Curso de Variable compleja

Números complejos

Los números complejos son una extensión de los números Reales, su uso no solo se limita a resolver ecuaciones con raíces negativas, sino que son parte fundamental del Álgebra, además tienen muchas aplicaciones a la Física, Ingeniería Eléctrica, Mecánica de fluidos, Termodinámica, Mecánica cuántica, etc…, por lo que se necesita una buena formación en Variable Compleja, para entender estos temas.

Definición del campo de los números complejos.

El campo de los números complejos es un campo cerrado, esto es cada polinomio de cualquier grado, tiene una raíz en este mismo campo, esta propiedad no lo cumplen los números reales, ya que cualquier polinomio de forma

$ x^2+A=0$ Con A positivo, no tiene solución en los números Reales. Por lo que los números complejos cumplen el teorema fundamental del álgebra.

Los números complejos son usualmente escritos de la siguiente manera.

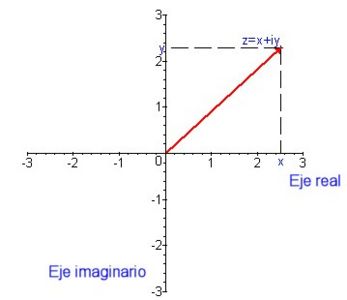
$z=x+i y$

Donde x es la parte real denotada por $x=Re(z)$.

y es la parte imaginaria $y=Im(z)$

i es la unidad imaginaria, que cumple que $i=\sqrt-1$

Donde x,y son números reales, es debido a estos elementos, que los números con parte real y la unidad imaginaria son llamados como Complejos y su campo es $\mathbb{C}$

Un número complejo $z_1=x_1+i y_1$ y $z_2=x_2+ i y_2$ son iguales solo si sus partes reales e imaginarias son iguales. Esto es:

$x_1=x_2$

$y_1=y_2$

De lo contrario se tratan de números complejos distintos.

Demostración de continuidad

Sea $f:\Omega \rightarrow C$ una función continua.

$(1)$ Si $\Omega$ es conexo, entonces $f(\Omega)$ también es conexo.

$(2)$ Si $\Omega$ es compacto, entonces $f(\Omega)$ también es compacto.

Demostración $(1)$

Supongamos que $\quad V\subseteq f(\Omega )$ es abierto y cerrado en $f(\Omega)$ y que $V\neq 0$.

Entonces, ${ f }^{ -1 }V\neq 0 \quad$ y $\quad { f }^{ -1 }V$ es abierto y cerrado en el conexo $\Omega$ por que $f$ es continua.

Se sigue que ${ f }^{ -1 }V=\Omega $ y así $V=f(\Omega)$ y por lo tanto $f(\Omega)$ es conexo.

Demostración $(2)$:

Si $\Omega =0 \quad$ entonces $f(\Omega)=0 \quad$ y no hay nada que probar.

Supongamos que $\Omega \neq 0 \quad$ y sea $\quad \left\{ { { V }_{ i } } \right\} \quad$ una cubierta abierta de $\quad f(\Omega) \quad$, es decir $\quad f(\Omega )\subseteq { U }_{ i }{ V }_{ i } \quad$.

Entonces $\left\{ { f }^{ -1 }{ V }_{ i } \right\} $ es una cubierta abierta de $\Omega$, y como $\Omega$ es compacto, entonces existe una subcubierta infinita, digamos $\Omega \subseteq { f }^{ -1 }{ V }_{ 1 }\cup .....\cup { f }^{ -1 }{ V }_{ n }. \quad$ Se sigue que:

$f(\Omega )\subseteq f({ f }^{ -1 }{ V }_{ 1 }\cup .....\cup { f }^{ -1 }{ V }_{ n })\subseteq f({ f }^{ -1 }{ V }_{ n })\cup .....\cup f({ f }^{ -1 }{ V }_{ n })\subseteq { V }_{ 1 }\cup ....\cup { V }_{ n }$

y por lo tanto ${ V }_{ 1 },.......,{ V }_{ n }$ es una sub-cubierta infinita de $f(\Omega)$.

Una función $f:\Omega \rightarrow C$ es uniformemente continua si para todo $\E >0$ existe un $\delta >0$ tal que $\left| f(z)-f(w) \right| <\E $ siempre que $\left| z-w \right| <\delta $. Claramente toda función uniformemente continua es continua.

---

Contribución de: Miguel Medina Armendariz (discusión) 12:48 5 jul 2015 (CDT)

Contribución de: Carlosmiranda (discusión) 15:09 21 nov 2020 (CST)

---

Operaciones básicas con números complejos.

Los números Complejos $\mathbb{C}$ y reales $\mathbb{R}$ satisfacen las mismas propiedades aritméticas.

Tales como la suma y resta.

Sean $z_1=x_1+i y_1$ , $z_2=x_2+ i y_2$

La suma o resta de estos números complejos se escribe de la siguiente manera:

$z_1 \pm z_2 = \left (x_1+x_2 \right )+i \left (y_1+y_2 \right )$

La multiplicación:

$z_1 \cdot z_2 = (x_1+i y_1) \cdot(x_2+i y_2)=\left [(x_1 \cdot x_2-y_1 \cdot y_2)+i (x_1 \cdot y_2+x_2 \cdot y_1) \right ]$

Además cumplen con los mismos axiomas de campo, asociativo conmutativo, neutro aditivo, neutro multiplicativo, inverso aditivo e inverso multiplicativo.

Números complejos y algunas propiedades

Plano complejo.

Un número complejo se puede representar mediante una expresión de la forma ${\displaystyle z=x+iy}$, donde ${\displaystyle x}$ y ${\displaystyle y}$son números reales, e ${\displaystyle i}$ es un símbolo con la propiedad de que ${\displaystyle i^{2}=-1}$. El número complejo ${\displaystyle x+iy}$ también se puede denotar por medio del par ordenado ${\displaystyle (x,y)}$y graficar como un punto en un plano llamado (plano de Argand), donde el eje ${\displaystyle x}$ es el eje real y el eje ${\displaystyle y}$, el eje imaginario, tal como se muestra en la figura 1.

Ver mas en: Plano complejo

Forma polar de números complejos.

Si consideramos todo número complejo

${\displaystyle z=x+iy}$

como un punto ${\displaystyle (x,y)}$ en el plano de Argand (figura 1)este puede representarse en términos de coordenadas polares.

^[1] ${\displaystyle (r,\theta )}$.

Ver mas en: Forma polar de los números complejos

Teorema de Moivre.

Las potencias enteras de un número complejo

\[ z^{n}=r^{n}\left ( \cos \theta +i \sin \theta \right )^{n} \]

La formula de Moivre es usada para encontrar las potencias de números complejos

\[ \left ( \cos \theta +i \sin \theta \right )^{n}=\cos n \theta + i \sin n \theta \]

Raíces de números complejos.

Las $n $ raíces de un numero complejo están dados por:

\[ w_{k}=r^{\frac{1}{n}}\left [ \cos\left ( \frac{\theta +2k \pi}{n} \right ) + i \sin\left ( \frac{\theta +2k \pi}{n} \right ) \right ] \]

Donde

\[ k=0,1,2,3,..., n-1 \]

Funciones de una variable compleja.

Una función compleja, es una función, cuyo dominio y rango son subconjuntos de números complejos. 

A diferencia de las funciones de variable real, las funciones de variable compleja involucran números complejos, muchas de las funciones de variable compleja son multivaluadas, por lo que se tiene que usar ramas para proporcionar soluciones continuas y analíticas.

Geometría de las funciones elementales.

Las funciones complejas tienen una representación en el plano complejo, estas funciones elementales incluyen:

Funciones exponenciales complejas y logarítmicas.

Ver ejercicios resueltos de: Exponencial Compleja y Logaritmo Complejo

Potencias Complejas.

Ver ejercicios resueltos de: Potencias complejas

Funciones Trigonométricas e Hiperbólicas

Ver ejercicios resueltos de: Funciones trigonométricas e Hiperbólicas.

Funciones multivaluadas.

Ramas

Superficies de Riemann

Calculo diferencial de funciones de una variable compleja.

Limites y continuidad.

Derivadas y funciones analíticas.

Mapeos conformes.

Condiciones de Cauchy-Riemann

Las ecuaciones de Cauchy Riemann constituyen una prueba necesaria pero no suficiente, para la derivabilidad de una función de variable compleja.

Demostración de Ecuaciones Cauchy-Riemann

Si

${\displaystyle f=\int fdt}$, $f=u+iv$, es decir, para $z(x,y)=x+iy$, escribiendo:

$f(z)=f(x,y)=f(x+iy)=u(x,y)+iv(x,y)$

donde $u,\quad v:\Omega \rightarrow R$ son funciones reales de dos variables reales, veamos como se comportan estas funciones al calcular el límite que define ${ f }^{ ´ }(z)$ a lo largo de las dos direcciones privilegiadas anteriores:

$(1)$. Supongamos que $h\rightarrow 0$ con $h\in R$. Entonces $z+h=(x+h)+iy=(x+h,y)$ y por lo tanto:

$\frac { f(z+h)-f(z) }{ h } =\frac { f(x+h,y)-f(x,y) }{ h } =\frac { u(x+h,y)+iv(x+h,y)-u(x,y)-iv(x,y) }{ h } =\frac { u(x+y,h)-u(x,y) }{ h } +i\frac { v(x+y,h)-v(x,y) }{ h } $

por lo que como ${ f }^{ ´ }(z)$ existe se debe tener que:

${ f }^{ ´ }(z)=\lim _{ h\rightarrow 0 }{ \frac { f(z+h)-f(z) }{ h } } =\lim _{ h\rightarrow 0 }{ \frac { u(x+h,y)-u(x,y) }{ h } } +i\lim _{ h\rightarrow 0 }{ \frac { v(x+h,y)-v(x,y) }{ h } } =\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}$

$(2)$. Similarmente, si $h\rightarrow 0$ con $h\in Ri$, escribiendo $h=ki$ con $k\in R$ se tiene que $k\rightarrow 0$ y por lo tanto $z+h=x+iy+ik=x+i(y+k)=(x,y+k)$ y asi:

$\frac { f(z+h)-f(z) }{ h } =\frac { f(x,y+k)-f(x,y) }{ ik } =\frac { u(x,y+k)+iv(x,y+k)-u(x,y)-iv(x,y) }{ ik } =\frac { 1 }{ i } \left( \frac { u(x,y+k)-u(x,y) }{ k } +i\frac { v(x,y+k)-v(x,y) }{ ik } \right) $

por lo que como ${ f }^{ ´ }(z)$ existe se debe tener que:

${ f }^{ ´ }(z)=\lim _{ h\rightarrow 0 }{ \frac { f(z+h)-f(z) }{ h } } =\frac { 1 }{ i } \lim _{ k\rightarrow 0 }{ \left( \frac { u(x,y+k)-u(x,y) }{ k } +i\frac { v(x,y+k)-v(x,y) }{ ik } \right) } =\frac { 1 }{ i } \lim _{ k\rightarrow o }{ \left( \frac { u(x,y+k)-u(x,y) }{ k } \right) } +\lim _{ k\rightarrow 0 }{ \left( \frac { v(x,y+k)-v(x,y) }{ ik } \right) } =-i\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}$

ya que $-i=\frac { 1 }{ i } $.

finalmente como ${ f }^{ ´ }(z)$ existe, las dos formas en que calculamos el límite deben coincidir, es decir:

$\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}=-i\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}$

E igualando partes reales y partes imaginarias se obtiene que:

$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$, $\quad \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$

A este par de ecuaciones diferenciales parciales se les conoce como las ecuaciones de Cauchy-Riemann.

---

Contribución de: Miguel Medina Armendariz (discusión) 13:43 5 jul 2015 (CDT)

Contribución de: Carlosmiranda (discusión) 15:05 21 nov 2020 (CST)

---

Funciones inversas.

Funciones armónicas.

Diferenciación de las funciones elementales.

Integración compleja.

Integrales de línea en el plano complejo y sus propiedades básicas.

Teorema fundamental del cálculo para integrales de línea.

Teorema integral de Cauchy.

Formulas integrales de Cauchy.

Formula integral de Cauchy para derivadas altas.

Representación en serie de funciones analíticas.

Series complejas.

Convergencia uniforme.

Series de funciones analíticas.

Criterios de convergencia.

Series de potencia y series de Taylor.

Series de Laurent.

Integración por el método de residuos.

Definición y calculo de residuos.

Evaluación de integrales definidas.

Teoremas del residuo.

Compleja: Teorema del residuo

Teorema de los residuos El teorema de los residuos es consecuencia directa del teorema integral de Cauchy y forma parte fundamental de la teoría matemática de análisis complejo.

Enunciado

Sea ${\displaystyle f\colon D\subset \mathbb {C} \to \mathbb {C} }$ una función analítica en un dominio simplemente conexo ${\displaystyle D}$, excepto en un número finito de puntos ${\displaystyle z_{k}}$ que constituyen singularidades aisladas de ${\displaystyle f}$. Sea ${\displaystyle C}$ una curva en ${\displaystyle D}$, simple, cerrada, regular a trozos, con orientación positiva y tal que el dominio que esta define contiene las singularidades de ${\displaystyle f}$. Entonces se tiene:

${\displaystyle \oint _{C}f(z)dz=2\pi i\sum _{k}\operatorname {Res} (f,z_{k})}$

donde ${\displaystyle \operatorname {Res} (f,z_{k})}$ es el Residuo de la función ${\displaystyle f}$ en el punto singular ${\displaystyle z_{k}}$.

Demostración

Sea ${\displaystyle f}$ holomorfa usando las ecuaciones de Cauchy-Riemann la forma diferencial ${\displaystyle f(z)\,dz}$ es cerrada. Por lo tanto, usando el corolario sobre las diferenciales de forma cerrada, un dominio simplemente conexo, sabemos que la integral ${\displaystyle \int _{C}f(z)\,dz}$ es igual a ${\displaystyle \int _{C'}f(z)\,dz}$ siempre que ${\displaystyle C'}$ sea una curva homotópica con ${\displaystyle C}$.

En específico, podemos considerar una curva tipo ${\displaystyle C'}$ la cual tiene una rotación alrededor de los puntos ${\displaystyle a_{j}}$ sobre círculos pequeños, cuando unimos todos estos pequeños círculos por medio de segmentos.

Ya que la curva ${\displaystyle C'}$ sigue cada segmento 2 veces con alineación opuesta, sólo necesitaremos sumar las integrales de ${\displaystyle f}$ alrededor de los círculos pequeños.

Consecuentemente sea ${\displaystyle z=a_{j}+\rho e^{i\theta }}$ parametrización de la curva alrededor del punto ${\displaystyle a_{j}}$, entonces tendremos ${\displaystyle dz=\rho ie^{i\theta }\,d\theta }$, por lo tanto:

${\displaystyle \int _{C}f(z)\,dz=\int _{C'}f(z)\,dz=\sum _{j}\eta (C,a_{j})\int _{\partial B_{\rho }(a_{j})}f(z)\,dz=\sum _{j}\eta (C,a_{j})\int _{0}^{2\pi }f(a_{j}+\rho e^{i\theta })\rho ie^{i\theta }\,d\theta }$

donde ${\displaystyle \rho >0}$, escogido tan extremadamente diminuto, tal que las esferas ${\displaystyle B_{\rho }(a_{j})}$ están todas desarticuladas y todas en un mismo dominio ${\displaystyle U}$. Entonces por medio de la linealidad en todas la singularidades, se demuestra que para toda ${\displaystyle j}$:

${\displaystyle i\int _{0}^{2\pi }f(a_{j}+\rho e^{i\theta })\rho e^{i\theta }\,d\theta =2\pi i\mathrm {Res} (f,a_{j}).}$

Sea ${\displaystyle j}$ fija y apliquemos la serie de Laurent para ${\displaystyle f}$ en ${\displaystyle a_{j}:}$

${\displaystyle f(z)=\sum _{k\in \mathbb {Z} }c_{k}(z-a_{j})^{k}}$

de tal forma que ${\displaystyle {\rm {{Res}(f,a_{j})=c_{-1}}}}$, donde c_-1, es el coeficiente de ${\displaystyle {1 \over (z-a_{j})}}$ en la serie de laurent. Entonces tenemos:

${\displaystyle \int _{0}^{2\pi }f(a_{j}+\rho e^{i\theta })\rho e^{i\theta }\,d\theta =\sum _{k}\int _{0}^{2\pi }c_{k}(\rho e^{i\theta })^{k}\rho e^{i\theta }\,d\theta =\rho ^{k+1}\sum _{k}c_{k}\int _{0}^{2\pi }e^{i(k+1)\theta }\,d\theta .}$

Observemos que si ${\displaystyle k=-1}$ , tendremos:

${\displaystyle \rho ^{k+1}c_{k}\int _{0}^{2\pi }e^{i(k+1)\theta }\,d\theta =c_{-1}\int _{0}^{2\pi }d\theta =2\pi c_{-1}=2\pi \,\mathrm {Res} (f,a_{j})}$

mientras que para ${\displaystyle k\neq -1}$ tenemos que los términos de la suma se anulan, debido a que:

${\displaystyle \int _{0}^{2\pi }e^{i(k+1)\theta }\,d\theta =\left[{\frac {e^{i(k+1)\theta }}{i(k+1)}}\right]_{0}^{2\pi }=0.}$

${\displaystyle \square }$

---

Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT) Carlosmiranda (discusión) 14:21 22 nov 2020 (CST)

---

Mapeos conformes y continuación analítica.

Teoría básica de los mapeos conformes.

Continuación analítica. Función gama.

Superficies de Riemann de funciones elementales.

Aplicaciones de Variable compleja.

El estudio de funciones de variable compleja tiene diversas aplicaciones por ejemplo:

Aplicaciones a flujo de fluidos, flujo de calor ... etc

Transformadas de Fourier

Ejercicios Resueltos de Variable Compleja

Libro A First Course in Complex Analysis with Applications de Zill y Shanahan Primera edición.

Ejercicios resueltos Zill

Libro Lascurain-Orive, Antonio: Curso básico de variable compleja, las prensas de ciencias, 2007

Ejercicios resueltos Libro Lascurain-Orive