Compleja:Zill-Cap2.3

Ejercicios del capítulo 2, sección 3 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.

---

Sección 2.3

Ejercicio 1

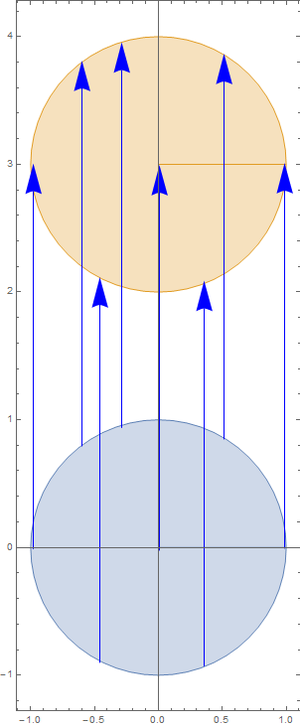
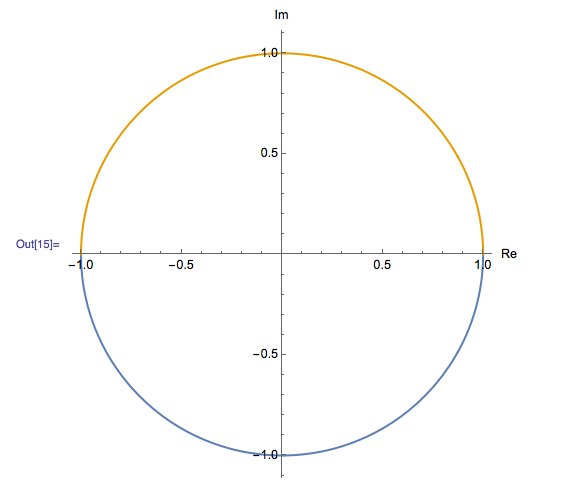
(a) Encuentre la imagen del disco cerrado $|z|\leq 1$ dentro del mapeo lineal $w=f(z)=z+3i$.

Inciso a

Para el caso de la suma de complejos, la transformación coincide con una traslación de 3 unidades hacia arriba. En la figura muestra la región inicial (en Azul) y el mapeo(en Rojo).

(b) Represente el mapeo lineal con una secuencia de puntos.

Inciso b

Los puntos se ilustran mediante flechas azules en la figura.

Gráfica

---

Realizado por:Tlacaelel Cruz (discusión) 19:22 22 mayo 2015 (CDT)

---

Ejercicio 3

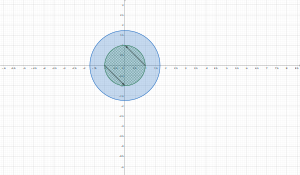
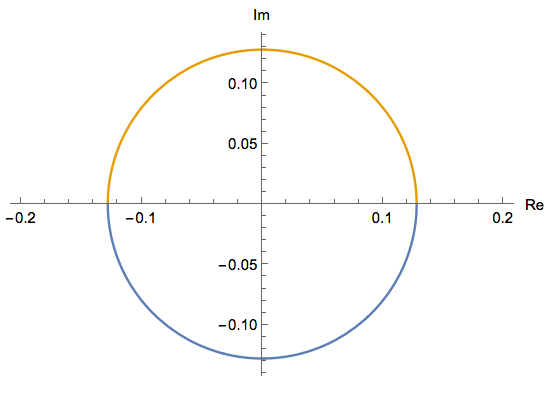
Encuentre la imagen del disco cerrado $|z|\leq 1$ dentro del mapeo lineal $w=f(z)=3iz$.

Tenemos que:

Procedimiento 

$x^2+y^2\leq 1$ $w=f(z)= 3iz$

$f(z)= 3i(x+iy)=(3xi-3y)=3(-y+xi)$

Donde

$Arg(\frac{3i}{3})=\frac{\pi}{4}$

y

$|3i|=3$

Por tanto podemos observar que al hacer el mapeo hay una rotación de $\frac{\pi}{4}$ con una amplificación de 3

Podemos concluir que al hacer el mapeo,la parte real de x pasó a ser imaginaria (al plano complejo) y la parte imaginaria de y pasó a los reales.

Gráfica

---

Realizado por: Samantha Martinez (discusión) 22:00 29 mayo 2015 (CDT)

---

Ejercicio 4

Encuentre la imagen del disco cerrado $|z|\leq 1$ dentro del mapeo lineal $w=f(z)=(1+i)z$.

Procedimiento

Tenemos que:

$w=f(z)= (1+i)z$

Pero: $z=x+iy$

Entonces:

$f(z)=(1+i)(x+iy)=(x+ix+iy+i^2y)=x-y+i(x+y)$

Determinamos el argumento y el modulo de $(1+i)$

$Arg(\frac{1}{1})=45°$

Y

$|1+i|=\sqrt{2}$

Por lo tanto hay una rotación de $\frac{\pi}{4}$ y una ampliación de $\sqrt{2}$

Gráfica

---

Realizado por:Nancy Martínez Durán (discusión) 03:43 30 mayo 2015 (CDT)

---

Ejercicio 5

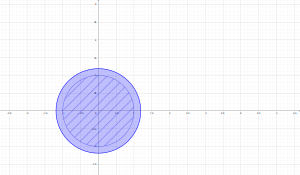
Encontrar la imagen del disco cerrado $|z|\leq 1$ bajo el mapeo lineal $w=f(z)$ y representar el mapeo lineal como una secuencia de puntos.

$f(z)=2z-i$

Inciso a

Como se puede apreciar:

$|2|=2$ y $Arg(2)=0$

Por lo tanto es unicamente un alargamiento del vector z (en este caso, del disco) y un desplazamiento en la dirección negativa del eje imaginario en una unidad. Por ello, la figura del disco original (azul) se transforma en el disco de color morado.

Gráfica

Nota: Solo se puso en la imagen el contorno del disco de color, pero tener en cuenta que realmente es el disco entero y no unicamente la frontera

---

Realizado por: Fernando Vazquez V. (discusión) 18:29 29 mayo 2015 (CDT)

---

Ejercicio 6

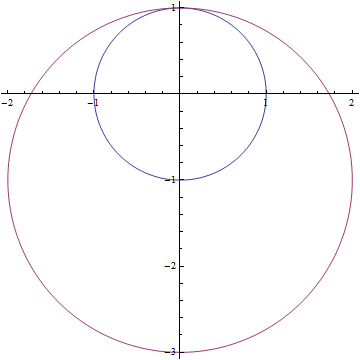
Encuentre la imagen del disco cerrado $|z|≤1$ dentro del mapeo lineal

$f\left(z\right)=\left(6-5i\right)z+1-3i$

Procedimiento 

$\left(a\right)$encuentre la imagen del disco cerrado $\left|z\right|\leqq1$bajo el mapeo lineal dado

$w=f\left(z\right)$

$\left(b\right)$represente el mapeo lineal con una secuencia de gráficas como en la figura 2.3.7

$\left(a\right)$:

Sea $S$ el disco cerrado $\left|z\right|\leqq1$ y sea $S\prime$ la imagen de $S$ bajo $f$ donde $z=x+iy$

El primer mapeo lineal se debe hacer con la expresión:

$f\left(z\right)=\left(6-5i\right)\left(x+iy\right)+1-3i=\left(6x+i6y-i5x+5y\right)+1-3i$

$f\left(z\right)=w=i\left(6y-5x-3\right)+6x+5y+1$

$\left|w\right|=36y^{2}-60xy-36y+25x^{2}+30x+9+36x^{2}+60xy+12x+25y^{2}+5y+1$

Por lo tanto $S\prime$será:

$\left|w\right|=61y^{2}+61x^{2}-31y+42x+10\leqq1$

$\left(b\right)$:

El mapeo lineal $f\left(z\right)=\left(6-5i\right)z+1-3i$ se puede ver como la composición

de una rotación, una ampliación y una rotación:

Como en $f\left(z\right)=\left(6-5i\right)z+1-3i$ el $\arg[6-5i]=-\arctan[\frac{5}{6}]$ y $\left|6-5i\right|=\sqrt{36+25}=\sqrt{61}$

$f$ actúa girando un ángulo de $39.8$ grados alrededor del origen, ampliando por $\sqrt{61}$ y luego

trasladando por $1-3i$

Secuencia de mapeos 

A continuación se mostrarán imágenes con esta secuencia de mapeos

1.-El círculo que se muestra a continuación se gira $39.8$ grados alrededor del origen, quedando exactamente igual.

2.-El círculo se amplía por $\sqrt{61}$

3.- Este último círculo se desplaza $1-3i$ en el plano complejo

---

Realizado por:Alejandro Juárez Toribio (discusión) 20:37 29 mayo 2015 (CDT)

---

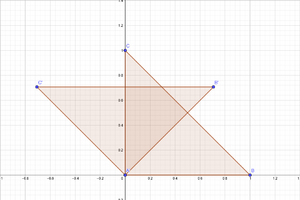
Ejercicio 7

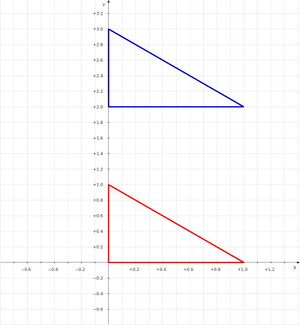
Encontrar la imagen del triangulo con vértices $0,1,i$ bajo el mapeo lineal $w=f(z)$ y b) representar el mapeo lineal bajo la secuencias de gráficas.

Solución:

Solución 

Siendo S el triángulo descrito y S' su imagen bajo el mapeo lineal $w=f(z)$ tenemos.

$f(z)=z+2i$

Que representa una traslación por lo que el triangulo conserva su orientación y tamaño, desplazándose 2 unidades hacia arriba en el plano complejo, para determinar la posición de los vértices bajo el mapeo se evalúa:

$f(0)=2i$

$f(1)=1+2i$

$f(3)=3i$

Gráfica

Los nuevos vértices del triángulo son:

$2i$,

$1+2i$,

$3i$.

---

Resuelto por: Luis Santos (discusión) 23:52 21 mayo 2015 (CDT)

---

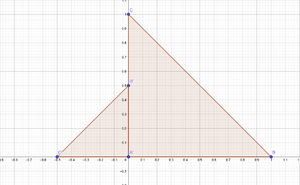
ejercicio 8

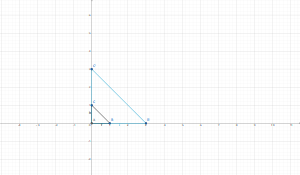
Determine la imagen del triángulo con vértices 0,1 e i bajo el mapeo lineal $f(z)=3z$

Solución 

vértice1 $f(0+0i)=3(0+0i)=0+0i$ {*}éste vértice no se mueve del origen (0,0)

vértice2 $f(1+0i)=3(1+0i)=3+0i$ {*}éste vértice se encuentra en el punto (3,0)

vértice3 $f(0+i)=3(0+i)=0+3i${*}éste vértice se encuentra en el punto (0,3)

el triángulo sólo sufrió una ampliación

Gráfica

Los vértices pasan:

$A=(0,0)$

$B'=(3,0)$

$C'=(0,3)$

En el plano $u,w$

---

Realizado por:Juan Daniel Rivera Bautista (discusión) 18:54 29 mayo 2015 (CDT)

---

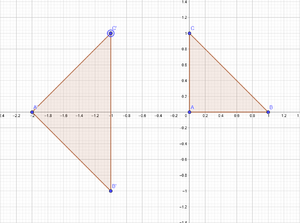
Ejercicio 9

Determine la imagen del triángulo con vértices 0,1 e i bajo el mapeo lineal

$f(z)= e^{i\dfrac{\pi}{4}}z$

Procedimiento 

$z=re^{i\theta}= r(\cos\theta+i \sin \theta)$

$f(z)= e^{i\dfrac{\pi}{4}}= \cos( \dfrac{\pi}{4}) + i \sin (\dfrac{\pi}{4}) = (\dfrac{\sqrt{2}}{2} + i \dfrac{\sqrt{2}}{2})$

Un triangulo con vértices en$(0, \dfrac{\sqrt{2}}{2} + i \dfrac{\sqrt{2}}{2}, -(\dfrac{\sqrt{2}}{2} + i \dfrac{\sqrt{2}}{2})$

Gráfica 

---

Realizado por: Esther Sarai (discusión) 13:56 27 mayo 2015 (CDT)Esther Sarai

---

Ejercicio 10

Determina la imagen del triangulo con vértices $0,1,i$ bajo el mapeo $w=f(z)$ y (b) Expresa el resultado del mapeo

Procedimiento 

$f(z)=\frac{1}{2}iz$

Como nos dan los puntos del triangulo se sustituyen en la función $f(z)$

$f(0)=\frac{1}{2}i(0)=0$

$f(1)=\frac{1}{2}i(1)=\frac{1}{2}i$

$f(i)=\frac{1}{2}i(i)=\frac{1}{2}(i^2)=\frac{-1}{2}$

Gráfica 

El mapeo del triangulo con vértices $0,1,i$ bajo la acción de la función $f(z)=\frac{1}{2}iz$ resulta en un triangulo rotado $\frac{\pi}{2}$ y se redujo ala mitad de su tamaño original

---

Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 22:07 28 mayo 2015 (CDT)

---

Ejercicio 11

Determine la imagen del triángulo con vértices $0,1,i$ bajo el mapeo lineal dado $w=f(z)$

$f(z)=-3z+i$

Procedimiento 

Tendremos entonces que sustituir en cada z por el número predeterminado a ser.

$f(0)=-3(0)+i=i$

Y el siguiente sería:

$f(1)=-3(1)+i=-3+i$

Ahora el siguiente

$f(i)=-3(i)+i=-2i$

Gráfica 

---

Realizado por:Francisco Medina Albino (discusión) 17:12 24 mayo 2015 (CDT)

---

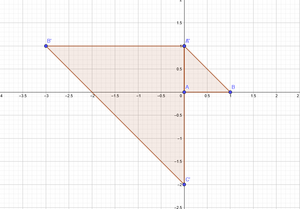
Ejercicio 12

Determine la imagen del triángulo con vértices en 0,1 e i bajo el mapeo $w=f\left(z\right)$

$f\left(z\right)=\left(1-i\right)z-2$

Procedimiento 

Para resolver este problema solamente debemos sustituir z en las condiciones dadas

$f\left(0\right)=\left(1-i\right)0-2=-2$

$f\left(1\right)=\left(1-i\right)1-2=-1-i$

$f\left(i\right)=\left(1-i\right)i-2=i-i^{2}-2=i-\left(-1\right)-2=-1+i$

Lo cual nos da como resultado un triángulo con vértices:

$v\left(-2,-1-i,-1+i\right)$

El cual sufrió una rotación y un desplazamiento de -2 unidades en el eje de los reales

Gráfica 

---

Resuelto porLuis Enrique Martínez Valverde (discusión) 18:47 28 mayo 2015 (CDT)

---

Ejercicio 13

Exprese el mapeo lineal dado w=f(z) como una composición de una rotación, una ampliación y una traslación. Luego describa la acción del mapeo lineal con palabras.

$f(z)=3iz+4$

Procedimiento 

Para poder expresar esta función como una rotación, una ampliación y una traslación sera necesario dejarla en la forma;

$f(z)=|a|{\frac {a}{|a|}}z+b$

En donde se puede identificar cada etapa del mapeo, esto es;

$|a|=$amplitud bajo el mapeo

$Arg(a)=$la rotacion de la imagen s bajo el mapeo

$b=$traslacion bajo el mapeo

Una vez especificado esto procederemos a identificar estas constantes en nuestra funcion, para esto pondremos la siguiente igualdad;

$f(z)=3iz+4=3({\frac {3i}{3}})z+4$

y asi de esta manera es claro identificar que;

$|a|=3$

$\theta ={\frac {\pi }{2}}$ nota;apesar de que aqui $Arctan(\frac{1}{0})$ no esta definido, el punto a=3i esta en el eje imaginario por lo cual $\theta=\frac{\pi}{2}$

$b=4$

Conclusión 

podemos concluir que la imagen S de el conjunto de puntos en en plano complejo x-y serán mapeados de la siguiente forma al plano u-v

sea S la imagen estará sera trasladad 4 unidades en el eje real $u$--Traslación

S sera ampliada por un factor de 3 (sera 3 veces mas grande)--Ampliación

S sera rotada $\frac{\pi}{2}$ en contra de la manecillas del reloj--Rotación

---

Realizado por:Cristian Alfredo Ruiz Castro (discusión) 17:32 29 mayo 2015 (CDT)

---

Ejercicio 15

Exprese el mapeo lineal dado $w=f(z)$ como una composición de una rotación , una ampliación , y una traslación .después describa con palabras la acción del mapeo lineal.

$f(z)=-{\frac {1}{2}}z+1-{\sqrt {3}}i$

Procedimiento 

Ahora bien para poder expresar la función como rotación, ampliación y traslación mapeo vamos a considerar:

$f(z)=|a|{\frac {a}{|a|}}z+b$

De donde tenemos;

$|a|=$amplitud

$Arg(a)=$la rotacion

$b=$traslacion bajo

Ahora bien de nuestra función tenemos que

$|a|={\frac {1}{2}}$

$\theta =tan^{-1}({\frac {1-{\sqrt {3}}i}{-{\frac {1}{2}}}})=0.9715$

$b=1-{\sqrt {3}}i=-0.73205$

Conclusión 

Ahora bien con lo anterior podemos observar que la imagen S en cuanto a la ampliación sera por 0.5 , pero de lo cual podemos ver que esta se reducirá, en cuanto a la rotación. esta sera indicada en contra a las manecillas del reloj y sera trasladado hacia el eje negativo.

---

Realizado por:Anahi Limas (discusión) 20:21 29 mayo 2015 (CDT)

---

Ejercicio 16

Exprese el mapeo lineal dado $w=f(z)$ como una composición de una rotación, una ampliación y una traslación. Luego describa la acción del mapeo lineal con palabras.

$f(z)=(3-2i)z+12$

Procedimiento 

Vemos que cada mapeo lineal complejo no constante es una composición de una rotación, una ampliación y una traslación. En este caso tenemos una rotación $R(z)$ a través de $Arg(a)$ donde $a=3-2i$ por lo que $Arg(a)=tan^{-1}(\frac{-2}{3})$.

Tenemos también una ampliación $M(z)$ a través de $|a|$ es decir $|a|=\sqrt{3^{2}+(-2)^{2}}=\sqrt{13}$ y una traslación $T(z)$ es una traslación por $b$ donde $b=12$ en este caso.

Entonces la composición $f(z)=T\circ M\circ R(z)=T(M(R(z)))$ es una función lineal compleja. Y se tiene que esta composición es un mapeo lineal siempre y cuando la forma básica no se vea comprometida por la transformación.

Conclusión 

Por tanto la acción del mapeo lineal es una rotación de $-33.69$ aprox., una ampliación de $\sqrt{13}$ y una traslación de $12$ sobre el eje real.

---

Realizado por: A. Martín R. Rabelo (discusión) 23:02 25 mayo 2015 (CDT)

---

Ejercicio 17

Determine un mapeo lineal que mapea el conjunto $S$ en el conjunto $S`$

$S$ es el triangulo con vértices $0$, $1$ y $1+i$.

$S`$ es el triangulo con vértices $2i$, $3i$, y $-1+3i$

Procedimiento 

Si para una función $f(z=0)=2i$, entonces debe haber una función que cumpla que para $z=0$ haya una función $f(0)=2i$ la cual seria $f(z=0)=z+2i$

Ahora dicha funciona debe cumplir que $f(z=1)=3i$ entonces debe haber una función que cumpla que para $z=1$ haya una función $3i$ la cual seria $f(z=1)=zi+2i=3i$

Por ultimo, comprobamos estas relaciones con la ultima expresión de $z=1+i$

Si $f(z)=zi+2i$, entonces para $f(z=1+i)=i(1+i)+2i=i-1+2i=-1+3i$

Conclusión 

Con lo que se cumple la relación, así concluimos que el mapeo lineal que mapea a $S$ en $S`$ es $f(z)=zi+2i$

---

Realizado por:Miguel Medina Armendariz (discusión) 01:38 22 mayo 2015 (CDT)

---

Ejercicio 19

Determine un mapeo en lineal que mapea al conjunto $S$ en el conjunto $S'$.

Procedimiento 

$S$ es el eje imaginario. $S'$ es la recta que pasa por los puntos $i$ y $1+2i$

Sea $S$ $x=0,-\infty \leq y\leq \infty$ y $S'i,$ $1+2i$

Entonces

$f(z=0)=i\Rightarrow f(0)=i$, la función recta $f(z=0)=z+i$

$f(z=0)=i+2i\Rightarrow f(0)=1+2i$, la función recta $f(z=0)=zi+i$; hay periocidad.

Se propone para que tenga la solución de mapeo lineal $f(z)=z*zi+i,$ donde $z$

$z=\exp(-\pi i/2)=\left[\cos \left(-{\frac {\pi }{2}}\right)+i\sin \left(-{\frac {\pi }{2}}\right)\right]=i$, para una sola $z$

Conclusión 

Con lo que se obtiene la función

$f(z)=\exp(-\pi i/2)z+i.$

---

Elaborado por --Ricardo Garcia Hernandez (discusión) 23:43 29 mayo 2015 (CDT)

---

Ejercicio 20

Determine un mapeo lineal que mapea el conjunto S en el conjunto S'

S es el cuadrado con vértices $1+i,-1+i,-1-i,\:y\:1-i.$S' es el cuadrado con vértices $1,2+i,1+2i,\:e\:i$

Procedimiento 

primero trasladamos los ejes $1+i$ unidades, entonces tendremos la función:

$T_{1}(z)=z+1+i$

así

$T_{1}(1+i)=(1+i)+1+i=2+2i$

$T_{1}(-1+i)=(-1+i)+1+i=0+2i$

$T_{1}(-1-i)=(-1-i)+1+i=0+0i$

$T_{1}(1-i)=(1-i)+1+i=2+0i$

después lo rotamos $\frac{\pi}{4}$ en la dirección de las manecillas del reloj quedándonos la función:

$R(z)=z(e^{-i\frac{\pi}{4}})=z(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i)$

entonces

$R(2+2i)=(2+2i)(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i)=\frac{2}{\sqrt{2}}-\frac{2}{\sqrt{2}}i+\frac{2}{\sqrt{2}}i-\frac{2}{\sqrt{2}}i^{2}=\frac{4}{\sqrt{2}}+0i$

$R(0+2i)=(0+2i)(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i)=\frac{2}{\sqrt{2}}i-\frac{2}{\sqrt{2}}i^{2}=\frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}}i$

$R(0+0i)=(0+0i)(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i)=0+0i$

$R(2+0i)=(2+0i)(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i)=\frac{2}{\sqrt{2}}-\frac{2}{\sqrt{2}}i$

sabiendo cual es el cuadrado en S' al que queremos mapear reducimos en un factor de $\frac{\sqrt{2}}{2}$ los lados del cuadrado en S, la función es:

$M(z)=z(\frac{\sqrt{2}}{2})$

de aquí que:

$M(\frac{4}{\sqrt{2}}+0i)=(\frac{4}{\sqrt{2}}+0i)(\frac{\sqrt{2}}{2})=2+0i$

$M(\frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}}i)=(\frac{2}{\sqrt{2}}+\frac{2}{\sqrt{2}}i)(\frac{\sqrt{2}}{2})=1+i$

$M(0+0i)=(0+0i)(\frac{\sqrt{2}}{2})=0+0i$

$M(\frac{2}{\sqrt{2}}-\frac{2}{\sqrt{2}}i)=(\frac{2}{\sqrt{2}}-\frac{2}{\sqrt{2}}i)(\frac{\sqrt{2}}{2})=1-i$

ademas lo trasladamos un factor de $i$

$T_{2}(z)=z+i$

de tal modo que:

$T_{2}(2+0i)=(2+0i)+i=2+i$

$T_{2}(1+i)=(1+i)+i=1+2i$

$T_{2}(0+0i)=(0+0i)+i=0+i$

$T_{2}(1-i)=(1-i)+i=1+0i$

como se quería,hemos encontrado que el mapeo lineal:

$f(z)=T_{2}\circ M\circ R\circ T_{1}(z)=(((z+1+i)(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i))(\frac{\sqrt{2}}{2}))+i=$

$=(z+1+i)(\frac{1}{2}-\frac{1}{2}i)+i=\frac{1}{2}z+\frac{1}{2}+\frac{1}{2}i-\frac{1}{2}zi-\frac{1}{2}i-\frac{1}{2}i^{2}+i=\frac{1}{2}z+1-\frac{1}{2}zi+i=\frac{1}{2}\left[(z+2)+(2-z)i\right]$

entonces:

$f(z)=\frac{1}{2}\left[(z+2)+(2-z)i\right]$

así

$f(1+i)=\frac{1}{2}\left[(1+i+2)+(2-1-i)i\right]=\frac{1}{2}\left[(3+i)+(1-i)i\right]=\frac{1}{2}\left[4+2i\right]=2+i$

$f(-1+i)=\frac{1}{2}\left[(-1+i+2)+(2-(-1+i))i\right]=\frac{1}{2}\left[(1+i)+(3-i)i\right]=\frac{1}{2}\left[(2+4i)\right]=1+2i$

$f(-1-i)=\frac{1}{2}\left[(-1-i+2)+(2-(-1-i))i\right]=\frac{1}{2}\left[(1-i)+(3+i)i\right]=\frac{1}{2}\left[(1-i)+(3+i)i\right]=\frac{1}{2}\left[(0+2i)\right]=i$

$f(1-i)=\frac{1}{2}\left[(1-i+2)+(2-(1-i))i\right]=\frac{1}{2}\left[(3-i)+(1+i)i\right]=\frac{1}{2}\left[(2+0i)\right]=1$

como se quería.

Conclusión 

$f(z)=\frac{1}{2}\left[(z+2)+(2-z)i\right]$

$f(z)$ mapea $S$ en $S'$

---

Realizado por: Francisco Medina Albino (discusión) 18:29 30 mayo 2015 (CDT)

---

Ejercicio 21

Encuentra dos aplicaciones lineales diferentes que mapean el cuadrado con vértices 0 , 1, 1 + i , i , al cuadrado con vértices: -1 , 0, i , -1 + i

Mapeo 1

tenemos el cuadrado de vértices 0 , 1, 1 + i , i y queremos mandarlo al siguiente cuadrado -1 , 0, i , -1 + i

podemos usar una traslación

traslación = -1

escrito como

$To\left(0,1,1+i,i\right)=-1,0,i,-1+i$

$f(z)=z-1$ dada

Mapeo 2

tenemos el cuadrado de vértices 0 , 1, 1 + i , i y queremos mandarlo al siguiente cuadrado -1 , 0, i , -1 + i

podemos usar la siguiente cadena:

rotación R = $e^{i\frac{\pi}{2}}$

Así los puntos:

$(0,1,1+i,i) \to (0,i,-1,-1+i)$

$f(z)=z e^{i\frac{\pi}{2}}$

---

Realizado por:Martin Flores Molina (discusión) 19:05 21 mayo 2015 (CDT)

---

Ejercicio 25

En las partes de $(a)\to(c)$ expresa la composición dada como un mapeo lineal de la forma $f(z)=az+b$

a) rotacion ${\frac {\pi }{4}}$, magnificación de 2, y una translacion de 1+ i.

Inciso a

La rotación vista desde forma polar es $R(z)=e^{i\rho }$ tiene la ventaja que $\rho$ es el ángulo que se desea rotar. La composición de función tiene la forma

$f_{1}(z)=T(M(R(z)))=T\circ M\circ R(z)=2e^{i{\frac {\pi }{4}}}(z)+(1+i)$

Donde primero rotamos, luego amplificamos y por último trasladamos.

b)magnificación por 2, trasladamos por ${\sqrt {2}}$ y rotamos ${\frac {\pi }{4}}$

Inciso b

Ahora tenemos primero que magnificar luego trasladar y por último rotamos

$f_{2}(z)=R(T(M(z)))=R\circ T\circ M(z)=e^{\frac {i\pi }{4}}((2(z))+{\sqrt {2}})$

c) traslación de ${\frac {\sqrt {2}}{2}}$, rotación de ${\frac {\pi }{4}}$ y una amplificación de 2

Inciso c

$f_{3}(z)=T(R(M(z)))=M\circ R\circ T(z)=2(e^{\frac {\pi }{4}}((z)+{\frac {\sqrt {2}}{2}}))$

d) ¿Qué puedes decir de (a)-(c)?

Inciso d

Si cambiamos el $f_{1}(z)$ a polares tenemos que

$f_{1}(z)=2e^{\frac {i\pi }{4}}(z)+{\sqrt {1+1}}e^{iarctan({\frac {1}{1}})}=2e^{\frac {i\pi }{4}}(z)+{\sqrt {2}}e^{\frac {i\pi }{4}}=e^{\frac {i\pi }{4}}(2(z)+{\sqrt {2}})=f_{2}(z)$

Ahora de $f_{3}(z)$ podemos hacer

$f_{3}(z)=2(e^{\frac {i\pi }{4}}((z)+{\frac {\sqrt {2}}{2}}))=2e^{\frac {i\pi }{4}}(z)+{\sqrt {2}}e^{\frac {i\pi }{4}}=2e^{\frac {i\pi }{4}}(z)+(1+i)=f_{1}(z)$

Por lo que decimos que si los incisos (a)=(b) y (b)=(c) por lo tanto (a)=(c).

Lo que podemos decir es que los incisos del (a)-(c) son iguales.

---

Realizado por: Pablo (discusión) 19:24 29 mayo 2015 (CDT)

---

Ejercicio 27

(a) Demostrar que la composición de dos traslaciones $T_1(z)=z+b_1; b_1 \neq0$ y $ T_2(z)=z+b_2; b_2 \neq0$ es una traslación. ¿Importa el orden de la composición?

(b) Demostrar que la composición de dos rotaciones $R_1(z)=a_1z; |a_1|=1 $ y $ R_2(z)=a_2z; |a_2|=1$ es una rotación. ¿Importa el orden de la composición?

(c) Demostrar que la composición de dos "magnificaciones" $M_1(z)=a_1z; a_1>0 $ y $ M_2(z)=a_2z; a_2>0$ es una "magnificación". ¿Importa el orden de la composición?

Solución:

(a) Sean: $T_1(z)=z+b_1; b_1 \neq0$ y $ T_2(z)=z+b_2; b_2 \neq0$. Entonces:

Inciso a

$(T_1\circ T_2)(z)=T_1(T_2(z))=T_1(z+b_2)=(z+b_2)+b_1=z+(b_2+b_1)$

$(T_2\circ T_1)(z)=T_2(T_1(z))=T_2(z+b_1)=(z+b_1)+b_2=z+(b_1+b_2)$.

si $b_1=-b_2$ entonces $b_1+b_2=b_2+b_1=0$, ya no sería traslación.

Por lo tanto la composición de dos traslaciones es una traslación (por asociatividad y por la forma)

No importa el orden, ya que que la suma es conmutativa en $\mathbb{C}$

(b) Sean: $R_1(z)=a_1z; |a_1|=1$ y $ R_2(z)=a_2z; |a_2|=1$. Entonces:

Inciso b

$(R_1\circ R_2)(z)=R_1(R_2(z))=R_1(a_2z)=a_1(a_2z)=(a_1a_2)z$ (con $|a_1a_2|=|a_1||a_2|=1)$

$(R_2\circ R_1)(z)=R_2(R_1(z))=R_2(a_1z)=a_2(a_1z)=(a_2a_1)z$ (con $|a_2a_1|=|a_2||a_1|=1)$.

Por lo tanto la composición de dos traslaciones es una traslación (por asociatividad,por la propiedad de la norma (producto) y por la forma)

No importa el orden, ya que que el producto es conmutativo en $\mathbb{C}$

(c) Sean: $M_1(z)=a_1z; a_1>0$ y $ M_2(z)=a_2z; a_2>$. Entonces:

Inciso c

$(M_1\circ M_2)(z)=M_1(M_2(z))=M_1(a_2z)=a_1(a_2z)=(a_1a_2)z ;(a_1>0\wedge a_2>0\rightarrow a_1a_2>0)$\\ $(M_2\circ M_1)(z)=M_2(M_1(z))=M_2(a_1z)=a_2(a_1z)=(a_2a_1)z ;(a_1>0\wedge a_2>0\rightarrow a_2a_1>0)$

Por lo tanto la composición de dos "magnificaciones" es una "magnificación" (por asociatividad, por la relación de orden de la multiplicación en $\mathbb{R}$ y por la forma).

No importa el orden (de las composiciones), ya que que el producto es conmutativo en $\mathbb{C}$

---

Realizado por:Alan Daniel Barrón Posadas (discusión) 21:02 29 mayo 2015 (CDT)

---

Ejercicio 29

Utilizando el mapeo $f(z)=\overline{z}$ y cualquier mapeo lineal, determinar un mapeo $g$ que refleje alrededor del eje imaginario. Es decir, exprese el mapeo $g(x+iy)=-x+iy$ en términos de constantes complejas y el símbolo $\overline{z}$.

Procedimiento

Si $z=x+iy$, su conjugada es $\overline{z}=x-iy$. Con $f(z)=\overline{z}$, por lo que un mapeo de reflexión alrededor del eje imaginario está dado por:

$g(z)=-f(z)=-\overline{z}=-(x-iy)=-x+iy$

$g(x+iy)=-x+iy$

---

Oscar Javier Gutierrez Varela (discusión) 18:34 21 mayo 2015 (CDT)

---

Ejercicio 30

Describa cómo obtener la imagen $w_{0}=f(z_{0})$ de un punto $z_{0}$ bajo el mapeo $f(z_{0})=a\overline{z_{0}}+b$ en términos de traslacion, rotación y ampliación y reflexión.

Conclusion

Dado un punto $z_{0}$ hacemos una reflexión respecto al eje real, eje ``$x$, si $a$ es una constante compleja al multiplicarla por el punto $z_{0}$ esta lo rota un angulo $\phi$ y hace una homotecia, viéndolo como vector, es decir, lo agranda o lo hace pequeño, por ultimo sumamos una constante $b$ que dependiendo si es real o compleja lo traslada en el eje real, imaginario o ambos.

---

Realizado por:Jose Emmanuel Flores Calderón (discusión) 19:44 29 mayo 2015 (CDT)

---