Compleja:Zill-Cap2.4
Ejercicios del capítulo 2, sección 4 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 2.4
Ejercicio 1
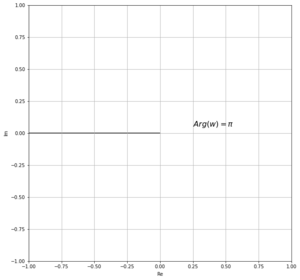
Encontrar la imagen del conjunto bajo la transformación $ w = z^2 .$ 1) El rayo : $arg(z)= \frac{\pi}{3}$
Solución:
La transformación
$w=z^2=(re^{i\theta}) = r^2 e^{i2 \theta}$
Dobla el ángulo por lo que si
$anrg(z)= \frac{\pi}{3}$
Se tiene que:
$arg(w)=\frac{2\pi}{3}$
Resuelto por: --Luis Santos (discusión) 00:26 22 mayo 2015 (CDT)
Ejercicio 2
Encontrar la imagen del conjunto en el mapeo $w=z^{2}$
El rayo $arg\left(z\right)=-\frac{3\pi}{4}$
Solución:
La transformación es:
$w=z^{2}=(re^{i\theta})^{2}=r^{2}e^{2i\theta}=r^{2}e^{2\left(-\frac{3\pi}{4}\right)}=r^{2}e^{-\frac{3\pi}{2}}=r^{2}e^{\frac{\pi}{2}}$
Lo cual nos dice que multiplica por el doble el $\arg\left(z\right)$
Resuelto por Luis Enrique Martínez Valverde (discusión) 19:06 28 mayo 2015 (CDT)
Ejercicio 3
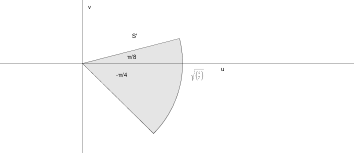
Encontrar la imagen del conjunto en el mapeo $w=z^{2}$
Para
Para poder encontrar la imagen S' bajo en mapeo sera nesesario realizar lo siguiente;
En este caso $z=x+iy=3+iy$ y tendremos que $z^{2}=(3+iy)^{2}=9+6iy-y^{2}$
por otro lado sabemos que;
por lo cual si igualamos partes reales y partes imaginarias tendremos que;
$u=9-y^{2}$......................(1)
$v=6iy$..........................(2)
despejando "y" de (2) y sustituyendo en (1) tenemos que
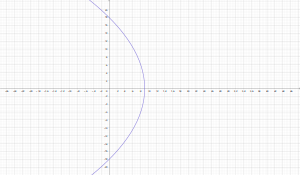
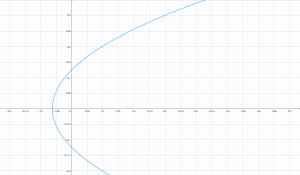
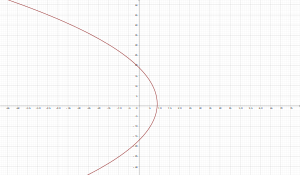
lo cual representa una parábola que abre hacia la izquierda con vértice en en punto $(9,0)$ en el plano $u-v$ y con intersección en el eje $v$ en los puntos $(0,±18)$
Conclusión
la imagen de la recta vertical $x=3$ es mapeada en una parabola con vertice en $(9,0)$ en el plano $u-v$ y dos intersecciones con el eje $v$ en $(0,±18)$ bajo el mapeo $w=z^{2}$
Gráficas
Realizado por: Cristian Alfredo Ruiz Castro (discusión) 19:20 29 mayo 2015 (CDT)
Ejercicio 4
Encontrar la imagen del conjunto de puntos dado, bajo el mapeo:
$w=z^{2}$.
La linea: $y=-5$
Procedimiento
Sabemos que
$w=(x^{2}-y^{2})+i2xy$
Entonces:
$u(x,y)=x^{2}-y^{2}$
$v(x,y)=2xy$
Pero la condición $y=-5$
$u=x^{2}-25$....1
$v=-10x$......2
De 2 tenemos que:
$x=\frac{v}{-10}$
Y sustituimos en 1
$u=(\frac{v}{-10})^{2}-25$
$u=\frac{v^{2}}{100}-25$
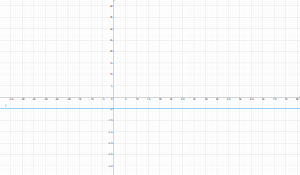
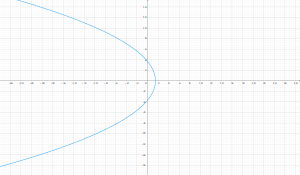
Conclusión
Entonces se observa que en el plano $uv$ la recta $y=-5$ se mapea como una parábola con vértice en $(-25,0)$ e intersecciones con $v$ en los puntos $(0,\pm50)$
Gráficas
Realizado por: Fernando Vazquez V. (discusión) 21:19 29 mayo 2015 (CDT)
Ejercicio 5
Encontrar la imagen del conjunto en el mapeo $w=z^{2}$ para la recta $y=- \frac{1}{4}$
Procedimiento
Tomamos que $z=x+iy$ sustituyendo en el mapeo w(f(z))
$w=(x+iy)^2$ $w=x^2-y^2+2xiy$
Donde:
$u= x^2-y^2$ $v= 2xy$
Donde $y=- \frac{1}{4}$
Por tanto
$u(y=- \frac{1}{4})= (x^2,-(-\frac{1}{4})^2) = x^2 -\frac{1}{16}$
$v(y=- \frac{1}{4})= 2x(-\frac{1}{4}) = -\frac{2}{4}x$
Por tanto
$x = -2v$
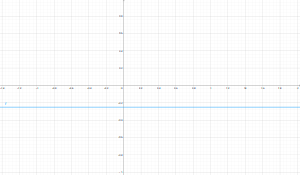
Conclusión
$u= x^2-y^2 = (-2v)^2 - (-\frac{1}{4})^2 = 4v^2-\frac{1}{16}$
Por lo tanto la recta y=- $\frac{1}{4}$ al mapearla en w se obtiene una parábola con vértice (-$\frac{1}{16}$,0) en el plano uv
Gráficas
Realizado por: Samantha Martinez (discusión) 21:14:20 29 mayo 2015 (CDT) Re elaborado por Manuel Rodríguez
Ejercicio 6
Encuentra la imagen del conjunto dado bajo el mapeo $w=z^2$ para la linea $x=\frac{3}{2}$
Procedimiento
$w=z^{2}=(x^{2}-y^{2})+2ixy$
Tenemos que:
$u(x,y)=x^{2}-y^{2}$
$v(x,y)=2xy$
Pero con la condición de que $x=\frac{3}{2}$
$u=\frac{9}{4}-y^{2}$......1
$v=3y$............2
Entonces de 2 sabemos que
$y=\frac{v}{3}$
Y lo sustituimos en 1
$u=\frac{9}{4}-(\frac{v}{3})^{2}=\frac{9}{4}-\frac{v^{2}}{9}$
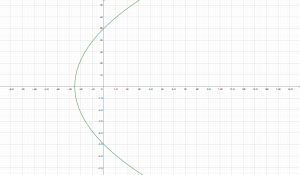
Conclusión
Entonces finalmente podemos decir que al mapear la recta $x=\frac{3}{2}$, en el plano $uv$ obtenemos la parábola con vértice en $(\frac{9}{4},0)$ e intersecciones en el eje $v$ en los puntos$(0,\pm\frac{9}{2})$
Gráficas
Corregido por: Fernando Vazquez V. (discusión) 20:33 29 mayo 2015 (CDT)
Ejercicio 7
Determine la imagen del conjunto dado bajo e mapeo $w=z^{2}$
El eje imaginario positivo
Tenemos que $f(z)=z^{2}$, dado un $z_{0}=0+ai$, donde $0<a<\infty$
\[ f(z_{0})=z_{0}^{2}=(0+ia)^{2}=(ia)^{2}=-a \]
Dado que a solo esta definido de cero a infinito, tenemos que siempre
el resultado es negativo, para cualquier punto en el eje imaginario
positivo.
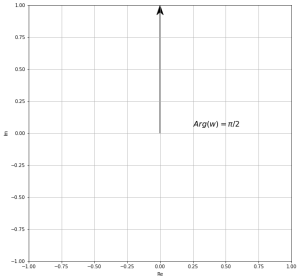
Así la imagen es el eje real negativo.
Realizado por: Jose Emmanuel Flores Calderón (discusión) 19:47 29 mayo 2015 (CDT)
Ejercicio 8
Encontrar la imagen del conjunto en el mapeo $w=z^{2}$
La línea $y=x$
Procedimiento
Si $z=x+iy$ entonces:
$w=\left(x+iy\right)^{2}=x^{2}-y^{2}+2ixy$
- $u\left(x,y\right)=x^{2}-y^{2}$; $v\left(x,y\right)=2xy$
Por lo que la imagen del conjunto dado bajo el mapeo anterior será:
$u\left(x,x\right)=x^{2}-x^{2}=0$; $v\left(x,x\right)=2.x.x=2x^{2}$
Conclusión
Por lo que:
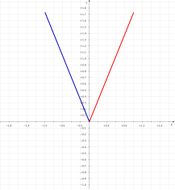
$w=2x^{2}$Entonces la línea $y=x$ bajo el mapeo se convertirá en una parábola
Ampliada en 2.
Realizado por: Alejandro Juárez Toribio (discusión) 07:23 30 mayo 2015 (CDT)
Ejercicio 09
Encontrar la imagen del conjunto dado bajo el mapeo w = z$^{2}$ . Representar al mapeo mediante la elaboración del conjunto y su imagen
Procedimiento
el arco de circulo $\left[z\right]=\frac{1}{2}$ en arco esta entre los ángulos $\theta=0,\theta=\pi$
nos piden encontrar el cuadrado de z y su representación gráfica
dado que w = z$^{2}$ tenemos que:
$\left[z^{2}\right]=\left(\frac{1}{2}\right)^{2}$
si utilizamos la forma exponencial tenemos que:
$z^{2}=R^{2}e^{i2\theta}$
si aplicamos esto para los valores inicial y final del arco dado por z tenemos que
para $\theta=0$
$z^{2}=\left(\frac{1}{2}\right)^{2}e^{i20}=\left(\frac{1}{4}\right)$
para $\theta=\pi$
$z^{2}=\left(\frac{1}{2}\right)^{2}e^{i2\pi}=\left(\frac{1}{4}\right)e^{i2\pi}$
por lo que en conclusión tenemos que:
Conclusión
El arco de circulo con radio $\frac{1}{2}$ dado por z , cuando es transformado por $z^{2}$ se convierte en un circulo completo pero de radio reducido a $\frac{1}{4}$
Gráficas
Realizado por: Martin Flores Molina (discusión) 22:15 21 mayo 2015 (CDT)
Ejercicio 10
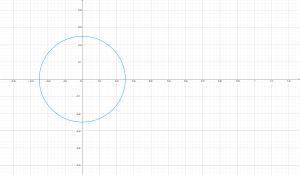
Encuentre la imagen del arco circular $|z|=\frac{4}{3}, \; \frac{\pi}{2}\leq arg(z) \leq \frac{\pi}{6}$ bajo el mapeo $w=z^{2}$. Represente dicho mapeo dibujando el conjunto y su imagen.
Procedimiento
En este caso es mucho as sencillo tratar al número complejo en su forma exponencial: \[ z={\frac{4}{3} e^{i \theta}, \; \frac{\pi}{2}\leq \theta \leq \frac{\pi}{6}} \] El mapeo lleva a: \[ w=z^{2}={\left(\frac{4}{3}\right)^{2} e^{2 i \theta}, \; \frac{\pi}{2}\leq \theta \leq \frac{\pi}{6}} \]
Conclusión
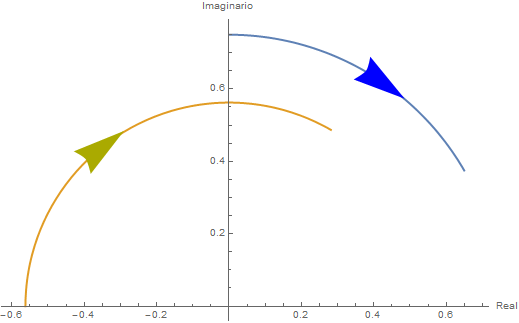
dicho de otro modo: \[ w=\frac{16}{9} e^{i \theta}, \; \pi\leq \theta \leq \frac{2\pi}{6}=\frac{\pi}{3} \]
Gráfica
La siguiente imagen muestra este mapeo, en Azul el arco original, en dorado el arco mapeado.
Realizado por: Tlacaelel Cruz (discusión) 21:50 22 mayo 2015 (CDT)
Ejercicio 18
Determinar la imagen del conjunto dado bajo la composición dada de una función lineal con la función potencia cuadrada.
$f(z)=-z^2+i$
La recta $y=-3$
Procedimiento
$f(z)=-z^{2}+i$
$f(x,y)=-(x^2-y^2+2xyi)+i$
$f(x,y)=-x^2+y^2+i(1-2xy)$
Separando en sus partes real e imaginaria:
$u=-x^2+y^2$
$v=-2xy+1$
Sustituyendo $y=-3$ $y^2=(-3)^2=9$
$u=-x^2+9$
$v=6x+1$
En el plano w=u+iv
Entonces $u=-x^{2}+9$ y $v=6x+1$ con $-\infty\leq x\leq\infty$
de $v$ se tiene que:
$\frac{v-1}{6}=x$
Sustituyendo esto en $u$, se tiene que:
Conclusión
$u=-\frac{(v-1)^2}{36}+9$
Gráficas
Se tienen:
Re elaborado por Manuel Rodríguez
Ejercicio 21
Encuentra la imagen del rayo bajo cada uno de los siguientes napeos
Inciso a
a)
Visualizando a z en polares tenemos que
Donde el argumento es igual a el angulo inicial, el rayo dado tiene la forma , r desde cero al infinito, por lo que al aplicarle el mapeo tenemos que
Donde r va desde el cero al infinito, Por lo tanto la imagen de es el rayo del .
Inciso b
b)
Realizando el mismo proceso anterior tenemos que
Como r puede tomar los valores de cero a infinito, decimos que: la imagen de es el rayo con un .
Inciso c
c)
Con los incisos (a) y (b), tenemos que la imagen del inciso (c) es el rayo con un
Realizado por:Pablo (discusión) 20:05 29 mayo 2015 (CDT)
Ejercicio 25
Solución:
Procedimiento
Primero obtenemos las magnitud de "r", y el angulo (argumento) de la expresión de dicho ejercicio:
Si , utilizando la función raíz-ésimal , sustituyendo al informacion obtenida se tiene:
Conclusión
Elaborado por --Ricardo Garcia Hernandez (discusión) 23:58 24 mayo 2015 (CDT)
Ejercicio 26
Encontrar el valor de la función raíz n-esima principal en el valor dado de $z$ Utilizando.
$z^{1/n}=\sqrt[n]{\mid z\mid}e^{\left[i\arg\left(z\right)/n\right]} $
$z^\frac{1}{2}= , z= 2+i$
Procedimiento
Lo primero que vamos a definir son los valores siguientes:
$\mid z\mid=\sqrt{(2)²+ (1)²}= \sqrt{5}$
$Arg(z)= sgn(y)arccos(\frac{x}{\mid z\mid})= +arccos(\frac{2}{\sqrt{5}})= 0.4636$
$n=2$
Ahora sustituyendo tenemos:
$z^{1/2}=((5)^\frac{1}{2})^\frac{1}{2}e^{{\frac{i(0.4636)}{2}}}$
$(2+i)^{1/2}=(5)^\frac{1}{4}e^{{\frac{i(0.4636)}{2}}} $
$(2+i)^{1/2}=(5)^\frac{1}{4}[cos(0.2318)+i sin(0.2318)] $
Solución
Por lo cual tenemos:
$(2+i)^{1/2}=1.4553+0.3435i $
Realizado por:Anahi Limas (discusión) 00:03 29 mayo 2015 (CDT)
Ejercicio 27
En los problemas 25 a 30 , use ( 14 ) para encontrar el valor de la función raíz enésima director dada en el valor dado de z.
$Z^{\frac{1}{3}},z=\text{\textminus}1$
utilizando la forma exponencial para la raíz tenemos
$z=R^{\frac{1}{n}}e^{i\text{\ensuremath{\left(\frac{\Theta+2kpi}{n}\right)}}}$donde k=0 hasta n-1
entonces para el ejercicio tenemos
$z^{\frac{1}{3}}=1^{\frac{1}{3}}e^{i\left(\frac{pi+2kpi}{3}\right)}$
Martin Flores Molina (Usuario discusión:Martin Flores Molina) 20:00 27 mayo 2015 (CDT)
Ejercicio 28
Encontrar el valor de la función raíz $n$-ésima principal en el valor z:
$z^{1/3}$
$z=-3+3i$
Procedimiento
Una forma de resolver este problema seria considerando que si $Arg(z)=\theta=\tan^{-1}\frac{y}{x}=\tan^{-1}\frac{3}{-3}=\tan^{-1}(-1)=-\frac{\pi}{4}$
Como $x<0$ entonces podemos considerar que $\theta=\tan^{-1}\frac{y}{x}+\pi=-\frac{\pi}{4}+\pi=\frac{3\pi}{4}$
Con $n=2$ y $r=3\sqrt{2}$
$z^{1/3}=(3\sqrt{2})^{1/3}exp(\frac{i3\pi}{4})(\frac{1}{3})=(3\sqrt{2})^{1/3}exp(\frac{i\pi}{4})$
$z^{1/3}=(3\sqrt{2})^{1/3}[\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}]$
Solución
$z^{1/3}=1.144+1.144i$
Corregido por:Miguel Medina Armendariz (discusión) 17:43 24 mayo 2015 (CDT)
Ejercicio 29
Encuentre el valor de la función raíz $n$-ésima principal en el valor dado de $z$
$z^{1/4}$
$z=-1+\sqrt{3}i$
Procedimiento
Para $z=-1+\sqrt{3}i$ tenemos que $r=2$ y $Arg(z)=\frac{-\pi}{3}+\pi=\frac{2\pi}{3}$
Sustituyendo en $z^\frac{1}{n}=r^\frac{1}{n} exp(\frac{i\theta}{n})$
donde $\theta=\frac{2\pi}{3}$ con $n=4$, tenemos
$(-1+\sqrt{3}i)^\frac{1}{4}=2^\frac{1}{4} exp(\frac{i2\pi}{3})(\frac{1}{4})=2^\frac{1}{4} exp(\frac{i\pi}{6})$
$(-1+\sqrt{3}i)^\frac{1}{4}=2^\frac{1}{4}[\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}]$
$(-1+\sqrt{3}i)^\frac{1}{4}=2^\frac{1}{4}[\frac{\sqrt{3}}{2}+\frac{1}{2}i]$
Solución
Finalmente obtendríamos que
$(-1+\sqrt{3}i)^\frac{1}{4}=1.029+0.594i$
Realizado por:Miguel Medina Armendariz (discusión) 02:39 22 mayo 2015 (CDT)
Ejercicio 30
Encontrar el valor de la función raíz $n$-ésima principal en el valor z:
$z^{1/5}$
$z=-4\sqrt{3}+4i$
Procedimiento
Primero se obtiene el módulo de "z" y el argumento ($\theta = Arg(z)$)
$r=|z|=\sqrt{48+16}=\sqrt{64}=8$
El $Arg(z)=\frac{5\pi}{6}$
Aplicando la fórmula para la raíz principal:
$z^{1/n}=r^\dfrac{1}{n}e^{(i\theta/n)}$
Donde: $n=5$
$z^{\frac{1}{5}}=(8)^{\frac{1}{5}}e^{i\frac{\frac{5\pi }{6}}{5}}=z^{\frac{1}{5}}=(8)^{\frac{1}{5}}\left (\cos\frac{\pi }{6} +i\sin\frac{\pi}{6} \right )$
Solución
$z^{1/5}=1.3126+i0.7579$
Re elaborado por Manuel Rodríguez
Ejercicio 35
Determine la imagen del conjunto dado bajo el mapeo de la raíz cuadrada principal de $w= z^\dfrac{1}{2}$ represente el mapeo dibujando el conjunto y su imagen
El arco $|z|= 9, \dfrac{-\pi}{2} \leq arg (z) \leq \pi$
Procedimiento
Definiendo en terminos de w
\[ w= \sqrt{|z|}\]
\[ |w| = 3\]
Para el argumento de z en w
\[ Arg (w) = \dfrac{1}{2} arg (z)\]
\[ \dfrac{-\pi}{4} \leq arg(w) \leq \dfrac{\pi}{2}\]
Solución
En el plano W se mapea:
$|w| = 3$ $-\dfrac{\pi}{4} \leq arg(w)\leq \dfrac{\pi}{2}$
Realizado por:Esther Sarai (discusión) 22:42 27 mayo 2015 (CDT)Esther Sarai
Ejercicio 36
Determine la imagen del conjunto dado bajo el mapeo de la raíz cuadrada principal de $w= z^{1/2}$ represente el mapeo dibujando el conjunto y su imagen.
El arco $|z|= \frac{4}{7}, \dfrac{-\pi}{2} \leq arg (z) \leq \dfrac{\pi}{4}$
Procedimiento
Sea $S'$ la imagen de $S$ bajo $w=z^{1/2}$
Ya que $|z|= \frac{4}{7}$ para puntos en $S$ y puesto que $z^{1/2}$ toma la raíz: $|w|=\sqrt{\frac{4}{7}}$, para puntos $w$ en $S'$
Además, ya que $\dfrac{-\pi}{2} \leq arg (z) \leq \dfrac{\pi}{4}$ para puntos en $S$ y ya que $z^{1/2}$ divide en dos el argumento de un punto, se tiene que:
Solución
$|z|= \frac{2}{\sqrt7}$ $\dfrac{-\pi}{4} \leq arg (w) \leq \dfrac{\pi}{8}$
Gráficas
Realizado por:Emmanuell Castro Flores (discusión) 22:38 29 mayo 2015 (CDT)
Ejercicio 49
(a) De acuerdo al ejemplo 6, muestra que la función $f(z)=az+b,a\neq0$ es uno-uno en el plano complejo.
(b) Encuentra una fórmula para la función inversa de (a)
Inciso a
(a) Sean: $f(z_1)=az_1+b$ y $f(z_2)=az_2+b$. Supongamos que $f(z_1)=f(z_2)$, entonces:
$az_1+b=az_2+b\Longleftrightarrow (az_1+b)-b=(az_2+b)-b\Longleftrightarrow (\frac{1}{a})az_1=(\frac{1}{a})az_2\Longleftrightarrow z_1=z_2$. Por lo tanto $f(z)=az+b,a\neq0$ es uno-uno .
Inciso b
(b) $w=az+b\Longleftrightarrow w-b=az \Longleftrightarrow \frac{w-b}{a}=z$. Por lo tanto $f^{-1}(z)=\frac{z-b}{a}$.
Comprobación: $f\circ f^{-1}(z)=f(f^{-1}(z))=a(\frac{z-b}{a})+b=(z-b)+b=z$
Realizado por: Alan Daniel Barrón Posadas (discusión) 21:38 29 mayo 2015 (CDT)
Ejercicio 50
a) demuestre que la función lineal compleja $f(z)=\frac{a}{z}+b,\;a\neq0$ , es univoca en el conjunto $\Vert z\Vert>0$
b) determine una formula para la función inversa de la función en
Inciso a
una función es univoca (inyectiva) si cada punto $w$ en el rango de $f$ es la imagen de un único punto $z$ es decir $f$es univoca si $f(z_{1})=f(z_{2})\iff z_{1}=z_{2}$
si $f$ es una función compleja univoca con dominio A y rango B, entonces, la función inversa de $f$ es la función con dominio B y rango A definida por $f^{-1}(z)=w\:si\:f(w)=z$
$f$ es univoca si $f(z_{1})=f(z_{2})\iff z_{1}=z_{2}$
a) $f(z)=\frac{a}{z}+b,\;a\neq0$
Inciso b
si $f(z_{1})=\frac{a}{z_{1}}+b,\;a\neq0,\Vert z_{1}\Vert>0\:y\:f(z_{2})=\frac{a}{z_{2}}+b,\;a\neq0,\Vert z_{2}\Vert>0\;supongamos\;que\;f(z_{1})=f(z_{2})\iff z_{1}=z_{2}$
entonces $\frac{a}{z_{1}}+b=\frac{a}{z_{2}}+b\iff\Vert z_{1}\Vert=\Vert z_{2}\Vert>0\therefore f(z)=\frac{a}{z}+b,\;a\neq0\;es\;univoca$
b) si $z=f(w)$ tenemos
$z=\frac{a}{w}+b$, asi $\frac{a}{w}=z-b\iff w=\frac{a}{z-b},(z-b)\neq0,z\neq b$ de aquí $f^{-1}(z)=\frac{a}{z-b}\:entonces\:f(f^{-1}(z))=\frac{a}{\frac{a}{z-b}}+b=\frac{a(z-b)}{a}+b=z-b+b=z$
por lo tanto se concluye que los mapeos son uno a uno como se esperaba.
Realizado por: Francisco Medina Albino (discusión) 00:39 30 mayo 2015 (CDT)
























![z^{1/n}=\sqrt[n]{\mid z\mid\exp\left[i\arg\left(z\right)/n\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fa362b89a2da651f82d6b97fc694a54a8ec810ac)