1. Demuestre que el producto de números complejos cumple con la ley asociativa
Sean  con
con 
Por demostrar 
 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
Por otra parte
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)
Entonces se cumple  .
.
Contribución de: Gabita 22:15 28 sep 2009 (UTC)
SECCIÓN 1.1.2
1. Demuestre que 
Sean 


![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)
Por otra parte

Contribución de: Gabita 22:15 28 sep 2009 (UTC)
2. Exprese  de la forma
de la forma 
Por las propiedades  ,
, 

Simplificando, se obtiene:

Resolviendo la división de números complejos, de la forma:
 :
:

= .
.
Contribución de:Josua Da Vinci 23:00 28 sep 2009 (UTC)
3. Demuestre que  es raiz de un polinomio real si y solo si
es raiz de un polinomio real si y solo si  lo es.
lo es.
Sea  solucion de un polinomio real,
solucion de un polinomio real,
entonces 
como  , por lo tanto
, por lo tanto  tambien es solucion.
tambien es solucion.
Contribución de: Luis Nava 06:35 30 sep 2009 (UTC)
5. Sean  tales que cumplen $\frac{z_2 - z_1}{z_3 - z_1} = \frac{z_1 - z_3}{z_2 - z_3}$, demuestre que estos tres puntos determinan un triángulo equilátero.
tales que cumplen $\frac{z_2 - z_1}{z_3 - z_1} = \frac{z_1 - z_3}{z_2 - z_3}$, demuestre que estos tres puntos determinan un triángulo equilátero.
Tenemos que
$
y, por lo tanto,

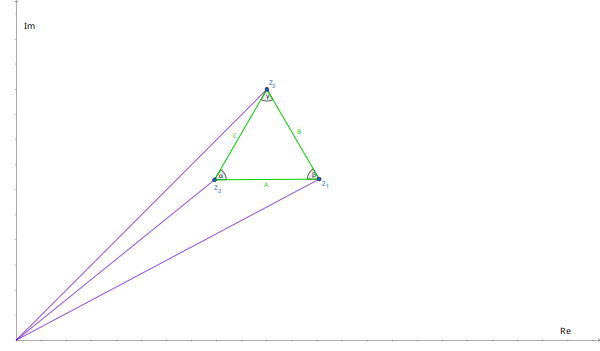
De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

De (2) y (3) tenemos que:

Por triángulos semejantes, se tiene que el ángulo  es igual al ángulo
es igual al ángulo  y éste a su vez al ángulo
y éste a su vez al ángulo  , es decir,
, es decir,

Y la ecuación (5) es precisamente la condición para que el triángulo ABC de la Figura 1 sea equilátero.
Contribución de:Belen 02:48 29 sep 2009 (UTC)
6. Sea  , pruebe que
, pruebe que 
Puesto que el número complejo z puede escribirse como

![{\left|{z}\right| = \sqrt{[Re(z)]^2+[Im(z)]^2} }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8e0198847b238989498ca0fdc303322f9e96db40)
Se deduce que


Como el cuadrado de un número real no puede ser negativo
![{{[\left|{Re(z)}\right|-\left|{Im(z)}\right|]^2}{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/978669b16b44e568056d312dc705389713ab77d3)
Entonces
![{[Re(z)]^2+[Im(z)]^2-2\left|{Re(z)}\right|\left|{Im(z)}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7b0f476c3d8973b1600fca31412b10b1ac7f73a)
O sea
![{{[Re(z)]^2+[Im(z)]^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fed125498b2c36e65792cd5398d4f6b6a81a0ed7)
O de otra manera

Sumando  , a ambos lados se tiene
, a ambos lados se tiene

Como

Entonces

De donde
![{{2\left|{z}\right|^2}{\ge }[\left|{Re(z)}\right|+\left|{Im(z)}\right|]^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/25881ff9f07d97b28f96aa6f6619afa320e7571b)
Sacando raíces cuadradas positivas

Por lo tanto

Contribución de: Ralf Gutierrez 19:18 29 sep 2009 (UTC)
6-bis. Sea  , pruebe que
, pruebe que

Tenemos que  , entonces de la teoria sabemos que
, entonces de la teoria sabemos que
![{\left|{z}\right| = \sqrt{[x]^2+[y]^2} }\qquad (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/29878428cc0a884b8bb46e7ebfc3dc55128b3e2d)


Tambien es inmediato que para z  ,
,  , y que el cuadrado de cualquier numero real es siempre positivo, entonces de esto se tiene que
, y que el cuadrado de cualquier numero real es siempre positivo, entonces de esto se tiene que
![{{[\left|{x}\right|-\left|{y}\right|]^2}{\ge}0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8fa44a4b80670114ab92e33372745f673d1898a)
Desarrollando el binomio se tiene que
![{[x]^2+[y]^2-2\left|{x}\right|\left|{y}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/713aec1fca2fe1b369986232bd50201f383ae306)
![{{[x]^2+[y]^2}{\ge }2\left|{x}\right|\left|{y}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c9e0cd7ac7b4884edd34e46175066247da7544c)
Y por la identidad (1) esto se puede escribir como

Ahora sumando en ambos lados  obtenemos lo siguiente
obtenemos lo siguiente

Pero ademas como  , lo sustituimos en el resultado anterior
, lo sustituimos en el resultado anterior

Es facil ver que
![{{[\left|{x}\right|+\left|{y}\right|]^2}={[x]^2+[y]^2+2\left|{x}\right|\left|{y}\right|}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a6f07c61fcbfff5a8e8ba6b651f1ffea8ea29339)
Utilizando este resultado se deduce que
![{{2\left|{z}\right|^2}{\ge }{[\left|{x}\right|+\left|{y}\right|]^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f96dc4fb554170cf471278862b51cbb43ca3cbe4)
Y tomando las raices positivas llegamos al siguiente resultado

Que es lo que se queria mostrar.
Contribución de: Oscar Adrian 03:56 1 oct 2009 (UTC)
REVISADO
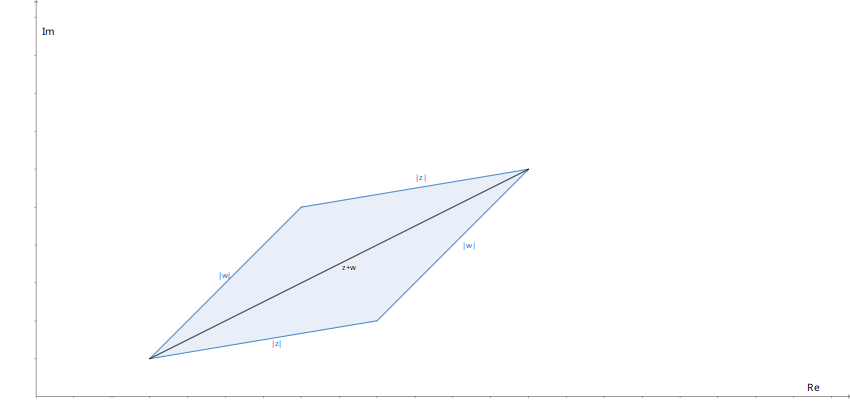
7. Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.
Sacamos las normas de los números complejos
|z|= |w|=
|w|=
Por algebra de vectores

Donde |h| es la resultante de |z|+|w|
 +
+ 
De la misma forma el dibujo nos indica q trasladamos la magnitudes de los vectores
|w| y |z| y por tanto también tendremos |z|+|w| =|h|
Entonces si |z|+|w| = |h|
Aplicando el teorema de pitagoras q nos dice
d = cateto
f = cateto

entonces tenemos que


Aplicamos pitagoras

Por tanto
 se cumple la suma de los cuadrados de los lados es igual a la suma de los cuadrados de la diagonal.
se cumple la suma de los cuadrados de los lados es igual a la suma de los cuadrados de la diagonal.
Contribución de:Karla 22:47 4 oct 2009 (UTC)Sanchez
Compleja:ej-cap1.1
Compleja:ej-cap1.2
Compleja:ej-cap1.3
Compleja:ej-cap1.4
Compleja:ej-cap2.1
Compleja:ej-cap2.2
Compleja:ej-cap2.3
Compleja:ej-cap2.4
Compleja:ej-cap2.5
Compleja:ej-cap3.1
Compleja:ej-cap3.2
Compleja:ej-cap3.3
Compleja:ej-cap3.4



 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)




![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)

























![{\left|{z}\right| = \sqrt{[Re(z)]^2+[Im(z)]^2} }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8e0198847b238989498ca0fdc303322f9e96db40)


![{{[\left|{Re(z)}\right|-\left|{Im(z)}\right|]^2}{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/978669b16b44e568056d312dc705389713ab77d3)
![{[Re(z)]^2+[Im(z)]^2-2\left|{Re(z)}\right|\left|{Im(z)}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7b0f476c3d8973b1600fca31412b10b1ac7f73a)
![{{[Re(z)]^2+[Im(z)]^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fed125498b2c36e65792cd5398d4f6b6a81a0ed7)





![{{2\left|{z}\right|^2}{\ge }[\left|{Re(z)}\right|+\left|{Im(z)}\right|]^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/25881ff9f07d97b28f96aa6f6619afa320e7571b)



![{\left|{z}\right| = \sqrt{[x]^2+[y]^2} }\qquad (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/29878428cc0a884b8bb46e7ebfc3dc55128b3e2d)




![{{[\left|{x}\right|-\left|{y}\right|]^2}{\ge}0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8fa44a4b80670114ab92e33372745f673d1898a)
![{[x]^2+[y]^2-2\left|{x}\right|\left|{y}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/713aec1fca2fe1b369986232bd50201f383ae306)
![{{[x]^2+[y]^2}{\ge }2\left|{x}\right|\left|{y}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c9e0cd7ac7b4884edd34e46175066247da7544c)




![{{[\left|{x}\right|+\left|{y}\right|]^2}={[x]^2+[y]^2+2\left|{x}\right|\left|{y}\right|}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a6f07c61fcbfff5a8e8ba6b651f1ffea8ea29339)
![{{2\left|{z}\right|^2}{\ge }{[\left|{x}\right|+\left|{y}\right|]^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f96dc4fb554170cf471278862b51cbb43ca3cbe4)