Compleja:Zill-Cap4.3
Ejercicios del capítulo 4, sección 3 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 4.3
Ejercicio 1
Exprese el valor de la función trigonométrica en la forma $a+ib$
$sen(4i)$
Procedimiento
Usamos la definición de seno complejo:
$sen(z)=\frac{e^{iz}-e^{-iz}}{2i}$
donde $z=4i$
Sustituyendo $z$ en la definición, obtenemos:
$sen(4i)=\frac{e^{i(4i)}-e^{-i(4i)}}{2i}$
Haciendo las operaciones correspondientes tenemos:
$sen(4i)=\frac{e^{-4}-e^{4}}{2i}= 0+27.28i$
Por lo tanto:
Solución
$sen(4i)\approx 0+27.28i$
Realizado por: Nancy Martínez Durán (discusión) 23:59 11 jun 2015 (CDT)
Ejercicio 3
Exprese el valor de la función trigonométrica dada en la función $a+ib$
$cos(2-4i)$
Procedimiento
Por definición la función coseno complejo puede escribirse como
$cos(z)=\frac{e^{iz}+e^{-iz}}{2}$
donde $z=2-4i$, entonces obtenemos que
$cos(2-4i)=\frac{e^{i(2-4i)}+e^{-i(2-4i)}}{2} $
$cos(2-4i)=\frac{e^{4+2i}+e^{-4-2i}}{2} $
$cos(2-4i)=\frac{e^{4}(cos2+isin2)+e^{-4}(cos(-2)+isin(-2))}{2} $
$cos(2-4i)=\frac{e^{4}cos2+e^{-4}cos(-2)+i[e^{4}sin(2)+e^{-4}sin(-2)]}{2} $
$cos(2-4i)=\frac{-22.76+i49.62}{2} $
simplificando obtenemos que la función $cos(2-4i)$ es igual a
Solución
$cos(2-4i)\approx-11.38+i24.81 $
Realizado por: Miguel Medina Armendariz (discusión) 18:24 9 jun 2015 (CDT)
Ejercicio 4
Exprese el valor de la función trigonométrica dada en la forma a+ib.
$\sin(\frac{\pi}{4}+i)$
Procedimiento
$\sin(\frac{\pi}{4}+i)=\frac{e^{i(\frac{\pi}{4}+i)}-e^{-i(\frac{\pi}{4}+i)}}{2i}=\frac{e^{(\frac{\pi}{4}i-1)}-e^{-(\frac{\pi}{4}i-1)}}{2i}=\frac{e^{(-1+\frac{\pi}{4}i)}-e^{(1-\frac{\pi}{4}i)}}{2i}=\frac{e^{-1}[\cos(\frac{\pi}{4})+i\sin(\frac{\pi}{4})]-e^{1}[\cos(\frac{\pi}{4})+\sin(-\frac{\pi}{4})]}{2i}=\frac{e^{-1}\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)-e^{1}\left(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right)}{2i}$
y ahora lo pasamos a la forma a+ib
$\frac{e^{-1}\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)-e^{1}\left(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right)}{2i}$, multiplicamos por un 1 inteligente, desarrollamos y simplificamos
$\frac{e^{-1}\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)-e^{1}\left(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right)}{2i}\left(\frac{i}{i}\right)=\frac{ie^{-1}\left(\frac{\sqrt{2}}{2}\right)-e^{-1}\left(\frac{\sqrt{2}}{2}\right)-e\left(\frac{\sqrt{2}}{2}i\right)-e\left(\frac{\sqrt{2}}{2}\right)}{-2}=\left(\frac{\sqrt{2}}{4e}+\frac{e\sqrt{2}}{4}\right)+i\left(-\frac{\sqrt{2}}{4e}+e\frac{\sqrt{2}}{4}\right)$
Solución
por lo tanto tenemos que
$\sin(\frac{\pi}{4}+i)=\left(\frac{\sqrt{2}}{4e}+\frac{e\sqrt{2}}{4}\right)+i\left(-\frac{\sqrt{2}}{4e}+e\frac{\sqrt{2}}{4}\right)$
$\sin(\frac{\pi}{4}+i)\approx1.091+i0.83$
Realizado por: Juan Daniel Rivera Bautista (discusión) 01:08 10 jun 2015 (CDT)
Ejercicio 5
Exprese el valor de la función trigonométrica dada en la forma $a+ib$
$\tan(2i)$
Primero encontramos el valor general para la $tan(z)$
Procedimiento
$tan(z)=\frac{sin(z)}{cos(z)}$
Por una parte sabemos que $sin(z)=\frac{e^{iz}-e^{-iz}}{2i}$ y que $cos(z)=\frac{e^{iz}+e^{-iz}}{2}$ ; entonces si simplificamos:
$tan(z)=\frac{e^{iz}-e^{-iz}}{(e^{iz}+e^{-iz})i}$
En este caso:
\[ tan(2i)=\frac{e^{i(2i)}-e^{-i(2i)}}{(e^{i(2i)}+e^{-i(2i)})i} \]
\[
tan(2i)=\frac{e^{-2}-e^{2}}{(e^{-2}+e^{2})i}
\]
\[
tan(2i)=\frac{e^{-2}-e^{2}}{(e^{-2}+e^{2})i}(\frac{-i}{-i})
\]
\[
tan(2i)=i\frac{e^{2}-e^{-2}}{e^{-2}+e^{2}}
\]
Entonces expresamos $tan(2i)=a+ib$ con $a=0$ y $b=\frac{e^{2}-e^{-2}}{e^{-2}+e^{2}}=tanh(2)$
\[
tan(2i)=0+i\frac{e^{2}-e^{-2}}{e^{-2}+e^{2}}
\]
Solución
\[ \tan(2i)\approx0.9640i \]
Realizado por: Fernando Vazquez V. (discusión) 23:03 7 jun 2015 (CDT)
Ejercicio 7
Exprese el valor de la función trigonométrica $\sec\left(\frac{\pi}{2} - i \right)$ en la forma $a+ib$.
Procedimiento
Sé que $\sec z=\frac{1}{cosz}$ , $\cos z=\frac{e^{iz} + e^{-iz}}{2}$
Entonces aplicando lo anterior tengo que:
$\sec\left(\frac{\pi}{2} - i \right)=\frac{1}{Cos\left(\frac{\pi}{2}-i\right)}$=$\frac{1}{\frac{e^{i\left(\frac{\pi}{2}-i\right)}+e^{-i\left(\frac{\pi}{2}-i\right) }}{2}}$=$\frac{1}{\frac{e^{\left(i\frac{\pi}{2}-i^2\right)}+e^{\left(-i\frac{\pi}{2}+i^2\right) }}{2}}$=$\frac{1}{\frac{e^{i\frac{\pi}{2}} e^{-i^2} + e^{-i \frac{\pi}{2}} e^{i^2}}{2}}$=$\frac{1}{\frac{e^{i \frac{\pi}{2}} e^{-(-1)} + e^{-i \frac{\pi}{2}}e^{-1}}{2}}$=...
y puesto que
$e^{i \frac{\pi}{2}}= Cos\left(\frac{\pi}{2}\right)+ i Sen\left(\frac{\pi}{2}\right)=i$, $e^{-i\frac{\pi}{2}}= Cos\left(\frac{\pi}{2}\right) -Sen\left(\frac{\pi}{2}\right)=-i$
...=$\frac{1}{\frac{ ie^{1}-ie^{-1} }{2}}$=$ \frac{1}{\frac{i(e^1-e^-1)}{2}}$=$\frac{1}{i senh 1}$
por que $senh z= \frac{e^z- e^{-z}}{2}$ en este caso pongo a $z=1$
después $csch z=\frac{1}{senh z}$ y multiplicando por $\frac{i}{i}$, finalmente tengo: $\frac{1}{i senh 1}$= $- i csch 1$
y en la forma $a+ib$:
Solución
$\sec\left(\frac{\pi}{2} - i \right) \approx0 - 0.850918 i $
Realizado por:Emmanuell Castro Flores (discusión) 00:33 10 jun 2015 (CDT)
Ejercicio 8
Expresar el valor de la función trigonométrica dada, en la forma $a+ib$
$\csc\left(1+i\right)$
Procedimiento
Sabemos que
$\csc (1+i)= \frac{1}{\sin(1+i)}$
Ademas, podemos expresar el seno de la siguiente forma:
$\sin(1+i)=\frac{e^{i(1+i)-e^{-i(1+i)}}}{2i}$
$\sin(1+i)=\frac{e^{i(1+i)-e^{-i(1+i)}}}{2i}$
$\sin(1+i)=\frac{e^{i-1}-e^{-i+1}}{2i}$
Por lo que se tendría que:
$\csc\left(1+i\right)=\frac{2i}{e^{-1}e^{i}-e^{1}e^{-i}})$
Escribiendo los números complejos en su forma trigonométrica.
$\csc\left(1+i\right)=\frac{2i}{e^{-1}(\cos1+i\sin1)-e^{1}(\cos1-i\sin1)}$
Reescribiendo la ecuación como:
$\csc\left(1+i\right)=\frac{\frac{1}{1}}{\frac{{e^{-1}e^{i}-e^{1}e^{-i}}}{2i}}$
$\csc\left(1+i\right)=\frac{1}{\frac{(e^{-1}e^{1})\sin1}{2}-i\frac{(e^{-1}-e^{1})\cos1}{2}}$
$\cos(1+i)=\frac{1}{\cosh1\sin1+i \cos1 \sinh1}$
$\cos(1+i)\approx \frac{1}{1.298+ i 0.6348}$
$\cos(1+i)\approx \frac{1}{1.30+ i 0.63}\approx \frac{1.30-i0.63}{2.086}$
Solución
$\cos(1+i)\approx 0.623-i0.302$
Alejandro Juárez Toribio (discusión) 20:14 12 jun 2015 (CDT)
Re elaborado por Manuel Rodríguez
Ejercicio 9
Determine todos los valores complejos $z$ que satisfacen la ecuación dada
$\sin z=i$
Procedimiento
como:
$\sin z=\frac{e^{iz}-e^{-iz}}{2i}$
entonces:
$\frac{e^{iz}-e^{-iz}}{2i}=i\Longleftrightarrow e^{iz}-e^{-iz}=2i^{2}=-2$
al multiplicar ambos lados de la ecuación por $e^{iz}$
tenemos:
$e^{iz}\left(e^{iz}-e^{-iz}\right)=-2e^{iz}\Longleftrightarrow e^{2iz}-1=-2e^{iz}\Longleftrightarrow e^{2iz}+2e^{iz}-1=0$
resolviendo esta ecuación como un polinomio de segundo grado:
$e^{iz}=\frac{-2\pm\sqrt{4-4(1)(-1)}}{2}=-1\pm\sqrt{2}$
aplicando el logaritmo en ambos lados de la ecuación,
$iz=ln(-1\pm\sqrt{2})$ por definición de logaritmo complejo
$ln(-1\pm\sqrt{2})=log_{e}\mid z\mid+iarg(z)$
para
$ln(-1+\sqrt{2})=log_{e}\mid-1+\sqrt{2}\mid+iarg(-1+\sqrt{2})=log_{e}(-1+\sqrt{2})+iarg(-1+\sqrt{2})=log_{e}(-1+\sqrt{2})+i2\pi n$, para $n=0,\pm1,\pm2,...$
$ln(-1-\sqrt{2})=log_{e}\mid-1-\sqrt{2}\mid+iarg(-1-\sqrt{2})=log_{e}(1+\sqrt{2})+iarg(1+\sqrt{2})=log_{e}(1+\sqrt{2})+i(2n+1)\pi$,
para $n=0,\pm1,\pm2,...$
esto es:
$iz=log_{e}(-1+\sqrt{2})+i2\pi n$ multiplicando en ambos lados:
$i$, $\Longrightarrow-z=ilog_{e}(-1+\sqrt{2})-2\pi n\Longleftrightarrow z=2\pi n-ilog_{e}(-1+\sqrt{2})$
para $n=0,\pm1,\pm2,...$
$iz=log_{e}(1+\sqrt{2})+i(2n+1)\pi$ multiplicando en ambos lados po $i$, $\Longrightarrow-z=ilog_{e}(1+\sqrt{2})-(2n+1)\pi\Longleftrightarrow z=(2n+1)\pi-ilog_{e}(1+\sqrt{2})$,
para $n=0,\pm1,\pm2,...$
de esto concluimos que todos los valores posibles para $z$ son:
$z=2\pi n-ilog_{e}(-1+\sqrt{2})$ ,para $n=0,\pm1,\pm2,...$
o
Solución
$z=(2n+1)\pi-ilog_{e}(1+\sqrt{2})$,para $n=0,\pm1,\pm2,...$
Francisco Medina Albino (discusión) 18:46 11 jun 2015 (CDT)
Ejercicio 10
Encontrar todos los valores complejos z, que satisfacen la ecuación dada.
$cos(z)=4$
Procedimiento
Por la definición de $cos(z)$ tenemos que:
$\frac{e^{iz}+e^{-iz}}{2}=4$
Entonces podemos resolver como sigue:
$e^{iz}+e^{-iz}=8$
$e^{iz}+e^{-iz}-8=0$
Ahora se multiplica por $e^{iz}$
$e^{iz}(e^{iz}+e^{-iz}-8)=0$
$e^{iz}e^{iz}+e^{iz}e^{-iz}-8e^{iz}=0$
$e^{2iz}-8e^{iz}+1=0$
Donde nos resulta una ecuación cuadrática que podemos resolver aplicando la fórmula general:
$e^{iz}=\frac{8\pm\sqrt{64-(4)(1)(1)}}{2}=\frac{8\pm\sqrt{60}}{2}=\frac{8\pm2\sqrt{15}}{2}=4\pm\sqrt{15}$
$\Longrightarrow e^{iz}=4\pm\sqrt{15}$
Entonces, para despejar $z$:
$iz=ln(4\pm\sqrt{15})$
Donde $ln(z)=log_{e}|z|+iarg(z)$
Y resolviendo para $\left(+\right)$, tenemos por tanto:
$iz=log_{e}(4+\sqrt{15})+i(2\pi n)$
Multiplicando finalmente por $-i$ debe quedar:
$z=-ilog_{e}(4+\sqrt{15})+(2\pi n)$
ó
$z=(2\pi n)-ilog_{e}(4+\sqrt{15})$
Solución
Entonces, los posibles valores para $z$ son:
$z_{1}=(2\pi n)-ilog_{e}(4+\sqrt{15})$ y $z_{2}=(2\pi n)-ilog_{e}(4-\sqrt{15})$
Para $n=0,\pm1,\pm2,\pm3,...$
Realizado por: A. Martín R. Rabelo (discusión) 00:40 12 jun 2015 (CDT)
Ejercicio 11
Determinar todos los valores complejos "z" que satisfacen la ecuación dada.
$sen(z)=cos(z)$
Procedimiento
Por definición se puede escribir como:
$\frac{e^{iz}-e^{-iz}}{2i}=\frac{e^{iz}+e^{-iz}}{2}$
Entonces reordenamos y resolvemos como sigue:
$e^{iz}-e^{-iz}=i(e^{iz}+e^{-iz})$
$e^{iz}-e^{-iz}-i(e^{iz}+e^{-iz})=0$
$e^{iz}-e^{-iz}-ie^{iz}-ie^{-iz}=0$
$e^{iz}-e^{-iz}-ie^{iz}-ie^{-iz}=0$
A partir de este punto multiplicamos por $e^{iz}$
$e^{iz}(e^{iz}-e^{-iz}-ie^{iz}-ie^{-iz})=0$
$e^{iz}e^{iz}-e^{iz}e^{-iz}-e^{iz}ie^{iz}-e^{iz}ie^{-iz}=0$
$e^{2iz}-1-ie^{2iz}-i=0$
$e^{2iz}-ie^{2iz}-i-1=0$
$e^{2iz}(1-i)-i-1=0$
Re acomodando ...
$e^{2iz}(1-i)=i+1$
$e^{2iz}=\frac{(i+1)}{(1-i)}$
Entonces multiplicamos por el conjugado para resolver la fracción compleja como sigue:
$e^{2iz}=\frac{(i+1)}{(1-i)}\frac{(1+i)}{(1+i)}=\frac{1-1+2i}{2}=i$
Entonces:
$e^{2iz}=i$
Y entonces, para saber $z$ despejamos haciendo uso del logaritmo y sus propiedades:
$ln(e^{2iz})=ln(i)$
$2iz=ln(i)$
Donde $ln$ es un logaritmo natura complejo definido como: $ln=log_{e}|z|+iarg(z)$ donde $|z|=1$ y $arg(z)=\frac{\pi}{2}+2n\pi$ dado que $z$ es un complejo puro. Por lo que tenemos entonces...
$2iz=log_{e}(1)+i(\frac{\pi}{2}+2n\pi)$
$2iz=log_{e}(1)+i(\frac{(4n+1)\pi}{2})$ pero $log_{e}(1)=0$
$\Longrightarrow2iz=i(\frac{(4n+1)\pi}{2})$
Para despejar $z$ se divide la ecuación entre $2$ y se multiplica por $-i$ como sigue:
Solución
$z=(\frac{(4n+1)\pi}{4})=\frac{1}{4}(4n+1)\pi$ para $n=0,\pm1,\pm2,\pm3....$
Realizado por: A. Martín R. Rabelo (discusión) 00:05 12 jun 2015 (CDT)
Ejercicio 13
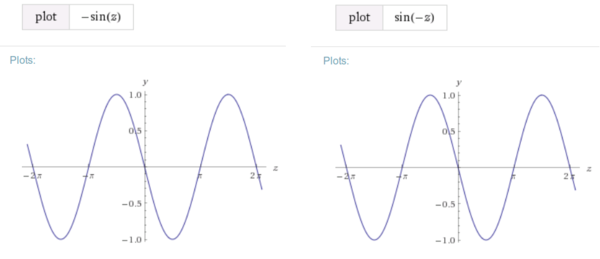
Verifique la identidad trigonométrica dada $sen(-z)=-sen(z)$
Sabemos que $z=x+iy$
Procedimiento
Entonces sustituyendo $z$ se tiene
$ sen(-z)=sen-(x+iy)=-sen(x+iy) $
Desarrollando $-sen(x+iy)$
$ sen(-z)=-[sen(x) cos(iy)+sen(iy) cosx] $
$ sen(-z)=-[sen(x) cosh(y)+isenh(y) cos(x)] $
Donde se demostrará que
$ - sen(z)= -[sen(x) cosh(y)+isenh(y) cos(x)], ---(*) $
Donde $ [sen(x) cosh(y)+isenh(y) cos(x)]$ está dada por:
$\left(\frac {e^{ix}-e^{-ix}}{2i}\right) \left(\frac {e^{iy}+e^{-iy}}{2}\right)+i \left(\frac {e^{iy}-e^{-iy}}{2i}\right) \left(\frac {e^{ix}+e^{-ix}}{2}\right)$
$ = \frac{[e^{i(x+y)}+e^{i(x-y)}-e^{i(-x+y)}-e^{-i(x+y)}]+i[e^{i(y+x)}+e^{i(y-x)}-e^{i(-y+x)}-e^{-i(y+x)}]}{4i}$
Eliminando términos
$ \frac{e^{i(x+y)}-ie^{-i(x+y)}}{2i}=sen(x+iy)=sen(z) $
$ \therefore sen(-z)=-sen(z) $
Grafica
Realizado por: Samantha Martinez (discusión) 19:01 11 Junio 2015 (CDT)
Ejercicio 14
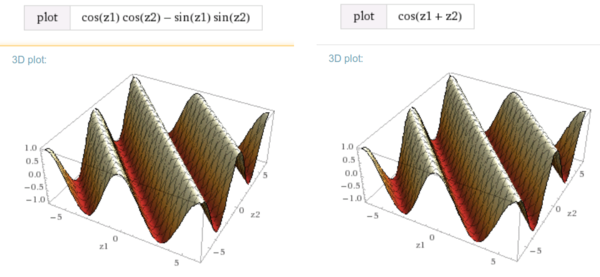
Verifique la identidad trigonométrica dada $cos(z_{1}+z_{2})=cosz_{1}cosz_{2}-senz_{1}senz_{2}$
Procedimiento
Tomando en cuenta que $cosz_{1}cosz_{2}-senz_{1}senz_{2}$ está dada por:
$\left(\frac {e^{iz_{1}}+e^{-iz_{1}}}{2}\right) \left(\frac {e^{iz_{2}}+e^{-iz_{2}}}{2}\right)- \left(\frac {e^{iz_{1}}-e^{-iz_{1}}}{2i}\right) \left(\frac {e^{iz_{2}}-e^{-iz_{2}}}{2i}\right)$
$ = \frac {[e^{i(z_{1}+z_{2})}+e^{i(z_{1}-z_{2})}+e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}]}{4}-\frac{e^{i(z_{1}+z_{2})}-e^{i(z_{1}-z_{2})} -e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}}{4i^2} $
$ = \frac {[e^{i(z_{1}+z_{2})}+e^{i(z_{1}-z_{2})}+e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}]}{4}+\frac{[e^{i(z_{1}+z_{2})}-e^{i(z_{1}-z_{2})} -e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}]}{4} $
$ = \frac {e^{i(z_{1}+z_{2})}+e^{i(z_{1}-z_{2})}+e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}+e^{i(z_{1}+z_{2})}-e^{i(z_{1}-z_{2})} -e^{i(-z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}}{4} $$ $$ \frac{e^{i(z_{1}+z_{2})}+e^{-i(z_{1}+z_{2})}}{2}=cos(z_{1}+z_{2}) $
$ \therefore cos(z_{1}+z_{2})=cosz_{1}cosz_{2}-senz_{1}senz_{2} $
Gráfica
Realizado por: Samantha Martinez (discusión) 19:01 11 Junio 2015 (CDT)
Ejercicio 15
Compruebe la identidad trigonométrica $\overline{\cos z}=\cos\overline{z}$
Procedimiento
Sabemos que:
$\cos z={\displaystyle \frac{e^{z}-e^{-z}}{2}}={\displaystyle \frac{e^{x}}{2}(\cos y+i\sin y)+{\displaystyle \frac{e^{-x}}{2}(\cos y-i\sin y)={\displaystyle (\frac{e^{x}+e^{-x}}{2})\cos y+i{\displaystyle (\frac{e^{x}-e^{-x}}{2}}}}})\sin y$
Por lo tanto:
$\overline{\cos z}={\displaystyle (\frac{e^{x}+e^{-x}}{2})\cos y-i\sin y({\displaystyle \frac{e^{x}-e^{-x}}{2})=\frac{(e^{x}\cos y+e^{-x}\cos y+ie^{x}\sin(-y)-ie^{x}\sin(-y))}{2}}}$
Que podemos escribir:
Conclusión
$\overline{\cos z}={\displaystyle \frac{e^{x}(\cos(-y)+i\sin(-y)+e^{-x}(\cos y+i\sin y)}{2}=\frac{e^{x-iy}+e^{-x+iy}}{2}}={\displaystyle \frac{e^{\overline{z}}+e^{\overline{-z}}}{2}=\cos\overline{z}}$
Realizado por: Jose Emmanuel Flores Calderón (discusión) 20:27 12 jun 2015 (CDT)
Ejercicio 16
Compruebe la identidad trigonométrica dada.
Procedimiento
Considerando que:
Sustituyendo tenemos que:
Evaluamos la funcion tenemos.
Ahora como
Al evaluar tenemos:
Por lo cual al sustituir tenemos:
Conociendo la definición de coseno tenemos que:
Conclusión
Realizado por: Anahi Limas (discusión) 22:45 12 jun 2015 (CDT)
Ejercicio 24
Expresa el valor de la función hiperbólica dada en la forma $a + ib$
$tanh(2 + 3i)$
Procedimiento
Como conocemos la expresión de la función tangente hiperbólica expresada en función de las exponenciales podemos hacer uso d ella la cual es:
$\tanh z = \frac{\sinh z}{\cosh z} = \frac{e^z - e^{-z}}{e^z + e^{-z}}$
Aplicando esta expresión a nuestro numero $z=2 +3i$
$\tanh (2 +3i) = \frac{e^{(2+3i)} - e^{-(2+3i)}}{e^{(2+3i)} + e^{-(2+3i)}} = \frac{e^2 e^{3i} - e^{-2} e^{-3i}}{e^2 e^{3i} + e^{-2} e^{-3i}}$
Desarrollando tenemos:
$\tanh (2 + 3i) =\frac{e^2(\cos3 + i\sin3) - e^{-2}(\cos{-3} + i\sin{-3})}{e^2(\cos3 + i\sin3) + e^{-2}(\cos{-3} + i\sin{-3})}$
$\approx{\frac{e^2(0.9986 + 0.0523i) - e^{-2}(0.9986 - 0.0523i)}{e^2(0.9986 + 0.0523i) + e^{-2}(0.9986 - 0.0523i)}}$
$\approx{\frac{(7.3890)(0.9986 + 0.0523i) - (0.1353)(0.09986 - 0.0523i)}{(7.3890)(0.9986 + 0.0523i) + (0.1353)(0.9986 - 0.0523i)}}$
$\approx{\frac{7.3786 + 0.3864i - 0.1351 + 0.0070i}{7.3786 + 0.3864i + 0.1351 - 0.0070i}}$
$\approx{\frac{7.2435 + 0.3934i}{7.5137 + 0.3794i}} = \frac{7.2435 + 0.3934i}{7.5137 + 0.3794i} * \frac{7.5137 - 0.3794i}{7.5137 - 0.3794i}$
Conclusión
$\approx{\frac{57.3783 - 2.8973i}{56.5995}}$
$\approx{1.0137 - 0.0511i}$
Como podemos ver al principio nos queda una división de números complejos es por ello que se multiplico por $\frac{z}{z*}$ para obtener un mero complejo de la forma $a + ib$
Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 14:24 11 jun 2015 (CDT)
Ejercicio 29
Comprobar la identidad hiperbólica
$cosh^{2}z-senh^{2}z=1$
Procedimiento
Partiendo de las definiciones:
\begin{equation} coshz=\frac{e^{z}+e^{-z}}{2}...(1) \end{equation}
\begin{equation} senhz=\frac{e^{z}-e^{-z}}{2}...(2) \end{equation}
Ahora sacamos cuadrados a (1) y (2) para obtener lo siguiente:
$cosh^{2}z=\left[\frac{e^{z}+e^{-z}}{2}\right]^{2}=\frac{\left(e^{z}+e^{-z}\right)^{2}}{4}=\frac{e^{2z}+2e^{z}e^{-z}+e^{2z}}{4}=\frac{e^{2z}+2+e^{-2z}}{4}$
$senh^{2}z=\left[\frac{e^{z}-e^{-z}}{2}\right]^{2}=\frac{\left(e^{z}-e^{-z}\right)^{2}}{4}=\frac{e^{2z}-2e^{z}e^{-z}+e^{2z}}{4}=\frac{e^{2z}-2+e^{-z}}{4}$
Recordando que:
$e^{z}e^{-z}=e^{z-z}=e^{0}=1$ y que $\left(e^{z}\right)^{2}=e^{2z}$
Ahora solo hacemos (1) menos (2) para así obtener:
$cosh^{2}z-senh^{2}z=\frac{e^{2z}+2+e^{-2z}}{4}-\left[\frac{e^{2z}-2+e^{-2z}}{4}\right]=\frac{e^{2z}+2+e^{-2z}}{4}+\frac{-e^{2z}+2-e^{-2z}}{4}=\frac{1}{4}\left[e^{2z}+2+e^{-2z}-e^{2z}+2-e^{-2z}\right]=\frac{1}{4}\left(2+2\right)=1$
Conclusión
Por lo tanto tenemos que:
$cosh^{2}z-senh^{2}z=1$ Q.E.D.
Resuelto por Luis Enrique Martínez Valverde (discusión) 21:37 11 jun 2015 (CDT)
Ejercicio 30
Demostrar las siguientes identidades
Procedimiento
Tenemos las siguientes relaciones trigonométricas e hiperbólicas, sí:
- , entonces
sustituimos en la identidad y factorizando la “i” en la expresión se tiene:
Conclusión
Acomodando términos se tiene la demostración:
Realizado por: Ricardo Garcia Hernandez (discusión) 11:23 12 jun 2015 (CDT)
Ejercicio 32
Compruebe que la identidad se cumple
Procedimiento
Retomando que para el seno hiperbólico y coseno hiperbólico
Tomando a con la forma , por lo que de la función coseno hiperbólico tenemos que cumple
Usando la forma de Moivre
Usando esta identidad en el coseno hiperbólico de z complejo, tenemos que
Al pedirnos solamente la parte imaginaria, usando la identidad de y la expresión inicial de seno hiperbólico, desarrollamos la ultima expresión
Conclusión
Por lo que hemos demostrado que
Realizado por: Pablo (discusión) 21:13 12 jun 2015 (CDT)
Ejercicio 37
Recordemos que la fórmula de Euler establece que $e^{i\theta}=\cos(\theta)+i\sin(\theta)$ para cualquier número real $\theta$. Demuestre que, de hecho $e^{i\,z}=\cos(z)+i\sin(z)$ , para cualquier número complejo $z$.'
Por definición de la exponencial compleja:
Procedimiento
\[ e^{w}=e^{Re(w)}\,\left[ cis (Im(w)) \right] \]
Si $w=iz=i(x+iy)=ix-y$.
\[ e^{iz}=e^{w}=e^{-y}\,\left[ cis (x) \right]=e^{-y}\,\left[ \left( \frac{e^{i x}+e^{-i x}}{2} \right)+i \left( \frac{e^{i x}-e^{-i x}}{2i} \right) \right]=e^{-y}\,\left( \frac{e^{i x}+e^{-i x}}{2} \right)+e^{-y}\,\left( \frac{e^{i x}-e^{-i x}}{2} \right) \]
\[ =\frac{e^{-y}\,e^{i x}+e^{-y}\,e^{-i x}+e^{-y}\,e^{i x}-e^{-y}\,e^{-i x}}{2}=\frac{e^{-y}\,e^{i x}+e^{-y}\,e^{i x}}{2} \]
Usando el teorema general aditivo: \[ =\frac{e^{ix-y}+e^{ix-y}}{2} \] Sumamos un $0$ especial $\frac{e^{-ix+y}-e^{-ix+y}}{2}$. \[ =\frac{e^{ix-y}+e^{ix-y}}{2}+\frac{e^{-ix+y}-e^{-ix+y}}{2}=\frac{e^{ix-y}+e^{ix-y}+e^{-ix+y}-e^{-ix+y}}{2} \] Reagrupando términos: \[ =\frac{e^{ix-y}+e^{-ix+y}}{2}+\frac{e^{ix-y}-e^{-ix+y}}{2} \] Se reescriben los argumentos como $iz=ix-y\,$ y $\,-iz=-ix+y$ \[ =\frac{e^{iz}+e^{-iz}}{2}+\frac{e^{iz}-e^{-iz}}{2} \] Se multiplica y divide por $i$ en el segundo término: \[ =\frac{e^{iz}+e^{-iz}}{2}+i\frac{e^{iz}-e^{-iz}}{2i} \]
Se observan claramente las definiciones del coseno de un número complejo en el primer término y la del seno en el segundo.
Conclusión
\[ e^{iz}=\cos(z)+i\,\sin(z)\;_\square \]
Realizado por: Tlacaelel Cruz (discusión) 23:37 4 jun 2015 (CDT)
Ejercicio 43
Encuentre las partes real e imaginaria de la función $\sin \overline{z}$ y utilícelas para demostrar que esta función no es analítica en ningún punto.
Procedimiento
Si $z=x+iy$, entonces $\overline{z}=x-iy$. La definción del seno complejo es:
$\sin z=\dfrac{e^{iz}-e^{-iz}}{2i}$, para el complejo conjugado simplemente sustituimos $\sin \overline{z}=\dfrac{e^{i\overline{z}}-e^{-i\overline{z}}}{2i}$
$\sin \overline{z}=\dfrac{e^{i\overline{z}}-e^{-i\overline{z}}}{2i}=\dfrac{e^{i(x-iy)}-e^{-i(x-iy)}}{2i}=\dfrac{e^{y+ix}-e^{-(y+ix)}}{2i}=\dfrac{e^ye^{ix}-e^{-y}e^{-ix}}{2i}=\dfrac{e^y(\cos x+i\sin x)-e^{-y}(\cos x-i\sin x)}{2i}$
$\sin \overline{z}=\dfrac{\cos x(e^y-e^{-y})+i\sin x(e^y+e^{-y})}{2i}=\dfrac{\cos x(e^y-e^{-y})}{2i}+\dfrac{i\sin x(e^y+e^{-y}}{2i}=\dfrac{\sin x(e^y+e^{-y})}{2}-i\dfrac{\cos x(e^y-e^{-y})}{2}$
$\sin \overline{z}=\sin x(\dfrac{e^y+e^{-y}}{2})-i\cos x(\dfrac{e^y-e^{-y}}{2})$
y con las funciones hiperbólicas $\sinh y=\dfrac{e^y-e^{-y}}{2}$, $\cosh y=\dfrac{e^y+e^{-y}}{2}$
$\sin \overline{z}=\sin x \cosh y-i\cos x \sinh y$
Identificando las partes real e imaginaria de la función:
$u(x,y)=\sin x \cosh y$, $v(x,y)=-\cos x \sinh y$
El criterio para la no analiticidad dice que si las ecuaciones de Cauchy-Riemann no se satisfacen en todos los puntos $z$ en un dominio $D$, entonces la función no puede ser analítica en $D$. Para demostrar que la función $\sin \overline{z}$ no es analítica en ningun punto, demostremos que sus partes real e imaginaria no satisfacen las ecuaciones de Cauchy-Riemann.
$\dfrac{\partial u}{\partial x}=\dfrac{\partial v}{\partial y}$, $-\dfrac{\partial u}{\partial y}=\dfrac{\partial v}{\partial x}$
Derivando las funciones parcialmente obtenemos
$\dfrac{\partial u}{\partial x}=\cos x\cosh y$, $\dfrac{\partial u}{\partial y}=\sin x\sinh y$
$\dfrac{\partial v}{\partial x}=\sin x\sinh y$, $\dfrac{\partial v}{\partial y}=-\cos x\cosh y$
Igualando términos
Conclusión
$\cos x\cosh y\neq -\cos x\cosh y$
$\sin x\sinh y\neq -\sin x\sinh y$
Por lo que hemos demostrado que la función $\sin \overline{z}$ no es analítica en ningún punto del plano complejo.
Realizado por: Oscar Javier Gutierrez Varela (discusión) 09:39 5 jun 2015 (CDT)
Ejercicio 45
Demuestre que $\sin z$ es uno-a-uno en el dominio: $-\pi/2<x<\pi/2$, $-\infty<y<\infty$.
Procedimiento
Sean: $z_1=x_1+iy_1$ y $z_2=x_2+iy_2$ números complejos tales que: $-\pi/2<x_1<\pi/2,-\pi/2<x_1<\pi/2$, $y_1,y_2\in \mathbb{R}$ arbitrarios. Sea $ f(z)=\sin z$.
Supongamos que $f(z_1)=f(z_2)$. Por demostrar $z_1=z_2$. Entonces:
\begin{align*}
\sin{z_1}&=\sin{z_2}&~~\textrm{f(z_1)=f(z_2)}\\\\
\end{align*}
\begin{align*}
\frac{e^{iz_1}-e^{-iz_1}}{2i}&=\frac{e^{iz_2}-e^{-iz_2}}{2i}&~~\textrm{(por definición)}\\\\
\end{align*}
\begin{align*}
e^{iz_1}-e^{-iz_1}-(e^{iz_2}-e^{-iz_2})&=0&~~\textrm{(despejando)}\\\\
\end{align*}
\begin{align*}
(e^{iz_1}-e^{iz_2})+(e^{-iz_2}-e^{-iz_1})&=0&~~\textrm{(por asociatividad)}\\\\
\end{align*}
\begin{align*} e^{\frac{i(z_1+z_2)}{2}}(e^{\frac{i(z_1-z_2)}{2}}-e^{\frac{-i(z_1-z_2)}{2}})+e^{\frac{-i(z_1+z_2)}{2}} (e^{\frac{i(z_1-z_2)}{2}}-e^{\frac{-i(z_1-z_2)}{2}})&=0&~~\textrm{(distributividad)}\\\\ \end{align*}
\begin{align*} (e^{\frac{i(z_1+z_2)}{2}}+e^{\frac{-i(z_1+z_2)}{2}})(e^{\frac{i(z_1-z_2)}{2}}-e^{\frac{-i(z_1-z_2)}{2}})&=0&~~\textrm{(distributividad)}\\\\ \end{align*}
\begin{align*} \Rightarrow [(e^{\frac{i(z_1+z_2)}{2}}+e^{\frac{-i(z_1+z_2)}{2}})=0] &\vee [(e^{\frac{i(z_1-z_2)}{2}}-e^{\frac{-i(z_1-z_2)}{2}})=0]&~~\textrm{(alguno o los dos factor(es) es cero.)}\\\\ \end{align*}
Dividiendo entre $e^{\frac{-i(z_1+z_2)}{2}}$ la primera, y la segunda entre $e^{\frac{-i(z_1-z_2)}{2}}$
\begin{align*} \Longleftrightarrow [\frac{e^{\frac{i(z_1+z_2)}{2}}}{e^{\frac{-i(z_1+z_2)}{2}}}+1=0] &\vee [\frac{e^{\frac{i(z_1-z_2)}{2}}}{e^{\frac{-i(z_1-z_2)}{2}}}-1=0] \end{align*}
\begin{align*} \Longleftrightarrow [e^{i(z_1+z_2)}=-1] &\vee [e^{i(z_1-z_2)}=1]&~~\textrm{(teorema 4.3 (ii))}\\\\ \end{align*}
\begin{align*} \Longleftrightarrow [e^{i(z_1+z_2)}=e^{i(\pi+2k\pi)}] &\vee [e^{i(z_1-z_2)}=e^{i(0+2l\pi)}]&~~\textrm{(forma de Euler de los complejos 1 y -1)} \end{align*}
\begin{align*} \Rightarrow [i(z_1+z_2)=i(\pi+2k\pi)] &\vee [i(z_1-z_2)=i(0+2l\pi)]&~~\textrm{(e^z es uno-a-uno en este dominio.)}\\\\ \end{align*}
\begin{align*} \Longleftrightarrow [(z_1+z_2)=(\pi+2k\pi)] &\vee [(z_1-z_2)=(0+2l\pi)]&~~\textrm{(multiplicando por 1/i)}\\\\ \end{align*}
\begin{align*} \Longleftrightarrow [(x_1+x_2=\pi + 2k\pi \wedge y_1+y_2=0)] &\vee [(x_1-x_2=2l\pi \wedge y_1-y_2=0)]&~~\textrm{(Por igualdad de números complejos.)}\\\\ \end{align*}
pero el hecho de que $x_1+x_2=\pi + 2k\pi,(k\in \mathbb{Z})$ implica que: $x_1\notin (-\pi/2,\pi/2)$ o $x_2\notin (-\pi/2,\pi/2)$, (ya que: Si $-\pi/2<x_1<\pi/2,-\pi/2<x_2<\pi/2 ~\Rightarrow -\pi<x_1+x_2<\pi$ ). De lo anterior $[(x_1+x_2=\pi + 2k\pi \wedge y_1+y_2=0)]$ no puede ocurrir.
Para que la disyunción sea verdadera,tiene que cumplirse $[(x_1-x_2=2l\pi),(l\in \mathbb{Z})) \wedge (y_1-y_2=0)]$ . Por otro lado si $-\pi/2<x_2<\pi/2 \Rightarrow -\pi/2<-x_2<\pi/2$, entonces: $-\pi<x_1-x_2<\pi$ y para que esto se cumpla, necesariamente $l=0$.
Conclusión
Entonces $x_1=x_2~~\wedge ~~y_1=y_2$. Por lo tanto $z_1=z_2$.
Por lo tanto: $\sin z$ es uno-a-uno en el dominio: $-\pi/2<x<\pi/2$, $-\infty<y<\infty$.
Realizado por: Alan Daniel Barrón Posadas (discusión) 14:38 11 jun 2015 (CDT)
Ejercicio 51
Compruebe las siguiente identidades:
$ (a)\sin (z+\pi)= -\sin z$
$ (b) \cos (z+\pi) = -\cos z$
Inciso a
$ (a)\sin (z+\pi)= -\sin z$
Por definición
$\sin z = \dfrac{e^{iz} - e^{-iz}}{2i}$
Sabemos que la periodicidad de $\sin = 2\pi$. Sustituyendo el periodo de esta función.
$\sin (z+\pi) = \dfrac{e^{i(z+\pi)} - e^{-i(z+\pi)}} {2i}$
Utilizando las propiedades de $e$. Tenemos
$\sin (z+\pi) =\dfrac{e^{iz}e^{i\pi}-e^{-iz}e^{-i\pi}}{2i}$
$e^{ix}= \cos x + i \sin x$ y $ e^{-ix} = \cos x - i \sin x $. Nos resulta
$\sin (z+\pi) =\dfrac{e^{iz}\cos (\pi) + i \sin (\pi) -e^{-iz}\cos (-\pi)- i \sin (-\pi)}{2i} = \dfrac{-e^{iz}+e^{-iz}}{2i} = -\dfrac{e^{iz}+e^{-iz}}{2i} = -\sin z$
$ (b) \cos (z+\pi) = -\cos z$
Inciso b
De igual forma demostramos (b)
$\ cos z = \dfrac{e^{iz} + e^{-iz}}{2}$
$\cos (z+ \pi) = \dfrac{e^{i(z+\pi)} +e^{-i(z+\pi)}} {2}$
Por las propiedades de $e$
$\cos (z+\pi) =\dfrac{e^{iz}e^{i\pi}+e^{-iz}e^{-i\pi}}{2}$
$e^{ix}= \cos x + i \sin x$ y $ e^{-ix} = \cos x - i \sin x $. Nos resulta
$\cos (z+\pi) =\dfrac{e^{iz}\cos (\pi) + i \sin (\pi) + e^{-iz}\cos (-\pi)- i \sin (-\pi)}{2i} = -\dfrac{-e^{iz}-e^{-iz}}{2i} = -\cos z$
Realizado por: Esther Sarai (discusión) 13:32 9 jun 2015 (CDT)Esther Sarai






![e^{0+\frac{i \pi}{2}}= e^0[cos \frac{\pi}{2} +i sen \frac{\pi}{2}]= i](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/63d06880bd54598eba309e497cbbaaec5f60cc7e)








![-isenh(iz_{1}+iz_{2})=[(-i)sen(iz_{1})cos(iz_{2})+cos(iz_{1})(-i)sen(iz_{2})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b0af7edf3884d09fa279deab8b079902f4a17c13)
![-isenh(iz_{1}+iz_{2})=-isen(iz_{1})cos(iz_{2})-icos(iz_{1})sen(iz_{2})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8e0a6bb797c65784083528611efee3c1d5f73b02)
![-isenh(iz_{1}+iz_{2})=-isen(iz_{1})cos(iz_{2})-isen(iz_{2})cos(iz_{1})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/892e615de71424bd0a0ce604942badfb8dc87957)








