Compleja:Zill-Cap6.5
Ejercicios del capítulo 6, sección 5 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 6.5
Ejercicio 3
Utilizar la serie de Laurent adecuada para encontrar el residuo indicado.
$f(z)=\frac{4z-6}{z(2-z)};Res(f(z),0)$
Procedimiento
Primero descomponemos en fracciones parciales para evaluar la serie de Laurent
$f(z)=\frac{4z-6}{z(2-z)}=\frac{A}{z}+\frac{B}{2-z}=\frac{2A-Az+Bz}{z(2-z)}=\frac{2A+z(-A+B)}{z(2-z)}$
De donde obtenemos el siguiente sistema
$B-A=4$--------(1)
$2A=-6$----------(2)
Entonces de (2) despejamos y queda que $A=-3$ para después sustituir en (1) y queda como:
$B+3=4\rightarrow B=1$
Por lo tanto tenemos que:
$f(z)=\frac{4z-6}{z(2-z)}=\frac{-3}{z}+\frac{1}{2-z}=f_{1}(z)+f_{2}(z)$
$f_2=\frac{1}{2-z}=\frac{1}{2(1-z/2)}$
Observamos que: $f_2$ es una serie geométrica y se puede escribir como:
$f_2=\frac{1}{2} \left [1+\frac{z}{2}+\left (\frac{z}{2} \right )^{2}+\left (\frac{z}{2} \right )^{3} + ... \right ]$
Valida cuando $|z/2|< 1$ esto es $|z|<2$
Por lo que la serie es valida cuando $0<|z|<1$
Conclusión
$f(z)=\frac{4z-6}{z(2-z)}=\frac{-3}{z-0}+\frac{1}{2} \left [1+\frac{z}{2}+\left (\frac{z}{2} \right )^{2}+\left (\frac{z}{2} \right )^{3} + ... \right ]$
Entonces:
$Res(f(z),0)=-3$
Re elaborado por Manuel Rodríguez
Ejercicio 7
Use (1) (2) o (4) para encontrar el residuo en cada polo de la función dada
(7) \[ f(z)=\dfrac{z}{z^{2}+16}\]
Procedimiento
Utilizando la ecuación (1), esta depende del numero de cero que contenga la función
\[ Res(f(z),z_{0}) = \lim_{z\rightarrow z_0}(z-z_{0})f(z)\]
Determinamos el numero de cero de la función haciendo una factorización del denominador
\[ f(z)=\dfrac{z}{(z+4i)(z-4i)}\]
De esto podemos concluir que la función tiene dos polos de orde uno o dos polos simples, por tanto emplearemos (1) de la siguiente forma:
\[
Res(f(z),z_{1}) = \lim_{z\rightarrow z_1}(z-z_{1})f(z)\]1
\[
Res(f(z),z_{2}) = \lim_{z\rightarrow z_2}(z-z_{2})f(z)\]
Conclusión
\[ Res(f(z), 4i) = \lim_{z\rightarrow 4i}(z-4i)\dfrac{z}{(z+4i)(z-4i)}=\lim_{z\rightarrow 4i}\dfrac{z}{(z+4i)}=\dfrac{4i}{8i}=\dfrac{1}{2} \]
\[ Res(f(z),-4i) = \lim_{z\rightarrow -4i}(z+4i)\dfrac{z}{(z+4i)(z-4i)}=\lim_{z\rightarrow -4i}\dfrac{z}{(z-4i)}=\dfrac{-4i}{-8i}=\dfrac{1}{2} \]
Realizado por: Esther Sarai (discusión) 11:35 3 jul 2015 (CDT)Esther Sarai
Ejercicio 8
Use (1) (2) o (4) para encontrar el residuo en cada polo de la función dada
$f(z)=\frac{4z+8}{2z-1}$
Procedimiento
Primero se puede reescribir como
$f(z)=\frac{4z+8}{2z-1}=\frac{4}{2}\frac{z+2}{z-1/2}=2[\frac{z+2}{z-1/2}]$
Entonces se puede ver que tiene un polo simple en $z=1/2$, por ello uso (1)
Conclusión
$Res(f(z),1/2)=\underset{z\rightarrow1/2}{lim}(z-1/2)[2[\frac{z+2}{z-1/2}]]=\underset{z\rightarrow1/2}{lim}2[z+2]=2[\frac{5}{2}]=5$
Resuelto por:Fernando Vazquez V. (discusión) 21:29 3 jul 2015 (CDT)
Ejercicio 9
Use $(1),(2)$ o $(4)$ para encontrar el residuo en cada polo de la función $f(z)=\frac{1}{z^{4} + z^{3} - 2z^{2} }$
Procedimiento
Tengo que
\[ f(z)=\frac{1}{z^{4} + z^{3} - 2z^{2} }= \frac{1}{ z^{2} \left( z^{2} +z -2 \right) }= \frac{1}{z^{2} \left( z+2 \right) \left( z-1 \right)} \]
La función $f(z) = \frac{1}{z^{2} \left( z+2 \right) \left( z-1 \right)}$ tiene dos polos simples en $z=1$ y en $z=-2$ , también un polo de orden 2 en $z=0$
Puesto que $z=1$ y $z=-2$ son polos simples, usamos $(1): $
\[
Res( f(z),1)= \lim_{z \to 1}(z-1) f(z)= \lim_{z \to 1} (z-1) \dfrac{1}{ z^{2} (z+2) (z-1)} = \lim_{z \to 1} \dfrac{1}{ z^{2} (z+2) } = \frac{1}{3}
\]
\[ \therefore Res( f(z),1)= \frac{1}{3} \]
\[
Res( f(z),-2)= \lim_{z \to -2}(z+2) f(z)= \lim_{z \to -2} (z+2) \dfrac{1}{ z^{2} (z+2) (z-1)} = \lim_{z \to -2} \dfrac{1}{ z^{2} (z-1) } = -\frac{1}{12}
\]
Res( f(z),-2)
\[ \therefore Res( f(z),-2)= -\frac{1}{12} \]
Ahora en el polo de orden 2, el resultado en $(2)$ da
\[ Res( f(z),0) = \frac{1}{ (2-1)! } \lim_{z \to 0 } \frac{ d^{2-1} }{ dz^{2-1} } \left[ \left( z-0 \right)^{2} f(z) \right]= \lim_{z \to 0 } \frac{d}{dz} \left[ z^{2} f(z) \right] = \lim_{z \to 0 } \frac{d}{dz} \left[ z^{2} \frac{1}{ z^{2}(z+2)(z-1) } \right]= \]
\[ \lim_{z \to 0 } \frac{d}{dz} \left[ \frac{1}{ (z+2)(z-1) } \right]= \lim_{z \to 0 } \left( - \frac{1}{ (z+2)^{2}(z-1)} - \frac{1}{ (z+2)(z-1)^{2} } \right) = \lim_{z \to 0 } \left( \frac{-2z-1}{ (z^{2}+z-2)^{2} } \right) = - \frac{1}{4} \]
Res( f(z),0)
\[ \therefore Res( f(z), 0)= - \frac{1}{4} \]
Realizado por: Emmanuell Castro Flores (discusión) 16:24 3 jul 2015 (CDT)
Ejercicio 10
Encuentre el residuo en cada polo de la función dada.
Procedimiento
Analizamos el denominador que se puede factorizar, para ello utilizaremos la frmula general y nos queda:
por los tanto
entonces:
Es un polo de orden n=2 en “z” subíndice uno y dos, aplicamos el teorema del residuo en un polo de orden n , el cuál es:
entonces:
por lo tanto
Residuos
Para el otro caso
Residuos
por lo tanto
Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 01:39 4 jul 2015 (CDT)
Ejercicio 11
Encontrar el residuo en cada polo de la función dada
$f(z)=\frac{5z^{2}-4z+3}{(z+1)(z+2)(z+3)}$
Procedimiento
tenemos tres polos simples : $z=-1$,$z=-2$,$z=-3$
usaremos el teorema :
$Res(f(z),z_{0})=lim_{z\rightarrow z_{0}}\left(z-z_{0}\right)f(z)$
para cada residuo.
Residuos
$Res(f(z),-1)=lim_{z\rightarrow-1}(z+1)f(z)=lim_{z\rightarrow-1}\frac{5z^{2}-4z+3}{(z+2)(z+3)}=\frac{5(1)-4(-1)+3}{(-1+2)(-1+3)}=\frac{5+4+3}{(1)(2)}=\frac{12}{2}=6$
$Res(f(z),-2)=lim_{z\rightarrow-2}(z+2)f(z)=lim_{z\rightarrow-2}\frac{5z^{2}-4z+3}{(z+1)(z+3)}=\frac{5(4)-4(-2)+3}{(-2+1)(-2+3)}=\frac{5(4)+4(2)+3}{(-1)(1)}=\frac{20+8+3}{-1}=-31$
$Res(f(z),-3)=lim_{z\rightarrow-3}(z+3)f(z)=lim_{z\rightarrow-3}\frac{5z^{2}-4z+3}{(z+1)(z+2)}=\frac{5(9)-4(-3)+3}{(-3+1)(-3+2)}=\frac{45+12+3}{2}=\frac{60}{2}=30$
Realizado por: Juan Daniel Rivera Bautista (discusión) 02:50 3 jul 2015 (CDT)
Ejercicio 12
Utilizar (1), (2) o (4) para encontrar el residuo de cada polo de la función dada
Procedimiento
$f\left(z\right)=\frac{2z-1}{\left(z-1\right)^{4}\left(z+3\right)}$
Usamos para el polo simple z+3
$Res\left(f\left(z\right),z_{0}\right)=\underset{z\rightarrow z_{0}}{lim}\left(z-z_{0}\right)f\left(z\right)$
Residuos
$Res\left(f\left(z\right),-3\right)=\underset{z\rightarrow-3}{lim}\left(z+3\right)f\left(z\right)=\underset{z\rightarrow-3}{lim}\frac{2z-1}{\left(z-1\right)^{4}}=-\frac{7}{256}$
Para el polo de orden cuatro usaremos:
$Res\left(f\left(z\right),1\right)=\frac{1}{3!}\underset{z\rightarrow1}{lim}\frac{d^{3}}{dz^{3}}\left[\left(z-1\right)^{4}f\left(z\right)\right]=\frac{1}{3!}\underset{z\rightarrow1}{lim}\frac{d^{3}}{dz^{3}}\left(\frac{2z-1}{z+3}\right)$
Tenemos que
$\frac{d^{3}}{dz^{3}}=\frac{42}{\left(z+3\right)^{4}}$
Entonces tenemos que:
Residuos
$Res\left(f\left(z\right),1\right)=\frac{1}{6}\underset{z\rightarrow1}{lim}\frac{42}{\left(z+3\right)^{4}}=\frac{42}{1536}=\frac{7}{256}$
Resuelto por Luis Enrique Martínez Valverde (discusión) 23:34 3 jul 2015 (CDT)
Ejercicio 13
Encontrar el residuo en cada polo de la función dada.
$f(z)=\frac{\cos z}{z^{2}(z-\pi)^{3}}$
Procedimiento
si $f$ tiene un polo de orden $n$ en $z=z_{0}$, entonces,
$Res(f(z),z_{0})=\frac{1}{(n-1)!}\lim_{z\rightarrow z_{0}}\frac{d^{n-1}}{dz^{n-1}}\left[(z-z_{0})^{n}f(z)\right]$
encuentre el residuo en cada polo de la función dada.
$f(z)=\frac{\cos z}{z^{2}(z-\pi)^{3}}$
como podemos ver la función $f(z)=\frac{\cos z}{z^{2}(z-\pi)^{3}}$ tiene un polo de orden 2 en $z=0$ y uno de orden 3 en $z=\pi$
usando el teorema para $z_{0}=0,\;y\;n=2$
$Res(f(z),z_{0}=0)=\frac{1}{(2-1)!}\lim_{z\rightarrow0}\frac{d}{dz}\left[(z-0)^{2}\frac{\cos z}{z^{2}(z-\pi)^{3}}\right]=\lim_{z\rightarrow0}\frac{d}{dz}\left[z^{2}\frac{\cos z}{z^{2}(z-\pi)^{3}}\right]=$
$\lim_{z\rightarrow0}\frac{d}{dz}\left[\frac{\cos z}{(z-\pi)^{3}}\right]=\lim_{z\rightarrow0}\frac{-\sin z(z-\pi)^{3}-3\cos z(z-\pi)^{2}}{(z-\pi)^{6}}=\lim_{z\rightarrow0}\frac{-\sin z(z-\pi)-3\cos z}{(z-\pi)^{4}}=\frac{-3}{(-\pi)^{4}}=\frac{-3}{\pi{}^{4}}$
ahora para $z_{0}=\pi,\;y\;n=3$
$Res(f(z),z_{0}=\pi)=\frac{1}{(3-1)!}\lim_{z\rightarrow\pi}\frac{d^{2}}{dz^{2}}\left[(z-\pi)^{3}\frac{\cos z}{z^{2}(z-\pi)^{3}}\right]=\frac{1}{2}\lim_{z\rightarrow\pi}\frac{d^{2}}{dz^{2}}\left[\frac{\cos z}{z^{2}}\right]=$
$=\frac{1}{2}\lim_{z\rightarrow\pi}\frac{d}{dz}\left[\frac{-\sin z*z^{2}-2z\cos z}{z^{4}}\right]=\frac{1}{2}\lim_{z\rightarrow\pi}\frac{d}{dz}\left[\frac{-\sin z*z-2\cos z}{z^{3}}\right]$
$=\frac{1}{2}\lim_{z\rightarrow\pi}\frac{\left(-\sin z-\cos z*z+2\sin z\right)z^{3}-3z^{2}\left(-\sin z*z-2\cos z\right)}{z^{6}}=\frac{1}{2}\lim_{z\rightarrow\pi}\frac{\left(-\sin z-\cos z*z+2\sin z\right)z^{3}-3z^{2}\left(-\sin z*z-2\cos z\right)}{z^{6}}=$
$=\frac{1}{2}\frac{\pi*\pi^{3}-3\pi^{2}(2)}{\pi^{6}}=\frac{\pi^{2}(\pi^{2}-6)}{2\pi^{6}}=\frac{(\pi^{2}-6)}{2\pi^{4}}$
así
Residuos
$Res(f(z),z_{0}=0)=\frac{-3}{\pi{}^{4}}$
$Res(f(z),z_{0}=\pi)=\frac{(\pi^{2}-6)}{2\pi^{4}}$
como se quería.
Realizado por: Francisco Medina Albino (discusión) 18:14 3 jul 2015 (CDT)
Ejercicio 14
Encuentre el residuo en cada polo de la función
$f(z)={\displaystyle \frac{e^{z}}{e^{z}-1}}$
Procedimiento
Analizando el denominador:
$e^{z}-1\neq 0$
$e^{z}\neq 1$
Esto sucede cuando
$z=i2\pi n$ con $n=\pm0,\pm1,\pm2$
Entonces $z=i2\pi n$ es un polo simple de la función $f(z)$
Reescribiendo $f(z)=\frac{e^{z}}{z-2in\pi}$
\[ Res(f(z),i2\pi n) = \lim_{z\rightarrow i2\pi n}(z-i2\pi n)\frac{e^{z}}{z-2in\pi}\]
Conclusión
\[ Res(f(z),i2\pi n) = e^{2ni\pi}\]
cuando $n=\pm0,\pm1,\pm2$
Re elaborado por Manuel Rodríguez
Ejercicio 15
Encontrar el residuo en cada polo de la función dada.
$f(z)=sec z$
Procedimiento
Utilizando la ecuación:
\[
Res(f(z),z_{0}) = \lim_{z\rightarrow z_0}(z-z_{0})f(z)\]
Determinamos los polos de la función:
$f(z) = sec z = \frac{1}{cos z} $
De esto podemos concluir, que la función tiene polos simples en los puntos donde $cos z = 0$.
$(2n+1)\frac{\pi}{2}$ con $n=0,\pm1,\pm2,...$
Conclusión
Por lo tanto:
$Res(f(z), (2n+1)\frac{\pi}{2}) = (-1)^{n+1}$
Realizado por: Nancy Martínez Durán (discusión) 02:58 4 jul 2015 (CDT)
Ejercicio 17
Utilice el teorema del residuo de Cauchy, donde sea apropiado, para evaluar la integral a lo rago del contorno indicado. \[ \oint_C \!\frac{1}{(z-1)(z+2)^2}dz \;\;\;\;\;\;\;(a)\,|z|=\frac{1}{2}\;\;\;(b)\,|z|=\frac{3}{2}\;\;\;(c)\,|z|=3 \]
Inciso a
Para el caso (a), ninguna singularidad (polo) esta dentro del contorno, por lo que:
\[
\oint_{C_a} \!\frac{1}{(z-1)(z+2)^2}dz=0
\]
Inciso b
Para el caso (b), unicamente $P_2 (1)$ esta dentro del contorno, por lo que: \[ \oint_{C_b} \!\frac{1}{(z-1)(z+2)^2}dz=2\pi\, i\, Res(f(z),1) \] \[ Res(f(z),1)=\lim_{z\to 1}{(z-1)\frac{1}{(z-1)(z+2)^2}}=\lim_{z\to 1}{\frac{1}{(z+2)^2}}=\frac{1}{1+2}=\frac{1}{3^2}=\frac{1}{9} \] \[ \oint_{C_b} \!\frac{1}{(z-1)(z+2)^2}dz=2\pi\, i\, Res(f(z),1)=\frac{2\pi\, i}{9} \]
Inciso c
Para el caso (c) ambas singularidades están dntro del contorno, por lo que: \[ \oint_{C_c} \!\frac{1}{(z-1)(z+2)^2}dz=2\pi\, i\, \left[Res(f(z),1)+Res(f(z),-2)\right] \] El primer residuo ya lo conocemos del incisio anterior, pero el segundo, es un polo de orden 2 por lo que se calcula como sigue: \[ Res(f(z),-2)=\lim_{z\to -2}{\frac{d}{dz}\left[(z+2)^2\frac{1}{(z-1)(z+2)^2}\right]}=\lim_{z\to -2}{\frac{d}{dz}\left[\frac{1}{(z-1)}\right]} \] \[ Res(f(z),-2)=\lim_{z\to -2}{-\left[\frac{1}{(z-1)^2}\right]}=-\frac{1}{(-2-1)^2}=-\frac{1}{3^2}=-\frac{1}{9} \] \[ \oint_{C_c} \!\frac{1}{(z-1)(z+2)^2}dz=2\pi\, i\, \left[\frac{1}{9}-\frac{1}{9}\right]=0 \]
Realizado por: Tlacaelel Cruz (discusión) 22:43 30 jun 2015 (CDT)
Ejercicio 21
Utilice el teorema del residuo de Cauchy, para evaluar la integral dada en el contorno dado: $\oint_C \frac{1}{z^2+4z+13}dz$
Sobre el contorno $C:|z-3i|=3$.
Procedimiento
Primero notemos que $z^2+4z+13=(z-(-2+3i))(z-(-2-3i))$. Con $(z_1=-2+3i) \wedge (z_2=-2-3i)$
Vea que $z_1=-2+3i$ satisface $|z-3i|<3$ y que $z_2=-2-3i$ no satisface $|z-3i|<3$, (pues $:|-2-3i-3i|=\sqrt{4+36}=2\sqrt{10}>3$).
Por lo anterior$\frac{1}{z^2+4z+13}$ es analítica en todos los puntos de $|z-3i|=3$, salvo $z_1=-2+3i$
Entonces, por el teorema 6.16:
$\oint_C \frac{1}{z^2+4z+13}dz=(2\pi i) res f(-2+3i)=(2\pi i) \lim_{z\to {z_1} } (\frac{1}{(z-(-2+3i))(z-(-2-3i))})(z-(-2+3i))=(2\pi i)\lim_{z\to {z_1} } \frac{1}{(z-(-2-3i))}=$
$=(2\pi i)\frac{1}{(-2+3i-(-2-3i))}=(2\pi i)\frac{1}{(-2+3i-(-2-3i))}=(2\pi i)\frac{1}{6i}=\frac{\pi}{3}.$
Conclusión
Por lo tanto: $\oint_C \frac{1}{z^2+4z+13}dz=\frac{\pi}{3}$,
en donde $C:|z-3i|=3$
Realizado por: Alan Daniel Barrón Posadas (discusión) 22:49 3 jul 2015 (CDT)
Ejercicio 22
En los problemas 21 a 34 , utilice el teorema de los residuos de Cauchy para evaluar la propuesta integral a lo largo del contorno indicado.
\begin{equation*} \oint _C\frac{1}{z^{3}\left(z-1\right)^{4}}dz \end{equation*}
en el contorno
$C:|z-2|=\frac{3}{2}$.
Procedimiento
Hay 2 polos, un polo de orden 3 en $z=0$ y de orden 4 $z=1$
Usando:
$Res(f(z),z_{0})=\frac{1}{(n-1)!}\lim_{z\rightarrow z_{0}}\frac{d^{n-1}}{dz^{n-1}}\left[(z-z_{0})^{n}f(z)\right]$
Para $z_0=0$ y $n=3$
$Res(f(z),0)=\frac{1}{(3-1)!}\lim_{z\rightarrow 0}\frac{d^{2}}{dz^{2}}\left[ \frac{1}{z^{3}\left(z-1\right)^{4}} \right]$
$Res(f(z),0)=\frac{1}{(2)!}\lim_{z\rightarrow 0}\frac{d^{2}}{dz^{2}}\left[ \frac{1}{\left(z-1\right)^{4}} \right]$
$Res(f(z),0)=\frac{1}{(2)!}\lim_{z\rightarrow 0} \frac{20}{\left (z-1 \right )^{6}}$
$Res(f(z),0)=\frac{20}{2}=10$
Para $z_0=1$ y $n=4$
$Res(f(z),1)=\frac{1}{(4-1)!}\lim_{z\rightarrow 1}\frac{d^{4-1}}{dz^{4-1}}\left[(z-1)^{4}\frac{1}{z^{3}\left(z-1\right)^{4}}\right]$
$Res(f(z),1)=\frac{1}{(2*3)}\lim_{z\rightarrow 1}\frac{d^{3}}{dz^{3}}\left[\frac{1}{z^{3}}\right]$
Haciendo las derivadas correspondientes:
$Res(f(z),1)=\frac{1}{(2*3)}\lim_{z\rightarrow 1}\frac{-60}{z^{6}}=-\frac{60}{6}= -10$
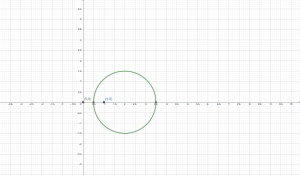
En la imagen se ve, que solo el polo $z=1$ esta dentro del contorno
Conclusión
Por lo que el valor de la integral esta dado por:
\begin{equation*} \oint _C\frac{1}{z^{3}\left(z-1\right)^{4}}dz = 2\pi i \left [Res(f(z),1) \right ] = -20 \pi i \end{equation*}
Re elaborado por Manuel Rodríguez
Ejercicio 23
Utilice el teorema de Cauchy del residuo para evaluar la integral a lo largo del contorno indicado
$\oint { \frac { z }{ { z }^{ 4 }-1 } } dz\quad \quad C:\left| z \right| =2$
Procedimiento
Del denominador ${ z }^{ 4 }-1=(z-1)(z+1)(z-i)(z+i),\quad $ tenemos polos simples de $n=1$ en $z=1,-1,i,-i$
Por lo tanto
$Re(f(z),1)=\lim _{ z\rightarrow 1 }{ \left[ (z-1)\frac { z }{ (z-1)(z+1)(z-i)(z+i) } \right] = } \lim _{ z\rightarrow 1 }{ \left[ \frac { z }{ (z+1)(z-i)(z+i) } \right] = } \frac { 1 }{ 4 } $
y para
$Re(f(z),-1)=\lim _{ z\rightarrow -1 }{ \left[ (z+1)\frac { z }{ (z-1)(z+1)(z-i)(z+i) } \right] = } \lim _{ z\rightarrow -1 }{ \left[ \frac { z }{ (z-1)(z-i)(z+i) } \right] = } \frac { 1 }{ 4 } $
ahora para
$Re(f(z),i)=\lim _{ z\rightarrow i }{ \left[ (z-i)\frac { z }{ (z-1)(z+1)(z-i)(z+i) } \right] = } \lim _{ z\rightarrow i }{ \left[ \frac { z }{ (z+1)(z-1)(z+i) } \right] = } \frac {- 1 }{ 4 } $
para finalizar
$Re(f(z),-i)=\lim _{ z\rightarrow -i }{ \left[ (z+i)\frac { z }{ (z-1)(z+1)(z-i)(z+i) } \right] = } \lim _{ z\rightarrow -i }{ \left[ \frac { z }{ (z+1)(z-1)(z-i) } \right] = } \frac {- 1 }{ 4 } $
Conclusión
Entonces sabemos que la integral quedaría de la siguiente manera
$\oint { \frac { z }{ { z }^{ 4 }-1 } dz\quad =\quad 2\pi i\left[ Re(f(z),1)+Re(f(z),-1)+Re(f(z),i)+Re(f(z),-i) \right] \quad =\quad 2\pi i\left[ \frac { 1 }{ 4 } +\frac { 1 }{ 4 } -\frac { 1 }{ 4 } -\frac { 1 }{ 4 } \right] } $
$\oint { \frac { z }{ { z }^{ 4 }-1 } dz\quad =\quad 0 } $
Realizado por: Miguel Medina Armendariz (discusión) 22:59 3 jul 2015 (CDT)
Forma alternativa
Utilice el teorema de Cauchy del residuo para elevar la integral a lo largo del contorno indicado.
- ,
Procedimiento
Factorizamos el denominador y se tiene:
- ya que:
- tiene 4 polos simples, y dado que todos estos puntos estan dentro del contorno C,
el teorema del residuo de Cauchy nos dice:
se deduce que:
Entonces tenemos
Solución
Sustituyendo en (1) se tiene finalmente que
Elaborado por Ricardo García Hernandez Ricardo Garcia Hernandez (discusión) 23:23 3 jul 2015 (CDT)
Ejercicio 25
Use el teorema del residuo de Cauchy´s para evaluar la integral dada a lo largo del contorno indicado
$\oint \frac{ze^z}{z^2 - 1} dz$ , $C: |z| = 2$
Procedimiento
Para conocer el valor de la integral a lo largo del contorno sabemos que tenemos el Teorema del residuo:
$\oint _c f)(z) dz = 2\pi i \sum_{k=1} ^{n} a_1$
Donde $a_1$ es el residuo de la integral, y para calcular este podemos hacer uso del teorema:
$a_1 = \lim_{z \rightarrow z_0} [(z - z_0) f(z)]$
Para esta función tenemos $z_0 = 1$ y $z_0 = -1$
Los dos cero están dentro del contorno por lo que podemos calcular los dos residuos
Aplicando el teorema con $z_0 = 1$
$\lim_{z \rightarrow 1} [(z - 1) \frac{ze^z}{z^2 - 1}] = \lim_{z \rightarrow 1} [(z -1) \frac{ze^z}{(z + 1) (z - 1)}] = \lim_{z \rightarrow 1} [\frac{ze^z}{(z + 1)}] = \frac{e}{2}$
Aplicando el teorema con $z_0 = -1$
$\lim_{z \rightarrow -1} [(z + 1) \frac{ze^z}{z^2 - 1}] = \lim_{z \rightarrow -1} [(z + 1) \frac{ze^z}{(z +1) (z - 1)}] = \lim_{z \rightarrow -1} [\frac{ze^z}{z - 1}] = \frac{e^{-1}}{2} = \frac{1}{2e}$
Conclusión
Regresando al teorema del residuo y sustituyendo los residuos tenemos:
$\int_{ |z| = 2} \frac{ze^z}{z^2 - 1} dz = 2\pi i (\frac{e}{2} + \frac{1}{2e})=2\pi i \cosh 1$
Y esta es nuestra integral evaluada.
Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 23:50 2 jul 2015 (CDT)
Ejercicio 26
Utilice el teorema de Cauchy del residuo para evaluar la integral a lo largo del contorno indicado. de nuestra integral observamos que existen dos ceros en , como podemos observar ambas se encuentran dentro de nuestro contorno, así pues procedemos a calcular los residuos correspondientes debido a que por el teorema:
Procedimiento
Para
Por otro lado para por ser de orden 2 tenemos:
Conclusión
Por lo cual:
Realizado por:Anahi Limas (discusión) 22:33 3 jul 2015 (CDT)
Ejercicio 30
Utilizar el teorema de Cauchy del residuo para evaluar la integral $\oint_C\dfrac{2z-1}{z^2(z^3+1)}dz$, donde $C$ es el rectángulo definido por $x=-2$, $x=1$, $y=-\frac{1}{2}$, $y=1$
Procedimiento
Se tiene que $z=0$ es un polo de orden 2, por lo que su residuo es
$Res(f(z),z_1)=\lim_{z\longrightarrow 0}\dfrac{d}{dz}[z^2\dfrac{2z-1}{z^2(z^3+1)}]=\lim_{z\longrightarrow 0}\dfrac{d}{dz}[\dfrac{2z-1}{(z^3+1)}]$
De la regla del cociente tenemos
$Res(f(z),z_1)=\lim_{z\longrightarrow 0}[\dfrac{(z^3+1)2-(2z-1)3z^2}{(z^3+1)^2}]=2$
El polinomio $z^3+1$ se puede factorizar como $(z-z_2)(z-z_3)(z-z_4)$ donde $z_2$, $z_3$ y $z_4$ son los tres ceros distintos de la ecuación $z^3+1=0$ (o lo que es lo mismo, los tres ceros cúbicos de -1), por lo que del teorema del polo de orden $n$ se deduce que la función $\dfrac{2z-1}{z^2(z^3+1)}$ tiene tres polos simples cada uno en $z_2$, $z_3$ y $z_4$. De la fórmula para las $n$ raíces de un número complejo
$w_k=^n\sqrt{r}[\cos \dfrac{\theta +2k\pi}{n}+i\sin \dfrac{\theta +2k\pi}{n}]$
Con $z=-1$, $|z|=r=1$, $n=3$ y $\theta = \pi$, buscamos los valores de las $n$ raices
$z_2=\cos \dfrac{\pi}{3}+i\sin \dfrac{\pi}{3}=\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$
$z_3=\cos \dfrac{\pi +2\pi}{3}+i\sin \dfrac{\pi +2\pi}{3}=\cos \dfrac{3\pi}{3}+i\sin \dfrac{3\pi}{3}=\cos \pi+i\sin \pi=-1$
$z_4=\cos \dfrac{\pi +4\pi}{3}+i\sin \dfrac{\pi +4\pi}{3}=\cos \dfrac{5\pi}{3}+i\sin \dfrac{5\pi}{3}=\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}$
Con lo anterior tenemos que $z_2=\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$, $z_3=-1$ y $z_4=\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}$ y notamos que la raíz $z_4$ está fuera del rectángulo dado por el problema, por lo que sólo se consideran $z_2$ y $z_3$. De la fórmula
$Res(f(z),z_0)=\dfrac{g(z_0)}{h'(z_0)}$
obtenemos los residuos considerando $g(z)=\dfrac{2z-1}{z^2}$, $h(z)=z^3+1$ y $h'(z)=3z^2$, así
$Res(f(z),z_2)=\dfrac{2(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2})-1}{(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2})^2}\dfrac{1}{3(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2})^2}=\dfrac{1+i\sqrt{3}-1}{-\dfrac{2}{4}+i\dfrac{\sqrt{3}}{2}}\dfrac{1}{3(-\dfrac{2}{4}+i\dfrac{\sqrt{3}}{2})}=\dfrac{i\sqrt{3}}{3(-\dfrac{2}{4}+i\dfrac{\sqrt{3}}{2})^2}=\dfrac{i\sqrt{3}}{3(-0.5-i\dfrac{\sqrt{3}}{2})}=\dfrac{i\sqrt{3}}{-1.5-i\dfrac{3\sqrt{3}}{2}}$
$Res(f(z),z_2)=\dfrac{i\sqrt{3}}{-1.5-i\dfrac{3\sqrt{3}}{2}}\dfrac{-1.5+i\dfrac{3\sqrt{3}}{2}}{-1.5+i\dfrac{3\sqrt{3}}{2}}=\dfrac{-\frac{9}{2}-i2.6}{\frac{9}{4}-\frac{27}{4}}=1+i0.577$
$Res(f(z),z_2)=1+i0.577$
$Res(f(z),z_3)=\dfrac{2(-1)-1}{(-1)^2}\dfrac{1}{3(-1)^2}=\dfrac{-3}{3}=-1$
$Res(f(z),z_3)=-1$
Conclusión
Del Teorema del residuo de Cauchy se tiene
$\oint_Cf(z)=2\pi i[(1+i0.577)-1]=2\pi i(i0.577)=-3.625$
Realizado por: Oscar Javier Gutierrez Varela (discusión) 18:57 2 jul 2015 (CDT)




![f(z)=\frac{1}{(z^{2}-2z+2)^{2}}=\frac{1}{\left[(z-(1+i))(z-(1-i))\right]^{2}}=\frac{1}{\left[(z-z_{1})(z-z_{2})\right]^{2}}=\frac{1}{(z-z_{1})^{2}(z-z_{2})^{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e6aec17071901b42ee941af3f8632c00a0648543)
![Res(f(z),z_{0})=\frac{1}{(n-1)\text{!}}\underset{z\rightarrow z_{0}}{l\acute{\imath}m}\frac{d^{n-1}}{dz^{n-1}}\left[(z-z_{0})^{n}f(z)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c52b3a4c66aab43d0a019037fe29a4be27c4799b)
![Res(f(z),z_{1})=\frac{1}{(2-1)\text{!}}\underset{z\rightarrow z_{1}}{l\acute{\imath}m}\frac{d^{1}}{dz^{1}}\left[(z-z_{1})^{2}\frac{1}{(z-z_{1})^{2}(z-z_{2})^{2}}\right]=\underset{z\rightarrow z_{1}}{l\acute{\imath}m}\frac{d}{dz}\left[\frac{1}{(z-z_{2})^{2}}\right]=\underset{z\rightarrow z_{1}}{l\acute{\imath}m}\left[-\frac{2}{(z-z_{2})^{3}}\right]=-\frac{2}{(z_{1}-z_{2})^{3}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3387e658b7897c15f5a47d20bd0299810a6cb5a1)
![Res(f(z),z_{2})=-\frac{2}{(z_{1}-z_{2})^{3}}=-\frac{2}{\left[(1+i)-(1-i)\right]^{3}}=-\frac{2}{\left[2i\right]^{3}}=-\frac{1}{4i^{3}}=\frac{1}{4i}=-\frac{i}{4}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1a83fcb52ec11af6bbfadacb42e9b3239a63a050)
![Res(f(z),z_{2})=\frac{1}{(2-1)\text{!}}\underset{z\rightarrow z_{2}}{l\acute{\imath}m}\frac{d^{1}}{dz^{1}}\left[(z-z_{2})^{2}\frac{1}{(z-z_{1})^{2}(z-z_{2})^{2}}\right]=\underset{z\rightarrow z_{2}}{l\acute{\imath}m}\frac{d}{dz}\left[\frac{1}{(z-z_{1})^{2}}\right]=\underset{z\rightarrow z_{2}}{l\acute{\imath}m}\left[-\frac{2}{(z-z_{1})^{3}}\right]=-\frac{2}{(z_{2}-z_{1})^{3}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3e55a48d846f1171acd5cde0492380bb553c5a4e)
![Res(f(z),z_{2})=-\frac{2}{(z_{2}-z_{1})^{3}}=-\frac{2}{\left[(1-i)-(1+i)\right]^{3}}=-\frac{2}{\left[-2i\right]^{3}}=\frac{1}{4i^{3}}=-\frac{1}{4i}=\frac{i}{4}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bd3c7aaf5e91cd9f2bcf89bd14a4a75ddd7965a1)




![\oint_{c}f(z)dz=
2\pi i\stackrel[k=1]{n}{\sum}Res(f(z),z_{k})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/14c315d8990b276906e0fb7553db0779a93030e3)
![\oint_{c}\frac{z}{(z^{2}-1)(z^{2}+1)}dz=
2\pi i\left[Res(f(z),+1)+Res(f(z),-1)+Res(f(z),+i)+Res(f(z),-i)\right]...(1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d35d2ae712a7867b5fc268e187968e10e94b5c30)
![Res(f(z),+1)=\underset{z\rightarrow+1}{l\acute{\imath}m}(z^{2}-1)f(z)=\underset{z\rightarrow+1}{l\acute{\imath}m}(z^{2}-1)\left[\frac{z}{(z^{2}-1)(z^{2}+1)}\right]=\underset{z\rightarrow+1}{l\acute{\imath}m}\frac{z}{z^{2}+1}=\frac{1}{(1)^{2}+1}=\frac{1}{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3961fe2cca06732bb0259fd744f9c01ec4e49e36)
![Res(f(z),-1)=\underset{z\rightarrow-1}{l\acute{\imath}m}(z^{2}-1)f(z)=\underset{z\rightarrow-1}{l\acute{\imath}m}(z^{2}-1)\left[\frac{z}{(z^{2}-1)(z^{2}+1)}\right]=\underset{z\rightarrow-1}{l\acute{\imath}m}\frac{z}{z^{2}+1}=\frac{-1}{(1)^{2}+1}=-\frac{1}{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ec0cc9ca5485ae5b2ff76672b40bccb2643b1695)
![Res(f(z),+i)=\underset{z\rightarrow+i}{l\acute{\imath}m}(z^{2}+1)f(z)=\underset{z\rightarrow+i}{l\acute{\imath}m}(z^{2}+1)\left[\frac{z}{(z^{2}-1)(z^{2}+1)}\right]=\underset{z\rightarrow+i}{l\acute{\imath}m}\frac{z}{z^{2}-1}=\frac{i}{-1-1}=-\frac{i}{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/036f94113e7de8d4c0ce0e72b941b6a6e8623f46)
![Res(f(z),-i)=\underset{z\rightarrow-i}{l\acute{\imath}m}(z^{2}+1)f(z)=\underset{z\rightarrow-i}{l\acute{\imath}m}(z^{2}+1)\left[\frac{z}{(z^{2}-1)(z^{2}+1)}\right]=\underset{z\rightarrow-i}{l\acute{\imath}m}\frac{z}{z^{2}-1}=\frac{-i}{-1-1}=\frac{i}{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f00c94c3454e276b70efb2333c672c2a6ecec980)
![\oint_{c}=\frac{z}{(z^{2}-1)(z^{2}+1)}dz=
2\pi i\left[Res(f(z),1)+Res(f(z),-1)+Res(f(z),i)+Res(f(z),-i)\right]
=\frac{1}{2}-\frac{1}{2}-\frac{i}{2}+\frac{i}{2}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f91f15565722ad09d86b2f8e3758b5a2d69641ce)






![Res(f(z),z_0=0)= \frac{1}{2-1}!\lim_{z \rightarrow 0}\frac{d}{dz} [z^2\frac{e^{z}}{z^2(z+2)}]=lim_{z \rightarrow 0} [\frac{e^{z}(z+2)-e^{z}}{(z+2)^2}]= lim_{z \rightarrow 0} \frac{e^{z}(z+1)}{z^2+4z+4}=\frac{1}{4}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6c979a5432cbebb2c22df1d6be00598783ad04eb)
![\oint_c \frac{e^{z}}{z^3+2z^2} dz = 2i\pi[Res(f(z),z_0=-2)+Res(f(z),z_0=0)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0f11959b075028e0ed8c6e1bb0c25bf0e820ea0a)
