Compleja:Zill-Cap6.6.2
Ejercicios del capítulo 6, sección 6.2 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 6.6.2
Ejercicio 1
Evalúe el valor Principal de Cauchy de la integrañ impropia $\int_{-\infty}^{\infty} \! \frac{dx}{x^2-2x+2}$.
Procedimiento
\[ \int_{-\infty}^{\infty} \! \frac{dx}{x^2-2x+2}=\lim_{R\to -\infty} \int_{R}^{0} \! \frac{dx}{x^2-2x+2}+\lim_{R \to \infty} \int_{0}^{R} \! \frac{dx}{x^2-2x+2}=\lim_{R\to -\infty} \int_{R}^{0} \! \frac{dx}{(x-1)^2+1}+\lim_{R \to \infty} \int_{0}^{R} \! \frac{dx}{(x-1)^2+1} \] Se hace $u=x-1$ y $du=dx$ \[ \int_{-\infty}^{\infty} \! \frac{dx}{x^2-2x+2}=\lim_{R\to -\infty} \int_{R-1}^{-1} \! \frac{du}{(u)^2+1}+\lim_{R \to \infty} \int_{-1}^{R-1} \! \frac{du}{(u)^2+1}=\lim_{R\to -\infty} (\arctan {(-1)}-\arctan {(R-1)}) +\lim_{R \to \infty} (\arctan {(R-1)}-\arctan {(-1)}) \] \[ =-\frac{\pi}{4}-\lim_{R\to -\infty} \arctan {(R-1)}+\lim_{R\to \infty} \arctan {(R-1)}+\frac{\pi}{4}=-\lim_{R\to -\infty} \arctan {(R-1)}+\lim_{R\to \infty} \arctan {(R-1)}=+\frac{\pi}{2}+\frac{\pi}{2}=\pi \]
Conclusion
\[ \int_{-\infty}^{\infty} \! \frac{dx}{x^2-2x+2}=\pi \]
Realizado por: Tlacaelel Cruz (discusión) 00:34 4 jul 2015 (CDT)
Ejercicio 2
Evalúe el valor Principal de Cauchy de la integral impropia
$\int_{-\infty}^{\infty}\frac{1}{x^{2}-6x+25}dx$ = I
Procedimiento
Para realizar la integral se necesita hacer varios pasos.
Primero tomamos el limite de integrales reales impropias
I= $\underset{R\rightarrow-\infty}{lim}\int_{R}^{0}\frac{1}{x^{2}-6x+25}dx+\underset{R\rightarrow\infty}{lim}\int_{0}^{R}\frac{1}{x^{2}-6x+25}$
Ahora sustituimos el denominador como sigue:
$x^{2}-6x+25=\left(x-3\right)^{2}+16$
Entonces sistituimos en I
I=$\underset{R\rightarrow-\infty}{lim}\int_{R}^{0}\frac{dx}{\left(x-3\right)^{2}+16}+\underset{R\rightarrow\infty}{lim}\int_{0}^{R}\frac{dx}{\left(x+3\right)^{2}+16}$
Ahora hacemos cambio de variable y sustituimos en la integral
$u=x-3\Rightarrow du=dx$
I=$\underset{R\rightarrow-\infty}{lim}\int_{R-3}^{-3}\frac{du}{u^{2}+16}+\underset{R\rightarrow\infty}{lim}\int_{-3}^{R-3}\frac{du}{u^{2}+16}$...II
Ahora resolvemos la integral por sustitución trigonometrica, para fines practicos se van a hacer sin limites de integración, al final regresaremos a la variable original X
$\int\frac{du}{u^{2}+16}$ ....III
De aqui sabemos que
$tan\theta=\frac{u}{4}\Rightarrow u=4tan\theta\Longrightarrow du=4sec^{2}\theta d\theta$
Ademas
$\theta=arctan\frac{u}{4}$ ...(1)
$sec^{2}\theta=tan^{2}\theta1$ ...(2)
Sustituyendo valores en la integral III y en su momento usando (1) y (2) y regresando a las ariables originales tenemos que:
$\int\frac{4sec^{2}\theta d\theta}{\left(4tan\theta\right)^{2}+16}=\int\frac{4sec^{2}\theta d\theta}{16tan^{2}\theta+16}=\frac{4}{16}\int\frac{sec^{2}\theta d\theta}{tan^{2}\theta+1}=\frac{1}{4}\int d\theta=\frac{1}{4}\theta=\frac{1}{4}arctn\frac{u}{4}=\frac{1}{4}arctan\frac{x-3}{4}$
Teniendo en cuenta los limites de integración de II
Ahora sustituyendo en I tenemos que:
I=$\underset{R\rightarrow-\infty}{lim}\left[\frac{1}{4}arctan-\frac{3}{4}-\frac{1}{4}arctan\frac{R-3}{4}\right]+\underset{R\rightarrow\infty}{lim}\left[\frac{1}{4}arctan\frac{R-3}{4}-\frac{1}{4}arctan-\frac{3}{4}\right]$
Por lo que
I=$\underset{R\rightarrow-\infty}{lim}\left[\frac{1}{4}-\frac{1}{4}arctan\frac{R-3}{4}\right]+\underset{R\rightarrow\infty}{lim}\left[\frac{1}{4}arctan\frac{R-3}{4}-\frac{1}{4}\right]$
Conclusión
Aplicando los limites tenemos
I=$\frac{1}{4}-\frac{1}{4}\left(-\frac{\pi}{2}\right)+\frac{1}{4}\frac{\pi}{2}-\frac{1}{4}=\frac{\pi}{4}$
Resuelto por Luis Enrique Martínez Valverde (discusión) 14:09 4 jul 2015 (CDT)
Ejercicio 3(17)
Evalue el valor principal de Cauchy de la integral impropia
\[ {\displaystyle \int_{-\infty}^{\infty}}{\displaystyle \frac{1}{(x^{2}+4)^{2}}dx} \]
Procedimiento
Sabemos que
\[ V.P.{\displaystyle \int_{-\infty}^{\infty}f(x)dx={\displaystyle \lim_{z\rightarrow z_{0}}{\displaystyle \int_{-R}^{R}f(x)dx=2\pi i{\displaystyle \sum_{k=1}^{n}Res\left(f(z),z_{k}\right)}}}} \]
Sabemos tambien que para poder hacer la integracion, es ncecesario
tener una superficie cerrada, pero existe un teorema que dice que
si la potencia del denominador es dos veces mas grande que la del
numerador, una parte de la integral tiende a cero, en simbolos
\[ \oint f(z)dz={\displaystyle \int_{C_{R}}f(z)dz+{\displaystyle \int_{-R}^{R}f(x)dx=2\pi i{\displaystyle \sum_{k=1}^{n}Res(f(z),z_{k})}}} \]
Donde ${\displaystyle \int_{C_{R}}f(z)dz\rightarrow0}$
Asi pues tenemos que
\[ {\displaystyle \oint}{\displaystyle \frac{1}{\left [(z+2i)(z-2i) \right ]^{2}}dz}=2\pi i{\displaystyle \sum_{k=1}^{n}Res\left(f(z),z_{k}\right)} \]
Podemos ver que hay dos polos de orden 2.
Usando
\[ Res\left(f(z),z_{0}\right)={\displaystyle \frac{1}{\left(n-1\right)!}{\displaystyle \lim_{z\rightarrow z_{0}}{\displaystyle \frac{d^{n-1}}{dz^{n-1}}\left[\left(z-z_{0}\right)^{n}f(z)\right]}}} \]
con $n=2$
Para $z=2i$
\[ Res\left(f(z),2i\right)={\displaystyle \lim_{z\rightarrow2i}{\displaystyle \frac{d}{dz}\left[\left(z-2i\right)^{2}{\displaystyle \frac{1}{\left(z+2i\right)^{2}\left(z-2\right)^{2}}}\right]}={\displaystyle \lim_{z\rightarrow2i}{\displaystyle \frac{d}{dz}\left[{\displaystyle \frac{1}{\left(z+2i\right)^{2}}}\right]={\displaystyle \lim_{z\rightarrow2i}\left[{\displaystyle \frac{-2}{\left(z+2i\right)^{3}}}\right]={\displaystyle -\frac{i}{32}}}}}} \]
Para $z=-2i$
\[ Res\left(f(z),2i\right)={\displaystyle \lim_{z\rightarrow-2i}{\displaystyle \frac{d}{dz}\left[\left(z+2i\right)^{2}{\displaystyle \frac{1}{\left(z+2i\right)^{2}\left(z-2\right)^{2}}}\right]}={\displaystyle \lim_{z\rightarrow-2i}{\displaystyle \frac{d}{dz}\left[{\displaystyle \frac{1}{\left(z-2i\right)^{2}}}\right]={\displaystyle \lim_{z\rightarrow-2i}\left[{\displaystyle \frac{-2}{\left(z+2i\right)^{3}}}\right]={\displaystyle \frac{i}{32}}}}}} \]
NOTA: Al hacer el semicírculo para el valor principal de Cauchy, solo se toma los residuos en la parte positiva del eje imaginario ( aquí 2i) -2i no se toma.
\[ \lim_{z\rightarrow z_{0}}{\displaystyle \int_{-R}^{R}f(x)dx=2\pi i{\displaystyle \sum_{k=1}^{n}Res\left(f(z),z_{k}\right)}}=2\pi i\left({\displaystyle \frac{-i}{32}}\right)=\frac{\pi}{16} \]
Conclusión
\[ \therefore{\displaystyle V.P.\int_{-\infty}^{\infty}}{\displaystyle \frac{1}{(x^{2}+4)^{2}}dx}=\frac{\pi}{16} \]
Realizado por: Jose Emmanuel Flores Calderón (discusión) 02:55 4 jul 2015 (CDT)
Ejercicio 4 (18)
Evaluar el valor principal de Cauchy de la integral impropia $\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx$
Procedimiento
Sol. Dividamos la integral en dos partes para evaluarlas como integrales impropias.
$\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=\int_{-\infty}^{0}\dfrac{x^2}{(x^2+1)^2}dx+\int_{0}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx$
$\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=lím_{R\longrightarrow -\infty}\int_{R}^{0}\dfrac{x^2}{(x^2+1)^2}dx+lím_{R\longrightarrow \infty}\int_{0}^{R}\dfrac{x^2}{(x^2+1)^2}dx$
Resolvamos primero la integral y después aplicamos límite. Sea $x=\tan \theta$, $dx=\sec^2\theta d\theta$, sustituimos
$\int \dfrac{x^2}{(x^2+1)^2}dx=\int \dfrac{\tan^2\theta\sec^2\theta d\theta}{(\tan^2\theta +1)^2}=\int\dfrac{\tan^2\theta\sec^2\theta d\theta}{\sec^4\theta}=\int\dfrac{\tan^2\theta d\theta}{\sec^2\theta}$
Con $\tan^2\theta =\dfrac{\sin^2\theta}{\cos^2\theta}$, $\sec^2\theta =\dfrac{1}{\cos^2\theta}$. Sustituimos
$\int \dfrac{x^2}{(x^2+1)^2}dx=\int\dfrac{\dfrac{\sin^2\theta}{\cos^2\theta} d\theta}{\dfrac{1}{\cos^2\theta}}=\int\sin^2\theta d\theta=\frac{1}{2}\int (1-\cos 2\theta)d\theta=\dfrac{\theta}{2}-\dfrac{1}{4}\sin 2\theta$
Volvemos a nuestras variables originales sustituyendo $\theta =\arctan x$ y evaluando límites
$\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=lím_{R\longrightarrow -\infty}[\dfrac{1}{2}\arctan x-\dfrac{1}{4}\sin (2\arctan x)]_R^0+lím_{R\longrightarrow \infty}[\dfrac{1}{2}\arctan x-\dfrac{1}{4}\sin (2\arctan x)]_0^R$
$\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=(\dfrac{1}{2}\arctan 0-\dfrac{1}{4}\sin (2\arctan 0))-lím_{R\longrightarrow -\infty}(\dfrac{1}{2}\arctan R-\dfrac{1}{4}\sin (2\arctan R))+(lím_{R\longrightarrow \infty}(\dfrac{1}{2}\arctan R-\dfrac{1}{4}\sin (2\arctan R))-(\dfrac{1}{2}\arctan 0-\dfrac{1}{4}\sin (2\arctan 0))$
$\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=-(\dfrac{1}{2}\dfrac{-\pi}{2}-\dfrac{1}{4}\sin (-\pi))+(\dfrac{1}{2}\dfrac{\pi}{2}-\dfrac{1}{4}\sin (\pi))=\dfrac{\pi}{4}+\dfrac{\pi}{4}=\dfrac{\pi}{2}$
Conclusión
Por tanto, escribimos
V.P. $\int_{-\infty}^{\infty}\dfrac{x^2}{(x^2+1)^2}dx=\dfrac{\pi}{2}$
Realizado por: Oscar Javier Gutierrez Varela (discusión) 17:53 4 jul 2015 (CDT)
Ejercicio 5(19)
Evalué el valor principal de Cauchy de la integral impropia dada,
Procedimiento
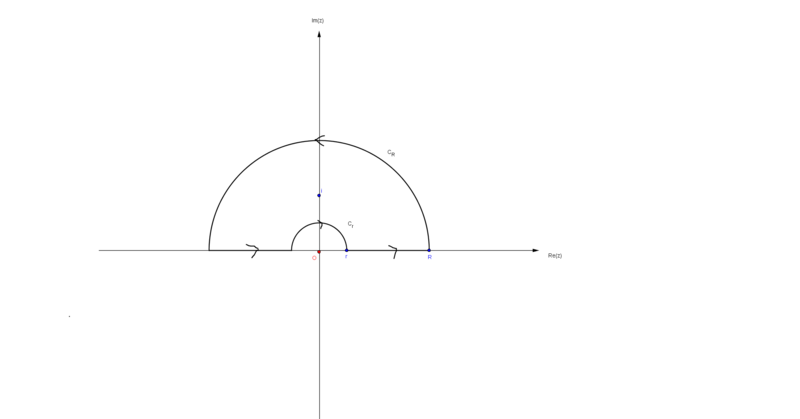
tomamos el contorno cerrado C que contiene el intervalo (-R,R) en el eje "x" y la semicircunferencia de radio Cr de radio R>i, como se observa a continuación
![\int_{-\infty}^{\infty}\frac{1}{(x^{2}+1)^{3}}dx=\underset{z\rightarrow z_{0}}{l\acute{\imath}m}\int_{-R}^{R}f(x)dx=2\pi i\stackrel[k=1]{n}{\sum}Res(f(z),z_{0})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2fc4684452d6fecee5c897e4fa9ae106a2d0dc45)
![\int_{-\infty}^{\infty}\frac{1}{(z^{2}+1)^{3}}dz=\underset{z\rightarrow z_{0}}{l\acute{\imath}m}\int_{-R}^{R}\frac{1}{(x^{2}+1)^{3}}dx+\int_{C_{R}}\frac{1}{\left[(z+i)(z-i)\right]^{3}}=I_{1}+I_{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9e011da8add4e7c3432631ee78334ca531017edf)
Tiene dos polos simples diferentes de orden 2 , ahora por el teorema del residuo, tenemos:
donde tomando en cuenta que el el polo z=i, de orden 3 encontramos respectivamente,
![Res(f(z),z_{0})=\frac{1}{(n-1)\text{!}}\underset{z\rightarrow z_{0}}{l\acute{\imath}m}\frac{d^{n-1}}{dz^{n-1}}\left[(z-z_{0})^{n}f(z)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c52b3a4c66aab43d0a019037fe29a4be27c4799b)
![Res(f(z),i)=\frac{1}{(3-1)\text{!}}\underset{z\rightarrow z_{0}}{l\acute{\imath}m}\frac{d^{2}}{dz^{2}}\left[(z-i)^{3}\frac{1}{(z-i)^{3}(z+i)^{3}}\right]=\frac{1}{2}\underset{z\rightarrow i}{l\acute{\imath}m}\frac{d^{2}}{dz^{2}}\left[\frac{1}{(z+1)^{3}}\right]
=\frac{1}{2}\underset{z\rightarrow i}{l\acute{\imath}m}\left[\frac{12}{(z+i)^{5}}\right]=\frac{1}{2}\left[\frac{12}{\left(i+i\right)^{5}}\right]=6\left[\frac{1}{32i}\right]=\frac{3}{16i}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b5cf6bc40e5f485e82f4b71e368f9aa62df7ed49)
Conclusión
Entonces el Valor principal es:
ó
Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 18:36 4 jul 2015 (CDT)
Ejercicio 6(20)
Evalué el valor principal de Cauchy de la integral impropia dada,
Procedimiento
Dividamos la integral en dos partes para evaluarlas como integrales impropias.
$\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=\int_{-\infty}^{0}\dfrac{x}{(x^2+4)^3}dx+\int_{0}^{\infty}\dfrac{x}{(x^2+4)^3}dx$
$\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=lím_{R\longrightarrow -\infty}\int_{R}^{0}\dfrac{x}{(x^2+4)^3}dx+lím_{R\longrightarrow \infty}\int_{0}^{R}\dfrac{x}{(x^2+4)^3}dx$
Resolveremos primero la integral
Para ello sea $x=2 \tan \phi$, $dx=2 \sec^2\phi d\phi$, sustituimos
$\int \dfrac{x}{(x^2+4)^3}dx=\int \dfrac{2 \tan \phi * 2 \sec^2\phi d\phi}{(4\tan^2\phi +4)^3}=\int\dfrac{4 \tan \phi \sec^2\phi d\phi}{4^3 \sec^6\phi}=\int\dfrac{\tan\phi d\phi}{16 \sec^4\phi}= \int\dfrac{\tan\phi \cos^4\phi d\phi}{16}$
Con $\tan\phi =\sin\phi \cos^{-1}\phi$
$\int\dfrac{\sin\phi \cos^{-1} \phi \cos^4\phi d\phi}{16}=\int\dfrac{\sin\phi \cos^3\phi d\phi}{16}$
Resolviendo por cambio de variable siendo $w=cos\phi $ y por lo tanto $dw= -sin\phi d\phi$
Por lo que la integral queda
$\int\dfrac{\sin\phi \cos^3\phi d\phi}{16}=\frac{-1}{16} \int w^3 dw = \frac{-1}{64} w^4$
Volvemos a nuestras variables originales sustituyendo $\phi =\arctan (\frac{x}{2})$ y evaluando límites
$ \frac{-1}{64} w^4= \frac{-1}{64} (cos(\phi))^4 = \frac{-1}{64} (cos(arc tan(\frac{x}{2})))^4$
$\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=lím_{R\longrightarrow -\infty}[\frac{-1}{64} (cos(arc tan(\frac{x}{2})))]_R^0+lím_{R\longrightarrow \infty}[\frac{-1}{64} (cos(arc tan(\frac{x}{2})))]_0^R$
$\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=(\frac{-1}{64} (cos(0))-\frac{-1}{64} (cos(0))-lím_{R\longrightarrow -\infty}(\frac{-1}{64} (cos(arc tan(\frac{R}{2}))))+lím_{R\longrightarrow \infty}(\frac{-1}{64} (cos(arc tan(\frac{R}{2}))))$
$\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=\frac{1}{64}(cos(\frac{\pi}{2}))+\frac{-1}{64} (cos(\frac{\pi}{2}))=0$
Conclusión
Por tanto, escribimos
V.P. $\int_{-\infty}^{\infty}\dfrac{x}{(x^2+4)^3}dx=0$
Realizado por: Pablo (discusión) 05:31 5 jul 2015 (CDT)
Forma alternativa
Primero reescribimos la integral en dos partes
$\int_{-\infty}^{^{\infty}}\frac{x}{(x^{2}+4)^{3}}dx=lim_{R\rightarrow-\infty}\int_{R}^{0}\frac{x}{(x^{2}+4)^{3}}dx+lim_{R\rightarrow-\infty}\int_{0}^{R}\frac{x}{(x^{2}+4)^{3}}dx$
Si hacemos el cambio de variable $u=x^{2}+4\rightarrow du=2xdx$ entonces:
$lim_{R\rightarrow-\infty}\int_{R^{2+4}}^{4}\frac{du/2}{u^{3}}+lim_{R\rightarrow\infty}\int_{4}^{R^{2}+4}\frac{du/2}{u^{3}}dx$
Ahora evaluamos
$lim_{R\rightarrow-\infty}-\frac{1}{4}[\frac{1}{4^{2}}-\frac{1}{(R^{2}+4)^{2}}]+lim_{R\rightarrow\infty}-\frac{1}{4}[\frac{1}{(R^{2}+4)^{2}}+\frac{1}{4^{2}}]$
Finalmente
$\int_{-\infty}^{\infty}\frac{x}{(x^{2}+4)^{3}}dx$=0
Realizado por: Fernando Vazquez V. (discusión) 05:48 5 jul 2015 (CDT)
Ejercicio 21
Evalue el valor principal de Cauchy de la integral impropia.
$ \int_{-\infty}^{\infty} \frac{2x^2-1}{x^4+5^2+4} $
Procedimiento
Si tomo $f(z)$ como:
$f(z)= \frac{2x^2-1}{x^4+5^2+4}$
Ahora factorizo :
$f(z)= \frac{2x^2-1}{x^4+5^2+4} = \frac{2x^2-1}{(z^2+1)(z^2+4)} $
Y claramente se ve que los polos de la función son: $z=\pm i$, $z=\pm2i$; son polos simples.
Ahora si integramos sobre como una circunferencia $C_{R}$, centrada en el origen de radio $R$; los polos $z=i$ y $z=2i $ estan en el interior de la curva. De modo que:
$\int_{-R}^{R} f(x) dx + \int_{C_{R}} f(z) dz = 2\pi i [Res(f(z),i)+Res(f(z),2i)]$
Obtenemos los residuos de los polos $z=i$ $z=2i$
$Res(f(z),i) = \frac{2x^2-1}{(z^2+1)(z^2+4)} |_{z=i} = -\frac{1}{2i}$
$Res(f(z),2i) = \frac{2x^2-1}{(z^2+1)(z^2+4)} |_{z=2i} = \frac{3}{4i}$
Conclusión
Por lo tanto:
$\int_{-R}^{R} f(x) dx + \int_{C_{R}} f(z) dz = 2\pi i (-\frac{1}{2i} + \frac{3}{4i}) = \frac{ \pi}{2}$
Realizado por:Nancy Martínez Durán (discusión) 06:20 5 jul 2015 (CDT)
Ejercicio 23.
Evalúe el valor principal de Cauchy de la integral impropia dada
$\int_{0}^{+\infty}\frac{x^{2}+1}{x^{4}+1}$
Procedimiento
Tomemos
$ \int_{0}^{\infty} \frac{x^2+1}{x^4+1}=\frac{1}{2}\int_{-\infty}^{\infty} \frac{x^2+1}{x^4+1} $
sea
$f(z)= \frac{x^2+1}{x^4+1}=\frac{(z+i)(z-i)}{(z^2+i)(z^2-i)}$
Teniendo polos de la función z=i, z=-i, y z=+1, z=-1
Y por definicion sabemos que:
$ \int_{-R}^{R} f(x)dx+ \int_{C_{R}}f(z)dz=2\pi i[Res(f(z),i)+Res(f(z),1)] $
Por tanto:
$ \int_{-R}^{R} \frac{x^2+1}{x^4+1}dx+ \int_{C_{R}}\frac{(z+i)(z-i)}{(z^2+i)(z^2-i)}dz=2\pi i[Res(f(z),i)+Res(f(z),1)] $
$ \int_{-R}^{R} \frac{x^2+1}{x^4+1}dx+ \int_{C_{R}}\frac{(z+i)(z-i)}{(z^2+i)(z^2-i)}dz=[\lim_{z\to i} \frac{(z+i)(z-i)i}{(z^2+i)(z^2-i)}+ \lim_{z\to 1} \frac{(z+i)(z-i)i}{(z^2+i)(z^2-i)}] $
$ \int_{-R}^{R} \frac{x^2+1}{x^4+1}dx+ \int_{C_{R}}\frac{(z+i)(z-i)}{(z^2+i)(z^2-i)}dz= 0+\frac{2\pi}{\sqrt{2}} $
$ \therefore \frac{1}{2} \int_{-\infty}^{\infty} \frac{x^2+1}{x^4+1}= \frac{2\pi}{\sqrt{2}}$
Conclusión
$ \therefore \int_{0}^{\infty} \frac{x^2+1}{x^4+1}= \frac{2\pi}{\sqrt{2}}$
Realizado por: Samantha Martinez (discusión) 23:30 5 jul 2015 (CDT)
Método alternativo
Evalúe el valor principal de Cauchy de la integral impropia dada
$\int_{0}^{+\infty}\frac{x^{2}+1}{x^{4}+1}$
Procedimiento
nosotros sabemos que
$\int_{0}^{+\infty}\frac{x^{2}+1}{x^{4}+1}=\frac{1}{2}\int_{-\infty}^{+\infty}\frac{x^{2}+1}{x^{4}+1}$
primero calcularemos
$V.P\int_{-\infty}^{+\infty}\frac{z^{2}+1}{z^{4}+1}=2\pi i\left[Res(f(z),z_{1})+Res(f(z),z_{2})\right]$
sólo tomaremos esos dos residuos ya que son los polos simples en la mitad superior del plano y estos son
$z_{1}=e^{\frac{\pi i}{4}}$, $z_{2}=e^{\frac{3\pi i}{4}}$
y del libro usamos el método alternativo para calcular el residuo en un polo simple
$Res(f(z),z_{1})=\frac{z_{1}^{2}+1}{4z_{1}^{3}}=\frac{e^{\frac{2\pi i}{4}}+1}{4e^{\frac{3\pi i}{4}}}=\frac{1}{4}e^{-\frac{\pi i}{4}}+\frac{1}{4}e^{-\frac{3\pi i}{4}}=-\frac{\sqrt{2}}{4}i$
$Res(f(z),z_{2})=\frac{z_{2}^{2}+1}{4z_{2}^{3}}=\frac{e^{\frac{6\pi i}{4}}}{4e^{\frac{9\pi i}{4}}}+\frac{1}{4}e^{-\frac{9\pi i}{4}}=\frac{1}{4}e^{-\frac{3\pi i}{4}}+\frac{1}{4}e^{-\frac{9\pi i}{4}}=-\frac{\sqrt{2}}{4}i$
tenemos que
$2\pi i\left[Res(f(z),z_{1})+Res(f(z),z_{2})\right]=2\pi i\left(-2\frac{\sqrt{2}i}{4}\right)=\sqrt{2}\pi$
Conclusión
pero por
$\int_{0}^{+\infty}\frac{x^{2}+1}{x^{4}+1}=\frac{1}{2}\int_{-\infty}^{+\infty}\frac{x^{2}+1}{x^{4}+1}=\pi i\left[Res(f(z),z_{1})+Res(f(z),z_{2})\right]=\frac{\sqrt{2}\pi}{2}$
Realizado por:Juan Daniel Rivera Bautista (discusión) 00:14 6 jul 2015 (CDT)
Ejercicio 24
Evalúa el valor principal de Cauchy de la integral impropia dada
$\oint_{0}^{\infty} \frac{1}{x^6 + 1} dx$
Procedimiento
La integral puede reescribirse como:
$I = \oint_{0}^{\infty} \frac{1}{x^6 + 1} dx = \frac{1}{2} \int_{- \infty}^{\infty} \frac{dx}{x^6 + 1}$
La función puede verse en el plano complejo como:
$f(z) = \frac{1}{z^6 + 1} = \frac{1}{(z + i) (z - i) (z^4 - z^2 + 1)}$
Y así podemos decir que la integral esta encerrada en un contorno que seria una circunferencia de radio $R$
$\oint_{C_R} \frac{dz}{(z + i) (z - i) (z^4 - z^2 + 1)} + \int_{-R}^{R} \frac{1}{x^6 + 1} dx $
Por Teorema de Residuo:
$\oint_{C_R} \frac{dz}{(z + i) (z - i) (z^4 - z^2 + 1)} + \int_{-R}^{R} \frac{1}{x^6 + 1} dx = 2\pi i \sum_{n=1}^{k} Res_{z_n} f(z)$
En este caso por el contorno solo nos interesa el $z_0 = i$ que es el punto que se encuentra encerrado en nuestro contorno, entonces el residuo nos queda:
$Res_{z=i} f(z) = \lim_{z \rightarrow i} [(z - i) f(z)] = \lim_{z \rightarrow i} [(z - i) \frac{1}{(z + i) (z - i) (z^4 - z^2 + 1)}] = \lim_{z \rightarrow i} [ \frac{1}{(z + i) (z^4 - z^2 + 1)}] = \frac{1}{6i}$
Sustituyendo este valor en nuestra integral tendríamos :
$\int_{-R}^{R} \frac{1}{x^6 + 1} dx = 2\pi i (\frac{1}{6i}) = \frac{\pi}{3}$
$I = \frac{1}{2} \int_{- \infty}^{\infty} \frac{dx}{x^6 + 1} = \frac{1}{2} ( \frac{\pi}{3})$
Conclusión
$I = \frac{1}{2} \int_{- \infty}^{\infty} \frac{dx}{x^6 + 1} = \frac{\pi}{6}$
Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 15:52 5 jul 2015 (CDT)
Ejercicio 25
Evalue el valor principal de Cauchy de la integral impropia
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx } $
Procedimiento
Como el integrando es una función par de $x$, podemos reescribir
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx }=\frac { 1 }{ 2 } \int _{ -\infty }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx } $
Reescribiendo la integral a una integral de contorno obtenemos que
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx } =\oint { \frac { { z }^{ 2 } }{ { z }^{ 6 }+1 } } dz$
que es lo mismo que escribir
$\int _{ { C }_{ R } }^{ }{ \frac { { z }^{ 2 } }{ { z }^{ 6 }+1 } dz } +\int _{ -R }^{ R }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx\quad =\quad 2\pi iRes(f(z),i) } $
donde $f(z)=\frac { { z }^{ 2 } }{ { z }^{ 6 }+1 } $
y el residuo es $\quad Res(f(z),i)=\frac { \pi }{ 3 } $
Conclusión
Por ultimo suponemos que
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx }=\frac { 1 }{ 2 } \int _{ -\infty }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx } = \frac { 1 }{ 2 } \left( \frac { \pi }{ 3 } \right) $
es decir
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx }=\frac { \pi }{ 6 }$
Realizado por:Miguel Medina Armendariz (discusión) 02:49 5 jul 2015 (CDT)
Comentario
Compañero cuando calculas el residuo de tu función $f(z) = \frac{z^2}{z^6 + 1}$ como solo nos importa un punto que es $z_0 = i$ por nuestro contorno que es solo la mitad de una circunferencia tenemos
$Res_{z=1} \lim_{z \rightarrow i} [(z- i) \frac{z^2}{(z + i) (z - i) (z^4 - z^2 + 1)}] = \lim_{z \rightarrow i} [ \frac{z^2}{(z + i) (z^4 - z^2 + 1)}] = \frac{-1}{6i}$
Y sustituyendo en: $ 2\pi iRes(f(z),i)$ tenemos $2\pi iRes(f(z),i) = 2\pi i (\frac{-1}{6i}) = \frac{- \pi}{3}$
Por lo que tu integral quedaría
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx }=\frac { 1 }{ 2 } \int _{ -\infty }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx } = \frac { 1 }{ 2 } \left( \frac {- \pi }{ 3 } \right) $
$\int _{ 0 }^{ \infty }{ \frac { { x }^{ 2 } }{ { x }^{ 6 }+1 } dx }=\frac {- \pi }{ 6 }$
Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 23:57 5 jul 2015 (CDT)
Ejercicio 27
Evalúe el valor principal de Cauchy de la integral impropia dada.
\[
\int_{-\infty}^{\infty}\frac{\cos x}{x^{2}+1}dx
\]
Procedimiento
Esta se puede reescribir como
\[ \oint_{C}\frac{e^{iz}}{z^{2}+1}dz \]
Por el teorema $6.5.3$ se tiene que:
\[ \int_{CR}\frac{1}{z^{2}+1}e^{iz}dz+\int_{-R}^{R}\frac{1}{x^{2}+1}e^{ix}dx=2\pi iRes\left(f\left(z\right)e^{iz},i\right) \]
Donde :
\[
Res\left(f\left(z\right)e^{iz},i\right)=lim_{z\rightarrow i}\frac{\left(z-i\right)e^{iz}}{\left(z+i\right)\left(z-i\right)}=lim_{z\rightarrow i}\frac{e^{iz}}{\left(z+i\right)}=\frac{e^{i^{2}}}{2i}
\]
Entonces:
\[
\int_{CR}\frac{1}{z^{2}+1}e^{iz}dz+\int_{-R}^{R}\frac{1}{x^{2}+1}e^{ix}dx=2\pi i\left(\frac{e^{i^{2}}}{2i}\right)=\pi e^{-1}
\]
Conclusión
\[ \therefore\int_{-\infty}^{\infty}\frac{\cos x}{x^{2}+1}dx=\pi e^{-1} \]
Realizado por: Alejandro Juárez Toribio (discusión) 00:56 6 jul 2015 (CDT)
Ejercicio 28
\[ \int_{-\infty}^{\infty} \! \dfrac { \cos 2x}{x^{2}+1}\, dx \]
Procedimiento
Se trata de una función par: $f(x)=f(-x)$
El limite de integración se encuentre de $-\infty$ a $\infty$ entonces podemos escribir la integral como:
\[
\dfrac {1}{2} \int_{-\infty}^{\infty} \! \dfrac { \cos 2x}{x^{2}+1}\, dx
\]
Usando el teorema 6.6.2, la integral se convierte en:
\[
\dfrac {1}{2} Re \int_{-\infty}^{\infty} \! \dfrac { e^{2xi}}{x^{2}+1}\, dx
\]
La función en términos de z
\[ g(z) =\dfrac{e^{2iz}}{z^{2}+1}\]
entonces
\[
\int_{c}g(z)dz=2πi∑Res\]
Sabemos que sus polos son simples y sus valores son $z=-i$ y $z=i$ evaluaremos en $z=i$ ya que $b>0$ entonces:
Conclusión
\[ Res (g,z) \lim_{z \to i}(z-i) (\dfrac{e^{i2z}}{(z+i)(z-i)}=\dfrac{e^{-2}}{2i}= \dfrac{1}{2}Res(2πi \dfrac{e^{-2}}{2i})= \dfrac{π}{e^{2}} \]
Realizado por: Esther Sarai (discusión) 18:49 5 jul 2015 (CDT)Esther Sarai
Ejercicio 29
Evalué el valor principal de Cauchy de la integral impropia dada.
\begin{equation*} \int_{-\infty}^{\infty}\frac{x \sin x}{x^2+1}dx \end{equation*}
Procedimiento
Tomando la función:
\begin{equation*} \frac{xe^{ix}}{x^2+1}=\frac{x \cos x}{x^2+1}+i \frac{x \sin x}{x^2+1} \end{equation*}
Ahora pasamos a variable compleja para sacar el valor principal de Cauchy:
\begin{equation*} \frac{ze^{iz}}{(z+i)(z-i)} \end{equation*}
Donde $f(z)$ es la función:
\begin{equation*} f(z)=\frac{e^{iz}}{(z+i)(z-i)} \end{equation*}
Integrando sobre la región:
Solo tomando los residuos en la parte superior e integrando:
\begin{equation*} \int_{CR} \frac{e^{iz}}{(z+i)(z-i)}+\int_{-R}^{R}\frac{x e^{ix}}{x^2+1}dx=2\pi i Res \left [f(z)e^{iz},i \right ] \end{equation*}
Ahora solo tenemos que encontrar el residuo: \begin{equation*} Res \left [f(z)e^{iz},i \right ]= \lim_{z \to i} z (z-i) \frac{e^{iz}}{(z+i)(z-i)}=\lim_{z \to i} z \frac{e^{iz}}{(z+i)}=\frac{ie^{-1}}{2i}=\frac{1}{2e} \end{equation*}
Por lo que la integral se puede reescribir como:
\begin{equation*} \int_{CR} \frac{e^{iz}}{(z+i)(z-i)}+\int_{-R}^{R}\frac{x e^{ix}}{x^2+1}dx=2\pi i \frac{1}{2e}=\frac{\pi i}{e} \end{equation*}
Por lo que el VP de Cauchy es:
\begin{equation*} \int_{-R}^{R}\frac{x e^{ix}}{x^2+1}dx=\int_{-R}^{R}\frac{x \cos x}{x^2+1}dx+ i \int_{-R}^{R}\frac{x \sin x}{x^2+1}dx= 0 + i \frac{\pi}{e} \end{equation*}
Conclusión
Igualando parte real e imaginaria, se tiene que el valor principal de Cauchy de la integral es:
\begin{equation*} \int_{-R}^{R}\frac{x \sin x}{x^2+1}dx=\frac{\pi}{e} \end{equation*}
Re elaborado por Manuel Rodríguez
Ejercicio 31
Evalúe el valor principal de Cauchy de la integral impropia \[ \int_{0}^{\infty} \! \frac{\cos 3x}{\left(x^{2}+1\right)^{2}} \, dx \]
Procedimiento
$Solución$. Primero observe que los límites de integración en la integral dada no son $-\infty$ a $\infty$ como lo requiere el método de V.P de Cauchy. Esto se puede remediar observando que, ya que el integrando es una función par de $x$, podemos escribir
\[ \int_{0}^{\infty} \! \frac{\cos 3x}{\left(x^{2}+1\right)^{2}} \, dx = \frac{1}{2} \int_{-\infty}^{\infty} \, \! \frac{\cos 3x}{\left(x^{2}+1\right)^{2}} \, dx \]
Con $\alpha=1$ ahora se forma la integral de contorno
\[ \oint_{C} \, \! \, \frac{1}{ \left( z^{2}+1\right )^{2} } e^{3iz} \, dz, \]
donde $C$ es el contorno cerrado $C$ que consiste en el intervalo $ [-R,R] $ en el eje $x$ y la semicircunferencia de radio $C_{R}$ de radio $R>1$. Por el Teorema del residuo de Cauchy
\[
\int_{ C_{R} } \, \! \, \frac{1}{ \left( z^{2} + 1\right )^{2} } \, e^{3iz} \, dz + \int_{-R}^{R} \, \! \,\frac{1}{ \left( x^{2}+1\right )^{2} } \, e^{3ix} \, dx= 2 \pi i \cdot Res\left( f(z) e^{3iz}, i \right)
\]
donde $f(z)= \frac{1}{\left( z^{2}+1\right )^{2} } $, y
\[
Res\left( f(z) e^{3iz}, i \right) = \frac{1}{1!} \lim_{z \to i} \frac{d}{dz} \left[ ( z-i)^{2} \cdot \frac{ e^{3iz} }{ \left( z+i \right)^{2} \left( z-i \right)^{2} } \right]= \lim_{z \to i} \left[ \frac{i e^{3 i z} (3 z+5 i)}{(z+i)^3} \right] = -\frac{i}{ e^{3} }
\]
Entonces, del $Teorema\, 6.6.2 \, Comportamiento\, de\, la\, integral\, cuando \, R \rightarrow \infty $ concluimos que $\int_{C_{R}} \! f(z) e^{3iz} \, dz \rightarrow 0 $ cuando $R \rightarrow \infty$, y así
\[ V.P \int_{-\infty}^{\infty} \, \! \, \frac{1}{\left( x^{2}+1\right )^{2} } e^{3ix} \, dx = 2 \pi i \left( -\frac{i}{ e^{3} } \right) = \frac{2 \pi }{e^3} \]
Pero por
\[
\int_{-\infty}^{\infty} \, \! \, f(x) e^{i \alpha x} \, dx= \int_{-\infty}^{\infty} \, \! \, f(x) \cos \alpha x \, dx + \int_{-\infty}^{\infty} \, \! \, f(x) \sin \alpha x \, dx
\]
Tengo que
\[
\int_{-\infty}^{\infty} \, \! \, \frac{1}{\left( x^{2}+1\right )^{2} } \, e^{3ix} \, dx = \int_{-\infty}^{\infty} \, \! \, \frac{ \cos 3x }{ \left( x^{2}+1 \right)^{2} } \, dx + i \int_{-\infty}^{\infty} \, \! \, \frac{ \sin 3x }{ \left( x^{2}+1 \right)^{2} } \, dx = \frac{2 \pi }{e^3}
\]
Igualando las partes reales e imaginarias en el último renglón se obtiene el resultado
\[ V.P. \int_{-\infty}^{\infty} \, \! \, \frac{ \cos 3x }{ \left( x^{2}+1 \right)^{2} } \, dx= \frac{2 \pi }{ e^3} \] junto con \[V.P. \int_{-\infty}^{\infty} \, \! \, \frac{ \sin 3x }{ \left( x^{2}+1 \right)^{2} } \, dx= 0 \]
Conclusión
Por último, considerando el hecho de que el integrando es una función par, obtenemos el valor de la integral indicada:
\[ \int_{0}^{\infty} \, \! \, \frac{\cos 3x}{\left(x^{2}+1\right)^{2}} \, dx = \frac{1}{2} \int_{-\infty}^{\infty} \! \, \frac{ \cos 3x }{ \left( x^{2}+1 \right)^{2} } \, dx=\left( \frac{1}{2} \right)\left( \frac{2 \pi }{ e^3} \right)= \frac{\pi}{e^{3}} \]
\[
\therefore \int_{0}^{\infty} \, \! \, \frac{\cos 3x}{\left(x^{2}+1\right)^{2}} \, dx = \frac{\pi}{ e^{3} } \]
Realizado por: Emmanuell Castro Flores (discusión) 17:19 5 jul 2015 (CDT)
Forma alternativa
Como podemos observar esta integral es la parte de real de la siguiente integral:
$\int_{0}^{\infty}\frac{e^{3ix}}{(x²+1)²}dx$
Por la teoría de los residuos reemplazamos x por la variable compleja z y se integra la función compleja $f$ en un contorno cerrado $C$ que consiste en el intervalo [-R,R] y en una semicircunferencia $C_R$de radio suficiente grande para incluir los polos de la función.
Por lo anterior tenemos:
$f(z)=\frac{e^{3iz}}{(z²+1)²}$
Con lo cual nuestra integral queda de la manera siguiente:
$\oint_C=\frac{e^{3iz}}{(z²+1)²} dz$
Como vemos los polos de nuestra integral son $z_0= -i,i$ asi pues la integral se reescribe como:
$\oint_C=\frac{e^{3iz}}{(z+i)²(z-i)²} dz$
Un polo que esta dentro de nuestro contorno es en $z_0=i $por lo cual por Cauchy calcularemos nuestro residuo.
$Res(f(z),i)=\lim_{z\rightarrow i}\frac{d}{dz}[(z-i)²f(z)]=\lim_{z\rightarrow i}\frac{d}{dz}[(z-i)² \frac{e^{3iz}}{(z+i)²(z-i)²}]=\lim_{z\rightarrow i}\frac{d}{dz}[\frac{e^{3iz}}{(z+i)²}]=\lim_{z\rightarrow i} \frac{3ie^{3iz}(z+i)²-e^{3iz}2(z+i)}{(z+i)⁴}=\frac{-i}{e^{3}}$
Asi :
$\int_{C_R} \frac{e^{3iz}}{(z²+1)²} dz + \int_{-R}^{R} \frac{e^{3ix}}{(x²+1)²}dx= 2i\pi Res(f(z),i)$
$\int_{C_R} \frac{e^{3iz}}{(z²+1)²} dz + \int_{-R}^{R} \frac{e^{3ix}}{(x²+1)²}dx= 2i\pi \frac{-i}{e^{3}}$
$\int_{C_R} \frac{e^{3iz}}{(z²+1)²} dz + \int_{-R}^{R} \frac{e^{3ix}}{(x²+1)²}dx=\frac{2\pi}{e^{3}}$
Pero este resultado es evaluando la integral de: $\int_{-\infty}^{\infty}\frac{\cos3x}{(x²+1)²}dx=\frac{2\pi}{e^{3}}$
Ahora bien por ser una función par podemos llegar a que : $\int_{0}^{\infty}\frac{\cos3x}{(x²+1)²}dx=\frac{1}{2} \int_{-\infty}^{\infty}\frac{\cos3x}{(x²+1)²}dx$ Por lo tanto:
$V.P \int_{0}^{\infty}\frac{\cos3x}{(x²+1)²}dx=\frac{\pi}{e^{3}}$
Realizado por: Anahi Limas (discusión) 17:11 5 jul 2015 (CDT)
Ejercicio 33
Evalué el valor principal de Cauchy de la integral impropia dada
$\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx$
Procedimiento
como se sabe el valor principal de Cauchy se escribe como
$V.P:\int_{\infty}^{-\infty}f(x)=\lim_{R\rightarrow\infty}\int_{-R}^{R}f(x)dx$
ademas:
$\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{\cos2x}{x^{4}+1}dx$
factorizando
$x^{4}+1=(x^{2}+i)(x^{2}-i)$
$=\frac{1}{2}\int_{-\infty}^{\infty}\frac{\cos2x}{(x^{2}+i)(x^{2}-i)}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{\cos2x}{(x^{2}+i)(x^{2}-i)}dx$
Escribiéndola como una integral de contorno
$\frac{1}{2}\int_{-\infty}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\oint_{c}\frac{1}{z^{4}+1}e^{i2z}dz=\oint_{c}\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}dz$
ademas
$z^{4}+1=(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})$
donde:
$z_{1}=e^{\pi i/4}=\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$
$z_{2}=e^{3\pi i/4}=\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4}=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$
$z_{3}=e^{5\pi i/4}=\cos\frac{5\pi}{4}+i\sin\frac{5\pi}{4}=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$
$z_{4}=e^{7\pi i/4}=\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i$
ademas como $z_{1}\;z_{2}\;z_{3}\;z_{4}$son polos simples
del teorema del residuo de un polo simple
$Res(f(z),z_{0})=\lim_{z\rightarrow z_{0}}(z-z_{0})f(z)$
$Res(f(z),z_{1})=\lim_{z\rightarrow z_{1}}(z-z_{1})f(z)=\lim_{z\rightarrow z_{1}}(z-z_{1})\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}=\lim_{z\rightarrow z_{1}}\frac{1}{(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}=$
$=\lim_{z\rightarrow e^{\pi i/4}}\frac{1}{(z-e^{3\pi i/4})(z-e^{5\pi i/4})(z-e^{7\pi i/4})}e^{i2z}=e^{i2z}\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]$
$Res(f(z),z_{2})=\lim_{z\rightarrow z_{2}}(z-z_{2})f(z)=\lim_{z\rightarrow z_{2}}(z-z_{2})\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}=\lim_{z\rightarrow z_{2}}\frac{1}{(z-z_{1})(z-z_{3})(z-z_{4})}e^{i2z}=$
$=\lim_{z\rightarrow e^{3\pi i/4}}\frac{1}{(z-e^{\pi i/4})(z-e^{5\pi i/4})(z-e^{7\pi i/4})}e^{i2z}=e^{i2z}\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]$
$Res(f(z),z_{3})=\lim_{z\rightarrow z_{3}}(z-z_{3})f(z)=\lim_{z\rightarrow z_{3}}(z-z_{3})\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}=\lim_{z\rightarrow z_{3}}\frac{1}{(z-z_{1})(z-z_{2})(z-z_{4})}e^{i2z}=$
$=\lim_{z\rightarrow e^{5\pi i/4}}\frac{1}{(z-e^{\pi i/4})(z-e^{3\pi i/4})(z-e^{7\pi i/4})}e^{i2z}=e^{i2z}\left[\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]$
$Res(f(z),z_{4})=\lim_{z\rightarrow z_{4}}(z-z_{4})f(z)=\lim_{z\rightarrow z_{4}}(z-z_{4})\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})(z-z_{4})}e^{i2z}=\lim_{z\rightarrow z_{4}}\frac{1}{(z-z_{1})(z-z_{2})(z-z_{3})}e^{i2z}=$
$=\lim_{z\rightarrow e^{7\pi i/4}}\frac{1}{(z-e^{\pi i/4})(z-e^{3\pi i/4})(z-e^{5\pi i/4})}e^{i2z}=e^{i2z}\left[-\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]$
El primer residuo.
$Res(f(z),z_{1})=e^{i2(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)}\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]=e^{-\sqrt{2}+\sqrt{2}i}\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]=$
$=(e^{-\sqrt{2}}\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]$
El segundo residuo.
$Res(f(z),z_{2})=e^{i2(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)}\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]=e^{-\sqrt{2}-\sqrt{2}i}\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]=$
$=(e^{-\sqrt{2}}\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]$
El tercer residuo.
$Res(f(z),z_{3})=e^{i2(-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}\left[\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]=e^{\sqrt{2}-\sqrt{2}i}\left[\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]=$
$=(e^{\sqrt{2}}\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]$
El cuarto residuo.
$Res(f(z),z_{4})=e^{i2(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)}\left[-\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]=e^{\sqrt{2}+\sqrt{2}i}\left[-\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]=$
$=(e^{\sqrt{2}}\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]$
Por el teorema del residuo de Cauchy
$\oint_{c}f(z)dz=2\pi i\sum_{k=1}^{n}Res(f(z),z_{k})$
$\int_{C_{R}}\frac{1}{z^{4}+1}e^{i2z}dz+\int_{-R}^{R}\frac{1}{x^{4}+1}e^{i2x}dx=2\pi i[Res(f(z),z_{1})+Res(f(z),z_{2})+Res(f(z),z_{3})+Res(f(z),z_{4})]$
donde
$f(z)=\frac{1}{z^{4}+1}e^{i2z},$
$\int_{C_{R}}\frac{1}{z^{4}+1}e^{i2z}dz+\int_{-R}^{R}\frac{1}{x^{4}+1}e^{i2x}dx=$
$=2\pi i[(e^{-\sqrt{2}}\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]+(e^{-\sqrt{2}}\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]+(e^{\sqrt{2}}\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]+(e^{\sqrt{2}}\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{4\sqrt{2}}+\frac{1}{4\sqrt{2}}i\right]]$
$=\pi[e^{-\sqrt{2}}(\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right])+i\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right])+e^{\sqrt{2}}(\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right]+i\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right])$
$=\pi[e^{-\sqrt{2}}\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right](\left[\cos\sqrt{2}+i\sin\sqrt{2}\right]+i\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])+e^{\sqrt{2}}\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right](\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right]+i\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])$
$=\pi[e^{-\sqrt{2}}\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right](\left[\cos\sqrt{2}+i\sin\sqrt{2}\right]+\left[i\cos\sqrt{2}+\sin\sqrt{2}\right])+e^{\sqrt{2}}\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right](\left[\cos\sqrt{2}-i\sin\sqrt{2}\right]+\left[i\cos\sqrt{2}-\sin\sqrt{2}\right])$
$=\pi[e^{-\sqrt{2}}\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right](1+i)(\left[\cos\sqrt{2}+\sin\sqrt{2}\right]+e^{\sqrt{2}}\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right](1+i)(\cos\sqrt{2}-\sin\sqrt{2})$
$=\pi(1+i)[e^{-\sqrt{2}}\left[\frac{1}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}i\right](\left[\cos\sqrt{2}+\sin\sqrt{2}\right]+e^{\sqrt{2}}\left[-\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}i\right](\cos\sqrt{2}-\sin\sqrt{2})$
=$\frac{\pi(1+i)(1-i)}{2\sqrt{2}}[e^{-\sqrt{2}}(\left[\cos\sqrt{2}+\sin\sqrt{2}\right]+e^{\sqrt{2}}(-\cos\sqrt{2}+\sin\sqrt{2})=\frac{\pi}{\sqrt{2}}(e^{-\sqrt{2}}(\left[\cos\sqrt{2}+\sin\sqrt{2}\right]+e^{\sqrt{2}}(-\cos\sqrt{2}+\sin\sqrt{2})=\frac{\pi}{\sqrt{2}}[e^{-\sqrt{2}}\cos\sqrt{2}+e^{-\sqrt{2}}\sin\sqrt{2}-e^{\sqrt{2}}\cos\sqrt{2}+e^{\sqrt{2}}\sin\sqrt{2}]$
$=\frac{\pi}{\sqrt{2}}[\cos\sqrt{2}(e^{-\sqrt{2}}-e^{\sqrt{2}})+\sin\sqrt{2}(e^{-\sqrt{2}}+e^{\sqrt{2}})]=\frac{\pi}{\sqrt{2}}[e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})+e^{\sqrt{2}}(-\cos\sqrt{2}+\sin\sqrt{2})]$
$=\frac{\pi}{\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})-\frac{\pi}{\sqrt{2}}e^{\sqrt{2}}(\cos\sqrt{2}-\sin\sqrt{2})$
pero solo tiene sentido calcular para $Res(f(z),z_{1})+Res(f(z),z_{2})$
así
$\int_{-\infty}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{\pi}{\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})$
pero como:
$\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{\cos2x}{x^{4}+1}dx$
entonces:
$\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{1}{2}\frac{\pi}{\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})$
$\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{\pi}{2\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})$
analizando solo
Conclusión
$Res(f(z),z_{1})+Res(f(z),z_{2})$
$\int_{C_{R}}\frac{1}{z^{4}+1}e^{i2z}dz+\int_{-R}^{R}\frac{1}{x^{4}+1}e^{i2x}dx=2\pi i[Res(f(z),z_{1})+Res(f(z),z_{2})]=2\pi i[(e^{-\sqrt{2}}\left[\cos\sqrt{2}+i\sin\sqrt{2}\right])\left[-\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]+(e^{-\sqrt{2}}\left[\cos-\sqrt{2}+i\sin-\sqrt{2}\right])\left[\frac{1}{4\sqrt{2}}-\frac{1}{4\sqrt{2}}i\right]$
$=\frac{\pi}{2\sqrt{2}}e^{-\sqrt{2}}(1-i)(\left[\cos\sqrt{2}+i\sin\sqrt{2}\right]+\left[i\cos\sqrt{2}+\sin\sqrt{2}\right])=\frac{\pi}{2\sqrt{2}}e^{-\sqrt{2}}(1-i)(\cos\sqrt{2}(1+i)+\sin\sqrt{2}(1+i))$
$=\frac{\pi}{2\sqrt{2}}e^{-\sqrt{2}}(1-i)(1+i)(\cos\sqrt{2}+\sin\sqrt{2})=\frac{\pi}{\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2})$
$\Longrightarrow\int_{0}^{\infty}\frac{\cos2x}{x^{4}+1}dx=\frac{\pi}{2\sqrt{2}}e^{-\sqrt{2}}(\cos\sqrt{2}+\sin\sqrt{2}$)
Realizado por: Francisco Medina Albino (discusión) 04:24 5 jul 2015 (CDT)
Ejercicio 34
Evaluar el valor principal de Cauchy de la integral impropia dada
$\int_{0}^{\infty}\frac{xsenx}{x^{4}+1}dx$
Procedimiento
Primero podemos ver que la integral dada no tiene los límite s de menos infinito hasta infinito como lo requiere el método,
sin embargo, se puede remediar observando que, ya que $senx$ es una función par, podemos escribir como sigue:
\[ \int_{0}^{\infty}\frac{xsenx}{x^{4}+1}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{xsenx}{x^{4}+1}dx \]
Entonces si $z=Re^{i\theta}$ considerando $0\leq\theta\leq\pi$ y
$\alpha>0$ entonces podemos escribir:
\[ \int_{Cr}f(z)e^{i\alpha z}dz\longrightarrow0 \]
Cuando $R\longrightarrow\infty$ con $\alpha=1$ ahora se forma la
integral de contorno:
\[ \oint_{C}\frac{z}{z^{4}+1}e^{iz}dz+\int_{-R}^{R}\frac{x}{x^{4}+1}e^{iz}dx=2\pi iRes(f(z)e^{iz},i) \]
Donde $f(z)=\frac{z}{z^{4}+1}$ y por tanto:
\[ Res(f(z)e^{iz},i)=\frac{1}{(n-1)!}lim_{z\rightarrow z_{0}}\frac{d^{n-1}}{dz^{n-1}}[(z-z_{0})f(z)]=lim_{z\rightarrow z_{0}}\frac{d^{n-1}}{dz^{n-1}}\left[(z-z_{0})\frac{z}{z^{4}+1}\right] \]
Tenemos un polo de orden 4 en $z=-1$
\[ Res(f(z)e^{iz},i)=lim_{z\rightarrow z_{0}}\frac{d}{dz}\left[(z+1)\frac{z}{z^{4}+1}\right]=lim_{z\rightarrow z_{0}}\left(\frac{-3z^{4}+4z^{3}+1}{z^{8}+2z^{4}+1}\right)=\frac{1}{4}e^{i} \]
Entonces concluimos que $\int_{Cr}f(z)e^{i\alpha z}dz\longrightarrow0$
cuando $R\longrightarrow\infty$, y así
\[ V.P.\int_{-\infty}^{\infty}\frac{xsenx}{x^{4}+1}dx=2\pi i\frac{1}{4}e^{i} \]
Conclusión
Finalmente, tomando en cuenta que la función es una función par, se obtiene el valor de la integral indicada.
\[ \int_{0}^{\infty}\frac{xsenx}{x^{4}+1}dx=\frac{1}{2}\int_{-\infty}^{\infty}\frac{xsenx}{x^{4}+1}dx=\frac{\pi }{4}e^{i} \]
Realizado por:A. Martín R. Rabelo (discusión) 23:43 5 jul 2015 (CDT)
Ejercicio 35
Evalué el valor principal de Cauchy de la la integral impropia dada.
$\int_{-\infty}^{\infty}\frac{cos x}{(x²+1)(x²+9)} dx$
Procedimiento
Como podemos observar esta integral es la parte de real de la siguiente integral. $\int_{-\infty}^{\infty}\frac{e^{ix}}{(x²+1)(x²+9)}dx$
Por la teoria de los residuos reemplazamos $x$ por la variable compleja $z$ y se integra la función compleja $f$ en un contorno cerrado $C$ que consiste en el intervalo $[-R,R]$ y en una semicircunferencia $C_R$de radio suficiente grande para incluir los polos de la función.
Por lo anterior tenemos:
$f(z)=\frac{e^{iz}}{(z²+1)(z²+9)}$, donde también lo podemos expresar de la forma:
$f(z)=\frac{e^{iz}}{(z-i)(z+i)(z-3i)(z+3i)}$
Como podemos observar tenemos polos en $z_0=i,-i,3i,-3i$, peor por lo propuesto anteriormente para hacer el cambio de variable la semicircunferencia es de radio $R>3$, por lo cual dentro de nuestro contorno solo están ubicados $z_0=i,3i$ para lo cuales calcularemos los residuos correspondientes.
para $z_0=i$, tenemos: $Res(f(z),i)=\lim_{z\rightarrow i}(z-i)f(z)=\lim_{z\rightarrow i}\frac{e^{iz}}{(z+i)(z-3i)(z+3i)}=\frac{e^{-1}}{16i}$
para $z_0=3i$, tenemos: $Res(f(z),3i)=\lim_{z\rightarrow 3i}(z-3i)f(z)=\lim_{z\rightarrow i}\frac{e^{iz}}{(z+i)(z-i)(z+3i)}=\frac{e^{-3}}{48i}$
Por lo cual tenemos que:
$\int_{-R}^{R}\frac{e^{ix}}{(x²+1)(x²+9)}dx + \int_{C_R}\frac{e^{iz}}{(z²+1)(z²+9)}dz= 2i\pi[Res(f(z),i)+Res(f(z),3i)]$
Sustituyendo:
$\int_{-R}^{R}\frac{e^{ix}}{(x²+1)(x²+9)}dx + \int_{C_R}\frac{e^{iz}}{(z²+1)(z²+9)}dz= 2i\pi[\frac{e^{-1}}{16i}+\frac{e^{-3}}{48i}]=\pi(\frac{e^{-1}}{8}-\frac{e^{-3}}{24})=\frac{\pi}{8}(e^{-1}-\frac{e^{-3}}{3})$
Conclusión
Así pues: $\int_{-\infty}^{\infty}\frac{cos x}{(x²+1)(x²+9)} dx=\frac{\pi}{8}(e^{-1}-\frac{e^{-3}}{3})$
Realizado por: Anahi Limas (discusión) 19:14 5 jul 2015 (CDT)
Ejercicio 39
Comprueba el resultado de la siguiente integral:
$ \int_{-\infty}^{\infty}\frac{sen x}{x} dx = \pi $
Procedimiento
La integral se puede escribir como:
$\int_{-\infty}^{\infty}\frac{sen x}{x}dx=\int_{-\infty}^{\infty} \frac{e^{iz}}{z} dz$
Hacemos uso del siguiente Teorema:
$ V.P. \int_{-\infty}^{\infty} f(x) dx = \lim_{R\longrightarrow \infty} \int_{-R}^{R}f(x)dx = 2i\pi \Sigma_{k=1}^{n} Res (f(z), z_{k})$
Si consideremos:
$ f(z) = \frac{1}{z} $
Encontramos los polos, que en este caso $f(z)$ tiene un polo simple en el origen $z_{0} = 0$. Y además con residuo $ \frac{e^{i 0}}{1} $ = 1 .
Entonces la integral queda:
$\int_{-\infty}^{\infty}\frac{sen x}{x}dx = \int_{-\infty}^{\infty} -i\frac{e^{ix}}{x} dx $
Ya que el integrando es par; y además:
$\int_{-\infty}^{\infty}\frac{cos x}{x}dx = 0$
Por lo tanto:
$\int_{-\infty}^{\infty}\frac{sen x}{x}dx = -i V.P. \int_{-\infty}^{\infty} \frac{e^{ix}}{x} dx$
Y recordando que $f(z)$ tiene un solo polo en $z=0$
$V.P. \int_{-\infty}^{\infty} \frac{e^{ix}}{x} dx = i \pi Res(e^{iz},0) = i \pi$
Conclusión
Y por consecuencia:
$ \int_{-\infty}^{\infty} \frac{sen x}{x} dx = \pi$
Realizado por: Nancy Martínez Durán (discusión) 04:43 5 jul 2015 (CDT)
Ejercicio 40
40. Utilice un contorno y residuos para encontar el V.P. de Cauchy para la integral impropia dada: $\int_{-\infty}^{\infty}\frac{\sin{x}}{x(x^2+1)}dx=\pi(1-e^{-1}) $
Procedimiento
Sea $f(z)=\frac{e^{iz}}{z(z^2+1)}$.Entonces: $\oint_C \frac{e^{iz}}{z(z^2+1)}dz=I_1+I_2+I_3+I_4...(1)$; donde:
$I_1 : \int_{C_R} f(z) dz$
$I_2 : \int_{-R}^{r}f(x)dx$
$I_3 : \int_{-C_r}f(z)dz$
$I_4 : \int_r^Rf(x)dx$
$C_R$ es el arco de la semicircunferencia con centro en $z=0$ y radio $R, (R>1)$ y $\theta \in [0,\pi]$. $C_r$ es es arco de la semicircunferencia con centro en $z=0$ y radio $r, (0<r<1)$
Si $(R\to\infty) \Longrightarrow (I_1\to 0)$ (teorema 6.18)
Por el teorema 6.19 se tiene: $\lim_{r\to 0}\int_{C_r}f(z)dz=\pi i res(f(z),z=0)$.
Regresando a (1):
$ \oint_C \frac{e^{iz}}{z(z^2+1)}dz=I_1+I_2+I_3+I_4=\int_{-\infty}^{0}f(x)dx-\pi i res(f(z),z=0)+\int_0^{\infty}f(x)dx $ .(Se utilizó el hecho : $\int_{-C_r}=-\int_{C_r}$).
Por otro lado:
$res(f(z),z=0)=\lim_{z\to0}(f(z))(z)=\lim_{z\to0}\frac{e^{iz}}{z^2+1}=\frac{e^0}{1}=1$
$res(f(z),z=i)=\lim_{z\to i}(f(z))(z-i)=\lim_{z\to i}\frac{e^{iz}}{z(z+i)}=\frac{e^{-1}}{2i^2}=-\frac{e^{-1}}{2}$
Sabemos que:$\oint_C \frac{e^{iz}}{z(z^2+1)}dz=2\pi ires(f(z),z=i)$.
Entonces:
\begin{align*} \int_{-\infty}^{0}f(x)dx-\pi i res(f(z),z=0)+\int_0^{\infty}f(x)dx=&2\pi ires(f(z),z=i)\\ \int_{-\infty}^{\infty}f(x)dx=&2\pi ires(f(z),z=i)+\pi i res(f(z),z=0)\\ \int_{-\infty}^{\infty}f(x)dx=&(\pi i)[2(-\frac{e^{-1}}{2})+(1)] \\ \int_{-\infty}^{\infty}f(x)dx=&(\pi i)[(-e^{-1})+(1)]\\ \int_{-\infty}^{\infty}f(x)dx=&\pi(1-e^{-1})i\\ \end{align*}
Por igualdad de números complejos tenemos: $ Im(\int_{-\infty}^{\infty}\frac{(\cos{x}+i\sin{x})}{x(x^2+1)}dx)=\pi(1-e^{-1}) $.
Conclusión
Por lo tanto: $\int_{-\infty}^{\infty}\frac{\sin{x}}{x(x^2+1)}dx=\pi(1-e^{-1})$.
Realizado por:Alan Daniel Barrón Posadas (discusión) 16:36 5 jul 2015 (CDT)
Ejercicio 42
Utilice un contorno y residuos para encontrar el V.P. de Cauchy para la integral impropia dada :$$\int_{-\infty}^{\infty}\frac{x\cos{x}}{x^2-3x+2}dx=\pi[\sin{1}-2\sin{2}] $$
Procedimiento
Sea $f(z)=\frac{ze^{iz}}{z^2-3z+2}$.
Entonces: $\oint_C\frac{ze^{iz}}{z^2-3z+2}=I_1+I_2+I_3+I_4+I_5+I_6...(1)$; donde:
$I_1 : \int_{C_R} f(z) dz$
$I_2 : \int_{-R}^{1-r_1}f(x)dx$
$I_3 : \int_{-C_{r_1}}f(z)dz$
$I_4 : \int_{1+r_1}^{2-r_2}f(x)dx$
$I_5 : \int_{-C_{r_2}}f(z)dz$
$I_6 : \int_{2+r_2}^Rf(x)dx$
Con: $0<r_1+r_2<1<2<R$.
Si $(R\to\infty) \Longrightarrow (I_1\to 0)$ (teorema 6.18)
Por el teorema 6.19 se tiene: $[\lim_{r_1\to 0}\int_{C_{r_1}}f(z)dz=\pi i res(f(z),z=1)] \wedge [\lim_{r_2\to 0}\int_{C_{r_2}}f(z)dz=\pi i res(f(z),z=2)] $.
Note además que $[z_1=1] \wedge [z_2=2]$ no están en la región limitada por $C$ y por ello $f(z)$ es analítica en dicho conjunto , entonces por el teorema de Cauchy $\oint_C\frac{ze^{iz}}{z^2-3z+2}=0$.
Por otro lado:
$res(f(z),z=1)=\lim_{z\to1}(f(z))(z-1)=\lim_{z\to1}\frac{ze^{iz}}{(z-2)}=-\frac{1e^i}{1}=-e^i=-(\cos{1}+i\sin{1})$
$res(f(z),z=2)=\lim_{z\to 2}(f(z))(z-2)=\lim_{z\to 2}\frac{ze^{iz}}{(z-1)}=\frac{2e^{2i}}{1}=2e^{2i}=2(\cos{2}+i\sin{2})$
Entonces en (1), tenemos:
\begin{align*} 0+\int_{-\infty}^{1}f(x)dx-\pi i res(f(z),z=1)+\int_{1}^{2}f(x)dx-\pi i res(f(z),z=2)+\int_{2}^{\infty}f(x)dx=&0\\ \int_{-\infty}^{1}f(x)dx+\int_{1}^{2}f(x)dx+\int_{2}^{\infty}f(x)dx=&\pi i [res(f(z),z=1)+res(f(z),z=2)]\\ \int_{-\infty}^{\infty}f(x)dx=&\pi i [res(f(z),z=1)+res(f(z),z=2)]\\ \int_{-\infty}^{\infty}f(x)dx=&\pi i [-(\cos{1}+i\sin{1})+2(\cos{2}+i\sin{2})]\\ \int_{-\infty}^{\infty}f(x)dx=&\pi [(-i\cos{1}+\sin{1})+2(i\cos{2}-\sin{2})]\\ \int_{-\infty}^{\infty}f(x)dx=&\pi(\sin{1}-2\sin{2})+i\pi(2\cos{2}-\cos{1})\\ \end{align*}
Por igualdad de números complejos se tiene: $Re(\int_{-\infty}^{\infty}f(x)dx)=\int_{-\infty}^{\infty}\frac{x\cos{x}}{x^2-3x+2}dx=Re(\pi(\sin{1}-2\sin{2})+i\pi(2\cos{2}-\cos{1})).$
Conclusión
Por lo tanto: $\int_{-\infty}^{\infty}\frac{x\cos{x}}{x^2-3x+2}dx=\pi(\sin{1}-2\sin{2})$
Realizado por:Alan Daniel Barrón Posadas (discusión) 18:53 5 jul 2015 (CDT)
Contribución
Como posible contribución:
Integrales de Fresnel\\
En el curso de Óptica (refracción), se emplean:
$\int_{0}^{\infty}\sin{x^2}dx \wedge \int_{0}^{\infty}\cos{x^2}dx$, que son iguales a $\frac{1}{2}\sqrt{\frac{\pi}{2}}$.
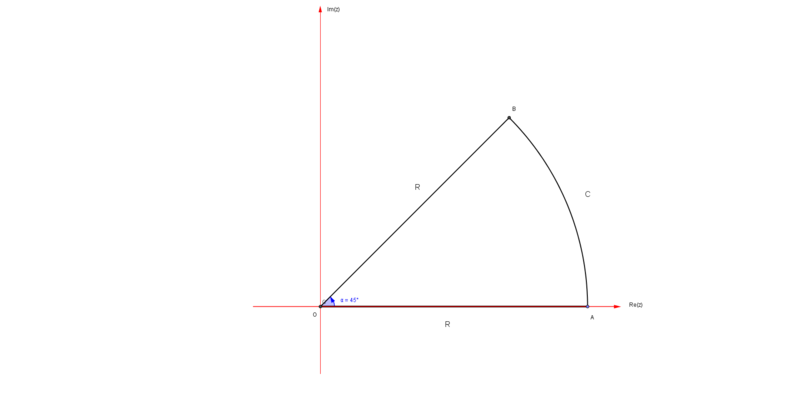
En efecto,sea $C$ el contorno mostrado en la figura, donde $AB$ es el arco de un círculo con centro en $O$ y radio $R$.Por el teorema de Cauchy $ \oint_C e^{iz^2}dz=0$.
$\int_{OA}e^{iz^2}dz+\int_{AB}e^{iz^2}dz+\int_{BO}e^{iz^2}dz=0$... (1)
Ahora sobre $OA, z=x$ (desde $x=0$ a $x=R$)
sobre $AB,z=Re^{i\theta}$ (desde $\theta=0$ a$\theta=\frac{\pi}{4}$ )
sobre $BO,z=re^{\frac{\pi i}{4}}$ (desde $r=R$ a $r=0$).
$$\int_{0}^{R}e^{ix^2}dx+\int_{0}^{\frac{\pi}{4}}e^{iR^2e^{2i\theta}}d\theta+\int_{R}^{0}e^{ir^2e^{\frac{\pi i}{2}}}e^{\frac{\pi i}{4}}dr=0...(2)$$
$$ \Longrightarrow \int_{0}^{R}(\cos{x^2}+i\sin{x^2})dx=e^{\frac{\pi i}{4}}\int_{0}^{R}e^{-r^2}dr-\int_{0}^{\frac{\pi}{4}}e^{iR^2\cos{2\theta}-R^2\sin{2\theta}}iRe^{i\theta} d\theta ...(3)$$
Si $R\to\infty$, entonces: $e^{\frac{\pi i}{4}}\int_{0}^{R}e^{-r^2}dr=\frac{\sqrt{\pi}}{2}e^{\frac{\pi i}{4}}=\frac{1}{2}\sqrt{\frac{\pi}{2}}+\frac{i}{2}\sqrt{\frac{\pi}{2}}$.
De la segunda integral de la derecha de (3):
\begin{align*} |\int_{0}^{\frac{\pi}{4}}e^{iR^2\cos{2\theta}-R^2\sin{2\theta}}iRe^{i\theta} d\theta|&\leq \int_{0}^{\frac{\pi}{4}}e^{-R^2\sin{2\theta}}Rd\theta\\ &=\frac{R}{2}\int_{0}^{\frac{\pi}{2}e^{R^2\sin{\phi}}}d\phi\\ &\leq\frac{R}{2}\int_{0}^{\frac{\pi}{2}e^{-2R^2\frac{\phi}{\pi}}}d\phi\\ &=\frac{\pi}{4R}(1-e^{-R^2}). \end{align*}
donde hemos usado la transformación $2\theta=\phi$ y la desigualdad $\sin{\phi}\geq\frac{2\phi}{\pi},0\leq\phi\leq\frac{\pi}{2}$. Esto muestra que cuando $R\to\infty$ la segunda integral a la derecha de (3) tiende a cero. Por lo anterior (3) se convierte en:
$$ \int_{0}^{\infty}(\cos{x^2}+i\sin{x^2})dx=\frac{1}{2}\sqrt{\frac{\pi}{2}}+\frac{i}{2}\sqrt{\frac{\pi}{2}}$$.
Por igualdad de números complejos se tiene:
$\int_{0}^{\infty}\sin{x^2}dx=\int_{0}^{\infty}\cos{x^2}dx=\frac{1}{2}\sqrt{\frac{\pi}{2}}$.\\
Referencia: Spiegel,Murray R. Variable Compleja. México: Editorial McGrawHill (serie Shaum), 1991.
Alan Daniel Barrón Posadas (discusión) 00:17 6 jul 2015 (CDT)
