La topología del plano complejo
1.13 Demuestre que las raíces n-ésimas de z=1 (diferentes de 1) satisfacen la ecuación ciclotómica:

Demostración
Sea  , se observa que:
, se observa que:
 entonces:
entonces:

por lo que las raíces de la ecuación ciclotómica son las mismas que las de la ecuación 
De la última ecuación se observa que  , luego
, luego  , es decir,
, es decir, ![u=\displaystyle{\sqrt[n]{1}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0bee50a989c38da767fcb71ac5d4a36ef6c49389) , con
, con 
Por lo tanto, las n-ésimas raices de  , diferentes de 1, satisfacen la ecuación ciclotómica.
, diferentes de 1, satisfacen la ecuación ciclotómica.
Realizado por: Pérez Córdoba Sabino (discusión) 12:43 4 dic 2012 (CST)
1.16.- Demuestre que un semi plano abierto es un conjunto abierto.
Demostración
Tenemos  del cual
del cual  . Decimos que
. Decimos que  . Elegimos un
. Elegimos un 












 (contradicción)
(contradicción)








 (contradicción)
(contradicción)

 .
.
Realizado por: Jean Carlo Cruz Venegas (discusión) 08:20 29 nov 2012 (CST)
1.19 Sea  . Demuestre que:
. Demuestre que:
(a)  es abierto si y sólo si
es abierto si y sólo si  .
.
(b)  es cerrado si y sólo si
es cerrado si y sólo si  .
.
Inciso a
(a) Si  es abierto, entonces para cada z ∈
es abierto, entonces para cada z ∈  existe un
existe un  tal que
tal que  . Vemos que la unión de todas las bolas
. Vemos que la unión de todas las bolas  es
es  . Además, esta unión es igual al interior de
. Además, esta unión es igual al interior de  a saber,
a saber,  , puesto que para cualquier subconjunto abierto
, puesto que para cualquier subconjunto abierto  de
de  se tiene que $ A \subset \bigcup \left \{ B(x,\epsilon) : x ∈ A \right \} $ Luego
se tiene que $ A \subset \bigcup \left \{ B(x,\epsilon) : x ∈ A \right \} $ Luego  .
.
Por otro lado, si  , entonces
, entonces  es abierto por que
es abierto por que  es abierto.
es abierto.
Inciso b
(b) Si  es cerrado, entonces
es cerrado, entonces  , por que
, por que  es el super conjunto cerrado más pequeño de
es el super conjunto cerrado más pequeño de  .
.
Por otra parte, si  entonces
entonces  es cerrado debido a que
es cerrado debido a que  es cerrado por definición.
es cerrado por definición.
Realizado por: Belen (discusión) 21:11 30 oct 2012 (UTC)
1.20 Sea  . Demuestre que:
. Demuestre que:
(a)  .
.
(b)  .
.
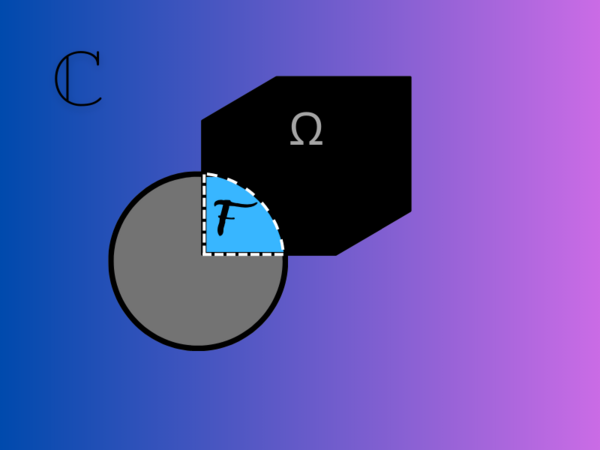
(c) $ ∂ \Omega = \Omega^{-} - \Omega ^{0} $.
(d) $ ∂ \Omega = \Omega^{-} \bigcap ( \mathbb{C} - \Omega ) ^{-} $.
Inciso a
(a)
- P.D.

Sabemos que 
Entonces  y es abierto, puesto que la cerradura es un conjunto cerrado y el complemento de un conjunto cerrado es abierto.
y es abierto, puesto que la cerradura es un conjunto cerrado y el complemento de un conjunto cerrado es abierto.
De manera que  , pues el interior de un conjunto (
, pues el interior de un conjunto ( ) es el mayor abierto contenido en ese conjunto (
) es el mayor abierto contenido en ese conjunto ( )
)
- P.D.

Sea $x \in (\mathbb{C} - \Omega )^{-}$, entonces $x \in \mathbb{C} - \Omega$ por que $\mathbb{C} - \Omega \subseteq ( \mathbb{C} - \Omega )^{-}$.
Como $ x ∈ \mathbb{C} - \Omega $, se tiene que $ x ∉ \Omega $ y también que $ x ∉ \Omega ^{0}$ ya que $\Omega ^{0} \subseteq \Omega $.
Puesto que $x \notin \Omega^{0} \Rightarrow x \in \mathbb{C} - \Omega ^{0}$, es decir, al complemento del interior de $\Omega$.
Tenemos entonces que  , de donde
, de donde  .
.
- Ya que
 y
y  , podemos decir que
, podemos decir que  .
.
Inciso b
(b)
Sabemos que ![\Omega^{-} = [\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1279895ddb03c3e8fd235b12c6208ec2a41b1a5c) .
.
Ahora, del inciso anterior,  , si
, si  . Sea
. Sea  ,
,
entonces: ![[\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bca850d56921e316fdcba71f427639eb39c41eec) .
.
Y así  .
.
Inciso c
(c)
Tenemos que ![{\displaystyle x\in \partial \ \Omega \Leftrightarrow x\in [\Omega \cap (\mathbb {C} -\Omega )]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76ae3ce4b398ed95d69339ad8a798ed44480246c) .
.
![{\displaystyle \Leftrightarrow x\in [\Omega ^{-}\cap (\mathbb {C} -\Omega )^{-}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e2cef5bbc36fab63d7a686b1c799f1ea308e4253) (puesto que
(puesto que  )
)
 y
y 
 y
y  (por el inciso anterior)
(por el inciso anterior)
 .
.
Inciso d
(d)
Veamos a la frontera  como el conjunto de puntos que NO están en el interior
como el conjunto de puntos que NO están en el interior  ni en el exterior (la unión de todos los abiertos ajenos con
ni en el exterior (la unión de todos los abiertos ajenos con  , es decir, la unión de todos los abiertos contenidos en
, es decir, la unión de todos los abiertos contenidos en  ). El exterior de
). El exterior de  es el interior de
es el interior de  , o sea el conjunto
, o sea el conjunto  .
.
Así, ![{\displaystyle \partial \Omega =\mathbb {C} -[\Omega ^{0}\cup (\mathbb {C} -\Omega )^{0}]=\mathbb {C} -\Omega ^{0}\cap \mathbb {C} -(\mathbb {C} -\Omega )^{0}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/47dcdffb8bac183f8331f40a8e72dc0370defd7c)
Sabemos del inciso (a) que  y del inciso (b) que
y del inciso (b) que  .
.
De tal forma que  .
.
Realizado por: Belen (discusión) 02:37 31 oct 2012 (UTC)
1.21 Sea  . Demuestre que:
. Demuestre que:
Inciso a
(a)  si y sólo si existe
si y sólo si existe  tal que
tal que  .
.
Si  entonces existe un
entonces existe un  tal que
tal que  , por que
, por que  es abierto. Como
es abierto. Como  , resulta que
, resulta que  . En la otra dirección, si
. En la otra dirección, si  para algún
para algún  , entonces por ser
, entonces por ser  un conjunto abierto, se tiene que
un conjunto abierto, se tiene que  , por que
, por que  es la unión de todos los subconjuntos abiertos de
es la unión de todos los subconjuntos abiertos de 
Inciso b
(b)  si y sólo si para todo
si y sólo si para todo  se tiene que
se tiene que 
Supóngase que  , por 1.20 (b)
, por 1.20 (b)  y de este modo
y de este modo  . Con esto y por el inciso anterior, se obtiene que para cada
. Con esto y por el inciso anterior, se obtiene que para cada  ,
,  . De esta forma, para cada
. De esta forma, para cada  hay un punto
hay un punto  que no pertenece a
que no pertenece a  , con lo cual
, con lo cual  , y así
, y así  . Ahora supóngase que
. Ahora supóngase que  , entonces
, entonces  , y por el inciso anterior existe un
, y por el inciso anterior existe un  tal que
tal que  . De esto se obtiene que
. De esto se obtiene que  .
.
Realizado por: Ricardo velasco bazán (discusión) 02:41 6 nov 2012 (UTC)
1.22 Sea  cualquier conjunto muestre que:
cualquier conjunto muestre que:
Ejercicio 1

Inciso a

 es abierto relativo en
es abierto relativo en  .
.
Puesto que dice que  puede ser cualquier conjunto, lo escogemos abierto, entonces
puede ser cualquier conjunto, lo escogemos abierto, entonces  será abierto relativo tal que exista un
será abierto relativo tal que exista un  , tal que
, tal que 
Dado que  contiene a
contiene a  , entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.
, entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.
Inciso b
 Si
Si  ,.....,
,....., son abiertos relativos,
son abiertos relativos,  es abierto relativo.
es abierto relativo.
Veamos, por el inciso , hemos dicho que
, hemos dicho que  , tal que
, tal que  , esto quiere decir que podemos tomar
, esto quiere decir que podemos tomar  , tal que
, tal que  , por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.
, por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.
Inciso c
 Si
Si  es cualquier familia de subconjuntos de
es cualquier familia de subconjuntos de  que son abiertos relativos, entonces
que son abiertos relativos, entonces  también es abierto relativo.
también es abierto relativo.
Hemos mostrado en  que
que  , y es abierto relativo por
, y es abierto relativo por  , ahora tenemos
, ahora tenemos  , tal que por ser abiertos y su unión es
, tal que por ser abiertos y su unión es  , lo cual sigue generando a nuestro abierto relativo.
, lo cual sigue generando a nuestro abierto relativo.
Ejercicio 2

Inciso a

 es cerrados relativo en
es cerrados relativo en  .
.
Puesto que dice que  puede ser cualquier conjunto, lo escogemos cerrado, entonces
puede ser cualquier conjunto, lo escogemos cerrado, entonces  será cerrado relativo tal que exista un
será cerrado relativo tal que exista un  , tal que
, tal que 
Inciso b
 Si
Si  ,.....,
,....., son cerrados relativos,
son cerrados relativos,  es cerrado relativo.
es cerrado relativo.
Entonces, por el inciso , hemos dicho que
, hemos dicho que  , tal que
, tal que  , esto quiere decir que podemos tomar
, esto quiere decir que podemos tomar  , tal que
, tal que  , por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.
, por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.
Inciso c
 Si
Si  es cualquier familia de subconjuntos de
es cualquier familia de subconjuntos de  que son cerrados relativos, entonces
que son cerrados relativos, entonces  también es cerrado relativo.
también es cerrado relativo.
Hemos mostrado en  que
que  , y es cerrado relativo por
, y es cerrado relativo por  , ahora tenemos
, ahora tenemos  , tal que por ser cerrados y su unión es
, tal que por ser cerrados y su unión es  , lo cual sigue generando a nuestro cerrado relativo.
, lo cual sigue generando a nuestro cerrado relativo.
Realizado por: Luis Antonio (discusión) 16:39 5 dic 2012 (CST)
1.23 Si  es abierto relativo, demuestre que
es abierto relativo, demuestre que  es cerrado relativo. Demuestre también que si
es cerrado relativo. Demuestre también que si  es cerrado relativo, entonces
es cerrado relativo, entonces  es abierto relativo
es abierto relativo
* Se dice que un subconjunto abierto  es abierto relativo en
es abierto relativo en  si existe un conjunto abierto
si existe un conjunto abierto  tal que
tal que  .
.
* Se dice que un subconjunto cerrado  es cerrado relativo en
es cerrado relativo en  si existe un conjunto cerrado
si existe un conjunto cerrado  tal que
tal que  .
.
Lo anterior es por el ejercicio 1.22
Podemos imaginar el analisis como el conjunto  es abierto relativo, su
es abierto relativo, su  será cerrado relativo, esto por que
será cerrado relativo, esto por que  podrá tocar sus puntos frontera. De manera similar si
podrá tocar sus puntos frontera. De manera similar si  es cerrado relativo, por entonces sus complemento
es cerrado relativo, por entonces sus complemento  , será abierto relativo por que
, será abierto relativo por que  no podrá tocar su frontera.
no podrá tocar su frontera.
Entonces se concluye lo que nos pide demostrar el enunciado enuciado.
Realizado por: Luis Antonio (discusión) 18:08 5 dic 2012 (CST)
1.24 Demuestre que  es conexo si y sólo si
es conexo si y sólo si  es un intervalo.
es un intervalo.
Sea ![I = [a,b], a,b \in \mathbb{R}, a < b](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4dc586451814d452d6c25abaa0f7fa1cb02ecf17) , y sea
, y sea  un subconjunto abierto de
un subconjunto abierto de  tal que
tal que  y
y  (como
(como  ,
,  no es abierto en
no es abierto en  , pero si en
, pero si en  , es decir,
, es decir,  es abierto relativo a
es abierto relativo a  ). Si se prueba que
). Si se prueba que  no es también cerrado, entonces se habrá probado que
no es también cerrado, entonces se habrá probado que  es conexo.
es conexo.
Puesto que  es abierto, existe un
es abierto, existe un  tal que
tal que  . Sea
. Sea  el mayor
el mayor  para el cual
para el cual  , es decir
, es decir  . De este modo se tiene que
. De este modo se tiene que  , pero
, pero  , por que de lo contrario, puesto que
, por que de lo contrario, puesto que  es abierto, habría un
es abierto, habría un  tal que
tal que  , contradiciendo la definición de
, contradiciendo la definición de  . Luego
. Luego  , y por tanto
, y por tanto  . Si
. Si  es también cerrado, entonces
es también cerrado, entonces  es abierto, y por tanto se puede encontrar un
es abierto, y por tanto se puede encontrar un  tal que
tal que  , lo cual contradice el hecho de que
, lo cual contradice el hecho de que  . Por lo tanto,
. Por lo tanto,  no puede ser cerrado.
no puede ser cerrado.
Ahora supóngase que  no es un intervalo, entonces existen dos puntos
no es un intervalo, entonces existen dos puntos  , tal que
, tal que  (un teorema afirma que
(un teorema afirma que  es un intervalo si y sólo si para cualquier par de puntos
es un intervalo si y sólo si para cualquier par de puntos  , con
, con  se tiene que
se tiene que  ). Entonces, existe un punto
). Entonces, existe un punto  tal que
tal que  . Como
. Como  y
y  se tiene que
se tiene que  , donde
, donde  y
y  son conjuntos disjuntos no vacíos. Por lo tanto,
son conjuntos disjuntos no vacíos. Por lo tanto,  no es conexo.
no es conexo.
Realizado por: Ricardo velasco bazán (discusión) 03:18 6 nov 2012 (UTC)
1.25 Un subconjunto  se dice que es convexo si para cualquiera dos puntos
se dice que es convexo si para cualquiera dos puntos 
 se tiene que el segmento
se tiene que el segmento ![[z,w]\subseteq](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c73b89b4ecbfcc4b203eb0a2ce0d46f6faa3f33c)
 .
.
- (1) Demuestre que cualquier disco abierto o cerrado es convexo.
- (2) Demuestre que cualquier semiplano abierto o cerrado es convexo.
- (3) Demuestre que la intersección de cualquier familia de subconjuntos convexos es convexa.
- Demostración
Inciso 1
(1) Por definición ![[z,w]:=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23f29c30fc0263283349c24de1046c77c2574852) {
{ }
}
Sean  , entonces
, entonces  ;
; .......................(*)
.......................(*)
Sea  arbitrario, pero fijo definido por
arbitrario, pero fijo definido por  , así todo punto del segmento [z,w] esta representado por
, así todo punto del segmento [z,w] esta representado por  .
.
- Por otra parte
 al sumar y restar
al sumar y restar  se tiene que
se tiene que
 agrupando y factorizando
agrupando y factorizando
 aplicando la desigualdad del triángiulo
aplicando la desigualdad del triángiulo
 n
Como
n
Como  , entonces
, entonces  y de las propiedades del valor absoluto tenemos que
y de las propiedades del valor absoluto tenemos que
 aplicando (*)
aplicando (*)
 por lo que
por lo que  Como
Como  fue arbitrario, entonces
fue arbitrario, entonces ![[z,w]\subseteq B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8f6e41e92495b3e8eaa7f8ff01b9e6149794d272)
Así, hemos dado dos elementos  cuyo segmento
cuyo segmento ![[z,w]\in B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4d01317c96326be3cacab1a4dca89f1a6dffebf7)
Por lo tanto, un disco abierto es convexo
Para un disco cerrado solo se reemplazan la desigualdad estricta de (*) por una desigualdad.
Sean  con
con  un semiplano abierto generado por
un semiplano abierto generado por  , luego
, luego  &
&  (**)
(**)
Sea ![z_t\in[x,y]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eb290cc604cfe09c6b9c7d64746eb13cff635cbc) arbitrario, entonces
arbitrario, entonces




Como  y de (**) se tiene que
y de (**) se tiene que
 , como
, como  fue arbitrario, entonces
fue arbitrario, entonces 
Por lo tanto un semiplano abierto es convexo.
Para el caso del semiplano cerrado basta con cambiar la condición (**).
Realizado por: Pérez Córdoba Sabino (discusión) 19:17 22 nov 2012 (CST)
1.27 Si  es abierto, demuestre que sus componentes conexas son abiertas también.
es abierto, demuestre que sus componentes conexas son abiertas también.
Tomemos una componente  y un punto
y un punto  , como
, como  y
y  es abierto, existe un disco
es abierto, existe un disco  . Recordando que un subconjunto
. Recordando que un subconjunto  no vacío, se puede descomponer como la unión de subconjuntos conexos (proposición 1.8),tenemos que la unión
no vacío, se puede descomponer como la unión de subconjuntos conexos (proposición 1.8),tenemos que la unión  es conexa; y por el hecho de que un conjunto se puede llenar por subconjuntos y los intersticios que hay entre ellos se llenan con conjuntos más pequeños, debe ser igual a
es conexa; y por el hecho de que un conjunto se puede llenar por subconjuntos y los intersticios que hay entre ellos se llenan con conjuntos más pequeños, debe ser igual a  . Con esto se entiende que
. Con esto se entiende que  y por tanto
y por tanto  es abierto.
es abierto.
Realizado por: Ignacio Peralta Martínez (discusión) 19:02 6 nov 2012 (UTC)
FUENTES (INFORMACIÓN ADICIONAL):
LEYES DE MORGAN
Compleja:z-ej-cap1.0
Compleja:z-ej-cap1.1
Compleja:z-ej-cap1.2
Compleja:z-ej-cap1.3
Compleja:z-ej-cap1.4
Compleja:z-ej-cap2.1
Compleja:z-ej-cap2.2







![u=\displaystyle{\sqrt[n]{1}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0bee50a989c38da767fcb71ac5d4a36ef6c49389)








































![\Omega^{-} = [\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1279895ddb03c3e8fd235b12c6208ec2a41b1a5c)



![[\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bca850d56921e316fdcba71f427639eb39c41eec)
![{\displaystyle x\in \partial \ \Omega \Leftrightarrow x\in [\Omega \cap (\mathbb {C} -\Omega )]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76ae3ce4b398ed95d69339ad8a798ed44480246c)
![{\displaystyle \Leftrightarrow x\in [\Omega ^{-}\cap (\mathbb {C} -\Omega )^{-}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e2cef5bbc36fab63d7a686b1c799f1ea308e4253)








![{\displaystyle \partial \Omega =\mathbb {C} -[\Omega ^{0}\cup (\mathbb {C} -\Omega )^{0}]=\mathbb {C} -\Omega ^{0}\cap \mathbb {C} -(\mathbb {C} -\Omega )^{0}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/47dcdffb8bac183f8331f40a8e72dc0370defd7c)



























































![I = [a,b], a,b \in \mathbb{R}, a < b](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4dc586451814d452d6c25abaa0f7fa1cb02ecf17)




























![[z,w]\subseteq](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c73b89b4ecbfcc4b203eb0a2ce0d46f6faa3f33c)
![[z,w]:=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23f29c30fc0263283349c24de1046c77c2574852)

















![[z,w]\subseteq B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8f6e41e92495b3e8eaa7f8ff01b9e6149794d272)

![[z,w]\in B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4d01317c96326be3cacab1a4dca89f1a6dffebf7)





![z_t\in[x,y]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eb290cc604cfe09c6b9c7d64746eb13cff635cbc)














