Usuario discusión:Ignacio Peralta Martínez
Bienvenido a Luz-wiki! Esperamos que contribuyas mucho y bien. Probablemente desearás leer las páginas de ayuda. Nuevamente, bienvenido y diviértete! mfg-wiki 01:02 10 feb 2012 (UTC)
1.61. Un punto se dice que es aislado si existe un disco con , tal que . Demuestre que si , entonces es un punto aislado o un punto de acumulación de .
En primer lugar supongamos que un punto aislado de , por lo que cumple que , veremos si es un punto de acumulación, entonces nos da una bola de radio pero sin su centro () y la intersección de nos da necesariamente el vacio pues eliminamos al único elemento de , . Por lo que nos es punto de acumulación.
Ahora supongamos que s un punto de acumulación por lo tanto cumple que Error al representar (error de sintaxis): \Omega\cap(B(z_{0};\varepsilon)-\left\{ z_{0}\right\} )\neq\textrm{Ø} veremos si es un punto aislado. Al ver este caso nos percatamos que el caso más extremo es aquel en el que el punto de acumulación está afuera y la bola toca solo un punto frontera de (los demás casos serían más simples de resolver), aquí vemos que no se encuentra en solo el punto al que nos referimos anteriormente. Por lo tanto no cumple con ser un punto aislado.
1.62. Si es un punto aislado, demuestre que cualquier función es continua en .
Como es punto aislado cumple con la definición dada en el ejercicio anterior, aplicando la definición de continuidad a los conjuntos vemos para que sea continua la función para el disco abierto en un plano uv, existe un disco abierto en el plano de xy, tal que para todo se tiene tiene . Lo cual es cierto para un punto aislado ya que bola en el plano xy con radio se interseca con solamente en por definición, para que cumpliera la continuidad ese elemento tiene que dar forzosamente a un punto en , en este caso es el centro; lo que era de esperarse pues era una condición impuesta al principio. Por lo tanto cualquier función es continua en un punto aislado.
--Ignacio Peralta Martínez (discusión) 03:45 29 nov 2012 (CST)
3.35 muestre que la función u del ejemplo 2.9 no tiene conjugada armónica. Sea
buscamos una función v tal que
por lo que para encontrar la v integramos respecto a y:
pero para verificar que es la buena veremos que cumpla con la condición de la segunda ecuación de Cauchy-Riemann
De igual forma integramos para obtener la v, pero ahora con respecto a x
como vemos los argumentos de la función no son iguales ni tampoco salió el signo negativo, por lo tanto la función no tiene armónica conjugada.
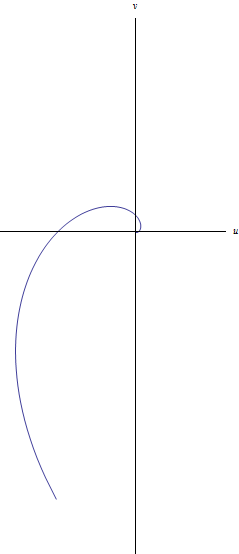
--Ignacio Peralta Martínez (discusión) 05:17 29 nov 2012 (CST) 2.34. Muestre que la imagen bajo la exponencial de la recta , para es una espiral logarítmica y bosqueje su imagen. Sea entonces
hacemos a entonces
con lo que comparamos y nos queda la solución
nota: la parte imaginaria de z en realidad se le suma donde k es cualquier entero.
Para el bosquejo simplemente se sustituye el valor de z en la exponencial compleja, y al pasarlas al plano uv, se puede graficar la espiral al darle valores a las siguientes componentes.
--Ignacio Peralta Martínez (discusión) 05:17 29 nov 2012 (CST)
_____________________________________________________________________________________________________________________
Problema 1.4 vibraciones
La solución es incorrecta. La ecuación que debes resolver es
--Ernesto (discusión) 14:10 29 may 2013 (CDT)
Problema 2.9 vibraciones
La solución es correcta.
--Ernesto (discusión) 20:59 18 jun 2013 (CDT)--Ernesto (discusión) 20:59 18 jun 2013 (CDT)
Problema 3.9 vibraciones
La solución es correcta.
--Ernesto (discusión) 10:50 3 jul 2013 (CDT)
Problema 4.5 vibraciones
El inciso b es incorrecto. En la última oscilación la amplitud está entre los valores $50 mm$ a la derecha y $35 mm$ a la izquierda del punto de equilibrio. Por lo que la fuerza máxima es
,
y la fuerza mínima es
--Ernesto (discusión) 10:41 3 jul 2013 (CDT)
Problema 5.8 vibraciones
La solución es correcta.
--Ernesto (discusión) 21:09 4 jul 2013 (CDT)
Problema 2.17 ondas
La solución es correcta
--Ernesto (discusión) 19:51 6 jul 2013 (CDT)
Problema 3.38 ondas
la solución es correcta
--Ernesto (discusión) 20:06 6 jul 2013 (CDT)
Punto de vista
La soluciòn al problema 1.4 es correcta Israel López (discusión) 04:27 26 ene 2014 (UTC)