--Luis Antonio (discusión) 23:03 10 dic 2012 (CST)
1.5 Sean  y
y 
 . Demostrar que:
. Demostrar que:
(a)

Veamos, sabemos que  , el conjugado de un número complejo es
, el conjugado de un número complejo es  , por ende nuestro número complejo conjugado tiene a su conjugado
, por ende nuestro número complejo conjugado tiene a su conjugado  esto es z.
esto es z.
Por lo tanto nuestra igualdad se cumple se cumple.
(b)
 .
.
Sean  ;
;  , entonces;
, entonces; 
Veamos
![[\overline{(a+bi)+(c+di)}]=[\overline{a+bi+c+di}]=[\overline{a+c+bi+di)}]=[\overline{(a+c)+(b+d)i}]=(a+c)-(b+d)i=(a+c)+(-b-d)i=a+c-bi-di=\overline{z}+\overline{w}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f386c2137bfcb5fcea2e5cbe3be13ca8a1cf33a5)
(c)
![[\overline{(a+bi)(c+di)}]=(a-bi)(c-di)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be9b5a43542ed75819cd7111402d090f5dd6ac6c)
![[\overline{(a+bi)(c+di)}]=[\overline{ac+adi+bci-bd}]=[\overline{(ac-bd)+(ad+bc)i}]={(ac-bd)-(ad+bc)i}=(a-bi)(c-di)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8faa660642747065eb3297f71af050f88df5c16b)
(d)
Si z≠0 entonces,  ;
;
![\overline{(a+bi)^-1}=[1/(\overline{a+bi})]=1/(a-bi)=(a-bi)^\left(-1\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c61398b37798007d3d92269da29bc3091cd13dd0)
Si z≠0, entonces 

1.7 Si z= a+bi, demostrar que
 e
e 
![R(z)=(1/2)[(z+\overline{z})=(1/2)[(a+bi]+(a-bi)]\,\!=(1/2)(a+bi+a-bi)\,\!=(1/2)(a+bi+a-bi)\,\!=(1/2)(2a)\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5180b26d32e41b15cfc9cfe489d3e7a31753f7df)

![\therefore R(z)=(1/2)[(z+\overline{z})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/44196c8b0430fbf9ca298728181e097ec7273485)
![Im(z)=(1/2i)[(a+bi]-(a-bi)]\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33846aa57690972f179b45b701218736b09f5cf1)



1.12. Calcule las raíces indicadas:
Raíces cuadradas de w=i
![\sqrt[n]{w}=[r_0 \exp{i(\theta\!+2k\pi\!)} ]^{1/n}= \sqrt[n]{r_0}\exp\left[\frac{i(\theta_0\! +2k\pi\!)}{n}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a7e2fc9277bc18e5e703b512521ffdd0e549d0c8)
1. Raíces cuadradas de w=
![i=1\left[cos\left(\frac{3\pi\!}{2}\right)-isin\left(\frac{3\pi\!}{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5587c20031834cf0e1add8510908cf7a79c53c11)
Observamos que  y
y  .
.
Entoces con nuestra definición
![\sqrt[2]{w}= \sqrt[2]{1}\exp\left[\frac{i(\left(\frac{3\pi\!}{2}\right) +2k\pi\!)}{2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a03133f1a146cb1ef164ecc3224ccaefb7fcd68b)
para 
![w_0=\sqrt[2]{1}\exp\left[i\left(\frac{3\pi\!}{4}\right)\right]=1\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=1\left(\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b3bc8e9b57b29b47215a874ae35d8f86b9498e26)
Para  ; tenemos que
; tenemos que 
![w_1=1\left[cos\left(\frac{7\pi\!}{4}\right)-isin\left(\frac{7\pi\!}{4}\right)\right]=1\left(\frac{\sqrt{2}}{2} +i\frac{\sqrt{2}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ab68cddb07a0440c9acfbfbed3b8b83dc62f8427)
Estas son las 2 raíces cuadradas para  Si le diéramos más valores a K lo único que estaríamos haciendo es darle vueltas a nuestro circulo de radio 1, donde se encuentran contenidas nuestras raíces.
Si le diéramos más valores a K lo único que estaríamos haciendo es darle vueltas a nuestro circulo de radio 1, donde se encuentran contenidas nuestras raíces.
2. Raíces cuartas de 
![w=-1+\sqrt{3}= 2\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c082533e0bb766b6772302bdbdcf0ca6dad6728a)
Observamos  y
y 
Nuestra formula de obtención de raíces queda;
![\sqrt[4]{2}\exp{i}\left(\frac{\pi\!}{3}+\frac{k\pi\!}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0dad568151ea79913809275fb9c19455c9be00ed)
Como ya sabemos K es lo que varía para obtener nuestras raíces

![w_0=\sqrt[4]{2}\exp{i}\left(\frac{\pi\!}{3}\right)=\sqrt[4]{2}\left[cos\left(\frac{\pi\!}{3}\right)-isin\left(\frac{\pi\!}{3}\right)\right]=\sqrt[4]{2}\left(\frac{1}{2}-i\frac{\sqrt{3}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e9990545a05586dfd28c46624ac46ddfbfb9b04b)

![w_1=\sqrt[4]{2}\exp{i}\left(\frac{5\pi\!}{6}\right)=\sqrt[4]{2}\left[cos\left(\frac{5\pi\!}{6}\right)-isin\left(\frac{5\pi\!}{6}\right)\right]=\sqrt[4]{2}\left(-\frac{\sqrt{3}}{2}-i\frac{1}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f1f28401ef8af112e7fdd5ef3041fd9a8239a9a2)

![w_2=\sqrt[4]{2}\exp{i}\left(\frac{4\pi\!}{3}\right)=\sqrt[4]{2}\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]=\sqrt[4]{2}\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7adcf00791efb1249ba2e8be346e8ace95edd8f4)

![w_3=\sqrt[4]{2}\exp{i}\left(\frac{11\pi\!}{6}\right)=\sqrt[4]{2}\left[cos\left(\frac{11\pi\!}{6}\right)-isin\left(\frac{11\pi\!}{6}\right)\right]=\sqrt[4]{2}\left(\frac{\sqrt{3}}{2}+i\frac{1}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/742cba82b2d219229802170f73a67647e80499da)
3. Raíces sextas de 
![w=1= 1\left[cos\left(0\right)-isin\left(0\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ddfc7be57132df19c9f983703899f9c7eace5231)
Vemos que

Entonces nuestra ecuaciòn de raíces queda;
![\sqrt[6]{1}\exp{i}\left(\frac{0}{6}+\frac{k\pi\!}{3}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1c8a912ef58cc1f65859d73a0f6e4c22c7ac5c87)

![w_0=\sqrt[6]{1}\left[cos\left(0\right)-isin\left(0\right)\right]=\sqrt[6]{1}\left(1-i\left(0\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9a74ca3d3a393a69f20c74a3b1a4f224c26a94cb)

![w_1=\sqrt[6]{1}\left[cos\left(\frac{\pi\!}{3}\right)-isin\left(\frac{\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fa1e76f693ff175d4c2068b2a4a336721cff05e4)

![w_2=\sqrt[6]{1}\left[cos\left(\frac{2\pi\!}{3}\right)-isin\left(\frac{2\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(-\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/191d62ce96655e76b3dd14e9d7814dfb2d1a0109)

![w_3=\sqrt[6]{1}\left[cos\left(\pi\!\right)-isin\left(\pi\!\right)\right]=\sqrt[6]{1}\left(-1-i\left(0\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9343572ba1c9b7e4f4ce07399932569f90c9ecd2)

![w_4=\sqrt[6]{1}\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f92c067935e53b2d724867f901964329fd525eb)

![w_5=\sqrt[6]{1}\left[cos\left(\frac{5\pi\!}{3}\right)-isin\left(\frac{5\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e5bf40e916996ae796ef46cd4151c589404cce6d)
4.Raíces cúbicas de 
![w=1-i= \sqrt{2}\left[cos\left(\frac{\pi\!}{4}\right)-isin\left(\frac{\pi\!}{4}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1c10c846d2f64a3fb83b9f8ddb2da793c65d82a3)
Vemos que

Nuestra ecuación queda;
![\sqrt[6]{2}\exp{i}\left(\frac{\pi\!}{12}+\frac{2k\pi\!}{3}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b4c4fd046a380ee5d1ca3f2ed042e6d1dd4ebdbe)

![w_0=\sqrt[6]{2}\exp{i}\left(\frac{\pi\!}{12}\right)=\sqrt[6]{2}\left[cos\left(\frac{\pi\!}{12}\right)-isin\left(\frac{\pi\!}{12}\right)\right]=\sqrt[6]{2}\left(0.9659-i\left(0.2588\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8cdb02cfb0242c5a660d83aae6eac8ee5d1ec9d9)

![w_1=\sqrt[6]{2}\exp{i}\left(\frac{3\pi\!}{4}\right)=\sqrt[6]{2}\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=\sqrt[6]{2}\left(-\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/948a91a570545d2d0bef9e80522dc5072082da31)

![w_2=\sqrt[6]{2}\exp{i}\left(\frac{17\pi\!}{12}\right)=\sqrt[6]{2}\left[cos\left(\frac{17\pi\!}{12}\right)-isin\left(\frac{17\pi\!}{12}\right)\right]=\sqrt[6]{2}\left(-0.2588-i\left(0.9656)\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a0aca186b9da9d077b004191ae5d6850ebf34a73)
5. Raíces cuartas de 
![w=-16= 16\left[cos\left(\pi\!\right)-isin\left(\pi\!\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0fd0cfed00dae4bd65da63214a6087ecbd4a6bb3)

Nuestra ecuación queda
![\sqrt[4]{16}\exp{i}\left(\frac{\pi\!}{4}+\frac{k\pi\!}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23b91472576f1043fdf2a41fdd0455f5da557d9e)

![w_0=\sqrt[4]{16}\exp{i}\left(\frac{\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{\pi\!}{4}\right)-isin\left(\frac{\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d305cb024abe606b05690343773cbf963d97064e)

![w_1=\sqrt[4]{16}\exp{i}\left(\frac{3\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(-\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d858d9210af895b96fef497e04631ab65ca1e7ae)

![w_2=\sqrt[4]{16}\exp{i}\left(\frac{5\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{5\pi\!}{4}\right)-isin\left(\frac{5\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(-\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5da7c9b454cb1a97e09c45a69dd3857dead63f79)

![w_3=\sqrt[4]{16}\exp{i}\left(\frac{7\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{7\pi\!}{4}\right)-isin\left(\frac{7\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2df3a75f264c8304250cbfe7affb02fdc11922cc)
6. Raíces quintas de 
![w=32i= 32\left[cos\left(-\frac{\pi\!}{2}\right)-isin\left(-\frac{\pi\!}{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0f84099369588e0c3b71a593b8120e7237486305)

Nuestra ecuación queda
![\sqrt[5]{32}\exp{i}\left(-\frac{\pi\!}{10}+\frac{2k\pi\!}{5}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b074f53ee2ea2b0981ff0043382fed61a51512ca)

![w_0=\sqrt[5]{32}\exp{i}\left(-\frac{\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(-\frac{\pi\!}{10}\right)-isin\left(-\frac{\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0.9510\right)+i\left(0.3090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/32f812e8458f4f16b8417cefa194a69a1f4916de)

![w_1=\sqrt[5]{32}\exp{i}\left(\frac{3\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{3\pi\!}{10}\right)-isin\left(\frac{3\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0.5877\right)-i\left(0.8090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e48fce49791327eff4a98fdf8f1aebe41472bb02)

![w_2=\sqrt[5]{32}\exp{i}\left(\frac{7\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{7\pi\!}{10}\right)-isin\left(\frac{7\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(-0.5877)\right)-i\left(0.8090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7a09076c808491941fdb5d6bd261846419f9498)

![w_3=\sqrt[5]{32}\exp{i}\left(\frac{11\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{11\pi\!}{10}\right)-isin\left(\frac{11\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0\right)+i\left(0.3090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85b5825edccb20cdc9b19c19776ceac84a43711c)

![w_4=\sqrt[5]{32}\exp{i}\left(\frac{3\pi\!}{2}\right)=\sqrt[5]{32}\left[cos\left(\frac{3\pi\!}{2}\right)-isin\left(\frac{3\pi\!}{2}\right)\right]=\sqrt[5]{32}\left(\left(0\right)+i\left(1\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5c27126e3607dd4c5cf8bf02917277beb5bff2e4)
1.22 Sea  cualquier conjunto muestre que:
cualquier conjunto muestre que:


 es abierto relativo en
es abierto relativo en  .
.
Puesto que dice que  puede ser cualquier conjunto, lo escogemos abierto, entonces
puede ser cualquier conjunto, lo escogemos abierto, entonces  será abierto relativo tal que exista un
será abierto relativo tal que exista un  , tal que
, tal que 
Dado que  contiene a
contiene a  , entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.
, entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.
 Si
Si  ,.....,
,....., son abiertos relativos,
son abiertos relativos,  es abierto relativo.
es abierto relativo.
Veamos, por el inciso , hemos dicho que
, hemos dicho que  , tal que
, tal que  , esto quiere decir que podemos tomar
, esto quiere decir que podemos tomar  , tal que
, tal que  , por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.
, por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.
 Si
Si  es cualquier familia de subconjuntos de
es cualquier familia de subconjuntos de  que son abiertos relativos, entonces
que son abiertos relativos, entonces  también es abierto relativo.
también es abierto relativo.
Hemos mostrado en  que
que  , y es abierto relativo por
, y es abierto relativo por  , ahora tenemos
, ahora tenemos  , tal que por ser abiertos y su unión es
, tal que por ser abiertos y su unión es  , lo cual sigue generando a nuestro abierto relativo.
, lo cual sigue generando a nuestro abierto relativo.


 es cerrados relativo en
es cerrados relativo en  .
.
Puesto que dice que  puede ser cualquier conjunto, lo escogemos cerrado, entonces
puede ser cualquier conjunto, lo escogemos cerrado, entonces  será cerrado relativo tal que exista un
será cerrado relativo tal que exista un  , tal que
, tal que 
 Si
Si  ,.....,
,....., son cerrados relativos,
son cerrados relativos,  es cerrado relativo.
es cerrado relativo.
Entonces, por el inciso , hemos dicho que
, hemos dicho que  , tal que
, tal que  , esto quiere decir que podemos tomar
, esto quiere decir que podemos tomar  , tal que
, tal que  , por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.
, por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.
 Si
Si  es cualquier familia de subconjuntos de
es cualquier familia de subconjuntos de  que son cerrados relativos, entonces
que son cerrados relativos, entonces  también es cerrado relativo.
también es cerrado relativo.
Hemos mostrado en  que
que  , y es cerrado relativo por
, y es cerrado relativo por  , ahora tenemos
, ahora tenemos  , tal que por ser cerrados y su unión es
, tal que por ser cerrados y su unión es  , lo cual sigue generando a nuestro cerrado relativo.
, lo cual sigue generando a nuestro cerrado relativo.
--Luis Antonio (discusión) 16:39 5 dic 2012 (CST)
1.23 Si  es abierto relativo, demuestre que
es abierto relativo, demuestre que  es cerrado relativo. Demuestre también que si
es cerrado relativo. Demuestre también que si  es cerrado relativo, entonces
es cerrado relativo, entonces  es abierto relativo
es abierto relativo
* Se dice que un subconjunto abierto  es abierto relativo en
es abierto relativo en  si existe un conjunto abierto
si existe un conjunto abierto  tal que
tal que  .
.
* Se dice que un subconjunto cerrado  es cerrado relativo en
es cerrado relativo en  si existe un conjunto cerrado
si existe un conjunto cerrado  tal que
tal que  .
.
Lo anterior es por el ejercicio 1.22

Podemos imaginar el analisis como el conjunto  es abierto relativo, su
es abierto relativo, su  será cerrado relativo, esto por que
será cerrado relativo, esto por que  podrá tocar sus puntos frontera. De manera similar si
podrá tocar sus puntos frontera. De manera similar si  es cerrado relativo, por entonces sus complemento
es cerrado relativo, por entonces sus complemento  , será abierto relativo por que
, será abierto relativo por que  no podrá tocar su frontera.
no podrá tocar su frontera.
Entonces se concluye lo que nos pide demostrar el enunciado enuciado.
1.32 Si  demuestre que
demuestre que es un punto de acumulación de
es un punto de acumulación de  .
.
Un punto  se dice que es un punto de acumulación
se dice que es un punto de acumulación  , si al menos alrededor de
, si al menos alrededor de  contiene un punto
contiene un punto  . Entonces si
. Entonces si  , este contiene todos sus puntos de acumulación
, este contiene todos sus puntos de acumulación
Ayudandonos del lema 1.12
si  , un punto de acumulción de
, un punto de acumulción de  si y sólo sí existe una sucesión
si y sólo sí existe una sucesión , tal que
, tal que
 .
.
Una sucesión convergente tiene exactamente un punto límite, su límite
 si
si  es un punto de acumulación de
es un punto de acumulación de  , y
, y  , por lo tanto
, por lo tanto 
Hay una bola  centrado en
centrado en  , y pasa que Error al representar (error de sintaxis): {\displaystyle \boldsymbol{\Omega}\cap\left(B\left(\mathcal{Z};\boldsymbol{\epsilon}\right)-\{\mathcal{Z}\}\right)\neq Ø}
.
, y pasa que Error al representar (error de sintaxis): {\displaystyle \boldsymbol{\Omega}\cap\left(B\left(\mathcal{Z};\boldsymbol{\epsilon}\right)-\{\mathcal{Z}\}\right)\neq Ø}
.
Por el ejercicio 1.21, tenemos que  , entonces si hay una sucesión
, entonces si hay una sucesión  , tal que sea convergente, osea
, tal que sea convergente, osea  .
.
1.56 Dé un ejemplo de una función continua que no es uniformemente continua.
Para mi  , no es uniformemente continua en el intervalo
, no es uniformemente continua en el intervalo  , o sea
, o sea  .
.
Del último párrafo de la pagina 30 del libro de Teoría de funciones de una variable compleja de Zaldivar Felipe. Podemos entender lo siguiente;
Si pensamos que  es uniformemente continua en el intervalo. Entonces para cualquier
es uniformemente continua en el intervalo. Entonces para cualquier  , debería ser posible encontrar
, debería ser posible encontrar  , entre 0 y 1, tal que
, entre 0 y 1, tal que  cuando
cuando  para todo
para todo  y
y  en el intervalo.
en el intervalo.
Para  y
y  .
.
 .
.
Por otro lado,
 ya que
ya que
De este modo tenemos una contradicción, y tenemos que  no es uniformemente continua en el intervalo.
no es uniformemente continua en el intervalo.
1.71.Si  ,
, , demuestre que
, demuestre que
 .
.
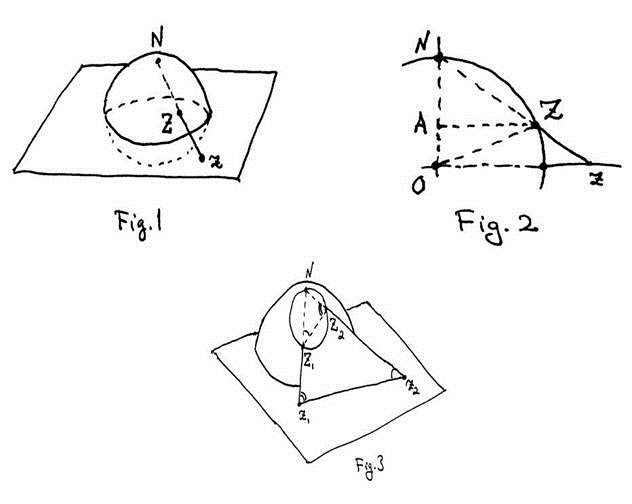
Sea  ,
,
Por triángulos semejantes  y
y
 , implica
, implica  .
.
Pero y
y  , entonces
, entonces
 y
y 
El plano N_z1z2, intersecta a S en un circulo, .
.
Vemos que ,
,
los triangulos N_z1z2 y N_Z1Z2, son semejantes, entonces;

Hacemos
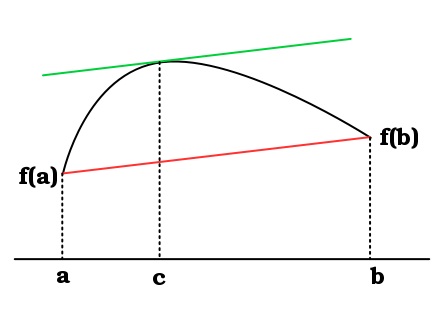
2.5 (Teorema del valor medio) Si  con
con ![a<b \mathcal{F} :\left[a,b\right]\rightarrow\mathbb{R}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b3525429d45d83e5d71b6b740aa78f59b0a0af28) , es continua y además es derivable en
, es continua y además es derivable en  , demuestre que existe un
, demuestre que existe un  , tal que:
, tal que:
Error al representar (error de sintaxis): \mathcal{F}^´\left(\epsilon\right) =\frac{\mathcal{F}\left(b\right)-\mathcal{F}\left(a\right)}{\left(b-a\right)}.
Suponemos una función  , como
, como  es continua en
es continua en ![\left[a,b\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa) , aparte la otra función
, aparte la otra función  , es continua en el intervalo entonces
, es continua en el intervalo entonces  también lo es.
también lo es.
Obtengamos su derivada;
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mathcal{g}^´ \left(x\right) = \mathcal{F}^´ \left(x\right)\left(b-a\right)-x\left(\mathcal{F}\left(b\right)-\mathcal{F}\left(a\right)\right).
Es diferenciable en  al igual que
al igual que 
Ahora, notemos;




El Teorema de Rolle, nos dice que exite  en
en  tal que;
tal que;
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 0=\mathcal{g}^´ \left(\epsilon\right)=\mathcal{F}^´ \left(\epsilon\right)\left(b-a\right)-\left(\mathcal{F} \left(b\right)-\mathcal{F} \left(a\right)\right)\Rightarrow \mathcal{F}\left(b\right)-\mathcal{F}\left(a\right)= \mathcal{F}^´ \left(\epsilon\right)\left(b-a\right).
2.29 Se definen las otras funciones trigonométricas complejas, en términos del seno y coseno complejos, como es usual:
 ;
; 
 ;
; 
Encuentre sus dominios y muestre que son holomorfas en su dominio y sus derivadas son las esperadas.
El dominio del primer par de funciones es todo 
El dominio del segundo par de funciones es todo 
Donde 
Para mostrar que son holomorfas en su dominio, basta demostrar las ecuaciones de Cauchy-Riemann. osea, que son diferenciables en su dominio, lo cual nos genera un intervalo abierto en el cual es diferenciable.
 y
y 
sabemos 
Entonces tenemos que la parte real;

y la parte imaginaria es ;

Comprobemos las ecucuaciones de Cauchy-Riemann.
![\mathcal{U}_x=\frac{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]2cos\left(2\mathcal{x}\right)- sen\left(2\mathcal{x}\right)\left(-2sen\left(2\mathcal{x}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}=\frac{2+2cos\left(2\mathcal{x}\right) \left( cosh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/89b5e2c3fab9eb67f8a116495f4cb8e52d5726dc)
![\mathcal{V}_y =\frac{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]2cosh\left(2\mathcal{y}\right)- senh\left(2\mathcal{y}\right)\left(-2senh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}=\frac{2+2cos\left(2\mathcal{x}\right) \left( cosh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f35a17f1888e041e7dfb5d9a5ca5f2827c2ce3a6)
De manera similar obtenemos;
![\mathcal{U}_y = \frac{-sin\left(2\mathcal{x}\right)\left[2senh\left(2\mathcal{y}\right)\right]}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2} =-\frac{2sen\left(2\mathcal{x}\right)senh\left(2\mathcal{y}\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b91d4602e9907dd2906e023136d5a32dc977384b)
![\mathcal{V}_x = \frac{-sinh\left(2\mathcal{y}\right)\left[-2sen\left(2\mathcal{x}\right)\right]}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2} =\frac{2sen\left(2\mathcal{x}\right)senh\left(2\mathcal{y}\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/36a8ce7757011a2ba9e687dfb24c179ba87c01bc)
Cumple con las ecuaciones de Cauchy-Riemann, en un intervalo diferenciable, por lo cual es Holomorfa(Analítica).
Ahora comprobemos sus derivadas respecto a z, y veamos que son las esperadas;
 y entonces Error al representar (error de sintaxis): Tan^´\left(\mathcal{z}\right)=\frac{cos(\left(\mathcal{z}\right)cos(\left(\mathcal{z}\right)-sen\left(\mathcal{z}\right)\left(-sen\left(\mathcal{z}\right)\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{cos^2\left(\mathcal{z}\right)+ sin^2\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{1}{cos^2\left(\mathcal{z}\right)}= sec^2\left(\mathcal{z}\right).
y entonces Error al representar (error de sintaxis): Tan^´\left(\mathcal{z}\right)=\frac{cos(\left(\mathcal{z}\right)cos(\left(\mathcal{z}\right)-sen\left(\mathcal{z}\right)\left(-sen\left(\mathcal{z}\right)\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{cos^2\left(\mathcal{z}\right)+ sin^2\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{1}{cos^2\left(\mathcal{z}\right)}= sec^2\left(\mathcal{z}\right).
 y entonces Error al representar (error de sintaxis): Sec^´\left(\mathcal{z}\right)=-\frac{-sen(\left(\mathcal{z}\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{sen\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{tan\left(\mathcal{z}\right)}{cos\left(\mathcal{z}\right)}= tan\left(\mathcal{z}\right)sec\left(\mathcal{z}\right).
y entonces Error al representar (error de sintaxis): Sec^´\left(\mathcal{z}\right)=-\frac{-sen(\left(\mathcal{z}\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{sen\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{tan\left(\mathcal{z}\right)}{cos\left(\mathcal{z}\right)}= tan\left(\mathcal{z}\right)sec\left(\mathcal{z}\right).
 y entonces Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): Cot^´\left(\mathcal{z}\right)=\frac{-sen\left(\mathcal{z}\right)sen\left(\mathcal{z}\right)-cos\left(\mathcal{z}\right)\left(cos\left(\mathcal{z}\right)\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=\frac{-sen^2\left(\mathcal{z}\right)- cos^2\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= \frac{-1}{sen^2\left(\mathcal{z}\right)}= -csc^2\left(\mathcal{z}\right).
y entonces Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): Cot^´\left(\mathcal{z}\right)=\frac{-sen\left(\mathcal{z}\right)sen\left(\mathcal{z}\right)-cos\left(\mathcal{z}\right)\left(cos\left(\mathcal{z}\right)\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=\frac{-sen^2\left(\mathcal{z}\right)- cos^2\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= \frac{-1}{sen^2\left(\mathcal{z}\right)}= -csc^2\left(\mathcal{z}\right).
 y entonces Error al representar (error de sintaxis): Csc^´\left(\mathcal{z}\right)=-\frac{-cos(\left(\mathcal{z}\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=-\frac{cos\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= -cot\left(\mathcal{z}\right)csc\left(\mathcal{z}\right).
y entonces Error al representar (error de sintaxis): Csc^´\left(\mathcal{z}\right)=-\frac{-cos(\left(\mathcal{z}\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=-\frac{cos\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= -cot\left(\mathcal{z}\right)csc\left(\mathcal{z}\right).
Vemos que sus derivadas son las correspondientes.
--Luis Antonio (discusión) 23:03 10 dic 2012 (CST)










![[\overline{(a+bi)+(c+di)}]=[\overline{a+bi+c+di}]=[\overline{a+c+bi+di)}]=[\overline{(a+c)+(b+d)i}]=(a+c)-(b+d)i=(a+c)+(-b-d)i=a+c-bi-di=\overline{z}+\overline{w}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f386c2137bfcb5fcea2e5cbe3be13ca8a1cf33a5)
![[\overline{(a+bi)(c+di)}]=(a-bi)(c-di)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/be9b5a43542ed75819cd7111402d090f5dd6ac6c)
![[\overline{(a+bi)(c+di)}]=[\overline{ac+adi+bci-bd}]=[\overline{(ac-bd)+(ad+bc)i}]={(ac-bd)-(ad+bc)i}=(a-bi)(c-di)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8faa660642747065eb3297f71af050f88df5c16b)

![\overline{(a+bi)^-1}=[1/(\overline{a+bi})]=1/(a-bi)=(a-bi)^\left(-1\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c61398b37798007d3d92269da29bc3091cd13dd0)




![R(z)=(1/2)[(z+\overline{z})=(1/2)[(a+bi]+(a-bi)]\,\!=(1/2)(a+bi+a-bi)\,\!=(1/2)(a+bi+a-bi)\,\!=(1/2)(2a)\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5180b26d32e41b15cfc9cfe489d3e7a31753f7df)

![\therefore R(z)=(1/2)[(z+\overline{z})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/44196c8b0430fbf9ca298728181e097ec7273485)
![Im(z)=(1/2i)[(a+bi]-(a-bi)]\,\!](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33846aa57690972f179b45b701218736b09f5cf1)



![\sqrt[n]{w}=[r_0 \exp{i(\theta\!+2k\pi\!)} ]^{1/n}= \sqrt[n]{r_0}\exp\left[\frac{i(\theta_0\! +2k\pi\!)}{n}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a7e2fc9277bc18e5e703b512521ffdd0e549d0c8)

![i=1\left[cos\left(\frac{3\pi\!}{2}\right)-isin\left(\frac{3\pi\!}{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5587c20031834cf0e1add8510908cf7a79c53c11)


![\sqrt[2]{w}= \sqrt[2]{1}\exp\left[\frac{i(\left(\frac{3\pi\!}{2}\right) +2k\pi\!)}{2}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a03133f1a146cb1ef164ecc3224ccaefb7fcd68b)

![w_0=\sqrt[2]{1}\exp\left[i\left(\frac{3\pi\!}{4}\right)\right]=1\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=1\left(\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b3bc8e9b57b29b47215a874ae35d8f86b9498e26)


![w_1=1\left[cos\left(\frac{7\pi\!}{4}\right)-isin\left(\frac{7\pi\!}{4}\right)\right]=1\left(\frac{\sqrt{2}}{2} +i\frac{\sqrt{2}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ab68cddb07a0440c9acfbfbed3b8b83dc62f8427)


![w=-1+\sqrt{3}= 2\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c082533e0bb766b6772302bdbdcf0ca6dad6728a)


![\sqrt[4]{2}\exp{i}\left(\frac{\pi\!}{3}+\frac{k\pi\!}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0dad568151ea79913809275fb9c19455c9be00ed)
![w_0=\sqrt[4]{2}\exp{i}\left(\frac{\pi\!}{3}\right)=\sqrt[4]{2}\left[cos\left(\frac{\pi\!}{3}\right)-isin\left(\frac{\pi\!}{3}\right)\right]=\sqrt[4]{2}\left(\frac{1}{2}-i\frac{\sqrt{3}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e9990545a05586dfd28c46624ac46ddfbfb9b04b)
![w_1=\sqrt[4]{2}\exp{i}\left(\frac{5\pi\!}{6}\right)=\sqrt[4]{2}\left[cos\left(\frac{5\pi\!}{6}\right)-isin\left(\frac{5\pi\!}{6}\right)\right]=\sqrt[4]{2}\left(-\frac{\sqrt{3}}{2}-i\frac{1}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f1f28401ef8af112e7fdd5ef3041fd9a8239a9a2)

![w_2=\sqrt[4]{2}\exp{i}\left(\frac{4\pi\!}{3}\right)=\sqrt[4]{2}\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]=\sqrt[4]{2}\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7adcf00791efb1249ba2e8be346e8ace95edd8f4)

![w_3=\sqrt[4]{2}\exp{i}\left(\frac{11\pi\!}{6}\right)=\sqrt[4]{2}\left[cos\left(\frac{11\pi\!}{6}\right)-isin\left(\frac{11\pi\!}{6}\right)\right]=\sqrt[4]{2}\left(\frac{\sqrt{3}}{2}+i\frac{1}{2}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/742cba82b2d219229802170f73a67647e80499da)

![w=1= 1\left[cos\left(0\right)-isin\left(0\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ddfc7be57132df19c9f983703899f9c7eace5231)

![\sqrt[6]{1}\exp{i}\left(\frac{0}{6}+\frac{k\pi\!}{3}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1c8a912ef58cc1f65859d73a0f6e4c22c7ac5c87)
![w_0=\sqrt[6]{1}\left[cos\left(0\right)-isin\left(0\right)\right]=\sqrt[6]{1}\left(1-i\left(0\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9a74ca3d3a393a69f20c74a3b1a4f224c26a94cb)
![w_1=\sqrt[6]{1}\left[cos\left(\frac{\pi\!}{3}\right)-isin\left(\frac{\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fa1e76f693ff175d4c2068b2a4a336721cff05e4)
![w_2=\sqrt[6]{1}\left[cos\left(\frac{2\pi\!}{3}\right)-isin\left(\frac{2\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(-\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/191d62ce96655e76b3dd14e9d7814dfb2d1a0109)
![w_3=\sqrt[6]{1}\left[cos\left(\pi\!\right)-isin\left(\pi\!\right)\right]=\sqrt[6]{1}\left(-1-i\left(0\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9343572ba1c9b7e4f4ce07399932569f90c9ecd2)

![w_4=\sqrt[6]{1}\left[cos\left(\frac{4\pi\!}{3}\right)-isin\left(\frac{4\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(-\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f92c067935e53b2d724867f901964329fd525eb)

![w_5=\sqrt[6]{1}\left[cos\left(\frac{5\pi\!}{3}\right)-isin\left(\frac{5\pi\!}{3}\right)\right]=\sqrt[6]{1}\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e5bf40e916996ae796ef46cd4151c589404cce6d)

![w=1-i= \sqrt{2}\left[cos\left(\frac{\pi\!}{4}\right)-isin\left(\frac{\pi\!}{4}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1c10c846d2f64a3fb83b9f8ddb2da793c65d82a3)

![\sqrt[6]{2}\exp{i}\left(\frac{\pi\!}{12}+\frac{2k\pi\!}{3}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b4c4fd046a380ee5d1ca3f2ed042e6d1dd4ebdbe)
![w_0=\sqrt[6]{2}\exp{i}\left(\frac{\pi\!}{12}\right)=\sqrt[6]{2}\left[cos\left(\frac{\pi\!}{12}\right)-isin\left(\frac{\pi\!}{12}\right)\right]=\sqrt[6]{2}\left(0.9659-i\left(0.2588\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8cdb02cfb0242c5a660d83aae6eac8ee5d1ec9d9)
![w_1=\sqrt[6]{2}\exp{i}\left(\frac{3\pi\!}{4}\right)=\sqrt[6]{2}\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=\sqrt[6]{2}\left(-\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/948a91a570545d2d0bef9e80522dc5072082da31)
![w_2=\sqrt[6]{2}\exp{i}\left(\frac{17\pi\!}{12}\right)=\sqrt[6]{2}\left[cos\left(\frac{17\pi\!}{12}\right)-isin\left(\frac{17\pi\!}{12}\right)\right]=\sqrt[6]{2}\left(-0.2588-i\left(0.9656)\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a0aca186b9da9d077b004191ae5d6850ebf34a73)

![w=-16= 16\left[cos\left(\pi\!\right)-isin\left(\pi\!\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0fd0cfed00dae4bd65da63214a6087ecbd4a6bb3)

![\sqrt[4]{16}\exp{i}\left(\frac{\pi\!}{4}+\frac{k\pi\!}{2}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23b91472576f1043fdf2a41fdd0455f5da557d9e)
![w_0=\sqrt[4]{16}\exp{i}\left(\frac{\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{\pi\!}{4}\right)-isin\left(\frac{\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d305cb024abe606b05690343773cbf963d97064e)
![w_1=\sqrt[4]{16}\exp{i}\left(\frac{3\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{3\pi\!}{4}\right)-isin\left(\frac{3\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(-\frac{1}{\sqrt{2}}-i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d858d9210af895b96fef497e04631ab65ca1e7ae)
![w_2=\sqrt[4]{16}\exp{i}\left(\frac{5\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{5\pi\!}{4}\right)-isin\left(\frac{5\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(-\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5da7c9b454cb1a97e09c45a69dd3857dead63f79)
![w_3=\sqrt[4]{16}\exp{i}\left(\frac{7\pi\!}{4}\right)=\sqrt[4]{16}\left[cos\left(\frac{7\pi\!}{4}\right)-isin\left(\frac{7\pi\!}{4}\right)\right]=\sqrt[4]{16}\left(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2df3a75f264c8304250cbfe7affb02fdc11922cc)

![w=32i= 32\left[cos\left(-\frac{\pi\!}{2}\right)-isin\left(-\frac{\pi\!}{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0f84099369588e0c3b71a593b8120e7237486305)

![\sqrt[5]{32}\exp{i}\left(-\frac{\pi\!}{10}+\frac{2k\pi\!}{5}\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b074f53ee2ea2b0981ff0043382fed61a51512ca)
![w_0=\sqrt[5]{32}\exp{i}\left(-\frac{\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(-\frac{\pi\!}{10}\right)-isin\left(-\frac{\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0.9510\right)+i\left(0.3090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/32f812e8458f4f16b8417cefa194a69a1f4916de)
![w_1=\sqrt[5]{32}\exp{i}\left(\frac{3\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{3\pi\!}{10}\right)-isin\left(\frac{3\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0.5877\right)-i\left(0.8090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e48fce49791327eff4a98fdf8f1aebe41472bb02)

![w_2=\sqrt[5]{32}\exp{i}\left(\frac{7\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{7\pi\!}{10}\right)-isin\left(\frac{7\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(-0.5877)\right)-i\left(0.8090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7a09076c808491941fdb5d6bd261846419f9498)

![w_3=\sqrt[5]{32}\exp{i}\left(\frac{11\pi\!}{10}\right)=\sqrt[5]{32}\left[cos\left(\frac{11\pi\!}{10}\right)-isin\left(\frac{11\pi\!}{10}\right)\right]=\sqrt[5]{32}\left(\left(0\right)+i\left(0.3090\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85b5825edccb20cdc9b19c19776ceac84a43711c)

![w_4=\sqrt[5]{32}\exp{i}\left(\frac{3\pi\!}{2}\right)=\sqrt[5]{32}\left[cos\left(\frac{3\pi\!}{2}\right)-isin\left(\frac{3\pi\!}{2}\right)\right]=\sqrt[5]{32}\left(\left(0\right)+i\left(1\right)\right)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5c27126e3607dd4c5cf8bf02917277beb5bff2e4)























































































![a<b \mathcal{F} :\left[a,b\right]\rightarrow\mathbb{R}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b3525429d45d83e5d71b6b740aa78f59b0a0af28)




![\left[a,b\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)





















![\mathcal{U}_x=\frac{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]2cos\left(2\mathcal{x}\right)- sen\left(2\mathcal{x}\right)\left(-2sen\left(2\mathcal{x}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}=\frac{2+2cos\left(2\mathcal{x}\right) \left( cosh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/89b5e2c3fab9eb67f8a116495f4cb8e52d5726dc)
![\mathcal{V}_y =\frac{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]2cosh\left(2\mathcal{y}\right)- senh\left(2\mathcal{y}\right)\left(-2senh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}=\frac{2+2cos\left(2\mathcal{x}\right) \left( cosh\left(2\mathcal{y}\right)\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f35a17f1888e041e7dfb5d9a5ca5f2827c2ce3a6)
![\mathcal{U}_y = \frac{-sin\left(2\mathcal{x}\right)\left[2senh\left(2\mathcal{y}\right)\right]}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2} =-\frac{2sen\left(2\mathcal{x}\right)senh\left(2\mathcal{y}\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b91d4602e9907dd2906e023136d5a32dc977384b)
![\mathcal{V}_x = \frac{-sinh\left(2\mathcal{y}\right)\left[-2sen\left(2\mathcal{x}\right)\right]}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2} =\frac{2sen\left(2\mathcal{x}\right)senh\left(2\mathcal{y}\right)}{\left[cos\left(2\mathcal{x}\right)+ cosh\left(2\mathcal{y}\right)\right]^2}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/36a8ce7757011a2ba9e687dfb24c179ba87c01bc)



