Transformadas de Fourier
Transformadas de Fourier
El objetivo de conocer las transformadas de Fourier es comprender el modo en que los sistemas ópticos procesan la luz para formar imágenes.
Al terminar solo nos centraremos en las amplitudes y las fases de las ondas luminosas que alcanzan el plano imagen.
Las Integrales de Fourier
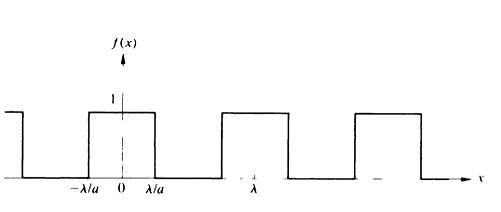
Imaginemos que tenemos una onda cuadrada como la de la imagen de la Figura 1, y que mantenemos constante el ancho de pico cuadrado, mientras que se incrementa sin limite. Al acercarse al infinito la función resultante ya no será periódica entonces tendríamos un pulso cuadrado único, estas ideas nos sugieren una forma posible de generalizar el método de las series de Fourier para incluir las funciones que no son periódicas.
Para ver como lograrlo particularizemos, para observar el comportamiento, tomemos un valor cualquiera, digamos y escojamos algún valor de cm. Entonces el pico tendrá un ancho de cm, es decir centrado en como se muestra en la Figura 2a.
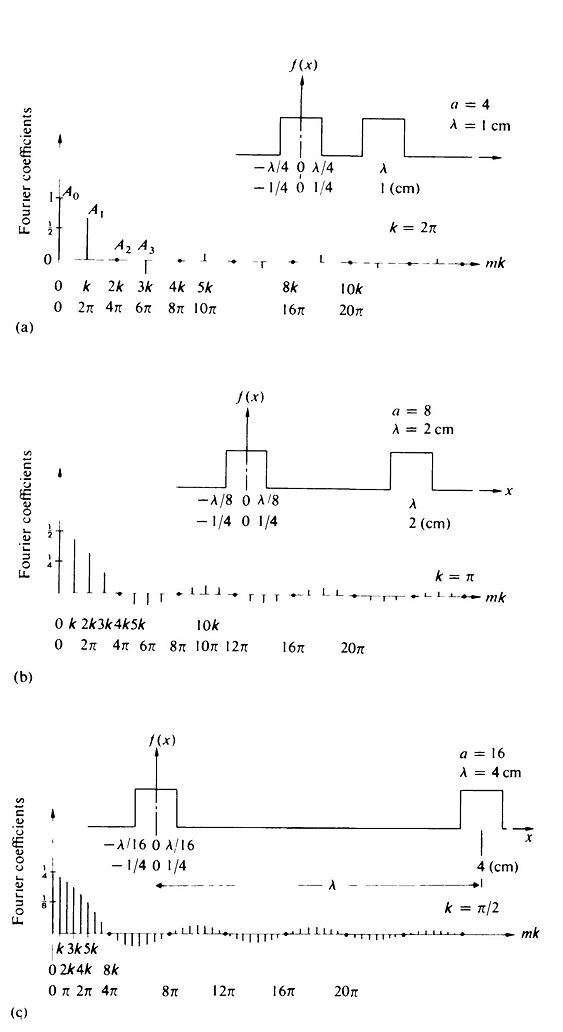
La importancia de cada frecuencia particular se apreciaria más facilmente examinando el valor del coeficiente de Fourier correspondiente en este caso (Vease Ondas: periódicas anarmónicas). Estos coeficientes los podemos considerar como factores de ponderación </math> que acentúan los distintos armónicos.En la Figura 2a se estiman distintos valores de (donde ) frente a mk para la onda cuadrada anterior. A esta curva se le denomina espectro de frecuencias espaciales.
Podemos considerar a como una función como función de que puede ser diferente de cero solamente para valores de .
Ahora si la cantidad le damos un valor de mientras que aumenta hasta el ancho de pico de no se verá afectado, notando que la única variación es la duplicación del ancho entre los picos. Sin embargo un cambio muy interesante se nota en el espectro de frecuencias espaciales véase la Figura 2b.
Ahora es fácil notar que la densidad de componentes a lo largo del eje ha aumentado considerablemente.
También observemos que es aún cero cuando , pero ya que el valor de es ahora en lugar de , habrá más términos entre estos puntos con valor cero. Finalmente sea y aumentemos . Notaremos ahora que la forma de los picos individuales permanecerá inalterada pero los términos en el espectro de frecuencias están ahora aún más compactos.
Notamos que eso era lo esperado, el pulso, comparado con , se está haciendo ahora cada vez más pequeño, por lo tanto se precisan frecuencias más elevadas para sintetizarlo.
Ahora es más fácil notar que la envolvente de la curva es mas perceptible y eso es evidente observando la Figura 2c.
Entonces concluimos que a medida que aumenta y que la función adquiere la apariencia de un pulso cuadrado simple, el espacio entre cada una de las contribuciones en el espectro decrecerá. las lineas espectrales discretas, al disminuir su amplitud se unirán gradualmente haciéndose gradualmente irresolubles.
"En el límite cuando tiende a las líneas espectrales se aproximan infinitamente unas a otras. A medida que se hace demasiado pequeña, se hace extremadamente grande para que sea perceptible.
Cambiando la notación:
(frecuencia angular de los armónicos), formada por términos discretos. El el límite se transformará en formada por una distribución continua de frecuencia. La función en el límite se convertirá en la envolvente mostrada en la Figura 2.
Entonces ya no podemos hablar de la frecuencia fundamental y sus armónicos ya que el pulso que se está sintetizando,, no tiene frecuencia fundamental aparente.
Sabemos de calculo que una integral es en realidad el límite de una suma a medida que el número de elementos se va al infinito y su tamaño se aproxima a cero.
Entonces podemos reemplazar a la serie de Fourier por la denominada Integral de Fourier( Deducción de la Integral de Fourier).
Transformadas Unidimensionales.
En la sección de INTEGRALES DE FOURIER, se vio que una función de una dimensión puede ser expresada como una combinación lineal de un número infinito de contribuciones armónicas, que se expresa como
Los factores de peso que determinan la importancia de las diversas contribuciones de frecuencia espacial angular ,es decir , y , son las transformadas de Fourier del seno y coseno dadas por:
respectivamente.Aqui la cantidad es una variable muda sobre la cual se lleva a cabo la integración,de manera que ni ni ,son funciones explicitas de y la selección del símbolo usado para indicarla no es importante.Las transformadas del seno y coseno pueden consolidarse dentro de una sola expresión exponencial compleja como sigue:
pero como esto se puede reescribir como:
La cantidad entre parentesis cuadrados es una funcion par de k por lo tanto, al cambiar los limites de sobre la integral externa,tendremos
Ya que estamos buscando una representación exponencial,nos viene a la memoria el teorema de Euler.Por consiguiente, observese que
Por lo que el factor entre paréntesis es una función impar de k.Al sumar esta dos ultimas expresiones,se obtiene la forma compleja de la integral de Fourier.
Por lo tanto podemos escribir
siempre que
habiendo puesto en la ecuación. La función en la transformada de Fourier de ,la cual se indica simbolicamente por
En realidad, en la literatura existen varias maneras equivalentes, ligeramente diferentes de definir la transformada. Por ejemplo, los signos en las exponenciales pueden intercambiarse o el factor de podría dividirse simétricamente entre y , es decir, cada uno tendría un coeficiente de . Obsérvese que es la parte real de mientras que es la imaginaria, es decir
Una cantidad compleja como ésta puede escribirse también en términos de amplitud de valor real, , el , y una fase de valor real,(k), el :
Precisamente como es la transformada de , es la transformada inversa Fourier de , o simbólicamente
{F(k)}={{}}
y y F(k)se denominan frecuentemente par de transformadas de Fourier. Es posible construir la transformada y su inversa de una forma aún más simétrica, en términos de la frecuencia espacial Sin embargo, independientemente de cómo se exprese, la transformada no será exactamente igual a la inversa por el signo negativo de la función exponencial. Por consiguiente, en la expresión presente,
En la mayoría de los casos, esto no tiene ninguna trascendencia, especialmente para funciones pares donde =,por lo tanto deberíamos esperar un alto nivel de paridad entre las funciones y sus transformadas.
Obviamente, si fuera una función del tiempo en vez del espacio, únicamente tendríamos que reemplazar por y entonces ,la frecuencia espacial angular, por , la frecuencia temporal angular, para obtener el par de transformadas oportuno en el dominio temporal, es decir
y
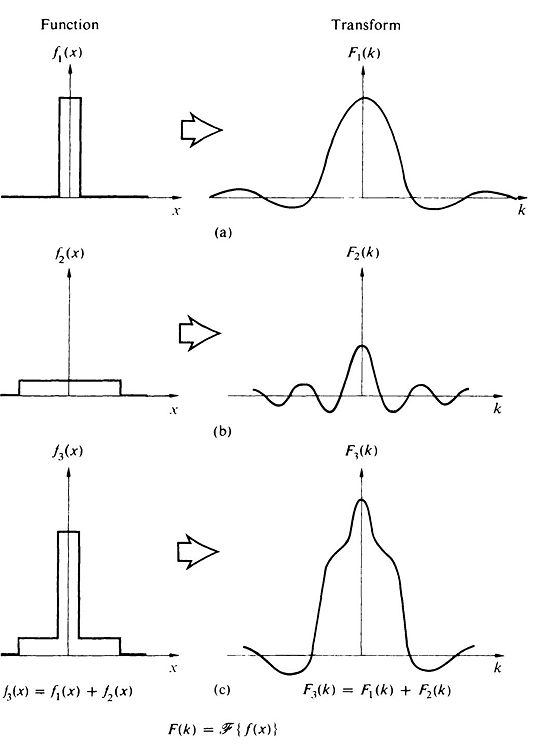
Cabe mencionar que si escribimos como una suma de funciones, su transformada, será evidentemente la suma de las transformadas de las competentes individuales de las funciones. A veces, esta forma de establecer las transformadas de funciones complicadas que pueden construirse a partir de componentes conocidas, puede resultar conveniente. La Figura 3 muestra claramente este procedimiento.
Transformada De La Función Gaussiana.
Sea la función:
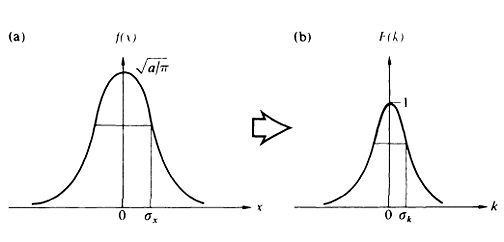
; donde: y es una constante. Si queremos podemos suponer que esto sea el perfil de un pulso para . La familiar curva con forma de campana. En óptica se encuentra con mucha frecuencia y se encuentra relacionada con paquetes de onda de fotones individuales, también en la distribución de la irradiancia transversal de un haz de luz láser en el modo y el tratamiento estadístico de luz térmica en la teoría de coherencia.
Su transformada de Fourier la obtenemos evaluando:
entonces si sustituimos la función gaussiana en está expresión obtenemos:
por propiedades de la exponencial esta expresión se ve como:
Al completar el cuadro, el exponente, , pasa a ser y haciendo que nos queda:
la integral definida puede encontrarse en las tablas y es igual a , por lo tanto:
la cual es nuevamente una función gaussiana, esta vez con como variable. La desviación estándar está definida como el rango de la viariable o en la cual la función disminuye un factor de de su valor máximo. Según vaya aumentando, se va estrechando mientras que, por el contrario, se ensancha. En conclusión cuanto más corta sea la longitud del pulso,más amplio será el ancho de banda de la frecuencia espacial.
Cabe mencionar que la transformada de una función, en general se mantiene como un espacio invariante, es decir mantiene la forma de la función pero cambia su tamaño o longitud.
Nota.- Para información sobre ondas Gaussianas visitar Ondas: Gaussianas.


























![f(z)=\frac{1}{\pi}\left [ \int_{0}^{\infty } A\cos(kz)\, dk + \int_{0}^{\infty } B\sin (kz)\, dk \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/94a218afe918904d8e9b1167e5c028ccd2bf9e3f)


![A(k)=\left [ \int_{-\infty}^{\infty }{f(z')} \cos (kz')\, dz' \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b168f3a438c8eb6de554406d03a00924a3f9814e)
![B(k)=\left [ \int_{-\infty}^{\infty }{f(z')} \sin (kz')\, dz' \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/74f01750955d378d32c3137611979f14a6545d7e)

![f(x)=\frac{1}{\pi}\left [\int_{0}^{\infty }\cos(kz)\, \int_{-\infty}^{\infty }{f(z')} \cos(kz')\, dz'dk + \int_{0}^{\infty }\sin(kz)\, \int_{-\infty}^{\infty }{f(z')} \sin(kz')\, dz'dk \right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d52292b8e1da7bdfc479e0b4fa39510cda1c610b)
![cos[k'(z-z')]=\cos(k_0)\cos(kz')+\sin(kz)\sin(kz')](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a839cec1261dc8be791a110efd207e72cb26c8d5)
![f(z)=\frac{1}{\pi}\int_{0}^{\infty } \left [ \int_{-\infty}^{\infty }{f(z')} \cos k(z'-z)\, dz' \right ]\,dk](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a3b79eb8d404b8ad2e2d582ef0e75e732a4cb180)
![f(z)=\frac{1}{2\pi}\int_{-\infty}^{\infty } \left [ \int_{-\infty}^{\infty }{f(z')} \cos k(z'-z)\, dz' \right ]\,dk](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6fe34f5345d6aff1a326370a9333b823bedfe953)
![f(z)=\frac{i}{2\pi}\int_{-\infty}^{\infty } \left [ \int_{-\infty}^{\infty }{f(z')} \sin k(z'-z)\, dz' \right ]\,dk =0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2ac3a12d98a48100835dc56bb31e1fb1dfc0f77d)
![f(z)=\frac{1}{2\pi}\int_{-\infty}^{\infty } \left [ \int_{-\infty}^{\infty }{f(z')} \mathbf{e}^{ikz'}\, dz' \right ]\mathbf{e}^{-ikz}\,dk](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/84fde0d32d92b20da1faa5d88b865c01407dd035)











































![\textstyle{F(k)}=\frac{C}{\sqrt{a}}\mathbf{e}^{\frac{-k^{2}}{4a}}\left [\textstyle \int_{-\infty }^{\infty } \mathbf{e}^{{-\beta}^{2}}\, d\beta\right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b400c99f54cc7e6b020e75c9bb13e49705d0a723)