Compleja:Zill-Cap5.2

Ejercicios del capítulo 5, sección 2 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.

---

Sección 5.2

Ejercicio 1

Evalué la integral a lo largo del contorno indicado

Procedimiento

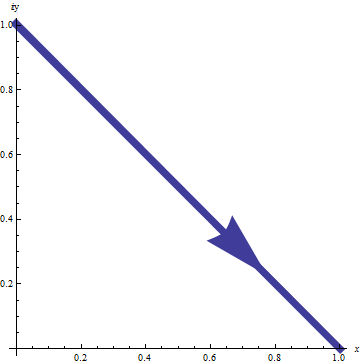
$\int_{c}\left(z+3\right)dz$ donde $C$ esta dada por $x=2t:y=4t-1;1\leq t\leq3$

para evaluar la integral de contorno sabemos que

$\int_{c}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt$

Si $z(t)=x+yi=2t+(4t-1)i$

$z(t)^{\prime}=2+4i$

y

$f(z(t))=(2t+3)+(4t-1)i$

por lo tanto

$\intop_{1}^{3} [(2t+3)+(4t-1)i](2+4i)dt$

$\intop_{1}^{3} [(-12t+10)+i(16t+10)]dt$

$\intop_{1}^{3} [(-12t+10)+i(16t+10)]dt = -6t^{2}+10t+i8t^{2}+i10t \mid_{1}^{3}$

$\intop_{1}^{3} [(-12t+10)+i(16t+10)]dt = (-24+102i)-(4+18i)$

y para finalizar simplificamos

Conclusión

$\intop_{1}^{3} [(-12t+10)+i(16t+10)]dt= -28+84i$

---

Realizado por: Miguel Medina Armendariz (discusión) 17:28 13 jun 2015 (CDT)

---

Ejercicio 2

Evaluar la integral dada, a lo largo del contorno indicado.

Procedimiento

$\int_{c}\left(2\bar{z}-z\right)dz:donde$ c esta dada por $x=-t:y=t^{2}+2;0\leq t\geq2$

utilizamos la siguiente relación para curvas parametrizadas:

$\int_{c}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt$

Que cumple con la forma de calcular trabajo en funciones vectoriales sobre curvas paramétricas

Entonces si utilizamos esta relación podremos resolver la integral compleja como sigue:

$f\left(z\right)=2\bar{z}-z=2\left(x-iy\right)-\left(x+iy\right)=2x-2iy-x-iy=x-3iy$

$f\left(z\left(t\right)\right)=-t-3i\left(t^{2}+2\right)$

$z=x+iy$ entonces $z\left(t\right)=-t+i\left(t^{2}+2\right)$

$z^{\prime}\left(t\right)=-1+2it$

Usando estos resultados podemos escribir la integral de este modo:

Conclusión

$\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt=\int_{0}^{2}\left(-t-3i\left(t^{2}+2\right)\right)\left(-1+2it\right)dt=\int_{0}^{2}\left(6t^{3}+13t\right)dt+i\int_{0}^{2}\left(t^{2}+6\right)dt=\left[\frac{6}{4}t^{4}+\frac{13}{2}t^{2}\right]_{0}^{2}+i\left[\frac{1}{3}t^{3}+6t\right]_{0}^{2}=50+i14.666$

---

Realizado por: Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT) ----

---

Ejercicio 3

Evalué la integral $\int_{c}(z^{2})dz$ a lo largo del contorno C dado $z(t) = 3t+2it$ con $-2\leq t\leq2$

Para resolver esta integral es necesario hacer uso de la expresión:

Procedimiento

$\int_{c}f\left(z\right)dz = \int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt$

donde:

$z(t) = 3t+2it$

$z^{\prime} (t) = 3 + 2i$

Sustituyendo estos valores en nuestra expresión para resolver la integral

$\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt=\int_{-2}^{2} (3t + 2it)^2 (3 + 2i)dt $

$= \int_{-2}^{2} (9t^2 + 2(6it^2) - 4t^2) (3 +2i)dt$

$= \int_{-2}^{2} (27t^2 + 36it^2 - 12t^2 + 18it^2 - 24t^2 - 8it^2)dt$

$= \int_{-2}^{2} (-9t^2 + 46it^2)dt$

$= -\int_{-2}^{2} 9t^2 dt + i\int_{-2}^{2} 46t^2 dt$

Evaluando la integral

$= -\frac{9}{3} [t^3]_{-2}^{2} + i\frac{46}{3} [t^3]_{-2}^{2}$

$= -3 (2^3 - (-2)^3) + i \frac{46}{3} (2^3 - (-2)^3)$

Conclusión

$\int_{c}f\left(z\right)dz= -48 + i \frac{736}{3}$

---

Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 00:24 14 jun 2015 (CDT)

---

Ejercicio 4

Evaluar la integral a lo largo del contorno dado'

$\int_{c}(3z^{2}-2z)dz$ donde C es $z(t)=t+it^{2}$ con $0\leq t\leq1$

Procedimiento

Como ya nos dan la parametrización sólo debemos derivar respecto a t y substituir en la integral.

$dz=1+2it$

$\Longrightarrow\int_{c}(3z^{2}-2z)dz=\int_{0}^{1}[3(t+it^{2})^{2}-2(t+it^{2})][1+2it]dt$

$=\int_{0}^{1}[3(t^{2}+2it^{3}-t^{4})-2t-2it^{2})][1+2it]dt$

$=\int_{0}^{1}[3t^{2}+6it^{3}-3t^{4}-2t-2it^{2}][1+2it]dt$

$=\int_{0}^{1}[3t^{2}+6it^{3}-3t^{4}-2t-2it^{2}+6it^{3}-12t^{4}-6it^{5}-4it^{2}+4t^{3}]dt$

$=\int_{0}^{1}[6it^{5}+12it^{3}-6it^{2}-15t^{4}+4t^{3}+3t^{2}-2t]dt$

Y haciendo la integral queda de la forma:

Solución

$=(it^{6}+3it^{4}-2it^{3}-3t^{5}+t^{4}+t^{3}-2)|_{0}^{1}$$=(i+3i-2i-3+1+1-2)=-3+2i$

---

Realizado por: A. Martín R. Rabelo (discusión) 20:36 12 jun 2015 (CDT)

---

Ejercicio 5

Evalué la integral a lo largo del contorno indicado.

$\intop_{C}\frac{z+1}{z}dz$ , donde $C$ es la mitad derecha de la circunferencia $\left|z\right|=1$ de

$z=-i$ a $z=i$

Procedimiento

$\left|z\right|=1$... $\left(1\right)$

Si $z=x+iy$...$\left(2\right)$ entonces

$x^{2}+y^{2}=1$... $\left(3\right)$

La ecuación $\left(2\right)$se puede parametrizar como :

$x=\cos\left(t\right)$ , $y=\sin\left(t\right)$, $-\frac{\pi}{2}\leq t\leq\frac{\pi}{2}$

entonces:

$z\left(t\right)=\cos\left(t\right)+i\sin\left(t\right)$

De modo que por el Teorema 5.2.1 :

$f\left(z\right)=\frac{z+1}{z}=\frac{\cos\left(t\right)+\sin\left(t\right)+1}{\cos\left(t\right)+\sin\left(t\right)}$

y además $z\prime\left(t\right)=-\sin\left(t\right)+i\cos\left(t\right)$

Entonces:

$\intop_{C}\frac{z+1}{z}dz=\intop_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left[\frac{\cos\left(t\right)+i\sin\left(t\right)+1}{\cos\left(t\right)+i\sin\left(t\right)}\right]\left[-\sin\left(t\right)+i\cos\left(t\right)\right]dt$

multiplicando la integral por:

$\frac{\cos\left(t\right)-i\sin\left(t\right)}{\cos\left(t\right)-i\sin\left(t\right)}$

se obtiene:

$\intop_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left[\frac{\cos\left(t\right)+i\sin\left(t\right)+1}{\cos\left(t\right)+i\sin\left(t\right)}\right]\left[-\sin\left(t\right)+i\cos\left(t\right)\right]\left[\frac{\cos\left(t\right)-i\sin\left(t\right)}{\cos\left(t\right)-i\sin\left(t\right)}\right]dt$

$=\intop_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left[\frac{\cos\left(t\right)+i\sin\left(t\right)+1}{1}\right]\left[i\right]dt$

$=i\intop_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left[\cos\left(t\right)+1\right]dt-\intop_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin\left(t\right)dt$

$=i\left[\sin\left(\frac{\pi}{2}\right)-\sin\left(-\frac{\pi}{2}\right)+\pi\right]-\left[\cos\left(\frac{\pi}{2}\right)-\cos\left(-\frac{\pi}{2}\right)\right]$

$=i\left[2+\pi\right]-\left[0-0\right]$

Solución

Por lo tanto:

$\intop_{C}\frac{z+1}{z}dz=\left[2+\pi\right]i$

---

Alejandro Juárez Toribio (discusión) 01:50 14 jun 2015 (CDT)

---

Ejercicio 6

Evalúe la integral a lo largo del contorno indicado

$\int_{c}|z|^{2}dz$ donde C es $x=t^{2}$, $y=\frac{1}{t}$, $1\leq t\leq2$

Procedimiento

Por las condiciones tenemos que:

$z(t)=t^{2}+i\frac{1}{t}$

$z'(t)=2t-i\frac{1}{t^{2}}$

Por otra parte, se observa que $|z|>0$, entonces

$\int_{c}|z|^{2}dz=\intop_{1}^{2}(t^{2}+i\frac{1}{t})^{2}(2t-i\frac{1}{t^{2}})dt=\intop_{1}^{2}(t^{4}+it-\frac{1}{t^{2}})(2t-i\frac{1}{t^{2}})dt=\intop_{1}^{2}(2t^{5}-it^{2}-\frac{2}{t}+i\frac{1}{t^{4}}+2it^{2}+\frac{1}{t})dt$

$=\intop_{1}^{2}(2t^{5}-\frac{1}{t})dt+i\intop_{1}^{2}(\frac{1}{t^{4}}+t^{2})dt=(\frac{1}{3}t^{5}-lnt)_{1}^{2}+i(\frac{-1}{3t^{3}}+2t)_{1}^{2}$

Evaluando

$(\frac{1}{3}t^{5}-lnt)_{1}^{2}+i(\frac{-1}{3t^{3}}+2t)_{1}^{2}=\frac{32}{3}-ln2-(\frac{1}{3}-ln1)+i[\frac{-1}{24}+4-(-\frac{1}{3}+2)]=\frac{31}{3}-ln2+i\frac{55}{24}$

Solución

$\intop_{1}^{2}(t^{2}+i\frac{1}{t})^{2}(2t-i\frac{1}{t^{2}})dt=\frac{31}{3}-ln2+i\frac{55}{24}$

---

Realizado por: Fernando Vazquez V. (discusión) 16:06 14 jun 2015 (CDT)

---

Ejercicio 7

Evalúe la integral a lo largo del contorno indicado.

$\oint_{c} Re(z) dz$ donde C es la circunferencia $|z|=1$

Procedimiento

Para nuestro caso la curva esta dada por $|z|=1$, pero sabemos que $z=x+iy$, por lo cual $x²+y²=1$. por lo cual podemos parametrizar de la siguiente manera.

$x(t)= \cos(t)$

$y(t)= \sin(t)$

$0\leq t\leq2\pi$

Ahora sustituimos a $z$ poniéndolo en términos de la parametrización propuesta.

$z(t)= \cos(t)+i \sin(t)$

$z'(t)= -\sin(t) + i \cos(t)$

como la integral solo nos la pide en la parte real de $z$tenemos:

$\intop_{0}^{2\pi}[cos(t)(-sen(t)+icos(t))]dt$

$\intop_{0}^{2\pi}-cos(t)sen(t) dt+i\intop_{0}^{2\pi}cos²(t)dt$

Integrando tenemos que

$\intop_{0}^{2\pi}[cos(t)(-sen(t)+icos(t))]dt= \frac{sen²(t)}{2}+\frac{t + sen(t)cos(t)}{2}|_{0}^{2\pi}$

evaluando tenemos: $\intop_{0}^{2\pi}[cos(t)(-sen(t)+icos(t))]dt=\frac{sen²(2\pi)}{2}+\frac{2\pi + sen(2\pi)cos(2\pi)}{2}-\frac{sen²(0)}{2}+\frac{0 + sen(t)cos(0)}{2}$

por lo cual para $c$ definida por $ |z|=1$

Conclusión

$\oint_{c} Re(z) dz= i\pi$

---

Realizado por: Anahi Limas (discusión) 20:10 14 jun 2015 (CDT)

---

Ejercicio 9

Evalua la siguiente integral definida

$\intop_{C}(x^2-iy^3)dz$

Procedimiento

Donde $C$ es la línea recta $1<t<i$

$z=(1+i)t$ y $dz=(1+i)$

Sustituyendo los valores anteriores en la integral, tenemos:

$\intop_{C}(x^2-iy^3)dz=\intop_{C}(t^2-i(it)^3)(1+i)dt= \intop_{C}(t^2+t^3(1+i)dt=$

$ \intop_{1}^{i}(t^2+t^3+it^2+it^3dt= \frac{-7}{12}+\frac{1}{12}i$

Conclusión

Por lo tanto:

$\intop_{C}(x^2-iy^3)dz=\frac{-7}{12}+\frac{1}{12}i$

---

Nancy Martínez Durán (discusión) 16:07 14 jun 2015 (CDT)

---

Ejercicio 14

Encuentra el valor de la integral, sobre el contorno dado. $\int_{C} dz$, donde C es la mitad izquierda de la elipse: $\frac{x^2}{36}+\frac{y^2}{4}=1$, desde:$z=2i$, hasta $z=-2i$.

Procedimiento

Usando el hecho de que: $\int_{C}f(z)dz=\int_{C}(udx-vdy)+i\int_{C}(vdx+udy)$; donde $f(z)=u(x,y)+iv(x,y); x,y\in\mathbb{R}$, se tiene:

$\int_{C} dz=\int_{C}dx+i\int_{C}dy$...(1)

Por otra parte: $\frac{x^2}{36}+\frac{y^2}{4}=1 \Longleftrightarrow x^2+9y^2=36\Longleftrightarrow x^2=36-9y^2\Longleftrightarrow |x|=\sqrt{36-9y^2} \Longrightarrow x=-\sqrt{36-9y^2}$. Como es la mitad izquierda de la elipse se toman las x's negativas.

de lo anterior: $x=-\sqrt{36-9y^2} \Longrightarrow dx=\frac{9ydy}{\sqrt{1-9y^2}}$.

Regresando a (1):

Conclusión

$\int_{C} dz=\int_{C}dx+i\int_{C}dy=\int_{2}^{-2} \frac{9ydy}{\sqrt{1-9y^2}}+i\int_{2}^{-2}dy=0+i(-2-2)=-4i$.

Por lo tanto: $\int_{C} dz=-4i$

---

Realizado por: Alan Daniel Barrón Posadas (discusión) 19:55 19 jun 2015 (CDT)

---

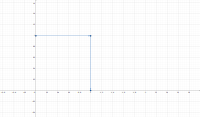
Ejercicio 19

Evale la integral a lo largo del contorno C dado en la figura

$\oint _{c}z^{2}dz$

Procedimiento

Como C es suave por tramos, integraremos sobre los tres tramos suaves

$\oint _{c}z^{2}dz=\int _{c_{1}}z^{2}dz+\int _{c_{2}}z^{2}dz+\int _{c_{3}}z^{2}dz$

Primero tomaremos a $C_{1}$ la parte del contorno que va del punto z= 0+ i0 al punto z= 1+ 0i, Por lo que $z_{1}=x_{1}(t)+y_{1}(t)$ su parametrización es, con $t\epsilon [0,1]$

$x_{1}(t)=t$ además $x'_{1}(t)=dt$

$y_{1}(t)=0$ además $y'_{1}(t)=0$

Por lo que para la primera curva suave tenemos que

$\int _{C_{1}}z_{1}^{2}dz=\int _{C_{1}}(x_{1}(t)+y_{1}(t))^{2}(x'_{1}(t)+y'_{1}(t))=\int _{0}^{1}(t+0i)^{2}(1)dt=[{\frac {t^{3}}{3}}]_{0}^{1}={\frac {1}{3}}$

Ahora para $c_{2}$ que va desde el punto z=1+0i al punto z= 1+i, tenemos que $z_{2}=x_{2}(t)+y_{2}(t)$ su parametrización es, con $t\epsilon [0,1]$

$x_{2}(t)=1$ además $x'_{2}(t)=0$

$y_{2}(t)=t$ además $y'_{2}(t)=dt$

Por lo que para la segunda curva tenemos que la integral cumple

$\int _{C_{2}}z_{2}^{2}dz=\int _{C_{2}}(x_{2}(t)+y_{2}(t))^{2}(x'_{2}(t)+y'_{2}(t))=\int _{0}^{1}(1+ti)^{2}(i)dt=i\int _{0}^{1}(1-t^{2})+2itdt=$

$\int _{0}^{1}i(1-t^{2})-2tdt=(-t^{2}+i(t-{\frac {t^{3}}{3}}))|_{0}^{1}=-1+{\frac {i2}{3}}$

Para $c_{3}$ que va desde el punto z=1+i al punto z= 0+0i, tenemos que $z_{3}=x_{3}(t)+y_{3}(t)$ su parametrización es, con $t\epsilon [1,0]$

$x_{3}(t)=t$ además $x'_{3}(t)=dt$

$y_{3}(t)=t$ además $y'_{3}(t)=dt$

Por lo que para la tercera integración

$\int _{C_{3}}z_{3}^{2}dz=\int _{C_{3}}(x_{3}(t)+y_{3}(t))^{2}(x'_{3}(t)+y'_{3}(t))=\int _{0}^{1}(t+ti)^{2}(1+i)dt=\int _{0}^{1}t^{2}(1+i)^{2}(1+i)dt=\int _{0}^{1}t^{2}(1+i)^{3}dt=$

$(1+i)^{3}\int _{0}^{1}t^{2}dt=(1+i)^{3}{\frac {t^{3}}{3}}|_{1}^{0}={\frac {(1+i)^{3}}{3}}$

Por lo que resolviendo, tenemos que

${\frac {(1+i)^{3}}{3}}={\frac {(1+i)(1+i)}{3}}(1+i)={\frac {2i}{3}}(1+i)$

Conclusión

Al sumar todas las partes tenemos que

$\oint _{c}z^{2}dz=\int _{c_{1}}z^{2}dz+\int _{c_{2}}z^{2}dz+\int _{c_{3}}z^{2}dz={\frac {1}{3}}-1+{\frac {2i}{3}}+{\frac {2}{3}}-{\frac {2i}{3}}=0$

---

Realizado por: Pablo (discusión) 18:05 14 jun 2015 (CDT)

---

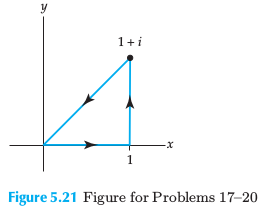
Ejercicio 21

Evalue $\int_{C} \! \left( z^2-z+2 \right) \, dz $, e el contorno ilustrado en la figura siguiente:

Procedimiento

Primeramente se encuentra la parametrización de ese contorno, la más evidente es que:

\[ z(t)=i+(1-i)t \;\;\;\;0\leqq t\leqq 1 \;\;\;\;\;\; y \;\;\;\;\;z'(t)=1-i \] Entonces: \[ z^2=(i+(1-i)t)^2=i^2+2i(1-i)t+(1-i)^2 t^2=-1+2(1+i)t-2it^2 \] \[ z(t)=i+(1-i)t \] \[ z^2-z+2=(-2i)t^2+(2+2i+i)t+(-1-1-i)=-(2i)t^2+(1+3i)t+(1-i) \] Se puede escribir la integral como: \[ \int_{C} \! \left( z^2-z+2 \right) \, dz =\int_{0}^{1} \! \left[ -(2i)t^2+(1+3i)t+(1-i) \right] \, (1-i)\,dt =(1-i) \left[ -2i\int_{0}^{1} \! t^2 \, dt +(1+3i)\int_{0}^{1} \! t \, dt+(1-i)\int_{0}^{1} \! 1 \, dt\right] ='"`UNIQ--h-12--QINU`"'(1-i) \left[ -2i\frac{(1^3-0^3)}{3} +(1+3i)\frac{(1^2-0^2)}{2}+(1-i)(1-0)\right]= \] \[ =(1-i) \left[ -2i\frac{1}{3} +(1+3i)\frac{1}{2}+(1-i)\right]=(1-i) \left[\frac{1}{2}+1+i\left(-\frac{2}{3}+\frac{3}{2}-1\right)\right]=(1-i)\left( \frac{3}{2}-i\frac{1}{6} \right)=\frac{4-5i}{3} \]

--Tlacaelel Cruz (discusión) 15:30 12 jun 2015 (CDT)

---

ejercicio 22

Evalúe $\intop_{c}\left(z^{2}-z+2\right)dz$ de i a 1 a lo largo del contorno C dado en la figura

Curva del problema 22 Capitulo 5.2 del Zill

primero definimos y desarrollamos las siguientes expresiones

$z=x+yi$

$z^{2}=x^{2}+2xiy-y^{2}$

$-z=-x-yi$

Procedimiento

Sustituimos y simplificamos la expresión

$\intop_{c}\left(x^{2}+2xiy-y^{2}-x-yi+2\right)dz$

por propiedades de la integral sabemos que

$\intop_{c}\left(x^{2}+2xiy-y^{2}-x-yi+2\right)dz=\intop_{c_{1}}\left(x^{2}+2xiy-y^{2}-x-yi+2\right)dz+\intop_{c2}\left(x^{2}+2xiy-y^{2}-x-yi+2\right)dz$

parametrizamos de la siguiente forma

$y=1$ , $0\leq x\leq1$

obtenemos que

$\intop_{c_{1}}(x^{2}+2xi-x-i+1)dz$

$z(x)=x+i=x+i$

$z'(x)=dx$

Entonces nuestra primera integral nos queda

$\intop_{c_{1}}(x^{2}+2xi-x-i+1)dx$

$\intop_{c_{1}}(x^{2}+2xi-x-i+1)dx=\frac{1}{3}+i-\frac{1}{2}-i+1= \frac{5}{6}$

Ahora haremos la segunda integral:

$\intop_{c_{2}}\left(x^{2}+2xiy-y^{2}-x-yi+2\right)dz$

parametrizamos de la siguiente forma

$x=1$ , $1\leq y\leq0$

$z(y)=1+yi$

$z'(y)=idy$

por los tanto nuestra integral nos queda

$\intop_{1}^{0}\left(1^{2}+2iy-y^{2}-1-iy+2\right)idy=\intop_{1}^{0}\left(-y^{2}+iy+2\right)idy=-\intop_{0}^{1}\left(-y^{2}i-y+2i\right)dy$

lo cual nos da como resultado al calcularla

$-\left[-\frac{y^{3}i}{3}-\frac{y^{2}}{2}+2iy\right]|_{0}^{1}=-\left[-\frac{i}{3}-\frac{1}{2}+2i\right]=\frac{1}{2}-\frac{5}{3}i$

por lo tanto nos queda:

Solución 

$\intop_{c}\left(z^{2}-z+2\right)dz= \frac{5}{6} + \frac{1}{2}-\frac{5}{3}i=\frac{4}{3}-\frac{5}{3}i$

---

Re elaborado por Manuel Rodríguez

Juan Daniel Rivera Bautista (discusión) 23:01 14 jun 2015 (CDT)

---

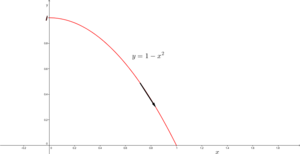
Ejercicio 23

Evalúe $\int_C (z^2-z+2)dz$ de $i$ a $1$ a lo largo del contorno $C$ dado en la figura.

Figura 5.2.10 figura para el problema 23

Procedimiento

Para parametrizar $y=-x^2+1$

Digo que: $x=t$ , $y=1-t^2$

Entonces : $\vec{z}(t)=<t,(1-t^2)>$ , $t\in[0,1]$

Si $z=x+iy$

$C:$ queda parametrizado por

$z(t)=t+i(1-t^2)$, $t[0,1]$

y $dz= (1-2it)dt$

Ahora: $z^{2}=\left(t+i(1-t)^{2}\right)^{2}$

y sustituyendo en mi función:

$z^2-z+2=(t+i(1-t^2))^{2}-\left(t+i(1-t^2)\right)+2=\left(1-i)-(1-2i)t+(3+i)t^{2}-2it^{3}-t^{4}\right)$

La integral queda: \[ \int_{C} \! \left( z^2-z+2 \right) \, dz =\int_{0}^{1} \! \left[ (1-i)-(1-2i)t+(3+i)t^{2}-2it^{3} -t^{4}\right] \, (1-2it)\,dt= \frac{4}{3}-\frac{5}{3}i \]

Por que:

\[ \int_{C} \! \left( z^2-z+2 \right) \, dz =\int_{0}^{1} \! \left[ (1-i)-(1-2i)t+(3+i)t^{2}-2it^{3}-t^{4}\right] \, (1-2it)\,dt= \]

\[ =(1-i) \int_{0}^{1} \! 1 \, dt - 3\int_{0}^{1} \! t \, dt + (7+3i) \int_{0}^{1} \! t^{2} \, dt + (2-8i) \int_{0}^{1} \! t^{3} \,dt - 5 \int_{0}^{1} \! t^{4} \,dt +2i \int_{0}^{1} \! t^{5} \,dt \]

Solución

\[ =1-i-\frac{3}{2}+\frac{7}{3}+i+\frac{1}{2}-2i-1+\frac{i}{3}=\frac{4}{3}-\frac{5}{3}i \]

---

Realizado por: Emmanuell Castro Flores (discusión) 20:13 14 jun 2015 (CDT)

---

---

Ejercicio 24

Evalué ${\displaystyle \int_{c}(z^{2}-z+2)dz}$ donde $c$ es el cuarto de circulo en el primer cuadrante con orientación negativa

Procedimiento

Proponemos la parametrización de $c=e^{it}$ con $\frac{\pi}{2}\leq t\leq0$

Sabemos que la integral esta dada por ${\displaystyle \int_{c}f(z)dz={\displaystyle \int_{a}^{b}f(z(t))z^{\prime}(t)dt}}$

Así, tendríamos que calcular

\[ {\displaystyle \int_{\pi/2}^{0}(z(t)^{2}-z(t)+2)z(t)^{\prime}dt=-{\displaystyle \int_{0}^{\pi/2}(e^{2it}-e^{it}+2)ie^{it}dt}} \]

\[ \Rightarrow-{\displaystyle i\int_{0}^{\pi/2}(e^{3it}-e^{2it}+2e^{it})dt=-i\left({\displaystyle \frac{e^{3it}}{3i}-{\displaystyle \frac{e^{2it}}{2i}+{\displaystyle \frac{2e^{it}}{i}}}}\right)|_{0}^{\pi/2}=\left({\displaystyle \frac{-e^{3it}}{3}+\frac{e^{2it}}{2}-2e^{it}}\right)|_{0}^{\pi/2}} \]

\[ \Rightarrow\left({\displaystyle \frac{-e^{3it}}{3}+\frac{e^{2it}}{2}-2e^{it}}\right)|_{0}^{\pi/2}=\left({\displaystyle \frac{-\cos3t}{3}}+{\displaystyle \frac{\cos2t}{2}-2\cos t}\right)|_{0}^{\pi/2}+i\left({\displaystyle \frac{-\sin3t}{3}+{\displaystyle \frac{\sin2t}{2}-2\sin t}}\right)|_{0}^{\pi/2} \]

Solución

\[ \Rightarrow\left({\displaystyle \frac{-e^{3it}}{3}+\frac{e^{2it}}{2}-2e^{it}}\right)|_{0}^{\pi/2}={\displaystyle \frac{4}{3}+i{\displaystyle \frac{5}{2}}} \]

---

Realizado por: Jose Emmanuel Flores Calderón (discusión) 18:47 14 jun 2015 (CDT)

---

Ejercicio 25

Determine una cota superior para el valor absoluto de la integral a lo largo del contorno indicado

$\oint {\frac {e^{z}}{z^{2}+1}}dz$ donde C es la circuferencia : $\mid z\mid =5$

Procedimiento

El teorema de acotamiento nos dice $\mid \int _{c}f(z)dz\mid \leq ML$, donde L es la longitud de la circunferencia(perímetro),

entonces:

$L=2\pi r=2\pi (5)=10\pi$ y $x=Re\mid z\mid =5$

Ahora:

$\mid {\frac {e^{z}}{z^{2}+1}}\mid ={\frac {\mid e^{z}\mid }{\mid z^{2}+1\mid }}$

analizamos el denominador:

La desiguealdad del triangulo nos dice que:

$\mid z_{1}+z_{2}\mid \geq \mid z_{1}\mid -\mid z_{2}\mid$ , entonces

$\mid z^{2}+1\mid \geq \mid z^{2}\mid -\mid 1\mid$

$\mid z^{2}\mid -\mid 1\mid \leq \mid z^{2}+1\mid$

${\frac {1}{\mid z^{2}+1\mid }}\leq {\frac {1}{\mid z^{2}\mid -\mid 1\mid }}$

${\frac {1}{\mid z^{2}+1\mid }}\leq {\frac {1}{\mid 5^{2}\mid -\mid 1\mid }}$

${\frac {1}{\mid z^{2}+1\mid }}\leq {\frac {1}{\mid 25\mid -\mid 1\mid }}$

${\frac {1}{\mid z^{2}+1\mid }}\leq {\frac {1}{24}}$

Por otro lado, la definición de una función exponencial compleja es:

$e^{z}=e^{x}cosy+ie^{x}seny$

sacando la magnitud(módulo)de ambos miembros de la ecuación, factorizando se tiene:

$\mid e^{z}\mid =\mid e^{x}cosy+ie^{x}seny\mid$

$\mid e^{z}\mid =\mid e^{x}(cosy+ie^{x}seny)\mid$

$\mid e^{z}\mid =\mid e^{x}\mid \mid cosy+iseny\mid$

$\mid e^{z}\mid =\mid e^{5}\mid {\sqrt {(cos^{2}y+sen^{2}y)}}$

$\mid e^{z}\mid =\mid e^{5}\mid (1)=e^{5}$

Juntando los resultados obtenidos se tiene finalmente:

Solución

$\mid \oint {\frac {e^{z}}{z^{2}+1}}dz\mid \leq {\frac {10\pi e^{5}}{24}}$

$\mid \oint {\frac {e^{z}}{z^{2}+1}}dz\mid \leq {\frac {5\pi e^{5}}{12}}$

---

Elaborado por Ricardo Garcia Hernandez--Ricardo Garcia Hernandez (discusión) 13:02 14 jun 2015 (CDT)

---

Ejercicio 26

Encontrar un límite superior para el valor absoluto de la integral dada a lo largo del contorno indicado.

$\oint_{c} \frac{1}{z^2-2i}dz $

donde C es la mitad derecha del círculo |z|=6 , de z=-6i a z=6i

Procedimiento

Tenemos una circunferencia con r=3

Tomamos el teorema de acotamiento

$ |\oint_{c}f(z)dz|\leq ML ....(1) $

Donde L es la longitud de la curva, por tanto

$ L=2\pi r=2\pi(3)=6\pi ....(2) $

Para encontrar el valor de la cota, tomamos el valor absoluto de la integral,donde

$ |\frac{1}{z^2-2i}|=\frac{|1|}{|z^2-2i|} ....(3) $

pero

$ |z_{1}+z_{2}|\geq |z_{1}|-|z_{2}| $ $ |z^2-2i|\geq |z^2|-|-2i| $ $ |z^2|-|-2i|\leq |z^2-2i| $ $ \frac{1}{|z^2-2i|}\leq \frac{1}{|z^2|-|-2i|} $ $ \frac{1}{|z^2-2i|}\leq \frac{1}{|36|-|-2i|} $ $ \frac{1}{|z^2-2i|}\leq \frac{1}{36-\sqrt{4}\sqrt{i^2}} $ $ \frac{1}{|z^2-2i|}\leq \frac{1}{36-2i} $ $ \therefore \frac{1}{36-2i}=M=(máximo)....(4)$

Solución

$ \therefore |\oint_{-6i}^{6i} \frac{1}{z^2-2i}dz|\leq \frac{6\pi}{36-2i} $

---

Realizado por: Samantha Martinez (discusión) 18:50 14 junio 2015 (CDT)

---

Ejercicio 27

Determine una cota superior para el valor absoluto de la integral a lo largo del contorno indicado.

$\int_{c}(z^{2}+4)dz$, donde$C$ es el segmento de recta $z=0\:a\:z=1+i$

Procedimiento

por el teorema de acotamiento

si $f$ es continua sobre una curva suave $C$y si $\mid f(z)\mid\leq M\;\forall,z\epsilon C$, entonces $\mid\int_{c}f(z)dz\mid\leq ML$, donde $L$ es la longitud de $C$

la longitud $L$ de $z=0\:a\:z=1+i$ utilizando el teorema de pitagoras

$L=\sqrt{2}$

podemos ver que el valor máximo que puede alcanzar $z$ es:

$\mid z\mid=\mid1+i\mid=\sqrt{1^{2}+1^{2}}=\sqrt{2}$

ademas:

$\mid z^{2}+4\mid\leq\mid z^{2}\mid+\mid4\mid=\mid z^{2}\mid+4=\mid z\mid^{2}+4=\sqrt{2}^{2}+4=2+4=6$

por el teorema de acotamiento tenemos:

$\mid\int_{c}(z^{2}+4)dz\mid\leq6\sqrt{2}$

Conclusión

por lo tanto podemos decir que $6\sqrt{2}$es una cota superior de $\mid\int_{c}(z^{2}+4)dz\mid$

---

Realizado por: Francisco Medina Albino (discusión) 18:02 14 jun 2015 (CDT)

---

Ejercicio 28

Determinar una cota superior para el valor absoluto de la integral $\int_{c}\frac{1}{z^{3}}dz$ donde c va de $z=4i$ a $z=4$ y $\left|z\right|=4$

Procedimiento

Para resolver el problema necesitaremos usar

$\left|\int_{c}f\left(z\right)dz\right|\leq ML$ ...(1)

Donde L es la longitud de arco dado por

$L=\int_{c}\sqrt{\left(\frac{d\phi}{dt}\right)^{2}+\left(\frac{d\psi}{dt}\right)^{2}}dt$ ...(2)

y M es una constante real

Tambien $\left|z\right|^{2}=16$ ...(3)

Lo primero que se resolverá va a ser L pero antes de eso sabemos que la integral es un cuarto de circulo con signo negativo ya que va de 4i a 4. Ahora resolvemos usando (2)

Antes definiremos las variables y sus derivadas

$x=\phi\left(t\right)=4cost\implies\frac{dx}{dt}=-4sent$ , $y=\psi\left(t\right)=4sent\Longrightarrow\frac{dy}{dt}=4cost$

Ya tenemos todo lo necesario para usar (2)

$L=\int\sqrt{\left(-4sent\right)^{2}+\left(4cost\right)^{2}}dt=\int\sqrt{16sen^{t}+16cos^{2}t}dt=\int\sqrt{\left(16\right)\left(sen^{2}t+cos^{2}t\right)}dt=\int\sqrt{16}=\int4dt$

Poniendo los limites de integracion adecuados tenemos que:

$L=4\int_{\frac{\pi}{2}}^{0}dt=4t\mid_{\frac{\pi}{2}}^{0}=4t\left(o-\frac{\pi}{2}\right)=-2\pi$ Recordando que el signo negativo nos da por la dirección.

Ahora sacaremos M y para hacerlo necesitamos tomar la norma de $\frac{1}{z^{3}}$ pero nos enfocaremos en $z^{3}$

$\left|z^{3}\right|=\left|z^{2}z\right|=\left|z^{2}\right|\left|z\right|=z^{2}\left|z\right|=4z^{2}=4(16)=64$ esto es posible gracias al dato de $\left|z\right|=4$ y a (3)

por lo tanto tenemos que

$\left|\frac{1}{z^{3}}\right|=\frac{1}{64}$

Multiplicamos Lpor M

$LM=-2\pi\left(\frac{1}{64}\right)=-\frac{\pi}{32}$

Ahora usando (1) obtenemos la solución del problema

Conclusión

$\left|\int_{c}\frac{1}{z^{3}}dz\right|\leq-\frac{\pi}{32}$

Nota: Salvo por el signo el ejercicio es correcto

$\left|\int_{c}\frac{1}{z^{3}}dz\right|\leq+\frac{\pi}{32}$

---

Resuelto por Luis Enrique Martínez Valverde (discusión) 15:56 14 jun 2015 (CDT)

---

Ejercicio 29

(a) utilice la definición 5.2.1 para demostrar que para cualquier curva suave C entre $z_0$ y $z_n$ se tiene que $\int_{c} dz = z_{n} - z_{n}$

Inciso a

Si $f$ es continua en una curva suave C dada por la parametrización $z(t) = x(t) iy(t), a \leq t \leq b$ , entonces

\[ \int_{c} f(z) dz = \int_{a}^{b} f(z(t)) z' (t) dt\]

Tenemos \[ \int_{z_{0}}^{z_{n}} dz = \int_{a}^{b} z' (t) dt\]

Entonces \[ \int_{a}^{b}[x'(t) + i y'(t)] dt = z\]

De acuerdo con el problema:

$b= z_{n} a= z_{0}$

\[ z_{n} - z_{0}\]

b)Usar los resultados en la parte (a) para verificar la respuesta del problema 14.

Inciso b

$z_0=2i$

$z_n=-2i$

$\int _c dz=-4i$

Que es el mismo resultado que el problema 14.

c) Cual es $\int _c dz $ si C es una curva simple cerrada.

Inciso c

Si es simple y cerrada:

$z_n = z_0$

Por lo que

$\int _c dz=0$

---

Realizado por: Esther Sarai (discusión) 11:45 13 jun 2015 (CDT)Esther Sarai

---

Ejercicio 30

Use la definición de la integral compleja para demostrar que para cualquier curva suave $C$ entre $z_0$ y $z_n$ se tiene que $\int_Czdz=\frac{1}{2}(z_n^2-z_0^2)$.

Procedimiento

Sol. La definición de la integral compleja es $\int_Cf(z)dz=\int_a^bf(z(t))z'(t)dt$, para nuestro problema $f(z)=z$ con $z=z(t)=x(t)+iy(t)$ donde $x$ e $y$ están parametrizadas en $t:[a,b]$ y definamos $z_0=z(t_0)=x(t_0)+iy(t_0)$, $z_n=z(t_n)=x(t_n)+iy(t_n)$ con $t_0=a$ y $t_n=b$.

Sustituimos en la definición:

$\int_Cf(z)dz=\int_a^bf(z(t))z'(t)dt=\int_{t_0}^{t_n}z(t)z'(t)dt$

Si $z(t)=x(t)+iy(t)$ entonces $z'(t)=x'(t)+iy'(t)$. Por comodidad se omitirá la notación $x(t)$ y demás considerándose que todas las variables son funciones implícitas de $t$.

Sustituyendo:

$\int_Cf(z)dz=\int_{t_0}^{t_n}z(t)z'(t)dt=\int_{t_0}^{t_n}(x+iy)(x'+iy')dt=\int_{t_0}^{t_n}[xx'+ixy'+iyx'-yy']dt$

$\int_Czdz=\int_{t_0}^{t_n}[(xx'-yy')+i(xy'+x'y)]dt=\int_{t_0}^{t_n}(xx'-yy')dt+i\int_{t_0}^{t_n}(xy'+x'y)dt$

e identificamos las partes de la integral

$\int_{a}^{b}f_1(t)dt=\int_{t_0}^{t_n}(xx'-yy')dt$ y $\int_{a}^{b}f_2(t)=\int_{t_0}^{t_n}(xy'+x'y)dt$

las cuales son integrales reales. Del teorema fundamental del cálculo se tiene que si $F(t)$ es una anti-derivada de una función continua (las cuales deben de ser para este problema dado que las funciones $x(t)$ e $y(t)$ son continuas en la curva $C$), es decir, $F$ es una función para la que $F'(t)=f(t)$, entonces la integral definida de $f$ en el intervalo $[a,b]$ es el número

$\int_a^bf(x)dx=F(x)|_a^b=F(b)-F(a)$

por lo que se procede a encontrar las funciones $F_1(t)$ y $F_2(t)$.

Para la parte real se tiene $\int_{t_0}^{t_n}(xx'-yy')dt$, por lo que una opción es $F_1(t)=\frac{1}{2}(x^2-y^2)$, lo cual puede comprobarse al derivar implícitamente respecto a $t$ con la regla de la cadena. Así, para la parte real de la integral $\int_Czdz$ se tiene

$\int_{t_0}^{t_n}(xx'-yy')dt=\frac{1}{2}(x^2-y^2)|_{t_0}^{t_n}=\frac{1}{2}[(x(t_n)^2-y(t_n)^2)-(x(t_0)^2-y(t_0)^2)]$

La parte imaginaria es $\int_{t_0}^{t_n}(xy'+x'y)dt$ y notamos que lo de entre paréntesis es la derivada de un producto por lo que $F_2(t)=xy$, así

$\int_{t_0}^{t_n}(xy'+x'y)dt=xy|_{t_0}^{t_n}=x(t_n)y(t_n)-x(t_0)y(t_0)$

Sustituyendo

$\int_Czdz=\frac{1}{2}[(x(t_n)^2-y(t_n)^2)-(x(t_0)^2-y(t_0)^2)]+i[x(t_n)y(t_n)-x(t_0)y(t_0)]$

$\int_Czdz=\frac{1}{2}[(x(t_n)^2-y(t_n)^2)+i(2x(t_n)y(t_n))]-\frac{1}{2}[(x(t_0)^2-y(t_0)^2)+i(2x(t_0)y(t_0))]$

Dado que $z_n=z(t_n)=x(t_n)+iy(t_n)$ y $z_0=z(t_0)=x(t_0)+iy(t_0)$, entonces por las reglas de multiplicación

$z_0^2=[x(t_0)+iy(t_0)]^2=[x(t_0)^2-y(t_0)^2]+i[2x(t_0)y(t_0)]$ y,

$z_n^2=[x(t_n)+iy(t_n)]^2=[x(t_n)^2-y(t_n)^2]+i[2x(t_n)y(t_n)]$

Sustituyendo

$\int_Czdz=\frac{1}{2}[(x(t_n)^2-y(t_n)^2)+i(2x(t_n)y(t_n))]-\frac{1}{2}[(x(t_0)^2-y(t_0)^2)+i(2x(t_0)y(t_0))]=\frac{1}{2}z_n^2-\frac{1}{2}z_0^2$

Por lo que hemos demostrado que:

Conclusión

$\int_Czdz=\frac{1}{2}(z_n^2-z_0^2)$

para toda curva $C$ suave entre los puntos $z_0$ y $z_n$.

---

Realizado por: Oscar Javier Gutierrez Varela (discusión) 20:20 13 jun 2015 (CDT)

---