SECCION 1.1.3
1. Calcule las raíces cuadradas de  y de
y de  .
.
Aplicando la formula para calcular raíces cuadradas de números complejos.
 si
si 
Por lo tanto las raices de  , son:
, son:



y para  , son:
, son:



Realizado por: Josua Da Vinci 23:44 30 sep 2009 (UTC)
REVISADO
2.- Calcule las raíces sextas de -64 y las raíces cubicas de 8i
Tenemos que  definicion en forma polar
definicion en forma polar
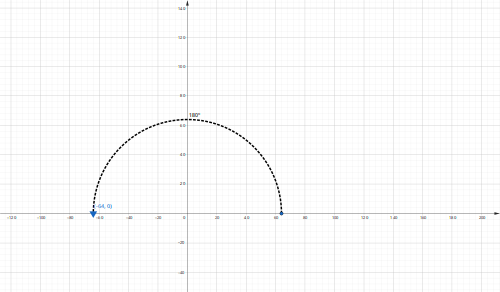
r=64
n=6 porque nos piden las raíces sextas
Entonces el argumento 
Si 
Entonces utilizando la Fórmula de Moivre para obtener las raíces

Ahora tenemos
 y g= raíz enesima
y g= raíz enesima  = = 2
= = 2
y  los
los  es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de
es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de  entonces sacando las raíces
entonces sacando las raíces
 k=0
k=0
 k=1
k=1
 k=2
k=2
 k=3
k=3
 k=4
k=4
 k=5
k=5
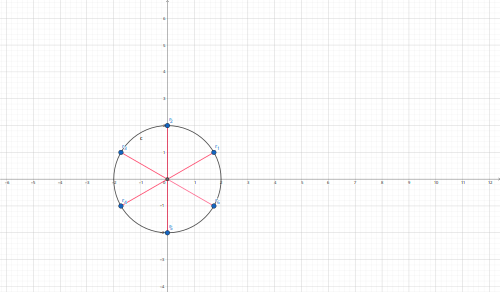
Las soluciones son
r1= 2 
r2= 2 
r3= 2 
r4= 2 
r5= 2 
r6= 2 
Graficando en coordenadas polares nos queda:
Haciendo algo similar para el 8i Tenemos

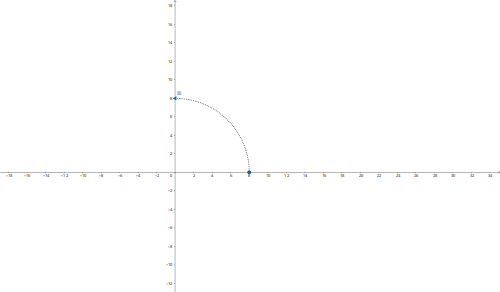
El argumento 
r= 8
n=3 porque nos piden las raíces cubicas
 y g= raíz enesima
y g= raíz enesima  = = 2
= = 2

 k=0
k=0
 k=1
k=1
 k=2
k=2
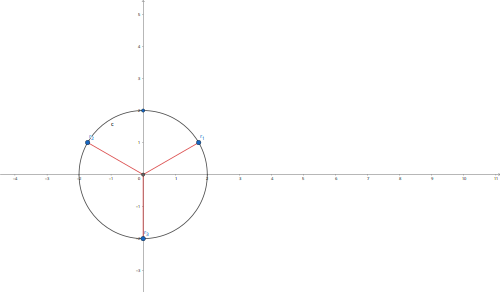
r1= 2 
r2= 2 
r3= 2 
Gráficando en coordenadas polares tenemos
Realizado por: Karla 21:35 4 oct 2009 (UTC)Sanchez
2.- Calcule las raíces sextas de -64 y las raíces cubicas de 8i
Sea 
Por la Fórmula de Moivre
 para k = 0,1,2,3,4,5
para k = 0,1,2,3,4,5
Evaluando k se obtiene
con k = 0

con k = 1

con k = 2

con k = 3

con k = 4

con k = 5

..............
Sea 
 para k = 0,1,2
para k = 0,1,2
Evaluando a k se obtiene
con k = 0

con k = 1

con k = 2

Realizado por: Luis Nava 21:07 3 oct 2009 (UTC)
3. Demuestre que  donde z es una raíz n-ésima de la unidad,
donde z es una raíz n-ésima de la unidad,

Sea 
Ahora multiplicamos ambos lados por Z

Restando la segunda ecuación de la primera

Tenemos que

entonces

De donde

Como z es una raíz enesima de la unidad



Entonces

y

porque

Por lo tanto

Realizado por: Ralf Gutierrez 22:00 2 oct 2009 (UTC)
4. Demuestre que:

Sugerencia: Factoriza la expresión  usando las raíces n-ésimas de la unidad, posteriormente evalue en
usando las raíces n-ésimas de la unidad, posteriormente evalue en  .
.
Solución:
Las raices de  son
son

entonces podemos escribir

dividiendo ambos lados por  y haciendo
y haciendo  :
:

de aqui hallamos que

tomando el conjugado complejo de ambos lados de (1)

Multiplicando la ecuación (1) por la (2) y aplicando que

tenemos

puesto que

la ecuación anterior se transforma en

despejando y sacando la raíz en ambos lados de la expresión:

lo que queda demostrada la igualdad.
Realizado por:Wendy 23:10 4 oct 2009 (UTC)
5. Demuestre que
 ,
,
donde  no es un multiplo par de
no es un multiplo par de  .
.
Esta identidad se le atribuye a Lagrange.
Sugerencia: calcular la parte real de
 , donde
, donde  .
.
Solucion.
Sea
 si multiplicamos por
si multiplicamos por  a
a  se tiene que
se tiene que
 ahora restemos estas dos ultimas expresiones
ahora restemos estas dos ultimas expresiones
 de lo que se obtiene que
de lo que se obtiene que

Si en esta última expresion utilizamos  entonces
entonces

toma la siguiente forma

que es equivalente a esta

Tomando el lado derecho de esta ultima expresión y llevar a cabo el producto con su conjugado , es decir:

Se obtiene del numerador lo siguiente

si tomamos solo la parte real se tiene que




por otra parte para el denominador se tiene:



al tomar la parte real de
 ,
,
sustituir lo encontrado para el numerador (parte real) y el denominador , y utilizar la siguiente
identidad

tenemos lo siguiente:

Lo cual es casi a lo que se queria llegar.
Realizado por: Dali 00:01 5 oct 2009 (UTC)
OTRA DEMOSTRACION DEL EJERCICIO1.1.3 NUMERO 5:
5. Demuestre que
 ,
,
donde  no es un multiplo par de
no es un multiplo par de  .
.
Esta identidad se le atribuye a Lagrange.
Sugerencia: calcular la parte real de
 , donde
, donde  .
.
Solucion.
Sea

y como  ..............& y por ser una serie geometrica la podemos escribir de la siguiente manera
..............& y por ser una serie geometrica la podemos escribir de la siguiente manera

Sea  , aplicando & con
, aplicando & con  se tiene lo siguiente
se tiene lo siguiente

y tomamos partes reales obtenemos
 .............%
.............%
desarrolandola se tiene :
![{\displaystyle \sum_{k=0}^{n}\cos k\theta=Re\dfrac{\left[1-e^{i\left(n+1\right)\theta}\right]\left[1-e^{-i\theta}\right]}{\left[1-e^{i\theta}\right]\left[1-e^{-i\theta}\right]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8d7744e877270d3a4dd56129b231a4d727852fb) =
=![\dfrac{1-\cos\theta+\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-cos\theta\right)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1acd2041b495052daa4b87e5f8f63098b599d569) =
=![\dfrac{1}{2}+\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b04257d7946a926963c3b0cf396245dec2c9a0ff) .
.
Con lo cual solo basta probar que
![\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}=\dfrac{\sin\left[\left(n+\frac{1}{2}\right)\theta\right]}{2\sin\frac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/df38fe02d60fe7ffbaf0dd3c905ede4ee6737ace)
Veamos la demostracion
![\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}=\dfrac{\sin\left[\left(n+\frac{1}{2}\right)\theta\right]}{2\sin\frac{\theta}{2}}\Longleftrightarrow](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce688b8e4e65f3b7326296aadf4842361ea3ea91)
![\left(\cos n\theta-\cos\left[\left(n+1\right)\theta\right]\right)\sin\frac{\theta}{2}=\left(1-\cos\theta\right)\sin\left[\left(n+\frac{1}{2}\right)\theta\right]\Longleftrightarrow](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eda6ac820a89616c39ec0f535266bf74038ec43d)

 ..............#
..............#
Si  la igualdad # es cierta. Si no, es equivalente a
la igualdad # es cierta. Si no, es equivalente a
 .
.
Lo cual es cierto por la formula de coseno diferencial . Por lo tanto queda demostrado que
 .
.
Realizado por:Diana Rodriguez Almaraz. 04:47 15 oct 2010 (UTC)
DEMOSTRACION ALTERNATIVA DEL EJERCICIO 5 CAP 1.1.3:
5. Demuestre que
 ,
,
donde  no es un multiplo par de
no es un multiplo par de  .
.
Sea

La expresión  la podemos expresar como una suma geométrica
la podemos expresar como una suma geométrica

Esta serie converge a la expresión:
![i\sin k\theta+\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8cdbbc2d3702a0c80e5b605a5c19004ec3457e22)
Como nos interesa solamente la parte real de la expresíon omitimos la parte imaginaria.
![Re[i\sin k\theta+\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]=\cos\dfrac{n\theta}{2}+\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0fd3758d02b4fad72cea41053fc41829da769d46)
Reescribiendo la parte real y sabiendo que 
![\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]=\dfrac{\cos\dfrac{n\theta}{2}+\sin[\dfrac{\theta(1+n)}{2}]}{\sin\dfrac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c5af21727a2c6b43025e1fadbc4630b845ade3a2)
Ahora bien, por la identidad
![\sin[a]\cos[b]=\dfrac{1}{2}[\sin[a+b]+\sin[a-b]]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3fbb640254d60794e89b67f9e661678ce00a45f7) Con
Con

Podemos reescrbir la expresión, para la sumas de senos y cosenos del numerador como:
![\dfrac{1}{2}[\sin[\dfrac{\theta}{2}+n\theta]+\sin\dfrac{\theta}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7234637c393445ce77011b4fe989b6000247376d)
Por último simplificando términos y reacomodando, llegamos al resultado
![\dfrac{\dfrac{1}{2}\sin[\dfrac{\theta}{2}+n\theta]+\sin\dfrac{\theta}{2}}{\sin\dfrac{\theta}{2}}=\dfrac{1}{2}+\dfrac{\sin[\dfrac{\theta}{2}+n\theta]}{2\sin\frac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5926b030ac724e9b6da88a14b62f6f9316acade8)
Realizado por: Carlos López Cobá 06:20 26 oct 2010 (UTC)
Compleja:ej-cap1.1
esta seccion ej-cap1.1.3
Compleja:ej-cap1.1.4
Compleja:ej-cap1.2
Compleja:ej-cap1.3
Compleja:ej-cap1.4

















































































































![{\displaystyle \sum_{k=0}^{n}\cos k\theta=Re\dfrac{\left[1-e^{i\left(n+1\right)\theta}\right]\left[1-e^{-i\theta}\right]}{\left[1-e^{i\theta}\right]\left[1-e^{-i\theta}\right]}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8d7744e877270d3a4dd56129b231a4d727852fb)
![\dfrac{1-\cos\theta+\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-cos\theta\right)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1acd2041b495052daa4b87e5f8f63098b599d569)
![\dfrac{1}{2}+\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b04257d7946a926963c3b0cf396245dec2c9a0ff)
![\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}=\dfrac{\sin\left[\left(n+\frac{1}{2}\right)\theta\right]}{2\sin\frac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/df38fe02d60fe7ffbaf0dd3c905ede4ee6737ace)
![\dfrac{\cos n\theta-\cos\left[\left(n+1\right)\theta\right]}{2\left(1-\cos\theta\right)}=\dfrac{\sin\left[\left(n+\frac{1}{2}\right)\theta\right]}{2\sin\frac{\theta}{2}}\Longleftrightarrow](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce688b8e4e65f3b7326296aadf4842361ea3ea91)
![\left(\cos n\theta-\cos\left[\left(n+1\right)\theta\right]\right)\sin\frac{\theta}{2}=\left(1-\cos\theta\right)\sin\left[\left(n+\frac{1}{2}\right)\theta\right]\Longleftrightarrow](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eda6ac820a89616c39ec0f535266bf74038ec43d)










![i\sin k\theta+\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8cdbbc2d3702a0c80e5b605a5c19004ec3457e22)
![Re[i\sin k\theta+\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]=\cos\dfrac{n\theta}{2}+\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0fd3758d02b4fad72cea41053fc41829da769d46)

![\cos\dfrac{n\theta}{2}\csc\dfrac{\theta}{2}\sin[\dfrac{\theta(1+n)}{2}]=\dfrac{\cos\dfrac{n\theta}{2}+\sin[\dfrac{\theta(1+n)}{2}]}{\sin\dfrac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c5af21727a2c6b43025e1fadbc4630b845ade3a2)
![\sin[a]\cos[b]=\dfrac{1}{2}[\sin[a+b]+\sin[a-b]]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3fbb640254d60794e89b67f9e661678ce00a45f7)


![\dfrac{1}{2}[\sin[\dfrac{\theta}{2}+n\theta]+\sin\dfrac{\theta}{2}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7234637c393445ce77011b4fe989b6000247376d)
![\dfrac{\dfrac{1}{2}\sin[\dfrac{\theta}{2}+n\theta]+\sin\dfrac{\theta}{2}}{\sin\dfrac{\theta}{2}}=\dfrac{1}{2}+\dfrac{\sin[\dfrac{\theta}{2}+n\theta]}{2\sin\frac{\theta}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5926b030ac724e9b6da88a14b62f6f9316acade8)