By using the programme Mandelbulber for the representation of fractal structures, it's important to make a correspondences between the coordinate system used by the program and the coordinates of the real scators space. That is, we need the connection $(x;y,z)\rightarrow (s;x,y).$ It seeks to associate each axis used in the programme with the axes used in scators space.
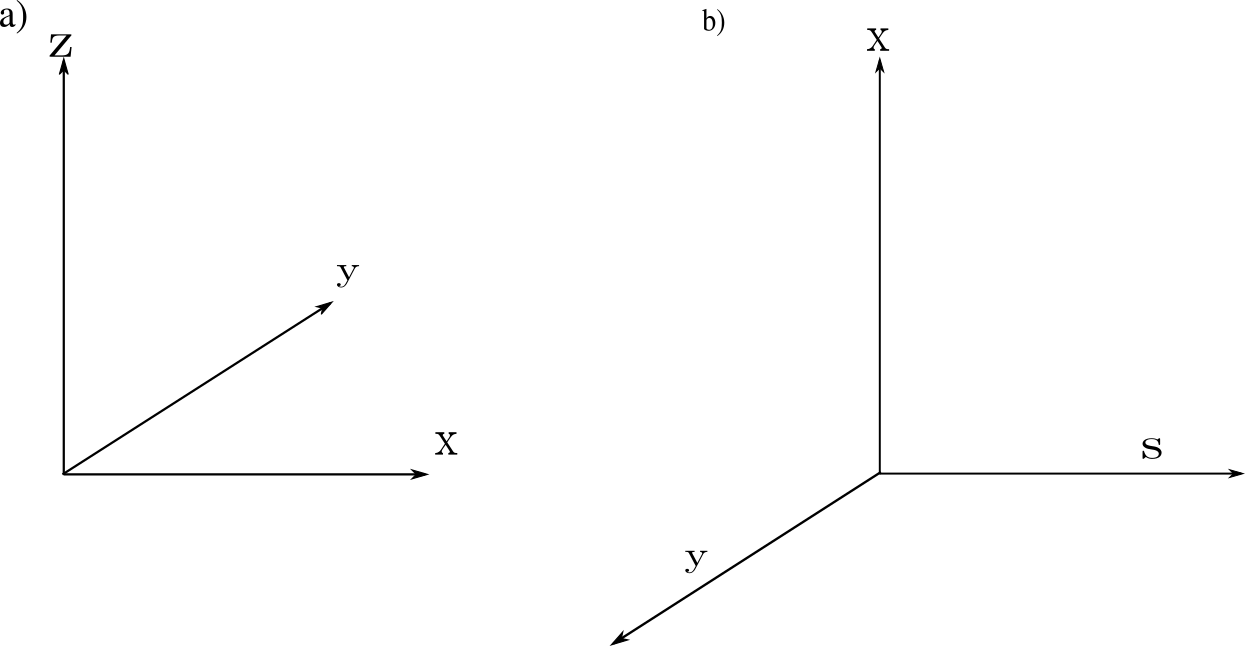
Then, if we want to label e interpret the images that the programme give us, you should use the following coordinate transformation: ($x\rightarrow s;\quad y\rightarrow -y,\quad z\rightarrow x$), thus, an image obtained in Mandelbulber have the coordinates $(1.5;0.5,0.6)$ will mean the real scators coordinates are $s=1.5; x=0.6,y=-0.5,$ with which we can to label or name the images according the scators coordinate system.

