Al hacer uso del programa Mandelbulber para la representación de las estructuras fractales, es importante hacer una correspondencia entre el sistema coordenado que usa dicho programa y las coordenadas del espacio de los escatores reales. Es decir, necesitamos las relación $(x;y,z)\rightarrow (s;x,y).$ Se busca hacer corresponder cada eje del sistema usado en Mandelbulber con cada eje del sistema usado en los escatores reales.
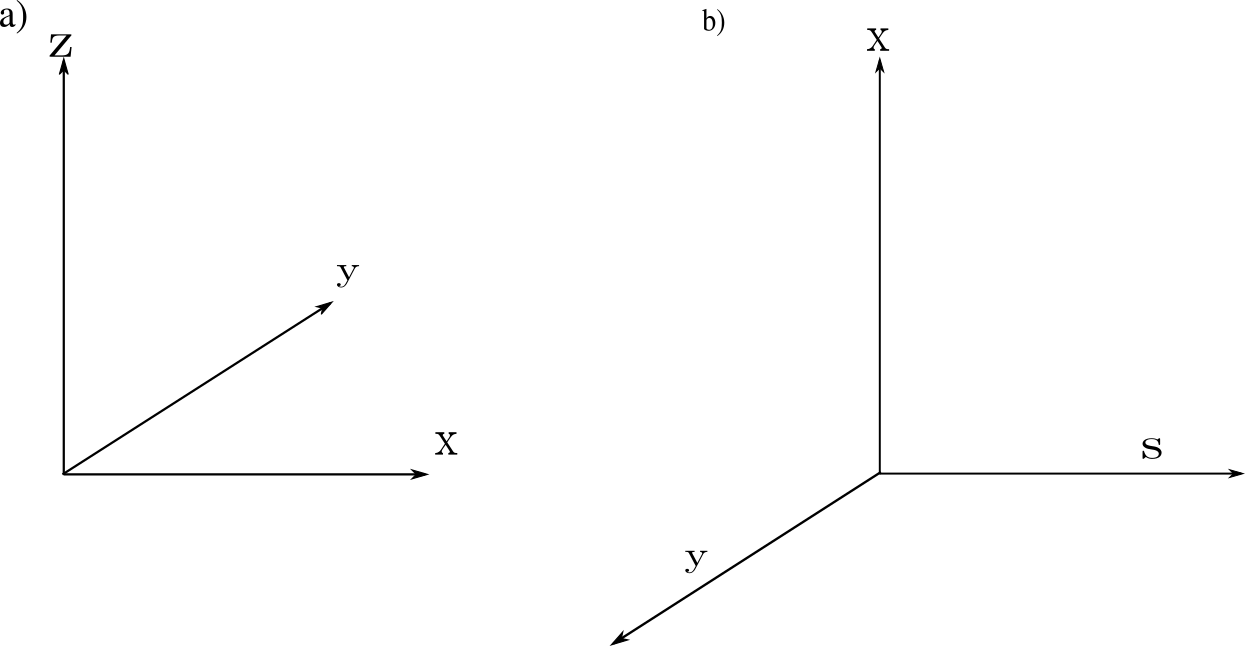
b) escatores, ambos sistemas son de mano derecha
Entonces, para poder etiquetar e interpretar las imágenes que brinda el Mandelbulber, es necesario usar la siguiente transformación de coordenadas: ($x\rightarrow s;\quad y\rightarrow -y,\quad z\rightarrow x$), de esta manera, si una imagen obtenida en Mandelbulber tiene por coordenadas $(1.5;0.5,0.6)$ querrá decir que $s=1.5; x=0.6,y=-0.5,$ y con ello se podrá nombrar o etiquetar cada imagen de acuerdo al sistema coordenado de los escatores, y no al que usa el programa.

