cúsfera o cusfera
escatores imaginarios en 1+2 dimensiones y la escala humana
Resumen
Se presenta una escultura que fusiona la vertiente artística y científica de una hiper-superficie de métrica constante y su relación con el cuerpo humano. Se propone la fabricación de la escultura a escala de dos metros cúbicos fundida en bronce y pulida al brillo. Se sugiere que se exponga en una ubicación apropiada que permita visualizarla desde tres ejes ortogonales. La cusfera será una cápsula de tiempo y seguramente se conformará como un símbolo emblemático del espacio y la institución donde se ubique.
1. la conjunción del arte y la ciencia
La fusión del arte y la ciencia, de la estética y la precisión es provocadoramente afín al ser humano. Desde el célebre dibujo de Leonardo da Vinci de las proporciones del hombre de Vitruvia ante el círculo y el cuadrado hasta algunas pinturas de los muralistas mexicanos invocando a la ciencia, se articulan dos esferas de saber y conocimiento, dos espacios complementarios pero elusivamente separados.
La escultura métrica que se presenta en éste proyecto se ubica en esta tradición de diversos artistas a lo largo de la historia de la humanidad que intentan fusionar la exactitud físico matemática y la libertad estética del arte.
2. la métrica
La métrica en un sistema matemático establece la definición de distancia, una medida de la cercanía o lejanía que permite establecer el concepto de vecindad. La métrica en física se vincula al concepto de tiempo y espacio así como la medición de eventos en esa matriz tempo-espacialoide. Ambas disciplinas se articulan para establecer la geometría del espacio y desde finales del siglo XIX del espacio-tiempo con las contribuciones iniciales entre otros de Poincaré, Grassmann y Lorentz y posteriormente de Einstein, Minkowski, Thomas y otros científicos.
La métrica de la geometría Euclideana se establece el teorema de Pitágoras. La distancia del origen a un punto con coordenadas cartesianas $(x,y,z)$ es igual a la raíz cuadrada de la suma de los cuadrados $\sqrt{x^2+y^2+z^2}$. La figura geométrica que se genera bajo la condición de distancia constante es una esfera, pues el origen de la esfera es equidistante a todos los puntos de la superficie de la esfera como se muestra en la figura 1.

En la métrica de Lorentz que se utiliza en relatividad especial, el punto de espacio - tiempo $(t,x,y,z)$ tiene una métrica hiperbólica $\sqrt{t^2-(x^2+y^2+z^2)}$. La métrica constante en el espacio de cuatro dimensiones da lugar a superficies hiperbólicas que no forman una figura acotada, es decir, la figura es como una sábana infinita con curvatura hiperbólica.
3. métrica de escatores imaginarios1
El álgebra de escatores es un álgebra que está en desarrollo y presenta afinidades con las álgebras gradadas de Clifford y con los números hiper-geométricos. El nombre de esca-tores proviene de la contracción de esca-lares y direc-tores (vectores o versores) pues sus elementos contienen una parte escalar que no posee la cualidad de dirección y una parte con dirección bien definida. Hay dos vertientes, una de escatores reales y otra de escatores imaginarios. El álgebra de escatores reales se puede concebir como una deformación de la métrica de Lorentz y como ella, genera superficies no acotadas. Los escatores imaginarios exhiben una métrica para coordenadas $(t;x,y,z)$
$\left\Vert \left(t;x,y,z\right)\right\Vert =t\sqrt{1+\frac{x^{2}}{t^{2}}}\sqrt{1+\frac{y^{2}}{t^{2}}}\sqrt{1+\frac{z^{2}}{t^{2}}}.$
Son necesarias cuatro dimensiones para visualizar a éstas cuatro variables. Sin embargo, se puede esbozar el tipo de superficies que se generan en tres dimensiones si se utiliza la dimensión temporal y dos de las dimensiones espaciales $(t;x,y)$. Si se impone la condición de métrica constante, digamos igual a cinco por ejemplo (= 4), la distancia a un punto origen para los escatores está dado por la ecuación
$t^{2}+x^{2}+y^{2}+\frac{x^{2}y^{2}}{t^{2}}=4.$
Ésta es precisamente la superficie que describe la escultura métrica que presentamos en la figura 2. La distancia al origen se aprecia distinta (en la métrica Euclideana), sin embargo, todos los puntos de la superficie se encuentran a la misma distancia del origen en la métrica de escatores imaginarios.

4. cusfera: escultura métrica en 1+2 dimensiones
La hiper-superficie reducida a 1+2 dimensiones se ha graficado con diversos programas de visualización matemática. A partir de ellos hemos realizado una escultura en barro, una aproximación en fomi, y un vaciado en bronce. Éstas esculturas son de pequeñas dimensiones de 6 centímetros de diámetro. Se realizó un modelo en una impresora 3D de la CyAD, UAM-A en tres dimensiones en polímero de 20 centímetros cúbicos, es decir se triplicó aproximadamente la escala previa. Este nuevo modelo se realizó asistido por computadora de manera que la precisión en las superficies es mucho mayor.
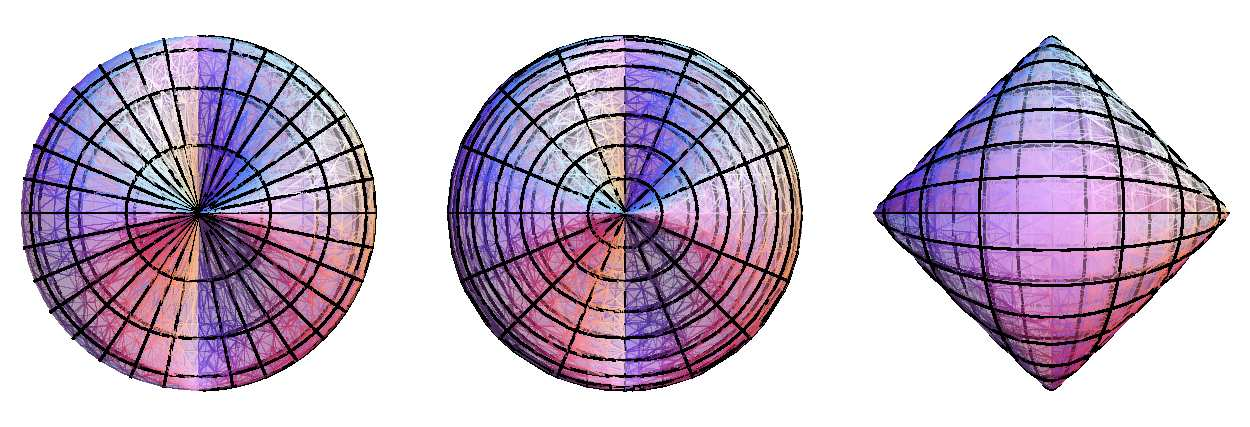
Una propiedad peculiar de la figura tridimensional es que el perímetro de sus proyecciones en dos planos perpendiculares forma círculos y sin embargo en el tercer plano perpendicular ¡forma un cuadrado! como se muestra en la figura 3. Por ésta peculiaridad, la figura se ha denominado con la contracción de 'cubo' y 'esfera', es decir, una cusfera.
5. la escultura expuesta en un espacio público universitario
Se propone una escultura de grandes dimensiones de la escultura métrica de escatores imaginarios fundida en metal. Escalar la figura a un modelo monumental de $2\times2\times2$ metros en bronce y pulida al brillo producirá un objeto impresionante.
Ubicada adecuadamente se podría observar desde distintos ángulos incluyendo las tres perspectivas antes mencionadas. Por ejemplo, imaginemos que se ubica en el cruce de dos corredores perpendiculares. El observador mira la silueta circular de la escultura al fondo del corredor. En el recorrido por la explanada o el pasillo tendrá oportunidad de observar perspectivas distintas de ésta escultura, en particular cuando llegue digamos al extremo oriente mirará otra silueta circular. Sin embargo, en la tercera dirección ortogonal desde la terraza del primer piso de posgrado o el corredor superior ad hoc con piso de vidrio, observará una silueta cuadrada. Con una iluminación adecuada que puede ser inclusive la luz solar es posible también proyectar la sombra de las siluetas antes descritas.
La idea es que a través de la experiencia estética el observador estimule su imaginación para concebir espacios multidimensionales no Euclideanos. El propósito de tener un terminado de metal al brillo permitirá que el observador mire el reflejo de su propia figura y el entorno en la escultura. Es decir, el sujeto se ve embebido en la superficie de espacio tiempo, que es por cierto, en donde se encuentra inmerso.
El acercamiento de los individuos al arte y la ciencia es radicalmente distinto. Del arte disfrutamos, de la ciencia aprendemos. Ésta concepción la queremos cambiar y tratar de empalmar las experiencias artísticas y científicas. El artista puede utilizar al arte para describir al mundo, su mundo. Asimismo, el físico matemático puede utilizar las matemáticas para conformar un sistema algebráico y otorgarle interpretación física a las variables. Intenta así describir también al mundo, otra faceta distinta a la que muestran los artistas o inclusive otros científicos. Sin embargo, desde esta perspectiva el quehacer artístico y el científico pueden no siempre estar tan alejados el uno del otro como pareciera en primera instancia. La belleza y el placer de disfrutarla es posible sin necesidad de ser un especialista.
Es necesario planear la ubicación específica, preparar el pedestal para depositarla así como la (posible) implementación de un pasillo de vidrio para observarla desde arriba.
La figura puede ser un símbolo emblemáticos del espacio y la institución donde se ubique. Se puede reproducir en serie en pequeña escala para su venta en materiales económicos sintéticos o en materiales tradicionales de escultura ya sea barro, metal o madera.
6. mensajes para la posteridad
Se propone que el interior hueco permanezca abierto una temporada para introducir documentos y pensamientos legados hacia el futuro. El vaciado de la figura se puede realizar en ocho piezas idénticas. Siete de las ocho piezas se pueden soldar y dejar un 'gajo' de un octavo descubierto con su 'cáscara' correspondiente a un lado.
Se sugiere invitar a la comunidad universitaria en primera instancia, y a la sociedad civil en general a proponer mensajes u objetos que se introduzcan en el interior. Después de un lapso apropiado, el último octavo de la escultura se suelda para completar la pieza. Se preparan instrucciones para que en un ciclo prehispánico completo de 52 años se abra el contenido de la cápsula de tiempo.
7. corolario
El álgebra de escatores es un álgebra asociativa y conmutativa pero no distributiva que ha sido concebida y esta siendo desarrollada por académicos mexicanos. Las figuras de métrica constante son originales y propias de éste tipo de álgebras. Desde éste punto de vista, la escultura métrica de escatores imaginarios tiene también una proyección en el ámbito internacional como una contribución original desde nuestra región mesoamericana.
Las muy distintas perspectivas de la pieza hacen del observador un sujeto activo e invitan a la reflexión sobre las posibilidades geométricas del espacio. Las imágenes del entorno reflejadas en la escultura evocan al mundo en el tiempo y espacio.

