Diferencia entre revisiones de «Optica: optica fisica»
Sin resumen de edición |
|||
| (No se muestran 140 ediciones intermedias de 7 usuarios) | |||
| Línea 1: | Línea 1: | ||
== | == Coherencia temporal y espacial== | ||
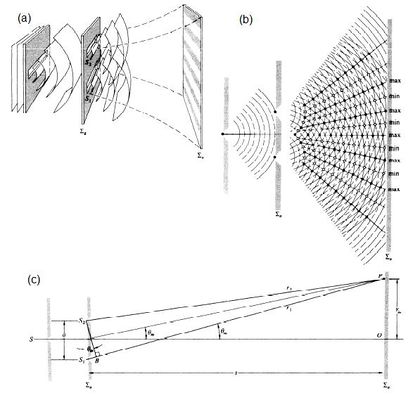
[[Imagen:young.jpg| | [[Imagen:young.jpg|600x400px|thumb|left|Figura 1. El experimento de Young, en la figura (a) tenemos la fuente luminosa que ilumina el plano paralelo que tiene dos rendijas que difractan la luz al pasar por ellas. En la figura (b) la fuente es puntual y pasa por los orificios S1 Y S2. ]] | ||
Si en la figura (a) | Si en la figura 1, la fuente primaria que se encuentra en el primer plano de la imagen (a), que llamaremos '''''S''''', se encoge hasta convertirse en una fuente puntual sobre el eje central como en la imagen (b) y tiene un ancho de banda de frecuencia finito, los efectos de [[Optica: Coherencia |coherencia]] temporal predominarán. | ||
Las perturbaciones ópticas en <math>{S}_1 y {S}_2 </math> son entonces idénticas. | Las perturbaciones ópticas en <math>{S}_1\ </math> y <math> {S}_2\ </math> son entonces idénticas, donde <math> {S}_1\ </math> y <math> {S}_2\ </math> son las ventanas que muestra la figura (b) en el plano intermedio. | ||
La coherencia mutua <math> \tilde{\Gamma}_{12}(\tau)=\left\langle \mathbf{V}_1(t)\mathbf{V}_2^{*}(t+\tau)\right\rangle </math> entre los dos puntos donde las perturbaciones son idénticas es en este caso la autocoherencia del campo. | |||
La coherencia mutua <math> \tilde{\Gamma}_{12}(\tau)=\left\langle \mathbf{V}_1(t)\mathbf{V}_2^{*}(t+\tau)\right\rangle </math> entre los dos puntos donde las perturbaciones son | |||
De aquí que podamos escribirla como | De aquí que podamos escribirla como | ||
| Línea 14: | Línea 13: | ||
<center><math> \tilde{\Gamma}(S_{1},S_{2},\tau)=\tilde{\Gamma}_{12}(\tau)=\tilde{\Gamma}_{11}(\tau)</math></center> | <center><math> \tilde{\Gamma}(S_{1},S_{2},\tau)=\tilde{\Gamma}_{12}(\tau)=\tilde{\Gamma}_{11}(\tau)</math></center> | ||
<center> | <center> o</center> | ||
<center><math>\tilde{\gamma}_{12}(\tau)=\tilde{\gamma}_{11}(\tau). </math></center> | <center><math>\tilde{\gamma}_{12}(\tau)=\tilde{\gamma}_{11}(\tau). </math></center> | ||
lo mismo obtenemos cuando <math> {S}_1 y {S}_2 </math> se | lo mismo obtenemos cuando <math> {S}_1\ </math> y <math> {S}_2\ </math> se combinan y <math> \tilde{\gamma}_{11}(\tau)</math> se denomina ''''' grado de coherencia temporal complejo''''' donde <math> \tau\ </math> es el intervalo de tiempo que se separan. | ||
Esta | Esta interpretación es un poco diferente para un interferómetro de división de amplitud (interferometro de Michelson[http://es.wikipedia.org/wiki/Interfer%C3%B3metro_de_Michelson]), donde <math> \tau\ </math> es igual a la diferencia de recorrido dividida por '''''c'''''. La expresión para la irradiancia '''''I''''' <math> I=I_{1}+I_{2}+2(I_{1}I_{2})^{\frac{1}{2}}Re\tilde{\gamma}_{12}(\tau), </math> contendra entonces a <math> \tilde{\gamma}_{11}(\tau)</math> en lugar de <math> \tilde{\gamma}_{12}(\tau)</math>. | ||
Ahora si una onda luminosa con el | Ahora si una onda luminosa con el interferómetro se divide en dos perturbaciones del campo idénticas de la forma <math>\tilde \mathbf{V}(t)=\mathbf{V}_0 e^{i\phi(t)} </math> donde <math> \phi\ (t) </math> se refiere a la fase de la onda y la tilde expresa en V que puede tener una representacion compleja, si el interferometro después las vuelve a combinar para generar una distribución de franjas, entonces | ||
<center><math> \tilde{\gamma}_{11}(\tau)=\frac{\left\langle \tilde\mathbf{V}(t+\tau)\tilde\mathbf{V}^{*}(t)\right\rangle}{\tilde {|\mathbf{V}|}^2} = \frac{\left\langle e^{i\phi(t+\tau)} e^{-i\phi(t)}\right\rangle}{\tilde {|\mathbf{V}|}^2}\tilde{|\mathbf{V}|}^2 =\left\langle e^{i\phi(t+\tau)} e^{-i\phi(t)}\right\rangle</math></center> | <center><math> \tilde{\gamma}_{11}(\tau)=\frac{\left\langle \tilde\mathbf{V}(t+\tau)\tilde\mathbf{V}^{*}(t)\right\rangle}{\tilde {|\mathbf{V}|}^2} = \frac{\left\langle e^{i\phi(t+\tau)} e^{-i\phi(t)}\right\rangle}{\tilde {|\mathbf{V}|}^2}\tilde{|\mathbf{V}|}^2 =\left\langle e^{i\phi(t+\tau)} e^{-i\phi(t)}\right\rangle</math></center> | ||
Para saber que tipo de resultados nos | Para saber que tipo de resultados nos generará la ecuación anterior y cómo varía veamos primero que pasa con una onda plana monocromática de longitud de coherencia infinita <math>\phi(t)= \mathbf{k \cdot r}-\omega t </math> | ||
Donde <math>\Delta\phi=\mathbf{k} {\cdot } \mathbf{r}-\omega(t+\tau)-\mathbf {k} \cdot \mathbf{r}+\omega t=-\omega\tau</math> que nos lleva a <math> \tilde{\gamma}_{11}(\tau)= e^{i\omega\tau}=\cos\omega\tau-i\sin\omega\tau</math> | |||
De tal modo que <math>|\tilde{\gamma}_{11}|=1</math>, llamada coherencia completa. | |||
Pasemos al caso opuesto, con una onda monocromática con <math> \tau >\ </math> longitud de coherencia de tal modo que <math> \Delta\phi\ </math> sera al azar, variando entre 0 y <math> 2\pi\ </math> de tal manera que la integral se promedia a cero, <math>|\tilde{\gamma}_{11}(\tau)|=0</math>, llamada incoherencia completa. | |||
Es importante entender que la [[Transformadas de Fourier|transformada de Fourier]] de la función de autocoherencia es el espectro energético que describe la distribución de la energía espectral de la luz, esto lo veremos más adelante cuando trabajemos con las aplicaciones del teorema que nos muestra la relación entre el grado de coherencia complejo en una región del espacio y la distribución de la irradiancia correspondiente en la fuente extensa que da lugar a los campos luminosos, este teorema es el '''''Teorema de Van Cittert Zernike,''''' | |||
== Teorema de van Cittert-Zernike == | |||
[[Archivo:Fuente incoherente.jpg|right|thumb|500x500px|Figura 2.- ''Fuente cuasimonocromática emisora de luz y plano de observación'']] | |||
El teorema de van Cittert - Zernike pude resumirse según se escribe a continuación. | |||
Sean <math> I(S) </math> la intensidad de radiación por unidad de área (irradiancia) de una fuente extendida <math> \sigma\ </math> y <math> J(P_{1},P_{2})</math> la [[Optica:_Coherencia#Funci.C3.B3n_de_coherencia_mutua_y_grado_de_coherencia|función de coherencia]] entre dos puntos <math>P_{1}</math> y <math> P_{2} </math>. | |||
Si la distancia entre <math> \sigma\ </math> y el plano <math> \Pi\ </math> que contiene a los puntos <math> P_{1} </math> y <math> P_{2} </math> es muy grande comparada con la distancia entre dichos puntos y las dimensiones de <math> \sigma\ </math>, entonces la función de coherencia mutua es la [[Transformadas de Fourier|transformada de Fourier]] de la intensidad de radiación por unidad de área. | |||
Esto es, si | |||
<center> <math> D << L_{\sigma} << R_{\sigma} , </math></center> | |||
entonces | |||
<center> <math> J(P_{1},P_{2})= \tilde F\ [I(S)].</math> </center> | |||
En donde | |||
<math> D -> </math> distancia entre <math> P_{1} </math> y <math> P_{2}. </math> | |||
<math>V_{m1}(t)=A_m\left(t-\frac{ | <math> L_{\sigma} -> </math> Arista de un cuadrado que enmarca a <math> {\sigma}. </math> | ||
<math> R_ {\sigma} -> </math> Distancia media entre <math> {\sigma} </math> y <math> {\Pi} .</math>. | |||
Este resultado se verifica a continuación. La prueba se divide en dos partes,la primera consta de la obtención de la expresión para el grado de coherencia (que en general será distinto de cero) y la segunda se centra en aplicar las aproximaciones correspondientes en tal expresión hallada. | |||
''Primera parte de la prueba'' | |||
En la figura 2 se presenta una fuente incoherente extensa cuasimonocromática, <math> {\sigma} </math>, situada a una distancia promedio <math> R_ {\sigma} </math> del plano <math> \Pi </math> y con una irradiancia proporcionada por <math> I(S)</math> (en donde S representa el área de <math> {\sigma} </math>). También se muestra una pantalla de observación (plano <math> \Pi </math> con origen de coordenadas en el punto medio entre <math> P_{1}\ </math> y <math> P_{2}\ </math>) en la que se hallan dos puntos, <math> P_{1}\ </math> y <math> P_{2}\ </math> a una distancia <math> r_{1}\ </math> y <math> r_{2}\ </math> respectivamente, desde un elemento "diminuto" de <math> {\sigma} </math>, ambos objetos colocados en un medio homogéneo. | |||
Vamos a determinar el grado de coherencia complejo <math> J(P_{1},P_{2}) </math> para los puntos <math> P_1\ </math> y <math> P_2\ </math> en la pantalla de observación iluminada por un haz de luz proveniente de <math> \sigma\ </math>. | |||
Imaginemos entonces que la fuente se divide en elementos <math> d\sigma_1\ , d\sigma_2, ...d\sigma_m </math> centrado en los puntos <math> S_1\ , S_2, ... </math> de dimensiones lineales pequeñas comparadas con la longitud de onda <math> \tilde\lambda\ </math> donde la tilde en este caso representa el promedio de <math> \lambda\ </math>. Es decir, si <math> V_{m1}(t)\ </math> y <math> V_{m2}(t)\ </math> son las perturbaciones del campo complejo en <math> P_1\ </math> y <math> P_2\ </math>, debido al elemento <math> d\sigma_1\ </math>, el total de las perturbaciones en estos puntos son ahora las vibraciones de luz que surgen de los diferentes elementos de la fuente, puede ser asumida como estadísticamente independientes (incoherentes entre sí), de modo que <math> V_1\ =\sum_{m} V_{m1}(t) </math> y <math> V_2\ =\sum_{m} V_{m2}(t) </math>. | |||
La función de coherencia, dada por la expresión | |||
<center><math> J(P_1,P_2)=\left\langle {V}_1(t){V}_2^{*}(t)\right\rangle,</math></center> | |||
puede reescribir como una suma, separandola en dos partes al no ser necesariamente los subíndices iguales. Es decir una cuando los subíndices son iguales y otra cuando no lo son. | |||
<center><math> J(P_1,P_2)=\sum_{m}\left\langle {V}_{m1}(t){V}_{m2}^{*}(t)\right\rangle + \sum\sum_{n m}\left\langle {V}_{m1}(t){V}_{n2}^{*}(t)\right\rangle. </math></center> | |||
Al ser una fuente incoherente, cuando m es distinto de n la suma vale cero. | |||
<center><math> J(P_1,P_2)=\sum_{m}\left\langle {V}_{m1}(t){V}_{m2}^{*}(t)\right\rangle + \sum\sum_{n m}0. </math></center> | |||
Si <math> r_{m1}\ </math> y <math> r_{m2}\ </math> son las distancias de <math> P_1\ </math> y <math> P_2\ </math> del elemento de origen <math> d\sigma_m\ </math> las perturbaciones del campo las podemos escribir como | |||
<center><math>V_{m1}(t)=A_m\left(t-\frac{r_{m1}}{v}\right)\frac{e^{-2i\tilde{\nu}\pi(t-\frac{r_{m1}}{v})}}{r_{m1}}</math></center>; | |||
<math>V_{m2}(t)=A_m\left(t-\frac{ | <center><math>V_{m2}(t)=A_m\left(t-\frac{r_{m2}}{v}\right)\frac{e^{-2i\tilde{\nu}\pi(t-\frac{r_{m2}}{v})}}{r_{m2}}</math></center> | ||
Donde <math> |A_m|\ </math> caracteriza a la intensidad I y el argumento <math> A_m\ </math> la fase de la de la radiación del elemento m-esimo, v es la velocidad de la luz en el medio entre la fuente y la pantalla. | |||
Por lo tanto | |||
<center><math> \left\langle \mathbf{v}_{m1}(t)\mathbf{v}_{m2}^{*}(t)\right\rangle= \left\langle A_m\left(t-\frac{ | <center><math> \left\langle \mathbf{v}_{m1}(t)\mathbf{v}_{m2}^{*}(t)\right\rangle= \left\langle A_m\left(t-\frac{r_{m1}}{v}\right)A_m^{*}\left(t-\frac{r_{m1}}{v}\right)\right\rangle \frac{e^{2i\pi\tilde{\nu}\frac{(r_{m1}- r_{m2})}{v}}}{r_{m1}r_{m2}}=\left\langle A_m\left(t\right)A_m^{*}\left(t-\frac{r_{m2}- r_{m1}}{v}\right)\right\rangle \frac{e^{2i\pi\tilde{\nu}\frac{(r_{m1}-r_{m2})}{v}}}{r_{m1}r_{m2}} </math></center> | ||
si la diferencia de caminos opticos <math> (r_{m1}- r_{m2})</math> es pequeña comparada con la longitud de coherencia de la Luz podemos despreciar el termino <math>\frac{(r_{m1}- r_{m2})}{v}</math> en el argumento de <math> A_m^{*}\ </math> y obtener | |||
<center><math> J(P_1,P_2)=\sum_{m}\left\langle A_m\left(t\right)A_m^{*}\left(t\right)\right\rangle \frac{e^{2i\pi\tilde{\nu}\frac{( | <center><math> J(P_1,P_2)=\sum_{m}\left\langle A_m\left(t\right)A_m^{*}\left(t\right)\right\rangle \frac{e^{2i\pi\tilde{\nu}\frac{(r_{m1}- r_{m2})}{v}}}{r_{m1}r_{m2}} </math></center> | ||
Se sigue que <math> \left\langle A_m\left(t\right)A_m^{*}\left(t\right)\right\rangle </math> caracteriza la intensidad de radiación de los elementos de la fuente <math> d\sigma\ </math> asi que podemos sustituirla por I(S) que es la intensidad por unidad de área de la fuente, dejándonos así | |||
<center><math> J(P_1,P_2)=\int_{\sigma}I(S)\frac{e^{i\tilde {k}( | <center><math> J(P_1,P_2)=\int_{\sigma}I(S)\frac{e^{i\tilde {k}(r_{1}-r_{2})}}{r_{1}r_{2}}dS</math></center> | ||
Regresando a la notación de <math> r_{1}\ </math> y <math> r_{2}\ </math> que ya definimos y el numero de onda en el medio como <math> \tilde k=\frac {2\pi \tilde{\nu}}{v}=\frac {2\pi}{\tilde {\lambda}}</math>, siendo las cantidades con tilde los promedios. | |||
el grado complejo de coherencia | De donde podemos calcular el grado complejo de coherencia normalizado | ||
<math> I(P_1)=J(P_1,P_1)=\int_{\sigma}\frac{I(S)}{{R_{1}}^2}dS</math> | <center><math> j(P_{1},P_{2}) = \frac{J(P_{1},P_{2})}{\sqrt{I(P_{1})I(P_{2})}}, </math></center> | ||
Con las intensidades de <math> P_1\ </math> y <math> P_2\ </math> | |||
<center><math> I(P_1)=J(P_1,P_1)=\int_{\sigma}\frac{I(S)}{{R_{1}}^2}dS</math></center> | |||
y | |||
<center><math> I(P_2)=J(P_2,P_2)=\int_{\sigma}\frac{I(S)}{{R_{2}}^2}dS</math></center> | |||
El cálculo da como resultado una integral con una estructura conocida cuya forma y cuyos resultados son iguales a los de una integral de difracción, con tal de que cada término se vuelva a interpretar correctamente. | |||
Notemos que esta integral (1), se puede calcular de una manera diferente, sobre la base del principio de [[Optica: Principio de Huygens-Fresnel|Huygens-Fresnel]], de la alteración compleja en el patrón de [[Optica: Difraccion|difracción ]] derivado de la difracción de una onda esférica en una apertura en una pantalla opaca. De manera más precisa, la integral (1) implica que la igualdad de grado de coherencia complejo, que describe la correlación de las vibraciones en un punto fijo <math> P_{2}\ </math> y el punto variable <math> P_{1}\ </math> en un plano iluminado por una fuente primaria extensa cuasimonocromática (incoherente), es igual a la normalización de la amplitud compleja en el punto correspondiente <math> P_1\ </math> en un cierto patrón de difracción, centrado en <math> P_{2}\ </math>. Este patrón se obtendría en la sustitución de la fuente por una abertura de difracción de la misma forma y tamaño de la fuente, y llenado con una onda esférica convergente para <math> P_{2}\ </math>, la apertura es proporcional a la distribución de intensidad a través de la fuente. | |||
=== Segunda parte de la prueba === | |||
De la figura 2, se tienen las siguientes expresiones. | |||
<center><math>\vec{r_{1}}= \vec{D_{1}} - \vec{r_{\sigma}},</math> | |||
</center> | |||
<center><math>\vec{r_{2}}= \vec{D_{2}} - \vec{r_{\sigma}},</math> | |||
</center> | |||
y | |||
<center><math>\vec{r_{\sigma}}= r_{\sigma}\hat{r_{\sigma}} </math> | |||
</center> | |||
De donde, | |||
<center><math> r_{1} = r_{\sigma} [1-2(\hat{r_{\sigma}} {\cdot } \hat{D_{1}})(\frac{D_{1}}{r_{\sigma}})+(\frac{D_{1}}{r_{\sigma}})^2]^{\frac{1}{2}} </math> </center> | |||
<center><math> r_{2} = r_{\sigma} [1-2(\hat{r_{\sigma}} {\cdot } \hat{D_{2}})(\frac{D_{2}}{r_{\sigma}})+(\frac{D_{2}}{r_{\sigma}})^2]^{\frac{1}{2}}. </math> </center> | |||
Luego, se las dimensiones lineales de <math>{\sigma}</math> son pequeñas comparadas con la distancia al plano de observación, es decir <math>L_{\sigma}<< r_{\sigma}</math>, entonces podemos considerarla aproximación <math>r_{\sigma}\thickapprox R_{\sigma} = cte </math> por lo que | |||
<center> <math> \vec{r_{\sigma}}\thickapprox R_{\sigma}\hat{r_{\sigma}}. </math> </center> | |||
Aproximando las expresiones anteriores mediante el binomio de Newton y despreciando los términos no lineales en la expansión se tiene que | |||
<center><math> r_{1} \thickapprox R_{\sigma} - \hat{r_{\sigma}}{\cdot } \vec{D_{1}} </math></center> | |||
<center><math> r_{2} \thickapprox R_{\sigma} - \hat{r_{\sigma}}{\cdot } \vec{D_{2}}. </math></center> | |||
Por lo que | |||
<center><math> r_{2}-r_{1} = \hat{r_{\sigma}} {\cdot } (\vec{D_{1}}-\vec{D_{2}}) = \hat{r_{\sigma}}{\cdot }\vec{D}</math></center> | |||
<center><math> r_{2}r_{1} \thickapprox R_{\sigma}^2. </math></center> | |||
Usando estas aproximaciones en la integral hallada en la primera sección de la demostración, se obtiene | |||
<center><math> J(P_1,P_2)=\int_{\sigma}I(S)\frac{e^{i\tilde {k}(\hat{r_{\sigma}}{\cdot }\vec{D})}}{R_{\sigma}^2}dS</math></center> | |||
Si ahora se reescribe a <math>dS</math> y a <math>\hat{r_{\sigma}}</math> en términos de los cosenos directores <math>(l,m,n)</math> se tiene | |||
<center><math>\hat{r_{\sigma}}{\cdot }\vec{D}= lx_{D} + my_{D} </math></center> | |||
<center><math> dS = R_{\sigma}^2dldm </math></center> | |||
Con lo que la integral se transforma en | |||
<center><math> J(P_1,P_2)=\int I(S) e^{i\tilde {k}(lx_{D} + my_{D})}dldm</math></center> | |||
Desde luego, dado que <math>I(s)</math> es nula fuera de la superficie de <math>\sigma </math>, los límites de integración pueden extenderse a todo el espacio. Dado lo anterior, la expresión hallada es precisamente la transformada de Fourier en 2 dimensiones de <math>I(s)</math>. | |||
Por tanto. | |||
<center> <math> J(P_{1},P_{2})= \tilde F\ [I(S)]</math> </center> | |||
Que era lo que se quería mostrar. | |||
''Aplicaciones. '' | |||
En la mayoría de las aplicaciones de la intensidad I(S) que puede suponerse como independiente de la posición de S en la superficie (la intensidad es uniforme). | |||
El problema de difracción correspondiente es entonces el de la difracción de una onda esférica de amplitud de uniforme por una abertura de la misma forma y tamaño de la fuente. | |||
Sean <math> (\epsilon,\eta)\ </math> las coordenadas de un punto de fuente típico S, en el plano sigma con el origen en 0, y <math>(X_1,Y_1)\ </math> y <math> (X_2,Y_2)\ </math> las coordenadas de <math> P_{1}\ </math> y <math> P_{2}\ </math>, en el plano paralelo A y con origenel 0´. Entonces, si R representa la distancia de 0 a 0´ | |||
<center><math> {R_1}^2=({X_1-\epsilon})^2+({Y_1-\eta})^2+R^2</math></center> | |||
<center><math> \psi=\frac{\tilde k[(X_1^2+Y_1^2)-({X_2}^2-{Y_2}^2)]}{R2}</math></center> | |||
Entonces, si las dimensiones lineales de una fuente y la distancia entre <math> P_{1}\ </math> y <math> P_{2}\ </math> son pequeñas comparadas con la distancia de esos puntos a la fuente, el grado de coherencia <math> j_{12}\ </math> es igual al valor absoluto de la [[Transformadas de Fourier|transformada de Fourier]] normalizada de la función intensidad de la fuente. | |||
<center><math> j(P_1,P_2)=\frac{e^{i\psi}\int\int_{\sigma}I(\epsilon,\eta)e^{i\tilde k(\frac{(X_1-X_2)\epsilon}{r}+\frac{(Y_1-Y_2)\eta}{r}}d\epsilon d\eta}{\int\int_{\sigma}I(\epsilon,\eta)d\epsilon d\eta} ...(2)</math></center> | |||
Para una fuente circular uniforme de radio <math> \rho\ </math> con centro en O, la expresión anterior la podemos reescribir como | |||
<center><math> j(P_1,P_2)=(\frac{2J_1(v)}{v})e^{i\psi}</math></center> | |||
donde | |||
<center><math> v=\frac{\tilde k\rho}{R}\sqrt{(X_1-X_2)^2+(Y_1-Y_2)^2} </math></center> | |||
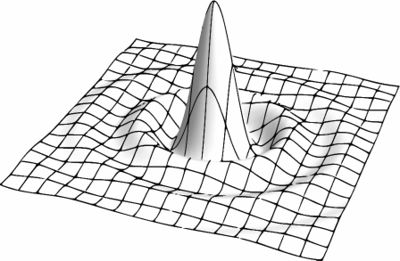
[[Imagen:figdif4.jpg|right|thumb|400x400px|Figura 4. Fuente circular donde <math> P_0\ </math> es <math> P_{2}\ </math> y <math> P\ </math> es <math> P_{1}\ </math> .]] | |||
[[Imagen:irrcirclista.jpg|center|thumb|400x400px|Figura 3. Distribución de la irradiancia para una apertura circular]] | |||
<math> J_1\ </math> es la función de Bessel[https://ccrma.stanford.edu/~juanig/articles/fundfm/Funciones_Bessel.html] de primer orden. Donde <math> |\frac{2J_1(v)}{v}|</math> decrece constantemente desde el valor 1 cuando <math> v=0\ </math>, al valor 0 cuando <math> v=3.83\ </math>; así como los puntos <math> P_{1}\ </math> y <math> P_{2}\ </math> son separados mas y mas, el grado de coherencia decrece constantemente y hay una completa incoherencia cuando <math> P_{1}\ </math> y <math> P_{2}\ </math> son separados por una distancia | |||
<math> P_1P_2=\sqrt{(X_1-X_2)^2+(Y_1-Y_2)^2}=\frac{0.61 R\tilde\lambda}{\rho}</math> | |||
Un incremento adicional en v reintroduce una cantidad pequeña de coherencia, pero el grado de coherencia permanece menor a 0.14, y hay una completa incoherencia para <math> v = 7.02\ </math>. Puesto que <math> J_1(v)\ </math> cambia de signo cada vez que v pasa a través de cada 0 de <math> J_1(v)\ </math> la fase <math> B_{12}\ </math> es equivalente al argumento de <math> j_{12}\ </math> cambia por <math> \pi\ </math>, en consecuencia la posición de las franjas oscuras y brillantes son intercambiadas después de cada desaparición de las franjas. | |||
<math> P_1P_2=\frac{0.16 R\tilde\lambda}{\rho}</math> | |||
Entonces <math> \tilde{\Gamma}_{12}(0)</math> es sencillamente una función sinc cuando la fuente es una rendija y una función Bessel cuando es circular. | |||
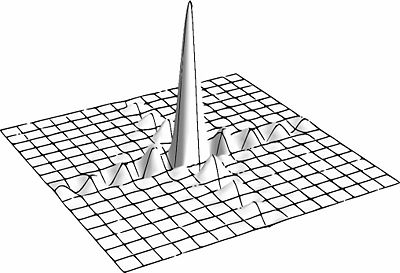
[[Imagen:figdi3.jpg|right|thumb|400x400px|Figura 6.Fuente rectangular donde <math> P_0\ </math> es <math> P_{1}\ </math> y <math> P\ </math> es <math> P_{2}\ </math> en nuestras ecuaciones]] | |||
[[Imagen:irradianciacuadro.jpg|center|thumb|400x400px|Figura 5. Distribución de la irradiancia para una apertura cuadrada]] | |||
<center><math> \beta=\frac{kb}{2}sen\theta </math></center> | <center><math> \beta=\frac{kb}{2}sen\theta </math></center> | ||
| Línea 151: | Línea 308: | ||
<center><math> \theta\thickapprox sen\theta. </math></center> | <center><math> \theta\thickapprox sen\theta. </math></center> | ||
<center><math>\beta=\frac{kb\theta}{2} </math></center> | <center><math>\beta=\frac{kb\theta}{2} </math></center> | ||
y | y | ||
<center><math> \theta=\frac{y}{l} | <center><math> \theta=\frac{y}{l} </math></center> | ||
por lo tanto <center><math> \left|\tilde{\gamma}_{12}(0)\right|= \left|sinc(\frac{\pi by}{l\lambda})\right|. </math></center> | por lo tanto <center><math> \left|\tilde{\gamma}_{12}(0)\right|= \left|sinc(\frac{\pi by}{l\lambda})\right|. </math></center> | ||
Otro ejemplo es el de la luz solar. | |||
Si consideramos al sol como un disco observado sobre la superficie de la tierra, el diámetro angular 2α que se genera con la proyección del disco solar es aproximadamente de 0 grados 32 min (0.0093 Rad). | |||
Entonces, si despreciamos la variación de la luminosidad del disco solar, esto es si consideramos que no se pueden detectar los cambios en la luminosidad de la fuente, el diámetro del área de coherencia es aproximadamente <math> 0.16\tilde\lambda\ </math> (tomando la media de la longitud de onda) que es el resultado que obtuvimos para la fuente circular, es decir los conceptos que utilizamos y el razonamiento serán aplicados de la misma manera para el disco solar. | |||
Tomando la longitud de onda promedio como 0.000055 cm, esto proporciona un diámetro de aproximadamente 0.019 mm. | |||
---- | |||
Aportacion de usuario: [[Usuario:Armando Trápala|Armando Trápala]] ([[Usuario discusión:Armando Trápala|discusión]]) 22:35 25 nov 2015 (CST) | |||
---- | |||
== Principio de Fermat== | |||
Cualquiera pensaría que el camino mas corto que seguiría la luz de un punto <math>P_1</math> a un punto <math>P2</math> en una superficie reflectora seria una trayectoria geométrica, pero no es así la trayectoria que sigue la luz es un camino que en óptica se conoce como un camino óptico. Son puntos de vista que llega mediante el principio de Fermat. | |||
Fermat reformuló la afirmación de Hero de la siguiente manera: la trayectoria real que adopta la luz entre dos puntos es aquella recorrida en el tiempo mas mínimo. | |||
El principio de Fermat puede enunciarse como sigue: La trayectoria real (rayo) que sigue la luz para viajar desde un punto <math>P_1</math> hasta otro punto <math>P_2</math> es aquella por la cual el camino óptico D entre ambos puntos es estacionario es decir | |||
\begin{equation} | |||
\delta C=\delta\int_{P_1}^{P_2}nds=0 | |||
\label{1} | |||
\end{equation} | |||
Donde el símbolo <math>\delta</math> significa variación y s es el parámetro del arco sobre la curva considerada. El camino óptico entre dos puntos a lo largo de un rayo puede ser máximo o mínimo o mantenerse constante con respecto a la trayectoria próximas a él. | |||
[[Imagen:Fermat.jpg]] | |||
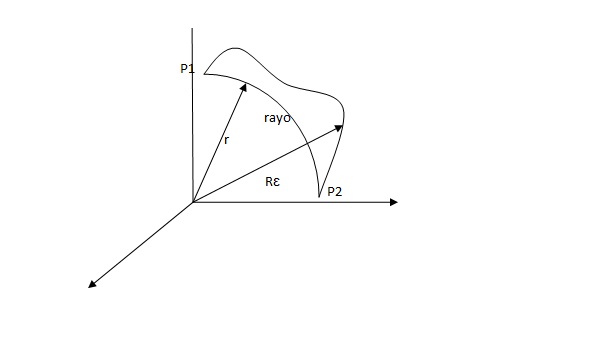
llamaremos <math>\mathbf r</math> al vector de posición de un cierto punto de la curva que representa el rayo que une los puntos <math>P_1</math> y <math>P_2</math> y sea <math>\mathbf R_\epsilon</math> el vector de posición asociada a una familia de curvas próximas al rayo | |||
\begin{equation} | |||
\mathbf R_{\varepsilon}=\mathbf r+\mathbf {\varepsilon} \mathbf f | |||
\label{2} | |||
\end{equation} | |||
donde <math>{\varepsilon}</math> es un numero real y f un vector (arbitrario pero fijo) función del punto tal que | |||
\begin{equation} | |||
\mathbf f(P_1)=\mathbf f(P_2)=0 | |||
\label{3} | |||
\end{equation} | |||
[[Imagen:Fermat2.jpg]] | |||
se tiene por lo tanto, <math>R_{\varepsilon}(P_i)=\mathbf r(P_i), i=1,2</math> El camino optico entre <math>P_1</math> y <math>P_2</math> a lo largo de una cualquiera de las curvas de la familia anterior viene dado por: | |||
\begin{equation} | |||
{[P_1 P_2]}_{R_{\varepsilon}} =\int_{P_1}^{P_2}n(\mathbf R_{\varepsilon})ds=D({\varepsilon})=0 | |||
\label{4} | |||
\end{equation} | |||
<math>\delta C=\delta\int_{P_1}^{P_2}nds=0</math> | |||
Donde la función D(ε) indica explícitamente que <math>[P_1P_2]</math> depende únicamente de ε (fijados f y el rayo). La condición 1.1 para D(ε) es equivalente, por tanto, a: | |||
\begin{equation} | |||
\frac{dD}{d{\varepsilon}}=0 | |||
\label{5} | |||
\end{equation} | |||
Demostraremos en lo que sigue que esta condición se satisface para <math>{\varepsilon}=0</math>, es decir cuando el camino óptico se calcula sobre el rayo. | |||
Si, en notación paramétrica, <math>{\mathbf R_{\varepsilon}}(\alpha)=(x(\alpha),y(\alpha),z(\alpha)</math>, se tiene entonces: | |||
\begin{equation} | |||
||\dot {\mathbf R_{\varepsilon}}||^2=(\frac{dx}{d\alpha})^2+(\frac{dy}{d\alpha})+(\frac{dz}{d\alpha})^2 | |||
\label{6} | |||
\end{equation} | |||
y sobre la curva, se cumple además | |||
\begin{equation} | |||
ds=||\dot {\mathbf R_{\varepsilon}}||d\alpha | |||
\label{7} | |||
\end{equation} | |||
Donde, de nuevo, el punto indica derivación con respecto a α (se esta suponiendo que <math>\mathbf f</math> admite derivada primera continua). La ecuación (4) se convierte, por tanto. | |||
\begin{equation} | |||
D(\varepsilon)=\int_{\alpha_1}^{\alpha_2}n(\mathbf R_{\varepsilon})||\dot {\mathbf R_{\varepsilon}}||d\alpha | |||
\label{8} | |||
\end{equation} | |||
Donde <math>\alpha_1</math> y <math>\alpha_2</math> son los valores que el parámetro α alcanza <math>P_1</math> y <math>P_2</math> respectivamente. La derivada del camino óptico con respecto a <math>\varepsilon</math> es, por tanto: | |||
\begin{equation} | |||
\frac{dD}{d\varepsilon}=\int_{\alpha_1}^{\alpha_2}\frac{d}{d\varepsilon}[n(\mathbf R_{\varepsilon})||\dot {\mathbf R_{\varepsilon}}||]d\alpha | |||
\label{9} | |||
\end{equation} | |||
Ahora bien, sobre la familia de curvas dada (2) se tiene | |||
\begin{equation} | |||
\frac{\mathrm{d} }{\mathrm{d} \varepsilon} (n||\dot{R}_\varepsilon)=\left \| \dot{R}_\varepsilon \right \| \nabla_n\cdot f+n\frac{\dot{R}_\varepsilon\cdot \dot{f}}{\left \| \dot{R}_\varepsilon \right \|} | |||
\label{10} | |||
\end{equation} | |||
De donde | |||
\begin{equation} | |||
\frac{\mathrm{d}D }{\mathrm{d} \varepsilon} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{R}_\varepsilon \right \| \nabla_n\cdot f d\alpha + \int_{\alpha_1 }^{\alpha_2}n\frac{\dot{R}_\varepsilon\cdot \dot{f}}{\left \| \dot{R}_\varepsilon \right \|} | |||
d\alpha | |||
\label{11} | |||
\end{equation} | |||
Integrando por partes la segunda integral de la ecuación anterior y teniendo en cuenta (3) se llega a: | |||
\begin{equation} | |||
\frac{\mathrm{d}D }{\mathrm{d} \varepsilon} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{R}_\varepsilon \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{R}_\varepsilon}{||\dot{R}_\varepsilon||}\cdot f \right ] d\alpha | |||
\label{12} | |||
\end{equation} | |||
En particular, si se hace <math>\varepsilon=0</math>, es decir, se considera estrictamente el rayo que une a <math>P_1</math> y <math>P_2</math>, la ecuación (12) toma la forma | |||
\begin{equation} | |||
\frac{\mathrm{d}D }{\mathrm{d} \varepsilon}\Big|_{\epsilon\rightarrow 0} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{r} \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{r}}{||\dot{r}||}\cdot f \right ] d\alpha | |||
\label{13} | |||
\end{equation} | |||
Donde <math>\mathbf r(\alpha)</math> satisface la ecuación de los rayos. Recuérdese que, en notación paramétrica, y esta dada por: | |||
\begin{equation} | |||
\frac{d}{d\alpha}(n\frac{\dot {\mathbf r}}{||\dot {\mathbf r}||})=||\dot {\mathbf r}||\nabla n | |||
\label{14} | |||
\end{equation} | |||
sustituyendo (14) en (13) se obtiene finalmente | |||
formula | |||
\begin{equation} | |||
\frac{dD}{d\epsilon}=0 | |||
\label{15} | |||
\end{equation} | |||
Como queríamos demostrar. Obsérvese que este resultado es independiente del vector f elegido. | |||
Si se considera ahora la demostración en sentido inverso, es decir partiendo del principio de Fermat, puede definirse un rayo luminoso como aquella curva que hace estacionario el camino óptico entre dos punto. Imponiendo entonces la condición (15) a D(ε) definido en (4) para una familia arbitraria de curvas, la demostración anterior conduce a la igualdad. | |||
\begin{equation} | |||
\int_{\alpha_1 }^{\alpha_2}\left \| \dot{r} \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{r}}{||\dot{r}||}\cdot f \right ] d\alpha = 0 | |||
\label{16} | |||
\end{equation} | |||
=== Ejemplo === | |||
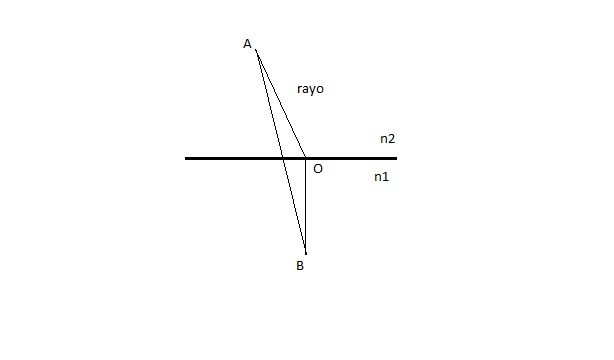
Sea un espejo esférico <math>\epsilon</math> de radio R y sean Ay B dos puntos alineados con centro del espejo, C, equidistantes de él. | |||
Supongamos, por simplicidad, que el medio que rodea el espejo es el vacío n=1 con esto determinaremos la trayectoria del radio que une A con B después de reflejarse en <math>\epsilon</math>. | |||
Figura | |||
para mayor facilidad tomemos coordenadas cartesianas con origen en C, respecto al cual las coordenadas de los puntos A y B son, respectivamente, (h,0) y (-h,0). Sea Q(x,y) un punto genérico de <math>\epsilon</math>. El camino óptico <math>[AB]_Q</math> correspondiente al recorrido AQB una vez que es reflejado en el espejo | |||
<math>\delta=[AB]_Q =[(x-h)^2+y^2]^{1/2}+[(x+h)^2 +y^2]^{1/2}</math>.............(1.1) | |||
esto es por geometría es decir como Q es un punto del espejo esférico se tiene además | |||
<math>x^2+y^2=R^2</math>.............(1.2) | |||
por lo tanto el principio de Fermat establece que la trayectoria del rayo que une a A con B tras reflejarse en <math<\epsilon</math> corresponde al punto <math<Q_0</math> que hace estacionario <math<\delta</math>. Dado que <math<\delta</math> debe considerarse una función de las coordenadas x,y del punto Q, la condición (1) se escribiría aquí en la forma | |||
<math>\delta \Delta=\frac{ \partial \Delta }{ \partial x }dx+\frac{ \partial \Delta }{ \partial y}dy</math>.............(1.3) | |||
debe cumplirse la condición de ligadura | |||
<math>f(x,y,z)=x^2+y^2-R^2=0</math>.............(1.4) | |||
Lo que implica | |||
<math>\frac{ \partial f }{ \partial x }dx+\frac{ \partial f }{ \partial dy}dy=0 \Rightarrow dy=-\frac{x}{y}dx </math>.............(1.5) | |||
Sustituimos esta relación en (1.3) se obtiene: | |||
<math>[\frac{ \partial \Delta }{ \partial x }-\frac{x}{y}\frac{ \partial \Delta }{ \partial y }]dx=0</math>.............(1.6) | |||
es decir: | |||
<math>\frac{ \partial \Delta }{ \partial x }=\frac{x}{y}\frac{ \partial \Delta }{ \partial y}</math>.............(1.7) | |||
finalmente recordando que <math>\delta</math> viene dado por (1.1) y teniendo en cuenta (1.2) la ecuación anterior conduce a: | |||
<math>(R^2+h^2+2hx)^{1/2}-(R^2+h^2-2hx)^2=0</math>.............(1.8) | |||
cuya solución es x=0. Las coordenadas del punto <math>Q_0</math> buscado son, por tanto <math>(0,R)</math>. | |||
Es importante darse cuenta de que, al despejar dy en (1.5), se han excluido los puntos del espejo con y=0. Se da además la circunstancia de que tales puntos <math>Q_0</math> de coordenadas (R,0), satisfacen el principio de Fermat (las trayectorias AQB son en consecuencia, físicamente admisibles). En un caso general, por lo tanto, hay que tener presente que, en la determinación del camino óptico estacionario, no se están excluyendo determinadas soluciones (o, al menos, se debe conocer cuáles son). | |||
| Línea 171: | Línea 549: | ||
'''''Sobre Fourier''''' | '''''Sobre Fourier''''' | ||
[[Optica: Optica de Fourier]] | [[Optica: Optica de Fourier]] | ||
---- | |||
Aportación de Usuario: [[Usuario:Yonatan Aldana Saldañas|Yonatan Aldana Saldañas]] 14:38 29 mar 2012 (UTC) | |||
---- | |||
==Referencias== | |||
1. Óptica, autor: Eugene Hecht, Tercera edición, Addison Wesley Iberoamericana, Madrid, 2000. | |||
2. Principles of optica, autores: Max Born y Emil Wolf, Quinta edición 1975, Pergamon Press. | |||
[[Category:optica]] | |||
[[category:investigacion]] | |||
Revisión actual - 08:17 5 oct 2023
Coherencia temporal y espacial
Si en la figura 1, la fuente primaria que se encuentra en el primer plano de la imagen (a), que llamaremos S, se encoge hasta convertirse en una fuente puntual sobre el eje central como en la imagen (b) y tiene un ancho de banda de frecuencia finito, los efectos de coherencia temporal predominarán.
Las perturbaciones ópticas en y son entonces idénticas, donde y son las ventanas que muestra la figura (b) en el plano intermedio. La coherencia mutua entre los dos puntos donde las perturbaciones son idénticas es en este caso la autocoherencia del campo.
De aquí que podamos escribirla como
lo mismo obtenemos cuando y se combinan y se denomina grado de coherencia temporal complejo donde es el intervalo de tiempo que se separan.
Esta interpretación es un poco diferente para un interferómetro de división de amplitud (interferometro de Michelson[1]), donde es igual a la diferencia de recorrido dividida por c. La expresión para la irradiancia I contendra entonces a en lugar de .
Ahora si una onda luminosa con el interferómetro se divide en dos perturbaciones del campo idénticas de la forma donde se refiere a la fase de la onda y la tilde expresa en V que puede tener una representacion compleja, si el interferometro después las vuelve a combinar para generar una distribución de franjas, entonces
Para saber que tipo de resultados nos generará la ecuación anterior y cómo varía veamos primero que pasa con una onda plana monocromática de longitud de coherencia infinita
Donde que nos lleva a
De tal modo que , llamada coherencia completa.
Pasemos al caso opuesto, con una onda monocromática con longitud de coherencia de tal modo que sera al azar, variando entre 0 y de tal manera que la integral se promedia a cero, , llamada incoherencia completa.
Es importante entender que la transformada de Fourier de la función de autocoherencia es el espectro energético que describe la distribución de la energía espectral de la luz, esto lo veremos más adelante cuando trabajemos con las aplicaciones del teorema que nos muestra la relación entre el grado de coherencia complejo en una región del espacio y la distribución de la irradiancia correspondiente en la fuente extensa que da lugar a los campos luminosos, este teorema es el Teorema de Van Cittert Zernike,
Teorema de van Cittert-Zernike
El teorema de van Cittert - Zernike pude resumirse según se escribe a continuación.
Sean la intensidad de radiación por unidad de área (irradiancia) de una fuente extendida y la función de coherencia entre dos puntos y .
Si la distancia entre y el plano que contiene a los puntos y es muy grande comparada con la distancia entre dichos puntos y las dimensiones de , entonces la función de coherencia mutua es la transformada de Fourier de la intensidad de radiación por unidad de área.
Esto es, si
entonces
En donde
distancia entre y
Arista de un cuadrado que enmarca a
Distancia media entre y .
Este resultado se verifica a continuación. La prueba se divide en dos partes,la primera consta de la obtención de la expresión para el grado de coherencia (que en general será distinto de cero) y la segunda se centra en aplicar las aproximaciones correspondientes en tal expresión hallada.
Primera parte de la prueba
En la figura 2 se presenta una fuente incoherente extensa cuasimonocromática, , situada a una distancia promedio del plano y con una irradiancia proporcionada por (en donde S representa el área de ). También se muestra una pantalla de observación (plano con origen de coordenadas en el punto medio entre y ) en la que se hallan dos puntos, y a una distancia y respectivamente, desde un elemento "diminuto" de , ambos objetos colocados en un medio homogéneo.
Vamos a determinar el grado de coherencia complejo para los puntos y en la pantalla de observación iluminada por un haz de luz proveniente de .
Imaginemos entonces que la fuente se divide en elementos centrado en los puntos de dimensiones lineales pequeñas comparadas con la longitud de onda donde la tilde en este caso representa el promedio de . Es decir, si y son las perturbaciones del campo complejo en y , debido al elemento , el total de las perturbaciones en estos puntos son ahora las vibraciones de luz que surgen de los diferentes elementos de la fuente, puede ser asumida como estadísticamente independientes (incoherentes entre sí), de modo que y .
La función de coherencia, dada por la expresión
puede reescribir como una suma, separandola en dos partes al no ser necesariamente los subíndices iguales. Es decir una cuando los subíndices son iguales y otra cuando no lo son.
Al ser una fuente incoherente, cuando m es distinto de n la suma vale cero.
Si y son las distancias de y del elemento de origen las perturbaciones del campo las podemos escribir como
;
Donde caracteriza a la intensidad I y el argumento la fase de la de la radiación del elemento m-esimo, v es la velocidad de la luz en el medio entre la fuente y la pantalla.
Por lo tanto
si la diferencia de caminos opticos es pequeña comparada con la longitud de coherencia de la Luz podemos despreciar el termino en el argumento de y obtener
Se sigue que caracteriza la intensidad de radiación de los elementos de la fuente asi que podemos sustituirla por I(S) que es la intensidad por unidad de área de la fuente, dejándonos así
Regresando a la notación de y que ya definimos y el numero de onda en el medio como , siendo las cantidades con tilde los promedios.
De donde podemos calcular el grado complejo de coherencia normalizado
Con las intensidades de y
y
El cálculo da como resultado una integral con una estructura conocida cuya forma y cuyos resultados son iguales a los de una integral de difracción, con tal de que cada término se vuelva a interpretar correctamente. Notemos que esta integral (1), se puede calcular de una manera diferente, sobre la base del principio de Huygens-Fresnel, de la alteración compleja en el patrón de difracción derivado de la difracción de una onda esférica en una apertura en una pantalla opaca. De manera más precisa, la integral (1) implica que la igualdad de grado de coherencia complejo, que describe la correlación de las vibraciones en un punto fijo y el punto variable en un plano iluminado por una fuente primaria extensa cuasimonocromática (incoherente), es igual a la normalización de la amplitud compleja en el punto correspondiente en un cierto patrón de difracción, centrado en . Este patrón se obtendría en la sustitución de la fuente por una abertura de difracción de la misma forma y tamaño de la fuente, y llenado con una onda esférica convergente para , la apertura es proporcional a la distribución de intensidad a través de la fuente.
Segunda parte de la prueba
De la figura 2, se tienen las siguientes expresiones.
y
De donde,
Luego, se las dimensiones lineales de son pequeñas comparadas con la distancia al plano de observación, es decir , entonces podemos considerarla aproximación por lo que
Aproximando las expresiones anteriores mediante el binomio de Newton y despreciando los términos no lineales en la expansión se tiene que
Por lo que
Usando estas aproximaciones en la integral hallada en la primera sección de la demostración, se obtiene
Si ahora se reescribe a y a en términos de los cosenos directores se tiene
Con lo que la integral se transforma en
Desde luego, dado que es nula fuera de la superficie de , los límites de integración pueden extenderse a todo el espacio. Dado lo anterior, la expresión hallada es precisamente la transformada de Fourier en 2 dimensiones de .
Por tanto.
Que era lo que se quería mostrar.
Aplicaciones.
En la mayoría de las aplicaciones de la intensidad I(S) que puede suponerse como independiente de la posición de S en la superficie (la intensidad es uniforme). El problema de difracción correspondiente es entonces el de la difracción de una onda esférica de amplitud de uniforme por una abertura de la misma forma y tamaño de la fuente.
Sean las coordenadas de un punto de fuente típico S, en el plano sigma con el origen en 0, y y las coordenadas de y , en el plano paralelo A y con origenel 0´. Entonces, si R representa la distancia de 0 a 0´
Entonces, si las dimensiones lineales de una fuente y la distancia entre y son pequeñas comparadas con la distancia de esos puntos a la fuente, el grado de coherencia es igual al valor absoluto de la transformada de Fourier normalizada de la función intensidad de la fuente.
Para una fuente circular uniforme de radio con centro en O, la expresión anterior la podemos reescribir como
donde
es la función de Bessel[2] de primer orden. Donde decrece constantemente desde el valor 1 cuando , al valor 0 cuando ; así como los puntos y son separados mas y mas, el grado de coherencia decrece constantemente y hay una completa incoherencia cuando y son separados por una distancia
Un incremento adicional en v reintroduce una cantidad pequeña de coherencia, pero el grado de coherencia permanece menor a 0.14, y hay una completa incoherencia para . Puesto que cambia de signo cada vez que v pasa a través de cada 0 de la fase es equivalente al argumento de cambia por , en consecuencia la posición de las franjas oscuras y brillantes son intercambiadas después de cada desaparición de las franjas.
Entonces es sencillamente una función sinc cuando la fuente es una rendija y una función Bessel cuando es circular.
y
y
por lo tanto
Otro ejemplo es el de la luz solar.
Si consideramos al sol como un disco observado sobre la superficie de la tierra, el diámetro angular 2α que se genera con la proyección del disco solar es aproximadamente de 0 grados 32 min (0.0093 Rad).
Entonces, si despreciamos la variación de la luminosidad del disco solar, esto es si consideramos que no se pueden detectar los cambios en la luminosidad de la fuente, el diámetro del área de coherencia es aproximadamente (tomando la media de la longitud de onda) que es el resultado que obtuvimos para la fuente circular, es decir los conceptos que utilizamos y el razonamiento serán aplicados de la misma manera para el disco solar. Tomando la longitud de onda promedio como 0.000055 cm, esto proporciona un diámetro de aproximadamente 0.019 mm.
Aportacion de usuario: Armando Trápala (discusión) 22:35 25 nov 2015 (CST)
Principio de Fermat
Cualquiera pensaría que el camino mas corto que seguiría la luz de un punto a un punto en una superficie reflectora seria una trayectoria geométrica, pero no es así la trayectoria que sigue la luz es un camino que en óptica se conoce como un camino óptico. Son puntos de vista que llega mediante el principio de Fermat.
Fermat reformuló la afirmación de Hero de la siguiente manera: la trayectoria real que adopta la luz entre dos puntos es aquella recorrida en el tiempo mas mínimo.
El principio de Fermat puede enunciarse como sigue: La trayectoria real (rayo) que sigue la luz para viajar desde un punto hasta otro punto es aquella por la cual el camino óptico D entre ambos puntos es estacionario es decir
\begin{equation} \delta C=\delta\int_{P_1}^{P_2}nds=0 \label{1} \end{equation}
Donde el símbolo significa variación y s es el parámetro del arco sobre la curva considerada. El camino óptico entre dos puntos a lo largo de un rayo puede ser máximo o mínimo o mantenerse constante con respecto a la trayectoria próximas a él.
llamaremos al vector de posición de un cierto punto de la curva que representa el rayo que une los puntos y y sea el vector de posición asociada a una familia de curvas próximas al rayo
\begin{equation} \mathbf R_{\varepsilon}=\mathbf r+\mathbf {\varepsilon} \mathbf f \label{2} \end{equation}
donde es un numero real y f un vector (arbitrario pero fijo) función del punto tal que
\begin{equation} \mathbf f(P_1)=\mathbf f(P_2)=0 \label{3} \end{equation}
se tiene por lo tanto, El camino optico entre y a lo largo de una cualquiera de las curvas de la familia anterior viene dado por:
\begin{equation}
{[P_1 P_2]}_{R_{\varepsilon}} =\int_{P_1}^{P_2}n(\mathbf R_{\varepsilon})ds=D({\varepsilon})=0
\label{4}
\end{equation}
Donde la función D(ε) indica explícitamente que depende únicamente de ε (fijados f y el rayo). La condición 1.1 para D(ε) es equivalente, por tanto, a:
\begin{equation} \frac{dD}{d{\varepsilon}}=0 \label{5} \end{equation}
Demostraremos en lo que sigue que esta condición se satisface para , es decir cuando el camino óptico se calcula sobre el rayo.
Si, en notación paramétrica, , se tiene entonces:
\begin{equation} ||\dot {\mathbf R_{\varepsilon}}||^2=(\frac{dx}{d\alpha})^2+(\frac{dy}{d\alpha})+(\frac{dz}{d\alpha})^2 \label{6} \end{equation}
y sobre la curva, se cumple además
\begin{equation} ds=||\dot {\mathbf R_{\varepsilon}}||d\alpha \label{7} \end{equation}
Donde, de nuevo, el punto indica derivación con respecto a α (se esta suponiendo que admite derivada primera continua). La ecuación (4) se convierte, por tanto.
\begin{equation} D(\varepsilon)=\int_{\alpha_1}^{\alpha_2}n(\mathbf R_{\varepsilon})||\dot {\mathbf R_{\varepsilon}}||d\alpha \label{8} \end{equation}
Donde y son los valores que el parámetro α alcanza y respectivamente. La derivada del camino óptico con respecto a es, por tanto:
\begin{equation}
\frac{dD}{d\varepsilon}=\int_{\alpha_1}^{\alpha_2}\frac{d}{d\varepsilon}[n(\mathbf R_{\varepsilon})||\dot {\mathbf R_{\varepsilon}}||]d\alpha
\label{9}
\end{equation}
Ahora bien, sobre la familia de curvas dada (2) se tiene
\begin{equation} \frac{\mathrm{d} }{\mathrm{d} \varepsilon} (n||\dot{R}_\varepsilon)=\left \| \dot{R}_\varepsilon \right \| \nabla_n\cdot f+n\frac{\dot{R}_\varepsilon\cdot \dot{f}}{\left \| \dot{R}_\varepsilon \right \|} \label{10} \end{equation}
De donde
\begin{equation}
\frac{\mathrm{d}D }{\mathrm{d} \varepsilon} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{R}_\varepsilon \right \| \nabla_n\cdot f d\alpha + \int_{\alpha_1 }^{\alpha_2}n\frac{\dot{R}_\varepsilon\cdot \dot{f}}{\left \| \dot{R}_\varepsilon \right \|}
d\alpha
\label{11}
\end{equation}
Integrando por partes la segunda integral de la ecuación anterior y teniendo en cuenta (3) se llega a:
\begin{equation} \frac{\mathrm{d}D }{\mathrm{d} \varepsilon} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{R}_\varepsilon \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{R}_\varepsilon}{||\dot{R}_\varepsilon||}\cdot f \right ] d\alpha \label{12} \end{equation}
En particular, si se hace , es decir, se considera estrictamente el rayo que une a y , la ecuación (12) toma la forma
\begin{equation} \frac{\mathrm{d}D }{\mathrm{d} \varepsilon}\Big|_{\epsilon\rightarrow 0} =\int_{\alpha_1 }^{\alpha_2}\left \| \dot{r} \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{r}}{||\dot{r}||}\cdot f \right ] d\alpha \label{13} \end{equation}
Donde satisface la ecuación de los rayos. Recuérdese que, en notación paramétrica, y esta dada por:
\begin{equation} \frac{d}{d\alpha}(n\frac{\dot {\mathbf r}}{||\dot {\mathbf r}||})=||\dot {\mathbf r}||\nabla n \label{14} \end{equation}
sustituyendo (14) en (13) se obtiene finalmente
formula
\begin{equation}
\frac{dD}{d\epsilon}=0
\label{15}
\end{equation}
Como queríamos demostrar. Obsérvese que este resultado es independiente del vector f elegido. Si se considera ahora la demostración en sentido inverso, es decir partiendo del principio de Fermat, puede definirse un rayo luminoso como aquella curva que hace estacionario el camino óptico entre dos punto. Imponiendo entonces la condición (15) a D(ε) definido en (4) para una familia arbitraria de curvas, la demostración anterior conduce a la igualdad.
\begin{equation} \int_{\alpha_1 }^{\alpha_2}\left \| \dot{r} \right \| \nabla_n - \frac{d}{d \alpha }\left [ n\frac{\dot{r}}{||\dot{r}||}\cdot f \right ] d\alpha = 0 \label{16} \end{equation}
Ejemplo
Sea un espejo esférico de radio R y sean Ay B dos puntos alineados con centro del espejo, C, equidistantes de él.
Supongamos, por simplicidad, que el medio que rodea el espejo es el vacío n=1 con esto determinaremos la trayectoria del radio que une A con B después de reflejarse en .
Figura
para mayor facilidad tomemos coordenadas cartesianas con origen en C, respecto al cual las coordenadas de los puntos A y B son, respectivamente, (h,0) y (-h,0). Sea Q(x,y) un punto genérico de . El camino óptico correspondiente al recorrido AQB una vez que es reflejado en el espejo
.............(1.1)
esto es por geometría es decir como Q es un punto del espejo esférico se tiene además
.............(1.2)
por lo tanto el principio de Fermat establece que la trayectoria del rayo que une a A con B tras reflejarse en <math<\epsilon</math> corresponde al punto <math<Q_0</math> que hace estacionario <math<\delta</math>. Dado que <math<\delta</math> debe considerarse una función de las coordenadas x,y del punto Q, la condición (1) se escribiría aquí en la forma
.............(1.3)
debe cumplirse la condición de ligadura
.............(1.4)
Lo que implica
.............(1.5)
Sustituimos esta relación en (1.3) se obtiene:
.............(1.6)
es decir:
.............(1.7)
finalmente recordando que viene dado por (1.1) y teniendo en cuenta (1.2) la ecuación anterior conduce a:
.............(1.8)
cuya solución es x=0. Las coordenadas del punto buscado son, por tanto .
Es importante darse cuenta de que, al despejar dy en (1.5), se han excluido los puntos del espejo con y=0. Se da además la circunstancia de que tales puntos de coordenadas (R,0), satisfacen el principio de Fermat (las trayectorias AQB son en consecuencia, físicamente admisibles). En un caso general, por lo tanto, hay que tener presente que, en la determinación del camino óptico estacionario, no se están excluyendo determinadas soluciones (o, al menos, se debe conocer cuáles son).
Mas sobre el teorema: [[3]] [[4]] [[5]]
Sobre Fourier Optica: Optica de Fourier
Aportación de Usuario: Yonatan Aldana Saldañas 14:38 29 mar 2012 (UTC)
Referencias
1. Óptica, autor: Eugene Hecht, Tercera edición, Addison Wesley Iberoamericana, Madrid, 2000.
2. Principles of optica, autores: Max Born y Emil Wolf, Quinta edición 1975, Pergamon Press.




























![J(P_{1},P_{2})= \tilde F\ [I(S)].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e0b5c3d4ecbb2753fc4f16b93f56abeae4ec814f)















































![{\displaystyle r_{1}=r_{\sigma }[1-2({\hat {r_{\sigma }}}{\cdot }{\hat {D_{1}}})({\frac {D_{1}}{r_{\sigma }}})+({\frac {D_{1}}{r_{\sigma }}})^{2}]^{\frac {1}{2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b851b63be67adb13bc08db6de7074db986441ea0)
![{\displaystyle r_{2}=r_{\sigma }[1-2({\hat {r_{\sigma }}}{\cdot }{\hat {D_{2}}})({\frac {D_{2}}{r_{\sigma }}})+({\frac {D_{2}}{r_{\sigma }}})^{2}]^{\frac {1}{2}}.}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/810061c8287851e8f23e8793355911dd31dd3aac)
















![J(P_{1},P_{2})= \tilde F\ [I(S)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/035ae952acc0a2e2fd5c6e4c242f01c071f2af49)




![\psi=\frac{\tilde k[(X_1^2+Y_1^2)-({X_2}^2-{Y_2}^2)]}{R2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fe19953bf56c6b39b1321029e38e2ba0781c32e4)

































![[P_1P_2]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d3ca578f9e64b644f78ff917285fab155ef047f1)









![[AB]_Q](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6fd64b135309ba8bfeeafd585e5b3868a25d0352)
![\delta=[AB]_Q =[(x-h)^2+y^2]^{1/2}+[(x+h)^2 +y^2]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/73fef4a62ddf91ad2da8ed6f5d6133c4738aebbf)




![[\frac{ \partial \Delta }{ \partial x }-\frac{x}{y}\frac{ \partial \Delta }{ \partial y }]dx=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/80e62fa3e622641e2003391c2f4b2c78484b452f)



