Optica: Difraccion
Considreaciones Preliminares
Francesco Grimaldi en el siglo XVII fue el primero en publicar un estudio detallado sobre esta desviación de la luz de su propagación rectilínea a la que llamo “difractio” El efecto es una característica de los fenómenos ondulatorios que ocurre donde quiera que una parte de un frente de onda este obstruida de alguna manera . Si al encontrar un obstáculo se altera la amplitud o la fase de una región del frente de onda, esto producirá difracción.
El Principio De Huygens-Fresnel
Establece que cada punto sin obstrucción de un frente de onda, en un instante de tiempo determinado sirve como fuente de trenes de onda secundarios esféricos (de la misma frecuencia como aquel de la onda primaria).
La amplitud del campo óptico en cualquier punto más allá es la superposición de todos estos trenes de onda (considerando sus amplitudes y fases relativas).
Si la longitud de onda es grande comparada con la abertura, las ondas se extenderán según ángulos grandes en la región más allá de la obstrucción.
Cuanto más pequeña sea la abertura , más circulares serán las ondas difractadas. Este principio tiene sus limitaciones (bastante hipotético) , mientras que la teoría de Kirchhoff es más rigurosa.
Difracción de Fraunhofer-Fresnel
Difracción de Fresnel o de campo cercano. Difracción de Fraunhofer o de campo lejano. Siempre que la onda incidente y la onda emitida sean planas (difiriendo de ello en una pequeña fracción de longitud de onda) en la extensión de las aberturas difractoras, se obtiene la difracción de Fraunhofer Cuando una fuente puntual distante y un punto de observación están demasiado cerca de la pantalla difractora, como para poder considerar despreciable la curvatura de los frentes de onda de incidencia y de emisión, prevalece la difracción de Fresnel. [1]
Osciladores Coherentes
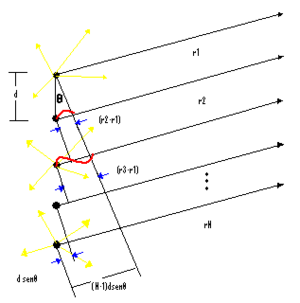
Considerando N osciladores lineales puntuales coherentes todos con el mismo ángulo de fase inicial , si el punto P donde se encuentren los rayos emitidos es muy distante, las amplitudes de onda individuales que lleguen a dicho punto serán esencialmente iguales es decir:
La suma de los trenes de onda esféricos Interferentes produce un campo eléctrico en P
No considerando la naturaleza vectorial de E tenemos que:
La diferencia de fase entre las fuentes adyacentes está dada por:
y como en un medio con indice n, ,de la fig. 1 podemos ver que , , etc. Así que:
Donde la serie geométrica tiene el valor de:
o bien:
=
Así el campo queda como:
O bien considerando se tiene que:
Finalmente, la distribución de densidad de flujo dentro de la distribución de difracción debido a N fuentes puntuales es proporcional a EE*/2 para E complejo o
Así que para N=0,I=1; N=1,; N=2, ó en función de :
Los máximos principales se dan en direcciones , tales que , (m=0,1,2,3,...) como , entonces , y como para ,
El valor de los máximos principales es
Examinemos Ahora una fuente lineal idealizada de osciladores electrónicos (es decir fuentes secundarias del principio de Huygens-Fresnel para una rendija larga cuyo ancho es mucho menor que iluminada por ondas planas). Cada punto emite una ondita esférica que escribimos como
donde =eficacia de la fuente
Dividiendo en diminutos segmentos tendremos que la contribución del segmento i a la intensidad del campo eléctrico en P es
Donde N=número de fuentes, D=longitud total del conjunto, y definiendo =eficacia de la fuente por unidad de longitud de la composición como:
Entonces el campo neto de todos los segmentos M esta dado por
Cuando se tiene que
Donde . La aproximación utilizada para evaluar la ecuación anterior debe depender de la posición de P con respecto al conjunto, marcando así la distinción entre la difracción de Fraunhofer y la de Fresnel[2].
La Rendija Única
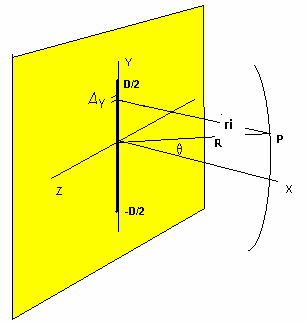
La difracción es junto con la interferencia un fenómeno típicamente ondulatorio. La difracción se observa cuando se distorsiona una onda por un obstáculo cuyas dimensiones son comparables a la longitud de onda. El caso más sencillo corresponde a la difracción Fraunhofer, en la que el obstáculo es una rendija estrecha y larga, de modo que podemos ignorar los efectos de los extremos. Supondremos que las ondas incidentes son normales al plano de la rendija, y que el observador se encuentra a una distancia grande en comparación con la anchura de la misma(R>>D). De la ecuación anterior se deduce que el campo en P, debido al segmento diferencial dy de la fuente, es
Donde es la amplitud, y podemos desarrollar r(y) como
El tercer término puede ignorarse siempre que su contribución a la fase sea despreciable aun cuando tiene que ser despreciable. Esto será cierto para todos los valores de cuando R sea muy grande. Así que consideramos unicamente los dos primeros términos, y sustituyendo en la ecuación (1) obtenemos:
Y finalmente
Para simplificar consideremos que , de tal forma que:
Lo que se puede medir rápidamente es la irradiancia que como recordaremos esta dada por , así que:
Cuando , y ,
Lo que corresponde al máximo principal. Así que la irradiancia en la aproximación de Fraunhofer esta dada por:
De donde podemos ver que cuando D>> , la irradiancia disminuye muy rápido conforme se desvía de cero.
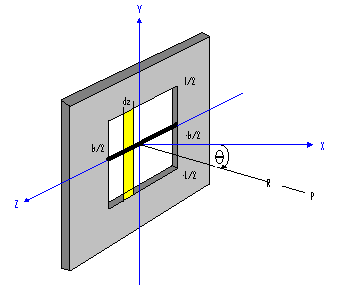
Considerando ahora el problema de la difracción de Fraunhofer por una rendija, donde el ancho puede ser de varios cientos de y pocos centímetros de longitud.Debemos dividir la rendija en una serie de tiras diferenciales (dz por l) paralelas al eje y, donde reconocemos a cada tira como una fuente lineal coherente larga, la cual podemos reemplazar por un punto emisor en el eje z. Donde cada punto emite una onda circular en el plano xz. Asi el problema se reduce al de encontrar el campo en el plano xz debido a un número infinito de fuentes puntuales que se extienden a través del ancho de la rendija a lo largo del eje z.Así que solo debemos calcular la integral de la contribución $"dE"$ de cada elemento $"dz"$ en la aproximación de Fraunhofer, pero esto es equivalente a fuente lineal coherente de manera que la solución completa esta dada, como hemos visto por:
Donde
Donde debemos tomar en cuenta que aun que la irradiancia disminuya rápidamente se observan unos máximos. Los extremos de los obtenemos mediante
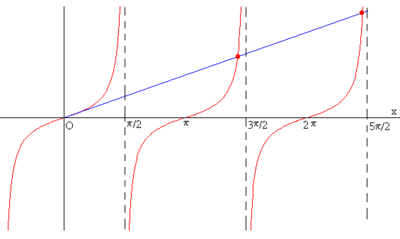
De dode podemos ver que tiene mínimos iguales a cero cuando , es decir en multiplos enteros de . Mientras que los máximos estan dados por la ecuación trascendente cuyas soluciones las podemos obtener gráficamente, donde algunas de las soluciones son
Sin embargo debemos aclarar que una de las principales fallas de en la teoría de Huygens-Fresnel es de que no toman en consideración las variaciones de la amplitud con el ángulo sobre la superficie de cada onda secundaria.
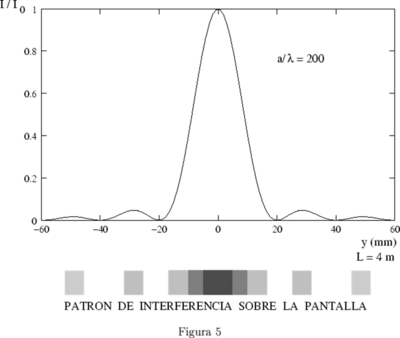
La gráfica siguiente muestra la densidad de flujo[3].
- ↑ HETCH, Eugene, Óptica, Adelphi University, Tercera ed., Addison-Wesley Iberoamerica,Madrid,2000 [cap.10]
- ↑ HETCH, Eugene, Óptica, Adelphi University, Tercera ed., Addison-Wesley Iberoamerica,Madrid,2000 [cap.10]
- ↑ HETCH, Eugene, Óptica, Adelphi University, Tercera ed., Addison-Wesley Iberoamerica,Madrid,2000 [cap.10]
Aportación de: jerifo 14:19 2 sep 2008 (CDT)--jerifo 13:13 2 sep 2008 (CDT)













![E=E_0(r)e^{-i\omega t}e^{i[kr_1+(N-1)\delta/2]}(\frac{\sin\N\delta/2}{\sin\delta/2})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/89acad1aba11bcd536564e379470d7ec986513d7)






![I=I_0\frac{\sin^2[N(kd/2)sin\theta]}{\sin^2[(kd/2)sin\theta}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2f6d1f4bdc23aa7bbac714f6e64454e6efbf8ca6)



















![E=\frac{\epsilon_L}{R}\int\limits_{-D/2}^{D/2}\sin[\omega t-k(R-y\sin\theta)]dy](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/11beb5f1b44af6da1a5bfb26d81de3e7fef490fb)
![E=\frac{\epsilon_LD}{R}\frac{\sin[(kD/2)\sin\theta]}{(kD/2)\sin\theta}\sin(\omega t-kR)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/490c2bdb3d4725bc528384e09649bc4690951a02)