Optica: Principio de Huygens-Fresnel

Principio de Huygens-Fresnel

El principio de Huygens fue establecido por el científico holandés Christian Huygens en 1678, es un método geométrico para encontrar a partir de la forma conocida de un frente de onda en algún instante dado, la forma de frente de onda un tiempo después. El principio establece:

"Dada punto de un frente de onda puede ser considerado como fuente secundaria de ondas que se expanden en todas direcciones con rapidez igual a la rapidez de propagación de la onda."

Así, el nuevo frente de onda en un tiempo posterior se encuentra construyendo una superficie tangente a las ondas secundarias o como se le conoce la envolvente de las ondas secundarias. Este principio expresa en esencia la idea de que cuando cada punto en un medio es perturbado por la onda, los efectos de dicha perturbación se mueven radialmente alejándose del punto en cuestión conforme pasa el tiempo.

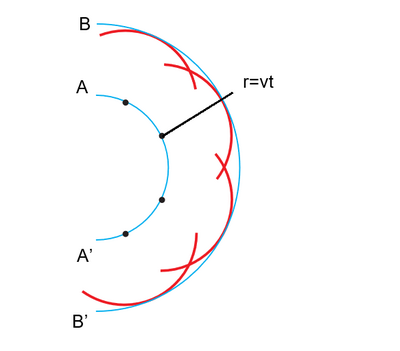
El principio de Huygens se muestra en la Fig. 1. El frente de onda original AA' se aleja de una fuente, como se indica con los pequeños puntos (fuerzas). Se quiere encontrar la forma del frente después del tiempo t. Sea v la rapidez de propagación de la onda; entonces en el tiempo t esta recorre una distancia vt; construimos varios círculos (ondas secundarias esféricas) de radio r=vt, centrados en los puntos a lo largo de AA'. La envolvente de estas ondas secundarias, que es el nuevo frente de onda, es la curva BB'; estamos suponiendo que v es la misma en todos los puntos y en todas las direcciones.

Figura 1 - Principio de Huygens

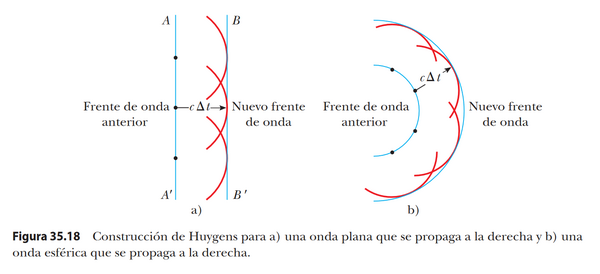
La figura 2 ilustra dos ejemplos sencillos de la construcción de Huygens. Primero considere una onda plana que se mueve por el espacio libre, como en la figura 2a. En t=0 el frente de onda esta indicado por el plano marcado AA'; en esta construcción cada uno de los puntos de este frente de onda se considera como una fuente puntual. Con estos puntos como fuentes para el tren de ondas, trazamos círculos de radio c Δt cada uno, donde c es la velocidad de la luz en el vacío y Δt es el periodo de propagación desde un frente de onda al siguiente. La superficie trazada tangente a estos trenes de ondas es el plano BB', que es paralelo a AA'. De un modo semejante, la figura 2b muestra la construcción para una onda esférica saliente.

Figura 2 -onda plana y onda esférica

Desarrollo matemático

Figura 3. Posición instantánea de una onda monocromática con radio $r_{o}$. Construcción de las zonas de Fresnel

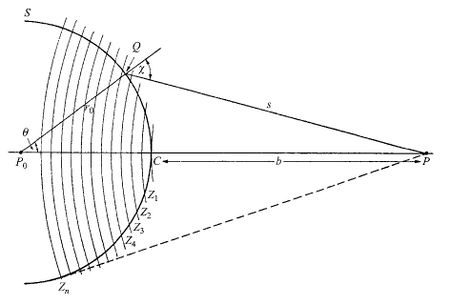
Consideremos $S$ la posición instantánea de una onda esférica monocromática con radio $r_{o}$ y centro en $P_{o}$. $P$ es el punto donde queremos ver la perturbación. El punto $Q$ está en la superficie de la esfera teniendo un ángulo $\theta$ respecto a la línea entre $P_{o}$ y $P$. Ahí existe una perturbación dada por \begin{equation}Q=A\quad { \frac { e }{ { r }_{ o } } }^{ { ikr }_{ o } }\end{equation} . Donde $A$ es la amplitud por unidad de tiempo.

Según el Principio de Huygens-Fresnel consideramos cada elemento del frente de onda como centro de una perturbación secundaria la cual se propaga en la forma de ondas esféricas. Tomemos un elemento de perturbación $dU$ debida al elemento S en Q:

\begin{equation}dU\left( P \right) =K\left( \chi \right) \frac { { e }^{ { ikr }_{ o } } }{ { r }_{ o } } \frac { { e }^{ { iks } } }{ s } dS\quad \quad \quad \quad \quad \quad \left( 1 \right)\end{equation}

Donde $s=QP$ y $K(\chi )$ es el factor de inclinación que describe la variación con dirección de la amplitud de las ondas secundarias y $\chi$ es el ángulo entre la normal en el punto $Q$ y la línea $s$.

$K(\chi )$ es máximo cuando $\chi =0$ y empieza a decrecer cuando $\chi$ va aumentando. $K(\chi )$ es cero cuando \begin{equation}\chi =\frac { \pi }{ 2 } \end{equation}.

Integrando la ecuación (1) obtenemos la perturbación total en $P$: \begin{equation}U\left( P \right) =\frac { { e }^{ { ikr }_{ o } } }{ { r }_{ o } } \iint _{ S }^{ }{ \frac { { e }^{ iks } }{ s } } K\left( \chi \right) \quad dS\quad \quad \quad \quad \left( 2 \right)\end{equation}.

Para evaluar esa ecuación es necesario construir las zonas de Fresnel.

Construcción de zonas de Fresnel

Tomemos varios círculos con centro en $P$ y diferentes radios: \begin{equation}b,b+\frac { \lambda }{ 2 } ,b+\frac { 2\lambda }{ 2 } ,b+\frac { 3\lambda }{ 2 } .............b+\frac { j\lambda }{ 2 }\end{equation}

Donde $b=CP$ y $C$ es el punto de intersección de $PP_{o}$ con el frente de onda $S$.

Las esféricas dividen a $S$ en varias zonas: $Z_{1},Z_{2},Z_{3},...,Z_{j},...$

Suponemos que $r_{o}$ y $b$ son mucho mayores que $\lambda$. Por lo tanto $K(\chi )$ debe tener el mismo valor $K_{j}$ en diferentes zonas (pues las $Z_{j}$ están muy pegadas).

Regresando al problema

De la Figura 3 vemos:

$s^{2}=r_{o}^{2}+(r_{o}+b)^{2}-2r_{o}(r_{o}+b)cos\theta$

Si derivamos respecto a $s$ tenemos:

$sds=r_{o}(r_{o}+b)sin\theta d\theta$

Por otro lado, tenemos el diferencial de la superficie $S$: \begin{equation}dS={ { r }_{ o } }^{ 2 }\sin { \theta } d\theta d\phi =\frac { { r }_{ o } }{ { r }_{ o }+b } sdsd\phi\end{equation}

Donde $\phi$ es el ángulo azimutal.

De la ecuación (2) vemos que es una doble integral. Por un lado integramos respecto a $\phi$ y nos da $2\pi$. Entonces nos queda una ecuación con una sola integral que describe la j-ésima contribución (de cada zona de Fresnel): \begin{equation}{ U }_{ j }\left( P \right) =2\pi \frac { { Ae }^{ { ikr }_{ o } } }{ { r }_{ o }+b } { K }_{ j }\int _{ b+\left( j-1 \right) \lambda /2 }^{ b+j\lambda /2 }{ { e }^{ iks }ds } \end{equation}

Resolviendo la integral y como $k\lambda =2\pi$: \begin{equation}{ U }_{ j }\left( P \right) =2i\lambda (-1{ ) }^{ j+1 }{ K }_{ j }\frac { { Ae }^{ { ik(r }_{ o }+b) } }{ { r }_{ o }+b } \quad \quad \quad \quad \quad \quad (3)\end{equation}

Re acomodando tenemos que el efecto total en P es la suma de todas las contribuciones: \begin{equation}{ U }_{ j }\left( P \right) =2i\lambda { K }_{ j }\frac { { Ae }^{ { ik(r }_{ o }+b) } }{ { r }_{ o }+b } \sum _{ j=1 }^{ n }{ { K }_{ j } } \quad (-1{ ) }^{ j+1 }\quad \quad \quad \quad \quad \quad (4)\end{equation}

Algo sobre series

En la ecuación (4) tenemos esta serie:

$\sum =\sum _{j=1}^{n}(-1)^{j+1}K_{j}=K_{1}-K_{2}+K_{3}-...+(-1)^{n+1}K_{n}$ (5)

La cual podemos desarrollar usando el método de Schuster, el cual consiste en separar elementos de la serie en dos partes y formar grupos:

\begin{equation}\quad \quad \sum { =\frac { { K }_{ 1 } }{ 2 } +\left( \frac { { K }_{ 1 } }{ 2 } -{ K }_{ 2 }+\frac { { K }_{ 3 } }{ 2 } \right) +\left( \frac { { K }_{ 3 } }{ 2 } -{ K }_{ 4 }+\frac { { K }_{ 5 } }{ 2 } \right) +.......... }\end{equation}

Donde el último término puede ser \begin{equation}\quad \quad \frac { 1 }{ 2 } { K }_{ n }\end{equation} o \begin{equation}\quad \quad \frac { 1 }{ 2 } { K }_{ n-1 }-{ K }_{ n }\end{equation} si n es impar o par, respectivamente.

Ahora, supongamos que $K_{j}$ es mayor que el promedio de sus vecinos $K_{j-1}$ y $K_{j+1}$. Entonces cada uno de los términos en los paréntesis de la ecuación aterior son negativos y resultaría (6):

\begin{equation}\sum { <\frac { { K }_{ 1 } }{ 2 } +\frac { { K }_{ n } }{ 2 } }\end{equation} para $n$ par.

\begin{equation}\sum { <\frac { { K }_{ 1 } }{ 2 } +\frac { { K }_{ n-1 } }{ 2 } } -{ K }_{ n }\end{equation}para $n$ impar.

Por otro lado, también la ecuación (5) podemos escribirla de la siguiente manera: \begin{equation}\sum { = } { K }_{ 1 }-\frac { { K }_{ 2 } }{ 2 } -\left( \frac { { K }_{ 2 } }{ 2 } -{ K }_{ 3 }+\frac { { K }_{ 4 } }{ 2 } \right) -\left( \frac { { K }_{ 4 } }{ 2 } -{ K }_{ 5 }+\frac { { K }_{ 6 } }{ 2 } \right) -......\end{equation}

Con el último termino siendo \begin{equation}-\frac { 1 }{ 2 } { K }_{ n-1 }+{ K }_{ n }\end{equation} con n par, \begin{equation} -\frac { 1 }{ 2 } { K }_{ n }\end{equation} para n impar. De forma similar al método de Schuster, la ecuación anterior resulta (7): \begin{equation}\sum { >{ K }_{ 1 }-\frac { { K }_{ 2 } }{ 2 } } -\frac { { K }_{ n-1 } }{ 2 } +{ K }_{ n }\end{equation}, para n par. \begin{equation}\sum { >{ K }_{ 1 }-\frac { { K }_{ 2 } }{ 2 } } -\frac { { K }_{ n } }{ 2 }\end{equation}, para n impar.

$K_{j}$ difiere muy poco de los valores de sus vecinos $K_{j-1}$ y $K_{j+1}$ por ello el lado derecho de las ecuaciones (6) y (7) son casi iguales, es decir (8):

$\sum ={\frac {K_{1}}{2}}+{\frac {K_{n}}{2}}$ si $n$ es par $\sum ={\frac {K_{1}}{2}}-{\frac {K_{n}}{2}}$ si $n$ es impar

Solución del problema

Tomando la ecuación (4) y sustituyendo las ecuaciones (8), tenemos (9):

$U(P)=i\lambda (K_{1}\pm K_{n}){\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Donde el signo $\pm$ es positivo o negativo si $n$ es par o impar.

De esta ecuación y la ecuación (3) para $U_{j}$:

$U(P)={\frac {1}{2}}[U_{1}(P)+U_{n}(P)]$

De aquí notamos que la perturbación total $U(P)$ depende solamente de la perturbación debida a la primera zona $U_{1}$ y la última $U_{n}$. Pero veamos qué pasa con la perturbación $U_{n}$.

Si tomamos la última zona de Fresnel $Z_{n}$, vemos que el la recta $s$ es tangente a la superfice $S$. Es decir, el ángulo $\chi ={\frac {\pi }{2}}$ y por lo tanto $K_{n}(\chi )=0$.

Entonces la ecuación (9) resultaría:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {1}{2}}U_{1}(P)$ (10)

Esto quiere decir que la perturbación total $U(P)$ es igual a la mitad de la perturbación debida a la primera zona.

Si tomamos la ecuación (10) para $U(P)$ y la ecuación (3) para $U_{1}(P)$ tendríamos que:

$i\lambda K_{1}=1\Rightarrow K_{1}=-{\frac {i}{\lambda }}={\frac {e^{-i{\frac {\pi }{2}}}}{\lambda }}$ (11)

Es decir, la ecuación (10) resultaría:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$ (12)

Obstrucción de un plano

Supongamos que tenemos un plano con una abertura muy pequeña circular perpendicular a $CP$ (ver Figura 1) y además que cubra todas las zonas salvo la mitad de la primera. Usando las ecuaciones (3) y (11), asumiendo que $j=1$ y multiplicando por ${\frac {1}{2}}$:

$U(P)=i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}={\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Que es el mismo resultado de la ecuación (12), es decir, da el mismo resultado si no tuvieramos el plano.

Ahora supongamos que tenemos un plano pero que cubre todas las zonas de Fresnel salvo la primera. Usando de nueva cuenta la ecuación (3), tenemos:

$U(P)=2i\lambda K_{1}{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}=2{\frac {Ae^{ik(r_{o}+b)}}{r_{o}+b}}$

Que es 4 veces mayor a que si el plano no estuviera (Comparado con la ecuación 10).

Con esto podemos ver que usando el plano, podemos aumentar o disminuir la perturbación sobre algún punto. Eso tiene gran aplicación en la ingeniería, por ejemplo en la construcción de lentes.

Placas zonales

Figura 4. Placa Zonal

En las consideraciones anteriores se recurrió al hecho según el cual las zonas sucesivas de Fresnel tendían a anularse unas a otras. Esto sugiere que observaríamos un enorme aumento de la irradiancia en P al eliminar todas las zonas pares o impares. una pantalla que altera la luz, bien sea en amplitud o fase, procedente de zonas de semiperíodo alternadas se denomina placa zonal. Supongamos que construimos una placa zonal que deje pasar solamente las primeras veinte zonas impares obstruyendo las pares. \begin{equation}E={ E }_{ 1 }+{ E }_{ 3 }+{ E }_{ 5 }+......{ +E }_{ 39 }\end{equation} siendo cada uno de estos términos aproximadamente igual. Para un frente de onda no obstruidos la perturbación en P seria \begin{equation}\frac { { E }_{ 1 } }{ 2 }\end{equation} mientras que con la placa zonal en su lugar,\begin{equation}E\approx { 20E }_{ 1 }\end{equation} La irradiancia se ha aumentado por un factor de 1600 veces.El mismo resultado seria si se hubiera dejado pasar a las zonas pares en lugar de las impares.

Lentes de Fresnel

El físico francés Augustin Fresnel ante la necesidad de construir una gran lente para un faro con una con una apropiada longitud focal,razono que seria la curvatura de la superficie lo que le daría la potencia de enfoque. Entonces reprodujo la curvatura de la superficie de la lente gruesa en secciones, manteniendo la misma longitud focal. La intensidad de lente (potencia) en dioptrías, se define como el inverso de la longitud focal en metros.

La calidad de la imagen dada por estas lentes no es muy buena debido a la dispersión que se produce en la unión de los anillos en que queda dividida la lente, lo que da ligeros anillos luminosos en el plano de la imagen. Las lentes de Fresnel son vidrios tallados o también plásticos fabricados de la misma forma cuya misión es hacer que los rayos de luz se comporten al atravesarlas como cuando atraviesan lentes plano convexas:

Los rayos de luz que llegan paralelos al eje óptico tienden a concentrarse en un punto o foco (se focalizan).

Los rayos que salen del foco atraviesan la lente y salen paralelos en un tubo de luz, es decir, colimados.

Figura 5. Lentes de Fresnel

Aplicaciones

LENTE DE FRESNEL EN EL CINE

Las lentes de Fresnel se han diseñado para aplicaciones de iluminación en televisión, cine y teatro ya sea para su aplicación en focos "spot" (luz concentrada) o focos "flood" (luz formando un abanico de 60°). La lente de Fresnel debe tener forma convexa a fin de acercar la lámpara el máximo posible a la lente. Para aplicaciones en las que se producen cargas térmicas muy altas se utilizan lentes de Fresnel especiales, endurecidas. Las características de la luz permanecen invariables: suave, uniforme y difuminada en los bordes. Se han desarrollado lentes de Fresnel con distancias focales cortas que proporcionan una iluminación uniforme y altamente eficiente. Modificando la distancia entre la lámpara y la lente se puede utilizar el foco tanto para situaciones de "spot" como de "flood".

COCINAS SOLARES

En las cocinas solares con reflectores parabólicos o lentes fresnel no es necesario el uso de una caja aislada pues la temperatura en el foco sobrepasa los 600 °C. Esta temperatura es demasiado alta para ser manejada con facilidad, por lo que si la vasija de cocción se sitúa fuera del foco, aumentará la superficie de caldeo al mismo tiempo que la temperatura será más baja. Este tipo de cocinas necesitan ser reorientadas con frecuencia para que la luz incida en la olla y no se desperdicie energía. De todos modos es conveniente evitar pérdidas de calor cubriendo los recipientes con una campana de cristal.

Referencia y links

Marx Born & Emil Wolf; Principles of Optics 6th Edition

Sears & Zemansky & Young & Freedman; Fisica Universidataria vol. II ed. Pearson Educacion

Raymond A. Serway; Fisica vol. II

Thomhas A. Moore; Fisica seis ideas fundamentales vol. II ed. Mc Graw Hill

Sobre los lentes de Fresnel: http://teleformacion.edu.aytolacoruna.es/FISICA/document/fisicaInteractiva/OptGeometrica/Instrumentos/fresnel/fresnel.htm

---

Aportación de Usuario : Aura Yazmin Bejarano Olvera (discusión) 23:57 23 nov 2015 (CST)

---