Compleja:Zill-Cap5.5
Ejercicios del capítulo 5, sección 5 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 5.5
Ejercicio 1
Evalue la integral dada a lo largo del contorno cerrado indicado
$ \oint_{c} \frac{4}{z-3i}dz $; $ |z|=5 $
Aqui observamos que $f(z)=4$ y $z_0=-i$ como un punto dentro de la circunferencia $C$.
Después observamos que la función $f$ es analítica en el contorno $C$
Y al aplicar la formula de Cauchy, obtenemos
$ \oint_{c} \frac{4}{z-3i}dz = 2\pi i f(-i) =2\pi i(4) $, asi tenemos
$ \oint_{c} \frac{4}{z-3i}dz = 8\pi i$
Miguel Medina Armendariz (discusión) 18:11 19 jun 2015 (CDT)
Ejercicio 2
'Utilizar los teoremas 5.5.1 y 5.5.2 (libro de Zill-Análisis complejo, pag:246;248) , cuando sea apropiado, para evaluar la integral dada a lo largo de o de los contornos cerrados.
$\oint\frac{z^{2}}{(z-3i)^{2}}dz$ con $|z|=5$
Al Examinar el integrando se ve que no es analítica en $z=3i$ por tanto acomodamos la función de forma que pueda usarse la forma integral de Cauchy.
$\oint\frac{z^{2}}{(z-3i)^{2}}dz=\oint\frac{z^{3}}{z(z-3i)^{2}}dz=\oint\frac{z^{3}}{\frac{(z-3i)^{2}}{z}}dz$
Identificamos $z_{0}$ y $f(z)=\frac{z^{3}}{(z-3i)^{2}}$
De donde se deduce que :
$\oint\frac{z^{2}}{(z-3i)^{2}}dz=\oint\frac{z^{3}}{z(z-3i)^{2}}dz=\oint\frac{z^{3}}{\frac{(z-3i)^{2}}{z}}dz=\frac{2\pi i}{1\text{!}}f'(i)=2\pi i(z-3i)=2\pi iz+6\pi$
--A. Martín R. Rabelo (discusión) 23:57 21 jun 2015 (CDT)
Ejercicio 3
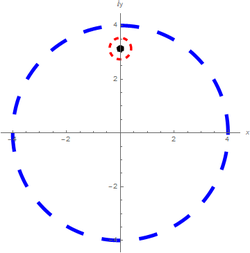
Use el teoremas 5.5.1 o 5.5.2, en su caso para evaluar la integral $\oint_{c} \! \frac{e^z}{z-i\pi}\,dz$ a lo largo de $|z|=4$.
La integral tiene una singularidad en $z=i\pi$, que se encuentra en el dominio de integración, por lo que no es analítica en ese punto y es preciso extraer ese punto, se muestra en la figura.
El teorema 5.5.1 indica que: \[ f(z_0)=\frac{1}{2\pi i}\oint_{C} \! \frac{f(z)}{z-z_0}\,dz \]
Para una $f(z)=e^z$ y una $z_0=i\pi$ tenemos: \[ f(i\pi)=\frac{1}{2\pi i}\oint_{C} \! \frac{e^z}{z-i\pi}\,dz \] Que claramente cohincide con nuestra integral, despejando nos queda: \[ \oint_{C} \! \frac{e^z}{z-i\pi}\,dz=f(i\pi)\,(2\pi i)=2i\pi e^{i\pi}=2i\pi\,[cis (\pi)]=2i\pi\,(-1)=-2i\pi \]
--Tlacaelel Cruz (discusión) 23:40 19 jun 2015 (CDT)
Ejercicio 4
Evalúe la integral dada a lo lardo del contorno cerrado indicado.
4.- $\oint_{c}\frac{1+e^{z}}{z}dz$, con $|z|=1$
Primero se ve que el unico punto donde el integrando no es analitico es en $z=0$ y que, en este caso, se encuentra dentro del contorno C, y
teniendo en cuenta el teorema 5.5.1 tenemos que:
$f(z)=1+e^{z}$
Y
$z-z_{0}=z-0$
Entonces:
$\oint_{c}\frac{1+e^{z}}{z}dz,=\oint_{c}\frac{f(z)}{z-z_{o}}dz=2\pi if(z_{0})=2\pi if(0)=2\pi i(1+1)$
Finalmente
\[ \oint_{c}\frac{1+e^{z}}{z}dz,=4\pi i \]
--Fernando Vazquez V. (discusión) 01:13 21 jun 2015 (CDT)
Ejercicio 5
Use el teoremas 5.5.1 o 5.5.2, en su caso para evaluar la integral a lo largo del contorno cerrado indicado.
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz $; $ |z|=3 $
Solución:
Primero, identificamos $f(z)=z^2-3z+4i$ y $z_0=-2i$ como un punto dentro del círculo C. Se observa que $f$ es analítica en todos los puntos dentro y en el contorno C. Así, por Cauchy (Teorema 5.5.1):
$ f(z_0)=\frac{1}{2\pi i}\oint_{c} \frac{f(z)}{z-z_0} dz $
Obtenemos:
$ 2\pi i f(-2i)= 2\pi i(-4+10i)= -8\pi i -20\pi = -\pi(20+8i) $
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz = 2\pi i f(-2i)= -\pi(20+8i)$
Nancy Martínez Durán (discusión) 21:56 18 jun 2015 (CDT)
Ejercicio 7
Evalúe la integral dada a lo largo de los contornos
a)
Analizando la función dada, la función tiene puntos donde no es analítica en los puntos y en el punto
reescribiendo la función
En donde para este contorno el término no está definido en el dominio, por lo que haremos que
Por lo que evaluando f(z) en , tenemos que
por lo que el resultado es
b)
Del inciso a) analizamos que f(z) no es analítica en en los puntos y en el punto
reescribiendo la función. Y lo escribimos de la forma
Por lo que hacemos el mismo proceso anterior, pero ahora solo para el punto dado que en esta región no es analítica en dicho punto. Por lo que tenemos que
Evaluando g(z) en tenemos que
Por lo que
--Pablo (discusión) 14:31 21 jun 2015 (CDT)
Ejercicio 11
Evalúe la integral dada a lo largo del contorno cerrado indicado.
Error al representar (error de sintaxis): \oint_{C}\frac{e^{z²}}{(z-i)³}dz ; |z-i|=1
Nuestro contorno esta definido por una circunferencia con centro en y radio .Ahora bien podemos notar de nuestra función que existe una singularidad cuando la cual se encuentra dentro de nuestro dominio , por lo cual no es analítica en ese punto.
Para la resolucion de este problema emplearemos lo siguiente:
por lo cual de nuestra integral a resolver identificamos:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): f(z)=e^{z²}
Error al representar (error de sintaxis): f'(z)=2z e^{z²}
Error al representar (error de sintaxis): f''(z)=2e^{z²}(2z²+1)
utilizando
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2 e^{z_0²}(2z_0²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz
sustituyendo :
Error al representar (error de sintaxis): 2 e^{(i)²}(2(i)²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz
Error al representar (error de sintaxis): 2 e^{-1}(-1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz
Despejando Error al representar (error de sintaxis): -2 e^{-1}i\pi=\oint_{C}\frac{e^{z²}}{(z-i)³}dz
Por lo cual nuestra solucion es
--Anahi Limas (discusión) 18:55 21 jun 2015 (CDT)
Ejercicio 15
evalúe la integral a lo largo de los contornos cerrados indicados
1.- $\oint_{C}\frac{2z+5}{z^{2}-2z}dz$; a) $\mid z\mid=\frac{1}{2}$ b) $\mid z+1\mid=2$ c) $\mid z-3\mid=2$, d) $\mid z+2i\mid=1$
$\oint_{C}\frac{2z+5}{z^{2}-2z}dz=\oint_{C}\frac{2z+5}{z(z-2)}dz$
y por fracciones parciales:
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\oint_{C}[\frac{A}{z}+\frac{B}{z-2}]dz=\oint_{C}\frac{A(z-2)+B(z)}{z(z-2)}\Longleftrightarrow2z+5=A(z-2)+B(z)$
resolviendo la ecuación para $A\;y\;B$ tenemos:
si
$z=0$
entonces:
$5=-2A\Longleftrightarrow A=-\frac{5}{2}$
si
$z=2$
entonces:
$9=2B\Longleftrightarrow B=\frac{9}{2}$
de esto:
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\oint_{C}[\frac{A}{z}+\frac{B}{z-2}]dz=\oint_{C}[-\frac{5}{2z}+\frac{9}{2z-4}]dz=-\frac{5}{2}\oint_{C}\frac{1}{z}dz+\frac{9}{2}\oint_{C}\frac{1}{z-2}dz$
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\frac{5}{2}\oint_{C}\frac{1}{z}dz+\frac{9}{2}\oint_{C}\frac{1}{z-2}dz$
evaluando la integral a lo largo de a) $\mid z\mid=\frac{1}{2}$
como se puede ver $\oint_{C}\frac{2z+5}{z(z-2)}dz$ no es una función analítica en $z=0\;y\;en\;z=2$
y como $\mid z\mid=\frac{1}{2}$ es una circunferencia de radio $\frac{1}{2}$ centrada en $0+0i$ entonces
por el teorema de Cauchy-Coursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
ademas como $-\frac{5}{2}\oint_{C}\frac{1}{z}dz$ no es analítica en $\mid z\mid=\frac{1}{2}$ entonces por la formula de la integral de Cauchy
$f(z_{0})=\frac{1}{2\pi i}\oint_{c}\frac{f(z)}{z-z_{0}}dz$
$\oint_{C}\frac{1}{z}dz=2\pi i\Longleftrightarrow-\frac{5}{2}\oint_{C}\frac{1}{z}dz=-\frac{5}{2}2\pi i=-5\pi i$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$
Ahora evaluando a lo largo de b) $\mid z+1\mid=2$, (circunferencia de radio $2$ centrada en $-1$) por el razonamiento anterior:
como $z=2$ no esta dentro del contorno $\mid z+1\mid=2$ entonces por el teorema de Cauchy-Coursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
como $z=0$ se encuentra dentro del contorno $\mid z+1\mid=2$
$\oint_{C}\frac{1}{z}dz=2\pi i\Longleftrightarrow-\frac{5}{2}\oint_{C}\frac{1}{z}dz=-\frac{5}{2}2\pi i=-5\pi i$
ademas
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$
ahora evaluando a lo largo de c) $\mid z-3\mid=2$,(circunferencia de radio $2$ centrada en $3$)
como $z=2$ esta sobre el contorno $\mid z-3\mid=2$ entonces
$\oint_{C}\frac{1}{z-2}dz=2\pi i\Longleftrightarrow\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=\frac{9}{2}2\pi i=9\pi i$
como $z=0$ no se encuentra dentro del contorno $\mid z+1\mid=2$ por el teorema de Cauchy-Coursat
$-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=9\pi i+0=9\pi i$
ahora evaluando a lo largo de d) $\mid z+2i\mid=1$(circunferencia de radio$1$ centrada en $-2i$ )
como $z=0\;y\;z=2$ no se encuentran dentro del contorno $\mid z+2i\mid=1$ entonces por el teorema de Cauchy-Coursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
$-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0+0=0$
--Francisco Medina Albino (discusión) 23:19 19 jun 2015 (CDT)
Ejercicio 17
Utilice los teoremas 5.5.1 y 5.5.2, cuando sea apropiado, evalúe la integral $ \oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz $ a lo largo de los contornos cerrados indicados.
$(a)$ $|z|=1$
$(b)$ $|z-1-i|= 1$
Solución del inciso $(a) : $
Al examinar el integrando se ve que no es analítica en $z=0$ y en $z=1+i$ pero sólo $z=0$ está dentro del contorno cerrado. Al escribir el integrando como
\[ \frac{z+2}{z^{2}(z-1-i)}=\frac{\frac{z+2}{z-1-i}}{z^{2}} \]
podemos identificar, $ z_{0}=0 $ y $ n=1 $ y $ f(z)=\frac{z+2}{z-1-i} $. La regla del cociente da $f'(z)= -\frac{3+i}{(z-(1+i))^2}$ y así $f'(0)=-\frac{1}{2}+\frac{3 i}{2} $. Por tanto, del teorema 5.5.2 se encuentra
\[
\oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz = \frac{2 \pi i }{1!} f'(0) = \left( \frac{2 \pi i }{1!} \right) \left( -\frac{1}{2}+\frac{3 i}{2} \right) = (-3-i) \pi
\]
Solución del inciso $(b) : $
Al examinar vemos que $1+i$ es el único punto en el contorno cerrado $C$ en que el integrando no es analítico. Entonces reescribiendo el integrando como
\[
\frac{z+2}{z^{2} (z-1-i) }= \frac{ \frac{z+2}{z^{2}} }{z-1-i}
\]
podemos identificar $f(z)= (z+2)/z^{2}$. La función $f$ es analítica en todos los puntos dentro y sobre el contorno $C$. Por tanto, de la fórmula integral de Cauchy del teorema 5.5.1 tenemos:
\[ \oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz = \int_{C} \! \frac{ \frac{z+2}{z^{2}} }{z-1-i} \,dz = 2 \pi i f(1+i)= ( 2 \pi i)\left( \frac{1}{2}-\frac{3 i}{2} \right)= (3+i) \pi \]
--Emmanuell Castro Flores (discusión) 21:05 20 jun 2015 (CDT)
Ejercicio 18 Sección 5.5.1
Usa el teorema 5.9 o 5.10 que sea apropiado para evaluar la integral dada a lo largo del contorno cerrado indicado
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz ; (a) |z| = 1 , (b) |z - 2| = 1$
(a) $|z| = 1$
Para este primer caso donde tenemos una circunferencia centrada en el origen como contorno es necesario re escribir la integral de la forma
$\oint_{C} \frac{\frac{1}{z^3}}{z - 4} dz$
La integral se re escribe de esta forma para poder hacer uno del Teorema 5.9 : $f(z_0) = \frac{1}{2\pi i } \oint_{C} \frac{f (z)}{z - z_0} dz$
Donde$f (z) = \frac{1}{z^3}$ y $z_0 = 4$
Aplicando el teorema a la integral tenemos:
$\oint_{C} \frac{\frac{1}{z^3}}{z - 4} dz = 2\pi i f(z_0)$
Donde $f(z_0) = \frac{1}{(4)^3} = \frac{1}{64}$
$\Rightarrow$
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = \oint_{C} \frac{\frac{1}{z^3}}{z - 4} dz= \frac{\pi i}{32}$
(b) $|z - 2| = 1$
Ahora tenemos una circunferencia con centro en 2 y de radio 1 es por ello que re escribiremos la integral de la siguiente forma:
$\oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz$
Ahora en este cao ahremos uso del teorema 5.10 : $f (z_0) = \frac{2}{2\pi i } \oint_{C} \frac{f (z)}{(z - z_0)^3} dz$
Donde:
$f = \frac{1}{z - 4}$
$z_0 = 0$
$f ' = \frac{d}{dz} (z - 4)^{-1} = \frac{-1}{(z - 4)^2}$
$f = \frac{d}{dz} (\frac{-1}{(z - 4)^2}) = \frac{2}{(z - 4)^3}$
Aplicando el teorema a la integral tenemos:
$\oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{2\pi i}{2} f (z_0)$
Con $f (z_0) = \frac{2}{(0 - 4)^3} = \frac{-2}{64} = frac{-1}{32}$
$\Rightarrow$
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = \oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{-\pi i}{32}$
Angelina Nohemi Mendoza Tavera (discusión) 15:20 21 jun 2015 (CDT)
Ejercicio 19
Ejercicio 19
Evaluar la integral dada a lo largo del contorno cerrado indicado:
$\oint_{c}\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz$ ; $\left|z\right|=6$
$\oint_{c}\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz$
$=\oint_{c}\frac{e^{2iz}}{z^{4}}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
$=\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$ ...$\left(1\right)$
por lo que podemos definir convenientemente:
$f\left(z_{1}\right)=e^{2iz}$ ...$\left(2\right)$ y
$f\left(z_{2}\right)=z^{4}$ ...$\left(3\right)$
También es claro que hay dos singularidades en:
1.- $z_{0,1}=0$ y
2.- $z_{0,2}=i$
{*} Para poder utilizar la fórmula integral de Cauchy las funciones
evaluadas en la integral deben ser analíticas en un dominio simplemente
conexo $D$ y $C$ debe ser cualquier contorno cerrado simple situado
totalmente en $D$. En nuestro ejemplo estas condiciones sí se cumplen. {*}
.
Cálculo de $\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz$ :
Por la fórmula integral de Cauchy se tiene:
$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz$
$=\frac{2\pi i.f\prime\prime\prime\left(z_{0,1}\right)_{1}}{3!}$
donde $f\prime\prime\prime\left(z_{1}\right)=-8ie^{2iz}$ es la derivada
de tercer orden de la ecuación $\left(2\right)$
Y por lo tanto
$f\prime\prime\prime\left(z_{0,1}\right)_{1}=-8i$
entonces:$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz=\frac{2\pi i\left(-8i\right)}{6}=\frac{8}{3}\pi$ ...$\left(4\right)$
Cálculo de $\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
Por la fórmula integral de Cauchy se tiene:
$\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
$=\frac{2\pi i\left(f\prime\prime\left(z_{0,2}\right)_{2}\right)}{2!}$
donde $f\prime\prime\left(z_{2}\right)=12z^{2}$es la segunda derivada de la ec $\left(3\right)$
Y por lo tanto :
$f\prime\prime\left(z_{0,2}\right)_{2}=12i^{2}$
Entonces:
$\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz=\frac{2\pi i\left(12i^{2}\right)}{2}=-12\pi i$ ... $\left(5\right)$
Finalmente sustituyendo los valores de las ecs. $\left(4\right)$y $\left(5\right)$en
la euación $\left(1\right)$ se obtiene:
$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz=\frac{8}{3}\pi+12\pi i$
$\therefore\oint_{c}=\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz=\pi\left(\frac{8}{3}+12i\right)$
Resuelto por:
Alejandro Juárez Toribio (discusión) 17:38 18 jun 2015 (CDT)
Ejercicio 21
Evalue la integral dada a lo largo del contorno cerrado indicado
- ;
Solución
Observamos que el centro de la curva es z=2 y tiene radio 5, entonces analizando la integral se ve que no es analítico en z=0 y z=1, pero ambos están dentro del contorno entonces es analítica la curva, procedemos a decir:
- , donde :
- , y entonces nos queda:
La formula integral de Cauchy para derivadas, para cualquier punto dentro de C es:
- , comparando con las integrales que tenemos, obtenemos:
Para la primera función
- , donde y
lo que nos dice n=1 ,es obtener la primera derivada de la funcion f1, y despues valuar en el punto 1,entonces:.
Para la segunda función
- , donde y
lo que nos dice n=2 ,es obtener la segunda derivada de la funcion f2 y despues valuar en el punto 0 ,entonces:.
Por lo tanto
Elaborado por Ricado García Hernández--Ricardo Garcia Hernandez (discusión) 15:23 20 jun 2015 (CDT)
Ejercicio 22
22.Utilice los teoremas 5.9 y 5.10, cuando sean apropiados, para evaluar la integral a lo largo de los contornos cerrados: $\oint_C \frac{1}{z^2(z^2+1)}dz; |z-i|=\frac{3}{2} $.
Solución:
Notemos que: $f(z)=\frac{1}{z+i}$ es analítica dentro del contorno dado, por otra parte: $z^2+1=(z+i)(z-i)$ y que $\frac{1}{z^2(z^2+1)}=\frac{\frac{1}{z+i}}{z^2(z-i)}$.
Entonces:
$\oint_C \frac{1}{z^2(z^2+1)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz$. Al descomponer $\frac{1}{z^2(z-i)}$ en fracciones parciales obtenemos que: $\frac{1}{z^2(z-i)}=\frac{1}{z^2}-\frac{1}{z-i}+\frac{1}{z}$. Por lo anterior $\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2}dz-\oint_C \frac{\frac{1}{z+i}}{(z-i)}dz+\oint_C \frac{\frac{1}{z+i}}{z}dz=\frac{2\pi if'(0)}{1!}-2\pi i f(i)+2\pi if(0)=2\pi i(\frac{-1}{(0+i)^2}-\frac{1}{2i}+\frac{1}{i})=2\pi i(1-\frac{1}{2i}+\frac{2}{2i})=2\pi i (1+\frac{1}{2i})=2\pi (\frac{1}{2}+i)=\pi(1+2i)$.
Por lo tanto: $\oint_C \frac{1}{z^2(z^2+1)}dz ;(|z-i|=\frac{3}{2})=\pi(1+2i) $
Alan Daniel Barrón Posadas (discusión) 13:07 28 jun 2015 (CDT)
Ejercicio 23
Evaluar la integral, donde C es la figura en forma de ocho
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz$
Solución:
Sabemos que C no es un contorno simple pero lo pensamos como si fueran dos solo que uno va en horario $-c_{1}$ y el otro antihorario $c_{2}$ por cual las integrales las escribiremos de la siguiente manera:
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=\oint_{c_{1}}\frac{3z+1}{z\left(z-2\right)^{2}}dz+\oint_{c_{2}}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\oint_{-c_{1}}\frac{\frac{3Z+1}{\left(Z-2\right)^{2}}}{Z}dz+\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=-I_{1}+I_{2}$
Para resolver $I_{1}$usaremos
$f\left(z_{0}\right)=\frac{1}{2\pi i}\oint_{c}\frac{f\left(z\right)}{z-z_{0}}dz$
Sacamos a $z_{0}$y a $f\left(z\right)$
$z_{0}=0$ $f\left(z\right)=\frac{3z+1}{\left(z-2\right)^{2}}$
entonces tenemos que:
$I_{1}=\oint_{-c_{1}}\frac{\frac{3Z+1}{\left(Z-2\right)^{2}}}{Z}dz=2\pi if\left(0\right)=2\pi i\left(\frac{1}{4}\right)=\frac{\pi}{2}i$
Pero nosotros queremos $-I$ entonces al resultado anterior lo multiplicamos por un signo menos y así tenemos que:
$-I=-\frac{\pi}{2}i$
Ahora para resolver $I_{2}$ utilizaremos
$f^{\left(n\right)}\left(z_{0}\right)=\frac{n!}{2\pi i}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
tenemos que
$z_{0}=2$ y $f\left(z\right)=3+\frac{1}{z}\Longrightarrow f^{,}\left(z\right)=-\frac{1}{Z^{2}}$y también $f\left(2\right)=-\frac{1}{4}$
Ahora resolvemos $I_{2}$
$I_{2}=\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=\frac{2\pi i}{1!}f^{\text{,}}\left(2\right)=2\pi i\left(-\frac{1}{4}\right)=-\frac{\pi}{2}i$
Finalmente sumamos las integrales y obtenemos el resultado requerido que es:
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\pi i$
Resuelto por Luis Enrique Martínez Valverde (discusión) 22:31 21 jun 2015 (CDT)
Ejercicio 24
In Problems 23 and 24, evaluate the given integral, where C is the figure-eight contour in the figure.
traduccion:
En los problemas 23 y 24 , evalúe la integral dada , donde C es la forma de ocho vertical contorno en la figura 5.47,
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ donde ces ese 8 vertical
para poder atacar este ejercicio tenemos los siguientes teoremas:
1.-Fórmula Integral Teorema 5.9 de Cauchy:
Supongamos que f es analítica en un dominio simplemente conexo D y C es cualquier contorno cerrado sencilla situada totalmente en D. Entonces, para cualquier punto z0 singular dentro de C ,
$f\left(z_{0}\right)=\frac{1}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)}dz$
2.-Fórmula Integral Teorema 5.10 de Cauchy para Derivados:
Supongamos que f es analítica en un dominio simplemente conexo D y C es cualquier contorno cerrado sencilla situada totalmente en D. Entonces, para cualquier punto z0 singular dentro de C
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
por lo cual devemos llevar la integral propuesta a alguna de las dos fromas anteriores para poder usar algun teorema:
pero antes devemos concidarar el contorno C y la integral $\ointclockwise_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ es obvio que el denominador tiene 2 singularidades las cuales son $z=i$ y tambien $z=-i$ y tambien es obvio que este corntorno no es simple ya que tiene un cruce con si mismo por lo cual procedemos a cortar este contorno en dos contornos de la siguiente manera:
$C=c_{1}+c_{2}$donde cada sumando es una porcion del contorno total pormlo que la interal original podemos partirla en dos integrales de la siguiente manera:
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$
haora si resolvemos cada integral por separado y aplicando los teoremas y despues las sumamos
3.- integral sobre c$_{1}$donde la singularidad es $z=i$:
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ arregrandola para poder usar algun teorema queda:
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=\oint c_{1}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ dejamos las singularidades en el denominador y subimos al numerador el resto de la siguiente manera:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)\left(z+i\right)}}{\left(\left(z-i\right)\right)\left(\left(z-i\right)\right)}dz$ desarrollando en el denominador tenemos:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz$ haora si podemos utilizar el teorema Fórmula Integral Teorema 5.10 de Cauchy para Derivados
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
$f^{1\prime}\left(z_{0}\right)=\frac{1!}{2ipi}\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz$ donde $f\left(z\right)=\frac{e^{iz}}{\left(z+i\right)^{2}}$la cual es analitica para c$_{1}$ y $z_{0}=i$
$f^{1\prime}\left(i\right)=\frac{\left(z+i\right)^{2}ie^{iz}-e^{iz}\left(2\left(z+i\right)\right)}{\left(\left(z+i\right)^{2}\right)^{2}}=\frac{-4e^{-1}}{\left(2i\right)^{3}}$ entonces la integral para c$_{1}$queda:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=2ipi\left(\frac{-4e^{-1}}{\left(2i\right)^{3}}\right)$
4.. 3.- integral sobre c$_{2}$donde la singularidad es $z=-i$:
$-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ arregrandola para poder usar algun teorema queda:
$-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=-\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=-\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ dejamos las singularidades en el denominador y subimos al numerador el resto de la siguiente manera:
$-\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z-i\right)\left(z-i\right)}}{\left(\left(z+i\right)\right)\left(\left(z+i\right)\right)}dz$ desarrollando en el denominador tenemos
$-\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z-i\right)^{2}}}{\left(z+i\right)^{2}}dz$ haora si podemos utilizar el teorema Fórmula Integral Teorema 5.10 de Cauchy para Derivados
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
$-f^{1\prime}\left(z_{0}\right)=-\frac{1!}{2ipi}\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z-i\right)^{2}}}{\left(z+i\right)^{2}}dz$ donde $f\left(z\right)=\frac{e^{iz}}{\left(z-i\right)^{2}}$ la cual es analitica en c$_{2}$y $z_{0}=-i$
$-f^{1\prime}\left(-i\right)=\frac{\left(z-i\right)^{2}ie^{iz}-e^{iz}\left(2\left(z-1\right)\right)}{\left(\left(z-i\right)^{2}\right)^{2}}=-\frac{\left\{ 0\right\} e^{-1}}{\left(-2i\right)^{3}}=-0$ entonces la integral para c$_{1}$queda:
$-\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=-2ipi\left(0\right)=0$
por lo tanto la integral total es igual a la suma de integrales para c1 y c2
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2ipi\left(\frac{-4e^{-1}}{\left(2i\right)^{3}}\right)-0$
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2ipi\left(\frac{-4e^{-1}}{-8i}\right)=\frac{-8pie^{-1}}{-8}=pie^{-1}$
--Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT) ----
Ejercicio 25
Proceder como el ejemplo 5 para encontrar el módulo máximo de la función dada en la región circular $|z|\leq 5$ para $f(z)=-iz+i$.
Sol. Factorizando en la función se tiene $f(z)=i(1-z)$ y del capítulo 1 se tuvo que $|z|^2=z\overline{z}$. Sustituyendo $z$ por $i(1-z)$
$|f(z)|^2=|i(1-z)|^2=i(1-z)\overline{i(1-z)}=i(1-z)[-i(1-\overline{z})]=(1-z)(1-\overline{z})=1-\overline{z}-z+z\overline{z}=1-\overline{z}-z+|z|^2$
$|f(z)|^2=1+|z|^2-(z+\overline{z})$
En el capítulo 1 se dedujo que
$Re(z)=\dfrac{z+\overline{z}}{2}$ y $Im(z)=\dfrac{z-\overline{z}}{2i}$
Por lo que despejando y sustituyendo en $|f(z)|^2$; $2Re(z)=z+\overline{z}$
$|f(z)|^2=1+|z|^2-2Re(z)$
Dado que $f(z)$ es un polinomio, es analítica en la región $|z|\leq 5$, por lo que del Teorema del módulo máximo, el máximo se alcanza cuando $|i(1-z)|$ está en la frontera, es decir $|z|=5$. Sustituyendo
$|f(z)|^2=1+|z|^2-2Re(z)=1+25-2Re(z)=26-2Re(z)$
$|f(z)|=\sqrt{26-2Re(z)}$
Y de igual manera, la expresión anterior obtiene su máximo en $|z|=5$ que es cuando $Re(z)=5$. Sustituimos
$|f(z)|=\sqrt{26-2Re(z)}=\sqrt{26-2(5)}=\sqrt{26-10}=\sqrt{16}=4$
Por lo tanto, el módulo máximo es:
$|f(z)|=4$
Oscar Javier Gutierrez Varela (discusión) 23:11 19 jun 2015 (CDT)
Ejercicio 26
proceda como en el ejemplo 5 para encontrar el módulo máximo de la función dada en la región circular cerrada indicada
$f(z)=z^{2}+4z$ ; $|z|\leq1$
sabemos que
$|z|^{2}=z\overline{z}$
entonces
$|z^{2}+4z|^{2}=\left(z^{2}+4z\right)\left(\overline{z^{2}+4z}\right)=\left(z^{2}+4z\right)\left(\overline{z^{2}}+4\overline{z}\right)=z^{2}\overline{z^{2}}+4z\overline{z^{2}}+4\overline{z}z^{2}+16z\overline{z}$
usando las propiedades de los números complejos siguientes
$\overline{z_{1}z_{2}}=\overline{z_{1}}*\overline{z_{2}}$
$|z|^{2}=z\overline{z}$
obtenemos
$z^{2}\overline{z^{2}}+4z\overline{z^{2}}+4\overline{z}z^{2}+16z\overline{z}=zz\overline{z}\overline{z}+4z\overline{z}\overline{z}+4\overline{z}zz+16z\overline{z}=|z|^{2}|z|^{2}+4|z|^{2}\overline{z}+4|z|^{2}z+16|z|^{2}$
nosotros sabemos que $m\acute{a}x_{|z|\leq1}|z^{2}+4z|$ ocurre cuando $|z|=1$
entonces sustituimos y simplificamos
$|z|^{2}|z|^{2}+4|z|^{2}\overline{z}+4|z|^{2}z+16|z|^{2}=(1^{2})(1^{2})+4(1)\overline{z}+4(1)z+16(1)^{2}=1+4\overline{z}+4z+16=17+4(z+\overline{z})$
ahora usamos otra propiedad
$*Re(z)=\frac{\overline{z}+z}{2}$
$2Re(z)=\overline{z}+z$
por lo tanto obtenemos
$17+4(z+\overline{z})=17+4\left(2Re(z)\right)=17+8Re(z)$
y la parte real vale 1 cuando alcanza su máximo en este caso, por lo tanto nos sale que
$17+8Re(z)=17+8=25$
entonces obtenemos que
$|z^{2}+4z|^{2}=25$
$|z^{2}+4z|=\sqrt{25}=5$
por lo tanto
$m\acute{a}x_{|z|\leq1}|z^{2}+4z|=5$
--Juan Daniel Rivera Bautista (discusión) 23:40 21 jun 2015 (CDT)
Ejercicio 28
Supongamos que $f$ es analítica dentro y sobre de la circunferencia C de radio r con el centro en $z_{0}$. Use (1) para obtener
\[ f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\]
Usando (1)
\[
f(z_{0}) = \dfrac{1}{2\pi} \oint_{C} \dfrac{f(z)}{z-z_{0}} dz \]
Como el radio de C es r entonces $|z-z_{0}|= r $ o $z= z_{0} +re^{i\theta}$. Así (1) se convierte en
\[ f(z_{0}) = \dfrac{1}{2\pi} \oint_{C} \dfrac{f(z_{0}+re_{i\theta} ) ire^{i\theta}}{re^{i\theta}} d\theta \]
Así llegamos al teorema del velor medio
\[ f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\] --Esther Sarai (discusión) 21:23 21 jun 2015 (CDT)Esther Sarai
Ejercicio 28, Solución alternativa
Se tiene la formula integral de Cauchy:
donde el problema nos dice que f es analítica , es el centro , y r el redio de la circuferencia C.
Recordemos que la forma exponencial de un numero complejo esta dada de la forma:
lo que nos permite expresar la forma polar de un número complejo distinto de cero.
Para nuestro caso y centro en z subíndice cero, se tiene que:
Entonces despejando “z” se tiene:
Ahora derivamos ambos miembros , uno con respecto a “z” y otrocon respecto a theta en el segundo miembro, y se tiene:
Sustituyendo en la formula integral de Cauchy (1),(2) y (3) se tiene:
Eliminado terminos se tiene:
en este contorno cerrado de la circuferenia nuestro ángulo theta va de 0 a 2 pi, entonces:
Lo cuál esta demostrado y ha este resultado se le conoce como el teorema del valor medio de Gauss,
y muestra que el valor de f en el centro z subíndice cero de la circuferencia es el promedio de todos
los valores de f en la circuferencia de C.
Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 00:28 22 jun 2015 (CDT)