Compleja:Zill-Cap1.2

Ejercicios del capítulo 1, sección 2 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.

---

Sección 1.2

Ejercicio 16

In Problems 15 and 16, determine which of the given two complex numbers is closest to the origin. Which is closest to 1 + i?

traduccion del enunciado:

En los problemas 15 y 16 , determinar cuál de los dos números complejos dados es más cercano al origen. ¿cual es más cercana a 1 + i ?

analisemos cual de los numeros es mas cercano al origen

\[ 16.z1=\frac{1}{2}\text{\textminus}\frac{1}{4}i,z2=\frac{2}{3}+\frac{1}{6}i,z0=0+0i \]

tenemos dos casos a comparar

caso 1 de z1 a z0 \[ dist\left(z1,z0\right)=\sqrt{\left(\frac{1}{2}\right)^{2}+\left(-\frac{1}{4}\right)^{2}}=0.5590 \]

caso 2 de z2 a z0

\[ dist\left(z2,z0\right)=\sqrt{\left(\frac{2}{3}\right)^{2}+\left(\frac{1}{6}\right)^{2}}=0.6871 \]

de estos casos se concluye que el numero mas cercano al origen es \[ z1=\frac{1}{2}\text{\textminus}\frac{1}{4}i \]

analisemos cual de los numeros es mas cercano a 1+1i

\[ 16.z1=\frac{1}{2}\frac{1}{4}i,z2=\frac{2}{3}+\frac{1}{6}i,z3=1+1i \]

caso 1 de z1 a z3

\[ dist\left(z1,z3\right)=\sqrt{\left(\frac{1}{2}-1\right)^{2}+\left(-\frac{1}{4}-1\right)^{2}}=1.34 \]

caso 2 de z2 a z3

\[ dist\left(z2,z3\right)=\sqrt{\left(\frac{2}{3}-1\right)^{2}+\left(\frac{1}{6}-1\right)^{2}}=0.89 \]

de estos casos se concluye que el numero mas cercano al 1+1i es

\[ z2=\frac{2}{3}+\frac{1}{6}i \]

Martin Flores Molina (discusión) 13:08 15 mayo 2015 (CDT)

---

---

Ejercicio 1

Interpreta $z_{1}$ y $z_{2}$ como vectores. Gráfica $z_{1}$, $z_{2}$ e indica cual es la suma y diferencia como vectores

$z_{1} = 4+2i, z_{2} = -2+5i; z_{1}+z_{2}, z_{1}-z_{2}$

• 

  Grafica de $z_{1}+z_{2}$

Nota: Si se desea visualizar la grafia, utilizar Mathematica con el siguiente pseudocodigo:

 Graphics[{
 Thick,
 Arrow[{{0, 0}, {4, 2}}],
 Arrow[{{0, 0}, {-2, 5}}],
 Blue,
 Arrow[{{0, 0}, {2, 7}}],
 Gray, Dashed,
 Arrow[{{0 + 4, 0 + 2}, {2, 7}}],
 Arrow[{{0 - 2, 0 + 5}, {2, 7}}]
 }, Frame -> True]

• 

  Grafica de $z_{1}-z_{2}$

Nota: Si se desea visualizar la grafia, utilizar Mathematica con el siguiente pseudocodigo:

 Graphics[{
 Thick,
 Arrow[{{0, 0}, {4, 2}}],
 Arrow[{{0, 0}, {-2, 5}}],
 Blue,
 Arrow[{{0 - 2, 0 + 5}, {4, 2}}]
 }, Frame -> True]

Para finalizar realizamos las operaciones deseadas.

La suma:

$z_{1}+z_{2} = (4+2i)+(-2+5i) = (4-2)+i(2+5) = 2+7i$

y la diferencia:

$z_{1}-z_{2} = (4+2i)-(-2+5i) = (4+2)+i(2-5) = 6-3i$

Miguel Medina Armendariz (discusión) 12:11 15 mayo 2015 (CDT)

---

Ejercicio 2

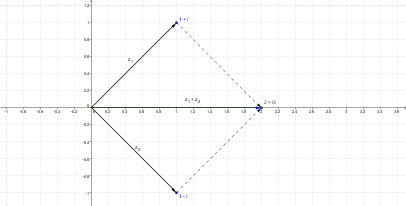
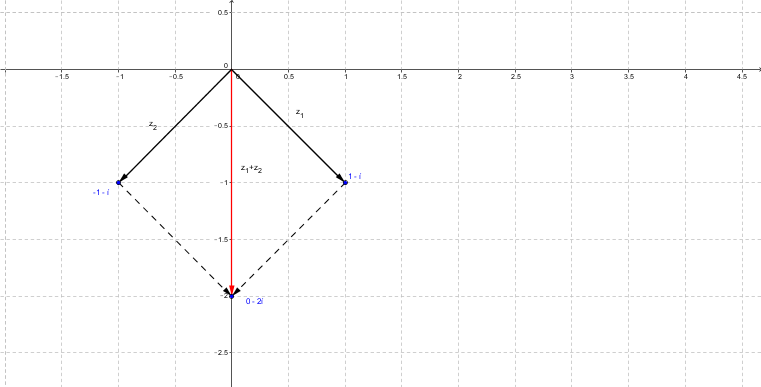
Interpreta $z_{1}$ y $z_{2}$ como vectores. Gráfica $z_{1}$, $z_{2}$ e indica cual es la suma y diferencia como vectores

$z_{1} = 1-i$ , $z_{2} = 1+i$ ; $z_{1}+z_{2}$ , $z_{1}-z_{2}$

La suma:

$z_{1}+z_{2} = (1-i)+(1+i) = (1+1)+(-1+1)i = 2+0i$

La diferencia:

$z_{1}-z_{2} = (1-i)-(1+i) = (1-1)+(-1-1)i = 0-2i$

--Emmanuell Castro Flores (discusión) 22:27 15 mayo 2015 (CDT)

---

Ejercicio 5

Dado que $z_{1}=5-2i$ y $z_{2}=-1-i$, encuentre el vector $z_{3}$ en la misma dirección que $z_{1}+z_{2}$ pero 4 veces más largo

Primeramente debemos calcular la suma $z_{1}+z_{2}$

$z_{1}+z_{2}=(5-2i)+(-1-i)=4-3i$

A continuación multiplicamos por 4 para cuadriplicar el tamaño

$4(z_{1}+z_{2})=4(4-3i)=16-12i$

--Tlacaelel Cruz (discusión) 21:10 12 mayo 2015 (CDT)

---

Ejercicio 7

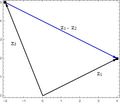
Determinar si los puntos $z_{1}$,$z_{2}$,$z_{3}$ sn los vértices de un triángulo rectángulo.

Tenemos que :

$z_{1}=-2-8i$

$z_{2}=3i$

$z_{3}=-6-5i$

Graficando $z_{1}$,$z_{2}$,$z_{3}$.

IMAGEN

Se observa que se a construido un triángulo rectángulo, con segmentos de rectas A,B,C. Si utilizamos el teorema de Pitágoras encontraremos la hipotensa C. donde

$c={\sqrt {a^{2}+b^{2}}}$

Por tanto es igual al módulo del número complejo Z.

$|z|={\sqrt {a^{2}+b^{2}}}=C$

Por tanto tomamos que :

$\left|{\frac {z_{2}-z_{1}}{z_{3}-z_{1}}}\right|=\left|{\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}\right|$

${\frac {|Z_{2}-Z_{1}|}{|Z_{3}-Z_{1}|}}={\frac {|Z_{1}-Z_{3}|}{|Z_{2}-Z_{3}|}}$

Entonces podemos construir los tres segmentos de rectas :

$A=|z_{1}-z_{2}|$

$B=|z_{3}-z_{1}|=|z_{1}-z_{3}|$

$C=|z_{2}-z_{3}|$

Por lo que tenemos una interpretación geométrica de módulos de los complejos $z_{1}$,$z_{2}$,$z_{3}$,que corresponden a las distancias entre los puntos.

Entonces A,B,C, forman los segmentos de los vértices $z_{1}$, $z_{2}$, $z_{3}$, formando un triángulo rectángulo.

--Samantha Martínez (Usuario discusión:Samantha Martínez) 23:13 15 mayo 2015 (CDT)

---

Ejercicio 9

Encuentra el módulo de:

9.-$(1-i)^{2}$

desarrollando el cuadrado se tiene :

$(1-i)^{2}=1-2i+i^{2}=1-2i-1=-2i$

Entonces:

$|-2i|=\sqrt{4}=2$

Así:

$|(1-i)^{2}|=2$

Además:

$|(1-i)|^{2}=(\sqrt{1+1})^{2}=(\sqrt{2})^{2}=2$

Elaborado por industrias--Francisco Medina Albino (discusión) 18:01 14 mayo 2015 (CDT)

---

Ejercicio 10

Encuentra el módulo de $i(2-i)-4(1+(\frac{1}{4})i)$:

para solucionar este problema debemos de realizar primera mete el producto para obtener:

$i(2-i)-4(1+{\frac {1}{4}})=(2i+1)-(4+i)$

después se realizaran la sumas y la restas correspondientes obteniendo:

$(2i+1)-(4+i)=-3+i$

así para sacar el valor absoluto de este numero bastara con sumar los cuadrados de la parte real y la parte que a acompaña ala unidad imaginaria y a esto sacarle la raíz cuadrada así tendremos:

$|-3+i|={\sqrt {(-3)^{2}+(1)^{2}}}={\sqrt {10}}$

finalmente:

$|i(2-i)-4(1+({\frac {1}{4}})i)|={\sqrt {10}}$

Realizado por --Cristian Alfredo Ruiz Castro (discusión) 19:49 14 mayo 2015 (CDT)

Ejercicio 11

Encontrar el módulo de: $\frac{2i}{3-4i}$

Primero se expresa el número de la forma $a+bi$ luego entonces:

Se multiplica por el conjugado

\[ \frac{2i}{3-4i}=(\frac{2i}{3-4i})(\frac{3+4i}{3+4i})=\frac{-8+6i}{9+16}=\frac{-8+6i}{25}=-\frac{8}{25}+\frac{6}{25}i \]

Ahora, esto implica que:

\[ |-\frac{8}{25}+\frac{6}{25}i|=\sqrt{\frac{64}{625}+\frac{36}{625}}=\sqrt{\frac{100}{625}}=\frac{10}{25} \]

Por tanto: $|\frac{2i}{3-4i}|=\frac{10}{25}$

Resuelto por --A. Martín R. Rabelo (discusión) 21:54 12 mayo 2015 (CDT)

---

Ejercicio 12

Encuentra el modulo de $\frac{1-2i}{1+i}+\frac{2-i}{1-i}$

Sea $z=\frac{1-2i}{1+i}+\frac{2-i}{1-i}$ lo reescibo de manera $z=a+ib$, para ello multiplico por su conjugado en cada parte y resuelvo

$z=(\frac{1-2i}{1+i})(\frac{1-i}{1-i})+(\frac{2-i}{1-i})(\frac{1+i}{1+i})=\frac{3-3i}{2}+\frac{3+i}{2}=\frac{3-3i+3+i}{2}=\frac{6-2i}{2}=3-i$

Ahora solo falta obtener el modulo

$|z|=|3-i|=\sqrt{9+1}=\sqrt{10}$

Por lo tanto

$|z|=|\frac{1-2i}{1+i}+\frac{2-i}{1-i}|=\sqrt{10}$

--Fernando Vazquez V. (discusión) 01:32 15 mayo 2015 (CDT)

---

Ejercicio 13

Dado z = x + iy. Expresar la cantidad en terminos de x e y.

$|z-1-3i|^{2}$

sustituimos z por la expresión que se nos dio

$|(x+yi)-1-3i|^{2}$

agrupamos las partes reales y las partes imaginarias y factorizamos i

$|(-1+x)+(-3i+yi)|^{2}$; $|(-1+x)+(-3+y)i|^{2}$

podemos hacer un cambio de variable para ilustrar de una forma óptima

$\alpha=-1+x$ y$\beta=-3+y$

$|\alpha+\beta i|^{2}$

sabemos que $|z|^{2}=\alpha^{2+}\beta^{2}$, donde $z=\alpha+\beta i$

sustituimos, desarrollamos y simplificamos

$(1+2x+x^{2})+(9-6y+y^{2})=x^{2}+y^{2}+2x-6y+10$

--Juan Daniel Rivera Bautista (discusión) 14:23 15 mayo 2015 (CDT)

Nota:

Si $\alpha = 1-x$ entonces $\alpha ^2=1+2(-x)+x^2=1-2x+x^2$. El resultado queda $|z|^2=x^{2}+y^{2}-2x-6y+10$.

Oscar Javier Gutierrez Varela (discusión) 21:35 15 mayo 2015 (CDT)

---

Ejercicio 14

Expresa $|z+5z*|$ en terminos de $x$ y $y$ si $z=x+iy$ Para poder obtener el modulo de la expresión es necesario determinar a $z$ y $z*$

$z=x+iy$

$z*=x-iy$

Se multiplica $z*$ por 5 y se realiza la suma de los numero complejos

$(x+iy)+(5x-5y)=6x-4iy$

Ahoratenemos un nuevo numero complejo $z_1$ y es a este al que se le sacara el modulo $|z_{1}|=\sqrt{(z_{1})(z_{1}*)}=\sqrt{(6x-4iy)(6x+4iy)}=\sqrt{(36(z)^2)+(16(y)^2)}$

Angelina Nohemi Mendoza Tavera (discusión) 09:56 15 mayo 2015 (CDT)

---

Ejercicio 15

Determinar cual de los dos números complejos dados es mas cercano al origen.¿Cual es mas cercano a $1+i$?:

$10+8i$ $11-6i$

Solución: Primeramente definimos:

$z_{0}=0+0i$(origen) $z_{1}=10+8i$ $z_{2}=11-6i$ $z'=1+i$

Por lo cual para conocer que número complejo es mas cercano al origen únicamente debemos considerar el modulo de cada uno de los números, por lo cual tenemos:

Error al representar (error de sintaxis): |z_1|= |10+8i|= \sqrt{10² + 8²}=\sqrt{100+64}=\sqrt{164}=2\sqrt{41}\approx{12.8} Error al representar (error de sintaxis): |z_2|= |11-6i|= \sqrt{11² + 6²}=\sqrt{121+36}=\sqrt{157}\approx{12.5}

Por lo anterior tenemos que: $|z_{2}|<|z_{1}|\therefore {z_{1}}$ es mas cercano al origen.

Ahora bien para conocer cual de los dos números es mas cercano a $z'$ procedemos a sacar la diferencia de $z_{1}$ con $z'$ y $z_{2}$ con $z'$.

Con lo cual tenemos:

Error al representar (error de sintaxis): |z_1 - z'|=\sqrt {(10-1)²+(8-1)²}=\sqrt{81+49}=\sqrt{130}\approx{11.4} Error al representar (error de sintaxis): |z_2 - z'|=\sqrt {(11-1)²+(-6-1)²}=\sqrt{100+49}=\sqrt{149}\approx{12.2}

Por lo anterior tenemos que: $|z_{2}-z'|>|z_{1}-z'|\therefore {z_{2}}$ es mas cercano a $z'$ .

--Anahi Limas (discusión) 22:36 14 mayo 2015 (CDT)

---

Ejercicio 16

Determinar cual de los dos números complejos esta más cercano al origen y cual esta más cercano a $1+i$

16.- $\frac{1}{2}-\frac{1}{4}i$, $\frac{2}{3}+\frac{1}{6}i$

Sean , $z_{1}=\frac{1}{2}-\frac{1}{4}i$ , $z_{2}=\frac{2}{3}+\frac{1}{6}i$ , $z_{0}=o+oi$ , $z_{u}=1+i$

Para saber cul esta más cerca del origen solo sacamos el modulo de $z_{1}$ y de $z_{2}$

$\left|z_{1}\right|=\sqrt{\left(\frac{1}{2}\right)^{2}+\left(-\frac{1}{4}\right)^{2}}=\sqrt{\frac{5}{16}}=0.5590$

$\left|z_{2}\right|=\sqrt{\left(\frac{2}{3}\right)^{2}+\left(\frac{1}{6}\right)^{2}}=\sqrt{\frac{17}{36}}=0.6871$

Por lo tanto tenemos que:

$\left|z_{1}\right|<\left|z_{2}\right|$

Ahora para conocer cual número complejo esta más cerca de 1+i hacemos la diferencia de $\left|z_{1}-z_{u}\right|$y de $\left|z_{2}-zu\right|$

$\left|z_{1}-z_{2}\right|=\sqrt{\left(\frac{1}{2}-1\right)^{2}+\left(-\frac{1}{4}-1\right)^{2}}=\sqrt{\frac{29}{16}}=1.3462$

$\left|z_{2}-z_{u}\right|=\sqrt{\left(\frac{2}{3}-1\right)^{2}+\left(\frac{1}{6}-1\right)^{^{2}}}=\sqrt{\frac{29}{16}}=1.3462$

Por lo cual los dos estan a la misma distancia de $z_{u}$Resuelto por: Luis Enrique Martínez Valverde (discusión) 17:51 15 mayo 2015 (CDT)

---

Ejercicio 17

Encuentre $z$ de tal manera que satisfaga la siguiente igualdad $$Re((1+i)z)-1=0....(1)$$ donde $z$ se expresa de la forma $z=(a+bi)$, entonces la igualdad se puede expresar de la siguiente forma $$Re((a+bi)(1+i)=1$$ Desarrollando el producto anterior obtenemos $$a+i(a+b)-b=1$$ Podemos ahora encontrar los valores para $a$ y $b$ con el siguiente sistema de ecuaciones $$a-b=1$$...(2) $$a+b=0$$ Pero ya que solo nos interesa la parte real solo utilizamos la siguiente igualdad $$a-b=1$$ Sustituyendo en la ecuación (1) $$Re(((b+1)+bi)(i+1))=1$$ desarrollando obtenemos: $$Re(b+1+bi+bi+i-b=1)$$ $$Re(1+(2b+1)i)=1$$ Así obtenemos $b$ cuyo valor es $$b=1/2$$ y por lo tanto $$a=\frac{3}{2}$$ Sustituyendo en la igualdad original obtenemos que $$Re((\frac{3}{2} + i\frac{1}{2})(1+i)-1)=0$$

---

Ejercicio 18

In problems 17-26, describe the set of the points z in the complex plane that satisfy the given ecuation.

$[Im (i (i\overline{z})]^2 = 2$

Tenemos que $z = a + ib$ y $\overline{z} = a - ib$

Entonces podemos escribir,

$[Im (i (a - ib)]^2 = 2$

Multiplicando i por el binomio tenemos,

$[Im (ai - bi^2)]^2 = 2$

Recordando que $i^2 = -1$, podemos escribir de manera equivalente,

$[Im (ai + b)]^2 = 2$

Posteriormente tomamos la parte imaginaria del binomio y la elevamos al cuadrado,

$ a^2 = 2 $, por lo que $a = \sqrt{2}$

Tenemos aquí una recta que corta al eje real en $\sqrt{2}$ a un ángulo de $\dfrac{\pi}{2}$.

--Arnold B. Herrera Rubert (discusión) 21:01 15 mayo 2015 (CDT)

---

Ejercicio 19

In Problems 17- 26, describe the set of points $z$ in the complex plane that satisfy the given equation.

19. $\arrowvert z-i\arrowvert=\arrowvert a-1\arrowvert$

Considerando $z=a+ib$ tenemos lo siguiente

\[ \arrowvert a+i(b-1\}\arrowvert=\arrowvert(a-1)+ib\arrowvert \]

\[ \sqrt{a^{2}+(b-1)^{2}}=\sqrt{(a-1)^{2}+b^{2}} \]

Elevando al cuadrado ambos terminos y desallorando

\[ a^{2}+b^{2}-2b+1=a^{2}-2a+1+b^{2} \]

De la ecuacion anterior tenemos que $b=a$, en terminos geometricos tendriamos una recta que pasa por el origen y que forma un angulo de $\pi/4$ conel eje real, haciendo una analogia con una funcion en los reales seria $f(x)=x$.

Jose Emmanuel Flores Calderón (discusión) 20:45 14 mayo 2015 (CDT)

---

Ejercicio 21

Describe the set of points Z in the complex plane that satisfy the given equation $$Im (z^{2})= 2$$

Definimos a $z = x +i y$ y tenemos:

$$Im ((x+ i y )^{2})= 2$$

$$2xy= 2 $$

$$xy= 1$$

El conjunto de puntos se describe como una hipérbola

--Esther Sarai (discusión) 22:29 14 mayo 2015 (CDT)Esther Sarai

Ejercicio 23

En los problemas 17-26, describa el conjunto de puntos z en el plano complejo que satisfacen la ecuación dada.

23.- $\left|z-1\right|=1$

Si $z=x+iy$, entonces :

$\left|z-1\right|=\left|(x-1)+iy\right|=\sqrt{(x-1)^{2}+y^{2}}=1$

$x^{2}-2x+1+y^{2}=1$ $y^{2}=-x^{2}+2x$ $y=\pm\sqrt{-x^{2}+2x}$

Por lo tanto el conjunto de puntos buscado se puede representar por medio de la función:

$z=x\pm i\sqrt{-x^{2}+2x}$, $x\epsilon\mathbb{R}$ Resuelto por :

Alejandro Juárez Toribio (discusión) 18:18 13 mayo 2015 (CDT)

Nota adicional: Creo que seria mas enriquecedor si especificaras que el conjunto de puntos que satisfacen la condición forman una circunferencia, se ve claramente desde la tercer ecuación, considero importante dar una descripción geométrica un poco mas rigurosa. Y te están pidiendo un conjunto de puntos que satisfagan la condición dada, no un nuevo numero complejo. Jose Emmanuel Flores Calderón (discusión) 21:10 14 mayo 2015 (CDT)

---

Ejercicios 29

29) Encuentra el límite superior para el módulo $3z^{2}+2z+1;\mid z\mid \leq 1$.

Solución

Se tiene que $3z^{2}+2z+1\leq M$, entonces

$\mid 3z^{2}+2z+1\mid \leq \mid \mid 3z^{2}\mid +\mid 2z+1\mid \mid$

$\mid 3z^{2}+2z+1\mid \leq \mid 3z^{2}\mid +\mid 2z+1\mid ;\mid 2z\mid +\mid 1\mid \geq 0$

$\mid 3z^{2}+2z+1\mid \leq \mid 3z^{2}\mid +(\mid 2z\mid +\mid 1\mid ),$

Sustituyendo y simplificando

$\mid 3z^{2}+2z+1\mid \leq \mid 3(1)+2(1)+1\mid$

$\mid 3z^{2}+2z+1\mid \leq \mid 6\mid$

Entonces $M=6$ y $\mid z\mid \leq 1$

$\therefore \mid 3z^{2}+2z+1\mid \leq 6$

Elaborado por --Ricardo Garcia Hernandez (discusión) 22:21 15 mayo 2015 (CDT)

---

Ejercicio 30

30) Encontrar el límite superior para el recíproco del módulo de $z^{4}-5z+6;\mid z\mid =2$.

Solución

Se tiene $z^{4}-5z+6=\left(z^{2}-3\right)\left(z^{2}-2\right),$

Entonces

${\frac {1}{\mid \left(z^{2}-3\right)\left(z^{2}-2\right)\mid }}\leq M$

Usando la propiedad $\mid z_{1}z_{2}\mid =\mid z_{1}\mid \cdot \mid z_{2}\mid$ y $\mid \mid z_{1}\mid -\mid z_{2}\mid \mid \leq \mid z_{1}-z_{2}\mid$

Error al representar (función desconocida «\cdotp»): \mid\left(z^{2}-3\right)\left(z^{2}-2\right)\mid=\mid z^{2}-3\mid\cdotp\mid z^{2}-2\mid,

Error al representar (función desconocida «\cdotp»): \mid z^{2}-3\mid\cdotp\mid z^{2}-2\mid\geq\mid\mid z^{2}\mid-3\mid\cdotp\mid\mid z^{2}\mid-2\mid,

sustituyendo y simplificando se tiene

Error al representar (función desconocida «\cdotp»): \mid z^{2}-3\mid\cdotp\mid z^{2}-2\mid\geq\mid4-3\mid\cdotp\mid4-2\mid,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \mid z^{2}-3\mid\cdotp\mid z^{2}-2\mid\geq2,

entonces si $M={\frac {1}{2}}$ y $z=2$

$\therefore {\frac {1}{\mid \left(z^{2}-3\right)\left(z^{2}-2\right)\mid }}\leq {\frac {1}{2}}.$

Elaborado por --Ricardo Garcia Hernandez (discusión) 20:36 15 mayo 2015 (CDT)

---

Ejercicios 31 y 32

31.- In Problem 31 and 32, find a number z than satisfies the given equatión.

31. $\bigl|z\bigr|-z=2+i$ $\qquad\qquad\qquad$32.$\bigl|z\bigr|^{2}+1+12i=6z$

Solución

Sea $z=a+ib$, el modulo de $z$ se define como:

$\bigl|z\bigr|=\sqrt{a^{2}+b^{2}}$

Además sean $z_{1}=a+ib$ y $z_{2}=a_{2}+ib_{2}$, tenemos que $z_{1}=z_{2}$sólo cuando $a=a_{2}$y $b=b_{2}$, bajo esto tenemos:

31.

$\bigl|z\bigr|-z=2+i$

$\sqrt{a^{2}+b^{2}}-(a+ib)=2+i$

$\left(\sqrt{a^{2}+b^{2}}-a\right)-ib=2+i$

Por lo que

$b=-1$

Ahora

$\sqrt{a^{2}+1}-a=2$

Resolviendo para $a$

$a^{2}+1=4+4a+a^{2}$

$4a+3=0$

$a=-\frac{3}{4}$

Por lo tanto la solución de la ecuación es:

$z=-\frac{3}{4}-i$

32.

$\bigl|z\bigr|^{2}+1+12i=6z$

$a^{2}+b^{2}+1+12i=6z$

$\left(a^{2}+b^{2}+1\right)+12i=6(a+ib)$

Igualando parte real e imaginaria se llega a:

$b=2$

y

$a^{2}+2^{2}+1=6a$

$a^{2}-6a+5=0$

Se tienen las soluciónes

$a=5$

y

$a=1$

Por lo que hay dos soluciónes a la ecuación planteada, estas son:

$z_{1}=5+2i$

$z_{2}=1+2i$

Ejercicio resuelto por: --Luis Santos (discusión) 16:15 12 mayo 2015 (CDT)

---

Ejercicio 36

¿Cuál es el único número complejo con módulo 0?

Definimos a $z\epsilon C$ en donde $z=a+bi$ con $a,b\epsilon R$, donde no sabemos cuales son los valores de a y b, a continuación obtenemos la magnitud de z.

$|z|={\sqrt {a^{2}+b^{2}}}$

Como buscamos un número cuya magnitud sea cero $|z|=0$

Por lo que, igualando las expresiones para en encontrar a y b.

${\sqrt {a^{2}+b^{2}}}=0$

Desarrollando

$a^{2}+b^{2}=0^{2}$

Donde podemos ver que

$a^{2}=-b^{2}$

Donde el único número real que cumple esta condición última, es el cero.

$a=b=0$

comprobando

$|z|={\sqrt {a^{2}+b^{2}}}={\sqrt {0^{2}+0^{2}}}=0$

--Pablo (discusión) 01:14 15 mayo 2015 (CDT)

---

Ejercicio 37

Bajo que circunstancias $|z_1+z_2|=|z_1|+|z_2|$.

Si $z_1=a_1+b_1i$ y $z_2=a_2+b_2i$, sus respectivas magnitudes son:

$|z_1|=\sqrt{a_1^2+b_1^2}$

$|z_2|=\sqrt{a_2^2+b_2^2}$

Su suma

$|z_1|+|z_2|=\sqrt{a_1^2+b_1^2}+\sqrt{a_2^2+b_2^2}$

Por otro lado, sumando los numeros:

$z_1+z_2=(a_1+a_2)+(b_1+b_2)i$

$|z_1+z_2|=\sqrt{(a_1+a_2)^2+(b_1+b_2)^2}=\sqrt{a_1^2+2a_1a_2+a_2^2+b_1^2+2b_1b_2+b_2^2}$

$|z_1+z_2|=\sqrt{a_1^2+a_2^2+b_1^2+b_2^2+2(a_1a_2+b_1b_2)}$

Igualando expresiones;

$\sqrt{a_1^2+b_1^2}+\sqrt{a_2^2+b_2^2}=\sqrt{a_1^2+a_2^2+b_1^2+b_2^2+2(a_1a_2+b_1b_2)}$

Por lo que para que la expresión anterior se satisfaga, se tiene que cumplir alguna de las siguientes condiciones:

$a_1=a_2=b_1=b_2=0$

$a_1 \neq 0, a_2=b_1=b_2=0$

O cualquier combinación como la anterior.

Oscar Javier Gutierrez Varela 22:57 12 mayo 2015 (CDT)

---

Ejercicio 44

Supongamos $z_1\neq z_2$. Interpretar: $Re(z_1{\bar z}_2)=0 $ geométricamente en términos de los vectores $z_1$ y $z_2$\\ Solución:\\ Sean: $z_1=a_1+ib_1$ y $z_2=a_2+ib_2$ números complejos. Entonces $z_1{\bar z}_2=(a_1+ib_1)(a_2-ib_2)=(a_1a_2+b_1b_2)+i(a_2b_1-a_1b_2)$. Con $Re(z_1{\bar z}_2)=a_1a_2+b_1b_2$. En plano complejo $z_1$ tiene coordenadas $(a_1,b_1)$ y $z_2$ tiene coordenadas $(a_2,b_2)$. Entonces $a_1a_2+b_1b_2=(a_1,b_1) \cdot (a_2,b_2)$ que lo anterior igualado a cero quiere decir que los vectores $z_1$ y $z_2$ son perpendiculares. Alan Daniel Barrón Posadas (discusión) 23:59 15 mayo 2015 (CDT)

---

Ejercicio 47

Demostrar:

a) |z|=|−z|

Soponer que  z=a+bi  y  -z=-(a+bi)

Y sabemos la definicion de modulo:

$|z|=\sqrt{a^2+b^2}$

Entonces

$|z|=\sqrt{a^2+b^2}$

Ademas sabemos que todo número negativo elevado al cuadrado da un número positivo; entonces:

$|-z|=\sqrt{a^2+b^2}$

Por lo tanto:

|z|=|-z|


b)|z|=|z*|

Suponer que  z=a+bi  y  z*=a-bi. Donde z* es el conjugado de z. Tomando en cuenta la definicion de modulo, tenemos:

$|z|=\sqrt{a^2+b^2}$

Por la razon anterior, no es necesario poner el signo menos en la siguiente igualdad.

$|z*|=\sqrt{a^2+b^2}$

Por lo tanto:

|z|=|z*|

Nancy Martínez Durán (discusión) 19:38 15 mayo 2015 (CDT)

---