Ondas: probs c7
Problemas capítulo 3y 7 Óptica Hecht, Teoría electromagnetica, fotones y luz Superposición de ondas
Ejercicios resueltos acerca de la Superposición de ondas. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.
Algunas ediciones del Hetch, tienen distintas numeraciones para problemas idénticos.
1ra Edición
Problema 7.9(Hecht 1ra ed.)
Imagine que golpeamos dos diapasones, uno con frecuencia de $340Hz$ y el otro de $342Hz$. ¿Qué oiremos?
Solución:
En este ejemplo se da el fenómeno del Batido, en el caso de que la frecuencia de ambas ondas no es igual ($\nu_1,\nu_2$), pero si son valores muy cercanos entre sí, la onda resultante es una onda modulada en amplitud por la llamada "frecuencia de batido" cuyo valor corresponde a $\nu_{\mbox{batido}}=\Delta \nu= | \nu_1 -\nu_2|$, la frecuencia de esta onda modulada corresponde a la media de las frecuencias que interfieren.
Nuestro sistema auditivo no es capaz de percibir separadamente las dos frecuencias presentes, sino que se percibe una frecuencia única promedio $(\nu_1 + \nu_2) / 2$, pero que cambia en amplitud a una frecuencia de $(\nu_2 - \nu_1) / 2$.
Es decir, si superponemos dos ondas senoidales de $340 Hz$ y $342 Hz$, nuestro sistema auditivo percibirá un único sonido cuya altura corresponde a una onda de $341 Hz$ y cuya amplitud varía con una frecuencia de $1 Hz$ (es decir, una veces por segundo) con $\nu_{\mbox{batido}}=\Delta \nu= | \nu_1 -\nu_2|=| 342Hz - 340Hz|=2Hz$ .
Realizado por: Luis Martínez (discusión) 13:18 28 mar 2015 (CDT)
Forma alternativa aunque incorrecto.
Imagine que golpeamos dos diapasones; uno con una frecuencia de 340Hz, el otro con una frecuencia de 342Hz.
¿Qué es lo que escucharemos?
SOLUCIÓN
Consideremos la perturbación derivada de la combinación de las ondas:
\[ E_{1}=E_{01}cos(k_{1}x-\omega_{1}t) \]
y también,
\[ E_{2}=E_{01}cos(k_{2}x-\omega_{2}t) \]
Las cuales tienen amplitudes iguales y un desfasamiento nulo. La onda
neta:
\[ E=E_{01}[cos(k_{1}x-\omega_{1}t)+cos(k_{2}x-\omega_{2}t)]\,\,\,\,\,\,\,\,\,\,\,\,(a) \]
Usando la identidad siguiente:
\[ cos\alpha+cos\beta=2cos\frac{1}{2}(\alpha+\beta)cos\frac{1}{2}(\alpha-\beta) \]
se puede reformular la ec.(a) de la siguiente manera:
\[ E=2E_{01}cos\frac{1}{2}[(k_{1}+k_{2})x-(\omega_{1}+\omega_{2})t]\times cos\frac{1}{2}[(k_{1}-k_{2})x-(\omega_{1}-\omega_{2})t] \]
De aquí se define que las cantidades $\bar{\omega}$ y $\bar{k}$
son el promedio de la frecuencia angular y número de propagación respectivamente
así como $\omega_{m}$ y $k_{m}$ son la modulación de frecuencia
y el número de propagación.
Tenemos entonces,
\[ \bar{\omega}\equiv\frac{1}{2}(\omega_{1}+\omega_{2})\,\,\,,\,\,\,\bar{k}\equiv\frac{1}{2}(k_{1}+k_{2}) \]
y también,
\[ \omega_{m}\equiv\frac{1}{2}(\omega_{1}-\omega_{2})\,\,\,,\,\,\, k_{m}\equiv\frac{1}{2}(k_{1}-k_{2}) \]
De aquí entonces obtenemos la frecuencia promedio mediante la relación
$\upsilon=\frac{\omega}{2\pi}$
Entonces $\bar{\upsilon}=\frac{\bar{\omega}}{2\pi}$, y ahora sólo substituimos los datos
\[ \bar{\omega}\equiv\frac{1}{2}(340Hz+342Hz)=341Hz \]
Que es precisamente lo que se escuchará.
Conclusión
Y la frecuencia del batido, o frecuencia de la pulsación $\omega_{m}$, o sea, la frecuencia con que varía la amplitud, lo da la semidiferencia entre las frecuencias originales:
\[ \omega_{m}\equiv\frac{1}{2}(342Hz-340Hz)=1Hz \]
Realizado por: A. Martín R. Rabelo (discusión) 16:21 30 mar 2015 (CDT)
3ra Edición en español
Problema 7.1 3ra Edición en español
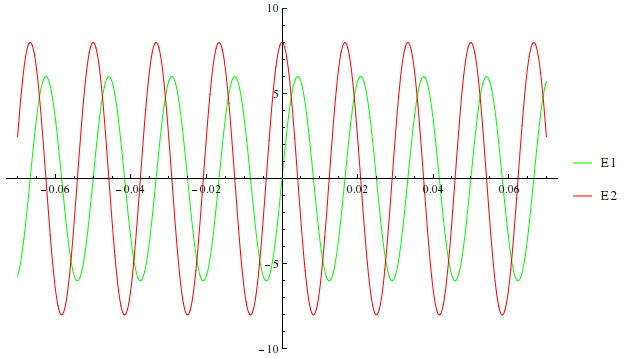
Determine la resultante de la superposición de las ondas paralelas $E_{1}=E_{01}\sin(\omega t+\epsilon_{1})$ y $E_{2}=E_{02}\sin(\omega t+\epsilon_{2})$ cuando $\omega=120\pi$, $E_{01}=6$, $E_{02}=8$, $\epsilon_{1}=0$ y $\epsilon_{2}=\frac{\pi}{2}$. Represente gráficamente cada función y la resultante.
Procedimiento
En la imagen se muestra la gráfica de las primeras dos funciones dadas.
Ahora bien sumemos ambas ondas, dado por
\[
E=E_{1}+E_{2}
\]
donde $E_{1}$ y $E_{2}$ están dadas por:
\[
E_{1}=E_{01}\sin(\omega t+\epsilon_{1})=E_{01}(\sin\omega t\cos\epsilon_{1}+\cos\omega t\sin\epsilon_{1})
\]
\[
E_{2}=E_{02}\sin(\omega t+\epsilon_{2})=E_{02}(\sin\omega t\cos\epsilon_{2}+\cos\omega t\sin\epsilon_{2})
\]
Al sumar y factorizar se obtiene
\[
E=(E_{01}\cos\epsilon_{1}+E_{02}\cos\epsilon_{2})\sin\omega t+(E_{01}\sin\epsilon_{1}+E_{02}\sin\epsilon_{2})\cos\omega t
\]
Ya que $\epsilon_{1}=0$ , $\epsilon_{2}=\frac{\pi}{2}$ , $\omega=120\pi$,
$E_{01}=6$ y $E_{02}=8$ nos queda
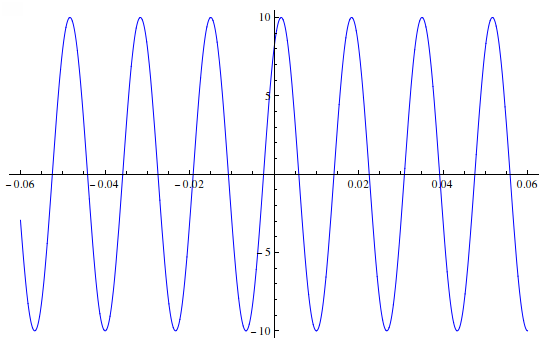
\[ E=6\sin120\pi t+8\cos120\pi t \]
La suma de ambas ondas se muestra gráficamente.
Realizado por: Luis Miguel Sánchez Mtz. (discusión) 17:22 28 mar 2014 (UTC)
Problema 7.2 3ra Edición en Español
Considerando la sección 7.1, suponga que empezamos el análisis con el fin de calcular $E = E_1 + E_2$ con dos funciones coseno $E_1=E_{01} \cos(\omega t + \alpha_1)$ y $E_2 E_{02} = \cos(\omega t + \alpha_2)$. Para facilitar algo la tarea, sea $E_{01} = E_{02}$ y $\alpha_1 = 0$. Sume las dos ondas algebraicamente y utilice la conocida identidad trigonométrica $\cos \theta + cos \phi = 2 \cos\left[1/2 (\theta + \phi)\right] \cos\left[1/2 (\theta - \phi)\right]$ para demostrar que $E = E_0 \cos(\omega t + \alpha)$, donde $E_0 = 2 E_{01} \cos(\alpha_2 / 2)$ y $\alpha = \alpha_2 / 2$. Ahora demuestre que estos mismos resultados se deducen de las ecuaciones 7.9 y 7.10.
Procedimiento
Comencemos desarrollando la suma algebraica de las dos ondas:
$ E = E_1 + E_2 = E_{01} \cos(\omega t + \alpha_1) + E_{02} \cos(\omega t + \alpha_2) $
y sabemos que $E_{01} = E_{02}$, además $\alpha_1 = 0$, por lo que, sustituyendo:
$ E = E_{01} \cos(\omega t + 0) + E_{01} \cos(\omega t + \alpha_2) = E_{01} \left[ \cos(\omega t) + \cos(\omega t + \alpha_2) \right] $
Y si definimos $\theta \equiv \omega t$ y $\phi \equiv \omega t + \alpha_2$, tenemos:
$ E = E_{01} \left[ \cos(\theta) + \cos(\phi) \right] $
y utilizando la identidad trigonométrica $\cos \theta + cos \phi = 2 \cos\left[1/2 (\theta + \phi)\right] \cos\left[1/2 (\theta - \phi)\right]$:
$ E = E_{01} \left[ 2 \cos\left[1/2 (\theta + \phi)\right] \cos\left[1/2 (\theta - \phi)\right] \right] $
y sustituyendo los valores de $\theta$ y $\phi$:
$ E = E_{01} \left\{ 2 \cos\left[1/2 (\omega t + \omega t + \alpha_2)\right] \cos\left[1/2 (\omega t - \omega t + \alpha_2)\right] \right\} \\ \Rightarrow E = E_{01} \left\{ 2 \cos\left[\dfrac{2 \omega t + \alpha_2}{2}\right] \cos\left[ \dfrac{\alpha_2}{2} \right] \right\} = E_{01} \left\{ 2 \cos\left[\omega t + \dfrac{\alpha_2}{2}\right] \cos\left[ \dfrac{\alpha_2}{2} \right] \right\} $
y definiendo $\alpha \equiv \alpha_2/2$:
![E = E_{01} \left[ 2 \cos\left(\omega t + \alpha \right) \cos\left( \alpha \right) \right]
= 2 E_{01} \cos(\alpha) \cos(\omega t + \alpha)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6cef0ae60a90f967a0d31a0ffb38af60e13a6259)
y como $E_0 = 2 E_{01} \cos(\alpha_2 / 2) = 2 E_{01} \cos(\alpha)$, entonces:
que es lo que queríamos mostrar.
Ahora, recordemos las ecuaciones (7.9) y (7.10):
$ E_0^2 = E_{01}^2 + E_{02}^2 + 2 E_{01} E_{02} \cos(\alpha_2 - \alpha_1) \hspace{20pt} \ldots \hspace{20pt} (7.9) \\ \tan(\alpha) = \dfrac{E_{01} \sin \alpha_1 + E_{02} \sin \alpha_2}{E_{01} \cos \alpha_1 + E_{02} \cos \alpha_2} \hspace{20pt} \ldots \hspace{20pt} (7.10) $
Tomando ahora la ecuación (7.10) y sustituyendo $\alpha_1 = 0$, tenemos que:
luego, como $E_{01} = E_{02}$:
y tenemos tres identidades trigonométricas importantes:
$ \sin \tfrac{\alpha_2}{2} = \sqrt{\frac{1 - \cos \alpha_2}{2}} \Rightarrow \sqrt{2} \sin \tfrac{\alpha_2}{2} = \sqrt{1 - \cos \alpha_2} \\ $
$ \cos \tfrac{\alpha_2}{2} = \sqrt{\frac{1 + \cos \alpha_2}{2}} \Rightarrow \sqrt{2} \cos \tfrac{\alpha_2}{2} = \sqrt{1 + \cos \alpha_2} \\ $
$ \sin^2 \alpha_2 + \cos^2 \alpha_2 = 1 \Rightarrow \sin \alpha_2 = \sqrt{1-\cos^2 \alpha_2} $
Por lo que siguiendo con el desarrollo de $\tan(\alpha)$:
$ \tan(\alpha) = \dfrac{\sin \alpha_2}{1 + \cos \alpha_2} = \dfrac{\sqrt{1-\cos^2 \alpha_2}}{1 + \cos \alpha_2} = \dfrac{\sqrt{(1-\cos\alpha_2) (1+\cos \alpha_2)}}{1 + \cos \alpha_2} \\ \Rightarrow \tan(\alpha) = \dfrac{\sqrt{1-\cos\alpha_2}}{\sqrt{1 + \cos \alpha_2}} = \dfrac{\sqrt{2} \sin(\alpha_2 / 2)}{\sqrt{2} \cos(\alpha_2 / 2)} = \tan(\alpha_2 / 2) \\ \Rightarrow \tan(\alpha) = \tan(\alpha_2 / 2) \\ \therefore \alpha = \alpha_2/2 $
Entonces, hemos llegado a uno de los resultados que se nos piden $\alpha = \alpha_2/2$. Tomemos ahora la ecuación (7.9) y sustituyamos $E_{01} = E_{02}$ y $\alpha_1 = 0$:
$ E_0^2 = E_{01}^2 + E_{01}^2 + 2 E_{01} E_{01} \cos(\alpha_2 - 0) = 2 E_{01}^2 + 2 E_{01}^2 \cos(\alpha_2) \\ \Rightarrow E_0^2 = 2 E_{01}^2 \left[ 1 + \cos(\alpha_2) \right] = 2 E_{01}^2 \left[ 2 \cos^2(\alpha_2 /2) \right]\\ \Rightarrow E_0 = \sqrt{4 E_{01}^2 \cos^2(\alpha_2 /2)} = 2 E_{01} \cos(\alpha_2 /2 ) \\ \therefore E_0 = 2 E_{01} \cos(\alpha_2 /2 ) $
con lo que hemos obtenido el segundo resultado deseado $E_0 = 2 E_{01} \cos(\alpha_2 /2 )$.
Conclusión
Entonces, de las ecuaciones (7.9) y (7.10) concluimos que:
$ E_0 = 2 E_{01} \cos(\alpha_2 /2 ) \\ \alpha = \alpha_2 /2 $
Realizado por: Ivan de Jesús Pompa García (discusión) 00:22 27 mar 2015 (CDT) Mfgwi (discusión) 09:08 8 oct 2020 (CDT) Mfgwi (discusión) 09:10 8 oct 2020 (CDT)
Problema 7.3 3ra Edición en español
Muestre que cuando las dos ondas de la ecuación. (7.5) están en fase, la amplitud resultante cuadrado es de un máximo igual a $ (E_ {01} + E_ {02}) ^ 2 $, y cuando están fuera de fase es un mínimo equivalente a $ (E_ {01} - E_ {02}) ^ 2 $
Solución:
De la ecuación 7.5 sabemos que
$E_{1}=E_{01}{Sen(\omega t+\beta_{1})}$
y
$E_{2}=E_{02}{Sen(\omega t+\beta_{2})}$
Para cuando están en fase:
$\beta_{1}=\beta_{2}{Cos(\beta_{2}-\beta_{1})}={Cos(0)}=1$
Usando (7.9)
$E_{0}^2=E_{01}^2+E_{02}^2+2E_{01}E_{02}{Cos(\beta_{2}-\beta_{1})}$
$E_{0}^2=E_{01}^2+E_{02}^2+2E_{01}E_{02}=(E_{01}+E_{02})^2$
Para cuando están fuera de fase:
$\beta_{1}-\beta_{2}=\pi$
$Cos(\beta_{2}-\beta_{1})=Cos{\pi}=-1$
Y por (7.9)
Conclusión
$E_{0}^2=E_{01}^2+E_{02}^2-2E_{01}E_{02}=(E_{01}-E_{02})^2$
Ejercicio resuelto por: Luis Velázquez (discusión) 20:57 27 mar 2015 (CDT)
Problema 7.4 3ra Edición en español
Demuestre que la longitud de camino óptico, definido como la suma de los productos de varios índices multiplicados por los espesores de los medios atravesados por un haz, es decir, ${\displaystyle \sum n_{i}x_{i}}$, equivale a la longitud del recorrido en el vacío que el haz tardaría el mismo tiempo en atravesar.
Solución:
Sea la longitud de camino óptico $L.C.O.=\sum n_{i}x_{i}$, si sabemos que el índice de refracción es $n=\frac{c}{v}$, con c la velocidad de la luz en el vacío y v la velocidad de la luz en un medio, podemos sustituir en nuestra primera ecuación.
$L.C.O.=\sum\frac{c}{v_{i}}x_{i}$
$L.C.O.=\sum\frac{ct_{i}}{x_{i}}x_{i}$
$L.C.O.=\sum ct_{i}$
que es justamente la longitud del recorrido en el vacío que la luz tardaría en ese tiempo en atravesar.
Realizado por: Edgar Ortega Roano (discusión) 12:36 25 mar 2014 (CDT)
Problema 7.5 3ra Edición en español
Responda lo siguiente:
Inciso a
(a) Cuántas longitudes de onda de luz $\lambda_{0}=500nm$ abarcarán una separación de 1 m en el vacío?
$\frac{1m}{500\times10^{-9}m}=0.2\times10^{7}=2,000,000$ ondas.
Inciso b
(b) Cómo las ondas que abarcan la brecha cuando una placa de vidrio de 5 cm piensa $\left(n=1.5\right)$ se inserta en el camino ?
En el vidrio
\[ 0.05/\lambda_{0}/n=0.05(1.5)/500nm=1.5\times10^{5} \]
En el aire
\[ 0.95/\lambda_{0}=0.19\times10^{7} \]
en total $2,050,000$ ondas.
Inciso c
(c) Determinar OPD entre las dos situaciones
Solución
\[ OPD=\left[\left(1.5\right)\left(0.05\right)+\left(1\right)\left(0.95\right)\right]-\left(1\right)\left(1\right) \]
\[
OPD=1.025-1.000=0.025m
\]
(d) Verificar que una corresponde a la diferencia entre las soluciones
de ( a) y ( b ) anteriores.
$\frac{\varLambda}{\lambda_{0}}=0.025/500\times10^{-9}m$ ondas.
Resuelto por: Rosario Maya (discusión) 04:02 30 mar 2015 (CDT)
Problema 7.6 3ra Edición en español
Determine la diferencia de camino óptico para las dos ondas A y B cuyas longitudes de onda en el vacío, ilustradas en la figura P.7.6, son ambas de 500 nm; el tanque de vidrio ($n=1.52$) se llena con agua ($n=1.33$). Si las ondas comienzan en fase y todos los números anteriores son exactos, encuentre su diferencia de fase relativa en la línea de meta.
Procedimiento
Tenemos que la longitud de camino óptico para cada onda (A y B) es:
\[ LCO_{B}=(1)_{aire}(100cm)=1m \]
\[
LCO_{A}=(1)_{aire}(89cm)+(1.52)_{vidrio}(2)(0.5cm)+(1.33)_{agua}(10cm)=103.8cm=1.038m
\]
Restando los caminos ópticos tendremos que:
\[ \Lambda=LCO_{A}-LCO_{B}=1.038m-1m=0.038m \]
Para hallar la diferencia de fase relativa tendremos que:
\[ \delta=k_{0}\Lambda=\left(\frac{2\pi}{\lambda_{0}}\right)\Lambda=\frac{2\pi\left(3.82x10^{-3}m\right)}{5x10^{-9}m}=7.64x10^{6}\pi \]
por lo cual, la diferencia de fase es:
\[ \delta=7.64x10^{6}\pi \]
Realizado por: Cesar Ivan Avila Vasquez 22:21 26 Marzo 2014
Forma alternativa
Determine la diferencia de camino óptico para las dos ondas Ay B cuyas longitudes de onda en el vacío,
son ambas de 500 nm
el tanque de vidrio ($n=1.52$) se llena con agua ($n=1.33$).
Si las ondas comienzan en fase y todos los números anteriores son exactos, encuentre su diferencia de fase relativa en
la línea de meta.
los caminos ópticos son diferentes para las dos ondas la onda B es mas rápida ya que no atraviesa nada al pasar al lado del estante de vidrio pero para la onda A es diferente ya que atraviesa dos medios el vidrio y el agua entonces en un poco mas lento
la ecuación es de la sig manera
\[ onda_{A-B}=(n)_{aire,A}(X)_A+(n)_{vidrio,A}(2)(X)_v+(n)_{agua,A}(X)_A - (n)_{aire.B}(X)_B \]
para la onda B
\[ Onda_{B}=(1)_{aire}(1m)=1m \]
para la onda A
\[ Onda_{A}=(1)_{aire}(.89m)+(1.52)_{vidrio}(2)(0.005m)+(1.33)_{agua}(.10m)=1.038m \]
para obtener la diferencia hay que restar los caminos
\[
Onda_{A-B}=onda_{A}-Onda_{B}=1.038m-1m=0.038m=\Lambda
\]
la diferencia de fase relativa esta dada por:
\[ \delta=k_{0}\Lambda \]
\[ \delta=k_{0}\Lambda=\left(\frac{2\pi}{\lambda_{0}}\right)\Lambda=\frac{2\pi\left(3.82x10^{-3}m\right)}{5x10^{-9}m}=7.64x10^{6}\pi \] por lo tanto
\[ \delta=7.64x10^{6}\pi \]
Realizado por: Jose de jesus (discusión) 19:57 30 mar 2015 (CDT)Jose de jesus Arizpe Flores 30/03/2015 18:30
Problema 7.7 3ra Edición en español
En este problema la primera parte de la solución es correcta, pero la segunda no, aqui se coloca la parte restante, y como lo realice:
7.7. Usando las ecuaciones (7.9), (7.10) y (7.11) demuestre que la resultante de las ondas
\[ E_{1}=E_{01}sen\left[wt-k(x+\Delta x)\right] \]
y
\[
E_{2}=E_{01}sen\left(wt-kx\right)
\]
es
\[
E=2E_{01}cos\left(\frac{k\Delta x}{2}\right)sen\left[wt-k\left(x+\frac{\Delta x}{2}\right)\right]
\]
Procedimiento
Primero, definamos las siguientes variables como $\alpha_{1}=-k(x+\Delta x)$ y $\alpha_{2}=-kx$, luego tendremos que:
\[ E_{1}=E_{01}sen(et+\alpha_{1}) \]
y
\[ E_{2}=E_{01}sen(wt+\alpha_{2}) \]
Asi, aplicando la ecuación (7.9) tendremos que:
\[ E_{0}^{2}=E_{01}^{2}+E_{01}^{2}+2E_{01}^{2}\left(cos\alpha_{1}cos\alpha_{2}+sen\alpha_{1}sen\alpha_{2}\right) \]
Factorizando tenemos:
\[ E_{0}^{2}=2E_{01}^{2}\left(1+cos\alpha_{1}cos\alpha_{2}+sen\alpha_{1}sen\alpha_{2}\right) \]
\[
E_{0}^{2}=2E_{01}^{2}\left(1+cos\left(\alpha_{2}-\alpha_{1}\right)\right)
\]
Haciendo $\alpha=\alpha_{2}-\alpha_{1}$
Usando la indentidad $\left(1+cos\alpha\right)=2cos\left(\frac{\alpha}{2}\right)$ tendremos:
\[ E_{0}^{2}=2E_{01}^{2}\left(2cos^{2}\left(\frac{\alpha}{2}\right)\right)=4E_{01}^{2}cos^{2}\left(\frac{\alpha_{2}-\alpha_{1}}{2}\right) \]
Finalmente:
\[ E_{0}^{2}=E_{01}^{2}cos^{2}\left(\frac{k\Delta x}{2}\right) \]
\[
E_{0}=E_{01}cos\left(\frac{k\Delta x}{2}\right)
\]
Luego, para hallar $\alpha$ usemos (7.10)
\[ tan\alpha=\frac{E_{01}sen\alpha_{1}+E_{01}sen\alpha_{2}}{E_{01}cos\alpha_{1}+E_{01}cos\alpha_{2}} \]
Realizando las operaciones pertinentes tendremos que:
\[ tan\alpha=\frac{sen\left(-kx-\frac{k\Delta x}{2}\right)}{cos\left(-kx-\frac{k\Delta x}{2}\right)}=tan\left(-kx-\frac{k\Delta x}{2}\right) \]
\[
\Rightarrow\alpha=-kx-\frac{k\Delta x}{2}
\]
\[
\alpha=-k\left(x+\frac{\Delta x}{2}\right)
\]
Conclusión
Por último, sustituyendo estos datos en la ecuación (7.11) tendremos:
\[ E=2E_{01}cos\left(\frac{k\Delta x}{2}\right)sen\left[wt-k\left(x+\frac{\Delta x}{2}\right)\right] \]
Realizado por: Cesar Ivan Avila Vasquez 22:13 26 Marzo 2014
Forma alternativa
Usando las ecuaciones:
Demostrar la resultante de las dos ondas.
es:
![E=2E_{01}cos(\frac{\triangle x}{2})sen[\omega t-k(x+\frac{\triangle x}{2})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/257453a38e28673ee1c17c0d719746c471aaff1f)
Sustituyendo en la primera relación tenemos:
Tras simplificar obtenemos.
![E_{0}^{2}=2E_{01}^{2}[1+cos(\triangle x)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/44b171b80be58adf63d32af32035d87f0f3d8fcb)
Utilizando una relación trigonométrica.
![E_{0}^{2}=4E_{01}^{2}[cos^{2}(\frac{\triangle x}{2})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e3bc9093359f0c9c9672a7040cc0f1e83cbfc807)
Sacando raíces de ambos lados.
Ahora en el caso de la fase.
De aquí, factorizamos del denominador un campo y este se hace uno con el campo del numerador
Utilizamos en el denominador 1. y en el numerador.
y sustituimos.
Tras simplificar.
Por definición de tangente.
Ahora por la ultima ecuación el campo.
Realizado por: Andrés Arturo Cerón Téllez ([[Usuario discusión:Andrés Arturo Cerón Téllez|discusión]]) 00:55 6 jul 2013 (CDT)
Problema 7.8 3ra Edición en español
Sume directamente las dos ondas del problema 7.7 para encontrar la ecuación (7.17)
Procedimiento
Las ondas del problema anterior son:
![{\displaystyle E_{1}=E_{01}\sin \left[\omega t-k(x+\Delta x)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9bcc4e974133c68d9f8e9926e4a86377f1d9fa94)
y:
![{\displaystyle E_{2}=E_{01}\sin \left[\omega t-kx\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c150908498df6a0ea033e15faed0195b045cd4d6)
Hacemos la suma directamente :
![{\displaystyle E=E_{01}\left\{\sin \left[\omega t-k(x+\Delta x)\right]+\sin \left[\omega t-kx\right]\right\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/48209cc032b9e240e42de01b2c38b3c0656719d4)
Desarrollamos el primer seno usando la regla trigonométrica de la suma de ángulos:
![{\displaystyle \sin \left[\omega t-k(x+\Delta x)\right]=\sin \left[\omega t-kx\right]\cos(k\Delta x)-\cos \left[\omega t-kx\right]\sin(k\Delta x)}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1ce2edfe87ae526b9d260680181f7d9005e4f667)
Desarrollamos
![{\displaystyle E=E_{01}\left\{\sin \left[\omega t-kx\right]\cos(k\Delta x)-\cos \left[\omega t-kx\right]\sin(k\Delta x)+\sin {\left[\omega t-kx\right]}\right\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f94562230982e78e5b2edbbec43e139ebd893164)
Factorizamos del primer y último término el seno de la fase:
![{\displaystyle E=E_{01}\left\{\sin \left[\omega t-kx\right]\left[\cos(k\Delta x)+1\right]-\cos \left[\omega t-kx\right]\sin(k\Delta x)\right\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a56a07a6ff8ad02fc314d1268384b3771982d2f8)
Utilizando las relaciones trigonométricas de los problemas anteriores se obtienen las siguientes expresiones para el seno y coseno:
Las ecuaciones de las ondas se ven como sigue:
![{\displaystyle E=E_{01}\left\{\sin \left[\omega t-kx\right]2\cos ^{2}({\frac {k\Delta x}{2}})-cos\left[\omega t-kx\right]2cos({\frac {k\Delta x}{2}})sen({\frac {k\Delta x}{2}})\right\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1a48fe0fa45037a10dfdd59fbb4ee0024851ad3f)
Si se factoriza un coseno de la mitad del ángulo y el coeficiente dos se tiene la siguiente ecuación de onda:
![E=2E_{01}cos(\frac{k\Delta x}{2})\left\{ sen\left[\omega t-kx\right]cos(\frac{k\Delta x}{2})-cos\left[\omega t-kx\right]sen(\frac{k\Delta x}{2})\right\}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9496fef5ebed9e7c1140f573654be249111d227d)
Arreglando la suma de ángulos del seno se tiene:
Conclusión
![{\displaystyle E=2E_{01}\cos \left({\frac {k\Delta x}{2}}\right)\sin \left[\omega t-k\left(x+{\frac {\Delta x}{2}}\right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2d20ea84d293a6eaba65397ba298e9b69ff97ea3)
que corresponde a la ecuación (7.17).
Realizado por: Brenda Pérez Vidal (discusión) 18:34 27 mar 2014 (UTC)
Problema 7.9 3ra Edición en español
Use la representación compleja para calcular la resultante de , donde
Y describa la onda compuesta.
Aplicando el método complejo
Entonces, la suma de ambas es:
Dado que
Entonces.
Desarrollando “”
![E=E_{0}[cos(kx)+\imath sen(kx)]2\imath sen(\omega t)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ff54c9570288637e6b37c2f78b1c87882fe611cb)
![E=E_{0}[2\imath cos(kx)sen(\omega t)-2sen(kx)sen(\omega t)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1b9c5bf91b8ff7341318476636d5198626c0b785)
Conclusión
Por tanto.
De esa forma se describe la onda compuesta, Siendo así que la onda es armónica y de la misma frecuencia que las constitutivas aunque su amplitud y fase son diferentes.
Realizado por:Mario Moranchel (discusión) 03:42 26 mar 2014 (UTC)
Problema 7.10 3ra Edición en español
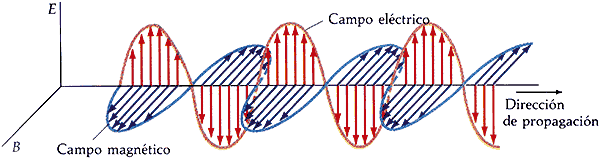
El campo eléctrico de una onda electromagnética estacionaria plana viene dado por \begin{equation} E(x,t)=2E_{0}sen(kx)cos(\omega t) \end{equation} Deduzca una expresión para $B(x,t)$.
Procedimiento
Dado.
\begin{equation} \frac{\partial E}{\partial t}=-\frac{\partial B}{\partial t} \end{equation}
Se busca una función de B dependiente de x y de t entonces integramos para obtener:
\begin{equation} B(x,t)=-\int \frac{\partial E}{\partial x}dt \end{equation}
\begin{equation} -\int \frac{\partial E}{\partial x}dt=-2E_{0}kcos(kx)\int cos(\omega t)dt \end{equation}
\begin{equation}
-2E_{0}kcos(kx)\int cos(\omega t)dt=-\frac{2E_{0}k}{\omega}cos(kx)sen(\omega t)
\end{equation}
Entonces
\begin{equation} B(x,t)=-\frac{2E_{0}k}{\omega}cos(kx)sen(\omega t) \end{equation}
Pero \begin{equation} \frac{E_{0}k}{\omega}=\frac{E_{0}}{c}=B_{0} \end{equation}
Conclusión
Por lo tanto:
\begin{equation} B(x,t)=-2B_{0}cos(kx)sen(\omega t) \end{equation}
Esquema de la onda estacionaria
Angel Nahir Molina Guadarrama (discusión) 03:45 28 mar 2014 (UTC)
Realizado por: Daniela López Martínez (discusión) 21:16 6 jul 2013 (CDT)
Forma alternativa
El campo eléctrico de una onda electromagnética estacionaria plana viene dado por Deduzca una expresión para
Regresando a la ecuación 3.27 de la sección 3.2 se tiene que:
Procedimiento
Se busca una función de B dependiente de x y de t
Entonces
Utilizamos la igualdad
Conclusión
Por lo que
que es la expresión que se busca
Realizado por: Hector Resendiz Héctor Reséndiz (discusión) 17:00 30 mar 2015 (CDT)
Problema 7.12 3ra Edición en español
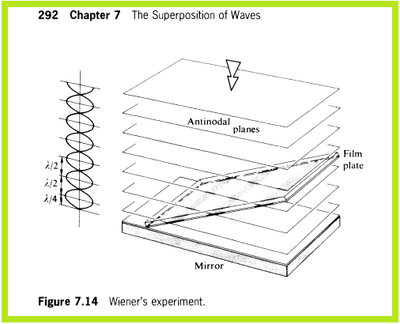
Considerando el experimento de Wiener ( Fig. 7.14 ) la luz monocromática de 550 nm de longitud de onda , si el plano de la película tiene un ángulo de 1.0° a la superficie reflectante , determinar el número de bandas brillantes por centímetro que aparecerán en él.
bandas que son espacios de $\frac{\lambda}{2}$ dispuestos verticalmente
\[ \sin\theta=\left(\frac{bandas}{cm}\right)\left(\frac{vertical}{\frac{bandas}{cm}}\right) \]
Conclusión
en la película;
$\frac{bandas}{cm}$en la pelicula$=\left[1/(\lambda/2)\right]/\sin\theta$ $=\left(1/5.50\times10^{-7}cm\right)/\sin\left(1\right)=1.04\times10^{8}cm^{-1}$
Resuelto por: Rosario Maya (discusión) 04:34 30 mar 2015 (CDT)
Forma alternativa
Considerando el experimento de Wiener (figura 7.11) en la luz monocromática cuya longitud de onda es de $550 nm$, si el plano de la película estuviera inclinado $1°$ con respecto a la superficie de reflexión, determine el número de franjas brillantes por centímetro que aparecerán en el plano.
Los planos antinodales están separados una distancia $\frac{\lambda}{2}$ uno del otro. El seno del ángulo de inclinación de la película se relaciona como sigue con el número de franjas brillantes y la separación entre los planos:
Con un simple despeje podemos obtener el número de franjas que hay por centímetro con la placa fotográfica inclinada $1°$ :
$\frac{No. franjas}{cm}=\frac{\frac{1}{\lambda/2}}{Sen \theta}=\frac{\frac{1}{5.5 * 10^{-7} cm}}{Sen (1°)} $
Por lo tanto, el número de franjas brillantes por centímetro que aparecen en el plano son:
Realizado por: Brenda Pérez Vidal (discusión) 19:04 27 mar 2014 (UTC)
Problema 7.12 3ra Edición en español
Microondas de frecuencia de $10^{10}Hz$ se emiten directamente en un reflector de metal. Despreciando el índice de refracción del aire, determinar el espaciado entre los nodos sucesivos en el patrón de onda estacionaria resultante.
Procedimiento
Nodos espaciados por $\lambda/2$ partes.
\[ c=\nu\lambda \]
entonces,
\[ \lambda=\frac{c}{\nu}=3\times10^{8}ms^{-1}/10^{10}Hz=0.03m \]
Solución
El espacio de los nodos es $0.015m$
Realizado por: Rosario Maya (discusión) 05:04 30 mar 2015 (CDT)
Problema 7.21 3ra Edición en español
Demuestre que la velocidad de grupo puede escribirse como:
\[V_g =\frac{C}{n+\omega (dn/d\omega)}\]
Solución:
La velocidad de grupo es: \[V_g = \frac{d\omega}{dk}= V +k \frac{dv}{dk}------(1)\]
Por otro lado, aplicando la regla de la cadena se tine que: \[ \frac{dv}{dk}=\frac{dv}{d\omega} \frac{d\omega}{dk}------(2) \]
Por lo que (1) se puede escribir como:
\[V_g = V +k\left( \frac{d\omega}{dk}\right)\frac{dv}{d\omega}------(3) \]
También sabemos que $v=C/n$ Por lo que: \[ \frac{dv}{d\omega}=\frac{dv}{dn}\frac{dn}{d\omega}=-\frac{C}{n^2}\frac{dn}{d\omega} \]
Sustituyendo en (3)
\[V_g = V - k\left( \frac{d\omega}{dk}\right)\left( \frac{C}{n^2} \frac{dn}{d\omega}\right) \]
\[V_g = V -k V_g \left( \frac{C}{n^2} \frac{dn}{d\omega}\right)------(4)\]
\[ V_g= \frac{V}{1+ \left( \frac{C}{n^2} \frac{dn}{d\omega}\right)k}------(5) \]
Conclusión
Finalmente:
\[ V_g=\frac{Vn}{n+ \left( \frac{C}{n^2} \frac{dn}{d\omega}\right)kn}=\frac{C}{n+\left(\frac{Ck}{n} \right)\frac{dn}{d\omega}} \]
\[V_g =\frac{C}{n+\omega \frac{dn}{d\omega}}\]
Resuelto por: Luis Santos (discusión) 01:59 27 mar 2015 (CDT)
Problema 7.25 3ra Edición en español
Un gas ionizado, o un plasma sirve como medio dispersor para ondas electromagnéticas. Puesto que la ecuación de dispersión es
donde es la frecuencia constante del plasma, determine las expresiones tanto de la fase como de las velocidades de grupo y demuestre que .
Solución
Se tiene que , elevando al cuadrado ambos componentes
- , entonces sustituyendo (2) en (1) se tiene
Invertimos
Despejando “v” nos queda
Ahora, por otro lado de la velocidad de grupo es
si , sustituyendo esta expresión en (3) se tiene
Conclusión
- :
![\left[c/\sqrt{1-\left(\frac{\omega_{p}}{\omega}\right)^{2}}\right]*\left[c\sqrt{1-\left(\frac{\omega_{p}}{\omega}\right)^{2}}\right]=c^{2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/13320c438b44b9a6b2fcaf7c85b1246582e8a382)
Elaborado por Ricardo García Hernández.--Ricardo Garcia Hernandez (discusión) 00:42 30 mar 2015 (CDT)
Forma alternativa
Un gas ionizado o un plasma sirve como medio dispersor para ondas electromagnéticas. Puesto que la ecuación de dispersión es:
Donde omega subíndice p es la constante del plasma, determine las expresiones tanto de la fase como de las velocidades de grupo y demuestre que
De la relación precedente.
por la definición de velocidad de grupo.
Obtenemos la derivada:
Al simplificar.
Entonces la velocidad de grupo.
Por otro lado en general la velocidad está dada por:
entonces podemos demostrar la propiedad de la segunda parte.
Simplificando obtenemos el resultado esperado.
Realizado por: Daniela López Martínez (discusión) 20:17 6 jul 2013 (CDT)
Problema 3.16 3ra Edición en español
Imagine que usted esta parado en una trayectoria de una antena que esta radiando ondas planas de frecuencia 100MHz y densidad de flujo $19.88x10^{-2} \frac{W}{m^2}$. Calcula la densidad fe flujo de fotones, es decir, el numero de fotones por unidad de tiempo por unidad de área.¿Cuantos fotones, en promedio, se encontraran en un metro cubico de esta región?
De la formula de la energía y usando la constante de Plank
Aplicaremos la formula para calcular el numero de fotones por metro cubico
Densidad de flujo de los fotones por unidad de tiempo, por unidad de área
Todos los fotones en el volumen V cruzan la unidad de área en un segundo
Fotones en promedio en un metro cubico
Realizado por: David Alberto Rojas Solis (discusión) 10:23 6 jul 2013 (CDT)
Problema 3.32 3ra Edición en español
¿Cuál es la velocidad de la luz en un diamante si el indice de refracción es de 2.42?
Procedimiento
"Se denomina índice de refracción al cociente entre la velocidad de la luz en el vacío y la velocidad de la luz en el medio cuyo índice se calcula. Se simboliza con la letra n y se trata de un valor adimensional.
n: es el indice de refracción
v: velocidad de la luz en el medio cuyo índice se calcula (agua, vidrio, diamante,etc.).
c: velocidad de la luz en el vació
De 1 se tiene que la velocidad de luz en el diamante (v) es igual a la velocidad de la luz en el vacío (c), entre el índice de refracción del diamante (2.42); o sea:
Realizado por: Anónimo
Problema 3.38 3ra Edición en español
La luz amarilla de una lámpara de sodio $\lambda=589nm$ cruza un depósito de glicerina (con índice de 1.47) de 20 cm de largo, en un tiempo $t_1$. Si la luz tarda $t_2$ en cruzar el mismo depósito cuando está lleno de disulfuro de carbono (índice 1.63), calcule el valor de $t_2-t_1$.
Procedimiento
Sabemos la relación del índice de refracción con la velocidad:
Tomando a la definición de la velocidad
despejando al tiempo en la última ecuación y sustituyéndola en la primera ecuación
haciendo lo mismo para el disulfuro de carbono
restando el segundo tiempo al primero
Conclusión
Sustituyendo los datos nos queda:
Realizado por: Ignacio Peralta Martínez (discusión) 02:03 6 jul 2013 (CDT)
MISS (discusión) 00:10 23 jun 2013 (CDT)
4ta Edición en Ingles
Problema 7.15 4ta Edición
Imagine que golpeamos dos diapasones, uno con frecuencia de $340Hz$ y el otro de $342Hz$. ¿Qué oiremos?
Solución:
En este ejemplo se da el fenómeno del Batido, en el caso de que la frecuencia de ambas ondas no es igual (), pero si son valores muy cercanos entre sí, la onda resultante es una onda modulada en amplitud por la llamada "frecuencia de batido" cuyo valor corresponde a , la frecuencia de esta onda modulada corresponde a la media de las frecuencias que interfieren.
Nuestro sistema auditivo no es capaz de percibir separadamente las dos frecuencias presentes, sino que se percibe una frecuencia única promedio $(\nu_1 + \nu_2) / 2$, pero que cambia en amplitud a una frecuencia de $(\nu_2 - \nu_1) / 2$.
Es decir, si superponemos dos ondas senoidales de $340 Hz$ y $342 Hz$, nuestro sistema auditivo percibirá un único sonido cuya altura corresponde a una onda de $341 Hz$ y cuya amplitud varía con una frecuencia de $1 Hz$ (es decir, una veces por segundo) con .
Realizado por: Luis Martínez (discusión) 13:18 28 mar 2015 (CDT)
Problema 7.22 4ta Edición
La velocidad de propagación de una onda superficial en un líquido cuya profundidad es mucho mayor que $\lambda$ viene dada por:
donde $g$=es la aceleración de la gravedad, $\lambda$=longuitud de onda, $\rho$=densidad, $\gamma$=tensión superficial. Calcule la velocidad de grupo de un pulso en el límite mayor de la longitud de onda(éstas reciben el nombre de ondas gravitacionales).
Solución:
tenemos que la velocidad de un pulso esta dada por:
la velocidad de grupo $v_{g}$ es:
donde:
Realizado por: Luis Martínez (discusión) 14:16 28 mar 2015 (CDT)
Problema 7.30 4ta Edición
Usando la ecuación de dispersión:
Demuestra que la velocidad de grupo está dada por: Para las ondas de alta frecuencia (por ejemplo los rayos X), tenga en cuenta que desde el son los factores de ponderación. ¿Qué es la velocidad de fase?, demostrar que
Procedimiento
Como hablamos para ondas de alta frecuencia, , por lo tanto en la ecuación de dispersión tenemos que, (acordándonos que :
Donde:
Usando la expansión binomial, para x<<1 Por lo tanto tenemos que: Calculando la derivada de con respecto de :
Empleando la ecuación para velocidad de grupo tenemos que: Sustituyendo:
por lo tanto:
Para el índice de refracción tenemos que: Por lo tanto tenemos que para la velocidad de fase es: Para tenemos que: Por expansión binomial tenemos que la velocidad de fase:
Dado que:
Por lo tanto demostramos que:
Realizado por:Pablo (discusión) 20:52 29 mar 2015 (CDT)
Problema 7.36 4ta Edición
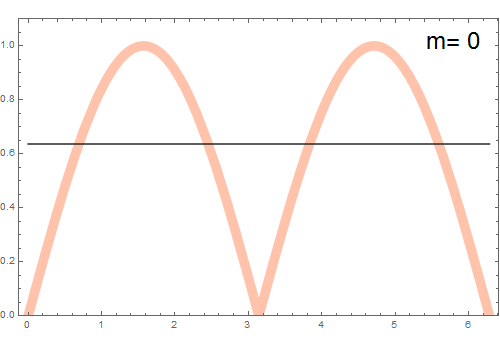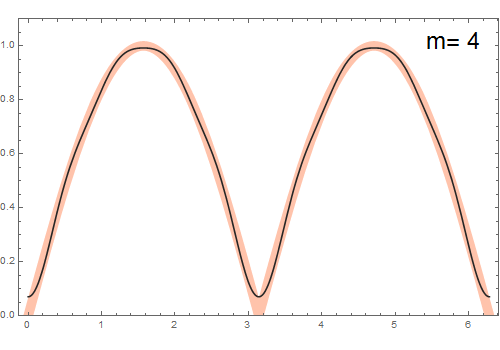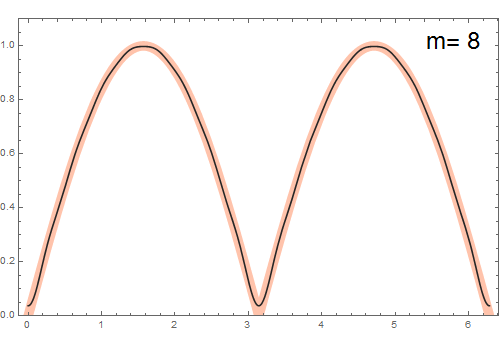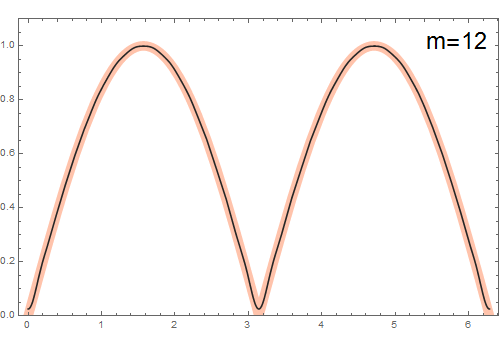
Muestre que la representación en serie de Fourier de la función $f(\theta) = |\sin(\theta)|$ es
\[ f(\theta)=\frac{2}{\pi}-\frac{4}{\pi} \sum_{m=1}^{\infty} \frac{\cos(2\,m\,\theta)}{4\,m^2-1} \]
Procedimiento
Para una función periódica, $f(x)$, su representación en una serie trigonométrica de Fourier es (ec. 7.42, Hecht, "Optics",4th edition)
\[ f(x)=\frac{1}{2}A_0 + \sum_{n=1}^{\infty} \bigg\lgroup A_n \cos(n\,k\,x)+B_n \sin(n\,k\,x) \bigg\rgroup \quad \text{con} \quad k=\frac{2\,\pi}{\lambda}\]
Y conociendo $f(x)$, los coeficientes son calculados usando (ecs. 7.47 y 7.48, Hecht, "Optics",4th edition)...
\[ A_n= \frac{2}{\lambda} \int_{0}^{\lambda} f(x) \cos(n\,k\,x) \, \mathrm{d}x \] \[ B_n= \frac{2}{\lambda} \int_{0}^{\lambda} f(x) \sin(n\,k\,x) \, \mathrm{d}x \]
Para problema expuesto, tenemos $f(\theta)=|\sin(\theta)|= \left\{\begin{array}{1} \quad \sin(\theta) & 0\leq \theta \leq \pi \\ \, -\sin(\theta) & \pi \leq \theta \leq 2\pi \end{array} \right.$ (véase la figura). Entonces podemos calcular los coeficientes considerando un intervalo $\lambda=2\,\pi$ que implica $k=1$.
Para $n=0$, calculamos $A_0$. \[ A_0= \frac{2}{2\,\pi} \int_{0}^{2\,\pi} |\sin(\theta)| \, \mathrm{d}\theta= \frac{1}{\pi} \left[ \int_{0}^{\pi} \sin(\theta) \, \mathrm{d}\theta-\int_{\pi}^{2\,\pi} \sin(\theta) \, \mathrm{d}\theta \right] = \frac{1}{\pi} \left( 2+2 \right) \]
Es decir, \begin{equation}\label{1} A_0=\frac{4}{\pi} \end{equation}
Para $n>0$, calculamos $A_n$.
\[ A_n= \frac{2}{2\,\pi} \int_{0}^{2\,\pi} |\sin(\theta)| \cos(n\,\theta) \, \mathrm{d}\theta=
\frac{1}{\pi} \left[ \int_{0}^{\pi} \sin(\theta) \cos(n\,\theta) \, \mathrm{d}\theta-\int_{\pi}^{2\,\pi} \sin(\theta) \cos(n\,\theta) \, \mathrm{d}\theta \right] =
\frac{1}{\pi} \left[ \frac{1+\cos(n\,\pi)}{1-n^2}-\frac{\cos(n\,\pi)+\cos(2\,n\,\pi)}{n^2-1} \right] =-\frac{2(1+(-1)^n)}{\pi(n^2-1)} \]
Considerando los caso $n$ par y $n$ impar obtenemos \[ A_n= \left\{\begin{array}{2} \;\;\; 0 & \quad\text{si} \;n\; \text{es impar} \\ -\frac{4}{\pi(n^2-1)} & \quad\text{si} \;n\; \text{es par} \end{array} \right.\]
Como $n$ es par, entonces podemos escribir $n=2m$ con $m\in\N$, y asi obtenemos
\begin{equation}\label{2} A_n=A_m= -\frac{4}{\pi(4m^2-1)}, \quad m\in\N ,\quad n=2m\end{equation}
Para $n>0$, calculamos $B_n$. \[ B_n= \frac{2}{2\,\pi} \int_{0}^{2\,\pi} |\sin(\theta)| \sin(n\,\theta) \, \mathrm{d}\theta= \frac{1}{\pi} \left[ \int_{0}^{\pi} \sin(\theta) \sin(n\,\theta) \, \mathrm{d}\theta-\int_{\pi}^{2\,\pi} \sin(\theta) \sin(n\,\theta) \, \mathrm{d}\theta \right] = \frac{1}{\pi} \left[ -\frac{\sin(n\,\pi)}{n^2-1}-\frac{\sin(n\,\pi)+\sin(2\,n\,\pi)}{n^2-1} \right] =\frac{1}{\pi}(-0-0)=0 \]
Así obtenemos \begin{equation}\label{3} B_n=0, \quad\forall n\in\N \end{equation}
Sustituyendo $(1)$, $(2)$ y $(3)$ en la serie trigonométrica de Fourier, obtenemos el resultado deseado.
\[ f(\theta)=\frac{1}{2}A_0 + \sum_{n=1}^{\infty} \bigg\lgroup A_n \cos(n\,k\,\theta)+B_n \sin(n\,k\,\theta) \bigg\rgroup =\frac{1}{2}\left( \frac{4}{\pi} \right) + \sum_{n=1}^{\infty} \bigg\lgroup \left( -\frac{4}{\pi(n^2-1)} \right) \cos(n\,k\,\theta)+(0) \sin(n\,k\,\theta) \bigg\rgroup \]
Pero $k=1$ y $n=2\,m$, entonces
\[ f(\theta)=\frac{2}{\pi} + \sum_{m=1}^{\infty} \left( -\frac{4}{\pi(4\,m^2-1)} \right) \cos(2\,m\,\theta) \]
Concluyendo
\[ f(\theta)=\frac{2}{\pi} -\frac{4}{\pi} \sum_{m=1}^{\infty} \frac{\cos(2\,m\,\theta)}{4\,m^2-1} \]
Problema resuelto por Adolfo Calderón Alcaraz (discusión) 17:07 30 mar 2015 (CDT).
Problema 7.23 4ta Edición
Mostrar que la velocidad de grupo puede ser escrita como:
Procedimiento
Sabemos que: así que:
:
:
:
si k*=k:
que se puede simplemente volver a renombrar:
Conclusión
o lo que es lo mismo:
Hecho por: Uziel Sanchez GUziel Sanchez Gutierrez (discusión) 19:46 30 mar 2015 (CDT)
5ta Edición en Ingles
Ejercicio 3.4 5ta Edición
Demostrar que la longitud del camino óptico, definido como la suma de los productos de varios indices multiplicados por los espesores de los medios atravesados por un haz, es decir equivale a la longitud del recorrido en el vació que el haz tardaría el mismo tiempo en atravesar.
Procedimiento
Sea la longitud del camino óptico L.C.O = si sabemos que el indice de fracción es con "c" la velocidad de la luz en el vació y v la velocidad de la luz en un medio, se puede sustituir en la primera ecuación :
L.C.O =
L.C.O=
L.C.O=
Que es la longitud del recorrido en el vació que la luz tardaría ese tiempo en atravesar
Realizado por:Luisa Alejandra Vega Sanchez (discusión) 17:23 30 mar 2015 (CDT)luisa alejandra vega sanchez
Problemas Adicionales
Problema Adicional 1
Tomado de : Vibraciones y ondas. A. P. FRENCH pág. 43. Problema 2-2.
Una partícula está sometida a dos movimientos armónicos simples de la misma frecuencia $\omega=\pi$ y en dirección de z, las amplitudes son 0.25mm y 0.20mm respectivamente y la de fase entre el primero y el segundo es de $45^º$. Hallar la resultante.
Procedimiento
Sabemos que la suma de dos ondas esta dada por
Donde
y
Desarrollando se obtiene:
Conclusión
y Sustituyendo:
Resuelto por:Luis Velázquez (discusión) 08:32 27 mar 2015 (CDT)
Problema adicional 2
Una cuerda de guitarra de $1 m$ de largo fija por ambos extremos vibra formando 4 nodos. Los puntos centrales de la cuerda tienen un desplazamiento máximo de $4 mm$. Si la velocidad de las ondas en la cuerda es $660 m/s$, halla la frecuencia con la que vibra la cuerda y la expresión de la función de la onda estacionaria.
Procedimiento
Para obtener la longitud de la cuerda usamos: $ L= 3\dfrac{\lambda}{2}\Rightarrow \lambda = \dfrac{2L}{3} = \dfrac{2*1}{3} = \dfrac{2}{3} m $$
Y la frecuencia de la vibración es $\ v =\dfrac{v}{\lambda} = \dfrac{660}{2/3} = 990 Hz$
La ecuación de onda estacionaria es :
$ y = 2 A\sin (k x) \cos (\omega t) = 2* 4 *10^{-3}\sin(\dfrac{2\pi}{2/3}x)\cos (2\pi 990 t) =8*10^{-3}\sin(3 \pi x)\cos (1980 \pi t)$
Realizado por: Esther Sarai (discusión) 00:05 29 mar 2015 (CDT)Esther Sarai García
Problema adicional 3
La ecuación de una onda, en unidades del SI, que se propaga por una cuerda es :
a) determinar las magnitudes características de la onda ( amplitud, frecuencia angular,numero de onda, longitud de onda, frecuencia, periodo,velocidad de propagación)
b) deducir las expresiones generales de la velocidad y aceleración transversal de un elemento de la cuerda y sus valores máximos
Inciso a
Para a) operando en la expresión de onda : y comparando con la expresión general :
se tiene que :
Frecuencia angular:
numero de onda :
longitud de onda :
frecuencia :
periodo :
velocidad de propagación : v=\lambda v =\frac{\omega}{k}= 0.5(4)=\frac{8\pi}{4\pi}</math>
Inciso b
para b) la velocidad de vibración :
donde la velocidad máxima =
la aceleración de vibración = a=\frac{dv}{dt}=-0.4\picos 2\pi(4t-2x)m/s</math>
donde la aceleración máxima =
Realizado por: Luisa Alejandra Vega Sanchez (discusión) 01:32 30 mar 2015 (CDT)luisa alejandra vega sanchez
Otra ediccion
3.12/7.12 Un láser emite unos pulsos de UV que dura cada uno y cuyo haz tiene un diámetro de . Suponiendo que la potencia de cada pulso tiene una energía de 6.0J: (a)calcule la extensión espacial de cada tren de ondas, y (b)calcule la energía media por unidad de volumen de tal pulso.
Inciso a
(a) conociendo la ecuación sustituimos los datos dados
Inciso b
(b)el volumen de un solo pulso esta dado por la formula
Por lo tanto
Realizado por: Leticia González Zamora (discusión) 16:01 20 jun 2013 (CDT)
