The constant magnitude hyper surface $c_1 \in \mathbb{R}$, in 1+2 dimensions, in the additive representation is
\begin{equation}\left\| \overset{o}{\varphi} \right\|=\bigl|f_{0}\bigr|\sqrt{1+\frac{f_{x}^{2}}{f_{0}^{2}}}\sqrt{1+\frac{f_{y}^{2}}{f_{0}^{2}}}=c_1.\label{eq:a to m-vars scal} \end{equation}
A visualization of this surface is given here below:
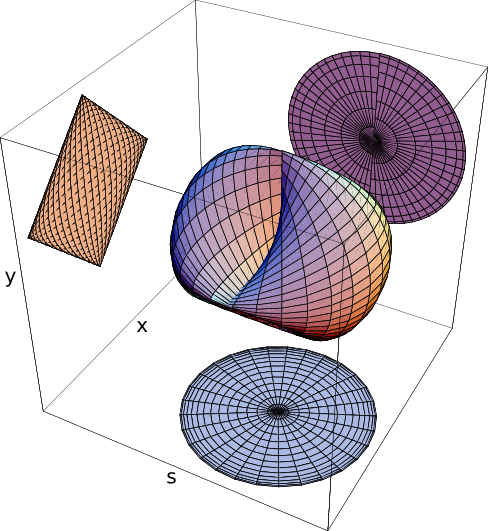
This three dimensional figure has the peculiarity that two of its orthogonal projections are circles while the remaining orthogonal projection is a square. For this reason, this figure is called a cusphere, a contraction of cube and sphere.
Publication: 2013d Escultura métrica: escatores imaginarios en 1+2 dimensiones y la escala humana.

