La hiper superficie de magnitud constante $c_1 \in \mathbb{R}$, en 1+2 dimensiones, en la representación aditiva está dada por
\begin{equation}\left\| \overset{o}{\varphi} \right\|=\bigl|f_{0}\bigr|\sqrt{1+\frac{f_{x}^{2}}{f_{0}^{2}}}\sqrt{1+\frac{f_{y}^{2}}{f_{0}^{2}}}=c_1.\label{eq:a to m-vars scal} \end{equation}
Una visualización de ésta superficie se muestra en la siguiente figura:
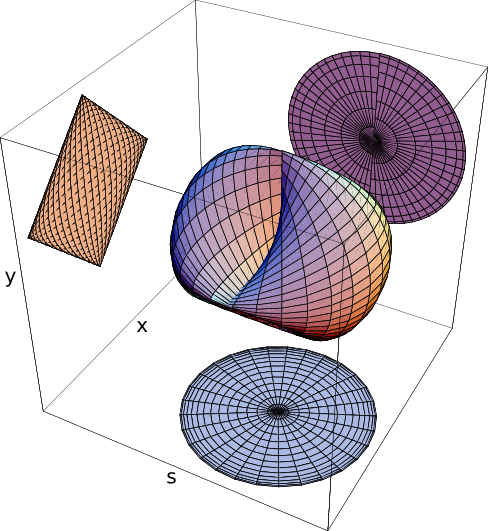
La figura tridimensional tiene la peculiaridad que dos de sus proyecciones ortogonales son círculos mientras que la proyección en la tercera dirección ortogonal es un cuadrado. Por este motivo, a esta figura se le llama cusfera, como contracción de cuadrado - esfera.
Mas información en * publicaciones
o directamente en 2023 cusfera

