Diferencia entre revisiones de «Vibra: probs c4»
Sin resumen de edición |
|||
| (No se muestran 84 ediciones intermedias de 10 usuarios) | |||
| Línea 1: | Línea 1: | ||
Main | Problemas capítulo 2 Amortiguamiento en la física. | ||
Ejercicios resueltos sobre osciladores amortiguados, para distintas areas de la física. | |||
Del libro ''Vibrations and waves in physics'' del autor Iain G. Main. Y algunos problemas adicionales de diversos libros. | |||
| Línea 6: | Línea 10: | ||
'''4.1 Show that the relaxation time for very heavily damped LCR circuit is RC. ''' | '''4.1 Show that the relaxation time for very heavily damped LCR circuit is RC. ''' | ||
'''Traducción''' | |||
4.1 Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC. | 4.1 Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC. | ||
'''Solución''' | |||
Conocemos la ecuación para el oscilador ligeramente amortiguado (ecuación 3.3 G. Main, Vibrations and waves in physics): | Conocemos la ecuación para el oscilador ligeramente amortiguado (ecuación 3.3 G. Main, Vibrations and waves in physics): | ||
| Línea 21: | Línea 30: | ||
Por regla de Kirchhoff(ecuación 4.1, G. Main) para un circuito LCR podemos escribir la siguiente ecuación: | Por regla de Kirchhoff(ecuación 4.1, G. Main) para un circuito LCR podemos escribir la siguiente ecuación: | ||
<math>L\left(\frac{d^{2}\psi}{dt^{2}}\right)+R\left(\frac{d\psi}{dt}\right)+\left(\frac{1}{C}\right)\psi=0 ...2</math> | <math>L\left(\frac{d^{2}\psi}{dt^{2}}\right)+R\left(\frac{d\psi}{dt}\right)+\left(\frac{1}{C}\right)\psi=0 ...(2)</math> | ||
| Línea 27: | Línea 36: | ||
\begin{equation}\frac{d^{2}\psi}{dt^{2}}+\frac{R}{L}\left(\frac{d\psi}{dt}\right)+\frac{1}{LC}\psi=0... (3)\end{equation} | \begin{equation}\frac{d^{2}\psi}{dt^{2}}+\frac{R}{L}\left(\frac{d\psi}{dt}\right)+\frac{1}{LC}\psi= 0 ...(3)\end{equation} | ||
\begin{equation}\gamma=\frac{R}{L}\end{equation} | \begin{equation}\gamma=\frac{R}{L}\end{equation} | ||
| Línea 36: | Línea 45: | ||
\begin{equation}\omega_{0}^{2}=\frac{1}{LC}\end{equation} | \begin{equation}\omega_{0}^{2}=\frac{1}{LC}\end{equation} | ||
Las ecuaciones 1 y 3 son ecuaciones análogas. | |||
El tiempo de relajación en una amortiguación critica está definida como: | |||
$\tau_{r}=\frac{\gamma}{\omega_{0}^{2}}$ | |||
Entonces | |||
$\tau_{r}=\frac{\frac{R}{L}}{\frac{1}{LC}}=\frac{RLC}{L}=RC$ | |||
Finalmente obtenemos | |||
\begin{equation}\tau_{r}=RC\end{equation} | \begin{equation}\tau_{r}=RC\end{equation} | ||
---- | |||
Aportación por usuarios: [[Usuario:Pedro Pablo Ramírez Martínez|Pedro Pablo Ramírez Martínez]] ([[Usuario discusión:Pedro Pablo Ramírez Martínez|discusión]]) 00:24 17 feb 2014 (UTC) , [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 18:56 1 mar 2015 (CST)Esther Sarai García González ,[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 13:15 11 mar 2015 (CDT) | |||
---- | ---- | ||
=== Forma alternativa 1 === | |||
'''Show that the relaxation time for very heavy damped LCR circuit is RC''' | |||
'''Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC.''' | '''Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC.''' | ||
Tomando como base las expresiones de los apuntes,para un circuito RCL muy pesadamente amortiguado en el cual <math>\gamma\succ\succ\succ w_{0} | Tomando como base las expresiones de los apuntes,para un circuito RCL muy pesadamente amortiguado en el cual <math>\gamma\succ\succ\succ w_{0} | ||
| Línea 61: | Línea 78: | ||
<math>\thickapprox A_{1}\exp\left(\frac{-W_{0}^{2}t}{\gamma}\right)\cdots\left(1\right) | <math>\thickapprox A_{1}\exp\left(\frac{-W_{0}^{2}t}{\gamma}\right)\cdots\left(1\right) | ||
</math> | </math> | ||
El tiempo de | |||
El tiempo de relación para este tipo de circuitos es aquel en el que el factor de decaimiento se reduce por un factor de | |||
<math>\frac{1}{e} | |||
</math> por lo tanto,igualamos el factor de decaimiento exponencial de la expresión <math>\left(1\right)</math> a <math>\frac{1}{e}</math> tenemos: | </math> por lo tanto,igualamos el factor de decaimiento exponencial de la expresión <math>\left(1\right)</math> a <math>\frac{1}{e}</math> tenemos: | ||
| Línea 108: | Línea 127: | ||
---- | ---- | ||
Aportación por usuarios: [[Usuario:MISS|MISS]] ([[Usuario discusión:MISS|discusión]]) 00:22 20 jun 2013 (CDT) , | |||
[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:36 28 feb 2015 (CST) | |||
---- | |||
==Problema 4.2 == | ==Problema 4.2 == | ||
'''4.2 A capacitor is charged to a voltage V and is then connected across a coil. If the damping is critical, show that the current rises to a maximun value 2V/eR, where R is the total resistance of the circuit made by the capacitor ant the coil.''' | '''4.2 A capacitor is charged to a voltage V and is then connected across a coil. If the damping is critical, show that the current rises to a maximun value 2V/eR, where R is the total resistance of the circuit made by the capacitor ant the coil.''' | ||
'''Traducción''' | |||
Un condensador se carga a una tensión V y es conectado a través de una bobina. Si el amortiguamiento es crítico, mostrar que la corriente aumenta a un valor máximo de 2V / eR, donde R es la resistencia total del circuito realizado por el condensador de la bobina. | Un condensador se carga a una tensión V y es conectado a través de una bobina. Si el amortiguamiento es crítico, mostrar que la corriente aumenta a un valor máximo de 2V / eR, donde R es la resistencia total del circuito realizado por el condensador de la bobina. | ||
'''Solución''' | |||
La solución para las ecuaciones (3.3) y (4.1) es: | |||
:<math>\psi(t)=(C_{1}+C_{2}w_{0}t)</math> | :<math>\psi(t)=(C_{1}+C_{2}w_{0}t)</math> | ||
Esto muestra que es una amortiguación critica | |||
| Línea 220: | Línea 244: | ||
:<math>i_{max}=\frac{2V_{1}}{\exp R}</math> | :<math>i_{max}=\frac{2V_{1}}{\exp R}</math> | ||
--[[Usuario:Mfgwiki|mfg-wiki]] ([[Usuario discusión:Mfgwiki|discusión]]) 12:00 9 may 2013 (CDT) | ---- | ||
Aportaciones por usuarios: [[Usuario:Mario Moranchel|Mario Moranchel]] ([[Usuario discusión:Mario Moranchel|discusión]]) 02:47 6 feb 2014 (UTC), [[Usuario:Mfgwiki|mfg-wiki]] ([[Usuario discusión:Mfgwiki|discusión]]) 12:00 9 may 2013 (CDT) , [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:56 28 feb 2015 (CST), [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 01:30 1 mar 2015 (CST), [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 20:06 1 mar 2015 (CST)Esther Sarai | |||
---- | ---- | ||
| Línea 238: | Línea 260: | ||
'''G is the constant defined as $G=\frac{\omega I}{g}$.''' | '''G is the constant defined as $G=\frac{\omega I}{g}$.''' | ||
''' [Traducción ] | ''' [Traducción ]''' | ||
Un galvanómetro con una bobina de resistencia $R{}_{G}$ está conectada en serie con una resistencia externa $R{}_{ext}$. | Un galvanómetro con una bobina de resistencia $R{}_{G}$ está conectada en serie con una resistencia externa $R{}_{ext}$. Mostrar que variando $R{}_{ext}$ podremos seleccionar valores de Q dentro de los límites | ||
$\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}\leq Q\leq Q_{m}$ | $\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}\leq Q\leq Q_{m}$ | ||
| Línea 246: | Línea 268: | ||
Donde $Q_{m}$ es la parte de Q debido a los efectos mecánicos y G es la constante definida como $G=\frac{\omega I}{g}$. | Donde $Q_{m}$ es la parte de Q debido a los efectos mecánicos y G es la constante definida como $G=\frac{\omega I}{g}$. | ||
Solución: | '''Solución:''' | ||
Primero tomemos en cuenta algo, sabemos que $Q=\frac{\omega}{\gamma}$ | Primero tomemos en cuenta algo, sabemos que $Q=\frac{\omega}{\gamma}$ | ||
| Línea 261: | Línea 283: | ||
donde Q son los llamados factores de calidad tanto mecánico, eléctrico y el total; como vemos | donde Q son los llamados factores de calidad tanto mecánico, eléctrico y el total; como vemos | ||
la frecuencia angular $\omega$es la misma para todo el sistema, por | la frecuencia angular $\omega$es la misma para todo el sistema, por | ||
lo que obtenemos $\frac{1}{Q}=\frac{1}{Q_{m}}+\frac{1}{Q_{e}}$, | lo que obtenemos $\frac{1}{Q}=\frac{1}{Q_{m}}+\frac{1}{Q_{e}}$, aquí | ||
hay que hacer las dos distinciones que nos pide el problema: | hay que hacer las dos distinciones que nos pide el problema: | ||
| Línea 282: | Línea 304: | ||
--[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:34 28 feb 2015 (CST) | ---- | ||
Aportaciones por usuarios:[[Usuario:Edgar Ortega Roano|Edgar Ortega Roano]] 09:58 12 feb 2014 (CDT) [[Usuario Discusión:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 16:51 25 Febrero 2014, [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:34 28 feb 2015 (CST) | |||
---- | ---- | ||
==Problema 4.4 == | ==Problema 4.4 == | ||
4.4 | |||
of a ballistic galvanometer | '''4.4 Asteady torque of $2.0x10^{-6}Nm,$ applied to the susppention of a ballistic galvanometer (by passing a suitable steady current), produces a steady delfection of 50º. Free vibratios of the suspension have a period og 2.5 s. Calculate the thow porducced by an angular impulse of $5.5x10^{-7}$Nm (applied by discharging a capacitor throw the coil).Neglect damping''' | ||
of 50º. Free vibratios of | '''Traducción''' | ||
by an angular impulse of | Una torca fija de $2.0x10^{-1}Nm$ es aplicada a la suspensión | ||
de un galvanómetro balistico (al pasar una corriente estable), | |||
coil).Neglect damping''' | produce una desviación fija de 50º. Vibraciones libres de la suspensión, | ||
'''Una torca fija de $2.0x10^{-1}Nm$ es aplicada a la suspensión | tienen un periodo 2.5 . Calcule el tiro producido por un impulso | ||
de un galvanómetro balistico (al pasar | angular de $5.5x10^{-7}Nm$ (que se aplica al descargar un capacitor), | ||
produce una | desprecie el amortiguamiento. | ||
tienen | |||
angular de $5.5x10^{-7}Nm$ (que se aplica al | |||
desprecie el amortiguamiento. | |||
Se tienen los siguientes datos: | Se tienen los siguientes datos: | ||
| Línea 314: | Línea 333: | ||
De donde se despeja $\Delta L$, que es el tiro; y se | De donde se despeja $\Delta L$, que es el tiro; y se obtiene: | ||
\[ | \[ | ||
| Línea 325: | Línea 344: | ||
$\Delta L=1.3x10^{-6}Ns^{2}$ | $\Delta L=1.3x10^{-6}Ns^{2}$ | ||
---- | |||
Aportación por usuario: [[Usuario:Ana Alarid|Ana Alarid]] ([[Usuario discusión:Ana Alarid|discusión]]) 03:05 22 feb 2014 (UTC) | |||
---- | |||
=== Forma alternativa === | |||
Una torca fija de $2.0\times10^{-6}Nm$, aplicada a la suspensión | |||
de un galvanometro balístico (al pasar una corriente estable), produce | |||
una desviación fija de 50º . Vibraciones libres de la suspensión, | |||
tienen un periodo de $2.5s$. Calcule el tiro producido por un impulso | |||
angular de $5.5\times10^{-7}Nms$(Que se aplica al descargar un capacitor, | |||
desprecie el amortiguamiento.) | |||
Solucion $\rightarrow$ | |||
Se conoce que | |||
\[ | |||
I=\frac{\Delta L}{\Delta t} | |||
\] | |||
Donde: | |||
I = impulso angular | |||
t = periodo | |||
L = Tiro | |||
Despejando $\triangle L$, tenemos | |||
\[ | |||
\Delta L=I\Delta t | |||
\] | |||
\[ | |||
\Delta L=(5.5\times10^{-7}Nm)(2.5s)=1.375\times10^{-6}Nms^{2} | |||
\] | |||
---- | |||
Aportación por usuario: [[Usuario:Rosario Maya|Rosario Maya]] ([[Usuario discusión:Rosario Maya|discusión]]) 11:28 06 marzo 2015 (UTC) | |||
---- | ---- | ||
| Línea 332: | Línea 394: | ||
'''4.5 Una masa 0.1kg es pegada a un resorte. Es jalado 200mm a la derecha de su posición cuando el resorte no esta ni estirado ni comprimido y entonces es liberado del reposo. Las vibraciones libres resultantes, que están amortiguadas por fricción tienen una frecuencia de 2.0Hz. Se observa que cada oscilación hacia la derecha la masa toma un punto 30mm hacia la izquierda de su límite previo. La masa finalmente llega al reposo a 235mm hacia la izquierda del punto del cual fue liberado. (a) Calcule la fuerza de fricción de deslizamiento.(b) Calcular los límites superior e inferior para la fuerza de pegado.''' | '''4.5 Una masa 0.1kg es pegada a un resorte. Es jalado 200mm a la derecha de su posición cuando el resorte no esta ni estirado ni comprimido y entonces es liberado del reposo. Las vibraciones libres resultantes, que están amortiguadas por fricción tienen una frecuencia de 2.0Hz. Se observa que cada oscilación hacia la derecha la masa toma un punto 30mm hacia la izquierda de su límite previo. La masa finalmente llega al reposo a 235mm hacia la izquierda del punto del cual fue liberado. (a) Calcule la fuerza de fricción de deslizamiento.(b) Calcular los límites superior e inferior para la fuerza de pegado.''' | ||
'''Solución''' | |||
La ecuación de movimiento del sistema es: | La ecuación de movimiento del sistema es: | ||
| Línea 396: | Línea 460: | ||
\] | \] | ||
---- | ---- | ||
Aportaciones por usuarios: [[Usuario:Luis Miguel Sánchez Mtz.|Luis Miguel Sánchez Mtz.]] ([[Usuario discusión:Luis Miguel Sánchez Mtz.|discusión]]) 19:17 8 feb 2014 (UTC), [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 18:50 28 feb 2015 (CST)Esther Sarai García Gonzalez, [[Usuario:Rosario Maya|Rosario Maya]] ([[Usuario discusión:Rosario Maya|discusión]]) 24:07 07 marzo 2015 (CST) | |||
---- | |||
==Problema 4.6 == | ==Problema 4.6 == | ||
'''Expresar el desplazamiento x(t) y la velocidad x'(t) del oscilador armónico sobre amortiguado utilizando funciones hiperbólicas''' | |||
'''Solución''' | |||
Para el caso sobre amortiguado x(t) y x'(t) se expresa | Para el caso sobre amortiguado x(t) y x'(t) se expresa | ||
$x(t)=e^{-\beta t}[A_{1}e^{\omega_{2}t}+A_{2}e^{-\omega_{2}t}]$ | |||
$x'(t)=e^{-\beta t}[-\beta(A_{1}e^{\omega_{2}t}+A_{2}e^{-\omega_{2}t})+(A_{1}\omega_{2}e^{\omega_{2}t}+A_{2}\omega_{2}e^{-\omega_{2}t})]$ | |||
| Línea 417: | Línea 483: | ||
$\omega_{2}=\sqrt{\beta^{2}-\omega_{0}^{2}}$ | |||
Las funciones hiperbólicas están definidas como: | Las funciones hiperbólicas están definidas como: | ||
$\cosh y=\frac{e^{y}+e^{-y}}{2}$ , $\sinh y=\frac{e^{y}-e^{-y}}{2}$ | |||
$e^{y}=\cosh y+\sinh y$ | |||
$e^{-y}=\cosh y-\sinh y$ | |||
| Línea 443: | Línea 509: | ||
<math> W=\frac{1}{2}m\omega^{2}A^{2}</math> | <math> W=\frac{1}{2}m\omega^{2}A^{2}</math> | ||
| Línea 474: | Línea 537: | ||
con 2\tau</math> | con 2\tau</math> | ||
---- | |||
Aportaciones por usuarios: [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 19:15 1 mar 2015 (CST)Esther Sarai García González , [[Usuario:David Alberto Rojas Solis|David Alberto Rojas Solis]] ([[Usuario discusión:David Alberto Rojas Solis|discusión]]) 06:17 6 jul 2013 (CDT) , [[Usuario:Sandyedid|sandy]] ([[Usuario discusión:Sandyedid|discusión]]) 21:31 6 jul 2013 (CDT)--[[Usuario:Sandyedid|sandy]] ([[Usuario discusión:Sandyedid|discusión]]) 21:31 6 jul 2013 (CDT) | |||
---- | |||
== Problema 4.6 bis == | |||
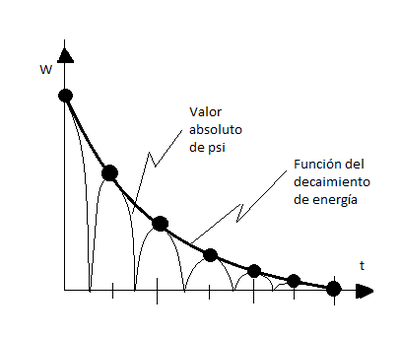
'''4.6 In fig. 4.6 values of the energy W at successive maxima of $|\psi(t)|$ | '''4.6 In fig. 4.6 values of the energy W at successive maxima of $|\psi(t)|$ | ||
| Línea 484: | Línea 549: | ||
'''(not the exponential curve obtained with standard damping) | '''(not the exponential curve obtained with standard damping) | ||
'''En la figura 4.4 los valores de la energía W en los máximos sucesivos | '''Traducción''' | ||
En la figura 4.4 los valores de la energía W en los máximos sucesivos | |||
de $|\psi(t)|$ están graficados contra el tiempo t, para la vibración | |||
amortiguada por fricción de la figura 4.3. Muestre que la curva que | |||
pasa a través de los puntos es una parábola (no la curva exponencial | |||
del amortiguamiento simple) | |||
[[Imagen:Problema_capitulo_4.png|400px|thumb|center|Imagen asociada al problema 4.6]] | [[Imagen:Problema_capitulo_4.png|400px|thumb|center|Imagen asociada al problema 4.6]] | ||
'''Solución''' | |||
Este problema se puede resolver con el hecho de que la energía de | Este problema se puede resolver con el hecho de que la energía de | ||
| Línea 508: | Línea 577: | ||
'''Nota: Este problema pertenece al Libro de Iain G. Main''' | '''Nota: Este problema pertenece al Libro de Iain G. Main''' | ||
--[[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 16:41 21 Febrero 2014 (CDT) | ---- | ||
Aportación por usuarios: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 16:41 21 Febrero 2014 (CDT) , | |||
[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:41 28 feb 2015 (CST) | |||
---- | ---- | ||
==Problema 4.7 == | ==Problema 4.7 == | ||
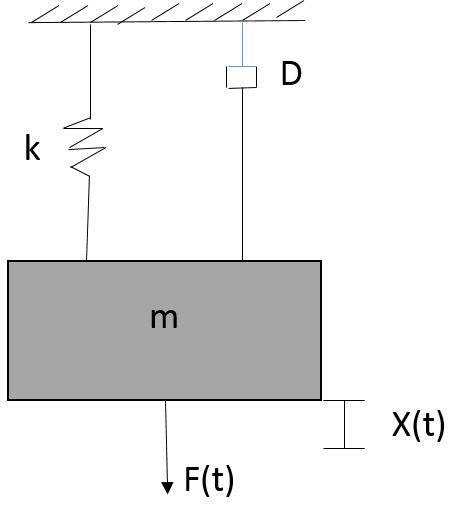
'''Del siguiente sistema mecánico, hallar la ecuación característica donde: $k=1250 [\frac{N}{m}]$, $D=2000 [\frac{N-s}{m}]$, m=10[Kg], F(t)=1[N]. ''' | |||
[[Archivo:sismec.png]] | [[Archivo:sismec.png]] | ||
'''Solución''' | |||
Se suman las fuerzas del resorte, del amortiguador y la fuerza de inercia y se iguala con la fuerza de excitación: | Se suman las fuerzas del resorte, del amortiguador y la fuerza de inercia y se iguala con la fuerza de excitación: | ||
\begin{ | \begin{eqnarray*} | ||
m\frac{d^2x}{dt^2}+D\frac{dx}{dt}+kx=F | m\frac{d^2x}{dt^2}+D\frac{dx}{dt}+kx=F \qquad\qquad (1) | ||
\end{ | \end{eqnarray*} | ||
Sustituyendo valores | Sustituyendo valores | ||
\begin{ | \begin{eqnarray*} | ||
(10)\frac{d^2x}{dt^2}+(2000)\frac{dx}{dt}+(1250)x=1 | (10)\frac{d^2x}{dt^2}+(2000)\frac{dx}{dt}+(1250)x=1 \qquad\qquad(2) | ||
\end{ | \end{eqnarray*} | ||
Utilizando la ecuación general de una ecuación diferencial de segundo orden | Utilizando la ecuación general de una ecuación diferencial de segundo orden | ||
\begin{ | |||
T^2\frac{d^2x}{dt^2}+2\epsilon T\frac{dx}{dt}+x= K | \begin{eqnarray*} | ||
\end{ | T^2\frac{d^2x}{dt^2}+2\epsilon T\frac{dx}{dt}+x= K \qquad\qquad(3) | ||
\end{eqnarray*} | |||
La ecuación (2) la reescribiremos de la forma que posee la ecuación (3), dividiremos la ec. (2) por 1250 para que esté equilibrada: | La ecuación (2) la reescribiremos de la forma que posee la ecuación (3), dividiremos la ec. (2) por 1250 para que esté equilibrada: | ||
\begin{ | |||
\begin{eqnarray*} | |||
(\frac{10}{1250})\frac{d^2x}{dt^2}+(\frac{2000}{1250})\frac{dx}{dt}+(\frac{1250}{1250})x=\frac{1}{1250} | (\frac{10}{1250})\frac{d^2x}{dt^2}+(\frac{2000}{1250})\frac{dx}{dt}+(\frac{1250}{1250})x=\frac{1}{1250} | ||
\end{ | \end{eqnarray*} | ||
\begin{ | \begin{eqnarray*} | ||
(8*10^{-3})\frac{d^2x}{dt^2}+(1.6)\frac{dx}{dt}+x=8*10^{-4} | (8*10^{-3})\frac{d^2x}{dt^2}+(1.6)\frac{dx}{dt}+x=8*10^{-4} \qquad\qquad(4) | ||
\end{ | \end{eqnarray*} | ||
Ahora que la ec. (3) y (4) son de la misma forma, nos dispondremos a encontrar los elementos de (3) para observar el comportamiento del sistema. | Ahora que la ec. (3) y (4) son de la misma forma, nos dispondremos a encontrar los elementos de (3) para observar el comportamiento del sistema. | ||
\begin{ | \begin{eqnarray*} | ||
T^2=8*10^{-3} | T^2=8*10^{-3} | ||
\end{ | \end{eqnarray*} | ||
Tiempo de respuesta del sistema | Tiempo de respuesta del sistema | ||
\begin{ | \begin{eqnarray*} | ||
T=0.089 | T=0.089 | ||
\end{ | \end{eqnarray*} | ||
\begin{ | \begin{eqnarray*} | ||
(2)(\epsilon)(T)=1.6 | (2)(\epsilon)(T)=1.6 | ||
\end{ | \end{eqnarray*} | ||
Despejando epsilon | Despejando epsilon | ||
\begin{ | \begin{eqnarray*} | ||
\epsilon=8.988; \epsilon > 1 | \epsilon=8.988; \epsilon > 1 | ||
\end{ | \end{eqnarray*} | ||
Observamos se trata de un caso sobre amortiguado, entonces calculamos sus polos: | Observamos se trata de un caso sobre amortiguado, entonces calculamos sus polos: | ||
\begin{ | \begin{eqnarray*} | ||
P_{{1},{2}}=\frac{-\epsilon\pm\sqrt{(\epsilon)^2-1}}{T} | P_{{1},{2}}=\frac{-\epsilon\pm\sqrt{(\epsilon)^2-1}}{T} | ||
\end{ | \end{eqnarray*} | ||
\begin{ | \begin{eqnarray*} | ||
P_{{1},{2}}=\frac{-8.988\pm\sqrt{(8.988)^2-1}}{0.089} | P_{{1},{2}}=\frac{-8.988\pm\sqrt{(8.988)^2-1}}{0.089} | ||
\end{ | \end{eqnarray*} | ||
Entonces: | Entonces: | ||
\begin{ | \begin{eqnarray*} | ||
P_{1}=-0.627 | P_{1}=-0.627 | ||
\end{ | \end{eqnarray*} | ||
\begin{ | \begin{eqnarray*} | ||
P_{2}=-199.4 | P_{2}=-199.4 | ||
\end{ | \end{eqnarray*} | ||
Como es un caso sobre amortiguado conlleva a: | Como es un caso sobre amortiguado conlleva a: | ||
\begin{ | \begin{eqnarray*} | ||
X(t)=\frac{KP_{2}}{P_{1}-P_{2}}*\exp^{P_{1}t}+\frac{KP_{1}}{P_{2}-P_{1}}*\exp^{P_{2}t}+K | X(t)=\frac{KP_{2}}{P_{1}-P_{2}}*\exp^{P_{1}t}+\frac{KP_{1}}{P_{2}-P_{1}}*\exp^{P_{2}t}+K | ||
\end{ | \end{eqnarray*} | ||
Sustituimos valores | Sustituimos valores | ||
\begin{ | \begin{eqnarray*} | ||
X(t)=\frac{(8*10^{-4})(-199.4)}{(-0.627)-(-199.4)}*\exp^{(-0.627)t}+\frac{(8*10^{-4})(-0.627)}{(-199.4)-(-0.627)}*\exp^{(-199.4)t}+8*10^{-4} | X(t)=\frac{(8*10^{-4})(-199.4)}{(-0.627)-(-199.4)}*\exp^{(-0.627)t}+\frac{(8*10^{-4})(-0.627)}{(-199.4)-(-0.627)}*\exp^{(-199.4)t}+8*10^{-4} | ||
\end{ | \end{eqnarray*} | ||
Por lo tanto, el comportamiento del sistema mecánico queda denotado por la siguiente expresión de segundo orden: | Por lo tanto, el comportamiento del sistema mecánico queda denotado por la siguiente expresión de segundo orden: | ||
\begin{ | \begin{eqnarray*} | ||
X(t)=-(8*10^{-4})*\exp^{(-0.627)t}(+2.52*10^{-6})*\exp^{(-199.4)t}+(8*10^{-4}) | X(t)=-(8*10^{-4})*\exp^{(-0.627)t}(+2.52*10^{-6})*\exp^{(-199.4)t}+(8*10^{-4}) | ||
\end{ | \end{eqnarray*} | ||
[[Usuario:Angel Nahir Molina Guadarrama|Angel Nahir Molina Guadarrama]] ([[Usuario discusión:Angel Nahir Molina Guadarrama|discusión]]) 11:05 21 feb 2014 (UTC) | ---- | ||
Aportaciones por usuarios: [[Usuario:Angel Nahir Molina Guadarrama|Angel Nahir Molina Guadarrama]] ([[Usuario discusión:Angel Nahir Molina Guadarrama|discusión]]) 11:05 21 feb 2014 (UTC) , [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:20 28 feb 2015 (CST) , [[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 13:28 11 mar 2015 (CDT) | |||
---- | |||
==Problema 4.9 Circuito RLC== | |||
'''¿Qué resistencia R se requiere(en términos de L y C) para impartir a un circuito LRC una frecuencia equivalente a la mitad de la frecuencia no amortiguada?''' | |||
''' | |||
'''Solución:''' | |||
Considerando la ecuación diferencial de un circuito LRC, por regla de Kirchhoff: | |||
: | |||
\begin{eqnarray*} | |||
L\left(\frac{d^{2}\psi}{dt^{2}}\right)+R\left(\frac{d\psi}{dt}\right)+\left(\frac{1}{C}\right)\psi=0 .\qquad\qquad (1) | |||
\end{eqnarray*} | |||
De la ecuación (1) dividimos entre L y obtenemos que: | |||
\begin{ | \begin{eqnarray*} | ||
\frac{d^{2}\psi}{dt^{2}}+\frac{R}{L}\left(\frac{d\psi}{dt}\right)+\frac{1}{LC}\psi=0 \qquad\qquad (2) | |||
\end{eqnarray*} | |||
Observamos la ecuación (2) se comporta en forma de una oscilación amortiguada [[Ondas: Atenuacion suave]]: | Observamos la ecuación (2) se comporta en forma de una oscilación amortiguada [[Ondas: Atenuacion suave]]: | ||
\begin{eqnarray*} | |||
\frac{d^{2}\psi}{dt^{2}}+\gamma\frac{d\psi}{dt}+\omega_{0}^{2}\psi=0 \qquad\qquad (3) | |||
\end{eqnarray*} | |||
Resolviendo la ecuación diferencial (3) para oscilaciones amortiguadas, obtenemos que la una solución es: | Resolviendo la ecuación diferencial (3) para oscilaciones amortiguadas, obtenemos que la una solución es: | ||
| Línea 662: | Línea 717: | ||
Donde | Donde | ||
\ | \begin{eqnarray*} | ||
\omega_{t}=\sqrt{\omega_{0}^{2}-(\frac{\gamma}{2})^{2}} \qquad\qquad (4) | |||
\end{eqnarray*} | |||
Por lo tanto usando la ecuación (4) obtenemos que la frecuencia angular en un circuito LRC, está dada por: | Por lo tanto usando la ecuación (4) obtenemos que la frecuencia angular en un circuito LRC, está dada por: | ||
\begin{eqnarray*} | |||
\omega= \sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}} \qquad\qquad (5) | |||
\end{eqnarray*} | |||
Usaremos la ecuación (5) para resolver el problema. Como el problema plantea que <math>\omega</math> tiene que ser la mitad de <math>\omega_{0}</math> . Donde <math>\omega_{0}=\frac{1}{\sqrt{LC}}</math> | Usaremos la ecuación (5) para resolver el problema. Como el problema plantea que <math>\omega</math> tiene que ser la mitad de <math>\omega_{0}</math> . Donde <math>\omega_{0}=\frac{1}{\sqrt{LC}}</math> | ||
| Línea 673: | Línea 731: | ||
Por lo tanto obtenemos que <math>\omega =\frac{\omega_{0}}{2}</math> sustituyendo los valores de las <math>\omega</math>: | Por lo tanto obtenemos que <math>\omega =\frac{\omega_{0}}{2}</math> sustituyendo los valores de las <math>\omega</math>: | ||
\begin{eqnarray*} | |||
\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}= \frac{1}{2 \sqrt{LC}} \qquad\qquad (6) | |||
\end{eqnarray*} | |||
Desarrollando la ecuación (6), primero elevando al cuadrado los dos lados de la ecuación (6): | Desarrollando la ecuación (6), primero elevando al cuadrado los dos lados de la ecuación (6): | ||
| Línea 691: | Línea 752: | ||
<math>R= \sqrt{\frac{3L}{C}}</math> | <math>R= \sqrt{\frac{3L}{C}}</math> | ||
--[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 23:58 28 feb 2015 (CST) | ---- | ||
Aportación por usuario: [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 23:58 28 feb 2015 (CST) | |||
---- | |||
== Problema Circuito RC en serie == | |||
Se aplica una fuerza electromotriz de $100V$ a un circuito en serie $RC$ en el que la resistencia es de $200 ohms$ y la capacitancia de <math>10^{-4} farads</math>. Determine la carga $q(t)$ del capacitor, si $q(0)=0$. Encuentre la corriente $i(t)$. | |||
[[Archivo:CircuitoRC2.png]] | |||
'''Solución:''' | |||
'''''para encontrar la carga $q(t)$ tenemos que:''''' | |||
Entonces, aplicando la ley de mallas de kirchoff al circuito de la Figura para las caídas de voltaje en función de la carga $q(t)$, tenemos: | |||
<math> R \frac{d q}{d t} + \frac{1}{C} q = E ( t) \qquad (1)</math> | |||
Donde $C, R$ son constantes conocidas como la capacitancia y resistencia, respectivamente. | |||
para encontrar la carga del circuito rc en serie, la ecuación diferencial a resolver, según la ecuación (1) y sustituyendo los valores del problema planteado, es: | |||
<math>200 \frac{d q}{d t} + \frac{1}{1 \times 10^{- 4}} q = 100 \qquad (2)</math> | |||
Resolviendo la ecuación (2) | |||
Forma estándar: | |||
<math> \frac{d y}{d x} + P ( x) y = g ( x) \Rightarrow \frac{d q}{d t} + 50 q = \frac{1}{2} </math> | |||
Factor Integrante: | |||
<math> e^{\int P ( x) d x} = e^{\int 50 d t} = e^{50 \int d t} = e^{50 t} </math> | |||
Forma de la solución: | |||
<math> y = y_c + y_p \Rightarrow q ( t) = q_{tr} ( t) + q_{s} ( t)</math> | |||
$ y_c = A e^{ -\int P ( x) d x} \Rightarrow q_{tr} ( t) = A e^{- \int 50 d t}\\ \Rightarrow q_{tr} ( t) = A e^{- 50 t} $ | |||
Donde $q_{tr}$ es la carga transitoria del capacitor en el circuito RC en serie. | |||
$y_p = \frac{1}{e^{\int P ( x) d x}} \int e^{\int P ( x) d x} f ( x) d x \Rightarrow q_s ( t) = \frac{1}{e^{50 t}} \int e^{50 t} \ast \frac{1}{2} d t\\ \Rightarrow q_s ( t) = \frac{1}{2 \ast 50 \ast e^{50 t}} \int e^{50 t} ( 50) d t\\ \Rightarrow q_s ( t) = \frac{1}{100 \ast e^{50 t}} \int e^{50 t} ( 50) d t\\ \Rightarrow q_s ( t) = \frac{1}{100} \ast e^{- 50 t} [ e^{50 t}]\\ \Rightarrow q_s ( t) = \frac{1}{100}$ | |||
$q_s$ es la carga estacionaria del capacitor. Por tanto la carga (total en el circuito), buscada es: | |||
$q ( t) = q _{tr} ( t) + q_s ( t) \nonumber\\ \qquad \qquad q(t) = A e^{- 50 t} + \frac{1}{100} \qquad (3) $ | |||
Para encontrar el valor de $A$ utilizamos los valores iniciales $q(0)=0$, cuando el tiempo $t=0$ la carga $q$ en el capacitor es 0 (como en un circuito abierto). Por tanto, sustituyendo estos valores en la ecuación (3) para la corriente resultante del circuito nos da: | |||
$ q ( t) = A e^{- 50 t} + \frac{1}{100}\\ 0 = A e^{- 50 ( 0)} + \frac{1}{100}\\ 0 = A ( 1) + \frac{1}{100}\\ 0 = A + \frac{1}{100}$ | |||
$\boxed{\therefore A = – \frac{1}{100}} $ | |||
De donde sustituyendo $A$ en (3) nos da la Carga en el capacitor: | |||
$ q ( t) = – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \, $ | |||
'''''Obteniendo la corriente $i(t)$, del circuito RC en serie''''' | |||
sabemos que : | |||
<math>Ri + \frac{1}{C}q = E(t)</math> | |||
sustituyendo los valores que conocemos, tenemos: | |||
$200 i + \frac{1}{1 \times 10^{- 4}} \left[ – \frac{1}{100} e^{- 50t} + \frac{1}{100} \right] = 100$ | |||
despejando $i(t)$ | |||
$200 i + \frac{1}{1 \times 10^{- 4}} \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = 100\\ i ( t) + \frac{10000}{200} \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = \frac{1}{2}\\ i ( t) + 50 \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = \frac{1}{2}\\ i ( t) – \frac{1}{2} e^{- 50 t} + \frac{1}{2} = \frac{1}{2}\\ i ( t) – \frac{1}{2} e^{- 50 t} = – \frac{1}{2} + \frac{1}{2}\\ i ( t) = \frac{1}{2} e^{- 50 t}$ | |||
la corriente en el circuito, es: | |||
$\boxed{ \therefore i( t) = \frac{1}{2} e^{- 50 t}} $ | |||
---- | |||
Aportación por usuarios: [[Usuario:Luis Martínez|Luis Martínez]] ([[Usuario discusión:Luis Martínez|discusión]]) 23:59 1 mar 2015 (CST) | |||
---- | |||
== Problema 4.10 == | |||
'''Un ratón de 0.3kg se mueve en el extremo de un resorte con $K=2.50N/m$ sometido a una acción de una fuerza amortiguadora $F{}_{x}=-b\upsilon_{x}$''' | |||
'''A)Si $b=.9 kg/s$ ¿Qué frecuencia de oscilación tiene el ratón ?''' | |||
'''B)¿Con qué valor de b la amortiguación resulta crítica?''' | |||
SOLUCIÓN: | |||
De la ecuación $\frac{d^{2}\psi}{dt^{2}}+\gamma\frac{d\psi}{dt}+\omega_{0}^{2}\psi=0\,\,\,\,\,\,\,\,\,(a)$ | |||
Proponemos la solución $\psi=Ae^{-\alpha t}cos(\omega t)$ | |||
Entonces: | |||
\[ | |||
\psi=Ae^{-\alpha t}cos(\omega t) | |||
\] | |||
\[ | |||
\dot{\psi}=-A\alpha e^{-\alpha t}cos(\omega t)-A\omega e^{-\alpha t}sen(\omega t) | |||
\] | |||
\[ | |||
\ddot{\psi}=A\alpha^{2}e^{-\alpha t}cos(\omega t)+2A\omega\alpha e^{-\alpha t}sen(\omega t)-A\omega^{2}e^{-\alpha t}cos(\omega t) | |||
\] | |||
Por lo que substituyendo en la ecuación $(a)$ tenemos: | |||
\[ | |||
A\alpha^{2}e^{-\alpha t}cos(\omega t)+2A\omega\alpha e^{-\alpha t}sen(\omega t)-A\omega^{2}e^{-\alpha t}cos(\omega t)-\gamma(A\alpha e^{-\alpha t}cos(\omega t)+A\omega e^{-\alpha t}sen(\omega t))+A\omega_{0}^{2}e^{-\alpha t}cos(\omega t)=... | |||
\] | |||
\[ | |||
=Ae^{-\alpha t}[\alpha^{2}cos(\omega t)+2\omega\alpha sen(\omega t)-\omega^{2}cos(\omega t)-\gamma(\alpha cos(\omega t)+\omega sen(\omega t))+\omega_{0}^{2}cos(\omega t)]=0 | |||
\] | |||
Sí, y sólo sí: | |||
\[ | |||
2\omega\alpha sen(\omega t)-\gamma\omega sen(\omega t)=0....(1) | |||
\] | |||
y, | |||
\[ | |||
\alpha^{2}cos(\omega t)-\omega^{2}cos(\omega t)-\gamma\alpha cos(\omega t)-\omega_{0}^{2}cos(\omega t)=0....(2) | |||
\] | |||
De $(1)$ podemos factorizar $omega$ y queda: | |||
\[ | |||
2\alpha sen(\omega t)-\gamma sen(\omega t)=0 | |||
\] | |||
\[ | |||
2\alpha sen(\omega t)=\gamma sen(\omega t) | |||
\] | |||
Por lo que $2\alpha=\gamma$ y $\alpha=\frac{\gamma}{2}$ . Entonces | |||
de (2) al factorizar $cos(\omega t)$ tenemos... | |||
\[ | |||
\alpha^{2}-\omega^{2}-\gamma\alpha+\omega_{0}^{2}=0 | |||
\] | |||
Dejando todo en términos de $\gamma$, | |||
\[ | |||
(\frac{\gamma}{2})^{2}-\omega^{2}-\gamma(\frac{\gamma}{2})+\omega_{0}^{2}=0 | |||
\] | |||
\[ | |||
\frac{\gamma}{4}^{2}-\omega^{2}-\frac{\gamma^{2}}{2}+\omega_{0}^{2}=0 | |||
\] | |||
Por lo tanto: | |||
\[ | |||
\omega=\pm\sqrt{\omega_{0}^{2}-\frac{1}{4}\gamma^{2}}\,\,\,\,\,\,(3) | |||
\] | |||
Y si recordamos que $\gamma=\frac{b}{m}$ y $\omega_{0}=\sqrt{\frac{k}{m}}$ | |||
, podemos escribir la ecuación como: | |||
\[ | |||
\omega=\pm\sqrt{\frac{k}{m}-(\frac{b}{2m}){}^{2}}\,\,\,\,\,\,(3') | |||
\] | |||
Entonces substituimos los datos en la ecuación (3') y obtenemos: | |||
\[ | |||
\omega=\pm\sqrt{\frac{2.50N/m}{.3kg}-(\frac{.9kg/s}{2(.3kg)}){}^{2}}=2.47rad/seg | |||
\] | |||
Pero esta es la frecuencia angular, para la frecuencia conocemos la | |||
relación $f=\frac{\omega}{2\pi}$ por lo que: | |||
\[ | |||
f=\frac{\omega}{2\pi}=.393Hz | |||
\] | |||
Y finalmente para encontrar el valor de $b$ para que la amortiguación | |||
sea crítica sabemos que $b=2\sqrt{km}$ por lo que: | |||
\[ | |||
b=2\sqrt{km}=2\sqrt{(2.50N/m)(.3kg)}=1.73kg/seg | |||
\] | |||
---- | |||
Resuelto por usuario: [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 21:25 5 mar 2015 (CST) | |||
---- | |||
= Ejercicios Adicionales = | |||
== Problema adicional 1 == | |||
'''Se inician oscilaciones eléctricas en un circuito en serie que contiene una capacitancia C, una inductancia L y una resistencia R. | |||
a) si <math>R\ll\sqrt{\frac{4L}{C}}</math> (amortiguamiento débil) ¿cuanto tiempo pasara antes de que la amplitud de la oscilación de la corriente disminuya a 50.0% de su valor inicial? | |||
b) ¿cuanto tiempo tarda en disminuir la energía a 50% de su valor inicial? ''' | |||
La ecuación para este tipo de problema es de la forma: | |||
<math>Q=Q_{max}\exp(-\frac{Rt}{2L})\cos\left(\omega_{d}t\right)</math> | |||
'''Inciso a''' | |||
a) | |||
con: | |||
<math>\omega_{d}=\sqrt{\frac{l}{LC}+\left(\frac{R}{2L}\right)^{2}}</math> | |||
Pero puesto que el tamaño de las oscilaciones decrecientes depende de la exponencial y el termino Q, solo se usara esa parte de la ecuación anterior, así a para encontrar el tiempo al que hay 50% de la carga inicial, se hace: | |||
<math>Q_{max}\exp(-\frac{Rt}{2L})=\frac{Q_{max}}{2}</math> | |||
: | |||
<math>\exp(-\frac{Rt}{2L})=\frac{1}{2}</math> | |||
: | |||
<math>-\frac{Rt}{2L}=\ln(\frac{1}{2})</math> | |||
: | |||
<math>t=-\frac{2L}{R}\ln\frac{1}{2}</math> | |||
'''Inciso b''' | |||
b) | |||
La energía para este caso esta expresada por: | |||
<math>E=\frac{1}{2C}Q_{max}^{2}</math> | |||
Dividiendo esta entre dos y despejando para t da: | |||
<math>E_{1}=\frac{Q_{max}^{2}}{4C}=\frac{1}{2C}\left(\frac{Q_{max}}{\sqrt{2}}\right)^{2}</math> | |||
: | |||
<math>\frac{Q_{max}}{\sqrt{2}}=Q_{max}\exp(-\frac{Rt}{2L})</math> | |||
: | |||
<math>\ln\left(\frac{1}{\sqrt{2}}\right)=-\frac{Rt}{2L}</math> | |||
: | |||
<math>t=-\frac{2L}{R}\ln\left(\frac{1}{\sqrt{2}}\right)</math> | |||
---- | |||
Resuelto por usuario: [[Usuario:Uziel Sanchez Gutierrez|Uziel Sanchez Gutierrez]] ([[Usuario discusión:Uziel Sanchez Gutierrez|discusión]]) 18:43 1 mar 2015 (CST) | |||
---- | |||
==PROBLEMA 1.50 Engineering vibration,3rd edition by Daniel J.Inman== | ==PROBLEMA 1.50 Engineering vibration,3rd edition by Daniel J.Inman== | ||
'''Resorte amortiguador del siguiente sistema mecánico hallar la ecuación característica donde : K= cte del resorte = 1250[N/m],D= cte del amortiguador =2000[Ns/m],M=masa= 10[kg],F(t)= 1N''' | '''Resorte amortiguador del siguiente sistema mecánico hallar la ecuación característica donde : K= cte del resorte = 1250[N/m],D= cte del amortiguador =2000[Ns/m],M=masa= 10[kg],F(t)= 1N''' | ||
\[M\frac{d^{2}x}{dt^{2}}+D\frac{dx}{dt}+Kx=F\] | '''Solución''' | ||
Primero se hace la suma de las 3 fuerzas y se igualan con la fuerza de excitación, empezando con la fuerza de inercia | |||
\[ | |||
M\frac{d^{2}x}{dt^{2}}+D\frac{dx}{dt}+Kx=F | |||
\] | |||
Sustituyendo valores | Sustituyendo valores | ||
Se pasa esta | $10 \frac{d^2x}{dt^2}+2000 \frac{dx}{dt}+1250x=1. $ | ||
se divide cada | Se pasa esta ecuación a una forma general para una ecuación diferencial de segundo orden | ||
$T^ 2 \frac{d^2x}{dt^2}+2 \gamma T \frac{dx}{dt}+x=K$ | |||
se divide cada termino de la ecuación entre 1250 para que este equilibrada | |||
$\frac{1}{125}\frac{d ^2x}{dt^2} + \frac{200}{125} \frac{dx}{dt} + \frac{125}{125}x = \frac{1}{1250}$ | |||
Obteniendo: | Obteniendo: | ||
Ya que $T^2=8 \times 10^{-3}$, entonces $T=\sqrt{8 \times 10^{-3}}$, | $8 \times 10^{-3}\frac{d^2x}{dt^2} + 1.6 \frac{dx}{dt}+ x= 8 \times 10^{-4}$ | ||
Teniendo la ecuación anterior podemos encontrar los elementos para analizar el comportamiento del sistema. Lo que se hace es calcular $T$. | |||
Ya que $T^2=8 \times 10^{-3}$, entonces $T=\sqrt{8 \times 10^{-3}}$, así $T=0.089$. Donde $T$ es el tiempo de respaldo del sistema. | |||
Teniendo que | Teniendo que | ||
$ 2 \gamma T = 1.6 $ | |||
Encontramos que $\gamma = 8.988 $. Se observa que $\gamma >1$, se trata de un caso sobreamortiguado. | |||
Encontramos que $\gamma = 8.988 $. Se observa que $\gamma >1$, se trata de un caso sobreamortiguado. | |||
Calculamos ahora ahora los polos del sistema: | Calculamos ahora ahora los polos del sistema: | ||
$P_{1,2} = \frac{- \gamma \pm \sqrt{\gamma^2 -1}}{ T }$ | |||
Por lo que $P_1 = -0.627$ y $P_2= -199.4$ | Por lo que $P_1 = -0.627$ y $P_2= -199.4$ | ||
Prosigue calcular el sistema. Como nos da un caso sobreamortiguado tenemos que | Prosigue calcular el sistema. Como nos da un caso sobreamortiguado tenemos que | ||
$ X(t) = \frac{kP_2}{P_1 - P_2} e^{P_1t} + \frac{kP_1}{P_2-P_1}e^{P_2t} + k $ | |||
Ahora sustituyendo los valores: | Ahora sustituyendo los valores: | ||
$x(t) = \frac{(8 \times 10^{-4})(-199.9) }{(-0.627)-(199)} e^{-0.627t} + \frac{(8 \times 10^{-4})(-0.06279}{199.9 - (-0.627)}e^{-199.9t} + 8 \times 10^{-4}$ | |||
$x(t)= -8 \times 10^{-4} e^{-0.627t } + (2.52 \times10^{-6}) e^{-0.199.4t}+ (8 \times 10^{-4})$ | |||
La ecuación anterior es la respuesta al sistema de segundo orden | |||
---- | |||
Aportaciones por usuarios: [[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 10:01 1 mar 2015 (CST)luisa alejandra vega sanchez | |||
---- | |||
==Problema 4.8 Serway== | |||
'''El sistema de la figura tiene una masa <math>1.52</math> | |||
'''y una constante de fuerza de <math>8.13N/m</math> la fuerza resistiva esta dada por <math>-v{(dx \over dt)}</math> | |||
'''donde <math>b=227g/s</math> | |||
'''suponiendo que se empuja el bloque a un lado a una distancia <math>12.5cm</math> y se suelta''' | |||
'''Inciso a''' | |||
a) calcule el intervalo temporal necesario para que la amplitud pierda un tercio de su valor inicial | |||
:solución: | |||
:tenemos que la energía esta dada por | |||
:<math>E(t)={{k A^2 exp(-2t/\gamma)}\over 2}</math> | |||
tenemos las condiciones iniciales en <math>t=0</math> es | |||
:<math>E(t)=k A^2</math> | |||
igualando las dos condiciones con <math>t=0</math> y a un tiempo <math>t</math> | |||
obtenemos lo siguiente: | |||
:<math>t=ln(3) \gamma</math> | |||
:<math>t=ln 3(0.0066) </math> | |||
'''Inciso b''' | |||
b) ¿cuántas oscilaciones realizó el bloque en este tiempo? | |||
para saber n oscilaciones tenemos la siguiente función | |||
:<math>A=A_0 exp(n\pi/Q)</math> | |||
despejando <math>n</math> tenemos | |||
:<math>n={ln 3 Q\over{\pi}}</math> | |||
donde | |||
:<math>Q={\omega_o\over {\gamma}}</math> | |||
--[[Usuario: | ---- | ||
Realizado por usuarios: [[Usuario:Jose de jesus|Jose de jesus]] ([[Usuario discusión:Jose de jesus|discusión]]) 21:06 27 feb 2015 (CST)jose de Jesus Arizpe Flores 27/02/2015 ,[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 01:49 28 feb 2015 (CST) | |||
---- | |||
==Problema 4.7 Waves. C.A. Coulson -A. Jeffrey . Ed Longman== | ==Problema 4.7 Waves. C.A. Coulson -A. Jeffrey . Ed Longman== | ||
''' En un circuito RLC, que una inductancia de 1 [H], una resistencia de 40 [$\Omega$] y un capacitor de $\frac{1}{4E^{4}}$ [F], se aplica un voltaje de V = 24 V. Determine el comportamiento de la carga y la intensidad de corriente en el circuito. ''' | |||
'''Solución''' | |||
La ecuación que describe el comportamiento del circuito: | |||
$L \frac{ d^{2}Q}{dt^{2}} + R \frac{dQ}{dt} + \frac{1}{C} Q = E(t) .\qquad\qquad (1)$ | |||
Derivando la ecuación (1) resulta: | Derivando la ecuación (1) resulta: | ||
$ L \frac{d^{2}I}{dt^{2}} + R\frac{dI}{dt}+\frac{1}{C}I(t)=\frac{dE(t)}{dt}.\qquad\qquad (2)$ | |||
Sustituir los datos en las ecuaciones (1) y (2) respectivamente. | Sustituir los datos en las ecuaciones (1) y (2) respectivamente. | ||
$\frac{ d^{2}Q}{dt^{2}} + 40 \frac{dQ}{dt} + 4E^{4} Q(t) = \frac{1}{2}$ | |||
$ \frac{d^{2}I}{dt^{2}} + 40\frac{dI}{dt}+ 4E^{4}I(t) = 0 $ | |||
Considerando la condiciones iniciales $Q(0) = 10^{-4}$ y $I=10^{-2}$ tenemos como solución. | Considerando la condiciones iniciales $Q(0) = 10^{-4}$ y $I=10^{-2}$ tenemos como solución. | ||
$Q(t) = \frac{1}{8E^{3}}e^{-20t}[\frac{47\sqrt{11}}{2.64E^{4}}\sin(\sqrt{1160t} + \frac{7}{8E^{3}}\cos(\sqrt{1160 t})]$ | |||
$I(t) = \frac{dQ}{dt}= e^{-20t}[\frac{1}{100}\cos(\sqrt{1160 t})-\frac{37\sqrt{11}}{6.6E^{3}}\sin(\sqrt{1160 t})] $ | |||
--[[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 16:31 1 mar 2015 (CST)Esther Sarai García Gonzalez | ---- | ||
Aportación por usuario: [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 16:31 1 mar 2015 (CST)Esther Sarai García Gonzalez | |||
---- | |||
== Problema Propuesto al Capítulo 4 == | |||
Un resorte vertical con constante de 6 lb/ft tiene suspendida una masa de 1/2 slug. Se aplica una fuerza externa dada por <math> f(t)=40\sin2t,t\geq0 | |||
</math>. Supóngase que actúa una fuerza amortiguadora numéricamente igual a dos veces la velocidad instantánea y que inicialmente el cuerpo está en reposo en su posición de equilibrio. Determine la posición del cuerpo en cualquier tiempo <math> t>0 | |||
</math>. | |||
'''Solución.''' | |||
Denotemos con <math> f(t) | |||
</math> la fuerza exterior que actúa sobre la masa. De la segunda ley de Newton, la ecuación diferencial del movimiento es | |||
: <math> m\frac{d^{2}x}{d^{2}t}=-kx-\beta\frac{dx}{dt}+f(t),...(4.1) | |||
</math> | |||
o bien | |||
: <math> \frac{d^{2}x}{d^{2}t}+2\lambda\frac{dx}{dt}+\omega^{2}x=F(t),...(4.2) | |||
</math> | |||
donde <math> 2\lambda=\beta/m,\omega^{2}=k/m | |||
</math> y <math> F(t)=f(t)/m | |||
</math>. | |||
Para resolver la ecuación no homogénea (4.2) podemos emplear el método de los coeficientes indeterminados o el de variación de parámetros, según sea más conveniente. | |||
Con los valores de <math> k=6lb/ft | |||
</math>, <math> m=1/2slug | |||
</math> y <math> \beta=2 | |||
</math>, la ecuación diferencial de movimiento resultante es | |||
: <math> \frac{d^{2}x}{d^{2}t}+4\frac{dx}{dt}+12x=80\sin2t,...(4.3) | |||
</math> | |||
La solución complementaria de (4.3) es | |||
: <math>x_{c}(t)=\exp\left(-2t\right)\left(c_{1}\cos2\sqrt{2}t+c_{2}\sin2\sqrt{2}t\right). | |||
</math> | |||
Usando el método de los coeficientes indeterminados proponemos una solución particular de (4.3) de la forma | |||
: <math> x_{p}(t)=A\cos(2t)+B\sin(2t). | |||
</math> | |||
En tal caso | |||
: <math> \dot{x}_{p}(t)=-2A\cos(2t)+2B\sin(2t) | |||
</math> | |||
: <math> \ddot{x}_{p}(t)=-4A\cos(2t)-4B\sin(2t). | |||
</math> | |||
Sustituyendo en (4.3), se sigue que | |||
: <math> (8A+8B)\cos(2t)+(8B-8A)\sin(2t)=80\sin(2t). | |||
</math> | |||
El sistema de ecuaciones resultante | |||
: <math> 8A+8B=0, | |||
</math> | |||
: <math> -8A+8B=80, | |||
</math> | |||
conduce a los valores A=-5 y B=5. Así que | |||
: <math> x(t)=\exp(-2t)\left(c_{1}\cos(2\sqrt{2}t)+c_{2}\sin(2\sqrt{2}t)\right)+5\left(\sin(2t)-\cos(2t)\right). | |||
</math> | |||
Empleando las condiciones iniciales <math> x(0)=0 | |||
</math> y <math> \dot{x}(0)=0 | |||
</math> encontramos que <math> c_{1}=5 | |||
</math> y <math> c_{2}=5 | |||
</math>.Por tanto | |||
: <math> x(t)=5\exp(-2t)\left(\cos(2\sqrt{2}t)\right)+5\left(\sin(2t)-\cos(2t)\right). | |||
</math> | |||
Obsérvese que en el problema, la solución complementaria | |||
: <math> x_{c}(t)=5\exp(-2t)\cos(2\sqrt{2}t) | |||
</math> | |||
tiene la propiedad de que | |||
: <math> lim_{t\rightarrow\infty}x_{c}(t)=0, | |||
</math> | |||
por lo que se dice que <math> x_{c}(t) | |||
</math> es un término transitorio o una solución transitoria. Así para valores grandes de t <math> x(t) | |||
</math> se aproxima a <math> x_{p}(t) | |||
</math>. A <math> x_{p}(t) | |||
</math> se le llama solución estacionario o de estado permanente. | |||
---- | |||
Bibliografía. | |||
Elizarraraz Martínez David, “Ecuaciones diferenciales: técnicas de solución y aplicaciones”, Primera Edición 2004, UAM-Azcapotzalco, México DF. | |||
---- | |||
Aportación por usuario: [[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 19:26 4 mar 2015 (CST) | |||
---- | |||
== Problema 3.16, Analytical Mechanics, Fowles & Cassiday, Seventh Edition == | |||
'''If a series LCR circuit is connected across the terminals of an electric generator that produces a voltage $V=V_0 e^{i\omega t}$, the flow of electrical charge $q$ through the circuit is given by the following second-order differential equation:''' | |||
<math> | |||
L \dfrac{d^2q}{dt^2} + R \dfrac{dq}{dt} + \dfrac{1}{C} q = V_0 e^{i \omega t} | |||
</math> | |||
'''a) Verify the correspondence shown in Table 3.6.1 between the parameters of a driven mechanical oscillator and the above driven electrical oscillator.''' | |||
'''b)Calculate the $Q$ of the electrical circuit in therms of the coefficients of the above differential equation.''' | |||
'''c) Show that, in the case of small damping, $Q$ can be written as $Q=R_0/R$, where $R_0=\sqrt{L/C}$ is the characteristic impedance of the circuit.''' | |||
---- | |||
'''Traducción''' | |||
'''Si un circuito en serie RCL es conectado en las terminales de un generador eléctrico que produce un voltaje $V=V_0 e^{i\omega t}$, el flujo de carga eléctrica $q$ a través del circuito está dado por la siguiente ecuación diferencial de segundo orden:''' | |||
<math> | |||
L \dfrac{d^2q}{dt^2} + R \dfrac{dq}{dt} + \dfrac{1}{C} q = V_0 e^{i \omega t} | |||
</math> | |||
'''a) Verifique la correspondencia mostrada en la Tabla 3.6.1 entre los parámetros del oscilador armónico forzado y el mencionado oscilador eléctrico forzado.''' | |||
'''b) Calcule $Q$ del circuito eléctrico en términos de los coeficientes de la anterior ecuación diferencial. ''' | |||
'''c) Muestre que, en el caso de un amortiguamiento ligero, $Q$ puede escribirse como $Q=R_0/R$, donde $R_0=\sqrt{L/C}$ es la impedancia característica del circuito. ''' | |||
---- | |||
'''Inciso a''' | |||
Tenemos para el inciso $a)$: | |||
$m(\text{masa}) \rightarrow L(\text{inductancia})$ | |||
$x(\text{desplazamiento}) \rightarrow q (\text{carga})$ | |||
$c(\text{coeficiente de amortiguamiento})\rightarrow R(\text{resistencia})$ | |||
$k(\text{constante de restitución})\rightarrow C^{-1}(\text{recíproco de la capacitancia})$ | |||
$F(\text{fuerza}) \rightarrow V(\text{diferencia de potencial})$ | |||
'''Inciso b''' | |||
Resolviendo $b)$: | |||
Sabemos que $Q=\omega_d / 2\gamma$, además $\omega_0^2=1/LC$ y $\gamma = R/2L$, por lo que: | |||
<math> | |||
Q = \dfrac{\omega_d}{2\gamma} = \dfrac{\sqrt{\omega_0^2 - \gamma^2}}{2\gamma} | |||
= \dfrac{\sqrt{\left(\dfrac{1}{LC}\right) - \left(\dfrac{R^2}{4L^2}\right)}}{2\left(\dfrac{R}{2L}\right)} | |||
</math> | |||
por lo que, simplificando, obtenemos que: | |||
<math> | |||
Q =\sqrt{\left(\dfrac{L}{R^2C}\right) - \dfrac{1}{4}} | |||
</math> | |||
Ahora, para el inciso $c)$: | |||
Sabemos que si el amortiguamiento es muy pequeño $\omega_d \approx \omega_0$, por lo que: | |||
<math> | |||
Q = \dfrac{\omega_0}{2\gamma} = \dfrac{\sqrt{L/C}}{R} | |||
</math> | |||
Por lo tanto, para un amortiguamiento pequeño, tenemos: | |||
<math> | |||
Q = \dfrac{R_0}{R} | |||
</math> | |||
donde $R_0 = \sqrt{L/C}$ | |||
---- | |||
Resuelto por usuario: [[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 21:32 10 mar 2015 (CDT) | |||
---- | |||
== Un problema de aplicación a circuitos eléctricos== | |||
Se tiene un circuito formado por una resistencia <math>R</math>, una bobina <math>L</math> y un capacitor <math>C</math> están conectados en serie a una fuente <math>V_{S}(t)=2e^{-t/3}</math> voltios en el tiempo <math>t</math> es decir, la resistencia de la fuente decae a una razón exponencial. | |||
Suponga que <math>R=4k\Omega, C=0.25\mu F, L=1.6Hz</math> El voltaje <math>v(t)</math> a través del capacitor es una solución de la ecuación de segundo orden | |||
'''Solución''' | |||
<math>LC\frac{d^{2}v}{dt^{2}}+RC\frac{dv}{dt}=V_{s}(t)</math> | |||
y con los valores proporcionados se tiene | |||
<math>0.4x10^{-6}\frac{d^{2}v}{dt^{2}}+10^{-3}\frac{dv}{dt}+v=2e^{-t/3}</math> | |||
Podemos transformar transformar esta ultima ecuación como sigue | |||
<math>\frac{d^{2}v}{dt^{2}}+2500\frac{dv}{dt}+2.5x10^{-6}v=5x10^{6}e^{-t/3}</math> | |||
calculando la solución tenemos: | |||
Los eigenvalores son <math>(-1.25\pm i\sqrt{0.93})x10^{3}</math>. Usando la aproximación <math>0.968</math> | |||
para <math>\sqrt{0.9375}</math> la solución es | |||
<math>v(t)=k_{1}e^{-1250t}\sin{(968t)}+k_{2}e^{-1250t}\cos{(968t)}</math> | |||
Donde <math>k_{1}, k_{2}</math> son constantes. | |||
Ahora para encontrar la solución para la ecuación no homogénea | |||
<math>\frac{d^{2}v}{dt^{2}}+2500\frac{dv}{dt}+2.5x10^{-6}v=5x10^{6}e^{-t/3}</math> | |||
suponemos que <math>v_{p}=ke^{-t/3}</math> donde <math>k </math> es el coeficiente indeterminado. Para encontrar el valor de <math>k </math> se sustituye en la ecuación diferencial anterior quedando | |||
<math>\frac{d^{2}v}{dt^{2}}+2500\frac{dv}{dt}+2.5x10^{-6}v=5x10^{6}e^{-t/3}=(1/9-2500/3+2.5x10^{6})ke^{t/3}</math> | |||
así que la solución particular queda como | |||
<math>v_{p}=2e^{-t/3}</math> | |||
Ahora determinamos la solución general con los resultados ya obtenidos, es decir, la solución homogénea y particular | |||
<math>v(t)=k_{1}e^{-1250t}\sin{(968t)}+k_{2}e^{-1250t}\cos{(968t)}+2e^{-t/3}</math>. | |||
---- | |||
Realizado por usuario: Hector Resendiz [[Usuario:Héctor Reséndiz|Héctor Reséndiz]] ([[Usuario discusión:Héctor Reséndiz|discusión]]) 21:59 29 mar 2015 (CDT) | |||
---- | |||
[[Categoría: Vibra]] | |||
Revisión actual - 04:42 6 oct 2023
Problemas capítulo 2 Amortiguamiento en la física.
Ejercicios resueltos sobre osciladores amortiguados, para distintas areas de la física.
Del libro Vibrations and waves in physics del autor Iain G. Main. Y algunos problemas adicionales de diversos libros.
Problema 4.1
4.1 Show that the relaxation time for very heavily damped LCR circuit is RC.
Traducción
4.1 Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC.
Solución
Conocemos la ecuación para el oscilador ligeramente amortiguado (ecuación 3.3 G. Main, Vibrations and waves in physics):
También sabemos que \begin{equation}\gamma=\frac{b}{m}\end{equation}
\begin{equation}\omega_{0}^{2}=\frac{s}{m}\end{equation}
Por regla de Kirchhoff(ecuación 4.1, G. Main) para un circuito LCR podemos escribir la siguiente ecuación:
Al multiplicar por obtenmos lo siguiente
\begin{equation}\frac{d^{2}\psi}{dt^{2}}+\frac{R}{L}\left(\frac{d\psi}{dt}\right)+\frac{1}{LC}\psi= 0 ...(3)\end{equation}
\begin{equation}\gamma=\frac{R}{L}\end{equation}
\begin{equation}\omega_{0}^{2}=\frac{1}{LC}\end{equation}
Las ecuaciones 1 y 3 son ecuaciones análogas.
El tiempo de relajación en una amortiguación critica está definida como:
$\tau_{r}=\frac{\gamma}{\omega_{0}^{2}}$
Entonces
$\tau_{r}=\frac{\frac{R}{L}}{\frac{1}{LC}}=\frac{RLC}{L}=RC$
Finalmente obtenemos
\begin{equation}\tau_{r}=RC\end{equation}
Aportación por usuarios: Pedro Pablo Ramírez Martínez (discusión) 00:24 17 feb 2014 (UTC) , Esther Sarai (discusión) 18:56 1 mar 2015 (CST)Esther Sarai García González ,Luis Santos (discusión) 13:15 11 mar 2015 (CDT)
Forma alternativa 1
Show that the relaxation time for very heavy damped LCR circuit is RC
Muestre que el tiempo de mitigación para cada circuito LCR severamente amortiguado es RC.
Tomando como base las expresiones de los apuntes,para un circuito RCL muy pesadamente amortiguado en el cual La amplitud del movimiento se reduce a:
El tiempo de relación para este tipo de circuitos es aquel en el que el factor de decaimiento se reduce por un factor de por lo tanto,igualamos el factor de decaimiento exponencial de la expresión a tenemos:
sacando logaritmo natural a ambos lados de la expresión
Despejando el tiempo de para el cual se cumple esta relación tenemos:
Pero:
Y
Sustituyendo en
Por lo tanto el tiempo de relajamiento para un circuito RLC pesadamente amortiguado es
Aportación por usuarios: MISS (discusión) 00:22 20 jun 2013 (CDT) , Pablo (discusión) 01:36 28 feb 2015 (CST)
Problema 4.2
4.2 A capacitor is charged to a voltage V and is then connected across a coil. If the damping is critical, show that the current rises to a maximun value 2V/eR, where R is the total resistance of the circuit made by the capacitor ant the coil.
Traducción
Un condensador se carga a una tensión V y es conectado a través de una bobina. Si el amortiguamiento es crítico, mostrar que la corriente aumenta a un valor máximo de 2V / eR, donde R es la resistencia total del circuito realizado por el condensador de la bobina.
Solución
La solución para las ecuaciones (3.3) y (4.1) es:
Esto muestra que es una amortiguación critica
Condiciones iniciales
Entonces, tenemos ahora:
Entonces
Así que
Así,
Con
Si entonces:
Así que:
Luego,
Con,
Puesto que la resistencia crítica de amortiguamiento es:
Así entonces,
Aportaciones por usuarios: Mario Moranchel (discusión) 02:47 6 feb 2014 (UTC), mfg-wiki (discusión) 12:00 9 may 2013 (CDT) , Pablo (discusión) 01:56 28 feb 2015 (CST), A. Martín R. Rabelo (discusión) 01:30 1 mar 2015 (CST), Esther Sarai (discusión) 20:06 1 mar 2015 (CST)Esther Sarai
Problema 4.3
A galvanometer with a coil of resistance $R{}_{G}$ is connected in series with an external resistance $R{}_{ext}$ . Show that by varying $R{}_{ext}$ we can select values of Q within the limits
$\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}\leq Q\leq Q_{m}$
where $Q_{m}$ is that part of Q due to the mechanical effects and G is the constant defined as $G=\frac{\omega I}{g}$.
[Traducción ]
Un galvanómetro con una bobina de resistencia $R{}_{G}$ está conectada en serie con una resistencia externa $R{}_{ext}$. Mostrar que variando $R{}_{ext}$ podremos seleccionar valores de Q dentro de los límites
$\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}\leq Q\leq Q_{m}$
Donde $Q_{m}$ es la parte de Q debido a los efectos mecánicos y G es la constante definida como $G=\frac{\omega I}{g}$.
Solución:
Primero tomemos en cuenta algo, sabemos que $Q=\frac{\omega}{\gamma}$ , donde $\gamma$ es el ancho del amortiguamiento. Si en este caso tenemos dos amortiguamientos, el mecánico $(\gamma_{m})$ y el eléctrico $(\gamma_{e})$, entonces el ancho total $(\gamma)$ es la suma de ambos.
$\gamma=\gamma_{m}+\gamma_{e}$. Entonces despejando $\gamma$ de la ecuación superior, obtenemos $\gamma=\frac{\omega}{Q}$, pero como $\gamma$ es la suma de la parte mecánica y la parte eléctrica entonces tenemos que $\gamma=\frac{\omega}{Q_{m}}+\frac{\omega}{Q_{e}}$ y asi $\frac{\omega}{Q}=\frac{\omega}{Q_{m}}+\frac{\omega}{Q_{e}}$, donde Q son los llamados factores de calidad tanto mecánico, eléctrico y el total; como vemos la frecuencia angular $\omega$es la misma para todo el sistema, por lo que obtenemos $\frac{1}{Q}=\frac{1}{Q_{m}}+\frac{1}{Q_{e}}$, aquí hay que hacer las dos distinciones que nos pide el problema:
Sabemos que $Q_{e}=GR_{G}+GR_{ext}$, si $R_{ext}$ es muy grande
entonces $\frac{1}{Q_{e}}$ tiende a cero con lo que se reduciría
a $\frac{1}{Q}=\frac{1}{Q_{m}}$ o mejor visto $Q=Q_{m}$ que es la
parte derecha de la desigualdad que queremos probar.
El otro caso es que $R_{ext}$ sea demasiado chiquito, casi cero,
entonces no nos interesaría su contribución, entonces se reduce simplemente
a $Q_{e}=GR_{G}$, con lo que $\frac{1}{Q}=\frac{1}{Q_{m}}+\frac{1}{GR_{G}}$,
y así $Q=\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}$ que es la parte izquierda
de la desigualdad que queremos comprobar.
Entonces los valores de Q quedan dados entre $\frac{GR_{G}Q_{m}}{GR_{G}+Q_{m}}\leq Q\leq Q_{m}$al
variar $R{}_{ext}$.
Aportaciones por usuarios:Edgar Ortega Roano 09:58 12 feb 2014 (CDT) Cesar Ivan Avila Vasquez 16:51 25 Febrero 2014, Pablo (discusión) 01:34 28 feb 2015 (CST)
Problema 4.4
4.4 Asteady torque of $2.0x10^{-6}Nm,$ applied to the susppention of a ballistic galvanometer (by passing a suitable steady current), produces a steady delfection of 50º. Free vibratios of the suspension have a period og 2.5 s. Calculate the thow porducced by an angular impulse of $5.5x10^{-7}$Nm (applied by discharging a capacitor throw the coil).Neglect damping
Traducción
Una torca fija de $2.0x10^{-1}Nm$ es aplicada a la suspensión de un galvanómetro balistico (al pasar una corriente estable), produce una desviación fija de 50º. Vibraciones libres de la suspensión, tienen un periodo 2.5 . Calcule el tiro producido por un impulso angular de $5.5x10^{-7}Nm$ (que se aplica al descargar un capacitor), desprecie el amortiguamiento.
Se tienen los siguientes datos:
$\Delta t=2.5$s y $T=2.0x10^{-7}$ $Imp=5.5x10^{-7}$Nms
Y se conoce la siguiente relación:
\[ Imp=\frac{\Delta L}{\Delta t} \]
De donde se despeja $\Delta L$, que es el tiro; y se obtiene:
\[ \Delta L=Imp\Delta t \]
Al sustituir los datos, se obtiene como resultado:
$\Delta L=1.3x10^{-6}Ns^{2}$
Aportación por usuario: Ana Alarid (discusión) 03:05 22 feb 2014 (UTC)
Forma alternativa
Una torca fija de $2.0\times10^{-6}Nm$, aplicada a la suspensión de un galvanometro balístico (al pasar una corriente estable), produce una desviación fija de 50º . Vibraciones libres de la suspensión, tienen un periodo de $2.5s$. Calcule el tiro producido por un impulso angular de $5.5\times10^{-7}Nms$(Que se aplica al descargar un capacitor, desprecie el amortiguamiento.)
Solucion $\rightarrow$
Se conoce que
\[ I=\frac{\Delta L}{\Delta t} \]
Donde:
I = impulso angular
t = periodo
L = Tiro
Despejando $\triangle L$, tenemos
\[ \Delta L=I\Delta t \]
\[
\Delta L=(5.5\times10^{-7}Nm)(2.5s)=1.375\times10^{-6}Nms^{2}
\]
Aportación por usuario: Rosario Maya (discusión) 11:28 06 marzo 2015 (UTC)
Problema 4.5
4.5 Una masa 0.1kg es pegada a un resorte. Es jalado 200mm a la derecha de su posición cuando el resorte no esta ni estirado ni comprimido y entonces es liberado del reposo. Las vibraciones libres resultantes, que están amortiguadas por fricción tienen una frecuencia de 2.0Hz. Se observa que cada oscilación hacia la derecha la masa toma un punto 30mm hacia la izquierda de su límite previo. La masa finalmente llega al reposo a 235mm hacia la izquierda del punto del cual fue liberado. (a) Calcule la fuerza de fricción de deslizamiento.(b) Calcular los límites superior e inferior para la fuerza de pegado.
Solución
La ecuación de movimiento del sistema es:
\[ m\ddot{\psi}+k\psi=F_{sl}...(1) \]
Dividiendo entre la masa resulta:
\[ \ddot{\psi}+w_{0}^{2}\psi=\frac{F_{sl}}{m}...(2) \]
la primera oscilación se detiene cuando $|\psi|=A_{0}-4\frac{F_{sl}}{s}$
$\;$
además sabemos que $4\frac{F_{sl}}{s}=30mm$, por otro lado $s=mw_{0}^{2}=m(2\pi f)^{2}$
$\;$
Entonces
\[ F_{sl}=\frac{30}{4}m(2\pi f)^{2}\quad...(3) con\; m=0.1kg\; y\; f=2Hz \]
\[
F_{sl}=0.12N
\]
(b) Sabemos que la fuerza de pegado es igual a
\[ F_{p}=s|\psi|...(1) \]
y además la última oscilación esta entre 50mm y 35mm, por lo que la
fuerza máxima es:
\[ F_{max}=(15.79)(50x10^{-3}) \]
\[
F_{max}=0.789N
\]
Lo que resulta
\[ F_{min}=(15.79)(35x10^{-3}) \]
\[
F_{min}=0.552N
\]
Aportaciones por usuarios: Luis Miguel Sánchez Mtz. (discusión) 19:17 8 feb 2014 (UTC), Esther Sarai (discusión) 18:50 28 feb 2015 (CST)Esther Sarai García Gonzalez, Rosario Maya (discusión) 24:07 07 marzo 2015 (CST)
Problema 4.6
Expresar el desplazamiento x(t) y la velocidad x'(t) del oscilador armónico sobre amortiguado utilizando funciones hiperbólicas
Solución
Para el caso sobre amortiguado x(t) y x'(t) se expresa
$x(t)=e^{-\beta t}[A_{1}e^{\omega_{2}t}+A_{2}e^{-\omega_{2}t}]$
$x'(t)=e^{-\beta t}[-\beta(A_{1}e^{\omega_{2}t}+A_{2}e^{-\omega_{2}t})+(A_{1}\omega_{2}e^{\omega_{2}t}+A_{2}\omega_{2}e^{-\omega_{2}t})]$
donde:
$\omega_{2}=\sqrt{\beta^{2}-\omega_{0}^{2}}$
Las funciones hiperbólicas están definidas como:
$\cosh y=\frac{e^{y}+e^{-y}}{2}$ , $\sinh y=\frac{e^{y}-e^{-y}}{2}$
$e^{y}=\cosh y+\sinh y$
$e^{-y}=\cosh y-\sinh y$
sustituyendo en las ecuaciones:
y
Aportaciones por usuarios: Esther Sarai (discusión) 19:15 1 mar 2015 (CST)Esther Sarai García González , David Alberto Rojas Solis (discusión) 06:17 6 jul 2013 (CDT) , sandy (discusión) 21:31 6 jul 2013 (CDT)--sandy (discusión) 21:31 6 jul 2013 (CDT)
Problema 4.6 bis
4.6 In fig. 4.6 values of the energy W at successive maxima of $|\psi(t)|$ are plotted againt the time t, for the friction-damped vibration of fig 4.3. Show that the smooth curve throught the points is a parabola (not the exponential curve obtained with standard damping)
Traducción
En la figura 4.4 los valores de la energía W en los máximos sucesivos de $|\psi(t)|$ están graficados contra el tiempo t, para la vibración amortiguada por fricción de la figura 4.3. Muestre que la curva que pasa a través de los puntos es una parábola (no la curva exponencial del amortiguamiento simple)
Solución
Este problema se puede resolver con el hecho de que la energía de un sistema amortiguado depende de lo siguiente:
\[ \frac{dW}{dt}=-b\psi^{2}\leq0 \]
ya que la función es un valor absoluto, tenemos que la curva pasa
por cada punto de la gráfica, es decir: $-b|\psi|^{2}=-b\psi^{2}$para
$\psi^{2}\geq0$, y $-b(-\psi)^{2}$ para $\psi^{2}<0$, entonces
la curva que pasa a través de $|\psi(t)|$ es la curva de decaimiento
de energía.
Nota: Este problema pertenece al Libro de Iain G. Main
Aportación por usuarios: Cesar Ivan Avila Vasquez 16:41 21 Febrero 2014 (CDT) , Pablo (discusión) 01:41 28 feb 2015 (CST)
Problema 4.7
Del siguiente sistema mecánico, hallar la ecuación característica donde: $k=1250 [\frac{N}{m}]$, $D=2000 [\frac{N-s}{m}]$, m=10[Kg], F(t)=1[N].
Solución
Se suman las fuerzas del resorte, del amortiguador y la fuerza de inercia y se iguala con la fuerza de excitación:
\begin{eqnarray*} m\frac{d^2x}{dt^2}+D\frac{dx}{dt}+kx=F \qquad\qquad (1) \end{eqnarray*}
Sustituyendo valores
\begin{eqnarray*} (10)\frac{d^2x}{dt^2}+(2000)\frac{dx}{dt}+(1250)x=1 \qquad\qquad(2) \end{eqnarray*}
Utilizando la ecuación general de una ecuación diferencial de segundo orden
\begin{eqnarray*} T^2\frac{d^2x}{dt^2}+2\epsilon T\frac{dx}{dt}+x= K \qquad\qquad(3) \end{eqnarray*}
La ecuación (2) la reescribiremos de la forma que posee la ecuación (3), dividiremos la ec. (2) por 1250 para que esté equilibrada:
\begin{eqnarray*}
(\frac{10}{1250})\frac{d^2x}{dt^2}+(\frac{2000}{1250})\frac{dx}{dt}+(\frac{1250}{1250})x=\frac{1}{1250}
\end{eqnarray*}
\begin{eqnarray*} (8*10^{-3})\frac{d^2x}{dt^2}+(1.6)\frac{dx}{dt}+x=8*10^{-4} \qquad\qquad(4) \end{eqnarray*}
Ahora que la ec. (3) y (4) son de la misma forma, nos dispondremos a encontrar los elementos de (3) para observar el comportamiento del sistema.
\begin{eqnarray*} T^2=8*10^{-3} \end{eqnarray*}
Tiempo de respuesta del sistema
\begin{eqnarray*} T=0.089 \end{eqnarray*}
\begin{eqnarray*} (2)(\epsilon)(T)=1.6 \end{eqnarray*}
Despejando epsilon
\begin{eqnarray*} \epsilon=8.988; \epsilon > 1 \end{eqnarray*}
Observamos se trata de un caso sobre amortiguado, entonces calculamos sus polos:
\begin{eqnarray*} P_{{1},{2}}=\frac{-\epsilon\pm\sqrt{(\epsilon)^2-1}}{T} \end{eqnarray*}
\begin{eqnarray*} P_{{1},{2}}=\frac{-8.988\pm\sqrt{(8.988)^2-1}}{0.089} \end{eqnarray*}
Entonces:
\begin{eqnarray*} P_{1}=-0.627 \end{eqnarray*}
\begin{eqnarray*} P_{2}=-199.4 \end{eqnarray*}
Como es un caso sobre amortiguado conlleva a:
\begin{eqnarray*} X(t)=\frac{KP_{2}}{P_{1}-P_{2}}*\exp^{P_{1}t}+\frac{KP_{1}}{P_{2}-P_{1}}*\exp^{P_{2}t}+K \end{eqnarray*}
Sustituimos valores
\begin{eqnarray*} X(t)=\frac{(8*10^{-4})(-199.4)}{(-0.627)-(-199.4)}*\exp^{(-0.627)t}+\frac{(8*10^{-4})(-0.627)}{(-199.4)-(-0.627)}*\exp^{(-199.4)t}+8*10^{-4} \end{eqnarray*}
Por lo tanto, el comportamiento del sistema mecánico queda denotado por la siguiente expresión de segundo orden:
\begin{eqnarray*} X(t)=-(8*10^{-4})*\exp^{(-0.627)t}(+2.52*10^{-6})*\exp^{(-199.4)t}+(8*10^{-4}) \end{eqnarray*}
Aportaciones por usuarios: Angel Nahir Molina Guadarrama (discusión) 11:05 21 feb 2014 (UTC) , Pablo (discusión) 01:20 28 feb 2015 (CST) , Luis Santos (discusión) 13:28 11 mar 2015 (CDT)
Problema 4.9 Circuito RLC
¿Qué resistencia R se requiere(en términos de L y C) para impartir a un circuito LRC una frecuencia equivalente a la mitad de la frecuencia no amortiguada?
Solución:
Considerando la ecuación diferencial de un circuito LRC, por regla de Kirchhoff:
\begin{eqnarray*}
L\left(\frac{d^{2}\psi}{dt^{2}}\right)+R\left(\frac{d\psi}{dt}\right)+\left(\frac{1}{C}\right)\psi=0 .\qquad\qquad (1)
\end{eqnarray*}
De la ecuación (1) dividimos entre L y obtenemos que:
\begin{eqnarray*}
\frac{d^{2}\psi}{dt^{2}}+\frac{R}{L}\left(\frac{d\psi}{dt}\right)+\frac{1}{LC}\psi=0 \qquad\qquad (2)
\end{eqnarray*}
Observamos la ecuación (2) se comporta en forma de una oscilación amortiguada Ondas: Atenuacion suave:
\begin{eqnarray*}
\frac{d^{2}\psi}{dt^{2}}+\gamma\frac{d\psi}{dt}+\omega_{0}^{2}\psi=0 \qquad\qquad (3)
\end{eqnarray*}
Resolviendo la ecuación diferencial (3) para oscilaciones amortiguadas, obtenemos que la una solución es:
\[\psi(t)=Ae^{-\gamma t/2}cos(\omega_{t}t+\psi)\]
Donde
\begin{eqnarray*} \omega_{t}=\sqrt{\omega_{0}^{2}-(\frac{\gamma}{2})^{2}} \qquad\qquad (4) \end{eqnarray*}
Por lo tanto usando la ecuación (4) obtenemos que la frecuencia angular en un circuito LRC, está dada por:
\begin{eqnarray*} \omega= \sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}} \qquad\qquad (5) \end{eqnarray*}
Usaremos la ecuación (5) para resolver el problema. Como el problema plantea que tiene que ser la mitad de . Donde
Por lo tanto obtenemos que sustituyendo los valores de las :
\begin{eqnarray*}
\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}= \frac{1}{2 \sqrt{LC}} \qquad\qquad (6)
\end{eqnarray*}
Desarrollando la ecuación (6), primero elevando al cuadrado los dos lados de la ecuación (6):
Si igualamos a cero:
Desarrollamos:
:
por lo tanto R en términos de L y C es igual a:
Aportación por usuario: Pablo (discusión) 23:58 28 feb 2015 (CST)
Problema Circuito RC en serie
Se aplica una fuerza electromotriz de $100V$ a un circuito en serie $RC$ en el que la resistencia es de $200 ohms$ y la capacitancia de . Determine la carga $q(t)$ del capacitor, si $q(0)=0$. Encuentre la corriente $i(t)$.
Solución:
para encontrar la carga $q(t)$ tenemos que:
Entonces, aplicando la ley de mallas de kirchoff al circuito de la Figura para las caídas de voltaje en función de la carga $q(t)$, tenemos:
Donde $C, R$ son constantes conocidas como la capacitancia y resistencia, respectivamente. para encontrar la carga del circuito rc en serie, la ecuación diferencial a resolver, según la ecuación (1) y sustituyendo los valores del problema planteado, es:
Resolviendo la ecuación (2)
Forma estándar:
Factor Integrante:
Forma de la solución:
$ y_c = A e^{ -\int P ( x) d x} \Rightarrow q_{tr} ( t) = A e^{- \int 50 d t}\\ \Rightarrow q_{tr} ( t) = A e^{- 50 t} $
Donde $q_{tr}$ es la carga transitoria del capacitor en el circuito RC en serie.
$y_p = \frac{1}{e^{\int P ( x) d x}} \int e^{\int P ( x) d x} f ( x) d x \Rightarrow q_s ( t) = \frac{1}{e^{50 t}} \int e^{50 t} \ast \frac{1}{2} d t\\ \Rightarrow q_s ( t) = \frac{1}{2 \ast 50 \ast e^{50 t}} \int e^{50 t} ( 50) d t\\ \Rightarrow q_s ( t) = \frac{1}{100 \ast e^{50 t}} \int e^{50 t} ( 50) d t\\ \Rightarrow q_s ( t) = \frac{1}{100} \ast e^{- 50 t} [ e^{50 t}]\\ \Rightarrow q_s ( t) = \frac{1}{100}$
$q_s$ es la carga estacionaria del capacitor. Por tanto la carga (total en el circuito), buscada es:
$q ( t) = q _{tr} ( t) + q_s ( t) \nonumber\\ \qquad \qquad q(t) = A e^{- 50 t} + \frac{1}{100} \qquad (3) $
Para encontrar el valor de $A$ utilizamos los valores iniciales $q(0)=0$, cuando el tiempo $t=0$ la carga $q$ en el capacitor es 0 (como en un circuito abierto). Por tanto, sustituyendo estos valores en la ecuación (3) para la corriente resultante del circuito nos da:
$ q ( t) = A e^{- 50 t} + \frac{1}{100}\\ 0 = A e^{- 50 ( 0)} + \frac{1}{100}\\ 0 = A ( 1) + \frac{1}{100}\\ 0 = A + \frac{1}{100}$
$\boxed{\therefore A = – \frac{1}{100}} $
De donde sustituyendo $A$ en (3) nos da la Carga en el capacitor:
$ q ( t) = – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \, $
Obteniendo la corriente $i(t)$, del circuito RC en serie
sabemos que :
sustituyendo los valores que conocemos, tenemos:
$200 i + \frac{1}{1 \times 10^{- 4}} \left[ – \frac{1}{100} e^{- 50t} + \frac{1}{100} \right] = 100$
despejando $i(t)$
$200 i + \frac{1}{1 \times 10^{- 4}} \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = 100\\ i ( t) + \frac{10000}{200} \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = \frac{1}{2}\\ i ( t) + 50 \left[ – \frac{1}{100} e^{- 50 t} + \frac{1}{100} \right] = \frac{1}{2}\\ i ( t) – \frac{1}{2} e^{- 50 t} + \frac{1}{2} = \frac{1}{2}\\ i ( t) – \frac{1}{2} e^{- 50 t} = – \frac{1}{2} + \frac{1}{2}\\ i ( t) = \frac{1}{2} e^{- 50 t}$
la corriente en el circuito, es:
$\boxed{ \therefore i( t) = \frac{1}{2} e^{- 50 t}} $
Aportación por usuarios: Luis Martínez (discusión) 23:59 1 mar 2015 (CST)
Problema 4.10
Un ratón de 0.3kg se mueve en el extremo de un resorte con $K=2.50N/m$ sometido a una acción de una fuerza amortiguadora $F{}_{x}=-b\upsilon_{x}$
A)Si $b=.9 kg/s$ ¿Qué frecuencia de oscilación tiene el ratón ?
B)¿Con qué valor de b la amortiguación resulta crítica?
SOLUCIÓN:
De la ecuación $\frac{d^{2}\psi}{dt^{2}}+\gamma\frac{d\psi}{dt}+\omega_{0}^{2}\psi=0\,\,\,\,\,\,\,\,\,(a)$
Proponemos la solución $\psi=Ae^{-\alpha t}cos(\omega t)$
Entonces:
\[ \psi=Ae^{-\alpha t}cos(\omega t) \]
\[
\dot{\psi}=-A\alpha e^{-\alpha t}cos(\omega t)-A\omega e^{-\alpha t}sen(\omega t)
\]
\[
\ddot{\psi}=A\alpha^{2}e^{-\alpha t}cos(\omega t)+2A\omega\alpha e^{-\alpha t}sen(\omega t)-A\omega^{2}e^{-\alpha t}cos(\omega t)
\]
Por lo que substituyendo en la ecuación $(a)$ tenemos:
\[ A\alpha^{2}e^{-\alpha t}cos(\omega t)+2A\omega\alpha e^{-\alpha t}sen(\omega t)-A\omega^{2}e^{-\alpha t}cos(\omega t)-\gamma(A\alpha e^{-\alpha t}cos(\omega t)+A\omega e^{-\alpha t}sen(\omega t))+A\omega_{0}^{2}e^{-\alpha t}cos(\omega t)=... \]
\[
=Ae^{-\alpha t}[\alpha^{2}cos(\omega t)+2\omega\alpha sen(\omega t)-\omega^{2}cos(\omega t)-\gamma(\alpha cos(\omega t)+\omega sen(\omega t))+\omega_{0}^{2}cos(\omega t)]=0
\]
Sí, y sólo sí:
\[ 2\omega\alpha sen(\omega t)-\gamma\omega sen(\omega t)=0....(1) \]
y,
\[ \alpha^{2}cos(\omega t)-\omega^{2}cos(\omega t)-\gamma\alpha cos(\omega t)-\omega_{0}^{2}cos(\omega t)=0....(2) \]
De $(1)$ podemos factorizar $omega$ y queda:
\[ 2\alpha sen(\omega t)-\gamma sen(\omega t)=0 \]
\[
2\alpha sen(\omega t)=\gamma sen(\omega t)
\]
Por lo que $2\alpha=\gamma$ y $\alpha=\frac{\gamma}{2}$ . Entonces
de (2) al factorizar $cos(\omega t)$ tenemos...
\[ \alpha^{2}-\omega^{2}-\gamma\alpha+\omega_{0}^{2}=0 \]
Dejando todo en términos de $\gamma$,
\[ (\frac{\gamma}{2})^{2}-\omega^{2}-\gamma(\frac{\gamma}{2})+\omega_{0}^{2}=0 \]
\[
\frac{\gamma}{4}^{2}-\omega^{2}-\frac{\gamma^{2}}{2}+\omega_{0}^{2}=0
\]
Por lo tanto:
\[ \omega=\pm\sqrt{\omega_{0}^{2}-\frac{1}{4}\gamma^{2}}\,\,\,\,\,\,(3) \]
Y si recordamos que $\gamma=\frac{b}{m}$ y $\omega_{0}=\sqrt{\frac{k}{m}}$
, podemos escribir la ecuación como:
\[ \omega=\pm\sqrt{\frac{k}{m}-(\frac{b}{2m}){}^{2}}\,\,\,\,\,\,(3') \]
Entonces substituimos los datos en la ecuación (3') y obtenemos:
\[ \omega=\pm\sqrt{\frac{2.50N/m}{.3kg}-(\frac{.9kg/s}{2(.3kg)}){}^{2}}=2.47rad/seg \]
Pero esta es la frecuencia angular, para la frecuencia conocemos la
relación $f=\frac{\omega}{2\pi}$ por lo que:
\[ f=\frac{\omega}{2\pi}=.393Hz \]
Y finalmente para encontrar el valor de $b$ para que la amortiguación
sea crítica sabemos que $b=2\sqrt{km}$ por lo que:
\[ b=2\sqrt{km}=2\sqrt{(2.50N/m)(.3kg)}=1.73kg/seg \]
Resuelto por usuario: A. Martín R. Rabelo (discusión) 21:25 5 mar 2015 (CST)
Ejercicios Adicionales
Problema adicional 1
Se inician oscilaciones eléctricas en un circuito en serie que contiene una capacitancia C, una inductancia L y una resistencia R.
a) si (amortiguamiento débil) ¿cuanto tiempo pasara antes de que la amplitud de la oscilación de la corriente disminuya a 50.0% de su valor inicial?
b) ¿cuanto tiempo tarda en disminuir la energía a 50% de su valor inicial?
La ecuación para este tipo de problema es de la forma:
Inciso a
a) con:
Pero puesto que el tamaño de las oscilaciones decrecientes depende de la exponencial y el termino Q, solo se usara esa parte de la ecuación anterior, así a para encontrar el tiempo al que hay 50% de la carga inicial, se hace:
Inciso b
b)
La energía para este caso esta expresada por:
Dividiendo esta entre dos y despejando para t da:
Resuelto por usuario: Uziel Sanchez Gutierrez (discusión) 18:43 1 mar 2015 (CST)
PROBLEMA 1.50 Engineering vibration,3rd edition by Daniel J.Inman
Resorte amortiguador del siguiente sistema mecánico hallar la ecuación característica donde : K= cte del resorte = 1250[N/m],D= cte del amortiguador =2000[Ns/m],M=masa= 10[kg],F(t)= 1N
Solución
Primero se hace la suma de las 3 fuerzas y se igualan con la fuerza de excitación, empezando con la fuerza de inercia
\[ M\frac{d^{2}x}{dt^{2}}+D\frac{dx}{dt}+Kx=F \]
Sustituyendo valores
$10 \frac{d^2x}{dt^2}+2000 \frac{dx}{dt}+1250x=1. $
Se pasa esta ecuación a una forma general para una ecuación diferencial de segundo orden
$T^ 2 \frac{d^2x}{dt^2}+2 \gamma T \frac{dx}{dt}+x=K$
se divide cada termino de la ecuación entre 1250 para que este equilibrada
$\frac{1}{125}\frac{d ^2x}{dt^2} + \frac{200}{125} \frac{dx}{dt} + \frac{125}{125}x = \frac{1}{1250}$
Obteniendo:
$8 \times 10^{-3}\frac{d^2x}{dt^2} + 1.6 \frac{dx}{dt}+ x= 8 \times 10^{-4}$
Teniendo la ecuación anterior podemos encontrar los elementos para analizar el comportamiento del sistema. Lo que se hace es calcular $T$.
Ya que $T^2=8 \times 10^{-3}$, entonces $T=\sqrt{8 \times 10^{-3}}$, así $T=0.089$. Donde $T$ es el tiempo de respaldo del sistema.
Teniendo que $ 2 \gamma T = 1.6 $
Encontramos que $\gamma = 8.988 $. Se observa que $\gamma >1$, se trata de un caso sobreamortiguado.
Calculamos ahora ahora los polos del sistema:
$P_{1,2} = \frac{- \gamma \pm \sqrt{\gamma^2 -1}}{ T }$
Por lo que $P_1 = -0.627$ y $P_2= -199.4$
Prosigue calcular el sistema. Como nos da un caso sobreamortiguado tenemos que $ X(t) = \frac{kP_2}{P_1 - P_2} e^{P_1t} + \frac{kP_1}{P_2-P_1}e^{P_2t} + k $
Ahora sustituyendo los valores:
$x(t) = \frac{(8 \times 10^{-4})(-199.9) }{(-0.627)-(199)} e^{-0.627t} + \frac{(8 \times 10^{-4})(-0.06279}{199.9 - (-0.627)}e^{-199.9t} + 8 \times 10^{-4}$
$x(t)= -8 \times 10^{-4} e^{-0.627t } + (2.52 \times10^{-6}) e^{-0.199.4t}+ (8 \times 10^{-4})$
La ecuación anterior es la respuesta al sistema de segundo orden
Aportaciones por usuarios: Luisa Alejandra Vega Sanchez (discusión) 10:01 1 mar 2015 (CST)luisa alejandra vega sanchez
Problema 4.8 Serway
El sistema de la figura tiene una masa y una constante de fuerza de la fuerza resistiva esta dada por donde suponiendo que se empuja el bloque a un lado a una distancia y se suelta
Inciso a
a) calcule el intervalo temporal necesario para que la amplitud pierda un tercio de su valor inicial
- solución:
- tenemos que la energía esta dada por
tenemos las condiciones iniciales en es
igualando las dos condiciones con y a un tiempo obtenemos lo siguiente:
Inciso b
b) ¿cuántas oscilaciones realizó el bloque en este tiempo? para saber n oscilaciones tenemos la siguiente función
despejando tenemos
donde
Realizado por usuarios: Jose de jesus (discusión) 21:06 27 feb 2015 (CST)jose de Jesus Arizpe Flores 27/02/2015 ,Pablo (discusión) 01:49 28 feb 2015 (CST)
Problema 4.7 Waves. C.A. Coulson -A. Jeffrey . Ed Longman
En un circuito RLC, que una inductancia de 1 [H], una resistencia de 40 [$\Omega$] y un capacitor de $\frac{1}{4E^{4}}$ [F], se aplica un voltaje de V = 24 V. Determine el comportamiento de la carga y la intensidad de corriente en el circuito.
Solución
La ecuación que describe el comportamiento del circuito:
$L \frac{ d^{2}Q}{dt^{2}} + R \frac{dQ}{dt} + \frac{1}{C} Q = E(t) .\qquad\qquad (1)$
Derivando la ecuación (1) resulta:
$ L \frac{d^{2}I}{dt^{2}} + R\frac{dI}{dt}+\frac{1}{C}I(t)=\frac{dE(t)}{dt}.\qquad\qquad (2)$
Sustituir los datos en las ecuaciones (1) y (2) respectivamente.
$\frac{ d^{2}Q}{dt^{2}} + 40 \frac{dQ}{dt} + 4E^{4} Q(t) = \frac{1}{2}$
$ \frac{d^{2}I}{dt^{2}} + 40\frac{dI}{dt}+ 4E^{4}I(t) = 0 $
Considerando la condiciones iniciales $Q(0) = 10^{-4}$ y $I=10^{-2}$ tenemos como solución.
$Q(t) = \frac{1}{8E^{3}}e^{-20t}[\frac{47\sqrt{11}}{2.64E^{4}}\sin(\sqrt{1160t} + \frac{7}{8E^{3}}\cos(\sqrt{1160 t})]$
$I(t) = \frac{dQ}{dt}= e^{-20t}[\frac{1}{100}\cos(\sqrt{1160 t})-\frac{37\sqrt{11}}{6.6E^{3}}\sin(\sqrt{1160 t})] $
Aportación por usuario: Esther Sarai (discusión) 16:31 1 mar 2015 (CST)Esther Sarai García Gonzalez
Problema Propuesto al Capítulo 4
Un resorte vertical con constante de 6 lb/ft tiene suspendida una masa de 1/2 slug. Se aplica una fuerza externa dada por . Supóngase que actúa una fuerza amortiguadora numéricamente igual a dos veces la velocidad instantánea y que inicialmente el cuerpo está en reposo en su posición de equilibrio. Determine la posición del cuerpo en cualquier tiempo .
Solución.
Denotemos con la fuerza exterior que actúa sobre la masa. De la segunda ley de Newton, la ecuación diferencial del movimiento es
o bien
donde y .
Para resolver la ecuación no homogénea (4.2) podemos emplear el método de los coeficientes indeterminados o el de variación de parámetros, según sea más conveniente.
Con los valores de , y , la ecuación diferencial de movimiento resultante es
La solución complementaria de (4.3) es
Usando el método de los coeficientes indeterminados proponemos una solución particular de (4.3) de la forma
En tal caso
Sustituyendo en (4.3), se sigue que
El sistema de ecuaciones resultante
conduce a los valores A=-5 y B=5. Así que
Empleando las condiciones iniciales y encontramos que y .Por tanto
Obsérvese que en el problema, la solución complementaria
tiene la propiedad de que
por lo que se dice que es un término transitorio o una solución transitoria. Así para valores grandes de t se aproxima a . A se le llama solución estacionario o de estado permanente.
Bibliografía.
Elizarraraz Martínez David, “Ecuaciones diferenciales: técnicas de solución y aplicaciones”, Primera Edición 2004, UAM-Azcapotzalco, México DF.
Aportación por usuario: Ricardo Garcia Hernandez (discusión) 19:26 4 mar 2015 (CST)
Problema 3.16, Analytical Mechanics, Fowles & Cassiday, Seventh Edition
If a series LCR circuit is connected across the terminals of an electric generator that produces a voltage $V=V_0 e^{i\omega t}$, the flow of electrical charge $q$ through the circuit is given by the following second-order differential equation:
a) Verify the correspondence shown in Table 3.6.1 between the parameters of a driven mechanical oscillator and the above driven electrical oscillator.
b)Calculate the $Q$ of the electrical circuit in therms of the coefficients of the above differential equation.
c) Show that, in the case of small damping, $Q$ can be written as $Q=R_0/R$, where $R_0=\sqrt{L/C}$ is the characteristic impedance of the circuit.
Traducción
Si un circuito en serie RCL es conectado en las terminales de un generador eléctrico que produce un voltaje $V=V_0 e^{i\omega t}$, el flujo de carga eléctrica $q$ a través del circuito está dado por la siguiente ecuación diferencial de segundo orden:
a) Verifique la correspondencia mostrada en la Tabla 3.6.1 entre los parámetros del oscilador armónico forzado y el mencionado oscilador eléctrico forzado.
b) Calcule $Q$ del circuito eléctrico en términos de los coeficientes de la anterior ecuación diferencial.
c) Muestre que, en el caso de un amortiguamiento ligero, $Q$ puede escribirse como $Q=R_0/R$, donde $R_0=\sqrt{L/C}$ es la impedancia característica del circuito.
Inciso a
Tenemos para el inciso $a)$:
$m(\text{masa}) \rightarrow L(\text{inductancia})$ $x(\text{desplazamiento}) \rightarrow q (\text{carga})$ $c(\text{coeficiente de amortiguamiento})\rightarrow R(\text{resistencia})$ $k(\text{constante de restitución})\rightarrow C^{-1}(\text{recíproco de la capacitancia})$ $F(\text{fuerza}) \rightarrow V(\text{diferencia de potencial})$
Inciso b
Resolviendo $b)$:
Sabemos que $Q=\omega_d / 2\gamma$, además $\omega_0^2=1/LC$ y $\gamma = R/2L$, por lo que:
por lo que, simplificando, obtenemos que:
Ahora, para el inciso $c)$:
Sabemos que si el amortiguamiento es muy pequeño $\omega_d \approx \omega_0$, por lo que:
Por lo tanto, para un amortiguamiento pequeño, tenemos:
donde $R_0 = \sqrt{L/C}$
Resuelto por usuario: Ivan de Jesús Pompa García (discusión) 21:32 10 mar 2015 (CDT)
Un problema de aplicación a circuitos eléctricos
Se tiene un circuito formado por una resistencia , una bobina y un capacitor están conectados en serie a una fuente voltios en el tiempo es decir, la resistencia de la fuente decae a una razón exponencial.
Suponga que El voltaje a través del capacitor es una solución de la ecuación de segundo orden
Solución
y con los valores proporcionados se tiene
Podemos transformar transformar esta ultima ecuación como sigue
calculando la solución tenemos:
Los eigenvalores son . Usando la aproximación
para la solución es
Donde son constantes.
Ahora para encontrar la solución para la ecuación no homogénea
suponemos que donde es el coeficiente indeterminado. Para encontrar el valor de se sustituye en la ecuación diferencial anterior quedando
así que la solución particular queda como
Ahora determinamos la solución general con los resultados ya obtenidos, es decir, la solución homogénea y particular
.
Realizado por usuario: Hector Resendiz Héctor Reséndiz (discusión) 21:59 29 mar 2015 (CDT)























![i(t)=\frac{d}{dt}\left[(C_{1}+C_{2}w_{0}t)\exp^{-w_{0}t}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f876978e21ba05cdfe8098012915ec17f0131946)







![\frac{di}{dt}=V_{1}Cw_{0}^{2}\left[\exp^{-w_{0}t}-w_{0}t\exp^{-w_{0}t}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/55d56cad8f8329bf2e0b8a3df8e7cafe3fe74adc)















![x(t)=(\cosh\beta t-\sinh\beta t)[(A_{1}+A_{2})\cosh\omega_{2}t+(A_{1}-A_{2})\sinh\omega_{2}t]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9b466d5915c848ecbebe84dc01cc8234cc4bc427)