Diferencia entre revisiones de «Compleja:Zill-Cap5.5»
| (No se muestran 36 ediciones intermedias del mismo usuario) | |||
| Línea 45: | Línea 45: | ||
Donde $C: |z|=5$ | Donde $C: |z|=5$ | ||
'''Procedimiento''' | |||
Usando la formula integral de Cauchy | Usando la formula integral de Cauchy | ||
| Línea 53: | Línea 55: | ||
Para $n=1$ , $z_0=3i$ y $f(z)=z^2$ | Para $n=1$ , $z_0=3i$ y $f(z)=z^2$ | ||
$f^{1}(3i)=\frac{1!}{2i\pi}\oint \frac{z^2}{(z-3i)^{2}}dz$ | |||
$f(z)=z^2$ | |||
$f'(z)=2z$ | |||
$f'(3i)=2(3i)=6i$ | |||
$6i(2i\pi)=\oint \frac{z^2}{(z-3i)^{2}}dz$ | |||
'''Solución''' | |||
\begin{equation*} | |||
\oint \frac{z^2}{(z-3i)^{2}}dz=-12\pi | |||
\end{equation*} | |||
---- | |||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | |||
===Ejercicio 3=== | ===Ejercicio 3=== | ||
| Línea 60: | Línea 82: | ||
[[Archivo:P5.5.3.png|250px|center]] | [[Archivo:P5.5.3.png|250px|center]] | ||
'''Procedimiento''' | |||
El teorema 5.5.1 indica que: | El teorema 5.5.1 indica que: | ||
| Línea 70: | Línea 94: | ||
f(i\pi)=\frac{1}{2\pi i}\oint_{C} \! \frac{e^z}{z-i\pi}\,dz | f(i\pi)=\frac{1}{2\pi i}\oint_{C} \! \frac{e^z}{z-i\pi}\,dz | ||
\] | \] | ||
Que claramente | Que claramente coincide con nuestra integral, despejando nos queda: | ||
'''Conclusión''' | |||
\[ | \[ | ||
\oint_{C} \! \frac{e^z}{z-i\pi}\,dz=f(i\pi)\,(2\pi i)=2i\pi e^{i\pi}=2i\pi\,[cis (\pi)]=2i\pi\,(-1)=-2i\pi | \oint_{C} \! \frac{e^z}{z-i\pi}\,dz=f(i\pi)\,(2\pi i)=2i\pi e^{i\pi}=2i\pi\,[cis (\pi)]=2i\pi\,(-1)=-2i\pi | ||
| Línea 76: | Línea 103: | ||
---- | ---- | ||
Realizado por:[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 23:40 19 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 4 === | ===Ejercicio 4 === | ||
| Línea 84: | Línea 111: | ||
Evalúe la integral dada a lo lardo del contorno cerrado indicado. | Evalúe la integral dada a lo lardo del contorno cerrado indicado. | ||
$\oint_{c}\frac{1+e^{z}}{z}dz$, con $|z|=1$ | |||
'''Procedimiento''' | |||
Primero se ve que el | Primero se ve que el único punto donde el integrando no es analítico es en $z=0$ y que, en este caso, se encuentra dentro del contorno C, y | ||
teniendo en cuenta el teorema 5.5.1 tenemos que: | teniendo en cuenta el teorema 5.5.1 tenemos que: | ||
| Línea 101: | Línea 129: | ||
$\oint_{c}\frac{1+e^{z}}{z}dz,=\oint_{c}\frac{f(z)}{z-z_{o}}dz=2\pi if(z_{0})=2\pi if(0)=2\pi i(1+1)$ | $\oint_{c}\frac{1+e^{z}}{z}dz,=\oint_{c}\frac{f(z)}{z-z_{o}}dz=2\pi if(z_{0})=2\pi if(0)=2\pi i(1+1)$ | ||
'''Conclusión''' | |||
Finalmente | Finalmente | ||
| Línea 109: | Línea 138: | ||
---- | ---- | ||
Realizado por:[[Usuario:Fernando Vazquez V.|Fernando Vazquez V.]] ([[Usuario discusión:Fernando Vazquez V.|discusión]]) 01:13 21 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 5 === | ===Ejercicio 5 === | ||
| Línea 122: | Línea 150: | ||
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz $; $ |z|=3 $ | $ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz $; $ |z|=3 $ | ||
'''Procedimiento''' | |||
Primero, identificamos $f(z)=z^2-3z+4i$ y $z_0=-2i$ como un punto dentro del círculo C. Se observa que $f$ es analítica en todos los puntos dentro y en el contorno C. Así, por Cauchy (Teorema 5.5.1): | Primero, identificamos $f(z)=z^2-3z+4i$ y $z_0=-2i$ como un punto dentro del círculo C. Se observa que $f$ es analítica en todos los puntos dentro y en el contorno C. Así, por Cauchy (Teorema 5.5.1): | ||
| Línea 131: | Línea 159: | ||
$ 2\pi i f(-2i)= 2\pi i(-4+10i)= -8\pi i -20\pi = -\pi(20+8i) $ | $ 2\pi i f(-2i)= 2\pi i(-4+10i)= -8\pi i -20\pi = -\pi(20+8i) $ | ||
'''Conclusión''' | |||
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz = 2\pi i f(-2i)= -\pi(20+8i)$ | $ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz = 2\pi i f(-2i)= -\pi(20+8i)$ | ||
---- | |||
Realizado por: [[Usuario:Nancy Martínez Durán|Nancy Martínez Durán]] ([[Usuario discusión:Nancy Martínez Durán|discusión]]) 21:56 18 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 7=== | ===Ejercicio 7=== | ||
'''Evalúe la integral dada a lo largo de los contornos''' | '''Evalúe la integral dada a lo largo de los contornos''' | ||
<math>\oint \frac{z^2}{z^2+4} dz</math> | <math>\oint \frac{z^2}{z^2+4} dz</math> | ||
'''Inciso a''' | |||
'''a)''' <math>|z-i|=2</math> | '''a)''' <math>|z-i|=2</math> | ||
| Línea 162: | Línea 195: | ||
<math>\oint \frac{z^2}{(z+2i)(z-2i)}= -2 \pi </math> | <math>\oint \frac{z^2}{(z+2i)(z-2i)}= -2 \pi </math> | ||
'''Inciso b''' | |||
'''b)''' <math>|z+2i|=1</math> | '''b)''' <math>|z+2i|=1</math> | ||
| Línea 189: | Línea 224: | ||
--[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 14:31 21 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 14:31 21 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 11=== | ===Ejercicio 11=== | ||
Evalúe la integral dada a lo largo del contorno cerrado indicado. | Evalúe la integral dada a lo largo del contorno cerrado indicado. | ||
$\oint_{C}\frac{e^{z²}}{(z-i)³}dz ; |z-i|=1$ | |||
'''Procedimiento''' | |||
Nuestro contorno esta definido por una circunferencia con centro en | Nuestro contorno esta definido por una circunferencia con centro en $i$ y radio $1$ .Ahora bien podemos notar de nuestra función que existe una singularidad cuando $z=i$ la cual se encuentra dentro de nuestro dominio , por lo cual no es analítica en ese punto. | ||
Para la | Para la resolución de este problema emplearemos lo siguiente: | ||
$f^{n}(z_0)=\frac{n!}{2i\pi}\oint \frac{f(z)}{(z-z_0)^{n+1}}dz..... (*)$ | |||
por lo cual de nuestra integral a resolver identificamos: | por lo cual de nuestra integral a resolver identificamos: | ||
$n=2$ | |||
$n!=2$ | |||
$f(z)=e^{z²}$ | |||
$f'(z)=2z e^{z²}$ | |||
\[ | |||
f''(z)=2e^{z²}(2z²+1) | |||
\] | |||
$z_0=i$ | |||
utilizando | utilizando $(*)$ | ||
$2 e^{z_0²}(2z_0²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$ | |||
sustituyendo : | sustituyendo : | ||
$2 e^{(i)²}(2(i)²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$ | |||
$2 e^{-1}(-1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$ | |||
'''Solución''' | |||
Despejando | Despejando | ||
$-2 e^{-1}i\pi=\oint_{C}\frac{e^{z²}}{(z-i)³}dz$ | |||
Por lo cual nuestra | Por lo cual nuestra solución es $-2ie^{-1}\pi$ | ||
--[[Usuario:Anahi Limas|Anahi Limas]] ([[Usuario discusión:Anahi Limas|discusión]]) 18:55 21 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Anahi Limas|Anahi Limas]] ([[Usuario discusión:Anahi Limas|discusión]]) 18:55 21 jun 2015 (CDT) | |||
---- | ---- | ||
===Ejercicio 15=== | ===Ejercicio 15=== | ||
Evalúe la integral a lo largo de los contornos cerrados indicados | |||
1.- $\oint_{C}\frac{2z+5}{z^{2}-2z}dz$; a) $\mid z\mid=\frac{1}{2}$ | 1.- $\oint_{C}\frac{2z+5}{z^{2}-2z}dz$; | ||
b) $\mid z+1\mid=2$ c) $\mid z-3\mid=2$ | a) $\mid z\mid=\frac{1}{2}$ | ||
b) $\mid z+1\mid=2$ | |||
c) $\mid z-3\mid=2$ | |||
d) $\mid z+2i\mid=1$ | |||
$\oint_{C}\frac{2z+5}{z^{2}-2z}dz=\oint_{C}\frac{2z+5}{z(z-2)}dz$ | $\oint_{C}\frac{2z+5}{z^{2}-2z}dz=\oint_{C}\frac{2z+5}{z(z-2)}dz$ | ||
'''Inciso a''' | |||
y por fracciones parciales: | y por fracciones parciales: | ||
| Línea 280: | Línea 330: | ||
centrada en $0+0i$ entonces | centrada en $0+0i$ entonces | ||
por el teorema de Cauchy- | por el teorema de Cauchy-Goursat | ||
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | $\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | ||
| Línea 296: | Línea 346: | ||
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$ | $\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$ | ||
'''Inciso b''' | |||
Ahora evaluando a lo largo de b) $\mid z+1\mid=2$, (circunferencia | Ahora evaluando a lo largo de b) $\mid z+1\mid=2$, (circunferencia | ||
de radio $2$ centrada en $-1$) por el razonamiento anterior: | de radio $2$ centrada en $-1$) por el razonamiento anterior: | ||
como $z=2$ no esta dentro del contorno $\mid z+1\mid=2$ entonces | como $z=2$ no esta dentro del contorno $\mid z+1\mid=2$ entonces | ||
por el teorema de Cauchy- | por el teorema de Cauchy-Goursat | ||
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | $\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | ||
| Línea 314: | Línea 365: | ||
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$ | $\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$ | ||
'''Inciso c''' | |||
Ahora evaluando a lo largo de c) $\mid z-3\mid=2$,(circunferencia | |||
de radio $2$ centrada en $3$) | de radio $2$ centrada en $3$) | ||
| Línea 322: | Línea 375: | ||
como $z=0$ no se encuentra dentro del contorno $\mid z+1\mid=2$ | como $z=0$ no se encuentra dentro del contorno $\mid z+1\mid=2$ | ||
por el teorema de Cauchy- | por el teorema de Cauchy-Goursat | ||
$-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$ | $-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$ | ||
| Línea 330: | Línea 383: | ||
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=9\pi i+0=9\pi i$ | $\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=9\pi i+0=9\pi i$ | ||
'''Inciso d''' | |||
ahora evaluando a lo largo de d) $\mid z+2i\mid=1$(circunferencia | ahora evaluando a lo largo de d) $\mid z+2i\mid=1$(circunferencia | ||
de radio$1$ centrada en $-2i$ ) | de radio$1$ centrada en $-2i$ ) | ||
como $z=0\;y\;z=2$ no se encuentran dentro del contorno $\mid z+2i\mid=1$ | como $z=0\;y\;z=2$ no se encuentran dentro del contorno $\mid z+2i\mid=1$ | ||
entonces por el teorema de Cauchy- | entonces por el teorema de Cauchy-Goursat | ||
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | $\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$ | ||
| Línea 344: | Línea 398: | ||
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0+0=0$ | $\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0+0=0$ | ||
---- | ---- | ||
Realizado por: [[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 23:19 19 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 17=== | ===Ejercicio 17=== | ||
| Línea 357: | Línea 411: | ||
$(b)$ $|z-1-i|= 1$ | $(b)$ $|z-1-i|= 1$ | ||
'''Inciso a''' | |||
Solución del inciso $(a) : $ | Solución del inciso $(a) : $ | ||
| Línea 376: | Línea 430: | ||
'''Inciso b''' | |||
Solución del inciso $(b) : $ | Solución del inciso $(b) : $ | ||
| Línea 398: | Línea 452: | ||
--[[Usuario:Emmanuell Castro Flores|Emmanuell Castro Flores]] ([[Usuario discusión:Emmanuell Castro Flores|discusión]]) 21:05 20 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Emmanuell Castro Flores|Emmanuell Castro Flores]] ([[Usuario discusión:Emmanuell Castro Flores|discusión]]) 21:05 20 jun 2015 (CDT) | |||
---- | ---- | ||
===Ejercicio 18 | ===Ejercicio 18=== | ||
| Línea 413: | Línea 466: | ||
'''Procedimiento''' | |||
(a) $|z| = 1$ | |||
$ | |||
Las singularidades de la integral son $z=0$ y $z=4$ | |||
$ | |||
| Línea 451: | Línea 480: | ||
Ahora en este | Ahora en este haremos uso del teorema 5.10 : | ||
\[ | |||
f ''(z_0) = \frac{2}{2\pi i } \oint_{C} \frac{f (z)}{(z - z_0)^3} dz | |||
\] | |||
Donde: | Donde: | ||
\[ | |||
f = \frac{1}{z - 4} | |||
\] | |||
\[ | |||
z_0 = 0 | |||
\] | |||
\[ | |||
f ' = \frac{d}{dz} (z - 4)^{-1} = \frac{-1}{(z - 4)^2} | |||
\] | |||
\[ | |||
f '' = \frac{d}{dz} (\frac{-1}{(z - 4)^2}) = \frac{2}{(z - 4)^3} | |||
\] | |||
Aplicando el teorema a la integral tenemos: | |||
\[ | |||
\oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{2\pi i}{2} f '' (z_0) | |||
\] | |||
Con | |||
\[ | |||
f '' (z_0) = \frac{2}{(0 - 4)^3} = \frac{-2}{64} = \frac{-1}{32} | |||
\] | |||
$\Rightarrow $ | |||
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = \oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{-\pi i}{32}$ | |||
'''Inciso b''' | |||
En este caso ambas singularidades están fuera del contorno, como se ve en la siguiente imagen: | |||
[[Archivo:Capitulo5.5Ejercicio18Zill.svg|sinmarco]] | |||
Dado que $f(z)$ es Analítica sobre la curva C, entonces la integral es 0, usando el teorema de Cauchy-Goursat. | |||
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = | $\oint_{C} \frac{1}{z^{3} (z - 4)} dz = 0$ | ||
---- | |||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | ---- | ||
| Línea 501: | Línea 552: | ||
$=\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$ | $=\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$ | ||
...$\left(1\right)$ | ...$\left(1\right)$ | ||
'''Procedimiento''' | |||
por lo que podemos definir convenientemente: | por lo que podemos definir convenientemente: | ||
| Línea 567: | Línea 620: | ||
$\left(5\right)$en | $\left(5\right)$en | ||
'''Conclusion''' | |||
la euación $\left(1\right)$ se obtiene: | la euación $\left(1\right)$ se obtiene: | ||
| Línea 574: | Línea 628: | ||
Resuelto por: | ---- | ||
Resuelto por: [[Usuario:Alejandro Juárez Toribio|Alejandro Juárez Toribio]] ([[Usuario discusión:Alejandro Juárez Toribio|discusión]]) 17:38 18 jun 2015 (CDT) | |||
[[Usuario:Alejandro Juárez Toribio|Alejandro Juárez Toribio]] ([[Usuario discusión:Alejandro Juárez Toribio|discusión]]) 17:38 18 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 588: | Línea 640: | ||
</math> | </math> | ||
'''Procedimiento''' | |||
Observamos que el centro de la curva es z=2 y tiene radio 5, entonces analizando la integral se ve que no es analítico en z=0 y z=1, pero ambos están dentro del contorno entonces es analítica la curva, procedemos a decir: | Observamos que el centro de la curva es z=2 y tiene radio 5, entonces analizando la integral se ve que no es analítico en z=0 y z=1, pero ambos están dentro del contorno entonces es analítica la curva, procedemos a decir: | ||
| Línea 652: | Línea 704: | ||
: <math> \oint_{c}\frac{f_{2}(z)}{(z-0)^{3}}dz=\frac{2\pi i}{2!}f_{2}^{'}(0)=\pi i(6)=6\pi i | : <math> \oint_{c}\frac{f_{2}(z)}{(z-0)^{3}}dz=\frac{2\pi i}{2!}f_{2}^{'}(0)=\pi i(6)=6\pi i | ||
</math> | </math> | ||
'''Solución''' | |||
Por lo tanto | Por lo tanto | ||
| Línea 661: | Línea 715: | ||
</math> | </math> | ||
Elaborado por Ricado García Hernández--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 15:23 20 jun 2015 (CDT) | ---- | ||
Elaborado por: Ricado García Hernández--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 15:23 20 jun 2015 (CDT) | |||
---- | ---- | ||
=== Ejercicio 22 === | === Ejercicio 22 === | ||
Utilice los teoremas 5.9 y 5.10, cuando sean apropiados, para evaluar la integral a lo largo de los contornos cerrados: | |||
$\oint_C \frac{1}{z^2(z^2+1)}dz; |z-i|=\frac{3}{2} $. | |||
'''Procedimiento''' | |||
Notemos que: $f(z)=\frac{1}{z+i}$ es analítica dentro del contorno dado, por otra parte: $z^2+1=(z+i)(z-i)$ y que $\frac{1}{z^2(z^2+1)}=\frac{\frac{1}{z+i}}{z^2(z-i)}$. | Notemos que: $f(z)=\frac{1}{z+i}$ es analítica dentro del contorno dado, por otra parte: $z^2+1=(z+i)(z-i)$ y que $\frac{1}{z^2(z^2+1)}=\frac{\frac{1}{z+i}}{z^2(z-i)}$. | ||
| Línea 675: | Línea 731: | ||
$\oint_C \frac{1}{z^2(z^2+1)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz$. Al descomponer $\frac{1}{z^2(z-i)}$ en fracciones parciales obtenemos que: $\frac{1}{z^2(z-i)}=\frac{1}{z^2}-\frac{1}{z-i}+\frac{1}{z}$. Por lo anterior $\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2}dz-\oint_C \frac{\frac{1}{z+i}}{(z-i)}dz+\oint_C \frac{\frac{1}{z+i}}{z}dz=\frac{2\pi if'(0)}{1!}-2\pi i f(i)+2\pi if(0)=2\pi i(\frac{-1}{(0+i)^2}-\frac{1}{2i}+\frac{1}{i})=2\pi i(1-\frac{1}{2i}+\frac{2}{2i})=2\pi i (1+\frac{1}{2i})=2\pi (\frac{1}{2}+i)=\pi(1+2i)$. | $\oint_C \frac{1}{z^2(z^2+1)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz$. Al descomponer $\frac{1}{z^2(z-i)}$ en fracciones parciales obtenemos que: $\frac{1}{z^2(z-i)}=\frac{1}{z^2}-\frac{1}{z-i}+\frac{1}{z}$. Por lo anterior $\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2}dz-\oint_C \frac{\frac{1}{z+i}}{(z-i)}dz+\oint_C \frac{\frac{1}{z+i}}{z}dz=\frac{2\pi if'(0)}{1!}-2\pi i f(i)+2\pi if(0)=2\pi i(\frac{-1}{(0+i)^2}-\frac{1}{2i}+\frac{1}{i})=2\pi i(1-\frac{1}{2i}+\frac{2}{2i})=2\pi i (1+\frac{1}{2i})=2\pi (\frac{1}{2}+i)=\pi(1+2i)$. | ||
'''Solución''' | |||
Por lo tanto: $\oint_C \frac{1}{z^2(z^2+1)}dz ;(|z-i|=\frac{3}{2})=\pi(1+2i) $ | Por lo tanto: $\oint_C \frac{1}{z^2(z^2+1)}dz ;(|z-i|=\frac{3}{2})=\pi(1+2i) $ | ||
---- | |||
[[Usuario:Alan Daniel Barrón Posadas|Alan Daniel Barrón Posadas]] ([[Usuario discusión:Alan Daniel Barrón Posadas|discusión]]) 13:07 28 jun 2015 (CDT) | Realizado por:[[Usuario:Alan Daniel Barrón Posadas|Alan Daniel Barrón Posadas]] ([[Usuario discusión:Alan Daniel Barrón Posadas|discusión]]) 13:07 28 jun 2015 (CDT) | ||
---- | ---- | ||
| Línea 687: | Línea 745: | ||
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz$ | $\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz$ | ||
'''Procedimiento''' | |||
Sabemos que C no es un contorno simple pero lo pensamos como si fueran | Sabemos que C no es un contorno simple pero lo pensamos como si fueran | ||
| Línea 724: | Línea 782: | ||
$I_{2}=\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=\frac{2\pi i}{1!}f^{\text{,}}\left(2\right)=2\pi i\left(-\frac{1}{4}\right)=-\frac{\pi}{2}i$ | $I_{2}=\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=\frac{2\pi i}{1!}f^{\text{,}}\left(2\right)=2\pi i\left(-\frac{1}{4}\right)=-\frac{\pi}{2}i$ | ||
'''Conclusión''' | |||
Finalmente sumamos las integrales y obtenemos el resultado requerido | Finalmente sumamos las integrales y obtenemos el resultado requerido | ||
| Línea 730: | Línea 790: | ||
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\pi i$ | $\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\pi i$ | ||
---- | ---- | ||
Resuelto por: [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 22:31 21 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 24=== | ===Ejercicio 24=== | ||
En los problemas 23 y 24 , evalúe la integral dada , donde C es la | En los problemas 23 y 24 , evalúe la integral dada , donde C es la | ||
forma de ocho vertical contorno en la figura 5.47, | forma de ocho vertical contorno en la figura 5.47, | ||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ donde | $\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ donde C | ||
es ese | |||
8 vertical | 8 vertical | ||
'''Procedimiento''' | |||
para poder atacar este ejercicio tenemos los siguientes teoremas: | para poder atacar este ejercicio tenemos los siguientes teoremas: | ||
| Línea 756: | Línea 812: | ||
Entonces, para cualquier punto z0 singular dentro de C , | Entonces, para cualquier punto z0 singular dentro de C , | ||
$f\left(z_{0}\right)=\frac{1}{ | $f\left(z_{0}\right)=\frac{1}{2i\pi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)}dz$ | ||
2.-Fórmula Integral Teorema 5.10 de Cauchy para Derivados: | 2.-Fórmula Integral Teorema 5.10 de Cauchy para Derivados: | ||
| Línea 764: | Línea 820: | ||
Entonces, para cualquier punto z0 singular dentro de C | Entonces, para cualquier punto z0 singular dentro de C | ||
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{ | $f^{n\prime}\left(z_{0}\right)=\frac{n!}{2i\pi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$ | ||
por lo cual | por lo cual debemos llevar la integral propuesta a alguna de las dos | ||
formas anteriores para poder usar algún teorema: | |||
pero antes | pero antes debemos considerar el contorno C y la integral | ||
es obvio que el denominador tiene 2 singularidades las cuales son | es obvio que el denominador tiene 2 singularidades las cuales son | ||
$z=i$ y tambien $z=-i$ y tambien es obvio que este | $z=i$ y tambien $z=-i$ y tambien es obvio que este contorno no | ||
es simple ya que tiene un cruce con si mismo por lo cual procedemos | es simple ya que tiene un cruce con si mismo por lo cual procedemos | ||
a cortar este contorno en dos contornos de la siguiente manera: | a cortar este contorno en dos contornos de la siguiente manera: | ||
$C=c_{1}+c_{2}$donde cada sumando es una | $C=c_{1}+c_{2}$donde cada sumando es una porción del contorno total | ||
por lo que la integral original podemos partirla en dos integrales | |||
de la siguiente manera: | de la siguiente manera: | ||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ | $\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ | ||
ahora si resolvemos cada integral por separado y aplicando los teoremas | |||
y | y después las sumamos | ||
3.- integral sobre c$_{1}$donde la singularidad es $z=i$: | 3.- integral sobre c$_{1}$donde la singularidad es $z=i$: | ||
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ | $\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ arregladora | ||
para poder usar | para poder usar algún teorema queda: | ||
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=\oint c_{1}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ | $\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=\oint c_{1}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ | ||
| Línea 836: | Línea 892: | ||
entonces la integral para c$_{1}$queda: | entonces la integral para c$_{1}$queda: | ||
$-\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=- | $-\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=-2i\pi \left(0\right)=0$ | ||
por lo tanto la integral total es igual a la suma de integrales para | por lo tanto la integral total es igual a la suma de integrales para | ||
| Línea 843: | Línea 899: | ||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ | $\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ | ||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz= | '''Solución''' | ||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2i\pi \left(\frac{-4e^{-1}}{\left(2i\right)^{3}}\right)-0$ | |||
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz= | $\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2i\pi \left(\frac{-4e^{-1}}{-8i}\right)=\frac{-8\pi e^{-1}}{-8}=\pi e^{-1}$ | ||
---- | |||
--[[Usuario:Martin Flores Molina|Martin Flores Molina]] ([[Usuario discusión:Martin Flores Molina|discusión]]) 13:05 15 mayo 2015 (CDT) | Realizado por:[[Usuario:Martin Flores Molina|Martin Flores Molina]] ([[Usuario discusión:Martin Flores Molina|discusión]]) 13:05 15 mayo 2015 (CDT) | ||
---- | ---- | ||
===Ejercicio 25=== | ===Ejercicio 25=== | ||
Proceder como el ejemplo 5 para encontrar el módulo máximo de la función dada en la región circular $|z|\leq 5$ para $f(z)=-iz+i$. | |||
'''Procedimiento''' | |||
$|f(z)|^2=f(z)\bar{f(z)}=(-iz+i)(i\bar{z}-i)=-i(z-1)(\bar{z}-1)i=-i^2\left [z\bar{z}-(z+\bar{z})+1 \right ]$ | |||
$|f(z)|=z\bar{z}-2Re(z)+1$ | |||
Entonces: | |||
$max|f(z)|^2=max|z\bar{z}-2Re(z)+1|$ | |||
$ | Donde el $max(z)=5$ Entonces: | ||
$max|f(z)|^2=max|z\bar{z}-2Re(z)+1|=5^2-2(-5)+1$ | |||
'''Solución''' | |||
$ | $max|f(z)|^2=25+10+1=36$ | ||
Entonces: | |||
$|f(z)|=6$ | |||
---- | |||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | ---- | ||
| Línea 909: | Línea 946: | ||
$f(z)=z^{2}+4z$ ; $|z|\leq1$ | $f(z)=z^{2}+4z$ ; $|z|\leq1$ | ||
'''Procedimiento''' | |||
sabemos que | sabemos que | ||
| Línea 955: | Línea 995: | ||
$|z^{2}+4z|=\sqrt{25}=5$ | $|z^{2}+4z|=\sqrt{25}=5$ | ||
'''Solución''' | |||
por lo tanto | por lo tanto | ||
| Línea 963: | Línea 1005: | ||
--[[Usuario:Juan Daniel Rivera Bautista|Juan Daniel Rivera Bautista]] ([[Usuario discusión:Juan Daniel Rivera Bautista|discusión]]) 23:40 21 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Juan Daniel Rivera Bautista|Juan Daniel Rivera Bautista]] ([[Usuario discusión:Juan Daniel Rivera Bautista|discusión]]) 23:40 21 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 974: | Línea 1015: | ||
f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\] | f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\] | ||
'''Procedimiento''' | |||
| Línea 989: | Línea 1032: | ||
Así llegamos al teorema del | Así llegamos al teorema del valor medio | ||
'''Conclusión''' | |||
\[ | \[ | ||
f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\] | f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\] | ||
---- | ---- | ||
Realizado por:[[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 21:23 21 jun 2015 (CDT)Esther Sarai | |||
---- | |||
'''Forma alternativa''' | |||
Se tiene la formula integral de Cauchy: | Se tiene la formula integral de Cauchy: | ||
| Línea 1004: | Línea 1051: | ||
donde el problema nos dice que f es analítica , <math> z_{0} | donde el problema nos dice que f es analítica , <math> z_{0} | ||
</math> es el centro , y r el | </math> es el centro , y r el radio de la circunferencia C. | ||
Recordemos que la forma exponencial de un numero complejo esta dada de la forma: | Recordemos que la forma exponencial de un numero complejo esta dada de la forma: | ||
| Línea 1023: | Línea 1070: | ||
</math> | </math> | ||
Ahora derivamos ambos miembros , uno con respecto a “z” y | Ahora derivamos ambos miembros , uno con respecto a “z” y otro con respecto a theta en el segundo miembro, y se tiene: | ||
: <math> z=z_{0}+re^{i\theta} | : <math> z=z_{0}+re^{i\theta} | ||
| Línea 1039: | Línea 1086: | ||
</math> | </math> | ||
Eliminado | Eliminado términos se tiene: | ||
: <math> f(z_{0})=\frac{1}{2\pi}\oint_{c}f(z_{0}+re^{i\theta})d\theta | : <math> f(z_{0})=\frac{1}{2\pi}\oint_{c}f(z_{0}+re^{i\theta})d\theta | ||
| Línea 1051: | Línea 1098: | ||
Lo cuál esta demostrado y ha este resultado se le conoce como el teorema del valor medio de Gauss, | Lo cuál esta demostrado y ha este resultado se le conoce como el teorema del valor medio de Gauss, | ||
y muestra que el valor de f en el centro z subíndice cero de la | y muestra que el valor de f en el centro z subíndice cero de la circunferencia es el promedio de todos | ||
los valores de f en la | los valores de f en la circunferencia de C. | ||
---- | |||
Elaborado por Ricardo García Hernández--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 00:28 22 jun 2015 (CDT) | Elaborado por Ricardo García Hernández--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 00:28 22 jun 2015 (CDT) | ||
---- | ---- | ||
Revisión actual - 00:13 25 mar 2023
Ejercicios del capítulo 5, sección 5 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 5.5
Ejercicio 1
Evalué la integral dada a lo largo del contorno cerrado indicado
$ \oint_{c} \frac{4}{z-3i}dz $; $ |z|=5 $
Procedimiento
Aquí observamos que $f(z)=4$ y $z_0=-i$ como un punto dentro de la circunferencia $C$.
Después observamos que la función $f$ es analítica en el contorno $C$
Y al aplicar la formula de Cauchy, obtenemos
$ \oint_{c} \frac{4}{z-3i}dz = 2\pi i f(-i) =2\pi i(4) $, así tenemos
Conclusión
$ \oint_{c} \frac{4}{z-3i}dz = 8\pi i$
Realizado por: Miguel Medina Armendariz (discusión) 18:11 19 jun 2015 (CDT)
Ejercicio 2
Evaluar la integral a lo largo del contorno indicado:
\begin{equation*}
\oint _C \frac{z^2}{\left (z-3i \right )^{2}}dz
\end{equation*}
Donde $C: |z|=5$
Procedimiento
Usando la formula integral de Cauchy
\begin{equation*} f^{n}(z_0)=\frac{n!}{2i\pi}\oint \frac{f(z)}{(z-z_0)^{n+1}}dz \end{equation*}
Para $n=1$ , $z_0=3i$ y $f(z)=z^2$
$f^{1}(3i)=\frac{1!}{2i\pi}\oint \frac{z^2}{(z-3i)^{2}}dz$
$f(z)=z^2$
$f'(z)=2z$
$f'(3i)=2(3i)=6i$
$6i(2i\pi)=\oint \frac{z^2}{(z-3i)^{2}}dz$
Solución
\begin{equation*} \oint \frac{z^2}{(z-3i)^{2}}dz=-12\pi \end{equation*}
Re elaborado por Manuel Rodríguez
Ejercicio 3
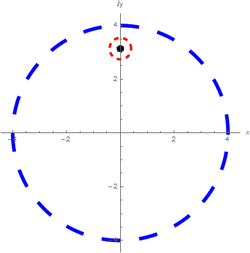
Use el teoremas 5.5.1 o 5.5.2, en su caso para evaluar la integral $\oint_{c} \! \frac{e^z}{z-i\pi}\,dz$ a lo largo de $|z|=4$.
La integral tiene una singularidad en $z=i\pi$, que se encuentra en el dominio de integración, por lo que no es analítica en ese punto y es preciso extraer ese punto, se muestra en la figura.
Procedimiento
El teorema 5.5.1 indica que: \[ f(z_0)=\frac{1}{2\pi i}\oint_{C} \! \frac{f(z)}{z-z_0}\,dz \]
Para una $f(z)=e^z$ y una $z_0=i\pi$ tenemos: \[ f(i\pi)=\frac{1}{2\pi i}\oint_{C} \! \frac{e^z}{z-i\pi}\,dz \] Que claramente coincide con nuestra integral, despejando nos queda:
Conclusión
\[ \oint_{C} \! \frac{e^z}{z-i\pi}\,dz=f(i\pi)\,(2\pi i)=2i\pi e^{i\pi}=2i\pi\,[cis (\pi)]=2i\pi\,(-1)=-2i\pi \]
Realizado por:Tlacaelel Cruz (discusión) 23:40 19 jun 2015 (CDT)
Ejercicio 4
Evalúe la integral dada a lo lardo del contorno cerrado indicado.
$\oint_{c}\frac{1+e^{z}}{z}dz$, con $|z|=1$
Procedimiento
Primero se ve que el único punto donde el integrando no es analítico es en $z=0$ y que, en este caso, se encuentra dentro del contorno C, y teniendo en cuenta el teorema 5.5.1 tenemos que:
$f(z)=1+e^{z}$
Y
$z-z_{0}=z-0$
Entonces:
$\oint_{c}\frac{1+e^{z}}{z}dz,=\oint_{c}\frac{f(z)}{z-z_{o}}dz=2\pi if(z_{0})=2\pi if(0)=2\pi i(1+1)$
Conclusión
Finalmente
\[ \oint_{c}\frac{1+e^{z}}{z}dz,=4\pi i \]
Realizado por:Fernando Vazquez V. (discusión) 01:13 21 jun 2015 (CDT)
Ejercicio 5
Use el teoremas 5.5.1 o 5.5.2, en su caso para evaluar la integral a lo largo del contorno cerrado indicado.
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz $; $ |z|=3 $
Procedimiento
Primero, identificamos $f(z)=z^2-3z+4i$ y $z_0=-2i$ como un punto dentro del círculo C. Se observa que $f$ es analítica en todos los puntos dentro y en el contorno C. Así, por Cauchy (Teorema 5.5.1):
$ f(z_0)=\frac{1}{2\pi i}\oint_{c} \frac{f(z)}{z-z_0} dz $
Obtenemos:
$ 2\pi i f(-2i)= 2\pi i(-4+10i)= -8\pi i -20\pi = -\pi(20+8i) $
Conclusión
$ \oint_{c} \frac{z^2-3z+4i}{z+2i}dz = 2\pi i f(-2i)= -\pi(20+8i)$
Realizado por: Nancy Martínez Durán (discusión) 21:56 18 jun 2015 (CDT)
Ejercicio 7
Evalúe la integral dada a lo largo de los contornos
Inciso a
a)
Analizando la función dada, la función tiene puntos donde no es analítica en los puntos y en el punto
reescribiendo la función
En donde para este contorno el término no está definido en el dominio, por lo que haremos que
Por lo que evaluando f(z) en , tenemos que
por lo que el resultado es
Inciso b
b)
Del inciso a) analizamos que f(z) no es analítica en en los puntos y en el punto
reescribiendo la función. Y lo escribimos de la forma
Por lo que hacemos el mismo proceso anterior, pero ahora solo para el punto dado que en esta región no es analítica en dicho punto. Por lo que tenemos que
Evaluando g(z) en tenemos que
Por lo que
Realizado por:Pablo (discusión) 14:31 21 jun 2015 (CDT)
Ejercicio 11
Evalúe la integral dada a lo largo del contorno cerrado indicado.
$\oint_{C}\frac{e^{z²}}{(z-i)³}dz ; |z-i|=1$
Procedimiento
Nuestro contorno esta definido por una circunferencia con centro en $i$ y radio $1$ .Ahora bien podemos notar de nuestra función que existe una singularidad cuando $z=i$ la cual se encuentra dentro de nuestro dominio , por lo cual no es analítica en ese punto.
Para la resolución de este problema emplearemos lo siguiente: $f^{n}(z_0)=\frac{n!}{2i\pi}\oint \frac{f(z)}{(z-z_0)^{n+1}}dz..... (*)$
por lo cual de nuestra integral a resolver identificamos:
$n=2$
$n!=2$
$f(z)=e^{z²}$
$f'(z)=2z e^{z²}$
\[ f''(z)=2e^{z²}(2z²+1) \]
$z_0=i$
utilizando $(*)$
$2 e^{z_0²}(2z_0²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$
sustituyendo :
$2 e^{(i)²}(2(i)²+1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$
$2 e^{-1}(-1)=\frac{2}{2i\pi}\oint_{C}\frac{e^{z²}}{(z-i)³}dz$
Solución
Despejando $-2 e^{-1}i\pi=\oint_{C}\frac{e^{z²}}{(z-i)³}dz$
Por lo cual nuestra solución es $-2ie^{-1}\pi$
Realizado por:Anahi Limas (discusión) 18:55 21 jun 2015 (CDT)
Ejercicio 15
Evalúe la integral a lo largo de los contornos cerrados indicados
1.- $\oint_{C}\frac{2z+5}{z^{2}-2z}dz$; a) $\mid z\mid=\frac{1}{2}$
b) $\mid z+1\mid=2$
c) $\mid z-3\mid=2$
d) $\mid z+2i\mid=1$
$\oint_{C}\frac{2z+5}{z^{2}-2z}dz=\oint_{C}\frac{2z+5}{z(z-2)}dz$
Inciso a
y por fracciones parciales:
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\oint_{C}[\frac{A}{z}+\frac{B}{z-2}]dz=\oint_{C}\frac{A(z-2)+B(z)}{z(z-2)}\Longleftrightarrow2z+5=A(z-2)+B(z)$
resolviendo la ecuación para $A\;y\;B$ tenemos:
si
$z=0$
entonces:
$5=-2A\Longleftrightarrow A=-\frac{5}{2}$
si
$z=2$
entonces:
$9=2B\Longleftrightarrow B=\frac{9}{2}$
de esto:
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\oint_{C}[\frac{A}{z}+\frac{B}{z-2}]dz=\oint_{C}[-\frac{5}{2z}+\frac{9}{2z-4}]dz=-\frac{5}{2}\oint_{C}\frac{1}{z}dz+\frac{9}{2}\oint_{C}\frac{1}{z-2}dz$
$\oint_{C}\frac{2z+5}{z(z-2)}dz=\frac{5}{2}\oint_{C}\frac{1}{z}dz+\frac{9}{2}\oint_{C}\frac{1}{z-2}dz$
evaluando la integral a lo largo de a) $\mid z\mid=\frac{1}{2}$
como se puede ver $\oint_{C}\frac{2z+5}{z(z-2)}dz$ no es una función analítica en $z=0\;y\;en\;z=2$
y como $\mid z\mid=\frac{1}{2}$ es una circunferencia de radio $\frac{1}{2}$ centrada en $0+0i$ entonces
por el teorema de Cauchy-Goursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
ademas como $-\frac{5}{2}\oint_{C}\frac{1}{z}dz$ no es analítica en $\mid z\mid=\frac{1}{2}$ entonces por la formula de la integral de Cauchy
$f(z_{0})=\frac{1}{2\pi i}\oint_{c}\frac{f(z)}{z-z_{0}}dz$
$\oint_{C}\frac{1}{z}dz=2\pi i\Longleftrightarrow-\frac{5}{2}\oint_{C}\frac{1}{z}dz=-\frac{5}{2}2\pi i=-5\pi i$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$
Inciso b
Ahora evaluando a lo largo de b) $\mid z+1\mid=2$, (circunferencia de radio $2$ centrada en $-1$) por el razonamiento anterior:
como $z=2$ no esta dentro del contorno $\mid z+1\mid=2$ entonces por el teorema de Cauchy-Goursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
como $z=0$ se encuentra dentro del contorno $\mid z+1\mid=2$
$\oint_{C}\frac{1}{z}dz=2\pi i\Longleftrightarrow-\frac{5}{2}\oint_{C}\frac{1}{z}dz=-\frac{5}{2}2\pi i=-5\pi i$
ademas
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0-5\pi i=-5\pi i$
Inciso c
Ahora evaluando a lo largo de c) $\mid z-3\mid=2$,(circunferencia de radio $2$ centrada en $3$)
como $z=2$ esta sobre el contorno $\mid z-3\mid=2$ entonces
$\oint_{C}\frac{1}{z-2}dz=2\pi i\Longleftrightarrow\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=\frac{9}{2}2\pi i=9\pi i$
como $z=0$ no se encuentra dentro del contorno $\mid z+1\mid=2$ por el teorema de Cauchy-Goursat
$-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=9\pi i+0=9\pi i$
Inciso d
ahora evaluando a lo largo de d) $\mid z+2i\mid=1$(circunferencia de radio$1$ centrada en $-2i$ )
como $z=0\;y\;z=2$ no se encuentran dentro del contorno $\mid z+2i\mid=1$ entonces por el teorema de Cauchy-Goursat
$\frac{9}{2}\oint_{C}\frac{1}{z-2}dz=0$
$-\frac{5}{2}\oint_{C}\frac{1}{z}dz=0$
entonces:
$\Longrightarrow\oint_{C}\frac{2z+5}{z(z-2)}dz=0+0=0$
Realizado por: Francisco Medina Albino (discusión) 23:19 19 jun 2015 (CDT)
Ejercicio 17
Utilice los teoremas 5.5.1 y 5.5.2, cuando sea apropiado, evalúe la integral $ \oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz $ a lo largo de los contornos cerrados indicados.
$(a)$ $|z|=1$
$(b)$ $|z-1-i|= 1$
Inciso a
Solución del inciso $(a) : $
Al examinar el integrando se ve que no es analítica en $z=0$ y en $z=1+i$ pero sólo $z=0$ está dentro del contorno cerrado. Al escribir el integrando como
\[ \frac{z+2}{z^{2}(z-1-i)}=\frac{\frac{z+2}{z-1-i}}{z^{2}} \]
podemos identificar, $ z_{0}=0 $ y $ n=1 $ y $ f(z)=\frac{z+2}{z-1-i} $. La regla del cociente da $f'(z)= -\frac{3+i}{(z-(1+i))^2}$ y así $f'(0)=-\frac{1}{2}+\frac{3 i}{2} $. Por tanto, del teorema 5.5.2 se encuentra
\[
\oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz = \frac{2 \pi i }{1!} f'(0) = \left( \frac{2 \pi i }{1!} \right) \left( -\frac{1}{2}+\frac{3 i}{2} \right) = (-3-i) \pi
\]
Inciso b
Solución del inciso $(b) : $
Al examinar vemos que $1+i$ es el único punto en el contorno cerrado $C$ en que el integrando no es analítico. Entonces reescribiendo el integrando como
\[
\frac{z+2}{z^{2} (z-1-i) }= \frac{ \frac{z+2}{z^{2}} }{z-1-i}
\]
podemos identificar $f(z)= (z+2)/z^{2}$. La función $f$ es analítica en todos los puntos dentro y sobre el contorno $C$. Por tanto, de la fórmula integral de Cauchy del teorema 5.5.1 tenemos:
\[ \oint_{C} \! \frac{z+2}{z^{2} (z-1-i)} \,dz = \int_{C} \! \frac{ \frac{z+2}{z^{2}} }{z-1-i} \,dz = 2 \pi i f(1+i)= ( 2 \pi i)\left( \frac{1}{2}-\frac{3 i}{2} \right)= (3+i) \pi \]
Realizado por: Emmanuell Castro Flores (discusión) 21:05 20 jun 2015 (CDT)
Ejercicio 18
Usa el teorema 5.9 o 5.10 que sea apropiado para evaluar la integral dada a lo largo del contorno cerrado indicado
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz ; (a) |z| = 1 , (b) |z - 2| = 1$
Procedimiento
(a) $|z| = 1$
Las singularidades de la integral son $z=0$ y $z=4$
Ahora tenemos una circunferencia con centro en 2 y de radio 1 es por ello que re escribiremos la integral de la siguiente forma:
$\oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz$
Ahora en este haremos uso del teorema 5.10 :
\[ f ''(z_0) = \frac{2}{2\pi i } \oint_{C} \frac{f (z)}{(z - z_0)^3} dz \]
Donde: \[ f = \frac{1}{z - 4} \]
\[ z_0 = 0 \]
\[ f ' = \frac{d}{dz} (z - 4)^{-1} = \frac{-1}{(z - 4)^2} \]
\[ f '' = \frac{d}{dz} (\frac{-1}{(z - 4)^2}) = \frac{2}{(z - 4)^3} \]
Aplicando el teorema a la integral tenemos:
\[ \oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{2\pi i}{2} f '' (z_0) \]
Con
\[ f '' (z_0) = \frac{2}{(0 - 4)^3} = \frac{-2}{64} = \frac{-1}{32} \]
$\Rightarrow $
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = \oint_{C} \frac{\frac{1}{z - 4}}{z^3} dz = \frac{-\pi i}{32}$
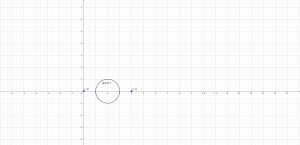
Inciso b
En este caso ambas singularidades están fuera del contorno, como se ve en la siguiente imagen:
Dado que $f(z)$ es Analítica sobre la curva C, entonces la integral es 0, usando el teorema de Cauchy-Goursat.
$\oint_{C} \frac{1}{z^{3} (z - 4)} dz = 0$
Re elaborado por Manuel Rodríguez
Ejercicio 19
Ejercicio 19
Evaluar la integral dada a lo largo del contorno cerrado indicado:
$\oint_{c}\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz$ ; $\left|z\right|=6$
$\oint_{c}\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz$
$=\oint_{c}\frac{e^{2iz}}{z^{4}}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
$=\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$ ...$\left(1\right)$
Procedimiento
por lo que podemos definir convenientemente:
$f\left(z_{1}\right)=e^{2iz}$ ...$\left(2\right)$ y
$f\left(z_{2}\right)=z^{4}$ ...$\left(3\right)$
También es claro que hay dos singularidades en:
1.- $z_{0,1}=0$ y
2.- $z_{0,2}=i$
{*} Para poder utilizar la fórmula integral de Cauchy las funciones
evaluadas en la integral deben ser analíticas en un dominio simplemente
conexo $D$ y $C$ debe ser cualquier contorno cerrado simple situado
totalmente en $D$. En nuestro ejemplo estas condiciones sí se cumplen. {*}
.
Cálculo de $\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz$ :
Por la fórmula integral de Cauchy se tiene:
$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz$
$=\frac{2\pi i.f\prime\prime\prime\left(z_{0,1}\right)_{1}}{3!}$
donde $f\prime\prime\prime\left(z_{1}\right)=-8ie^{2iz}$ es la derivada
de tercer orden de la ecuación $\left(2\right)$
Y por lo tanto
$f\prime\prime\prime\left(z_{0,1}\right)_{1}=-8i$
entonces:$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz=\frac{2\pi i\left(-8i\right)}{6}=\frac{8}{3}\pi$ ...$\left(4\right)$
Cálculo de $\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
Por la fórmula integral de Cauchy se tiene:
$\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz$
$=\frac{2\pi i\left(f\prime\prime\left(z_{0,2}\right)_{2}\right)}{2!}$
donde $f\prime\prime\left(z_{2}\right)=12z^{2}$es la segunda derivada de la ec $\left(3\right)$
Y por lo tanto :
$f\prime\prime\left(z_{0,2}\right)_{2}=12i^{2}$
Entonces:
$\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz=\frac{2\pi i\left(12i^{2}\right)}{2}=-12\pi i$ ... $\left(5\right)$
Finalmente sustituyendo los valores de las ecs. $\left(4\right)$y $\left(5\right)$en
Conclusion
la euación $\left(1\right)$ se obtiene:
$\oint_{c}\frac{e^{2i\pi}}{\left(z-0\right)4}dz-\oint_{c}\frac{z^{4}}{\left(z-i\right)^{3}}dz=\frac{8}{3}\pi+12\pi i$
$\therefore\oint_{c}=\left(\frac{e^{2iz}}{z^{4}}-\frac{z^{4}}{\left(z-i\right)^{3}}\right)dz=\pi\left(\frac{8}{3}+12i\right)$
Resuelto por: Alejandro Juárez Toribio (discusión) 17:38 18 jun 2015 (CDT)
Ejercicio 21
Evalue la integral dada a lo largo del contorno cerrado indicado
- ;
Procedimiento
Observamos que el centro de la curva es z=2 y tiene radio 5, entonces analizando la integral se ve que no es analítico en z=0 y z=1, pero ambos están dentro del contorno entonces es analítica la curva, procedemos a decir:
- , donde :
- , y entonces nos queda:
La formula integral de Cauchy para derivadas, para cualquier punto dentro de C es:
- , comparando con las integrales que tenemos, obtenemos:
Para la primera función
- , donde y
lo que nos dice n=1 ,es obtener la primera derivada de la funcion f1, y despues valuar en el punto 1,entonces:.
Para la segunda función
- , donde y
lo que nos dice n=2 ,es obtener la segunda derivada de la funcion f2 y despues valuar en el punto 0 ,entonces:.
Solución
Por lo tanto
Elaborado por: Ricado García Hernández--Ricardo Garcia Hernandez (discusión) 15:23 20 jun 2015 (CDT)
Ejercicio 22
Utilice los teoremas 5.9 y 5.10, cuando sean apropiados, para evaluar la integral a lo largo de los contornos cerrados:
$\oint_C \frac{1}{z^2(z^2+1)}dz; |z-i|=\frac{3}{2} $.
Procedimiento
Notemos que: $f(z)=\frac{1}{z+i}$ es analítica dentro del contorno dado, por otra parte: $z^2+1=(z+i)(z-i)$ y que $\frac{1}{z^2(z^2+1)}=\frac{\frac{1}{z+i}}{z^2(z-i)}$.
Entonces:
$\oint_C \frac{1}{z^2(z^2+1)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz$. Al descomponer $\frac{1}{z^2(z-i)}$ en fracciones parciales obtenemos que: $\frac{1}{z^2(z-i)}=\frac{1}{z^2}-\frac{1}{z-i}+\frac{1}{z}$. Por lo anterior $\oint_C \frac{\frac{1}{z+i}}{z^2(z-i)}dz=\oint_C \frac{\frac{1}{z+i}}{z^2}dz-\oint_C \frac{\frac{1}{z+i}}{(z-i)}dz+\oint_C \frac{\frac{1}{z+i}}{z}dz=\frac{2\pi if'(0)}{1!}-2\pi i f(i)+2\pi if(0)=2\pi i(\frac{-1}{(0+i)^2}-\frac{1}{2i}+\frac{1}{i})=2\pi i(1-\frac{1}{2i}+\frac{2}{2i})=2\pi i (1+\frac{1}{2i})=2\pi (\frac{1}{2}+i)=\pi(1+2i)$.
Solución
Por lo tanto: $\oint_C \frac{1}{z^2(z^2+1)}dz ;(|z-i|=\frac{3}{2})=\pi(1+2i) $
Realizado por:Alan Daniel Barrón Posadas (discusión) 13:07 28 jun 2015 (CDT)
Ejercicio 23
Evaluar la integral, donde C es la figura en forma de ocho
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz$
Procedimiento
Sabemos que C no es un contorno simple pero lo pensamos como si fueran dos solo que uno va en horario $-c_{1}$ y el otro antihorario $c_{2}$ por cual las integrales las escribiremos de la siguiente manera:
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=\oint_{c_{1}}\frac{3z+1}{z\left(z-2\right)^{2}}dz+\oint_{c_{2}}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\oint_{-c_{1}}\frac{\frac{3Z+1}{\left(Z-2\right)^{2}}}{Z}dz+\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=-I_{1}+I_{2}$
Para resolver $I_{1}$usaremos
$f\left(z_{0}\right)=\frac{1}{2\pi i}\oint_{c}\frac{f\left(z\right)}{z-z_{0}}dz$
Sacamos a $z_{0}$y a $f\left(z\right)$
$z_{0}=0$ $f\left(z\right)=\frac{3z+1}{\left(z-2\right)^{2}}$
entonces tenemos que:
$I_{1}=\oint_{-c_{1}}\frac{\frac{3Z+1}{\left(Z-2\right)^{2}}}{Z}dz=2\pi if\left(0\right)=2\pi i\left(\frac{1}{4}\right)=\frac{\pi}{2}i$
Pero nosotros queremos $-I$ entonces al resultado anterior lo multiplicamos por un signo menos y así tenemos que:
$-I=-\frac{\pi}{2}i$
Ahora para resolver $I_{2}$ utilizaremos
$f^{\left(n\right)}\left(z_{0}\right)=\frac{n!}{2\pi i}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
tenemos que
$z_{0}=2$ y $f\left(z\right)=3+\frac{1}{z}\Longrightarrow f^{,}\left(z\right)=-\frac{1}{Z^{2}}$y también $f\left(2\right)=-\frac{1}{4}$
Ahora resolvemos $I_{2}$
$I_{2}=\oint_{c_{2}}\frac{\frac{3Z+1}{Z}}{\left(Z-2\right)^{2}}dz=\frac{2\pi i}{1!}f^{\text{,}}\left(2\right)=2\pi i\left(-\frac{1}{4}\right)=-\frac{\pi}{2}i$
Conclusión
Finalmente sumamos las integrales y obtenemos el resultado requerido que es:
$\oint_{c}\frac{3z+1}{z\left(z-2\right)^{2}}dz=-\pi i$
Resuelto por: Luis Enrique Martínez Valverde (discusión) 22:31 21 jun 2015 (CDT)
Ejercicio 24
En los problemas 23 y 24 , evalúe la integral dada , donde C es la forma de ocho vertical contorno en la figura 5.47,
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ donde C es ese 8 vertical
Procedimiento
para poder atacar este ejercicio tenemos los siguientes teoremas:
1.-Fórmula Integral Teorema 5.9 de Cauchy:
Supongamos que f es analítica en un dominio simplemente conexo D y C es cualquier contorno cerrado sencilla situada totalmente en D. Entonces, para cualquier punto z0 singular dentro de C ,
$f\left(z_{0}\right)=\frac{1}{2i\pi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)}dz$
2.-Fórmula Integral Teorema 5.10 de Cauchy para Derivados:
Supongamos que f es analítica en un dominio simplemente conexo D y C es cualquier contorno cerrado sencilla situada totalmente en D. Entonces, para cualquier punto z0 singular dentro de C
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2i\pi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
por lo cual debemos llevar la integral propuesta a alguna de las dos formas anteriores para poder usar algún teorema:
pero antes debemos considerar el contorno C y la integral es obvio que el denominador tiene 2 singularidades las cuales son $z=i$ y tambien $z=-i$ y tambien es obvio que este contorno no es simple ya que tiene un cruce con si mismo por lo cual procedemos a cortar este contorno en dos contornos de la siguiente manera:
$C=c_{1}+c_{2}$donde cada sumando es una porción del contorno total por lo que la integral original podemos partirla en dos integrales de la siguiente manera:
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$
ahora si resolvemos cada integral por separado y aplicando los teoremas y después las sumamos
3.- integral sobre c$_{1}$donde la singularidad es $z=i$:
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ arregladora para poder usar algún teorema queda:
$\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=\oint c_{1}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ dejamos las singularidades en el denominador y subimos al numerador el resto de la siguiente manera:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)\left(z+i\right)}}{\left(\left(z-i\right)\right)\left(\left(z-i\right)\right)}dz$ desarrollando en el denominador tenemos:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz$ haora si podemos utilizar el teorema Fórmula Integral Teorema 5.10 de Cauchy para Derivados
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
$f^{1\prime}\left(z_{0}\right)=\frac{1!}{2ipi}\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz$ donde $f\left(z\right)=\frac{e^{iz}}{\left(z+i\right)^{2}}$la cual es analitica para c$_{1}$ y $z_{0}=i$
$f^{1\prime}\left(i\right)=\frac{\left(z+i\right)^{2}ie^{iz}-e^{iz}\left(2\left(z+i\right)\right)}{\left(\left(z+i\right)^{2}\right)^{2}}=\frac{-4e^{-1}}{\left(2i\right)^{3}}$ entonces la integral para c$_{1}$queda:
$\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=2ipi\left(\frac{-4e^{-1}}{\left(2i\right)^{3}}\right)$
4.. 3.- integral sobre c$_{2}$donde la singularidad es $z=-i$:
$-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$ arregrandola para poder usar algun teorema queda:
$-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=-\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)^{2}}dz=-\oint_{c_{1}}\frac{e^{iz}}{\left(\left(z+i\right)\left(z-i\right)\right)\left(\left(z+i\right)\left(z-i\right)\right)}dz$ dejamos las singularidades en el denominador y subimos al numerador el resto de la siguiente manera:
$-\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z-i\right)\left(z-i\right)}}{\left(\left(z+i\right)\right)\left(\left(z+i\right)\right)}dz$ desarrollando en el denominador tenemos
$-\oint_{c_{1}}\frac{\frac{e^{iz}}{\left(z-i\right)^{2}}}{\left(z+i\right)^{2}}dz$ haora si podemos utilizar el teorema Fórmula Integral Teorema 5.10 de Cauchy para Derivados
$f^{n\prime}\left(z_{0}\right)=\frac{n!}{2ipi}\oint_{c}\frac{f\left(z\right)}{\left(z-z_{0}\right)^{n+1}}dz$
$-f^{1\prime}\left(z_{0}\right)=-\frac{1!}{2ipi}\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z-i\right)^{2}}}{\left(z+i\right)^{2}}dz$ donde $f\left(z\right)=\frac{e^{iz}}{\left(z-i\right)^{2}}$ la cual es analitica en c$_{2}$y $z_{0}=-i$
$-f^{1\prime}\left(-i\right)=\frac{\left(z-i\right)^{2}ie^{iz}-e^{iz}\left(2\left(z-1\right)\right)}{\left(\left(z-i\right)^{2}\right)^{2}}=-\frac{\left\{ 0\right\} e^{-1}}{\left(-2i\right)^{3}}=-0$ entonces la integral para c$_{1}$queda:
$-\oint_{c_{2}}\frac{\frac{e^{iz}}{\left(z+i\right)^{2}}}{\left(z-i\right)^{2}}dz=-2i\pi \left(0\right)=0$
por lo tanto la integral total es igual a la suma de integrales para c1 y c2
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=\oint_{c_{1}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz-\oint_{c_{2}}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz$
Solución
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2i\pi \left(\frac{-4e^{-1}}{\left(2i\right)^{3}}\right)-0$
$\oint_{c}\frac{e^{iz}}{\left(z^{2}+1\right)^{2}}dz=2i\pi \left(\frac{-4e^{-1}}{-8i}\right)=\frac{-8\pi e^{-1}}{-8}=\pi e^{-1}$
Realizado por:Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT)
Ejercicio 25
Proceder como el ejemplo 5 para encontrar el módulo máximo de la función dada en la región circular $|z|\leq 5$ para $f(z)=-iz+i$.
Procedimiento
$|f(z)|^2=f(z)\bar{f(z)}=(-iz+i)(i\bar{z}-i)=-i(z-1)(\bar{z}-1)i=-i^2\left [z\bar{z}-(z+\bar{z})+1 \right ]$
$|f(z)|=z\bar{z}-2Re(z)+1$
Entonces:
$max|f(z)|^2=max|z\bar{z}-2Re(z)+1|$
Donde el $max(z)=5$ Entonces:
$max|f(z)|^2=max|z\bar{z}-2Re(z)+1|=5^2-2(-5)+1$
Solución
$max|f(z)|^2=25+10+1=36$
Entonces:
$|f(z)|=6$
Re elaborado por Manuel Rodríguez
Ejercicio 26
proceda como en el ejemplo 5 para encontrar el módulo máximo de la función dada en la región circular cerrada indicada
$f(z)=z^{2}+4z$ ; $|z|\leq1$
Procedimiento
sabemos que
$|z|^{2}=z\overline{z}$
entonces
$|z^{2}+4z|^{2}=\left(z^{2}+4z\right)\left(\overline{z^{2}+4z}\right)=\left(z^{2}+4z\right)\left(\overline{z^{2}}+4\overline{z}\right)=z^{2}\overline{z^{2}}+4z\overline{z^{2}}+4\overline{z}z^{2}+16z\overline{z}$
usando las propiedades de los números complejos siguientes
$\overline{z_{1}z_{2}}=\overline{z_{1}}*\overline{z_{2}}$
$|z|^{2}=z\overline{z}$
obtenemos
$z^{2}\overline{z^{2}}+4z\overline{z^{2}}+4\overline{z}z^{2}+16z\overline{z}=zz\overline{z}\overline{z}+4z\overline{z}\overline{z}+4\overline{z}zz+16z\overline{z}=|z|^{2}|z|^{2}+4|z|^{2}\overline{z}+4|z|^{2}z+16|z|^{2}$
nosotros sabemos que $m\acute{a}x_{|z|\leq1}|z^{2}+4z|$ ocurre cuando $|z|=1$
entonces sustituimos y simplificamos
$|z|^{2}|z|^{2}+4|z|^{2}\overline{z}+4|z|^{2}z+16|z|^{2}=(1^{2})(1^{2})+4(1)\overline{z}+4(1)z+16(1)^{2}=1+4\overline{z}+4z+16=17+4(z+\overline{z})$
ahora usamos otra propiedad
$*Re(z)=\frac{\overline{z}+z}{2}$
$2Re(z)=\overline{z}+z$
por lo tanto obtenemos
$17+4(z+\overline{z})=17+4\left(2Re(z)\right)=17+8Re(z)$
y la parte real vale 1 cuando alcanza su máximo en este caso, por lo tanto nos sale que
$17+8Re(z)=17+8=25$
entonces obtenemos que
$|z^{2}+4z|^{2}=25$
$|z^{2}+4z|=\sqrt{25}=5$
Solución
por lo tanto
$m\acute{a}x_{|z|\leq1}|z^{2}+4z|=5$
Realizado por: Juan Daniel Rivera Bautista (discusión) 23:40 21 jun 2015 (CDT)
Ejercicio 28
Supongamos que $f$ es analítica dentro y sobre de la circunferencia C de radio r con el centro en $z_{0}$. Use (1) para obtener
\[ f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\]
Procedimiento
Usando (1)
\[
f(z_{0}) = \dfrac{1}{2\pi} \oint_{C} \dfrac{f(z)}{z-z_{0}} dz \]
Como el radio de C es r entonces $|z-z_{0}|= r $ o $z= z_{0} +re^{i\theta}$. Así (1) se convierte en
\[ f(z_{0}) = \dfrac{1}{2\pi} \oint_{C} \dfrac{f(z_{0}+re_{i\theta} ) ire^{i\theta}}{re^{i\theta}} d\theta \]
Así llegamos al teorema del valor medio
Conclusión
\[ f(z_{0}) \dfrac{1}{2\pi}\int^{2\pi}_{0} f(z_{0}+re^{i \theta})d\theta\]
Realizado por:Esther Sarai (discusión) 21:23 21 jun 2015 (CDT)Esther Sarai
Forma alternativa
Se tiene la formula integral de Cauchy:
donde el problema nos dice que f es analítica , es el centro , y r el radio de la circunferencia C.
Recordemos que la forma exponencial de un numero complejo esta dada de la forma:
lo que nos permite expresar la forma polar de un número complejo distinto de cero.
Para nuestro caso y centro en z subíndice cero, se tiene que:
Entonces despejando “z” se tiene:
Ahora derivamos ambos miembros , uno con respecto a “z” y otro con respecto a theta en el segundo miembro, y se tiene:
Sustituyendo en la formula integral de Cauchy (1),(2) y (3) se tiene:
Eliminado términos se tiene:
en este contorno cerrado de la circuferenia nuestro ángulo theta va de 0 a 2 pi, entonces:
Lo cuál esta demostrado y ha este resultado se le conoce como el teorema del valor medio de Gauss,
y muestra que el valor de f en el centro z subíndice cero de la circunferencia es el promedio de todos
los valores de f en la circunferencia de C.
Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 00:28 22 jun 2015 (CDT)