Diferencia entre revisiones de «Compleja:Zill-Cap5.3»
(Página creada con «Category:Compleja Ejercicios del capítulo 5, sección 3 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan. ---- ==Sección 5.3== ...») |
|||
| (No se muestran 50 ediciones intermedias del mismo usuario) | |||
| Línea 8: | Línea 8: | ||
==Sección 5.3== | ==Sección 5.3== | ||
| Línea 14: | Línea 17: | ||
Naturalmente surgen dos formas de resolver este ejercicio, la primera, más directa es parametrizar la curva, evaluar la función e integrar; si bien es fácil pensar de esta forma puede se transparente, es sin duda laboriosa. La segunda, consiste en usar el teorema de Cauchy para asumir que el resultado es 0, bastando así comprobar as condiciones de cauchy para la función dentro del dominio, a continuación presento ambos razonamientos: | Naturalmente surgen dos formas de resolver este ejercicio, la primera, más directa es parametrizar la curva, evaluar la función e integrar; si bien es fácil pensar de esta forma puede se transparente, es sin duda laboriosa. La segunda, consiste en usar el teorema de Cauchy para asumir que el resultado es 0, bastando así comprobar as condiciones de cauchy para la función dentro del dominio, a continuación presento ambos razonamientos: | ||
'''Procedimiento''' | |||
Parametrizando: | Parametrizando: | ||
| Línea 24: | Línea 30: | ||
Entonces: | Entonces: | ||
\[ | \[ | ||
\oint_{C} \! f(z)\,dz=\int_{0}^{2 \pi} \! \left[ \left(\cos (t)+ i\,\sin (t)\right)^3 -1+3i\right]\left[-\sin (t)+ i\,\cos (t)\right]\, dt | \oint_{C} \! f(z)\,dz=\int_{0}^{2 \pi} \! \left[ \left(\cos (t)+ i\,\sin (t)\right)^3 -1+3i\right]\left[-\sin (t)+ i\,\cos (t)\right]\, dt | ||
\] | |||
\[ | |||
\int_{0}^{2 \pi} \! \left[ \cos (3t) +i\,\sin(3t) -1+3i\right]\left[-\sin (t)+ i\,\cos (t)\right]\, dt | |||
\] | \] | ||
\[ | \[ | ||
\int_{0}^{2 \pi} \! \left[ (-3-i)\cos(t) + i\,\cos(t) \cos(3t) + (1-3i) \sin(t) -\cos(3t) \sin(t) -\cos(t) \sin(3t) -i\,\sin(t) \sin(3t) \right]\, dt= | |||
\] | \] | ||
\[ | |||
=\int_{0}^{2 \pi} \! \left[ (-3-i)\cos(t) + i\,\cos(4t) + (1-3i)\sin[t]-\sin(4t)\right]\, dt | |||
\] | |||
\[ | \[ | ||
=(-3-i)\int_{0}^{2 \pi} \! \cos(t) \, dt+i\int_{0}^{2 \pi} \! \cos(4t) \, dt+(1-3i)\int_{0}^{2 \pi} \! \sin(t) \, dt-\int_{0}^{2 \pi} \! \sin(4t) \, dt | =(-3-i)\int_{0}^{2 \pi} \! \cos(t) \, dt+i\int_{0}^{2 \pi} \! \cos(4t) \, dt+(1-3i)\int_{0}^{2 \pi} \! \sin(t) \, dt-\int_{0}^{2 \pi} \! \sin(4t) \, dt | ||
| Línea 58: | Línea 74: | ||
\frac{\partial v}{\partial y}=\frac{\partial (3x^2y-y^3+3)}{\partial y}=3x^2-3y^2 | \frac{\partial v}{\partial y}=\frac{\partial (3x^2y-y^3+3)}{\partial y}=3x^2-3y^2 | ||
\] | \] | ||
Donde se | |||
'''Conclusión''' | |||
Donde se verifica la analiticidad de $f$ para todo $\mathbb{C}$, y por lo tanto: | |||
\[ | \[ | ||
\therefore \oint_{C} \! f(z)\,dz=0 \blacksquare | \therefore \oint_{C} \! f(z)\,dz=0 \blacksquare | ||
\] | \] | ||
--[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 22:57 16 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Tlacaelel Cruz|Tlacaelel Cruz]] ([[Usuario discusión:Tlacaelel Cruz|discusión]]) 22:57 16 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 72: | Línea 92: | ||
$f(z)=\frac{senz}{(z^{2}-25)(z^{2}+9)}$ | $f(z)=\frac{senz}{(z^{2}-25)(z^{2}+9)}$ | ||
'''Procedimiento''' | |||
Entonces: | Entonces: | ||
| Línea 77: | Línea 99: | ||
$\oint_{C}f(z)dz=\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz$ | $\oint_{C}f(z)dz=\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz$ | ||
Vemos que tenemos | Vemos que tenemos singularidades en:$z=\left\{ 5;-5;\right\} $ , | ||
sin embargo, estas no están dentro de la circunferencia $|z|=1$. | sin embargo, estas no están dentro de la circunferencia $|z|=1$. | ||
| Línea 106: | Línea 128: | ||
$(A+C+D)z^{3}+(B+3iC-3iD)z^{2}+(9A-25D)z+9B-75iC+75iD$ | $(A+C+D)z^{3}+(B+3iC-3iD)z^{2}+(9A-25D)z+9B-75iC+75iD$ | ||
Entonces, igualando términos | Entonces, igualando términos semejantes, formamos un sistema de ecuaciones de | ||
la siguiente manera: | la siguiente manera: | ||
| Línea 132: | Línea 154: | ||
$=\frac{2}{43}\oint_{C}\frac{senz}{z^{2}-25}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z-3)}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z+3)}dz=0$ | $=\frac{2}{43}\oint_{C}\frac{senz}{z^{2}-25}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z-3)}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z+3)}dz=0$ | ||
'''Conclusión''' | |||
De aquí vemos que cada fracción parcial cumple con los criterios de | De aquí vemos que cada fracción parcial cumple con los criterios de | ||
| Línea 138: | Línea 162: | ||
--[[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 19:08 21 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 19:08 21 jun 2015 (CDT) | |||
---- | |||
---- | ---- | ||
=== Ejercicio 6 === | === Ejercicio 6 === | ||
| Línea 151: | Línea 175: | ||
$f\left(z\right)=\frac{e^{z}}{2z^{2}+11z+15}$ y $\left|z\right|=1$ | $f\left(z\right)=\frac{e^{z}}{2z^{2}+11z+15}$ y $\left|z\right|=1$ | ||
'''Procedimiento''' | |||
Mostrar que: | Mostrar que: | ||
| Línea 174: | Línea 199: | ||
$f\left(z\right)$sí es analítica dentro y sobre C. | $f\left(z\right)$sí es analítica dentro y sobre C. | ||
'''Solución''' | |||
Por lo que según el teorema de Cauchy-Goursat | Por lo que según el teorema de Cauchy-Goursat | ||
| Línea 180: | Línea 207: | ||
---- | |||
Realizado por: [[Usuario:Alejandro Juárez Toribio|Alejandro Juárez Toribio]] ([[Usuario discusión:Alejandro Juárez Toribio|discusión]]) 13:36 18 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 190: | Línea 215: | ||
Muestre que $\oint_{C} \! f(z)\,dz=0$, donde $f$ es la | Muestre que $\oint_{C} \! f(z)\,dz=0$, donde $f$ es la función dada y $C$ es la circunferencia unitaria $|z|=1$ | ||
$f(z)=tanz$ | $f(z)=tanz$ | ||
'''Procedimiento''' | |||
Donde $z=cost+isint$ y $dz=(-sint+icost)dt$ | Donde $z=cost+isint$ y $dz=(-sint+icost)dt$ | ||
| Línea 219: | Línea 245: | ||
$\oint_{1}^{1} \! tan(u)\,du = -ln(cosu)\mid_{1}^{1}$ | $\oint_{1}^{1} \! tan(u)\,du = -ln(cosu)\mid_{1}^{1}$ | ||
'''Solución''' | |||
$\oint_{1}^{1} \! tan(u)\,du = -ln(cos1)+ln(cos1) $, entonces | $\oint_{1}^{1} \! tan(u)\,du = -ln(cos1)+ln(cos1) $, entonces | ||
| Línea 225: | Línea 252: | ||
$\oint_{1}^{1} \! tan(u)\,du = 0$ | $\oint_{1}^{1} \! tan(u)\,du = 0$ | ||
---- | |||
[[Usuario:Miguel Medina Armendariz|Miguel Medina Armendariz]] ([[Usuario discusión:Miguel Medina Armendariz|discusión]]) 17:27 19 jun 2015 (CDT) | Realizado por: [[Usuario:Miguel Medina Armendariz|Miguel Medina Armendariz]] ([[Usuario discusión:Miguel Medina Armendariz|discusión]]) 17:27 19 jun 2015 (CDT) | ||
---- | ---- | ||
===Ejercicio 9=== | ===Ejercicio 9=== | ||
Evaluar $\oint_{c}\frac{1}{Z}dz$, Donde C es el contorno mostrado | |||
en la Figura. | |||
[[Archivo:Problema9Capitulo5.3Zill.png|sinmarco]] | |||
'''Procedimiento''' | |||
Reescribiendo la integral: | |||
$\oint_{c}\frac{1}{\left(z+0\right)^{1}}dz$ | |||
Entonces teniendo la integral resuelta por el teorema anterior de | |||
la siguiente manera: | |||
$\oint_{c}\frac{1}{\left(z+0\right)^{1}}dz=2i\pi$ | |||
'''Comentario''' | |||
Lo que se usó fue deformación de contornos: | |||
$ | Con la parametrización $z=e^{it}$ | ||
$ | Sobre la curva Cerrada $0 \leq t\leq 2\pi$ | ||
Derivando z | |||
$ | $dz=ie^{it} dt$ | ||
Con todo esto la integral puede reescribirse como: | |||
$\frac{ | $\oint_C \frac{1}{z}dz= \int_{0}^{2\pi} \frac{ie^{it}}{e^{it}}dt=i2\pi$ | ||
---- | |||
Realizado por:[[Usuario:Martin Flores Molina|Martin Flores Molina]] ([[Usuario discusión:Martin Flores Molina|discusión]]) 13:05 15 mayo 2015 (CDT) | |||
Comentario [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | |||
===Ejercicio 11=== | |||
Evalúa la integral: | |||
$\oint (z + \frac{1}{z})dz$ | |||
A lo largo del contorno: | |||
$|z|=2$ | |||
'''Procedimiento''' | |||
[[Archivo:Problema11Capitulo5.3Zill.svg|miniaturadeimagen|alt=El Circulo Verde corresponde al contorno original, el circulo azul a la deformación del contorno]] | |||
Separando la integral en dos partes: | |||
$\oint (z + \frac{1}{z})dz=\oint _Czdz+\oint _C\frac{1}{z}dz=0+\oint _C\frac{1}{z}dz$ | |||
La primera integral es 0 dado que es la función es analítica sobre todo el contorno $|z|=2$ | |||
Usando deformación de contornos, para la segunda integral: | |||
Con la parametrización $z=e^{it}$ | |||
la | |||
Sobre la curva Cerrada azul $0 \leq t\leq 2\pi$ | |||
Derivando z | |||
$ | $dz=ie^{it} dt$ | ||
Con todo esto la integral puede reescribirse como: | |||
$\oint_C \frac{1}{z}dz= \int_{0}^{2\pi} \frac{ie^{it}}{e^{it}}dt=i2\pi$ | |||
'''Solución''' | |||
Por lo que la integral: | |||
$\oint _Cz+\frac{1}{z}dz=i2\pi$ | |||
---- | |||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | ---- | ||
===Ejercicio | ===Ejercicio 12=== | ||
Utilice cualquiera de los resultados de esta sección para evaluar la integral a lo largo del contorno indicado cerrado. | |||
$\oint(z+\frac{1}{z²})dz$; | |||
$\oint (z + \frac{1}{ | |||
A lo largo del contorno: | |||
$|z|=2$ | $|z|=2$ | ||
'''Procedimiento''' | |||
para analizar la integral anterior podemos hacer: | para analizar la integral anterior podemos hacer: | ||
$\oint_{C}z dz +\oint_{C}\frac{1}{z²}dz$ | |||
Analizando la primera integral y tomando f(z)=z, vemos que la función puede ser cualquier función entera,por lo cual es analítica en cualquier contorno cerrado, | Analizando la primera integral y tomando f(z)=z, vemos que la función puede ser cualquier función entera,por lo cual es analítica en cualquier contorno cerrado, así pues : | ||
$\oint_{C}z dz=0$ | |||
Analizando la segunda integral tenemos que nuestra | Analizando la segunda integral tenemos que nuestra función tiene una singularidad para <math>z=0</math>, la cual pertenece al dominio. | ||
\begin{equation} | \begin{equation} | ||
| Línea 396: | Línea 370: | ||
\end{equation} | \end{equation} | ||
Tomando en cuenta para nuestra integral que | Tomando en cuenta para nuestra integral que $n=2$ y $z_0=0$, y tomando en cuenta que existe una singularidad en la función, podemos obtener de la condición anterior que : | ||
$\oint_{C}\frac{1}{z²}dz=0$ | |||
'''Solución''' | |||
Por lo cual para esta integral. | Por lo cual para esta integral. | ||
$\oint(z+\frac{1}{z²})dz=0$ | |||
---- | ---- | ||
Realizado por: [[Usuario:Anahi Limas|Anahi Limas]] ([[Usuario discusión:Anahi Limas|discusión]]) 21:06 21 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 13=== | ===Ejercicio 13=== | ||
| Línea 411: | Línea 389: | ||
$|z|=3$ | $|z|=3$ | ||
'''Procedimiento''' | |||
Consideramos la siguiente definición: | Consideramos la siguiente definición: | ||
| Línea 426: | Línea 406: | ||
\] | \] | ||
Resolvemos la integral por el método de fracciones parciales | Resolvemos la integral por el método de fracciones parciales | ||
| Línea 451: | Línea 430: | ||
De acuerdo al teorema de Cauchy-Goursat la integral no esta en el contorno, es | '''Solución''' | ||
De acuerdo al teorema de Cauchy-Goursat la integral no esta en el contorno, es analítica en todos los puntos,así que es 0. | |||
$ \oint_{C} \! \frac{z}{z^{2}-\pi^2} \,dz = 0 $ | $ \oint_{C} \! \frac{z}{z^{2}-\pi^2} \,dz = 0 $ | ||
---- | ---- | ||
Realizado por:[[Usuario:Nancy Martínez Durán|Nancy Martínez Durán]] ([[Usuario discusión:Nancy Martínez Durán|discusión]]) 09:28 18 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 511: | Línea 446: | ||
$\oint_{c}\frac{2z+1}{z^{2}+z}dz$ con los contornos (a) $|z|=\frac{1}{2}$, (b) $|z|=2$ y (c) $|z-3i|=1$ | $\oint_{c}\frac{2z+1}{z^{2}+z}dz$ con los contornos (a) $|z|=\frac{1}{2}$, (b) $|z|=2$ y (c) $|z-3i|=1$ | ||
'''Procedimiento''' | |||
Primero notamos que: | Primero notamos que: | ||
| Línea 522: | Línea 460: | ||
Entonces $A=1$ y $B=1$, y | Entonces $A=1$ y $B=1$, y así tenemos que | ||
$\oint_{c}\frac{2z+1}{z^{2}+z}dz=\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z+1}dz$ | $\oint_{c}\frac{2z+1}{z^{2}+z}dz=\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z+1}dz$ | ||
Se observa que el denominador de la integral no es | Se observa que el denominador de la integral no es analítico en $z=0$ y $z=-1$ | ||
| Línea 535: | Línea 473: | ||
$\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z-(-1)}dz=2\pi i+0$ | $\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z-(-1)}dz=2\pi i+0$ | ||
'''Inciso a''' | |||
\[ | \[ | ||
| Línea 548: | Línea 486: | ||
Tenemos: | Tenemos: | ||
'''Inciso b''' | |||
\[ | \[ | ||
| Línea 557: | Línea 496: | ||
Y para (c), ninguno de los puntos esta dentro, entonces: | Y para (c), ninguno de los puntos esta dentro, entonces: | ||
'''Inciso c''' | |||
\[ | \[ | ||
| Línea 564: | Línea 504: | ||
--[[Usuario:Fernando Vazquez V.|Fernando Vazquez V.]] ([[Usuario discusión:Fernando Vazquez V.|discusión]]) 19:58 18 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Fernando Vazquez V.|Fernando Vazquez V.]] ([[Usuario discusión:Fernando Vazquez V.|discusión]]) 19:58 18 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 573: | Línea 512: | ||
evalúe la integral a lo largo de los contornos indicados cerrados | evalúe la integral a lo largo de los contornos indicados cerrados | ||
$\oint_{C}\frac{2z}{z^{2}+3}dz$; | |||
a) $\mid z\mid=1$ | |||
b) $\mid z-2i\mid=1$ | |||
c) $\mid z\mid=4$ | c) $\mid z\mid=4$ | ||
'''Procedimiento''' | |||
$\oint_{C}\frac{2z}{z^{2}+3}dz=\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$ | $\oint_{C}\frac{2z}{z^{2}+3}dz=\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$ | ||
| Línea 607: | Línea 553: | ||
evaluando la integral a lo largo de a) $\mid z\mid=1$ | evaluando la integral a lo largo de a) $\mid z\mid=1$ | ||
'''Inciso a''' | |||
como se puede ver $\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$ | como se puede ver $\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$ | ||
| Línea 622: | Línea 569: | ||
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=0$ | $\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=0$ | ||
'''Inciso b''' | |||
evaluando a lo largo de b) $\mid z-2i\mid=1$, (circunferencia de | evaluando a lo largo de b) $\mid z-2i\mid=1$, (circunferencia de | ||
| Línea 646: | Línea 595: | ||
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=2\pi i$ | $\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=2\pi i$ | ||
'''Inciso c''' | |||
evaluando a lo largo de c) $\mid z\mid=4$ (circunferencia de radio | evaluando a lo largo de c) $\mid z\mid=4$ (circunferencia de radio | ||
| Línea 660: | Línea 611: | ||
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=4\pi i$ | $\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=4\pi i$ | ||
---- | ---- | ||
Realizado por: [[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 21:51 19 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 17=== | ===Ejercicio 17=== | ||
| Línea 687: | Línea 638: | ||
\] | \] | ||
'''Procedimiento''' | |||
| Línea 718: | Línea 670: | ||
y así, | y así, | ||
'''Inciso a''' | |||
\[ | \[ | ||
| Línea 740: | Línea 694: | ||
y así, | y así, | ||
'''Inciso b''' | |||
\[ | \[ | ||
| Línea 752: | Línea 707: | ||
--[[Usuario:Emmanuell Castro Flores|Emmanuell Castro Flores]] ([[Usuario discusión:Emmanuell Castro Flores|discusión]]) 20:45 17 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Emmanuell Castro Flores|Emmanuell Castro Flores]] ([[Usuario discusión:Emmanuell Castro Flores|discusión]]) 20:45 17 jun 2015 (CDT) | |||
---- | |||
---- | |||
===Ejercicio 18=== | ===Ejercicio 18=== | ||
Calcular la integral a lo largo de los contornos indicados | |||
<math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz</math> | <math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz</math> | ||
'''Inciso a''' | |||
'''a)''' <math>|z|=5</math> | '''a)''' <math>|z|=5</math> | ||
| Línea 774: | Línea 733: | ||
con C1 que va en el intervalo de <math>\theta \epsilon [0,2 \pi]</math> y C2 que va en el intervalo <math>\phi \epsilon [0, 2\pi ]</math> | con C1 que va en el intervalo de <math>\theta \epsilon [0,2 \pi]</math> y C2 que va en el intervalo <math>\phi \epsilon [0, 2\pi ]</math> | ||
Por lo que la integral queda definida como | Por lo que la integral queda definida como: | ||
'''Solución''' | |||
<math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz= \int_{c1} (\frac{3}{z+2}) dz - \int_{c2} (\frac{1}{z-2i}) dz = \int_{c1} \frac{3 i e^{i \theta}}{e^{i \theta}}d \theta - \int_{c2} \frac{ie^{i \phi}}{e^{i \phi}} d \phi = \int_0^{2 \pi} 3 i d \theta - \int_0^{2 \pi} i d \phi= 6i \pi - 2i \pi= 4 \pi i </math> | <math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz= \int_{c1} (\frac{3}{z+2}) dz - \int_{c2} (\frac{1}{z-2i}) dz = \int_{c1} \frac{3 i e^{i \theta}}{e^{i \theta}}d \theta - \int_{c2} \frac{ie^{i \phi}}{e^{i \phi}} d \phi = \int_0^{2 \pi} 3 i d \theta - \int_0^{2 \pi} i d \phi= 6i \pi - 2i \pi= 4 \pi i </math> | ||
| Línea 783: | Línea 743: | ||
<math>\oint (\frac{3}{z+2}- \frac{1}{z-2i})dz= 3(2i \pi)- 2i \pi= 4i \pi</math> | <math>\oint (\frac{3}{z+2}- \frac{1}{z-2i})dz= 3(2i \pi)- 2i \pi= 4i \pi</math> | ||
'''Inciso b''' | |||
'''b)''' <math>|z-2i|=\frac{1}{2}</math> | '''b)''' <math>|z-2i|=\frac{1}{2}</math> | ||
| Línea 802: | Línea 763: | ||
por lo que para el segundo contorno el resultado es | por lo que para el segundo contorno el resultado es | ||
'''Solución''' | |||
<math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz= -2i \pi</math> | <math>\oint (\frac{3}{z+2}- \frac{1}{z-2i}) dz= -2i \pi</math> | ||
--[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 10:37 21 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 10:37 21 jun 2015 (CDT) | |||
---- | ---- | ||
===Ejercicio 19=== | |||
Integrar a lo largo del contorno | |||
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}dz$ | |||
donde | |||
$\left|z-i\right|=\frac{1}{2}$ | |||
'''Procedimiento''' | |||
Resolveremos la integra como fracciones parciales de la siguiente | |||
manera: | |||
$\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}=\frac{A}{z}+\frac{B}{z-i}+\frac{C}{z-3i}=\frac{A\left(z-i\right)\left(z-3i\right)+Bz\left(z-3i\right)+Cz\left(z-i\right)}{z\left(z-i\right)\left(z-3i\right)}$ | |||
Entoces: | |||
$z-1=A\left(z-i\right)\left(z-3i\right)+Bz\left(z-3i\right)+Cz\left(z-1\right)$ | |||
Resolviendo el sistema obtenemos los siguientes valores: | |||
$A=\frac{1}{3}$ , $B=\frac{i-1}{2}$ , $C=\frac{1-3i}{6}$ | |||
Por lo tanto solamente sustituimos: | |||
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}=\frac{1}{3}\oint_{c}\frac{dz}{z}+\frac{1}{2}\oint_{c}\frac{\left(i-1\right)}{z-i}dz+\frac{1}{6}\oint_{c}\frac{\left(1-3i\right)}{z-3i}dz$ | |||
Pero sabemos por Cauchy-Goursat que el valor de la primera y tercer | |||
integral es cero por lo tanto nos enfocamos en la segunda integral. | |||
Pero también sabemos que el valor de esa integral es $2i\pi$, entonces | |||
tenemos los sig: | |||
$\frac{1}{2}\oint_{c}\frac{\left(i-1\right)}{\left(z-1\right)}dz=\frac{i-1}{2}\oint_{c}\frac{dz}{z-1}=\frac{\left(i-1\right)}{2}\left(2\pi i\right)=-\pi\left(1+i\right)$ | |||
'''Solución''' | |||
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}dz=-\pi\left(1+i\right)$ | |||
---- | |||
Resuelto por [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 21:38 16 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 23=== | ===Ejercicio 23=== | ||
Evalue :<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz | Evalue :<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz | ||
</math> , donde C es la “forma de ocho” del contorno de la figura 5.3.11. | |||
[Sugerencia. Exprese C como la unión de dos curvas cerradas C1 y C2] | [Sugerencia. Exprese C como la unión de dos curvas cerradas C1 y C2] | ||
'''Procedimiento''' | |||
:<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz=\oint_{c}\frac{8z-3}{z(z-1)}dz=\oint_{c}\frac{A}{z}dz+\oint_{c}\frac{B}{z-1}dz=\left[\oint_{c_{1}}\frac{A}{z}dz+\oint_{c_{1}}\frac{B}{z-1}dz\right]+\left[\oint_{c_{2}}\frac{A}{z}dz+\oint_{c_{2}}\frac{B}{z-1}dz\right] | :<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz=\oint_{c}\frac{8z-3}{z(z-1)}dz=\oint_{c}\frac{A}{z}dz+\oint_{c}\frac{B}{z-1}dz=\left[\oint_{c_{1}}\frac{A}{z}dz+\oint_{c_{1}}\frac{B}{z-1}dz\right]+\left[\oint_{c_{2}}\frac{A}{z}dz+\oint_{c_{2}}\frac{B}{z-1}dz\right] | ||
| Línea 856: | Línea 865: | ||
Para la primera integral C1, z=0 esta dentro del contorno, y tiene valor de 2pi i; la segunda integral z =1 | Para la primera integral C1, z=0 esta dentro del contorno, y tiene valor de 2pi i; la segunda integral z =1 | ||
no esta dentro del contorno, no es | no esta dentro del contorno, no es analítica,así que es 0; | ||
para C2 la primera integral no esta dentro del contorno y es 0 ,la segunda integral por medio el teorema | para C2 la primera integral no esta dentro del contorno y es 0 ,la segunda integral por medio el teorema | ||
| Línea 864: | Línea 873: | ||
:<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz=3(2\pi i)+5(0)-3(0)-5(2\pi i)=6\pi i-10\pi i=-4\pi i | :<math>\oint_{c}\frac{8z-3}{z^{2}-z}dz=3(2\pi i)+5(0)-3(0)-5(2\pi i)=6\pi i-10\pi i=-4\pi i | ||
</math> | </math> | ||
'''Conclusión''' | |||
por lo tanto: | por lo tanto: | ||
| Línea 870: | Línea 881: | ||
</math> | </math> | ||
---- | |||
Elaborado por Ricardo Garcia Hernandez--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 23:33 17 jun 2015 (CDT) | Elaborado por Ricardo Garcia Hernandez--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 23:33 17 jun 2015 (CDT) | ||
---- | ---- | ||
=== | ===Ejercicio 24=== | ||
'''Supongamos que $z_{0}$ es cualquier numero complejo constante interior a cualquier curva simple cerrada del contorno C. Muestre que para un entero positivo n.''' | '''Supongamos que $z_{0}$ es cualquier numero complejo constante interior a cualquier curva simple cerrada del contorno C. Muestre que para un entero positivo n.''' | ||
'''Procedimiento''' | |||
\[ | \[ | ||
\oint_{c}\dfrac{dz}{(z-z_{0})^{n}} = \left\lbrace | \oint_{c}\dfrac{dz}{(z-z_{0})^{n}} = \left\lbrace | ||
| Línea 892: | Línea 904: | ||
\oint_{c}\dfrac{dz}{z-z_{0}} = \int^{2\pi}_{o} \dfrac{Re^{i\theta}}{Re^{i\theta}}= i \int^{2\pi}_{0}d \theta = 2i \pi\] | \oint_{c}\dfrac{dz}{z-z_{0}} = \int^{2\pi}_{o} \dfrac{Re^{i\theta}}{Re^{i\theta}}= i \int^{2\pi}_{0}d \theta = 2i \pi\] | ||
'''Conclusión''' | |||
Si $n>1$ esto implica que $z_{0}$ está fuera de la curva por tanto la función es analítica y se cumple el teorema de Cauchy. | Si $n>1$ esto implica que $z_{0}$ está fuera de la curva por tanto la función es analítica y se cumple el teorema de Cauchy. | ||
| Línea 898: | Línea 910: | ||
\oint_{c} f(z) dz = 0\] | \oint_{c} f(z) dz = 0\] | ||
--[[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 20:32 18 jun 2015 (CDT)Esther Sarai | ---- | ||
Realizado por:[[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 20:32 18 jun 2015 (CDT)Esther Sarai | |||
---- | |||
===Ejercicio 30=== | ===Ejercicio 30=== | ||
| Línea 904: | Línea 918: | ||
'''Evalúe $\int_Ce^zdz$ de $z=0$ a $z=2+2i$ sobre el contorno $C$ de la figura 5.3.12 (consultar el libro) que consiste en la recta $y=x$ y una circunferencia tangente a la recta en $(1,1)$.''' | '''Evalúe $\int_Ce^zdz$ de $z=0$ a $z=2+2i$ sobre el contorno $C$ de la figura 5.3.12 (consultar el libro) que consiste en la recta $y=x$ y una circunferencia tangente a la recta en $(1,1)$.''' | ||
'''Procedimiento''' | |||
'''Sol.''' (Se omite la figura, para mayor claridad consultar la imagen en el libro). | '''Sol.''' (Se omite la figura, para mayor claridad consultar la imagen en el libro). | ||
| Línea 931: | Línea 946: | ||
factorizando $e^t$ en cada termino y posteriormente | factorizando $e^t$ en cada termino y posteriormente sumamos y restamos: | ||
| Línea 967: | Línea 982: | ||
'''Conclusión''' | |||
Por lo tanto: | Por lo tanto: | ||
| Línea 972: | Línea 988: | ||
$\int_Cf(z)dz=(e^2\cos 2-1)+i(e^2\sin 2)$ | $\int_Cf(z)dz=(e^2\cos 2-1)+i(e^2\sin 2)$ | ||
---- | |||
[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 19:01 16 jun 2015 (CDT) | [[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 19:01 16 jun 2015 (CDT) | ||
---- | ---- | ||
===Ejercicio 31=== | ===Ejercicio 31=== | ||
En particular use $|z|=1$como $C$ y la | En particular use $|z|=1$como $C$ y la parametrización $z=e^{i\theta}$,$0\leq\theta\leq2\pi,$para | ||
determinar el valor de las | determinar el valor de las integrales reales. | ||
'''Procedimiento''' | |||
\[ | \[ | ||
| Línea 1001: | Línea 1018: | ||
\Rightarrow{\displaystyle \frac{1}{2}}{\displaystyle \int_{a}^{b}}(-e^{z}+e^{z^{-1}}z^{-2})dz={\displaystyle -\frac{1}{2}\left(e^{z^{-1}}+e^{z}\right)|_{a}^{b}=-{\displaystyle \frac{1}{2}(e^{(\cos\theta-i\sin\theta)}+e^{(\cos\theta+i\sin\theta)})|_{0}^{2\pi}}}=0 | \Rightarrow{\displaystyle \frac{1}{2}}{\displaystyle \int_{a}^{b}}(-e^{z}+e^{z^{-1}}z^{-2})dz={\displaystyle -\frac{1}{2}\left(e^{z^{-1}}+e^{z}\right)|_{a}^{b}=-{\displaystyle \frac{1}{2}(e^{(\cos\theta-i\sin\theta)}+e^{(\cos\theta+i\sin\theta)})|_{0}^{2\pi}}}=0 | ||
\] | \] | ||
'''Solución''' | |||
\[ | \[ | ||
| Línea 1007: | Línea 1024: | ||
\] | \] | ||
[[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 19:43 21 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 19:43 21 jun 2015 (CDT) | |||
---- | ---- | ||
---- | ---- | ||
Revisión actual - 07:17 11 mar 2023
Ejercicios del capítulo 5, sección 3 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 5.3
Ejercicio 1
Muestre que $\oint_{C} \! f(z)\,dz=0$, donde $f(z)=z^3-1+3i$ y $C$ es la circunferencia unitaria $|z|=1$.
Naturalmente surgen dos formas de resolver este ejercicio, la primera, más directa es parametrizar la curva, evaluar la función e integrar; si bien es fácil pensar de esta forma puede se transparente, es sin duda laboriosa. La segunda, consiste en usar el teorema de Cauchy para asumir que el resultado es 0, bastando así comprobar as condiciones de cauchy para la función dentro del dominio, a continuación presento ambos razonamientos:
Procedimiento
Parametrizando: \[ z(t)=\cos (t)+ i\,\sin (t)\;\;\;\;0\leq t \le 2\pi \] \[ dz=\left[-\sin (t)+ i\,\cos (t)\right]\, dt \] Entonces: \[ \oint_{C} \! f(z)\,dz=\int_{0}^{2 \pi} \! \left[ \left(\cos (t)+ i\,\sin (t)\right)^3 -1+3i\right]\left[-\sin (t)+ i\,\cos (t)\right]\, dt \]
\[ \int_{0}^{2 \pi} \! \left[ \cos (3t) +i\,\sin(3t) -1+3i\right]\left[-\sin (t)+ i\,\cos (t)\right]\, dt \]
\[ \int_{0}^{2 \pi} \! \left[ (-3-i)\cos(t) + i\,\cos(t) \cos(3t) + (1-3i) \sin(t) -\cos(3t) \sin(t) -\cos(t) \sin(3t) -i\,\sin(t) \sin(3t) \right]\, dt= \]
\[ =\int_{0}^{2 \pi} \! \left[ (-3-i)\cos(t) + i\,\cos(4t) + (1-3i)\sin[t]-\sin(4t)\right]\, dt \]
\[ =(-3-i)\int_{0}^{2 \pi} \! \cos(t) \, dt+i\int_{0}^{2 \pi} \! \cos(4t) \, dt+(1-3i)\int_{0}^{2 \pi} \! \sin(t) \, dt-\int_{0}^{2 \pi} \! \sin(4t) \, dt \] Claramente todas estas integrales valen 0 pues se integra en multiplos del periodo de estas funciones trigonometricas. \[ \therefore \oint_{C} \! f(z)\,dz=(-3-i)(0)+i(0)+(1-3i)(0)-0=0+0+0+0=0 \blacksquare \]
De la otra forma, basta con verificar que $f$ sea analítica en el dominio. Bastaria con observar que $f$ esta formada por combinación de funciones elementales que son analíticas, pero a fin de qu este razonamiento sean contundente se procede del siguiente modo:
Descomponemos $f$: \[ f(z)=f(x+iy)=u(x,y)+i\,v(x,y)=z^3-1+3i=(x+iy)^3-1+3i=(x^3+3ix^2y-3xy^2-iy^3)-1+3i=(x^3-3xy^2-1)+i(3x^2y-y^3+3) \] \[ \therefore \; u(x,y)=x^3-3xy^2-1 \;\;\;\;\;\;v(x,y)=3x^2y-y^3+3 \] Para que $f$ sea analítica debe cumplir que: \[ \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\;\;\;\;\;\;\;\;\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y} \] \[ \frac{\partial u}{\partial x}=\frac{\partial (x^3-3xy^2-1)}{\partial x}=3x^2-3y^2 \;\;\;\;\; \frac{\partial u}{\partial y}=\frac{\partial (x^3-3xy^2-1)}{\partial y}=-6xy \] \[ \frac{\partial v}{\partial x}=\frac{\partial (3x^2y-y^3+3)}{\partial x}=6xy \;\;\;\;\; \frac{\partial v}{\partial y}=\frac{\partial (3x^2y-y^3+3)}{\partial y}=3x^2-3y^2 \]
Conclusión
Donde se verifica la analiticidad de $f$ para todo $\mathbb{C}$, y por lo tanto: \[ \therefore \oint_{C} \! f(z)\,dz=0 \blacksquare \]
Realizado por:Tlacaelel Cruz (discusión) 22:57 16 jun 2015 (CDT)
Ejercicio 5
Mostrar que $\oint_{C}f(z)dz=0$, donde $f$ es una función dada y $C$ es la circunferencia unitaria $|z|=1$.
$f(z)=\frac{senz}{(z^{2}-25)(z^{2}+9)}$
Procedimiento
Entonces:
$\oint_{C}f(z)dz=\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz$
Vemos que tenemos singularidades en:$z=\left\{ 5;-5;\right\} $ , sin embargo, estas no están dentro de la circunferencia $|z|=1$.
Por tanto, se puede demostrar que, efectivamente, la integral de contorno es igual a cero.
Se sigue por tanto que esta función es...
$\oint_{C}f(z)dz=\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz=0$
Para ver que esto se cumple, y no dejarlo a la fé, resolviendo la integral...
Primero resolvemos por fracciones parciales como sigue
Factorizando como más convenga...
$\frac{senz}{(z^{2}-25)(z^{2}+9)}=\frac{senz}{(z-5i)(z-5i)(z+3)(z-3)}=\frac{senz}{(z-5i)^{2}(z+3)(z-3)}=\frac{Az+B}{z^{2}-25}+\frac{C}{(z-3)}+\frac{D}{(z+3)}$
Desarrollando nos queda de la forma:
$Az+B(z-3i)(z+3i)+C(z+3i)(z^{2}-25)+D(z-3i)(z^{2}-25)$
$=Az^{3}+9Az+Bz^{2}+9B+Cz^{3}+3Cz^{2}i+75Ci+Dz^{3}-3Dz^{2}i-25Dz+75Di$
Agrupando:
$(A+C+D)z^{3}+(B+3iC-3iD)z^{2}+(9A-25D)z+9B-75iC+75iD$
Entonces, igualando términos semejantes, formamos un sistema de ecuaciones de la siguiente manera:
$A+C+D=0$
$B+3iC-3iD=0$
$9A-25D=0$
$9B-75iC+75iD=senz$
Se puede comprobar que
$A=\frac{2}{43}senz$
$B=0$
$C=-\frac{1}{43}senz$
$D=\frac{senz}{43}$
Y con esto podemos resolver como sigue:
$\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz=\oint_{C}\frac{senz}{(z^{2}-25)(z^{2}+9)}dz=\oint_{C}\frac{senz}{(z-5i)(z-5i)(z+3)(z-3)}dz=\oint_{C}\frac{senz}{(z-5i)^{2}(z+3)(z-3)}dz=\oint_{C}\frac{Az+B}{z^{2}-25}dz+\oint_{C}\frac{C}{(z-3)}dz+\oint_{C}\frac{D}{(z+3)}dz$
$=\frac{2}{43}\oint_{C}\frac{senz}{z^{2}-25}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z-3)}dz-\frac{1}{43}\oint_{C}\frac{senz}{(z+3)}dz=0$
Conclusión
De aquí vemos que cada fracción parcial cumple con los criterios de la condición que se pide para que sea cero. Ya que se cumple que cada singularidad está fuera de la circunferencia de radio 1.
Realizado por: A. Martín R. Rabelo (discusión) 19:08 21 jun 2015 (CDT)
Ejercicio 6
Ejercicio 6
$f\left(z\right)=\frac{e^{z}}{2z^{2}+11z+15}$ y $\left|z\right|=1$
Procedimiento
Mostrar que:
$\oint_{c}f\left(z\right)dz=0$
$f\left(z\right)=\frac{e^{z}}{2z^{2}+11z+15}=\frac{e^{z}}{\left(2z+5\right)\left(z+3\right)}$ ...$\left(1\right)$
$f\left(z\right)$es analítica porque en el denominador tenemos una función polinomial $g\left(z\right)$que es
analítica porque $g\prime\left(z\right)=4z+11$y en el numerador tenemos $p\left(z\right)=e^{z}$que es analítica porque
$p\prime\left(z\right)=e^{z}$
Pero de la función $f\left(z\right)$ se puede ver que existen dos singularidades en
$z=-\frac{5}{2}$ y en $z=-3$
Pero ambas singularidades se encuentran fuera de C por lo que
$f\left(z\right)$sí es analítica dentro y sobre C.
Solución
Por lo que según el teorema de Cauchy-Goursat
$\oint_{c}f\left(z\right)dz=0$
Realizado por: Alejandro Juárez Toribio (discusión) 13:36 18 jun 2015 (CDT)
Ejercicio 7
Muestre que $\oint_{C} \! f(z)\,dz=0$, donde $f$ es la función dada y $C$ es la circunferencia unitaria $|z|=1$
$f(z)=tanz$
Procedimiento
Donde $z=cost+isint$ y $dz=(-sint+icost)dt$
Entonces tendríamos
$\oint_{0}^{2\pi} \! tan(cost+isint)\,(-sint+icost)dt$
Haciendo un cambio de variable
$u=cost+isint$ y $du=(-sint+icost)dt$
y si $t=0$ entonces $u=1$
y $t=2\pi$ entonces $u=1$, sustituimos valores
$\oint_{1}^{1} \! tan(u)\,du = -ln(cosu)\mid_{1}^{1}$
Solución
$\oint_{1}^{1} \! tan(u)\,du = -ln(cos1)+ln(cos1) $, entonces
$\oint_{1}^{1} \! tan(u)\,du = 0$
Realizado por: Miguel Medina Armendariz (discusión) 17:27 19 jun 2015 (CDT)
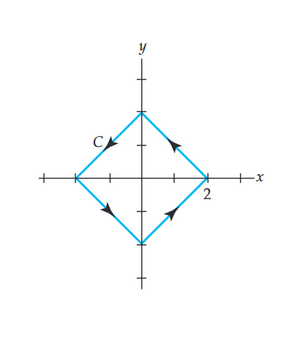
Ejercicio 9
Evaluar $\oint_{c}\frac{1}{Z}dz$, Donde C es el contorno mostrado en la Figura.
Procedimiento
Reescribiendo la integral:
$\oint_{c}\frac{1}{\left(z+0\right)^{1}}dz$
Entonces teniendo la integral resuelta por el teorema anterior de la siguiente manera:
$\oint_{c}\frac{1}{\left(z+0\right)^{1}}dz=2i\pi$
Comentario
Lo que se usó fue deformación de contornos:
Con la parametrización $z=e^{it}$
Sobre la curva Cerrada $0 \leq t\leq 2\pi$
Derivando z
$dz=ie^{it} dt$
Con todo esto la integral puede reescribirse como:
$\oint_C \frac{1}{z}dz= \int_{0}^{2\pi} \frac{ie^{it}}{e^{it}}dt=i2\pi$
Realizado por:Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT)
Comentario Manuel Rodríguez
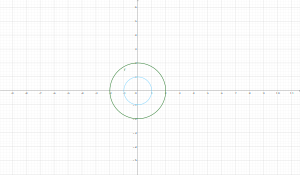
Ejercicio 11
Evalúa la integral:
$\oint (z + \frac{1}{z})dz$
A lo largo del contorno: $|z|=2$
Procedimiento
Separando la integral en dos partes:
$\oint (z + \frac{1}{z})dz=\oint _Czdz+\oint _C\frac{1}{z}dz=0+\oint _C\frac{1}{z}dz$
La primera integral es 0 dado que es la función es analítica sobre todo el contorno $|z|=2$
Usando deformación de contornos, para la segunda integral:
Con la parametrización $z=e^{it}$
Sobre la curva Cerrada azul $0 \leq t\leq 2\pi$
Derivando z
$dz=ie^{it} dt$
Con todo esto la integral puede reescribirse como:
$\oint_C \frac{1}{z}dz= \int_{0}^{2\pi} \frac{ie^{it}}{e^{it}}dt=i2\pi$
Solución
Por lo que la integral:
$\oint _Cz+\frac{1}{z}dz=i2\pi$
Re elaborado por Manuel Rodríguez
Ejercicio 12
Utilice cualquiera de los resultados de esta sección para evaluar la integral a lo largo del contorno indicado cerrado.
$\oint(z+\frac{1}{z²})dz$;
A lo largo del contorno: $|z|=2$
Procedimiento
para analizar la integral anterior podemos hacer:
$\oint_{C}z dz +\oint_{C}\frac{1}{z²}dz$
Analizando la primera integral y tomando f(z)=z, vemos que la función puede ser cualquier función entera,por lo cual es analítica en cualquier contorno cerrado, así pues : $\oint_{C}z dz=0$
Analizando la segunda integral tenemos que nuestra función tiene una singularidad para , la cual pertenece al dominio.
\begin{equation} \oint_{C} \! \frac{1}{\left(z-z_{o}\right)^n} = \left\lbrace \begin{array}{ll} 2 \pi i & n=1\\ 0, & n\neq 1 \end{array} \right. \end{equation}
Tomando en cuenta para nuestra integral que $n=2$ y $z_0=0$, y tomando en cuenta que existe una singularidad en la función, podemos obtener de la condición anterior que : $\oint_{C}\frac{1}{z²}dz=0$
Solución
Por lo cual para esta integral. $\oint(z+\frac{1}{z²})dz=0$
Realizado por: Anahi Limas (discusión) 21:06 21 jun 2015 (CDT)
Ejercicio 13
Evaluar la integral a lo largo del contorno indicado.
$ \oint_{C} \! \frac{z}{z^{2}-\pi^2} \,dz $
$|z|=3$
Procedimiento
Consideramos la siguiente definición:
\begin{equation} \oint_{C} \! \frac{1}{\left(z-z_{o}\right)^n} = \left\lbrace \begin{array}{ll} 2 \pi i & n=1\\ 0, & n\neq 1 \end{array} \right. \end{equation} \[ \]
Resolvemos la integral por el método de fracciones parciales
Factorizando el denominador tenemos:
${z^{2}-\pi^2} = (z+\pi)(z-\pi)$
$ \frac{z}{z^2-\pi^2}=\frac{A}{z+\pi}+\frac{B}{z-\pi}=\frac{(A+B)z+(B-A)\pi} {(2+\pi)(z-\pi)} $
$A=\frac{1}{2}$ , $B=\frac{1}{2}$
Entonces la integral queda:
\[ \oint_{C} \! \frac{z}{z^{2}-\pi^2} \,dz= \frac{1}{2} \oint_{C} \! \frac{1}{z+\pi}\,dz + \frac{1}{2} \oint_{C} \! \frac{1}{z-\pi} \,dz \]
Solución
De acuerdo al teorema de Cauchy-Goursat la integral no esta en el contorno, es analítica en todos los puntos,así que es 0.
$ \oint_{C} \! \frac{z}{z^{2}-\pi^2} \,dz = 0 $
Realizado por:Nancy Martínez Durán (discusión) 09:28 18 jun 2015 (CDT)
Ejercicio 15
Utilice cualquiera de los resultados de esta sección para evaluar la integral a lo largo del(los) contorno(s) indicado(s) cerrados(s).
$\oint_{c}\frac{2z+1}{z^{2}+z}dz$ con los contornos (a) $|z|=\frac{1}{2}$, (b) $|z|=2$ y (c) $|z-3i|=1$
Procedimiento
Primero notamos que:
$\oint_{c}\frac{2z+1}{z^{2}+z}dz=\oint_{c}\frac{2z+1}{z(z+1)}dz$
Ahora por fracciones parciales
$\frac{2z+1}{z(z+1)}=\frac{A}{z}+\frac{B}{z+1}\Longrightarrow2z+1=A(z+1)+Bz$
Entonces $A=1$ y $B=1$, y así tenemos que
$\oint_{c}\frac{2z+1}{z^{2}+z}dz=\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z+1}dz$
Se observa que el denominador de la integral no es analítico en $z=0$ y $z=-1$
Para (a), el punto $z=0$ sí esta dentro de c, pero $z=-1$ no lo esta. Por ello:
$\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z-(-1)}dz=2\pi i+0$
Inciso a
\[ (a)\longrightarrow\oint_{c}\frac{2z+1}{z^{2}+z}dz=2\pi i \]
Para (b), ambos puntos se encuentran dentro de c, entonces:
$\oint_{c}\frac{1}{z}dz+\oint_{c}\frac{1}{z-(-1)}dz=2\pi i+2\pi i$
Tenemos:
Inciso b
\[ (b)\longrightarrow\oint_{c}\frac{2z+1}{z^{2}+z}dz=4i\pi \]
Y para (c), ninguno de los puntos esta dentro, entonces:
Inciso c
\[ (c)\longrightarrow\oint_{c}\frac{2z+1}{z^{2}+z}dz=0 \]
Realizado por:Fernando Vazquez V. (discusión) 19:58 18 jun 2015 (CDT)
Ejercicio 16
evalúe la integral a lo largo de los contornos indicados cerrados
$\oint_{C}\frac{2z}{z^{2}+3}dz$;
a) $\mid z\mid=1$
b) $\mid z-2i\mid=1$
c) $\mid z\mid=4$
Procedimiento
$\oint_{C}\frac{2z}{z^{2}+3}dz=\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$
y por fracciones parciales:
$\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=\oint_{C}[\frac{A}{(z+i\sqrt{3})}+\frac{B}{(z-i\sqrt{3})}]dz=\oint_{C}[\frac{A(z-i\sqrt{3})+B(z+i\sqrt{3})}{(z+i\sqrt{3})(z-i\sqrt{3})}]dz\Longleftrightarrow2z=A(z-i\sqrt{3})+B(z+i\sqrt{3})$
resolviendo la ecuación para $A\;y\;B$ tenemos:
si
$z=-i\sqrt{3}$
entonces:
$-i2\sqrt{3}=-Ai2\sqrt{3}\Longleftrightarrow A=1$
si
$z=i\sqrt{3}$
entonces:
$i2\sqrt{3}=Bi2\sqrt{3}\Longleftrightarrow B=1$
de esto:
$\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=\oint_{C}[\frac{A}{(z+i\sqrt{3})}+\frac{B}{(z-i\sqrt{3})}]dz=\oint_{C}[\frac{1}{(z+i\sqrt{3})}+\frac{1}{(z-i\sqrt{3})}]dz=\oint_{C}\frac{1}{(z+i\sqrt{3})}dz+\oint_{C}\frac{1}{(z-i\sqrt{3})}dz$
$\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=\oint_{C}\frac{1}{(z+i\sqrt{3})}dz+\oint_{C}\frac{1}{(z-i\sqrt{3})}dz$
evaluando la integral a lo largo de a) $\mid z\mid=1$
Inciso a
como se puede ver $\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz$ no es una función a analítica en $z=i\sqrt{3}\;y\;en\;z=-i\sqrt{3}$ y como estos puntos no se encuentran dentro del contorno $\mid z\mid=1$ entonces
es analítica en todo su dominio $D$ ,dentro y sobre $C$
así por el teorema de Cauchy-Coursat
$\oint_{C}\frac{1}{(z+i\sqrt{3})}dz=0$
$\oint_{C}\frac{1}{(z-i\sqrt{3})}dz=0$
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=0$
Inciso b
evaluando a lo largo de b) $\mid z-2i\mid=1$, (circunferencia de radio $1$ centrada en $2i$)
por el razonamiento anterior $z=-i\sqrt{3}$ no se encuentra dentro del contorno $\mid z-2i\mid=1$ y asi
$\oint_{C}\frac{1}{(z+i\sqrt{3})}dz=0$
pero $z=i\sqrt{3}$ se encuentra dentro del contorno, entonces:
$\oint_{C}\frac{1}{(z-i\sqrt{3})}dz=2\pi i$ esto se deduce de:
si $z_{0}$es cualquier numero complejo constante interior a cualquier contorno cerrado simple $C$, entonces para un entero n tenemos
$\oint_{c}\frac{dz}{(z-z_{0})^{n}}=\begin{cases} 2\pi i & n=1\\ 0 & n\neq1 \end{cases}$
entonces:
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=2\pi i$
Inciso c
evaluando a lo largo de c) $\mid z\mid=4$ (circunferencia de radio $4$ centrada en $0+0i$)
de lo anterior podemos concluir:
$\oint_{C}\frac{1}{(z-(-i\sqrt{3}))}dz=2\pi i$
$\oint_{C}\frac{1}{(z-i\sqrt{3})}dz=2\pi i$
así:
$\Longrightarrow\oint_{C}\frac{2z}{(z+i\sqrt{3})(z-i\sqrt{3})}dz=4\pi i$
Realizado por: Francisco Medina Albino (discusión) 21:51 19 jun 2015 (CDT)
Ejercicio 17
Utilice cualquiera de los resultados de esta sección para evaluar la integral a lo largo del(los) contorno(s) indicado(s) cerrados(s).
$ \oint_{C} \! \frac{-3z+2}{z^{2}-8z+12} \,dz=0 $
$(a)$ $|z-5|=2$
$(b)$ $|z|=9$
\begin{equation}
\oint_{C} \! \frac{1}{\left(z-z_{o}\right)^n} = \left\lbrace
\begin{array}{ll}
2 \pi i & n=1\\
0, & n\neq 1
\end{array}
\right.
\end{equation}
\[
(6)
\]
Procedimiento
$(a)$ $|z-5|=2$
Factorizando el denominador
$z^{2}-8z+12 = (z-6)(z-2)$ el integrando no es analítico en $z=6$ y en $z=2$. De estos dos puntos sólo $z=6$ se encuentra dentro del contorno $C$, que es una
circunferencia centrada en $z=5$ de $r= 2$.
Ahora por fracciones parciales
\[ \frac{-3z+2}{z^{2}-8z+12}=\frac{A}{z-6}+\frac{B}{z-2}=\frac{A(z-2)+B(z-6)}{(z-6)(z-2)}= \frac{(A+B)z-2A-6B}{(z-6)(z-2)} \] $z: A+B=-3$
$c: -2A-6B=2$
Resolviendo tengo que:
$A=-4$ , $B=1$
\[
\frac{-3z+2}{z^{2}-8z+12}=\frac{-4}{z-6}+\frac{1}{z-2}
\]
y así,
Inciso a
\[ \oint_{C} \! \frac{-3z+2}{z^{2}-8z+12} \,dz=-4 \oint_{C} \! \frac{1}{z-6}\,dz + \oint_{C} \! \frac{1}{z-2} \,dz ...(1) \]
De acuerdo con el resultado $(6)$, la primera integral en $(1)$ tiene el valor de $2 \pi i$, mientras que por el teorema de Cauchy-Gousart el valor de la segunda integral es 0. Por tanto $(1)$, se convierte en
\[ \oint_{C} \! \frac{-3z+2}{z^{2}-8z+12} \,dz= -4(2 \pi)i + 1(0)= -8 \pi i. \]
$(b)$ $|z|=9$
Factorizando el denominador
$z^{2}-8z+12 = (z-6)(z-2)$ el integrando no es analítico en $z=6$ y en $z=2$. Los dos puntos se encuentran dentro del contorno $C$, que es una circunferencia centrada en $z=0$ de $r= 9$.
y así,
Inciso b
\[ \oint_{C} \! \frac{-3z+2}{z^{2}-8z+12} \,dz=-4 \oint_{C} \! \frac{1}{z-6}\,dz + \oint_{C} \! \frac{1}{z-2} \,dz ...(2) \]
De acuerdo con el resultado $(6)$, las dos integrales en $(2)$ tiene el valor de $2 \pi i$. Por tanto, se convierte en
\[ -4 (2 \pi)i + 1(2 \pi)i =-8( \pi )i+(2 \pi) i = - 6 \pi i. \]
Realizado por:Emmanuell Castro Flores (discusión) 20:45 17 jun 2015 (CDT)
Ejercicio 18
Calcular la integral a lo largo de los contornos indicados
Inciso a
a)
Analizando la función tenemos que las dos partes de la integral no son analíticas en puntos del dominio de la circunferencia de radio 5, es decir que
La función no es analitica en y además en y ambos puntos están dentro del dominio de la circunferencia de radio 5.
Por lo que procederemos a formar dos contornos circulares al rededor de cada punto respectivamente
en donde
en donde
con C1 que va en el intervalo de y C2 que va en el intervalo
Por lo que la integral queda definida como:
Solución
Otra forma de ver es, dado si esto si hay puntos en donde la función no es analítica el dominio del contorno. Por lo mismo tenemos que
Inciso b
b)
Analizando el contorno y la funcion
únicamente la primera parte es analítica en el dominio dado que está fuera del dominio de la región, por otra parte, la segunda fracción de la función no es analítica en dicha región.
Tenemos por Cauchy-Goursat que
y por si , tenemos
por lo que para el segundo contorno el resultado es
Solución
Realizado por:Pablo (discusión) 10:37 21 jun 2015 (CDT)
Ejercicio 19
Integrar a lo largo del contorno
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}dz$
donde $\left|z-i\right|=\frac{1}{2}$
Procedimiento
Resolveremos la integra como fracciones parciales de la siguiente manera:
$\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}=\frac{A}{z}+\frac{B}{z-i}+\frac{C}{z-3i}=\frac{A\left(z-i\right)\left(z-3i\right)+Bz\left(z-3i\right)+Cz\left(z-i\right)}{z\left(z-i\right)\left(z-3i\right)}$
Entoces:
$z-1=A\left(z-i\right)\left(z-3i\right)+Bz\left(z-3i\right)+Cz\left(z-1\right)$
Resolviendo el sistema obtenemos los siguientes valores:
$A=\frac{1}{3}$ , $B=\frac{i-1}{2}$ , $C=\frac{1-3i}{6}$
Por lo tanto solamente sustituimos:
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}=\frac{1}{3}\oint_{c}\frac{dz}{z}+\frac{1}{2}\oint_{c}\frac{\left(i-1\right)}{z-i}dz+\frac{1}{6}\oint_{c}\frac{\left(1-3i\right)}{z-3i}dz$
Pero sabemos por Cauchy-Goursat que el valor de la primera y tercer integral es cero por lo tanto nos enfocamos en la segunda integral. Pero también sabemos que el valor de esa integral es $2i\pi$, entonces tenemos los sig:
$\frac{1}{2}\oint_{c}\frac{\left(i-1\right)}{\left(z-1\right)}dz=\frac{i-1}{2}\oint_{c}\frac{dz}{z-1}=\frac{\left(i-1\right)}{2}\left(2\pi i\right)=-\pi\left(1+i\right)$
Solución
$\oint_{c}\frac{z-1}{z\left(z-i\right)\left(z-3i\right)}dz=-\pi\left(1+i\right)$
Resuelto por Luis Enrique Martínez Valverde (discusión) 21:38 16 jun 2015 (CDT)
Ejercicio 23
Evalue : , donde C es la “forma de ocho” del contorno de la figura 5.3.11.
[Sugerencia. Exprese C como la unión de dos curvas cerradas C1 y C2]
Procedimiento
Resolviendo la integral por fracciones parciales se tiene:
entonces:
Sustituyendo (2) en (1), y despejando “B” esta ultima que:
por lo tanto
Para la primera integral C1, z=0 esta dentro del contorno, y tiene valor de 2pi i; la segunda integral z =1
no esta dentro del contorno, no es analítica,así que es 0;
para C2 la primera integral no esta dentro del contorno y es 0 ,la segunda integral por medio el teorema
de Cauchy-Goursat, la segunda integral esta dentro del contorno y tiene valor de 2pi i; simplificando se tiene:
Conclusión
por lo tanto:
Elaborado por Ricardo Garcia Hernandez--Ricardo Garcia Hernandez (discusión) 23:33 17 jun 2015 (CDT)
Ejercicio 24
Supongamos que $z_{0}$ es cualquier numero complejo constante interior a cualquier curva simple cerrada del contorno C. Muestre que para un entero positivo n.
Procedimiento
\[ \oint_{c}\dfrac{dz}{(z-z_{0})^{n}} = \left\lbrace \begin{array}{ll} n= 1 & 2\pi i\\ n>1 & 0 \end{array} \right.\]
Tomamos como cualquier curva cerrada a una circunferencia centrada en $z=z_{0}$ y a $\gamma$ como otra curva que aísla a $z_{0}$ con un radio $|z-z_{0}|= R$. Entonces, si hacemos esto $z-z_{0}= \overline{z} = Re^{i \theta}$. Utilizando el teorema de Cauchy.
\[ \oint_{c}\dfrac{dz}{z-z_{0}} = \int^{2\pi}_{o} \dfrac{Re^{i\theta}}{Re^{i\theta}}= i \int^{2\pi}_{0}d \theta = 2i \pi\]
Conclusión
Si $n>1$ esto implica que $z_{0}$ está fuera de la curva por tanto la función es analítica y se cumple el teorema de Cauchy.
\[ \oint_{c} f(z) dz = 0\]
Realizado por:Esther Sarai (discusión) 20:32 18 jun 2015 (CDT)Esther Sarai
Ejercicio 30
Evalúe $\int_Ce^zdz$ de $z=0$ a $z=2+2i$ sobre el contorno $C$ de la figura 5.3.12 (consultar el libro) que consiste en la recta $y=x$ y una circunferencia tangente a la recta en $(1,1)$.
Procedimiento
Sol. (Se omite la figura, para mayor claridad consultar la imagen en el libro).
La curva $C$ esta dada en 3 segmentos $C_1$, $C_2$ y $C_3$. Se procede primero a calcular la integral de contorno sobre $C_1$.
Se tiene que la integral de contorno es $\int_Cf(z)dz=\int_a^bf(z(t))z'(t)dt$. Con $f(z)=e^z=e^x(\cos y+i\sin y)$, la curva sobre la que se integra es la recta $y=x$. Sea $x=t$ con $t\epsilon [0,1]$ (de la figura) como el parámetro, por lo tanto $y=t$ y si $z=x+iy=t+it=z(t)$, entonces $z'(t)=1+i$. Sustituyendo en la definición de la integral:
$\int_{C_1}f(z)dz=\int_a^bf(z(t))z'(t)dt=\int_0^1e^t(\cos t+i\sin t)(1+i)dt=\int_0^1e^t(\cos t+i\cos t+i\sin t-\sin t)dt=\int_0^1e^t(\cos t-\sin t)+i\int_0^1e^t(\cos t +\sin t)dt$
$\int_{C_1}f(z)dz=\int_0^1(e^t\cos t-e^t\sin t)+i\int_0^1(e^t\cos t +e^t\sin t)dt$
Las integrales se obtienen de tablas y son:
$\int e^x\cos xdx=\frac{1}{2}e^x(\sin x+\cos x)$ y $\int e^x\sin xdx=\frac{1}{2}e^x(\sin x-\cos x)$
Sustituyendo:
$\int_{C_1}f(z)dz=\frac{1}{2}[e^t(\sin t+\cos t)-e^t(\sin t-\cos t)]_0^1+i\frac{1}{2}[e^t(\sin t+\cos t)+e^t(\sin t-\cos t)]_0^1$
factorizando $e^t$ en cada termino y posteriormente sumamos y restamos:
$\int_{C_1}f(z)dz=\frac{1}{2}(2e^t\cos t)|_0^1+i\frac{1}{2}(2e^t\sin t)|_0^1=(e\cos 1-1)+i(e\sin 1)$
Así $\int_{C_1}f(z)dz=(e\cos 1-1)+i(e\sin 1)$
Para la curva $C_2$ que corresponde a la circunferencia tangente a la recta en $(1,1)$ se toma en cuenta que la función $f(z)=e^z$ es una función analítica en todo el plano complejo, lo cual es fácil comprobarse con el criterio del Teorema de Cauchy-Riemann. Dado lo anterior y del Teorema de Cauchy-Goursat, se tiene que la integral sobre el contorno cerrado $C_2$ es cero
$\int_{C_2}f(z)dz=0$
Para la curva $C_3$ se procede de igual forma que para $C_1$, sólo que los límites de la integral ésta vez cambian dado que el parámetro $t$ ahora se define para $t\epsilon [1,2]$. Así, simplemente sustituyendo límites:
$\int_{C_3}f(z)dz=(e^t\cos t)|_1^2+i(e^t\sin t)|_1^2=[e^2\cos 2-e\cos 1]+i[e^2\sin 2-e\sin 1]$
$\int_{C_3}f(z)dz=[e^2\cos 2-e\cos 1]+i[e^2\sin 2-e\sin 1]$
Se tiene que para la integral sobre el contorno $C$ conformada por los segmentos $C_1$, $C_2$ y $C_3$ es
$\int_Cf(z)dz=\int_{C_1}f(z)dz+\int_{C_2}f(z)dz+\int_{C_3}f(z)dz$
Sustituyendo cantidades:
$\int_Cf(z)dz=(e\cos 1-1)+i(e\sin 1)+(e^2\cos 2-e\cos 1)+i(e^2\sin 2-e\sin 1)=(e\cos 1-1+e^2\cos 2-e\cos 1)+i(e\sin 1+e^2\sin 2-e\sin 1)$
Conclusión
Por lo tanto:
$\int_Cf(z)dz=(e^2\cos 2-1)+i(e^2\sin 2)$
Oscar Javier Gutierrez Varela (discusión) 19:01 16 jun 2015 (CDT)
Ejercicio 31
En particular use $|z|=1$como $C$ y la parametrización $z=e^{i\theta}$,$0\leq\theta\leq2\pi,$para determinar el valor de las integrales reales.
Procedimiento
\[ {\displaystyle \int_{0}^{2\pi}e^{\cos\theta}\sin(\theta+\sin\theta)d\theta}={\displaystyle \frac{1}{2i}{\displaystyle \int_{0}^{2\pi}e^{\cos\theta}(e^{i(\theta+\sin\theta)}-e^{-i(\theta+\sin\theta)}d\theta}=}{\displaystyle \frac{1}{2i}{\displaystyle \int_{0}^{2\pi}e^{(\cos\theta+i(\theta+\sin\theta))}-e^{(\cos\theta-i(\theta+\sin\theta))}}} \]
\[
\Rightarrow{\displaystyle {\displaystyle \frac{1}{2i}}\int_{0}^{2\pi}e^{(\cos\theta+i\sin\theta)+i\theta}-e^{(\cos\theta-i\sin\theta)-i\theta}d\theta={\displaystyle \frac{1}{2i}}}{\displaystyle \int_{0}^{2\pi}{\displaystyle e^{e^{i\theta}}e^{i\theta}-e^{e^{-i\theta}}e^{-i\theta}d\theta}}
\]
Usando $z=e^{i\theta}\Rightarrow d\theta={\displaystyle \frac{dz}{ie^{i\theta}}={\displaystyle \frac{dz}{iz}}}$
tenemos que
\[ {\displaystyle \frac{1}{2i}}\int_{0}^{2\pi}{\displaystyle e^{e^{i\theta}}e^{i\theta}-e^{e^{-i\theta}}e^{-i\theta}d\theta={\displaystyle \frac{1}{2i}\int_{a}^{b}\left(e^{z}z-{\displaystyle \frac{e^{1/z}}{z}}\right)\frac{dz}{iz}=\frac{1}{2}{\displaystyle \int_{a}^{b}(-e^{z}+e^{z^{-1}}z^{-2})dz}}} \]
\[
\Rightarrow{\displaystyle \frac{1}{2}}{\displaystyle \int_{a}^{b}}(-e^{z}+e^{z^{-1}}z^{-2})dz={\displaystyle -\frac{1}{2}\left(e^{z^{-1}}+e^{z}\right)|_{a}^{b}=-{\displaystyle \frac{1}{2}(e^{(\cos\theta-i\sin\theta)}+e^{(\cos\theta+i\sin\theta)})|_{0}^{2\pi}}}=0
\]
Solución
\[ \therefore\int_{0}^{2\pi}e^{\cos\theta}\sin(\theta+\sin\theta)d\theta=0 \]
Realizado por:Jose Emmanuel Flores Calderón (discusión) 19:43 21 jun 2015 (CDT)









![\theta \epsilon [0,2 \pi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31b2bcea4b374acb1e5096a234d90ef56baae316)
![\phi \epsilon [0, 2\pi ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f562fe13ec22297908a5fe9c8a419a6569ee89b)









![\oint_{c}\frac{8z-3}{z^{2}-z}dz=\oint_{c}\frac{8z-3}{z(z-1)}dz=\oint_{c}\frac{A}{z}dz+\oint_{c}\frac{B}{z-1}dz=\left[\oint_{c_{1}}\frac{A}{z}dz+\oint_{c_{1}}\frac{B}{z-1}dz\right]+\left[\oint_{c_{2}}\frac{A}{z}dz+\oint_{c_{2}}\frac{B}{z-1}dz\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e73d387e6f1a2e109e98635c884d8e25e3750e6e)





![\oint_{c}\frac{8z-3}{z^{2}-z}dz=\oint_{c}\frac{8z-3}{z(z-1)}dz=\left[\oint_{c_{1}}\frac{3}{z}dz+\oint_{c_{1}}\frac{5}{z-1}dz\right]+\left[\oint_{c_{2}}\frac{3}{z}dz+\oint_{c_{2}}\frac{5}{Z-1}dz\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cf0437fd6f92633dd80045e05151be6d9ce17f68)
![\oint_{c}\frac{8z-3}{z^{2}-z}dz=\left[3\oint_{c_{1}}\frac{dz}{z}+5\oint_{c_{1}}\frac{dz}{z-1}\right]+\left[3\oint_{c_{2}}\frac{dz}{z}+5\oint_{c_{2}}\frac{dz}{Z-1}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5049e0f2afe526c1d6b4558f97afbe8e0225f572)

