Diferencia entre revisiones de «Compleja:Zill-Cap5.1»
| (No se muestran 25 ediciones intermedias del mismo usuario) | |||
| Línea 46: | Línea 46: | ||
'''Solución''' | '''Solución''' | ||
Por lo que la | Por lo que la solución a la integral dada. | ||
\begin{equation*} | \begin{equation*} | ||
| Línea 427: | Línea 427: | ||
Siendo este nuestro resultado final | Siendo este nuestro resultado final | ||
---- | |||
[[Usuario:Angelina Nohemi Mendoza Tavera|Angelina Nohemi Mendoza Tavera]] ([[Usuario discusión:Angelina Nohemi Mendoza Tavera|discusión]]) 23:25 13 jun 2015 (CDT) | Realizado por: [[Usuario:Angelina Nohemi Mendoza Tavera|Angelina Nohemi Mendoza Tavera]] ([[Usuario discusión:Angelina Nohemi Mendoza Tavera|discusión]]) 23:25 13 jun 2015 (CDT) | ||
---- | ---- | ||
| Línea 510: | Línea 509: | ||
---- | ---- | ||
[[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 20:43 12 jun 2015 (CDT) | Realizado por: [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 20:43 12 jun 2015 (CDT) | ||
---- | ---- | ||
| Línea 683: | Línea 682: | ||
Evalué la integral | |||
\begin{equation*} | |||
\int_{c}(x^{2}+y^{2})dx-2xydy | |||
\end{equation*} | |||
En la curva cerrada dada $x^2+y^2=4$ | |||
'''Procedimiento''' | |||
La curva está dada por una circunferencia con $r=2$ por tanto parametrizamos como | La curva está dada por una circunferencia con $r=2$ por tanto parametrizamos como | ||
$x=2 cost ..... dx=-2sent dt$ | |||
$y=2 sent ..... dy=2cost dt$ | |||
$ 0\leq t\leq\pi $ | |||
[[ | [[Archivo:Problema27Capitulo5.2Zill-modified.png|sinmarco]] | ||
Sustituyendo en la integral se tiene que | Sustituyendo en la integral se tiene que | ||
$ \int_{c} (2cost)^2+(2sent)^2 (-2sent dt)-2(2cost)(2sent)(2cost dt) $ | |||
$ \int_{0}^{\pi} (4cos^{2}t+4sen^{2}t)(-2sent)dt-(8cost sent)(2cost)dt $ | |||
$ \int_{0}^{\pi} (-8 cos^{2}t sent-8 sen^{3}t)dt-(8 cos^{2}t sent)dt $ | |||
$ \int_{0}^{\pi} (-16 cos^{2}t sent-8 sen^{3}t)dt $ | |||
$ -16\int_{0}^{\pi} cos^{2}t sent dt-8\int_{0}^{\pi} sen^{3}t dt $ | |||
Para la primera integral se toma un cambio de variable $u=cost$ $du=-sent dt$ | Para la primera integral se toma un cambio de variable $u=cost$ $du=-sent dt$ | ||
| Línea 714: | Línea 720: | ||
Por tanto la integral es igual a | Por tanto la integral es igual a | ||
$ \frac{16}{3}cos^{3}t-\frac{2}{3}(cos(3t)-9 cost) |_{0}^{\pi} $ | |||
$ \frac{16}{3}cos^{3}t+6 cost-\frac{2}{3}cos(3t) |_{0}^{\pi} $ | |||
$ \frac{2}{3}(15 cost+cos3t) |_{0}^{\pi} $ | |||
'''Solución''' | |||
-- | $ \therefore \int_{c}(x^{2}+y^{2})dx-2xydy=-\frac{64}{3} $ | ||
---- | |||
[[Usuario:Samantha Martinez|Samantha Martinez]] ([[Usuario discusión:Samantha Martinez|discusión]]) 00:37 14 jun 2015 (CDT) | |||
---- | ---- | ||
===Ejercicio 28=== | |||
En el problema evalué | |||
\begin{equation*} | |||
\oint_{c}(x^{2}+y^{2})dx-2xydy | |||
\end{equation*} | |||
sobre la curva cerrada, mostrada en la figura (PONER FIGURA) | |||
[[Archivo:28zill.png|250px]] | |||
'''Procedimiento''' | |||
Como vemos la función es una curva suave por trozos, procederemos a calcular la integral de linea pero haciéndolo sobre trayectorias suaves. | |||
<math>\oint_{c}(x^{2}+y^{2})dx-2xydy = \int_{c_1}(x^{2}+y^{2})dx-2xydy + \int_{c_2}(x^{2}+y^{2})dx-2xydy </math> | |||
Calculando primero para la primera curva suave tenemos que <math>c_{1}</math> es la curva definida de la función <math>y= x^2</math>, que va desde el punto (0,0) al punto (1,1), por lo que tomaremos a x como el parámetro de la curva, con <math>x \epsilon [0,1]</math>, por lo que tenemos que | |||
$y= x^2$ ; $dy = 2x dx$ | |||
Por lo que la integral de linea para la curva $c_{1}$ es | |||
$\int_{c_1}(x^{2}+y^{2})dx-2xydy = \int_{c_1} (x^{2}+(x^2)^{2})dx-2x(x^2)(2x dx)= \int_{c_1} (x^2 - 3 x^4) dx= \intop_{0}^{1} (x^2 - 3 x^4) dx = \frac{x^3}{3}- \frac{3x^5}{5}= \frac{1}{3}- \frac{3}{5}= \frac{-4}{15}$ | |||
Ahora para la segunda curva tenemos que cumple con la función <math>y = \sqrt{x}</math>, que va desde el punto (1,1) al (0,0), por lo que tomaremos a y como el parámetro, con <math>y \epsilon [1,0]</math>, en donde | |||
$y^2= x$ además de que $2y dy= dx$ | |||
Por lo que tenemos que la integral de linea para esta curva cumple que | |||
$\int_{c_2}(x^{2}+y^{2})dx-2(xy)dy= \int_{c_2}((y^2)^{2}+y^{2})(2 y dy)-2(y^2)ydy= \intop_{1}^{0} 2y^5 dy$ | |||
Dado que | |||
$\int_{b}^{a}du=-\int_{a}^{b}du$ | |||
$-\intop_{0}^{1} 2y^5 dy= -[\frac{2y^6}{6}]^{1}_{0}= -\frac{2}{6}$ | |||
'''Procedimiento''' | |||
Por lo que al sumar las dos partes tenemos que | Por lo que al sumar las dos partes tenemos que | ||
$\oint_{c}(x^{2}+y^{2})dx-2xydy = \int_{c_1}(x^{2}+y^{2})dx-2xydy + \int_{c_2}(x^{2}+y^{2})dx-2xydy = -\frac{4}{15} -\frac{2}{6}= -\frac{3}{5}$ | |||
---- | |||
[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 14:31 14 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 815: | Línea 798: | ||
=== Ejercicio 30 === | === Ejercicio 30 === | ||
Evalúa: $\oint_{C}{x^2y^3dx-xy^2dy}$ en la curva cerrada dada. | |||
'''Procedimiento''' | |||
Sea $\Gamma$ la trayectoria cerrada compuesta por los segmentos de recta: $\overline{OA},\overline{AB}, \overline{BO}$, donde: $O(0,0), A(2,4), B(0,4)$. Sean: $\Gamma_1$ la trayectoria $\overline{OA}$, $\Gamma_2$ la trayectoria $\overline{AB}$, $\Gamma_3$ la trayectoria $\overline{BO}$. Entonces: | Sea $\Gamma$ la trayectoria cerrada compuesta por los segmentos de recta: $\overline{OA},\overline{AB}, \overline{BO}$, donde: $O(0,0), A(2,4), B(0,4)$. Sean: $\Gamma_1$ la trayectoria $\overline{OA}$, $\Gamma_2$ la trayectoria $\overline{AB}$, $\Gamma_3$ la trayectoria $\overline{BO}$. Entonces: | ||
| Línea 841: | Línea 825: | ||
$$\oint_{C}{x^2y^3dx-xy^2dy}=\oint_{\Gamma}{x^2y^3dx-xy^2dy}=8(\frac{2^6}{6}-\frac{2^4}{4}) -64(\frac{2^3}{3})=8(\frac{64-24}{6})-\frac{8^3}{3}=\frac{8}{3}(20-64)=-\frac{352}{3}$$ | $$\oint_{C}{x^2y^3dx-xy^2dy}=\oint_{\Gamma}{x^2y^3dx-xy^2dy}=8(\frac{2^6}{6}-\frac{2^4}{4}) -64(\frac{2^3}{3})=8(\frac{64-24}{6})-\frac{8^3}{3}=\frac{8}{3}(20-64)=-\frac{352}{3}$$ | ||
'''Solución''' | |||
Por lo tanto : $\oint_{C}{x^2y^3dx-xy^2dy}=-\frac{352}{3}$ | Por lo tanto : $\oint_{C}{x^2y^3dx-xy^2dy}=-\frac{352}{3}$ | ||
[[Usuario:Alan Daniel Barrón Posadas|Alan Daniel Barrón Posadas]] ([[Usuario discusión:Alan Daniel Barrón Posadas|discusión]]) 14:45 16 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Alan Daniel Barrón Posadas|Alan Daniel Barrón Posadas]] ([[Usuario discusión:Alan Daniel Barrón Posadas|discusión]]) 14:45 16 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 850: | Línea 836: | ||
evalué $\oint_{c}(x^{2}-y^{2})ds$, donde $C$ esta dada por $x=5\cos t,y=5\sin t,0\leq t\leq2\pi$ | evalué $\oint_{c}(x^{2}-y^{2})ds$, donde $C$ esta dada por $x=5\cos t,y=5\sin t,0\leq t\leq2\pi$ | ||
'''Procedimiento''' | |||
por definición | por definición | ||
| Línea 873: | Línea 861: | ||
$\oint_{c}(x^{2}-y^{2})ds=\int_{0}^{2\pi}(25\cos^{2}t-25\sin^{2}t)\sqrt{1+\left[-\arctan t\right]^{2}}(-5\sin t)dt=25\int_{0}^{2\pi}(-5\sin t)(\cos^{2}t-\sin^{2}t)\sqrt{1+\arctan^{2}t}dt=25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt$ | $\oint_{c}(x^{2}-y^{2})ds=\int_{0}^{2\pi}(25\cos^{2}t-25\sin^{2}t)\sqrt{1+\left[-\arctan t\right]^{2}}(-5\sin t)dt=25\int_{0}^{2\pi}(-5\sin t)(\cos^{2}t-\sin^{2}t)\sqrt{1+\arctan^{2}t}dt=25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt$ | ||
$25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt=\frac{5}{2}\cos t\sqrt{\sec^{2}t}(\cos2t)-2\log(cost)\mid_{0}^{2\pi}=\frac{5}{2}\cos2\pi\sqrt{\sec^{2}2\pi}(\cos4\pi)-2\log(cos2\pi)-\frac{5}{2}\cos0\sqrt{\sec^{2}0}(\cos20)+2\log(cos0)=1-1=0$ | $25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt=\frac{5}{2}\cos t\sqrt{\sec^{2}t}(\cos2t)-2\log(cost)\mid_{0}^{2\pi}=$ | ||
$=\frac{5}{2}\cos2\pi\sqrt{\sec^{2}2\pi}(\cos4\pi)-2\log(cos2\pi)-\frac{5}{2}\cos0\sqrt{\sec^{2}0}(\cos20)+2\log(cos0)=1-1=0$ | |||
'''Solución''' | |||
así | así | ||
| Línea 881: | Línea 873: | ||
--[[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 22:53 11 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 22:53 11 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 889: | Línea 882: | ||
y $t\epsilon\left[0,\pi\right]$ | y $t\epsilon\left[0,\pi\right]$ | ||
'''Procedimiento''' | |||
Recordemos que $\int_{-c}=-\int_{c}$ ...(1) , también que $cos^{2}t+sen^{2}t=1$ | Recordemos que $\int_{-c}=-\int_{c}$ ...(1) , también que $cos^{2}t+sen^{2}t=1$ | ||
| Línea 911: | Línea 905: | ||
cero y pi, por lo tanto poniendo los limites de integración y resolviendo | cero y pi, por lo tanto poniendo los limites de integración y resolviendo | ||
la integral tenemos: | la integral tenemos: | ||
'''Solución''' | |||
$6\int_{0}^{\pi}dt=6t\mid_{0}^{\pi}=6\pi$ | $6\int_{0}^{\pi}dt=6t\mid_{0}^{\pi}=6\pi$ | ||
---- | |||
Resuelto por [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 11:42 14 jun 2015 (CDT) | Resuelto por [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 11:42 14 jun 2015 (CDT) | ||
---- | ---- | ||
===Ejercicio 33=== | ===Ejercicio 33=== | ||
| Línea 931: | Línea 925: | ||
$ C_1: x= 2t+1, y=4t+2$ $0<t<1$ | $ C_1: x= 2t+1, y=4t+2$ $0<t<1$ | ||
'''Procedimiento''' | |||
| Línea 966: | Línea 962: | ||
$ dx=\frac{dt}{t}, dy=\frac{2dt}{t}$ | $ dx=\frac{dt}{t}, dy=\frac{2dt}{t}$ | ||
'''Solución''' | |||
$\int_{c}y^2dx+xydy=\int_{c}[2\ln{t}]^2\frac{dt}{t}+[\ | $\int_{c}y^2dx+xydy=\int_{c}[2\ln {t}]^2\frac{dt}{t}+[\ln t][2\ln t][\dfrac{2dt}{t}= \frac{208}{3} $ | ||
---- | ---- | ||
Realizado por:[[Usuario:Nancy Martínez Durán|Nancy Martínez Durán]] ([[Usuario discusión:Nancy Martínez Durán|discusión]]) 09:14 14 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 35=== | ===Ejercicio 35=== | ||
'''Si $\rho (x,y)$ es la densidad de un alambre (masa por unidad de longitud), entonces la masa del alambre es $m=\int_C\rho (x,y)ds$. Determine la masa de un alambre que tiene la forma de una semicircunferencia $x=1+\cos t$, $y=\sin t$, $0\leq t\leq \pi$, si la densidad en un punto $P$ es directamente proporcional a la distancia del eje $y$.''' | '''Si $\rho (x,y)$ es la densidad de un alambre (masa por unidad de longitud), entonces la masa del alambre es $m=\int_C\rho (x,y)ds$. Determine la masa de un alambre que tiene la forma de una semicircunferencia $x=1+\cos t$, $y=\sin t$, $0\leq t\leq \pi$, si la densidad en un punto $P$ es directamente proporcional a la distancia del eje $y$.''' | ||
'''Solución''' | |||
Si $\rho (x,y)=ky$ con $k$ como la constante de proporcionalidad. La función de masa es la integral de línea de la densidad sobre la curva del alambre. En este caso el alambre tiene la forma de la semicircunferencia de radio 1 y centro en $(1,0)$ que tiene por ecuaciones paramétricas $x=1+\cos t$ $y=\sin t$. La definición de integral de línea de a lo largo de $C$ es | |||
| Línea 994: | Línea 992: | ||
[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 19:25 11 jun 2015 (CDT) | ---- | ||
Realizado por:[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 19:25 11 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 1000: | Línea 999: | ||
=== Ejercicio 36 === | === Ejercicio 36 === | ||
Las coordenadas del centro de masa de un alambre con densidad variable | Las coordenadas del centro de masa de un alambre con densidad variable | ||
estan dadas por $\overline{x}=M_{y}/m\hspace{1em}y\hspace{1em}\overline{y}=M_{x}/m$ | |||
donde | donde | ||
| Línea 1009: | Línea 1008: | ||
Encuentre el centro de masa del alambre en el problema 35. | Encuentre el centro de masa del alambre en el problema 35. | ||
'''Procedimiento''' | |||
De acuerdo al problema 35, sabemos que la curva $c$ esta parametrizada | De acuerdo al problema 35, sabemos que la curva $c$ esta parametrizada | ||
| Línea 1025: | Línea 1025: | ||
Así | |||
\[ | \[ | ||
| Línea 1031: | Línea 1031: | ||
\] | \] | ||
'''Conclusión''' | |||
Por lo tanto las coordenadas son $\overline{x}=1,\overline{y}={\displaystyle \frac{\pi}{4}}$ | Por lo tanto las coordenadas son $\overline{x}=1,\overline{y}={\displaystyle \frac{\pi}{4}}$ | ||
---- | |||
[[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 17:30 14 jun 2015 (CDT) | [[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 17:30 14 jun 2015 (CDT) | ||
---- | ---- | ||
Revisión actual - 09:52 12 mar 2023
Ejercicios del capítulo 5, sección 1 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 5.1
En los problemas 1-16, evaluar la integral definida. Si es necesario, revisar las técnicas de integración de libros de cálculo.
Ejercicio 1
Evalué la integral definida
\begin{equation*} \int_{-1}^{3}x\left ( x-1 \right )\left ( x+2 \right )dx \end{equation*}
Procedimiento
Resolviendo los productos que están adentro de la integral.
$x \left ( x-1 \right )\left ( x+2 \right )=x(x^{2}+2x-x-2)=x^{3}+x^{2}-2x$
Por lo que la integral puede escribirse como:
$ \int_{-1}^{3}x\left ( x-1 \right )\left ( x+2 \right )dx= \int_{-1}^{3}(x^{3}+x^{2}-2x) dx$
Fácilmente se puede solucionar esta integral separando en sumas de integrales, por lo que el resultado de la integral es:
$\int_{-1}^{3}(x^{3}+x^{2}-2x) dx=\frac{x^{4}}{4}+\frac{x^{3}}{3}-x^{2} \Bigg|_{-1}^{3}$
Aplicando los limites de integración:
$\frac{x^{4}}{4}+\frac{x^{3}}{3}-x^{2} \Bigg|_{-1}^{3}$=
Resolviendo las potencias de las fracciones nos da el siguiente resultado:
$\left [ \frac{81}{4}+\frac{27}{3}-9 \right ]-\left [ \frac{1}{4}-\frac{1}{3}-1 \right ]$
$\left [\frac{81}{4} \right ]-\left [-\frac{13}{12} \right ]= \frac{64}{3}$
Solución
Por lo que la solución a la integral dada.
\begin{equation*} \int_{-1}^{3}x\left ( x-1 \right )\left ( x+2 \right )dx=\frac{64}{3} \end{equation*}
Elaborado por --Ricardo Garcia Hernandez (discusión) 00:20 15 jun 2015 (CDT)
Re elaborado por Manuel Rodríguez
Ejercicio 3
Evalué la integral definida
\begin{equation*} \int_{\frac{1}{2}}^{1} \sin(2\pi x) dx \end{equation*}
Procedimiento
$\int_{\frac{1}{2}}^{1} \sin(2\pi x) dx= \left [ \frac{-\cos(2\pi x)}{2\pi} \right ]\Bigg|_{-\frac{1}{2}}^{1}$
Aplicando los limites
$\left [ \frac{-\cos(2\pi x)}{2\pi} \right ]\Bigg|_{-\frac{1}{2}}^{1}=\left [ \frac{-\cos(2\pi )}{2\pi} \right ]-\left [ \frac{-\cos(-\pi)}{2\pi} \right ]$
Usando la propiedad del $cos(-u)=cos(u)$ y sustituyendo el valor de coseno:
$\left [ \frac{-\cos(2\pi x)}{2\pi} \right ]\Bigg|_{-\frac{1}{2}}^{1}=\left [ -\frac{1}{2\pi} \right ]-\left [ \frac{1}{2\pi} \right ]$
Solución
Por lo que el resultado de la Integral propuesta es:
\begin{equation*} \int_{\frac{1}{2}}^{1} \sin(2\pi x) dx= -\frac{1}{\pi} \end{equation*}
Alejandro Juárez Toribio (discusión) 23:37 13 jun 2015 (CDT)
Ejercicio 5
Evalúe la integral definida
\begin{equation*} \int_{0}^{4}\frac{1}{2x+1} dx \end{equation*}
Procedimiento
Para resolver la integral hacemos un cambio de variable:
$u=2x+1$ ; $du=2dx$
Usando el cambio de Variable propuesto:
$\int_{0}^{4}\frac{1}{2}\frac{1}{u}du=\frac{1}{2}\int_{0}^{4}\frac{1}{u}du$
En este caso, la solución a la integral, es la función logaritmo
$\int \frac{1}{x}dx=\ln(x)+Constante$
Usando los limites de integracion
$\frac{1}{2}\int_{0}^{4}\frac{1}{u}du= \frac{1}{2}\ln(u)\Bigg|_{0}^{4}$
Regresando a la variable original
$ \intop_{0}^{4} \frac{dx}{2x+1} = \intop_{0}^{4} \frac{du}{2u} = \dfrac{1}{2}\ln[u]_{0}^{4} = \dfrac{1}{2}\ln[2x+1]_{0}^{4} = \frac{1}{2}\ln(9)-\frac{1}{2}\ln(1)$
Solución
Dado que $ln(1)=0$, la solución a la Integral es:
\begin{equation*} \int_{0}^{4}\frac{1}{2x+1} dx=\frac{1}{2}\ln(9) \end{equation*}
Nancy Martínez Durán (discusión) 19:56 13 jun 2015 (CDT)
Ejercicio 6
Evalúe la integral definida
\begin{equation*} \intop_{ln2}^{ln3}e^{-x} dx \end{equation*}
Procedimiento
Usando que $\int_{a}^{b}e^{x}dx=e^{x}\Bigg|_{a}^{b}$
$\intop_{ln2}^{ln3}e^{-x}=-e^{-x}\mid_{ln2}^{ln3}=\left [ -e^{-ln3} \right ]-\left [ -e^{-ln2} \right ]$
Dado que $e^{\ln u}=u$ y usando la conocida propiedad de los logaritmos $\ln\left ( \frac{x}{y} \right )=\ln(x)-\ln(y)$ ; si $x=1$ entonces $-\ln(y)=\ln\left ( \frac{1}{y} \right )$
Por lo que
$\left [ -e^{-ln3} \right ]-\left [ -e^{-ln2} \right ]=\left [-e^{ln\left ( \frac{1}{3} \right )} \right ]-\left [-e^{ln\left ( \frac{1}{2} \right )} \right ]=\left [ -\frac{1}{3} \right ]-\left [ -\frac{1}{2} \right ]$
Solución
Entonces el valor de la integral es:
\begin{equation*} \intop_{ln2}^{ln3}e^{-x} dx=\frac{-2+3}{6}=\frac{1}{6} \end{equation*} --- Juan Daniel Rivera Bautista (discusión) 23:38 12 jun 2015 (CDT)
Ejercicio 7
Evalúe la integral definida
\begin{equation*} \intop_{2}^{4} xe^{\frac{-x}{2}}dx \end{equation*}
Procedimiento
Para resolver esta integral emplearemos la técnica de integración por partes donde se define como $\int udv=uv-\intop v du$
donde
$u=x$ por lo tanto $du=dx$
$dv=e^{\frac{-x}{2}}dx$ así tenemos $v=-2e^{\frac{-x}{2}}$
Evaluamos $uv-\intop v du$ y tenemos
$-2xe^{\frac{-x}{2}}+2\intop e^{\frac{-x}{2}}dx=-2xe^{\frac{-x}{2}}-4e^{\frac{-x}{2}}$
$\intop_{2}^{4} xe^{\frac{-x}{2}}dx = 2xe^{\frac{-x}{2}}-4e^{\frac{-x}{2}}\mid_{2}^{4}$
$\intop_{2}^{4} xe^{\frac{-x}{2}}dx = [-8e^{-2}-4e^{-2}]-[-4e^{-1}-4e^{-1}]$
Solución
Por lo que la solución es:
\begin{equation*}
\intop_{2}^{4} xe^{\frac{-x}{2}}dx = -12e^{-2}+8e^{-1}
\end{equation*}
Miguel Medina Armendariz (discusión) 16:43 13 jun 2015 (CDT)
Ejercicio 8
Evalúe la integral definida.
\begin{equation*} \intop_{1}^{e}\ln(x)dx \end{equation*}
Procedimiento
Integrando por partes:
$\int udv=uv-\intop v du$
Donde $u=\ln(x)$, $du=dx/x$, $dv=dx$ y $v=x$, tenemos que:
$\intop_{1}^{e}\ln(x)dx=[x \ln(x)-x]_{1}^{e}=[x(\ln(x)-1)]_{1}^{e}$
Evaluando:
$[x(\ln(x)-1)]_{1}^{e}=e(\ln(e)-1)-1(\ln(1)-1)=1$
Solución
$\therefore\intop_{1}^{e}\ln(x)dx=1$
Fernando Vazquez V. (discusión) 15:15 14 jun 2015 (CDT)
Ejercicio 9
Evalúe la integral definida
\begin{equation*} \int_{2}^{4} \frac{dx}{x^{2}-6x+5} \end{equation*}
Procedimiento
La integral puede ser solucionada por fracciones parciales
$\frac{1}{(x-5)(x-1)}=\frac{A}{x-5}+\frac{B}{x-1}=\frac{A(x-1)+B(x-5)}{(x-5)(x-1)}=\frac{Ax-1A+Bx-B}{(x-5)(x-1)}=\frac{(A+B)x-1A-5B}{(x-5)(x-1)}$
Igualando las partes del numerador
$x: A+B=0$
$C: -1A-5B=1$
Resolviendo tengo que: $A=\frac{1}{4}$, $B=-\frac{1}{4}$
Así tengo que:
$\int_{2}^{4} \frac{dx}{x^{2}-6x+5}=\int_{2}^{4} \frac{A}{(x-5)}+\frac{B}{(x-1)}= \int_{2}^{4} \frac{1/4}{(x-5)}+\frac{-1/4}{(x-1)}=$
$\frac{1}{4} ln(x-5)\mid_{2}^{4}-\frac{1}{4} ln(x-1)\mid_{2}^{4}=$
$\frac{1}{4} ln(4-5)-\frac{1}{4} ln(2-5)-\frac{1}{4} ln(4-1)-\left(-\frac{1}{4} ln(2-1)\right)=$
$\frac{1}{4} ln(-1)-\frac{1}{4} ln(-3)-\frac{1}{4} ln(3)+\frac{1}{4} ln(1)$
Dado que el logaritmo natural no tiene solución en el campo de los números reales, ampliando al campo complejo y tomando la primera rama del logaritmo.
Ahora $ln(-1)$, y sé que $lnz=log_{e}|z|+i Arg(z)$
Si $z=-1$, $|z|=|-1|=1$, $Arg(z)=Arg(-1)=\pi$
Entonces: $ln(-1)=log_{e}1+i \pi=i \pi$
Y $ln(-3)$, $z=-3$, $|z|=|-3|=3$, $Arg(z)=Arg(-3)=\pi$
Entonces: $ln(-3)=log_{e}3+i\pi$
Con $\ln(1)=0$ y el $log_{e}=ln$ Sustituyendo:
$\frac{1}{4} ln(-1)-\frac{1}{4} ln(-3)-\frac{1}{4} ln(3)+\frac{1}{4} ln(1)$= $\frac{1}{4} i\pi-\frac{1}{4} \left(ln(3)+i\pi\right)-\frac{1}{4} ln(3)+\frac{1}{4} \cdot 0$= $\frac{1}{4} i\pi-\frac{1}{4} ln(3)-\frac{1}{4} i\pi-\frac{1}{4} ln(3)$= $-\frac{1}{4} ln(3)-\frac{1}{4} ln(3)$= $-\frac{1}{2} ln(3)$
Por lo tanto:
Solución
\begin{equation*} \int_{2}^{4} \frac{dx}{x^{2}-6x+5}=-\frac{1}{2} ln 3 \end{equation*}
Emmanuell Castro Flores (discusión) 16:05 14 jun 2015 (CDT)
Ejercicio 11
In Problems 11\textendash 14, evaluate the line integrals
C G(x, y) dx,
C G(x, y) dy, and C G(x, y) dl on the indicated curve C.
traduccion
En los problemas 11 a 14 , evaluar las integrales de línea
C G ( x , y) dx,
C G ( x , y) dy, y C dl de la curva indicada C. G ( x , y)
$11-.G\left(X,Y\right)=2XY:X=5COS\left(t\right),Y=5SEN\left(t\right),0\leq t\geq\frac{PI}{4}$
primero encuentro $G\left(X,Y\right)$en funcion de t y las derivadas tambien con respecto de t
$G\left(\left(X,Y\right)T\right)=2\left(5COS\left(t\right)5SEN\left(t\right)\right)=50COS\left(t\right)SEN\left(t\right)$
$X^{\prime}\left(t\right)=-5SEN\left(t\right)$
$Y^{\prime}\left(t\right)=5COS\left(t\right)$
$\left[l^{\prime}\right]=\sqrt{\left(X^{\prime}\left(t\right)\right)^{2}+\left(Y^{\prime}\left(t\right)\right)^{2}}=\sqrt{\left(-5SEN\left(t\right)\right)^{2}+\left(5COS\left(t\right)\right)^{2}}=5$
HAORA , RESOLVEMOS LA PRIMERA INTEGRAL:
$\int_{c}G\left(X,Y\right)dX=\int_{0}^{\frac{pi}{4}}G\left(t\right)X^{\prime}\left(t\right)dt=\int_{0}^{\frac{pi}{4}}50COS\left(t\right)SEN\left(t\right)\left(-5SEN\left(t\right)\right)dt=\int_{0}^{\frac{pi}{4}}-250SEN^{2}\left(t\right)COS\left(t\right)dt=\left[-\frac{250}{3}SEN^{3}\left(t\right)\right]_{0}^{\frac{pi}{4}}=-29.46$
RESOLVEMOS LA SEGUNDA INTEGRAL:
$\int_{c}G\left(X,Y\right)dY=\int_{0}^{\frac{pi}{4}}G\left(t\right)Y^{\prime}\left(t\right)dt=\int_{0}^{\frac{pi}{4}}50COS\left(t\right)SEN\left(t\right)\left(5COS\left(t\right)\right)dt=\int_{0}^{\frac{pi}{4}}-250COS^{2}\left(t\right)SE\left(t\right)dt=\left[\frac{250}{3}COS^{3}\left(t\right)\right]_{0}^{\frac{pi}{4}}=-53.87$
RESOLVEMOS LA TERCERA INTEGRAL:
$\int_{c}G\left(X,Y\right)dl=\int_{0}^{\frac{pi}{4}}G\left(t\right)\left[l^{\prime}\right]dt=\int_{0}^{\frac{pi}{4}}50COS\left(t\right)SEN\left(t\right)5dt=\int_{0}^{\frac{pi}{4}}250CO\left(t\right)SE\left(t\right)dt=\left[\frac{250}{2}SEN^{2}\left(t\right)\right]_{0}^{\frac{pi}{4}}=62.50$
--Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT) ----
Ejercicio 16
Evalué la integral
\begin{equation*} \int_{C} \! (2x + y)\,dx + xy\,dy \end{equation*}
Procedimiento
en la curva $y = x^2 + 1$ dada de (-1, 2) a (2, 5)
En este caso elegimos a $x $ como variable de integración, entonces tenemos:
$y = x^2 + 1$
$dy = 2x dx$
Reescribiendo la integral sustituyendo $y$ y $dy$
$\int_{C} \! (x^2 + 1)\,dx + xy\,dy = \int_{C} [2x + (x^2 + 1)]dx + x(x^2 + 1)2x dx$
$=\int_{-1}^{2} (2x + x^2 + 1 + 2x^4 + 2x^2)dx = \int_{-1}^{2} (2x^4 + 3x^2 + 2x + 1)dx$
Evaluando la integral
$=[\frac{2}{5} x^5 + x^3 + x^2 + x]_{-1}^{2} = \frac{2}{5} (2^5 - (-1)^5) + (2^3 - (-1)^3) + (2^2 - (-1)^2) + (2 + 1)$
$=\frac{2}{5} (33) + 9 + 6 = \frac{66}{5} + 15 = \frac{141}{5}$
Solución
\begin{equation*} \int_{C} \! (2x + y)\,dx + xy\,dy= \frac{141}{5} \end{equation*}
Siendo este nuestro resultado final
Realizado por: Angelina Nohemi Mendoza Tavera (discusión) 23:25 13 jun 2015 (CDT)
Ejercicio 19
Evalúe
\begin{equation*} \int_{C} \! y\,dx + x\,dy \,dx \end{equation*}
sobre la curva dada ($y=x^2$) de $(0,0)$ a $(1,1)$.
Se pueden escoger cualquier variable para parametrizar, o bien, un parámetro a continuación ilustro los 2 procedimientos
Procedimiento 1
Eligiendo x como variable de integración: \[ y=x^2 \;\;\;\Rightarrow\;\;\;dy=2\,x\,dx \] Luego podemos escribir la integral como: \[ \int_{C} \! y\,dx + x\,dy = \int_{C} \! {\left[ (x^2)dx + x(2x\,dx) \right]} dx==\int_{-2}^{2} \! \left( x^2 + 2 x^2 \right) \,dx=\int_{0}^{1} \! 3 x^2 \,dx=1^3-0^3=1 \]
Procedimiento 2
Si se escoge $y$ como variable de integración se tiene: \[ x=\sqrt{y} \;\;\;\Rightarrow\;\;\;dx=\frac {dy}{2\,x}=\frac{dy}{2\,\sqrt{y}} \] Luego podemos escribir la integral como: \[ \int_{C} \! y\,dx + x\,dy \,dx= \int_{C} \! \left( y\, \frac {dy}{2\,\sqrt{y}} + \sqrt{y}\,dy \right) \,dy=\int_{0}^{1} \! \left( \frac{y}{2 \sqrt{y}}+\sqrt{y} \right) \,dy=\frac{3}{2}\int_{0}^{1} \! \left( \sqrt{y} \right) \,dy=1^{\frac{3}{2}}-0^{\frac{3}{2}}=1-0=1 \]
Como se ve, ambos métodos son equivalentes, n obstante algebraicamente pueden ser mas o menos complicados; nótese que en el segundo se pudo usar $x=\sqrt{y}\,$ y no $x=\pm\sqrt{y}$, porque tanto $y$ como $x$ están contenidos en el primer cuadrante.
Solución
\begin{equation*} \int_{C} \! y\,dx + x\,dy \,dx=1 \end{equation*}
Tlacaelel Cruz (discusión) 14:33 12 jun 2015 (CDT)
Método alterno Parametrización de la función
Evaluar $\int_{c}ydx+xdy$sobre la curva dada de (0,0) a (1,1).
$y=x^{2}$
Primero parametrizamos la función.
$x(t)=t$
$y(t)=t^{2}$
Con $0\leq t\leq1$
Y sustituyendo en la integral:
$\Longrightarrow\int[(t^{2})(1)dt+t(2t)dt]$
Resolviendo
$\int(t^{2})dt+\int2t^{2}dt=\frac{1}{3}t^{3}|_{0}^{1}+\frac{2}{3}t^{3}|_{0}^{1}=\frac{1}{3}+\frac{2}{3}=1$
Solución
Por lo que el valor de la integral es el mismo que en los dos métodos anteriores
\begin{equation*} \int_{C} \! y\,dx + x\,dy \,dx=1 \end{equation*}
Realizado por: A. Martín R. Rabelo (discusión) 20:43 12 jun 2015 (CDT)
Ejercicio 23
Evalué la integral.
\begin{equation*} \int_{c}(6x^{2}+2y^{2})dx+4xydy \end{equation*}
Donde C está dado por $x=\sqrt{t}$ , $y=t$ con $4\leq t\leq9$
Procedimiento
$ x=\sqrt{t} ..... dx=\frac{1}{2\sqrt{t}} $
$ y=t .... dy=dt $
$ 4\leq t\leq9 $
Sustituyendo en la integral
$\int_{c}(6x^{2}+2y^{2})dx+4xydy=\int_{4}^{9}[6(\sqrt{t})^2+2(t)^2]\frac{1}{2\sqrt{t}}dt+[4\sqrt{t} t]dt $
$ \int_{4}^{9} [6t+2t^2]\frac{1}{2\sqrt{t}}dt+[4\sqrt{t} t]dt $
$ \int_{4}^{9} [\frac{6t}{2\sqrt{t}}+\frac{2t^2}{2\sqrt{t}}+4\sqrt{t} t]dt $
$ \int_{4}^{9}[3\frac{t}{\sqrt{t}}+\frac{t^2}{\sqrt{t}}+4\sqrt{t} t]dt] $
$ \int_{4}^{9}[3t^{\frac{1}{2}}+t^{\frac{3}{2}}+4t^{\frac{3}{2}}]dt $
$ =(2t^{\frac{3}{2}}+\frac{2}{5}t^{\frac{5}{2}}+\frac{8}{5}t^{\frac{5}{2}}) |_{4}^{9} $
$ 2t^{\frac{3}{2}}+t^{\frac{5}{2}}(\frac{2}{5}+\frac{8}{5}) |_{4}^{9} $
$ 2t^{\frac{3}{2}}+t^{\frac{5}{2}}(2) |_{4}^{9} $
$ 2 (t^{\frac{3}{2}}+t^{\frac{5}{2}}) |_{4}^{9}$
$ 2 t^{\frac{3}{2}}(1+t) |_{4}^{9} $
$ \therefore \int_{c}(6x^{2}+2y^{2})dx+4xydy=460 $
Solución
La solución a la integral es:
\begin{equation*}
\int_{c}(6x^{2}+2y^{2})dx+4xydy=460
\end{equation*}
Ejercicio corregido por:Samantha Martinez (discusión) 01:20:41 14 jun 2015 (CDT)
Ejercicio incorrecto
$\int_{c}[(6t+2t^{2})(\frac{1}{2}t^{-2})+4t^{\frac{1}{2}}(t)]dt=\int_{4}^{9}[(6t+2t^{2})(\frac{1}{2}t^{-2})+4t^{\frac{1}{2}}(t)]dt=\int_{4}^{9}[3t^{-1}+1+4t^{\frac{3}{2}}]dt$
Integrando queda de la forma:
$\int_{4}^{9}[3t^{-1}+1+4t^{\frac{3}{2}}]dt=(3log_{e}(t)+t+\frac{8}{5}t^{\frac{5}{2}})|_{4}^{9}=(3log_{e}(9)+9+\frac{8}{5}9^{\frac{5}{2}})-(3log_{e}(4)+4+\frac{8}{5}4^{\frac{5}{2}})=345.032$
A. Martín R. Rabelo (discusión) 23:41 12 jun 2015 (CDT)
Ejercicio 24
Evalué la integral sobre el contorno C.
\begin{equation*} \int_{c}-y² dx + xy dy \end{equation*}
donde C esta dada por $x=2t$, $y=t³$, $0\leq t\leq2$.
Procedimiento
para calcular la integral tenemos que:
$x= 2t ...... dx= 2 dt$
$y= t³ ...... dy= 3t²dt$
$0\leq t\leq2$
Por lo cual sustituyendo en la integral tenemos:
$\int_{c}-y² dx + xy dy= \int_{0}^{2} [-(t³)²(2 dt)]+[(2t)(t³)(3t² dt)]$
Desarrollando y simplificando tenemos:
$\int_{0}^{2} -(t⁶)(2 dt)+(2t⁴)(3t² dt)$
$\int_{0}^{2} -2t⁶ dt + 6t⁶ dt$
$\int_{0}^{2} 4t⁶ dt$
$\int_{0}^{2} 4t⁶ dt= \frac{4t⁷}{7}|_{0}^{2} = \frac{512}{7}\approx {73.1428}$
Solución
por lo cual:
\begin{equation*} \int_{c}-y² dx + xy dy= \frac{512}{7} \end{equation*}
Anahi Limas (discusión) 12:16 14 jun 2015 (CDT)
Ejercicio 25
Evalué la Integral:
\begin{equation*} \int_{C} 2x^{3}y dx +(3x+y) dy \end{equation*}
Donde C esta dada por $x= y^{2}$ $(1,-1)$ a $(1,1)$
Procedimiento
La curva de es $x= y^{2}$ tomamos un parámetro $ t$ y definimos $ y= t$, en la curva $y^{2}=t^{2}$.
Entonces el intervalo a evaluar es $(-1,1)$
Por lo que la integral parametrizada quedaría
$\int_{C} 2x^{3}y dx +(3x+y) dy =\int_{-1}^{1}4t^{8}+3t^{2}+t dt$
$\int_{-1}^{1}4t^{8}+3t^{2}+t dt$
Por lo que el resultado de la suma de integrales:
$\left [4\frac{t^{9}}{9}+3\frac{t^{3}}{3}+\frac{t^{2}}{2} \right ]\Bigg|_{-1}^{1}$
Evaluando los limites.
$\left [\frac{4}{9}+1+\frac{1}{2} \right ]-\left [-\frac{4}{9}-1+\frac{1}{2} \right ]=\frac{8}{9}+2$
Solución
\begin{equation*} \int_{C} 2x^{3}y dx +(3x+y) dy =\frac{26}{9} \end{equation*}
Esther Sarai (discusión) 12:27 14 jun 2015 (CDT)Esther Sarai
Ejercicio 27
Evalué la integral
\begin{equation*}
\int_{c}(x^{2}+y^{2})dx-2xydy
\end{equation*}
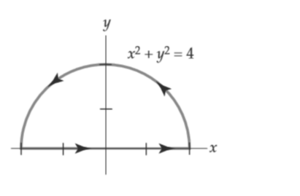
En la curva cerrada dada $x^2+y^2=4$
Procedimiento
La curva está dada por una circunferencia con $r=2$ por tanto parametrizamos como
$x=2 cost ..... dx=-2sent dt$ $y=2 sent ..... dy=2cost dt$
$ 0\leq t\leq\pi $
Sustituyendo en la integral se tiene que
$ \int_{c} (2cost)^2+(2sent)^2 (-2sent dt)-2(2cost)(2sent)(2cost dt) $
$ \int_{0}^{\pi} (4cos^{2}t+4sen^{2}t)(-2sent)dt-(8cost sent)(2cost)dt $
$ \int_{0}^{\pi} (-8 cos^{2}t sent-8 sen^{3}t)dt-(8 cos^{2}t sent)dt $
$ \int_{0}^{\pi} (-16 cos^{2}t sent-8 sen^{3}t)dt $
$ -16\int_{0}^{\pi} cos^{2}t sent dt-8\int_{0}^{\pi} sen^{3}t dt $
Para la primera integral se toma un cambio de variable $u=cost$ $du=-sent dt$
Y para la segunda integral se toma en cuenta la siguiente formulita $\int sen^{m}t dt=-\frac{cost sen^{m-1}t}{m}+\frac{m-1}{m} $
Por tanto la integral es igual a
$ \frac{16}{3}cos^{3}t-\frac{2}{3}(cos(3t)-9 cost) |_{0}^{\pi} $
$ \frac{16}{3}cos^{3}t+6 cost-\frac{2}{3}cos(3t) |_{0}^{\pi} $
$ \frac{2}{3}(15 cost+cos3t) |_{0}^{\pi} $
Solución
$ \therefore \int_{c}(x^{2}+y^{2})dx-2xydy=-\frac{64}{3} $
Samantha Martinez (discusión) 00:37 14 jun 2015 (CDT)
Ejercicio 28
En el problema evalué
\begin{equation*} \oint_{c}(x^{2}+y^{2})dx-2xydy \end{equation*}
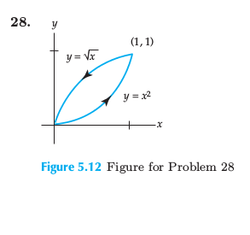
sobre la curva cerrada, mostrada en la figura (PONER FIGURA)
Procedimiento
Como vemos la función es una curva suave por trozos, procederemos a calcular la integral de linea pero haciéndolo sobre trayectorias suaves.
Calculando primero para la primera curva suave tenemos que es la curva definida de la función , que va desde el punto (0,0) al punto (1,1), por lo que tomaremos a x como el parámetro de la curva, con , por lo que tenemos que
$y= x^2$ ; $dy = 2x dx$
Por lo que la integral de linea para la curva $c_{1}$ es
$\int_{c_1}(x^{2}+y^{2})dx-2xydy = \int_{c_1} (x^{2}+(x^2)^{2})dx-2x(x^2)(2x dx)= \int_{c_1} (x^2 - 3 x^4) dx= \intop_{0}^{1} (x^2 - 3 x^4) dx = \frac{x^3}{3}- \frac{3x^5}{5}= \frac{1}{3}- \frac{3}{5}= \frac{-4}{15}$
Ahora para la segunda curva tenemos que cumple con la función , que va desde el punto (1,1) al (0,0), por lo que tomaremos a y como el parámetro, con , en donde
$y^2= x$ además de que $2y dy= dx$
Por lo que tenemos que la integral de linea para esta curva cumple que
$\int_{c_2}(x^{2}+y^{2})dx-2(xy)dy= \int_{c_2}((y^2)^{2}+y^{2})(2 y dy)-2(y^2)ydy= \intop_{1}^{0} 2y^5 dy$
Dado que
$\int_{b}^{a}du=-\int_{a}^{b}du$
$-\intop_{0}^{1} 2y^5 dy= -[\frac{2y^6}{6}]^{1}_{0}= -\frac{2}{6}$
Procedimiento
Por lo que al sumar las dos partes tenemos que
$\oint_{c}(x^{2}+y^{2})dx-2xydy = \int_{c_1}(x^{2}+y^{2})dx-2xydy + \int_{c_2}(x^{2}+y^{2})dx-2xydy = -\frac{4}{15} -\frac{2}{6}= -\frac{3}{5}$
Pablo (discusión) 14:31 14 jun 2015 (CDT)
Ejercicio 30
Evalúa: $\oint_{C}{x^2y^3dx-xy^2dy}$ en la curva cerrada dada.
Procedimiento
Sea $\Gamma$ la trayectoria cerrada compuesta por los segmentos de recta: $\overline{OA},\overline{AB}, \overline{BO}$, donde: $O(0,0), A(2,4), B(0,4)$. Sean: $\Gamma_1$ la trayectoria $\overline{OA}$, $\Gamma_2$ la trayectoria $\overline{AB}$, $\Gamma_3$ la trayectoria $\overline{BO}$. Entonces:
$$\oint_{C}{x^2y^3dx-xy^2dy}=\oint_{\Gamma}{x^2y^3dx-xy^2dy}=\int_{\Gamma_1}{x^2y^3dx-xy^2dy}+\int_{\Gamma_2}{x^2y^3dx-xy^2dy}+\int_{\Gamma_3}{x^2y^3dx-xy^2dy}$$
Para $\Gamma_1$: el segmento de recta recorrido es el $\overline{OA}$, con $y=2x \Rightarrow dy=2dx$, además $x\in[0,2]$. Entonces:
$\int_{\Gamma_1}{x^2y^3dx-xy^2dy}=\int_{0}^{2}{x^2(2x)^3dx-x(2x)^2(2dx)}=\int_{0}^{2}{(8x^5-8x^3)dx}=8(\tfrac{1}{6} x^6 \Big|_0^2 \ - \tfrac{1}{4} x^4 \Big|_0^2 \ )=8(\frac{2^6}{6}-\frac{2^4}{4})$
Para $\Gamma_2$: el segmento de recta recorrido es el $\overline{AB}$, con $y=4 \Rightarrow dy=0$, además $x=x\Rightarrow dx=dx$ ,$x\in[0,2]$, entonces:
$\int_{\Gamma_2}{x^2y^3dx-xy^2dy}=\int_{2}^{0}{x^2(4)^3dx}=\int_{2}^{0}{64x^2dx}=64(\tfrac{1}{3} x^3 \Big|_2^0 \ )= -64(\tfrac{1}{3} x^3 \Big|_0^2 \ )=-64(\frac{2^3}{3})$
Para $\Gamma_3$: el segmento de recta recorrido es el $\overline{BO}$, con $x=0 \Rightarrow dx=0$, además $y=y\Rightarrow dy=dy$, $y\in[0,4]$, entonces:
$\int_{\Gamma_3}{x^2y^3dx-xy^2dy}=\int_{4}^{0}{(0)^2y^3(0)-(0)y^2(0)}=0$\\
Por consiguiente:
$$\oint_{C}{x^2y^3dx-xy^2dy}=\oint_{\Gamma}{x^2y^3dx-xy^2dy}=8(\frac{2^6}{6}-\frac{2^4}{4}) -64(\frac{2^3}{3})=8(\frac{64-24}{6})-\frac{8^3}{3}=\frac{8}{3}(20-64)=-\frac{352}{3}$$
Solución
Por lo tanto : $\oint_{C}{x^2y^3dx-xy^2dy}=-\frac{352}{3}$
Realizado por: Alan Daniel Barrón Posadas (discusión) 14:45 16 jun 2015 (CDT)
Ejercicio 31
evalué $\oint_{c}(x^{2}-y^{2})ds$, donde $C$ esta dada por $x=5\cos t,y=5\sin t,0\leq t\leq2\pi$
Procedimiento
por definición
$\int_{c}G(x,y)ds=\int_{b}^{a}G(x,f(x))\sqrt{1+\left[f'(x)\right]^{2}}dx$
como
$ds=\sqrt{1+\left[f'(x)\right]^{2}}dx$
$\frac{dx}{dt}=-5\sin t\Longleftrightarrow dx=-5\sin tdt$
$\frac{dy}{dt}=5\cos t$
$dy=f'(x)dx\Longleftrightarrow\frac{dy}{dx}=f'(x)$
$f'(x)=\frac{5\cos t}{-5\sin t}=-\arctan t$
$ds=\sqrt{1+\left[-\arctan t\right]^{2}}(-5\sin t)dt$
entonces
$\oint_{c}(x^{2}-y^{2})ds=\int_{0}^{2\pi}(25\cos^{2}t-25\sin^{2}t)\sqrt{1+\left[-\arctan t\right]^{2}}(-5\sin t)dt=25\int_{0}^{2\pi}(-5\sin t)(\cos^{2}t-\sin^{2}t)\sqrt{1+\arctan^{2}t}dt=25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt$
$25\int_{0}^{2\pi}(-5\sin t)(\cos2t)\sqrt{1+\arctan^{2}t}dt=\frac{5}{2}\cos t\sqrt{\sec^{2}t}(\cos2t)-2\log(cost)\mid_{0}^{2\pi}=$
$=\frac{5}{2}\cos2\pi\sqrt{\sec^{2}2\pi}(\cos4\pi)-2\log(cos2\pi)-\frac{5}{2}\cos0\sqrt{\sec^{2}0}(\cos20)+2\log(cos0)=1-1=0$
Solución
así
$\oint_{c}(x^{2}-y^{2})ds=0$ donde $C$ esta dada por $x=5\cos t,y=5\sin t,0\leq t\leq2\pi$
Realizado por:Francisco Medina Albino (discusión) 22:53 11 jun 2015 (CDT)
Ejercicio 32
Evaluar $\int_{-c}ydx-xdy$ donde c esta dado por $x=2cost$ , $y=3sent$ y $t\epsilon\left[0,\pi\right]$
Procedimiento
Recordemos que $\int_{-c}=-\int_{c}$ ...(1) , también que $cos^{2}t+sen^{2}t=1$
...(2)
Ahora derivamos a x respecto a t y de igual manera a y
$dx=-2sentdt$ , $dy=3costdt$
Entonces de (1) tenemos en nuestro ejercicio
$-\int ydx-xdy=\int xdy-ydx$
Sustituimos valores, tanto de las datos dados como de las derivadas
$\int2cost3costdt-3sent\left(-2sent\right)dt=\int6cos^{2}tdt+6sen^{2}tdt=6\int\left(cos^{2}t+sen^{2}t\right)dt$
y por (2) tenemos que la integral es:
$6\int dt$ pero en este ejercicio tenemos una integral definida entre cero y pi, por lo tanto poniendo los limites de integración y resolviendo la integral tenemos:
Solución
$6\int_{0}^{\pi}dt=6t\mid_{0}^{\pi}=6\pi$
Resuelto por Luis Enrique Martínez Valverde (discusión) 11:42 14 jun 2015 (CDT)
Ejercicio 33
Verificar que la integral de linea tiene el mismo valor para cada una de las siguientes parametrizaciones
$\int_{c}y^2dx+xydy$
$ C_1: x= 2t+1, y=4t+2$ $0<t<1$
Procedimiento
Derivamos $x$ y $y$ y sustituimos en la integral:
$ dx=2dt, dy=4$
$\int_{c}y^2dx+xydy=\int_{c}2(4t+2)^2dt+(2t+1)(4t+2)(4dt)=\int_{c}2(16t^2+16t+4)dt+4(8t^2+4t+4t+2)dt=$
$ =2[\frac{16}{3}t^3+8t^2+4t]_{0}^{1}+4[\dfrac{8}{3}t^3+4t^2+2t]_{0}^{1}=\frac{208}{3}$
$ C_2: x= t^2, y=2t^2$ $1<t<\sqrt{3}$
Derivamos $x$ y $y$ y sustituimos en la integral:
$ dx=2tdt, dy=4t$
$\int_{c}y^2dx+xydy=\int_{c}2t(2t^2)^2dt+(t^2)(2t^2)(4tdt)=\int_{c}(8t^5+8t^5)dt=[\frac{16}{6}]_{1}^{\sqrt{3}= \frac{208}{3}}$
$ C_3: x= lnt, y=2lnt$ $e<t<e^{3}$
Derivamos $x$ y $y$ y sustituimos en la integral:
$ dx=\frac{dt}{t}, dy=\frac{2dt}{t}$
Solución
$\int_{c}y^2dx+xydy=\int_{c}[2\ln {t}]^2\frac{dt}{t}+[\ln t][2\ln t][\dfrac{2dt}{t}= \frac{208}{3} $
Realizado por:Nancy Martínez Durán (discusión) 09:14 14 jun 2015 (CDT)
Ejercicio 35
Si $\rho (x,y)$ es la densidad de un alambre (masa por unidad de longitud), entonces la masa del alambre es $m=\int_C\rho (x,y)ds$. Determine la masa de un alambre que tiene la forma de una semicircunferencia $x=1+\cos t$, $y=\sin t$, $0\leq t\leq \pi$, si la densidad en un punto $P$ es directamente proporcional a la distancia del eje $y$.
Solución
Si $\rho (x,y)=ky$ con $k$ como la constante de proporcionalidad. La función de masa es la integral de línea de la densidad sobre la curva del alambre. En este caso el alambre tiene la forma de la semicircunferencia de radio 1 y centro en $(1,0)$ que tiene por ecuaciones paramétricas $x=1+\cos t$ $y=\sin t$. La definición de integral de línea de a lo largo de $C$ es
$\int_C G(x,y)ds=\int_a^b G(x(t),y(t))\sqrt{[x'(t)]^2+[y'(t)]^2}dt$
Con $G(x,y)=\rho (x,y)=ky$, $x'(t)=-\sin t$, $y'(t)=\cos t$ y $ds=\sqrt{(-\sin t)^2+(\cos t)^2}dt=dt$
$m=\int_C G(x,y)ds=\int_C\rho (x(t),y(t))ds=\int_a^{b}kyds=k\int_0^{\pi}\sin t dt=k(-\cos t|_0^{\pi})=k(1+1)=2k$
Por lo que la masa del alambre es $m=2k$.
Realizado por:Oscar Javier Gutierrez Varela (discusión) 19:25 11 jun 2015 (CDT)
Ejercicio 36
Las coordenadas del centro de masa de un alambre con densidad variable estan dadas por $\overline{x}=M_{y}/m\hspace{1em}y\hspace{1em}\overline{y}=M_{x}/m$ donde
\[ m={\displaystyle \int_{c}\rho(x,y)ds}\hspace{1em},\hspace{1em}M_{x}={\displaystyle \int_{c}y\rho(x,y)ds\hspace{1em},\hspace{1em}M_{y}={\displaystyle \int_{c}x\rho(x,y)ds}} \]
Encuentre el centro de masa del alambre en el problema 35.
Procedimiento
De acuerdo al problema 35, sabemos que la curva $c$ esta parametrizada de la siguiente manera $c=(1+\cos t,\sin t)$ con $0\leq t\leq\pi$, asi que solo es cuestion de resolver las integrales para $M_{y},\hspace{1em}y\hspace{1em}M_{x}$, asi tambien sabemos que $m=2\alpha$. y que $\rho(x,y)=\alpha y$
\[ M_{x}={\displaystyle \int_{c}y}\rho(x,y)ds={\displaystyle \int_{0}^{\pi}y(t)\rho(x(t),y(t))dt={\displaystyle \int_{0}^{\pi}\sin t\alpha\sin tdt={\displaystyle \alpha\int_{0}^{\pi}{\displaystyle \frac{(1-\cos2t)}{2}dt={\displaystyle \frac{\alpha}{2}}|_{0}^{\pi}-{\displaystyle \frac{\sin t}{4}|_{0}^{\pi}={\displaystyle \frac{\alpha\pi}{2}}}}}}} \]
\[
M_{y}={\displaystyle \int_{c}x\rho(x,y)ds={\displaystyle \int_{0}^{\pi}x(t)\rho(x(t),y(t))dt={\displaystyle \int_{0}^{\pi}(1+\cos t)\alpha\sin tdt=\alpha{\displaystyle \int_{0}^{\pi}(\sin t+\sin t\cos t)dt=\alpha\left(-\cos t|_{0}^{\pi}+{\displaystyle \frac{\sin^{2}t}{4}|_{0}^{\pi}}\right)=2\alpha}}}}
\]
Así
\[ \overline{x}={\displaystyle \frac{M_{y}}{m}={\displaystyle \frac{2\alpha}{2\alpha}=1\hspace{1em}y\hspace{1em}\overline{y}={\displaystyle \frac{M_{x}}{m}={\displaystyle \frac{\alpha\pi}{2(2\alpha)}={\displaystyle \frac{\pi}{4}}}}}} \]
Conclusión
Por lo tanto las coordenadas son $\overline{x}=1,\overline{y}={\displaystyle \frac{\pi}{4}}$
Jose Emmanuel Flores Calderón (discusión) 17:30 14 jun 2015 (CDT)
![{\displaystyle \left[{\frac {3^{4}}{4}}+{\frac {3^{3}}{3}}-3^{2}\right]-\left[{\frac {(-1)^{4}}{4}}+{\frac {(-1)^{3}}{3}}-(-1)^{2}\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ac9fb210de91423be23fd7a663bd6e128bdfef46)



![x \epsilon [0,1]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e72112e68a6c82db584143621ce4e21ab8ef3e92)

![y \epsilon [1,0]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2d442eff57da6c63b1f0b7e7837e951f5bae59bf)