Diferencia entre revisiones de «Compleja:Zill-Cap3.4»
Sin resumen de edición |
|||
| (No se muestran 21 ediciones intermedias del mismo usuario) | |||
| Línea 266: | Línea 266: | ||
$\left(-\frac{\ | $\left(-\frac{\partial u / \partial x}{\partial u / \partial y} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)$ = $\left(\frac{\partial v / \partial y}{\partial v / \partial x} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)=-1$ | ||
| Línea 279: | Línea 279: | ||
$\left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)= \left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)=-1$ | $\left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)= \left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)=-1$ | ||
Por lo que se concluye que la familia de curvas son ortogonales. | |||
---- | ---- | ||
Realizado por:[[Usuario:Nancy Martínez Durán|Nancy Martínez Durán]] ([[Usuario discusión:Nancy Martínez Durán|discusión]]) 03:10 5 jun 2015 (CDT) | Realizado por:[[Usuario:Nancy Martínez Durán|Nancy Martínez Durán]] ([[Usuario discusión:Nancy Martínez Durán|discusión]]) 03:10 5 jun 2015 (CDT) | ||
| Línea 284: | Línea 285: | ||
===Ejercicio 7=== | ===Ejercicio 7=== | ||
La | La función analítica dada <math>f(z)= u+iv</math> define dos familias de curvas de nivel de <math>u(x,y)=c_1</math> y <math>v(x,y)=c_2</math>. Use derivación implícita para calcular <math>\frac{dy}{dx}</math> para cada familia y compruebe que las familias son ortogonales. | ||
<math>f(z)= e^{-x}cos y + ie^{-x}sen y</math> | <math>f(z)= e^{-x}cos y + ie^{-x}sen y</math> | ||
'''Procedimiento''' | |||
Ahora identificamos a : | Ahora identificamos a : | ||
| Línea 301: | Línea 304: | ||
<math>\frac{\partial v}{\partial x}=-e^{-x}sen y ; \frac{\partial v}{\partial y}=e^{-x}cos y</math> | <math>\frac{\partial v}{\partial x}=-e^{-x}sen y ; \frac{\partial v}{\partial y}=e^{-x}cos y</math> | ||
Ahora bien derivando | Ahora bien derivando implícitamente: | ||
<math>\frac{dy}{dx}=-\frac{-e^{-x}cos y }{-e^{-x}sen y}=-\frac{\frac{\partial u}{\partial x}}{ \frac{\partial u}{\partial y}}=-\frac{e^{-x}cos y }{e^{-x}sen y }</math> | <math>\frac{dy}{dx}=-\frac{-e^{-x}cos y }{-e^{-x}sen y}=-\frac{\frac{\partial u}{\partial x}}{ \frac{\partial u}{\partial y}}=-\frac{e^{-x}cos y }{e^{-x}sen y }</math> | ||
| Línea 311: | Línea 314: | ||
<math>(-\frac{\frac{\partial u}{\partial x}}{ \frac{\partial u}{\partial y}})(-\frac{\frac{\partial v}{\partial x}}{ \frac{\partial v}{\partial y}})=(\frac{\frac{\partial v}{\partial y}}{ \frac{\partial v}{\partial v}})(-\frac{\frac{\partial v}{\partial x}}{ \frac{\partial v}{\partial y}})=-1</math> | <math>(-\frac{\frac{\partial u}{\partial x}}{ \frac{\partial u}{\partial y}})(-\frac{\frac{\partial v}{\partial x}}{ \frac{\partial v}{\partial y}})=(\frac{\frac{\partial v}{\partial y}}{ \frac{\partial v}{\partial v}})(-\frac{\frac{\partial v}{\partial x}}{ \frac{\partial v}{\partial y}})=-1</math> | ||
'''Conclusión''' | |||
sustituyendo: | sustituyendo: | ||
| Línea 318: | Línea 322: | ||
Por lo cual son ortogonales. | Por lo cual son ortogonales. | ||
---- | ---- | ||
Realizado por: [[Usuario:Anahi Limas|Anahi Limas]] ([[Usuario discusión:Anahi Limas|discusión]]) 12:29 5 jun 2015 (CDT) | |||
---- | |||
=== Ejercicio 8 === | === Ejercicio 8 === | ||
La | La función analítica dada <math>f(z)= u+iv</math> define dos familias de curvas de nivel de <math>u(x,y)=c_1</math> y <math>v(x,y)=c_2</math>. Use derivación implícita para calcular <math>\frac{dy}{dx}</math> para cada familia y compruebe que las familias son ortogonales. | ||
: <math> f(z)=x+\frac{x}{x^{2}+y^{2}}+i\left(y-\frac{y}{x^{2}+y^{2}}\right) | : <math> f(z)=x+\frac{x}{x^{2}+y^{2}}+i\left(y-\frac{y}{x^{2}+y^{2}}\right) | ||
</math> | </math> | ||
'''Solución''' | '''Solución''' | ||
Se tiene que | Se tiene que | ||
| Línea 374: | Línea 380: | ||
Por lo tanto, sustituyendo y simplificando en el producto de la derivación implícita, el cual se desea comprobar la otorgonalida es | Por lo tanto, sustituyendo y simplificando en el producto de la derivación implícita, el cual se desea comprobar la otorgonalida es | ||
'''Conclusión''' | |||
::<math> -\frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}}*\frac{\frac{\partial v}{\partial x}}{\frac{\partial v}{\partial y}}=-\frac{1+\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}*\frac{1-\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}=-\frac{1-\frac{\left(x^{2}-y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}*\frac{1-\frac{\left(x^{2}-y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}=-1. | ::<math> -\frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}}*\frac{\frac{\partial v}{\partial x}}{\frac{\partial v}{\partial y}}=-\frac{1+\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}*\frac{1-\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}=-\frac{1-\frac{\left(x^{2}-y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}*\frac{1-\frac{\left(x^{2}-y^{2}\right)}{\left(x^{2}+y^{2}\right)^{2}}}{-\frac{2xy}{\left(x^{2}+y^{2}\right)^{2}}}=-1. | ||
| Línea 380: | Línea 388: | ||
Con esto probamos que las familias son ortogonales. | Con esto probamos que las familias son ortogonales. | ||
--[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 23:50 5 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 23:50 5 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 386: | Línea 395: | ||
===Ejercicio 9=== | ===Ejercicio 9=== | ||
'''La | '''La función dada de valor real $\phi$ es el potencial de velocidad para un fluido incomprensible e irrotacional, encuentre el campo de velocidad $\vec{F}$ suponga un dominio adecuado $D$ del plano''' | ||
<math>\phi(x,y)=\frac{x}{x^{2}+y^{2}}</math> | <math>\phi(x,y)=\frac{x}{x^{2}+y^{2}}</math> | ||
'''Procedimiento''' | |||
Para poder encontrar el campo | Para poder encontrar el campo vectorial $\vec{F}$ sera necesario recordar que; | ||
\[\vec{F}=\nabla\phi\] | \[\vec{F}=\nabla\phi\] | ||
Por lo cual, solo basta encontrar el | Por lo cual, solo basta encontrar el gradiente del potencial $\phi$ | ||
así tendremos; | |||
\[\nabla\phi(x,y)=(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}) \] | \[\nabla\phi(x,y)=(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}) \] | ||
| Línea 405: | Línea 415: | ||
notar que el dominio $D$ es el | notar que el dominio $D$ es el conjunto de las {$x$,$y$} tal que $x^{2}+y^{2} ≠ 0$ | ||
''' | '''Conclusión''' | ||
-- | '''Así concluimos que \[\vec{F}=\nabla\phi=(\frac{y^{2}-x^{2}}{(x^{2}+y^{2})^{2}},-\frac{2xy}{(x^{2}+y^{2})^{2}})\]''' | ||
---- | ---- | ||
Realizado por: [[Usuario:Cristian Alfredo Ruiz Castro|Cristian Alfredo Ruiz Castro]] ([[Usuario discusión:Cristian Alfredo Ruiz Castro|discusión]]) 17:24 5 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 10=== | ===Ejercicio 10=== | ||
<math>\phi (x,y)= \frac{1}{2} A log_e (x^2 + (y+1)^2) , A> 0</math> | La función dada de valor real $\phi$ es el potencial de velocidad para un fluido incomprensible e irrotacional, encuentre el campo de velocidad $\vec{F}$ suponga un dominio adecuado $D$ del plano | ||
<math>\phi (x,y)= \frac{1}{2} A \log_e (x^2 + (y+1)^2) , A> 0</math> | |||
'''Procedimiento''' | |||
El campo vectorial esta dado por | El campo vectorial esta dado por | ||
| Línea 439: | Línea 457: | ||
Con A>0 y con | Con A>0 y con $x^2+(y+1)^2 ≠ 0 $ | ||
--[[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 23:30 5 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 23:30 5 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 450: | Línea 469: | ||
'''Procedimiento''' | |||
| Línea 483: | Línea 502: | ||
dado que satisface la | dado que satisface la ecuación de Laplace en $D$, $\phi$ es una función armónica. | ||
| Línea 492: | Línea 511: | ||
Integrando la primera | Integrando la primera ecuación tenemos | ||
| Línea 500: | Línea 519: | ||
$\psi(y)=-50y$ | $\psi(y)=-50y$ | ||
'''Conclusión''' | |||
La función potencial compleja para el problema de Dirichlet es | La función potencial compleja para el problema de Dirichlet es | ||
| Línea 509: | Línea 528: | ||
$Ω(z)=-50x+50-50yi$ | $Ω(z)=-50x+50-50yi$ | ||
---- | ---- | ||
Realizado por: [[Usuario:Miguel Medina Armendariz|Miguel Medina Armendariz]] ([[Usuario discusión:Miguel Medina Armendariz|discusión]]) 23:16 3 jun 2015 (CDT) | |||
---- | |||
===Ejercicio 12=== | ===Ejercicio 12=== | ||
| Línea 525: | Línea 543: | ||
c)Dibujar las curvas equipotenciales y las líneas de fuerzas | c)Dibujar las curvas equipotenciales y las líneas de fuerzas | ||
'''Procedimiento''' | |||
Para determinar el potencial | Para determinar el potencial necesitamos saber que la función dada | ||
cumpla con la ecuación de Laplace | cumpla con la ecuación de Laplace | ||
| Línea 552: | Línea 570: | ||
$\phi\left(2\right)=2c_{1}+c_{2}=20$ | $\phi\left(2\right)=2c_{1}+c_{2}=20$ | ||
Resolviendo el sistema de ecuaciones tenemos | Resolviendo el sistema de ecuaciones tenemos: | ||
$c_{1}=\frac{10}{3}$ y $c_{2}=\frac{40}{3}$ | $c_{1}=\frac{10}{3}$ y $c_{2}=\frac{40}{3}$ | ||
| Línea 585: | Línea 603: | ||
$\varOmega\left(z\right)=\left[\frac{10}{3}y+\frac{40}{3}\right]+i\left[\frac{10}{3}x\right]$ | $\varOmega\left(z\right)=\left[\frac{10}{3}y+\frac{40}{3}\right]+i\left[\frac{10}{3}x\right]$ | ||
---- | |||
Resuelto por [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 00:38 6 jun 2015 (CDT) | Resuelto por [[Usuario:Luis Enrique Martínez Valverde|Luis Enrique Martínez Valverde]] ([[Usuario discusión:Luis Enrique Martínez Valverde|discusión]]) 00:38 6 jun 2015 (CDT) | ||
| Línea 593: | Línea 611: | ||
El potencial $\phi(\theta)$ entre las dos placas de longitud infinita que forman la cuña infinita que se muestra en la figura 3.4.11 | |||
satisface la | satisface la ecuación de Laplace en coordenadas polares de la forma: | ||
| Línea 602: | Línea 620: | ||
(a) Resuelva la | (a) Resuelva la ecuación diferencial sujeta a las condiciones frontera | ||
de $\phi(\pi/4)=30$ y $\phi(0)=0$ | de $\phi(\pi/4)=30$ y $\phi(0)=0$ | ||
'''Inciso a''' | |||
-Resolviendo la | -Resolviendo la ecuación diferencial se obtiene que: | ||
\[ | \[ | ||
| Línea 642: | Línea 661: | ||
'''Inciso b''' | |||
(b) Determine el potencial complejo $\Omega(z)$ | (b) Determine el potencial complejo $\Omega(z)$ | ||
| Línea 696: | Línea 716: | ||
\] | \] | ||
'''Inciso c''' | |||
(c) De las curvas equipotenciales y las lineas de fuerza | (c) De las curvas equipotenciales y las lineas de fuerza | ||
| Línea 703: | Línea 723: | ||
--[[Usuario:Fernando Vazquez V.|Fernando Vazquez V.]] ([[Usuario discusión:Fernando Vazquez V.|discusión]]) 20:21 6 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Fernando Vazquez V.|Fernando Vazquez V.]] ([[Usuario discusión:Fernando Vazquez V.|discusión]]) 20:21 6 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 710: | Línea 730: | ||
La temperatura en estado estacionario $\phi(r)$ entre dos conductores | La temperatura en estado estacionario $\phi(r)$ entre dos conductores | ||
cilíndricos satisface la ecuación de Laplace en coordenadas polares | |||
de la forma | de la forma | ||
| Línea 718: | Línea 738: | ||
'''Inciso a''' | |||
(a) Demostrar que la EDO sujeta a las dos condiciones de frontera | (a) Demostrar que la EDO sujeta a las dos condiciones de frontera | ||
$\phi(a)=k_{0}$ y $\phi(b)=k_{1}$ donde $k_{1}$ y $k_{0}$ son | $\phi(a)=k_{0}$ y $\phi(b)=k_{1}$ donde $k_{1}$ y $k_{0}$ son | ||
| Línea 727: | Línea 748: | ||
Tenemos que la EDO es del tipo Cauchy-Euler, por lo tanto proponemos | Tenemos que la EDO es del tipo Cauchy-Euler, por lo tanto proponemos | ||
una | una solución de la forma $\phi=r^{m}$, derivando y sustituyendo en | ||
la | la ecuación diferencial, tenemos lo siguiente: | ||
\[ | \[ | ||
| Línea 735: | Línea 756: | ||
La | La única solución para $m$ es que sea igual a cero. | ||
Como la EDO es de segundo orden necesitamos dos funciones linealmente | Como la EDO es de segundo orden necesitamos dos funciones linealmente | ||
independientes para formar el espacio | independientes para formar el espacio solución: | ||
\[ | \[ | ||
| Línea 745: | Línea 766: | ||
Pero como $m_{1}=m_{2}=m=0$, usamos | Pero como $m_{1}=m_{2}=m=0$, usamos variación de parámetros para | ||
encontrar la segunda | encontrar la segunda solución, la cual esta dada por: | ||
\[ | \[ | ||
| Línea 767: | Línea 788: | ||
$\phi(b)=k_{1}=A+Blnb$ | $\phi(b)=k_{1}=A+Blnb$ | ||
Despejando $A$ en la | Despejando $A$ en la ecuación (1) y sustiyudendolo en (2), tenemos | ||
lo siguiente | lo siguiente | ||
| Línea 775: | Línea 796: | ||
Despejando $B$en (1) y sustituyendo en 2 e introduciendo el valor | |||
que encontramos para $B$ tenemos lo siguiente | que encontramos para $B$ tenemos lo siguiente | ||
| Línea 782: | Línea 803: | ||
\] | \] | ||
---- | ---- | ||
Realizado por:[[Usuario:Jose Emmanuel Flores Calderón|Jose Emmanuel Flores Calderón]] ([[Usuario discusión:Jose Emmanuel Flores Calderón|discusión]]) 22:06 5 jun 2015 (CDT) | |||
---- | |||
$ r^2 \frac{d^2 φ}{dr^2}+r \frac{d φ}{dr}=0 $ | |||
'''Inciso a''' | |||
A) Mostrar que una solución de la ecuación diferencial sujeta a las condiciones de contorno $φ(A) = k_{0}$ y $φ(B) = k_{1}$, donde $k_{0}$ y $k_{1}$ son constantes potenciales, está dada por $φ(r) = a + log_{e}r + B$, donde: | |||
$ A=\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} $ | |||
$ B=\frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} $ | |||
Sustituimos las condiciones iniciales en $ φ(r)$ | |||
$ φ(r)= \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} + log_{e}r + \frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} $ | |||
donde $φ(r)= φ $ | |||
Sacando derivadas parciales | |||
$\frac{\partial φ}{\partial r} = \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} =A \frac{1}{r} $ | |||
$ \frac{\partial^{2} φ}{\partial r} = - \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r^2} = -A \frac{1}{r^2} $ | |||
Sustituyendo en la ecuación de Laplace-Euler | |||
$ r^2 \frac{d^2 φ}{dr^2}+r \frac{d φ}{dr}=0 $ | |||
$ r^2 (-\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r^2}) + r (\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} =0 $ | |||
$ \therefore -\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} + \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} =0 $ | |||
$\therefore φ(r)$ es solución a la ecuación de Laplace-Euler. | |||
'''B) Encuentre el potencial complejo''' | |||
'''Inciso b''' | |||
Tomamos las ecuaciones de C-R | |||
$\frac{\partial φ}{\partial r}= \frac{\partial φ*}{\partial r'} ---- (1)$ | |||
$\frac{\partial φ}{\partial r'}=- \frac{\partial φ*}{\partial r}$ | |||
Donde $φ*$ es el potencial complejo | |||
De la ecuación (1) | |||
$\frac{\partial φ}{\partial r}=\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r}= \frac{\partial φ*}{\partial r'} $ | |||
Integrando | |||
$ \int{\partial φ}= \int{ A \frac{1}{r} dr'}$ | |||
$ φ= A \frac{1}{r} r' + h(r) | |||
$ h(r)=Cte.=0 $ | |||
$ φ= A \frac{1}{r} r' $ | |||
$\therefore W(r,r')= φ + i φ* $ | |||
$\therefore W(r,r')= A log_{e} r + B + i(A \frac{1}{r} r') $ | |||
$\therefore W(r,r')= \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} log_{e} r + \frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} + i(\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} r') $ | |||
---- | |||
Elaborado por --[[Usuario:Samantha Martinez|Samantha Martinez]] ([[Usuario discusión:Samantha Martinez|discusión]]) 22:15 05 de Junio 2015 (CDT) | |||
---- | |||
===Ejercicio 15=== | ===Ejercicio 15=== | ||
| Línea 791: | Línea 878: | ||
'''Sol.''' Si $z=x+iy$ | '''Sol.''' | ||
Si $z=x+iy$ | |||
| Línea 805: | Línea 894: | ||
Y es fácil observar que la curva $v(x,y)$ es una circunferencia de radio 1 centrada en el origen. | Y es fácil observar que la curva $v(x,y)$ es una circunferencia de radio 1 centrada en el origen. | ||
[[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 20:21 1 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Oscar Javier Gutierrez Varela|Oscar Javier Gutierrez Varela]] ([[Usuario discusión:Oscar Javier Gutierrez Varela|discusión]]) 20:21 1 jun 2015 (CDT) | |||
---- | ---- | ||
===Ejercicio 16=== | ===Ejercicio 16=== | ||
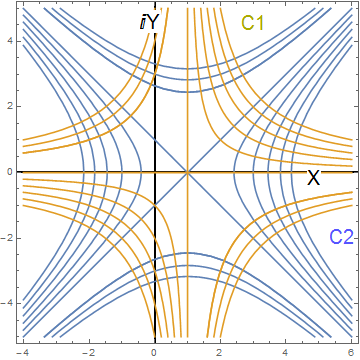
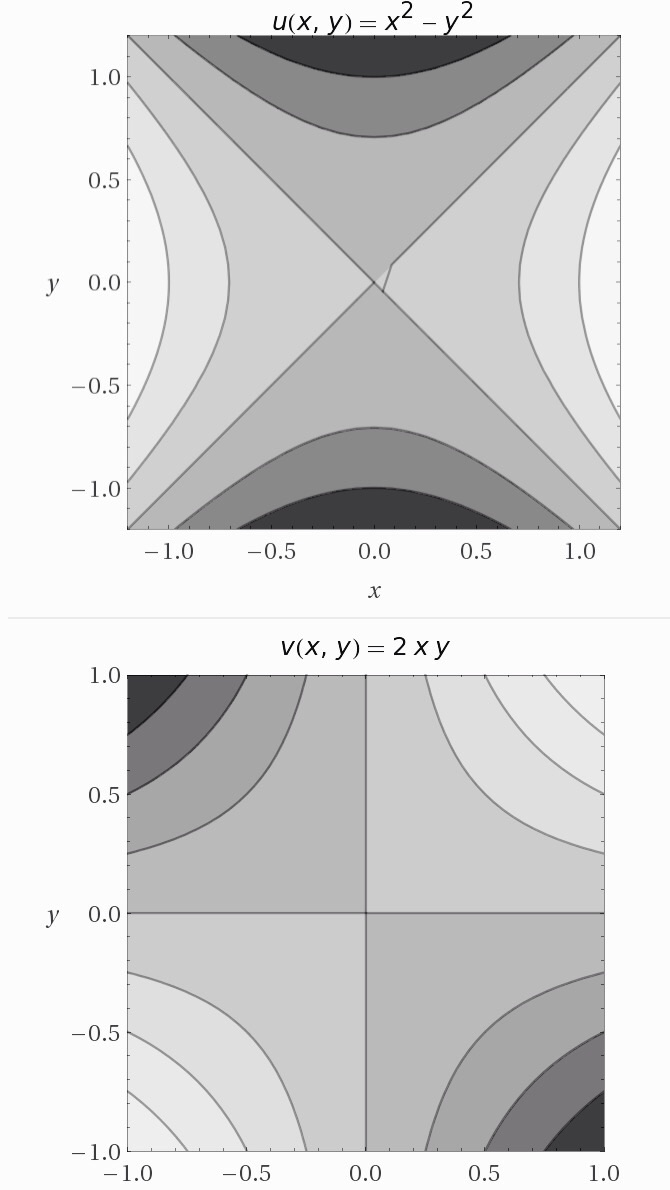
Las curvas de nivel de $u(x,y) = x^{2}-y^{2}$ y la | Las curvas de nivel de $u(x,y) = x^{2}-y^{2}$ y la ecuación $v(x,y)= 2xy$ Analizadas en el ejemplo 1 se intersectan z=0. Dibuje las curvas de nivel que se intersectan en z=0. Explique por que estas curvas de nivel no son ortogonales. | ||
'''Gráficas''' | |||
[[Archivo:Image.jpg]] | [[Archivo:Image.jpg]] | ||
| Línea 818: | Línea 909: | ||
--[[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 23:05 6 jun 2015 (CDT)Esther Sarai | ---- | ||
Realizado por: [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 23:05 6 jun 2015 (CDT)Esther Sarai | |||
---- | |||
===Ejercicio 17=== | ===Ejercicio 17=== | ||
| Línea 859: | Línea 952: | ||
en los que $f'(z_{0})\neq0$ | en los que $f'(z_{0})\neq0$ | ||
--[[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 00:48 5 jun 2015 (CDT) | ---- | ||
Realizado por: [[Usuario:Francisco Medina Albino|Francisco Medina Albino]] ([[Usuario discusión:Francisco Medina Albino|discusión]]) 00:48 5 jun 2015 (CDT) | |||
---- | ---- | ||
| Línea 868: | Línea 962: | ||
$f(x)=u(x,y)+iv(x,y)$ necesariamente analítica en D?''' | $f(x)=u(x,y)+iv(x,y)$ necesariamente analítica en D?''' | ||
'''Procedimiento''' | |||
Sabemos que si tenemos una función $f(x)=u(x,y)+iv(x,y)$ que es analítica | Sabemos que si tenemos una función $f(x)=u(x,y)+iv(x,y)$ que es analítica | ||
| Línea 919: | Línea 1014: | ||
y que $(\frac{\partial v}{\partial x})=(\frac{\partial v}{\partial y})$ | y que $(\frac{\partial v}{\partial x})=(\frac{\partial v}{\partial y})$ | ||
pero esto no cumple con la igualdad (1), por lo que es irrelevante. | pero esto no cumple con la igualdad (1), por lo que es irrelevante. | ||
'''Conclusión''' | |||
Pero no podríamos decir mucho acerca de su continuidad aunque si sea | Pero no podríamos decir mucho acerca de su continuidad aunque si sea | ||
| Línea 926: | Línea 1024: | ||
y analiticidad entre funciones. No es suficiente para decir que así | y analiticidad entre funciones. No es suficiente para decir que así | ||
sea. | sea. | ||
---- | ---- | ||
Realizado por: [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 21:49 7 jun 2015 (CDT) | |||
---- | ---- | ||
Revisión actual - 04:38 10 mar 2023
Ejercicios del capítulo 3, sección 4 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.
Sección 3.4
Ejercicio 1
Identifique las dos familias de curvas de nivel definidas por la función analítica f dada. A mano, dibuje dos curvas de cada familia en los mismos ejes coordenados
$f(z)=2iz-3+i$
Procedimiento
tomamos en cuenta que $z=x+iy$ ,sustituimos, desarrollamos y simplificamos
$2i(x+iy)-3+i=2ix+2yi^{2}-3-i=(-2y-3)+i(2x+1)$
$u(x,y)=-2y-3$
$v(x,y)=2x+1$
por lo tanto nuestras familias de curvas de nivel parten de esto
$c_{1}=-2y-3$
$c_{2}=2x+1$
Gráficas
Para dos puntos por ejemplo:
$z_0=1+i$ $z_1=2+2i$
$-2y-3=-5$ $-2y-3=-7$
en color azul
$2x+1=3$ $2x+1=5$
en color rojo
Realizado por: Juan Daniel Rivera Bautista (discusión) 14:34 3 jun 2015 (CDT)
Ejercicio 2
Identifique las dos familias de curvas de nivel definidas por la función analítica f dada. A mano, dibuje dos curvas de cada familia en los mismos ejes coordenados
Procedimiento
\[ f(z)=(z-1)^2 \]
\[ f(z)=f(x+iy)=\left[(x+iy)-1\right]^2=(x-1+iy)^2=(x-1)^2+2(x-1)(iy)+(iy)^2 \]
\[ =(x-1)^2+2(ixy-iy)-y^2=(x-1)^2-y^2+2iy(x-1) \]
Recordemos que $f(z)=f(x+iy)=u(x,y)+iv(x,y)$, entonces:
\[ u(x,y)=(x-1)^2-y^2 \;\;\;\; y \;\;\;\; v(x,y)=2y(x-1) \]
Y por ende familias de curvas de nivel parten de:
\[ c_1=(x-1)^2-y^2 \;\;\;\; y \;\;\;\; c_2=2y(x-1) \]
Para visualizar mejor como son estas curvas dividimos entre $c_1$ la primera expresión y despejamos $y$ de la segunda.
\[ 1=\left(\frac{x-1}{\sqrt {c_1}}\right)^2-\left(\frac{y}{\sqrt {c_1}}\right)^2\;\;\;\; y \;\;\;\; y=\frac{c_2}{2(x-1)} \]
Haciendo $k_1=\sqrt {c_1}$ y $k_2=\frac{c_2}{2}$, quedando así:
\[ 1=\left(\frac{x-1}{k_1}\right)^2-\left(\frac{y}{k_1}\right)^2\;\;\;\; y \;\;\;\; y=\frac{k_2}{x-1} \]
Ahora resulta evidente que la primer familia de curvas corresponde a hipérbolas equiláteras centradas en (1,0) que aumentan de tamaño con $k_1$, cuando $k_1$ es negativa son verticales y cuando es positiva horizontales. En cero colapsa en las asíntotas de estas hipérbolas.
La segunda familia corresponde también a hipérbolas equiláteras centradas en (1,0) que aumentan de tamaño con $k_1$, pero estas están rotadas $\pi/20$.
A continuación se muestran:
Gráficas
- NOTA: Pese a que el ejercicio pide que se bosquejen a mano, opto por subirlas usando mathematica
Realizado por:Tlacaelel Cruz (discusión) 20:57 4 jun 2015 (CDT)
Ejercicio 3
Identifique las dos familias de curvas de nivel definidas por la función analítica f dada. A mano, dibuje dos curvas de cada familia en los mismos ejes coordenados
$f\left(z\right)=\frac{1}{z}$
Procedimiento
viendo el numero complejo z como
$z=x+iy$
desarrollamos a f$\left(z\right)$
$f\left(z\right)=\frac{1}{x+iy}=\frac{1}{x+iy}\left(\frac{x-iy}{x-iy}\right)=\frac{x-iy}{x^{2}+y^{2}}$
poniendo f$\left(z\right)$en funcion de $u\left(x,y\right)+iv\left(x,y\right)$
$U\left(x,y\right)=\frac{x}{x^{2}+y^{2}}$
$V\left(x,y\right)=\frac{-y}{x^{2}+y^{2}}$
por tanto nuestras familias de curvas de nivel quedan
$C_{1}=\frac{x}{x^{2}+y^{2}}$
$C_{2}=\frac{-y}{x^{2}+y^{2}}$
Gráficas
Para dos puntos por ejemplo:
$z_0=1+i$
$z_1=2+2i$
Realizado por: Martin Flores Molina (discusión) 19:05 21 mayo 2015 (CDT)
Ejercicio 4
Identificar a las dos familias de curvas de nivel definidas por función analítica $f$. A mano, dibujar dos curvas de cada familia en la misma coordenada ejes
$f(z)= z + \frac{1}{z}$
Sabemos que $z = x + iy$, entonces sustituyendo en la función $F$ tenemos:
$f(z) = (x+iy) + \frac{1}{x+iy} = \frac{(x+iy)^2 + 1}{x+iy} = \frac{(x^2 - y^2 + 1) + 2ixy}{x+iy} = \frac{(x^2 - y^2 + 1) + 2ixy}{x+iy} .\frac{x-iy}{x-iy}$
$f(z) = \frac{(x^3 - xy^2 + x + 2xy^2) + i(x^2 y + y^3)}{x^2 + y^2}$
Como sabemos podemos ver alas función $f$ como $f(z)=u(x,y)+iv(x,y)$, entonces tendíamos que:
$u(x,y)=\frac{(x^3 - xy^2 + x + 2xy^2)}{x^2 + y^2}$
$v(x,y)=\frac{(x^2 y + y^3)}{x^2 + y^2}$
De estas ecuaciones podemos decir que las familias de curvas son:
$c_{1}=\frac{(x^3 - xy^2 + x + 2xy^2)}{x^2 + y^2}$
$c_{2}=\frac{(x^2 y + y^3)}{x^2 + y^2}$
Angelina Nohemi Mendoza Tavera (discusión) 15:46 4 jun 2015 (CDT)
Ejercicio 5
La función analítica dada $f(z)= u+iv$ define dos familias de curvas de nivel de $u(x,y)= c_{1}$ y $v(x,y)= c_{2}$ Primero use derivación implícita para calcular $dy/dx$ para cada familia y compruebe que las familias son ortogonales.
$f(z)= x-2x^2+2y^2+ i(y-4xy)$
Procedimiento
Identificamos $u(x,y)= x-2x^2+2y^2$ y $v(x,y)=y-4xy$
Para esta función las familias de las curva de nivel $x-2x^2+2y^2=c_{1}$ y $y-4xy=c_{2}$ son dos familias de
Para probar que $L_{1}$ y $L_{2}$ (las rectas tangentes a las curvas de nivel) son perpendiculares en $z_{0}$ demostramos que la pendiente de una tangente es el recíproco negativo de la pendiente de la otra, demostrando que el producto de las dos pendientes es -1.
Derivando a $u(x,y)=u_{0}$ y $v(x,y)=v_{0}$
$\frac{dy}{dx}= -\frac{1-4x}{4y}$ = $-\frac{\partial u / \partial x}{\partial u / \partial y}$ , $\frac{dy}{dx}= -\frac{-4y}{1-4x}$= $-\frac{\partial v / \partial x}{\partial v / \partial y}$ ...(1)
En $\left(x_{0},y_{0}\right)$ vemos de (1), las ecuaciones de Cauchy-Reimann $u_{x}=v_{y}$ , $u_{y}=-v_{x}$ y de $f'(z_{0})\neq0$ , que el producto de la dos funciones pendiente es
$\left(-\frac{\partial u / \partial x}{\partial u / \partial y} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)$ = $\left(\frac{\partial v / \partial y}{\partial v / \partial x} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)$
Conclusión
Sustituyendo:
$\left(-\frac{1-4x}{4y}\right) \left(-\frac{-4y}{1-4x}\right)= \left(\frac{1-4x}{-4y}\right) \left(-\frac{-4y}{1-4x}\right)=-1$
Por lo que se concluye que la familia de curvas son ortogonales.
Realizado por: Emmanuell Castro Flores (discusión) 22:51 4 jun 2015 (CDT)
Ejercicio 6
La función analítica dada $f(z)= u+iv$ define dos familias de curvas de nivel de $u(x,y)= c_{1}$ y $v(x,y)= c_{2}$ Primero use derivación implícita para calcular $dy/dx$ para cada familia y compruebe que las familias son ortogonales.
$f(z)= x^3-3xy^2+ i(3x^2y-y^3)$
Procedimiento
Identificamos $u(x,y)= x^3-3xy^2$ y $v(x,y)=3x^2y-y^3$
Entonces las familias de curvas de nivel son:
$x^3-3xy^2=c_{1}$ y $3x^2y-y^3=c_{2}$
Para probar que las rectas tangentes a las curvas de nivel son perpendiculares, debemos de tomar en cuenta las Ecuaciones de Cauchy-Riemann:
$\left(-\frac{\partial u / \partial x}{\partial u / \partial y} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)$ = $\left(\frac{\partial v / \partial y}{\partial v / \partial x} \right)$ $\left(-\frac{\partial v / \partial x}{\partial v / \partial y} \right)=-1$
Ahora derivamos $u(x,y)=u_{0}$ y $v(x,y)=v_{0}$
$\frac{dy}{dx}= -\frac{6xy}{3x^2-3y^2}$ = $-\frac{\partial u / \partial x}{\partial u / \partial y}$ , $\frac{dy}{dx}= \frac{3x^2-3y^2}{6xy}$= $-\frac{\partial v / \partial x}{\partial v / \partial y}$
Conclusión
Por lo tanto, sustituyendo las derivadas anteriores en las ecuaciones de Cauchy-Riemann, tenemos:
$\left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)= \left(\frac{6xy}{3x^2-3y^2}\right) \left(-\frac{3x^2-3y^2}{6xy}\right)=-1$
Por lo que se concluye que la familia de curvas son ortogonales.
Realizado por:Nancy Martínez Durán (discusión) 03:10 5 jun 2015 (CDT)
Ejercicio 7
La función analítica dada define dos familias de curvas de nivel de y . Use derivación implícita para calcular para cada familia y compruebe que las familias son ortogonales.
Procedimiento
Ahora identificamos a :
;
Por lo cual las familias de curvas de nivel son:
;
Derivando a y
Ahora bien derivando implícitamente:
Ahora para probar que las rectas tangentes a las curvas de nivel son perpendiculares, debemos de tomar el siguiente:
Conclusión
sustituyendo:
Por lo cual son ortogonales.
Realizado por: Anahi Limas (discusión) 12:29 5 jun 2015 (CDT)
Ejercicio 8
La función analítica dada define dos familias de curvas de nivel de y . Use derivación implícita para calcular para cada familia y compruebe que las familias son ortogonales.
Solución
Se tiene que
y el problema nos proporciona la información que
entonces; igualando la ecuación (1) con (2) se tiene
Estas son familias de curvas de nivel.
Para probar que las rectas tangentes a las curvas de nivel son perpendiculares, tomaremos las ecuaciones de Cauchy-Riemann; entonces
Por lo tanto, sustituyendo y simplificando en el producto de la derivación implícita, el cual se desea comprobar la otorgonalida es
Conclusión
Con esto probamos que las familias son ortogonales.
Realizado por: Ricardo Garcia Hernandez (discusión) 23:50 5 jun 2015 (CDT)
Ejercicio 9
La función dada de valor real $\phi$ es el potencial de velocidad para un fluido incomprensible e irrotacional, encuentre el campo de velocidad $\vec{F}$ suponga un dominio adecuado $D$ del plano
Procedimiento
Para poder encontrar el campo vectorial $\vec{F}$ sera necesario recordar que;
\[\vec{F}=\nabla\phi\]
Por lo cual, solo basta encontrar el gradiente del potencial $\phi$
así tendremos;
\[\nabla\phi(x,y)=(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}) \]
y resolviendo las respectivas derivadas, obtendremos;
\[\nabla\phi(x,y)=(\frac{y^{2}-x^{2}}{(x^{2}+y^{2})^{2}},-\frac{2xy}{(x^{2}+y^{2})^{2}}) \]
notar que el dominio $D$ es el conjunto de las {$x$,$y$} tal que $x^{2}+y^{2} ≠ 0$
Conclusión
Así concluimos que \[\vec{F}=\nabla\phi=(\frac{y^{2}-x^{2}}{(x^{2}+y^{2})^{2}},-\frac{2xy}{(x^{2}+y^{2})^{2}})\]
Realizado por: Cristian Alfredo Ruiz Castro (discusión) 17:24 5 jun 2015 (CDT)
Ejercicio 10
La función dada de valor real $\phi$ es el potencial de velocidad para un fluido incomprensible e irrotacional, encuentre el campo de velocidad $\vec{F}$ suponga un dominio adecuado $D$ del plano
Procedimiento
El campo vectorial esta dado por
\[\vec{F}=\nabla\phi\]
Por lo que encontraremos el gradiente de lo que es
\[\nabla\phi(x,y)=(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y}) \]
Obteniendo las derivadas parciales con respecto de x y de y obtenemos que
Por lo que el campo vectorial está definido como
Con A>0 y con $x^2+(y+1)^2 ≠ 0 $
Realizado por: Pablo (discusión) 23:30 5 jun 2015 (CDT)
Ejercicio 11
Determine el potencial $\phi$ si el dominio $D$ en la figura 3.4.8 se sustituye por $0<x<1$, $-\infty<y<\infty$ y los potenciales en las fronteras son $\phi(0,y)=50$, $\phi(1,y)=0$
Procedimiento
Resolvemos para
$\frac{\partial^{2}\phi}{\partial x^{2}}+\frac{\partial^{2}\phi}{\partial y^{2}}=0$, $0<x<1$, $-\infty<y<\infty$
Sujeto a $\phi(0,y)=50$, $\phi(1,y)=0$
Con esto la ecuación de Laplace se convierte en
$\frac{\partial^{2}\phi}{\partial x^{2}}=0$
Integrando dos veces se obtiene
$\phi(x)=ax+b$, con condiciones de frontera $\phi(0)=50$ y $\phi(1)=0$
debemos tener $a(0)+b=50$ y $a(1)+b=0$, respectivamente así los valores de $a$ y $b$ son
$b=50$ y $a=-b=-50$
por lo tanto tenemos que la solución del problema de Dirichlet es $\phi(x)=-50x+50$
dado que satisface la ecuación de Laplace en $D$, $\phi$ es una función armónica.
Por tanto una armónica conjugada $\psi$ se puede encontrar de la siguiente forma
$\frac{\partial\psi}{\partial y}=\frac{\partial\phi}{\partial x}=-50$ y $\frac{\partial\psi}{\partial x}=-\frac{\partial\phi}{\partial y}=0$
Integrando la primera ecuación tenemos
$\psi(y)=-50y+C$, donde $C=0$
$\psi(y)=-50y$
Conclusión
La función potencial compleja para el problema de Dirichlet es
$Ω(z)=\phi(x)+i\psi(y)$
$Ω(z)=-50x+50-50yi$
Realizado por: Miguel Medina Armendariz (discusión) 23:16 3 jun 2015 (CDT)
Ejercicio 12
a)Determinar el potencial entre las placas infinitas paralelas al eje x, si los potenciales de las fronteras son:
$\phi\left(x,-1\right)=10$ y $\phi\left(x,2\right)=20$
b)Determinar el potencial complejo
c)Dibujar las curvas equipotenciales y las líneas de fuerzas
Procedimiento
Para determinar el potencial necesitamos saber que la función dada cumpla con la ecuación de Laplace
$\frac{\partial^{2}\phi}{\partial x^{2}}+\frac{\partial^{2}\phi}{\partial y^{2}}=0$
Pero podemos reescribir esta ecuación ya que la placa no va a depender de x, entonces nos queda:
$\frac{\partial^{2}\phi}{\partial y^{2}}=0$
De hecho esta ecuación como no depende de x podemos reescribirla como una ecación diferencial ordinaria.
$\frac{d^{2}\phi}{dy^{2}}=0$
Resolviendo la ecuación diferencial ordinaria tenemos:
$\phi\left(y\right)=c_{1}y+c_{2}$
Aplicando las condiciones iniciales tenemos:
$\phi\left(-1\right)=-c_{1}+c_{2}=10$
$\phi\left(2\right)=2c_{1}+c_{2}=20$
Resolviendo el sistema de ecuaciones tenemos:
$c_{1}=\frac{10}{3}$ y $c_{2}=\frac{40}{3}$
Por lo que la solución es:
$\phi\left(x,y\right)=\frac{10}{3}y+\frac{40}{3}$...(1)
Para sacar el potencial complejo necesitamos apoyarnos de las ecuaciones de Cauchy-Riemann
$\frac{\partial\phi}{\partial x}=\frac{\partial\Psi}{\partial y}$...(1.1) y $\frac{\partial\Psi}{\partial x}=-\frac{\partial\phi}{\partial y}$...(1.2)
De (1) tenemos
$\frac{\partial\phi}{\partial x}=0=\frac{\partial\Psi}{\partial y}$
$\frac{\partial\phi}{\partial y}=\frac{10}{3}=\frac{\partial\Psi}{\partial x}$...(2)
Integrando (2) tenemos
$\Psi=\frac{10}{3}x+G\left(y\right)$
Derivamos respecto a y
$\frac{\partial\Psi}{\partial y}=\frac{\partial G}{\partial y}=0$ Por (1.1 ) Por lo tanto nuestro potencial complejo es
$\varOmega\left(z\right)=\left[\frac{10}{3}y+\frac{40}{3}\right]+i\left[\frac{10}{3}x\right]$
Resuelto por Luis Enrique Martínez Valverde (discusión) 00:38 6 jun 2015 (CDT)
Ejercicio 13
El potencial $\phi(\theta)$ entre las dos placas de longitud infinita que forman la cuña infinita que se muestra en la figura 3.4.11 satisface la ecuación de Laplace en coordenadas polares de la forma:
\[
\frac{d^{2}\phi}{d\theta^{2}}=0
\]
(a) Resuelva la ecuación diferencial sujeta a las condiciones frontera
de $\phi(\pi/4)=30$ y $\phi(0)=0$
Inciso a
-Resolviendo la ecuación diferencial se obtiene que:
\[ \phi(r,\theta)=c\theta+k \]
Evaluando las condiciones de frontera se tiene que
$\phi(\pi/4)=30=c(\pi/4)+k$
Y
$\phi(0)=0=c0+k$
Entonces:
\[ c=\frac{120}{\pi} \]
\[
k=0
\]
Sustituyendo los valores tenemos:
\[ \phi(r,\theta)=\frac{120}{\pi}\theta \]
Inciso b
(b) Determine el potencial complejo $\Omega(z)$
-Para ello nos auxiliaremos de las ecuaciones de Cauchy-Riemann en forma polar
\[ \frac{\partial\phi}{\partial r}=\frac{1}{r}\frac{\partial\psi}{\partial\theta}...(1) \]
\[
\frac{\partial\phi}{\partial\theta}=-r\frac{\partial\psi}{\partial r}...(2)
\]
Ocupando (1) y (2)
\[ \frac{\partial\phi}{\partial r}=0=\frac{1}{r}\frac{\partial\psi}{\partial\theta} \]
\[
\frac{\partial\phi}{\partial\theta}=\frac{120}{\pi}=-r\frac{\partial\psi}{\partial r}
\]
Por lo tanto
$\frac{\partial\psi}{\partial r}=-\frac{120}{\pi r}$
$\psi(r,\theta)=-\frac{120}{\pi}log_{e}r+G(\theta)$
Pero:
$\frac{\partial\phi}{\partial r}=0=\frac{1}{r}\frac{\partial\psi}{\partial\theta}=G(\theta)$
\[ \psi(r,\theta)=-\frac{120}{\pi}log_{e}r \]
Finalmente:
$\Omega(r,\theta)=\phi(r,\theta)+i\psi(r,\theta)$
\[ \Omega(r,\theta)=\frac{120}{\pi}\theta-i\frac{120}{\pi}log_{e}r \]
Inciso c
(c) De las curvas equipotenciales y las lineas de fuerza
-Para esta ultima parte sabemos que las curvas equipotenciales satisfacen que $\frac{120}{\pi}\theta=c_{1}$ y que $\frac{120}{\pi}log_{e}r=c_{2}$
Realizado por: Fernando Vazquez V. (discusión) 20:21 6 jun 2015 (CDT)
Ejercicio 14
La temperatura en estado estacionario $\phi(r)$ entre dos conductores cilíndricos satisface la ecuación de Laplace en coordenadas polares de la forma
\[ r^{2}{\displaystyle \frac{d^{2}\phi}{dr^{2}}+r{\displaystyle \frac{d\phi}{dr}=0}} \]
Inciso a
(a) Demostrar que la EDO sujeta a las dos condiciones de frontera $\phi(a)=k_{0}$ y $\phi(b)=k_{1}$ donde $k_{1}$ y $k_{0}$ son potenciales constantes, está dada por $\phi(r)=BLog_{e}r+A$
$B={\displaystyle \frac{k_{0}-k_{1}}{log_{e}(a/b)}}$
$A={\displaystyle \frac{k_{1}log_{e}a-k_{0}log_{e}b}{log_{e}(a/b)}}$
Tenemos que la EDO es del tipo Cauchy-Euler, por lo tanto proponemos una solución de la forma $\phi=r^{m}$, derivando y sustituyendo en la ecuación diferencial, tenemos lo siguiente:
\[ r^{2}(m(m-1)r^{m-2})+mrr^{m-1}=r^{m}(m^{2})=0 \]
La única solución para $m$ es que sea igual a cero.
Como la EDO es de segundo orden necesitamos dos funciones linealmente independientes para formar el espacio solución:
\[ \phi(r)=Ar^{m_{1}}+Br^{m_{2}} \]
Pero como $m_{1}=m_{2}=m=0$, usamos variación de parámetros para
encontrar la segunda solución, la cual esta dada por:
\[ \phi_{2}=r^{m}{\displaystyle \int{\displaystyle \frac{e^{-lnr}}{x^{2m}}dr}=logr} \]
Por lo tanto la solucion es de la forma
\begin{equation} \phi(r)=A+Blogr \end{equation}
\begin{equation}
\phi(a)=k_{0}=A+Bloga
\end{equation}
$\phi(b)=k_{1}=A+Blnb$
Despejando $A$ en la ecuación (1) y sustiyudendolo en (2), tenemos lo siguiente
\[ B={\displaystyle \frac{k_{1}-k_{0}}{log(a/b)}} \]
Despejando $B$en (1) y sustituyendo en 2 e introduciendo el valor
que encontramos para $B$ tenemos lo siguiente
\[ A={\displaystyle \frac{kloga-k_{0}logb}{ln(a/b)}} \]
Realizado por:Jose Emmanuel Flores Calderón (discusión) 22:06 5 jun 2015 (CDT)
$ r^2 \frac{d^2 φ}{dr^2}+r \frac{d φ}{dr}=0 $
Inciso a
A) Mostrar que una solución de la ecuación diferencial sujeta a las condiciones de contorno $φ(A) = k_{0}$ y $φ(B) = k_{1}$, donde $k_{0}$ y $k_{1}$ son constantes potenciales, está dada por $φ(r) = a + log_{e}r + B$, donde:
$ A=\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} $ $ B=\frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} $
Sustituimos las condiciones iniciales en $ φ(r)$
$ φ(r)= \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} + log_{e}r + \frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} $
donde $φ(r)= φ $
Sacando derivadas parciales
$\frac{\partial φ}{\partial r} = \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} =A \frac{1}{r} $
$ \frac{\partial^{2} φ}{\partial r} = - \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r^2} = -A \frac{1}{r^2} $
Sustituyendo en la ecuación de Laplace-Euler
$ r^2 \frac{d^2 φ}{dr^2}+r \frac{d φ}{dr}=0 $
$ r^2 (-\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r^2}) + r (\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} =0 $
$ \therefore -\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} + \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} =0 $
$\therefore φ(r)$ es solución a la ecuación de Laplace-Euler.
B) Encuentre el potencial complejo
Inciso b
Tomamos las ecuaciones de C-R
$\frac{\partial φ}{\partial r}= \frac{\partial φ*}{\partial r'} ---- (1)$ $\frac{\partial φ}{\partial r'}=- \frac{\partial φ*}{\partial r}$
Donde $φ*$ es el potencial complejo
De la ecuación (1)
$\frac{\partial φ}{\partial r}=\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r}= \frac{\partial φ*}{\partial r'} $
Integrando
$ \int{\partial φ}= \int{ A \frac{1}{r} dr'}$
$ φ= A \frac{1}{r} r' + h(r) $ h(r)=Cte.=0 $
$ φ= A \frac{1}{r} r' $
$\therefore W(r,r')= φ + i φ* $
$\therefore W(r,r')= A log_{e} r + B + i(A \frac{1}{r} r') $
$\therefore W(r,r')= \frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} log_{e} r + \frac{-k_{0}log_{e}b+k_{1}log_{e}a}{log_{e}(\frac{a}{b})} + i(\frac{k_{0}-k_{1}}{log_{e}(\frac{a}{b})} \frac{1}{r} r') $
Elaborado por --Samantha Martinez (discusión) 22:15 05 de Junio 2015 (CDT)
Ejercicio 15
Considere la función $f(z)=z+\dfrac{1}{z}$. Describa la curva de nivel $v(x,y)=0$.
Sol.
Si $z=x+iy$
$f(z)=z+\dfrac{1}{z}=z+\dfrac{1}{z}\dfrac{\overline{z}}{\overline{z}}=z+\dfrac{\overline{z}}{|z|}=(x+iy)+\dfrac{x-iy}{\sqrt{x^2+y^2}}=x(1+\dfrac{1}{\sqrt{x^2+y^2}})+iy(1-\dfrac{1}{\sqrt{x^2+y^2}})$
Con $v(x,y)=y(1-\dfrac{1}{\sqrt{x^2+y^2}})=0$
$1-\dfrac{1}{\sqrt{x^2+y^2}}=0$, $\dfrac{1}{\sqrt{x^2+y^2}}=1$, $\sqrt{x^2+y^2}=1$, $x^2+y^2=1$
Y es fácil observar que la curva $v(x,y)$ es una circunferencia de radio 1 centrada en el origen.
Realizado por: Oscar Javier Gutierrez Varela (discusión) 20:21 1 jun 2015 (CDT)
Ejercicio 16
Las curvas de nivel de $u(x,y) = x^{2}-y^{2}$ y la ecuación $v(x,y)= 2xy$ Analizadas en el ejemplo 1 se intersectan z=0. Dibuje las curvas de nivel que se intersectan en z=0. Explique por que estas curvas de nivel no son ortogonales.
Gráficas
En el gráfico se han representado las dos familias que son ortogonales entre sí, salvo en z=0
Realizado por: Esther Sarai (discusión) 23:05 6 jun 2015 (CDT)Esther Sarai
Ejercicio 17
suponga que la función $f(z)=u(x,y)+iv(x,y)$ es analítica en un dominio D.Entonces las partes real e imaginaria de $f$ se pueden utilizar para definir dos familias de curvas en D.las ecuaciones
$u(x,y)=c_{1}$
$v(x,y)=c_{2}$
donde $c_{1}\:y\:c_{2}$ son constantes reales arbitrarias, se llaman curvas de nivel de $u$ y $v$ respectivamente.Mas precisamente, en un punto de intersección
$z_{0}=x_{0}+iy_{0},$ donde supondremos que $f'(z_{0})\neq0$ , la recta tangente $L_{1}$a la curva de nivel $u(x,y)=u_{0}$ y la recta tangente $L_{2}$a la curva de nivel $v(x,y)=v_{0}$son perpendiculares.
¿Por que se suponemos que $f'(z_{0})\neq0$ ?
sea $f$ una función analítica en un dominio $\mathbb{D\subset C}$ y sea $z_{0}\in D$ si ponemos $f(z)-f(z_{0})\approx f_{0}(z_{0})*(z-z_{0})$ (por la def. de derivada), entonces cuando $f'(z_{0})\neq0$ la derivada puede interpretarse geometricamente como:
$\mid f(z)-f(z_{0})\mid\approx\mid f_{0}(z_{0})\mid*\mid(z-z_{0})\mid$para $z\approx z_{0}$
siendo $\mid f'_{0}(z_{0})\mid$el factor de escala de las distancias entre las imágenes de los puntos, y el $Arg(f'_{0}(z_{0}))$ es una rotación,
así
$Arg(f(z)-f(z_{0}))=Arg(f_{0}(z_{0}))+Arg(z-z_{0})$
esto es, las funciones analíticas conservan los ángulos en los puntos en los que $f'(z_{0})\neq0$
Realizado por: Francisco Medina Albino (discusión) 00:48 5 jun 2015 (CDT)
Eercicio 18
Supongamos que las dos familias de curvas $u(x,y)=c_{1}$y $v(x,y)=c_{2,}$, son trayectorias ortogonales en un dominio D. Analice ¿Es la función $f(x)=u(x,y)+iv(x,y)$ necesariamente analítica en D?
Procedimiento
Sabemos que si tenemos una función $f(x)=u(x,y)+iv(x,y)$ que es analítica en un cierto dominio D las partes real e imaginaria de esta función, a las que llamamos curvas de nivel de $u$ y $v$, respectivamente, son familias ortogonales.
Sabemos esto al analizar algún punto de intersección entre ambas familias y obtener sus rectas tangentes a través de sus respectivas derivadas. Entonces se puede demostrar que son ortogonales si comparamos las pendientes de las rectas tangentes respectivas y ver que la pendiente de una es el recíproco negativo de la otra.
............
Pero si tenemos dos familias ortogonales de alguna función $f(x)=u(x,y)+iv(x,y)$ ¿Podemos decir si estas son análiticas?
Para que sean analíticas tendrían que ser necesariamente continuas y satisfacer con las ecuasiones de cauchy-riemann.
Entonces tomamos a dos curvas de nivel $u(x,y)=c_{1}$y $v(x,y)=c_{2,}$ y sabiendo que se cumple que el produnto de las funciones pendiente es :
$(-\frac{(\frac{\partial u}{\partial x})}{(\frac{\partial u}{\partial y}))})(-\frac{(\frac{\partial v}{\partial x})}{(\frac{\partial v}{\partial y})})=(\frac{(\frac{\partial v}{\partial y})}{(\frac{\partial v}{\partial x})})(-\frac{(\frac{\partial v}{\partial x})}{(\frac{\partial u}{\partial y})})=-1................(1)$
Vemos que de la primera parte de estas relaciones podemos obtener las ecuasiones de cauchy riemann como sigue:
$(-\frac{(\frac{\partial u}{\partial x})}{(\frac{\partial u}{\partial y})})(-\frac{(\frac{\partial v}{\partial x})}{(\frac{\partial v}{\partial y})})=-1$
Dada esta relación podemos reordenar de la forma:
$(\frac{\partial u}{\partial x})(\frac{\partial v}{\partial x})=-(\frac{\partial u}{\partial y})(\frac{\partial v}{\partial y})$
y de esta igualdad se puede decir que necesariamente
$(\frac{\partial u}{\partial x})=(\frac{\partial v}{\partial y})$ y que $(\frac{\partial v}{\partial x})=-(\frac{\partial u}{\partial y})$
Las cuales son las ecuasiones de cauchy-riemann que son una condición necesaria para la analiticidad. Sin embargo, podría decirse que la ecuación que tomamos que demuestra la perpendicularidad también puede relacionarse como sigue:
$(\frac{\partial u}{\partial x})=-(\frac{\partial u}{\partial y})$ y que $(\frac{\partial v}{\partial x})=(\frac{\partial v}{\partial y})$ pero esto no cumple con la igualdad (1), por lo que es irrelevante.
Conclusión
Pero no podríamos decir mucho acerca de su continuidad aunque si sea derivable en algún punto evaluado.
Por tanto, aunque todo esto sugiere una doble implicación entre perpendicularidad y analiticidad entre funciones. No es suficiente para decir que así sea.
Realizado por: A. Martín R. Rabelo (discusión) 21:49 7 jun 2015 (CDT)