Vibra: probs c5
Problemas capítulo 5 Vibraciones Forzadas.
Ejercicios resueltos acerca de Vibraciones Forzadas.
Del libro Vibrations and waves in physics del autor Iain G. Main. 3ra Edición.
Así como algunos ejercicios del libro Vibraciones y ondas del autor A.P. Fench
Y algunos ejercicios extras.
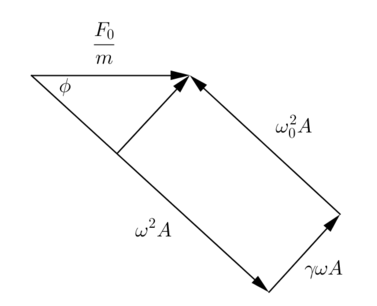
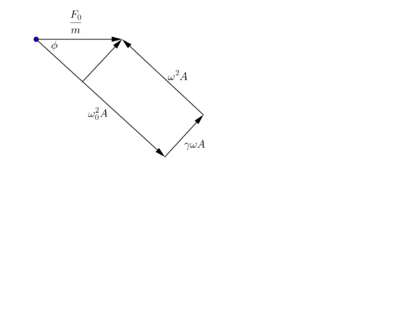
Problema 5.1
For a very lightly damped system, make sketches like fig 5.2 for
(a) ,
(b) ,
(c) ,
(d) , and
(e) . Use these sketches to verify directly the value of A and derived elsewhere.
Traducción:
Para un sistema muy poco amortiguado, hacer diagramas como los de la fig 5.2 para (a) , (b) , (c) , (d) , y (e) . Usar esos diagramas para verificar los valores de A y mostrados antes.
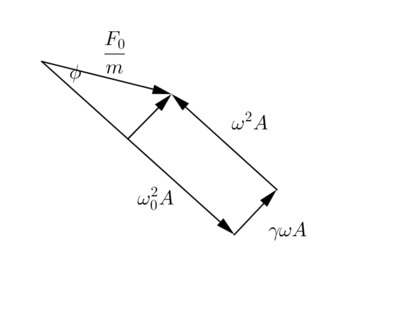
Inciso a
(a)
En este caso tenemos una división de un numero muy chico ( ) entre uno comparado con el muy grande , de ahí que resulte cero:
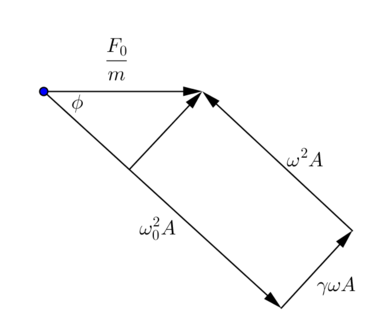
y para la amplitud: por el teorema de Pitágoras, aplicado en el triangulo que se forma en la parte superior de la figura 2:
donde nuevamente se ha usado el argumento de que es relativamente chico y que
Inciso b
(b)
: : Y para la amplitud: : :
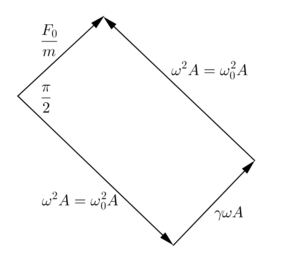
Inciso c
(c)
En este caso podemos empezar escribiendo las ecuaciones a partir del primer diagrama:
pero sabiendo que se tiene una singularidad, que solo ocurre en primera instancia en
Para la amplitud, la ecuación:
se transforma en:
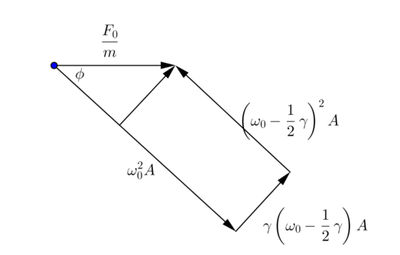
Inciso d
(d) se tiene a partir de la figura 5 que:
:
:
y: : :
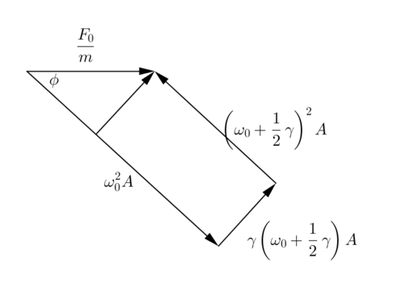
Inciso e
(e)
Procediendo como antes pero en la ultima figura se tiene : : : Y para la amplitud: : : : : :
Aportación por usuario: Uziel Sanchez Gutierrez (discusión) 01:47 16 mar 2015 (CDT) SaraVel (discusión) 15:00 25 jun 2020 (CDT)
Problema 5.2
A system with $m=0.010$ , y is driven by a harmonically varying force of amplitude N. Find the amplitude and the phase constant of the steady-state motion when the angular frequency is: a), b) y c).
Un sistema con , y es impulsado por una fuerza que varía armónicamente de amplitud N. Encuentra la amplitud y la constante de fase del estado estacionario de movimiento cuando la frecuencia es: a), b) y c).
Solución:
La amplitud de un sistema amortiguado es: \[ A=\frac{F_0}{m}\lbrace\frac{1}{(\omega^2 _0 - \omega^2)^2+\gamma^2 \omega^2}\rbrace ^{1/2} --------(1) \]
Con: \[\omega\ ^2_0 = \frac{s}{m}=\frac{36 N m^{⁻1}}{0.01 kg}=3600 s^{-2}--------(2) \]
\[ \gamma^2= \left( \frac{b}{m} \right)^2= \left( \frac{0.5 kg s^{-1}}{0.01kg}\right)^2=2500 -------(3)\]
Sustituyendo los valores de (2) y (3) en (1), así como la fuerza y masa. \[ A=\frac{3.6N}{0.01kg}\lbrace\frac{1}{(3600 s^{-1} - \omega^2)^2+(2500 s^{-2}) \omega^2}\rbrace ^{1/2}=360 N kg^{-1} \lbrace\frac{1}{(3600 s^{-1} - \omega^2)^2+(2500 s^{-2}) \omega^2}\rbrace ^{1/2}--------(4) \]
Por otro lado, el ángulo de fase es:
\[ \phi = angtg \left( -\frac{\gamma \omega}{\omega_0 ^2 - \omega^2}\right)=angtg\left( -\frac{5 0\omega s^{-2}}{3600 s^{-2} - \omega^2}\right)--------(5) \]
Empleando (4) y(5) se obtine:
Para $\omega =8.0 s^{-1}$
\[
A=100mm
\]
\[
\phi=-6.5°
\]
Para $\omega=80 s^{-1}$ \[ A=74mm \] \[ \phi=55 ^o \approx-125^o \]
Para $\omega=800 s^{-1}$ \[ A=0.56mm \]
\[ \phi=3.59^o \approx-176° \]
Resuelto por Luis Santos Luis Santos (discusión) 00:42 8 mar 2015 (CST)MISS (discusión) 01:12 21 may 2013 (CDT) Aportaciones por: Brenda Pérez Vidal (discusión) 01:42 17 feb 2014 (UTC)
Problema 5.3
Solución 1
Show that the displacement amplitud A is a maxium at the driving frequency given by $\omega_{R}^{2}=\omega_{0}^{2}-\frac{1}{2}\gamma^{2}$
Traducción
Muestre que la amplitud del desplazamiento A es máxima cuando la frecuencia está dada por $\omega_{R}^{2}=\omega_{0}^{2}-\frac{1}{2}\gamma^{2}$ .
Solución
Partimos de la ecuación de movimiento para un movimiento forzado y amortiguado
\[ \ddot{\psi}+\gamma\dot{\psi}+\omega_{0}^{2}\psi=\frac{F_{0}}{m}\cos\omega t\qquad\ \]
teniendo como solución la combinación lineal de su solución homogénea
y su solución particular
\[ \psi_{h}(t)=e^{-\beta t}[A_{1}e^{\sqrt{\beta^{2}-\omega_{0}^{2}}t}+A_{2}e^{-\sqrt{\beta^{2}-\omega_{0}^{2}}t}]\quad;\;\beta=\frac{\gamma}{2} \]
\[
\psi_{p}(t)=D\cos(\omega t+\phi)
\]
por sustitución en la ecuación de movimiento y desarrollando $\cos(\omega t-\delta)$
y $\sin(\omega t-\delta)$ obtenemos:
\[ \{A-D[(\omega_{0}^{2}-\omega^{2})\cos\delta+2\omega\beta\sin\delta]\}\cos\omega t-\{D[(\omega_{0}^{2}-\omega^{2})\sin\delta-2\omega\beta\cos\delta]\}\sin\omega t=0 \]
del primer término se obtiene la relación para la amplitud dada por
\[ D=\frac{A}{(\omega_{0}^{2}-\omega^{2})\cos\delta+2\omega\beta\sin\delta}\qquad(1) \]
y la relación para $\cos\delta$ y $\sin\delta$ se obtiene del segundo término
\[ \tan\delta=\frac{2\omega\beta}{\omega_{0}^{2}-\omega^{2}} \]
\[
\sin\delta=\frac{2\omega\beta}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}\gamma^{2}}}
\]
\[
\cos\delta=\frac{\omega_{0}^{2}-\omega^{2}}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}\beta^{2}}}
\]
y así, sustituyendo estas dos últimas expresiones en (1) obtenemos
\[ D=\frac{A}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\omega^{2}\beta^{2}}} \]
Para hallar la pulsación $\omega_{R}$ para la cual la amplitud D
es máxima efectuamos la derivación
\[ \frac{dD}{d\omega}|_{\omega=\omega_{R}}=0 \]
- $\frac{dD}{d\omega}=-\frac{1}{2}\frac{A[-4\omega_{R}(\omega_{0}^{2}-\omega_{R}^{2})+8\omega_{R}\beta^{2}]}{[(\omega_{0}^{2}-\omega_{R}^{2})^{2}+4\omega_{R}^{2}\beta^{2}]^{3/2}}=0\quad\Rightarrow8\omega\beta^{2}=4\omega(\omega_{0}^{2}-\omega_{R}^{2})\;\Rightarrow2\beta^{2}=\omega_{0}^{2}-\omega_{R}^{2}$
y por la tanto así queda demostrado
\[ \omega_{R}^{2}=\omega_{0}^{2}-2\beta^{2}\quad;\;\beta=\frac{\gamma}{2} \]
\[
\omega_{R}^{2}=\omega_{0}^{2}-\frac{1}{2}\gamma^{2}
\]
Aportación por usuario: Luis Miguel Sánchez Mtz. (discusión) 17:33 15 feb 2014 (UTC)
Solución 2
Show that the displacement amplitude $A$ is a maximun at the driving frequency given by $\;\omega^2=\omega_0^2-\tfrac{1}{2}\gamma^2 $.
Muestre que la amplitud del desplazamiento $A$ es máxima cuando la frecuencia está dada por $\;\omega^2=\omega_0^2-\tfrac{1}{2}\gamma^2 $.
SOLUCIÓN:
Sabemos que para un sistema forzado amortiguado, la solución para el estado estable del sistema es:
\[ \psi=A \, \cos(\omega \, t +\phi) \]
De donde la amplitud es \[ A=\frac{F_0}{b\,\omega} \left( \frac{\gamma^2 \, \omega^2}{(\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2} \right)^{1/2} =\frac{(F_0/b)\, \gamma}{ \left[ (\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2 \right]^{1/2}}\]
Para obtener el punto $\omega$ en el cual la amplitud $A$ es máxima, usamos el criterio de la derivada, i.e., \[ \left. \frac{\mathrm{d}A}{\mathrm{d}\omega} \right|_{\omega_{max}} =0 \]
Y resolviendo la derivada obtenemos la frecuencia de resonancia, $\omega$.
\[ \frac{\mathrm{d}}{\mathrm{d}\omega} \left[ \frac{(F_0/b)\, \gamma}{ \left[ (\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2 \right]^{1/2}} \right] = \left( -\frac{F_0 \, \gamma}{b} \, \omega \right) \left( \frac{2(\omega_0^2-\omega^2)-\gamma^2}{\left[ (\omega_0^2-\omega^2)^2+\gamma^2 \, \omega^2 \right]^{3/2}} \right) =0 \]
Como $\frac{F_0 \, \gamma}{b} \,\omega \neq 0$, entonces
\[ 2(\omega_0^2-\omega^2)-\gamma^2=0 \quad \Longrightarrow \quad \omega^2=\omega_0^2-\frac{1}{2}\gamma^2 \]
Solución hecha por: Adolfo Calderón Alcaraz (discusión) 20:27 15 mar 2015 (CDT)
Problema 5.4
Solución 1
Show that the acceleration amplitude $\omega^{2}A$ is a maximum at the driving frequency given by
$\omega^{2}=\omega_{0}^{2}/(1-\gamma^{2}/2\omega_{0}^{2})\simeq\omega_{0}^{2}+\frac{1}{2}\gamma^{2}$
where the approximation is good when the damping is very light.
Traducción
Muestre que la amplitud de la aceleración $\omega^{2}A$ es máxima cuando la frecuencia está dada por
$\omega^{2}=\omega_{0}^{2}/(1-\gamma^{2}/2\omega_{0}^{2})\simeq\omega_{0}^{2}+\frac{1}{2}\gamma^{2}$
donde la aproximación es buena para un amortiguamiento muy ligero.
Solución:
Primero nombremos $\omega^{2}=z$ y $\omega_{0}^{2}=x$ por facilidad de escritura, entonces tenemos que la amplitud de aceleración es $zA$, y esto es igual a $\frac{F_{0}\omega}{B}\left[\frac{\gamma^{2}\omega^{2}}{(\omega_{0}^{2}-\omega^{2})+\gamma^{2}\omega^{2}}\right]^{1/2}$ o $\frac{F_{0}}{B}\left[\frac{\gamma^{2}z^{2}}{(x-z)+\gamma^{2}z}\right]^{1/2}$ simplemente haciendo las sustituciones propuestas.
Por lo que $zA=\frac{F_{0}}{B}\left[\frac{\gamma^{2}z^{2}}{(x-z)+\gamma^{2}z}\right]^{1/2}$ , al derivar esto con respecto a z e igualarlo a cero para hacerlo un máximo, vemos que el factor $\frac{F_{0}}{B}$
y la parte inferior de la derivada del cociente desaparecen al igual que el cociente de la raíz, por lo que
sólo nos va a interesar la parte superior de la derivada, y lo escribimos.
$\left[(x-z)^{2}+\gamma^{2}z\right](2\gamma^{2}z)-\gamma^{2}z^{2}\left[-2(x-z)+\gamma^{2}\right]=0$
Haciendo algunas simplificaciones algebraicas sencillas
$2(x^{2}-2xz+z^{2})+\gamma^{2}z=-2z(x-z)$
Por lo que
$-2xz+\gamma^{2}z+2x^{2}=0$
$z(-2x+\gamma^{2})=-2x^{2}$
$z=\frac{-2x^{2}}{-2x+\gamma2}$
$z=\frac{x}{1-\frac{\gamma^{2}}{2x}}$
O resustituyendo
$\omega^{2}=\omega_{0}^{2}/(1-\gamma^{2}/2\omega_{0}^{2})\simeq\omega_{0}^{2}+\frac{1}{2}\gamma^{2}$
Nota: Tomar en cuenta que la parte de las simplificaciones fue omitida puesto que es pura álgebra y el lector la puede hacer fácilmente.
Resuelto por usuario: Edgar Ortega Roano 09:58 12 feb 2014 (CDT)
Solución 2
Show that the acceleration amplitude $\; \omega^2\,A \;$ is a maximun at the driving frequency given by $\; \omega^2=\omega_0^2/(1-\gamma^2/2\omega_0^2) \approx \omega_0^2 + \tfrac{1}{2}\gamma^2$, where the approximation is good when the damping is very light.
La solución a un sistema amortiguado y forzado es
\[ \psi(t)=A\,\cos(\omega\,t+\phi) = \left(\frac{F_0}{b\,\omega}\right) \left( \frac{\gamma^2 \, \omega^2}{(\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2} \right)^{1/2} \cos(\omega\,t+\phi) \]
Derivando la aceleración...
\[ \ddot{\psi}(t)=-\left(\frac{F_0 \, \omega}{b}\right) \left( \frac{\gamma^2 \, \omega^2}{(\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2} \right)^{1/2} \cos(\omega\,t+\phi) \]
Derivando la amplitud con respecto a $\omega$ e igualando a cero...
\[ \frac{\mathrm{d\,(A\,\omega^2)}}{\mathrm{d}\omega} =\frac{\mathrm{d}}{\mathrm{d}\omega} \left[ \left(\frac{F_0 \, \omega}{b}\right) \left( \frac{\gamma^2 \, \omega^2}{(\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2} \right)^{1/2} \right] = \frac{\mathrm{d}}{\mathrm{d}\omega} \left[ \left(\frac{F_0}{b}\right) \frac{\gamma \, \omega^2}{\left( (\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2 \right)^{1/2}} \right] =0\] \[ \Longrightarrow \quad \left( \frac{F_0}{b} \right) \left[ \frac{2\,\omega}{((\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2)^{1/2}} -\frac{\tfrac{1}{2}\omega^2(2(-2\omega)(\omega_0^2-\omega^2)+2\gamma^2\omega)}{((\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2)^{3/2}} \right]=0 \]
\[ \Longrightarrow \quad \frac{2\omega(\omega_0^2-\omega^2)+2\omega^3(\omega_0^2-\omega^2)+2\gamma^2\,\omega^3-\gamma^2\,\omega^3}{((\omega_0^2-\omega^2)^2+\gamma^2\,\omega^2)^{3/2}} =0 \]
Lo anterior solo es posible cuando el numerador es igual a cero.
\[ \Longrightarrow 2\omega(\omega_0^2-\omega^2)+2\omega^3(\omega_0^2-\omega^2)+2\gamma^2\,\omega^3-\gamma^2\,\omega^3=0 \]
Dividiendo entre $\omega$. \[ \Longrightarrow 2(\omega_0^2-\omega^2)^2+2\omega_0^2\,\omega^2-2\omega^4+\gamma^2\,\omega^2=0 \]
Despejando $\omega$ de la ecuación anterior...
\[ 2(\omega^4-2\omega_0^2\,\omega^2+\omega^4)+2\omega_0^2\,\omega^2-2\omega^4+\gamma^2\,\omega^2=\omega_0^4-\omega_0^2\omega^2+\frac{1}{2}\gamma^2\,\omega^2=0 \]
\[ \omega_0^4-\omega^2(\omega_0^2-\frac{1}{2}\gamma^2)=0 \]
\[ \omega^2=\frac{\omega^4_0}{\omega_0^2-\tfrac{1}{2}\gamma^2} \]
Dividiendo el numerador y el denominador por $\omega^2$...
\begin{equation}\label{2.1}\tag{2.1} \omega^2=\frac{\omega_0^2}{1-\gamma^2/(2\,\omega_0^2)} \end{equation}
Podemos aplicar la aproximación
\begin{equation}\label{2.2}\tag{2.2} (1-2\,x^2)^{-1} \approx 1+2\,x^2 \end{equation}
, para $x\ll1$ lo suficientemente pequeña, a la ec. $(2.1)$. Por eso si elegimos $x=\frac{\gamma}{2\,\omega_0}$, entonces como $x=\frac{\gamma}{2\,\omega_0}\ll1$ implica que $\gamma\ll2\,\omega_0$ que es la relación que describe un amortiguamiento muy ligero.
\[ \omega^2=\omega_0^2 \left( 1-\frac{\gamma^2}{2\,\omega_0^2} \right)^{-1} =\omega_0^2 \left( 1-2\left(\frac{\gamma}{2\,\omega_0}\right)^2 \right)^{-1} \]
Elegimos $x=\frac{\gamma}{2\,\omega_0}$ y aplicamos la ec. $(2.2)$
\[ \omega^2 \approx \omega_0^2 \left( 1+2 \left( \frac{\gamma}{2\,\omega_0} \right)^2 \right) \]
Simplificando....
\begin{equation}\label{2.3}\tag{2.3} \omega^2 \approx \omega_0^2+\frac{1}{2}\gamma^2 \end{equation}
Resuelto por usuario: Rosario Maya (discusión) 23:13 15 mar 2015 (CDT)
Problema 5.5
A certain system has $\nu_{0}=$50 Hz exactly and Q=10 excactly. Compare the numericale values of:
a) A the resonance angular frecuency $\omega_{0},b)$ the angular frecuency of the free vibrations $\omega_{f},$ c)the value of $\omega$ at which the displacement amplitude A is a maximun, and d) the value of $\omega$ at which the aceleration amplitude $\omega^{2}$is a maximun.
Traducción
Cierto sistema tiene $\nu_{0}=$50 Hz exactamente y Q=10 exactamente. Compare los valores numéricos de:
a) La frecuencia angular de resonancia $\omega_{0}$:
Solución
Inciso a
Para calcular $\omega_{0},$se utiliza la siguiente definición: $\omega=2\pi\nu$ que para $\omega_{0}$, se convierte en $\omega_{0}=2\pi\nu0$.
Al sustituir los valores dados, dentro de la ecuación, se obtiene:
\[ \omega_{0}=2\pi(50Hz)=314.16rad/seg \]
Inciso b
b)La frecuencia angular para vibraciones libres:
Para obtener la frecuencia angular para vibraciones libres, se ocupa la siguiente definición:
\[ \omega=\omega_{0}\left[1-\left(\gamma/2\omega_{0}\right)^{2}\right]^{1/2} \]
En donde se utiliza la siguiente relación: $\gamma=\frac{\omega_{0}}{Q}$
Al sustituir las ecuaciones anteriores con los datos, se obtiene:
\[ \gamma=31.416 \]
\[
\omega=314.16\left[1-(31.416/628.31)^{2}\right]^{1/2}=313.76rad/seg
\]
Se puede observar que $\omega$ y $\omega_{0},$ valen prácticamente
lo mismo.
Inciso c
c)El valor de $\omega$ en el que la amplitud A, sea un máximo:
Primero se utiliza la siguiente relación:
\[ x(t)=Asen(\omega t+\phi) \]
Que se deriva para obtener el punto crítico en el que A es un máximo,
y se obtiene:
\[ Cos(\omega t+\phi)=0 \]
En donde se aplica el arcoseno con el propósito de despejar a $\omega$:
\[ \omega t=\frac{\pi}{2}-\phi \]
\[
\omega=\frac{\pi}{2t}=\frac{\pi}{2\nu_{0}}
\]
Al sustituir, con los valores dados, se obtiene: $\omega=0.314$ rad/seg
d)El valor de $\omega$ para el cual la amplitud de la aceleración y $\omega^{2}A$ es un máximo:
Este valor, se obtiene con la segunda derivada de la siguiente ecuación:
\[ \frac{}{} \] \[ \frac{d^{2}x}{dt}Asen(\omega t+\phi)=-A\omega sen(\omega t) \]
\[
-A\omega sen\omega t=0
\]
Al despejar el $\omega$ utilizando el arcoseno, se obtiene:
\[ 0=\omega t \]
Por ende, $\omega=0$
Resuelto por usuario: Ana Alarid (discusión) 03:31 26 feb 2014 (UTC)
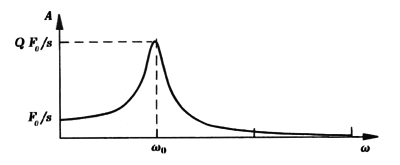
Problema 5.6
Show that value of the displacement amplitude A at the exact maximum of its response curve is
Traducción:
Muestre que el valor de desplazamiento de la amplitud A en el máximo exacto de su curva de respuesta es:
\[ A_{max}=\left(\frac{QF_{0}}{s}\right)\left(1-\frac{1}{4Q^{2}}\right)^{-1/2}\thickapprox\left(\frac{QF_{0}}{s}\right)\left(1+\frac{1}{8Q^{2}}\right) \]
Como ya sabemos la amplitud esta dada por la siguiente ecuación:
\[ A=\frac{F_{0}}{m}\left[\frac{1}{(\omega_{0}^{2}-\omega^{2})^{2}+\gamma^{2}\omega^{2}}\right]^{1/2}\qquad\qquad (1) \]
También conocemos las siguientes ecuaciones:
\[
Q=\frac{\omega_{0}}{\gamma}
\]
Cuanto mayor es el valor de Q menor es el efecto disipativo y mayor
el numero de ciclos de oscilaciones libres para una disminución dada
de amplitud.
\[ \omega^{2}=\frac{s}{m} \]
\[
\gamma=\frac{b}{m}
\]
Ahora bien haciendo álgebra y utilizando las ec. anteriores podemos llegar a:
\[ A=\frac{F_{0}}{m\omega_{0}}\frac{\omega/\omega_{0}}{\left[\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}+\frac{1}{Q^{2}}\right]^{1/2}}\qquad\qquad (2) \]
O bien:
\[ A=\frac{F_{0}}{s}\frac{\omega_{0/}\omega}{\left[\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}+\frac{1}{Q^{2}}\right]^{1/2}} \]
La mayor parte de la variación de la fase se produce en un intervalo
de frecuencias que va aproximadamente desde $\omega_{0}\left(1-\frac{1}{Q}\right)$hasta
$\omega_{0}\left(1+\frac{1}{Q}\right),$en el limite $Q\rightarrow\infty$.
La amplitud A pasa por un máximo para cualquier valor de Q mayor de $1/\sqrt{2}$, es decir, para todos los sistemas excepto los amortiguados con mayor intensidad.
Esta amplitud máxima se presenta, a una frecuencia $\omega_{m}$que es menor que $\omega_{0}$. Si llamamos Ao a la amplitud $\frac{F_{0}}{s}$ obtenida para $\omega\rightarrow0$, se obtendrán las siguientes ecuaciones:
\[ \omega_{m}=\omega_{0}\left(1-\frac{1}{2Q^{2}}\right)^{1/2} \]
\[
A_{m}=A_{0}\frac{Q}{\left(1-\frac{1}{4Q^{2}}\right)^{1/2}}
\]
Por lo tanto queda demostrado que:
\[ A_{m}=\frac{F_{0}}{s}\frac{Q}{\left(1-\frac{1}{4Q^{2}}\right)^{1/2}}\thickapprox\frac{F_{0}}{s}\frac{Q}{\left(1+\frac{1}{8Q^{2}}\right)} \]
Aquí el álgebra para llegar de (1) a (2).
Se tiene la ecuación: \[A=\frac{F_0}{m}=\left[\frac{1}{(\omega_0 ^2 -\omega^2)^2+\gamma^2 \omega^2} \right]\]
y las relaciones:
\[ \omega_0 ^2 =\frac{s}{m} \] \[ \gamma=\frac{b}{m} \] \[ Q=\frac{\omega_0}{\gamma} \]
Por lo que podemos escribir los siguiente:
\[ A=\frac{F_0}{m}\frac{\omega_0}{\omega}\frac{\frac{\omega}{\omega_0}}{\left[(\omega_0 ^2-\omega^2)^2 + \gamma^2 \omega^2 \right]^{1/2} } \]
\[ A=\frac{F_0}{m}\frac{\frac{\omega}{\omega_0}}{{\left[\left(\frac{\omega}{\omega_0} \right)^2 (\omega_0 ^2 -\omega^2)^2 + \left( \frac{\omega}{\omega_0}\right)^2\gamma^2\omega^2 \right]^{1/2} } } \]
\[ A=\frac{F_0}{m}\frac{\frac{\omega}{\omega_0}}{{\left[\left(\frac{\omega}{\omega_0} \right)^2 (\omega_0 ^2 -\omega^2)^2 + \frac{1}{Q} \omega^4\right]^{1/2} } } \]
\[
A=\frac{F_0}{m\omega_0 ^2}\frac{\frac{\omega}{\omega_0}}{{\left[\left(\frac{1}{\omega_0 \omega} \right)^2 (\omega_0 ^2 -\omega^2)^2 + \frac{1}{Q}\right]^{1/2} } }
\]
Finalmente:
\[ A=\frac{F_0}{m\omega_0 ^2}\frac{\frac{\omega}{\omega_0}}{{\left[ (\frac{\omega_0}{\omega} -\frac{\omega}{\omega_0})^2 + \frac{1}{Q}\right]^{1/2} } }=\frac{F_0}{s}\frac{\frac{\omega}{\omega_0}}{{\left[ (\frac{\omega_0}{\omega} -\frac{\omega}{\omega_0})^2 + \frac{1}{Q}\right]^{1/2} } } \]
Aportación por usuarios: Luis Santos (discusión) 00:24 9 mar 2015 (CDT) , Usuario:Daniel Olvera Moreno 22:40 21 de feb 2014 Cesar Ivan Avila Vasquez (discusión) 17:10 25 Febrero 2014
Problema 5.7
Show that the value of the acceleration amplitude $\omega^{2}A$ at the exact maximum of its response curve is
\[ \left(\omega^{2}A\right)_{m}=\left(QF_{0}/m\right)\left(1-1/4Q^{2}\right)^{-1/2}\thickapprox\left(QF_{0}/m\right)\left(1+1/8Q^{2}\right) \]
Ya que anteriormente habíamos calculado $A_{m}$
\[ A_{m}=\frac{F_{0}}{s}\frac{Q}{\left(1-\frac{1}{4Q^{2}}\right)^{1/2}} \]
lo único que debemos hacer es multiplicar en los dos lados de la ecuación
por $\omega^{2}$y sabiendo también que $\omega^{2}=\frac{s}{m}$
obtendremos que
\[ \left(\omega^{2}A\right)_{m}=\frac{F_{0}}{m}\frac{Q}{\left(1-\frac{1}{4Q^{2}}\right)^{1/2}}\thickapprox\frac{F_{0}}{m}\frac{Q}{\left(1+\frac{1}{8Q^{2}}\right)} \]
Aportacion por usuario: Usuario:Daniel Olvera Moreno 23:05 21 de feb 2014
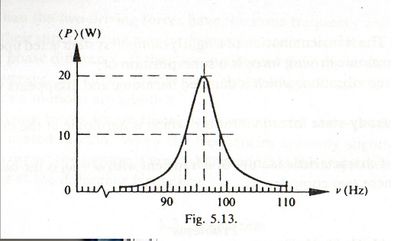
Problema 5.8
Figure 5.13 shows the mean power absorption (P) in watts, as a function of driving frequency in the resonance region. Find the numerical vaules of a) , b), and c) Q. d) If driving force is removed, after how many subsequent cycles will the energy of the system be of its initial vaule?
Traducción
La figura 5.13 muestra la media de absorción de potencia (P) en watts, en función de la potencia de la frecuencia. Encontrar los valores numéricos de (a) , (b) , y (c) Q. Si se retira la fuerza motriz, ¿después de cuantos ciclos posteriores la energía del sistema es de su valor inicial.
Solución
Inciso a
a) Directamente de la figura 5.13, se observa que en su punto más alto la frecuencia es de 96Hz, por lo que
Inciso b
b) Como esta dado por el ancho de la gráfica cuando su potencia es de la mitad de la máxima, de la figura se observa fácilmente que
Inciso c
c) De la ecuación 3.14 se tiene que
Inciso d
d) De las ecuaciones 3.12 se sabe que la energía decae por un factor al tiempo , es decir
Como
se tiene que el número de ciclos esta dado por
Realizado por usuario: Pérez Córdoba Sabino (discusión) 04:54 25 feb 2014 (UTC) Imagen Pablo (discusión) 00:15 15 mar 2015 (CDT)
Problema 5.9
If the system in problem 5.8 has m=0-010 Kg, calculate the force amplitude $F_o$
Traducción
Si en el problema 5.8 se tiene m=0-010 Kg, calcule la fuerza $F_o$
Solución
Primeramente escribimos los datos obtenidos del problema anterior
$\omega_{0}=600\frac{rad}{s}$ $Q=16$$\gamma=38Hz$
Ahora bien para calcular Fo podemos acudir a la ecuación:
\[ P=\frac{F_{0}^{2}}{2M\gamma}\left[\frac{\gamma^{2}\omega^{2}}{\left(\omega_{0}^{2}-\omega^{2}\right)^{2}+\gamma^{2}\omega^{2}}\right] \]
Esta es la ecuación para obtener P y la usaremos ya que del problema
anterior podemos observar en la gráfica que P es 20 W esto es porque
el problema dice que esta en resonancia, y cuando esta en resonancia
P alcanza su máximo, de aquí también se observa que $\omega=\omega_{0}$
, esta ecuación se reducirá a la siguiente
\[ P=\frac{F_{0}^{2}\omega_{0}Q}{2\gamma} \]
Y esta ecuación puede convertirse en
\[ P=\frac{QF_{0}^{2}}{2m\omega_{0}} \]
Ya que anteriormente se explico que se conoce P de la ecuación se despejara
para obtener Fo y tenemos que:
\[ F_{0}=\left[\frac{2Pm\omega_{0}}{Q}\right]^{1/2} \]
Por lo tanto
\[
F_{0}=3.87N\backsimeq3.9N
\]
Realizado por usuario: Usuario:Daniel Olvera Moreno 21:26 25 de feb 2014
Problema 5.11
In form B the steady-state forced vibration is written \[ \psi= B_{p}\cos\omega t + B_{q}\sin \omega t\] show that $\langle P\rangle = \dfrac{1}{2}\omega F_{0}B_{q}$
Traducción
En la forma B el estado estacionario de una vibración forzada se escribe como \[ \psi= B_{p}\cos\omega t + B_{q}\sin \omega t\] muestre que $\langle P\rangle = \dfrac{1}{2}\omega F_{0}B_{q}$
Solución
En la forma B; $B_{q}$ se define como :
\[ B_{q} = -A\sin\phi\]
Utilizando la figura 5.2 del libro encontraremos a $\sin B\phi$ y de ahí obtendremos la amplitud, la cual resulta :
\[ A=\frac{F_{0}mB_{q}}{\gamma \omega} \]
De acuerdo con el libro $\dot{\psi}= A\omega [R(\omega)]^\dfrac{1}{2}$ y $\langle\dot{\psi^{2}}\rangle=\dfrac{1}{2}(\omega A)^{2}$ entonces:
\[
\langle\dot{\psi^{2}}\rangle=\dfrac{1}{2}(\frac{F_{0}B_{q}}{b}[R(\omega)]
\]
Utilizando la ecuación 5.11 del libro $\langle P\rangle = b\dot{\psi^{2}}$ tenemos que:
\[ \langle P\rangle = \dfrac{1}{2}\omega F_{0}B_{q} \]
Aportación por usuario: Esther Sarai (discusión) 16:38 15 mar 2015 (CDT)Esther Sarai
Problema 5.12
Show that, for driving frequencies close to resonance $(\omega\thickapprox\omega_{0})$ in a very lightly damped system, the response function (5.7) may be approximated by the Lorentzian
Traducción:
Muestre que para frecuencias cerca de la resonancia $\left(\omega\approx\omega_{0}\right)$ en un sistema muy ligeramente amortiguado, la función de respuesta (5.7) puede ser aproximada por el Lorentziano:
Solución
\[ L(\omega)=\frac{\frac{1}{4}\gamma^{2}}{(\omega_{0}-\omega)^{2}+\frac{1}{4}\gamma^{2}} \]
Sabemos que:
\[ R(\omega)=\frac{\gamma^{2}\omega^{2}}{\left(\omega_{0}^{2}-\omega^{2}\right)^{2}+\gamma^{2}\omega^{2}} \]
Además tenemos que $\omega\thickapprox\omega_{0}$ y dado que el movimiento
es muy ligeramente amortiguado también tenemos que $\omega_{0}\gg\frac{\gamma}{2}$
y por lo cual $\omega\gg\frac{\gamma}{2}$ entonces:
\[ R(\omega)=\frac{\gamma^{2}\omega^{2}}{\left(\omega_{0}+\omega\right)^{2}\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}\omega^{2}} \]
\[
R(\omega)=\frac{\gamma^{2}\omega^{2}}{\left(\omega\left(\frac{\omega_{0}}{\omega}+1\right)\right)^{2}\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}\omega^{2}}
\]
\[
R(\omega)=\frac{\gamma^{2}\omega^{2}}{\omega^{2}\left(\frac{\omega_{0}}{\omega}+1\right)^{2}\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}\omega^{2}}=\frac{\gamma^{2}}{\left(\frac{\omega_{0}}{\omega}+1\right)^{2}\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}}
\]
Luego, con $\omega_{0}\thickapprox\omega$ tenemos que:
\[ R(\omega)\cong\frac{\gamma^{2}}{\left(1+1\right)^{2}\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}}=\frac{\gamma^{2}}{4\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}} \]
\[
R(\omega)=\left(\frac{\frac{1}{4}}{\frac{1}{4}}\right)\frac{\gamma^{2}}{4\left(\omega_{0}-\omega\right)^{2}+\gamma^{2}}
\]
Finalmente:
\[ \Rightarrow\frac{\frac{\gamma^{2}}{4}}{\left(\omega_{0}-\omega\right)^{2}+\frac{\gamma^{2}}{4}}=L(\omega) \]
Aportación por usuario: Cesar Ivan Avila Vasquez 00:01 20 Febrero 2014 (CDT) Esther Sarai (discusión) 22:11 15 mar 2015 (CDT)Esther Sarai
Problema 5.14
By finding the value of $\omega$ which makes the compliance $\left|K(\omega)\right|$ a maximum, confirm the result of problem 5.3.
Traducción
A través de encontrar el valor de $\omega$ la cual hace que se cumpla que $\left|K(\omega)\right|$ sea máximo, confirme el resultado del problema 5.3.
Solución
Sea $K(\omega)=\frac{1}{(s-m\omega^{2})+ib\omega}$
si queremos que $K(\omega)$ sea máximo esto sucede cuando el denominador tiende a cero y para eso resolvemos $s-m\omega^{2}+ib\omega=0$ obteniendo entonces que
\[\omega=\frac{ib}{2m}\pm(\frac{s}{m}-\left(\frac{b}{m}\right)^{2})^{\frac{1}{2}}\]
Si ahora consideramos solamente la parte real donde $K(\omega)$ tiene un máximo (según la gráfica 5.8 de la página 66 de G.Main) tendremos que
$\omega=\pm(\frac{s}{m}-\left(\frac{b}{m}\right)^{2})^{\frac{1}{2}}$
Resuelto por usuarios: Pedro Pablo Ramírez Martínez (discusión) 04:32 28 mar 2014 (UTC) , Imagen por usuario: Pablo (discusión) 00:52 15 mar 2015 (CDT)
Problema 5.16
For the motion find (a) the frequency, and (b) the time interval separating sucessive beats.
Traducción
Para el movimiento encuentra (a) la frecuencia, y (b) el intervalo que separa las pulsaciones sucesivas.
Inciso a
(a) Se tiene un movimiento que resulta de la superposición de dos movimientos, la vibración libre y una vibración forzada, por lo tanto se tienen diferentes frecuencias angulares y , entonces la frecuencia estará dada como sigue:
donde se tienen dos valores distintos para :
y:
Entonces las frecuencias correspondientes a cada son:
y:
Así la frecuencia correspondiente al movimiento es:
Inciso b
(b) Dado que el periodo se relaciona de la siguiente forma con :
Y es:
Se tiene:
Y finalmente al sustituir obtenemos el valor del periodo:
Resuelto por usuario: Brenda Pérez Vidal (discusión) 23:32 19 feb 2014 (UTC)
Problema 5.17
A single driving force produces a steady-state forced vibrations with amplitude $10mm$. A second driving force of the same frequency as the first, acting on the same system, produces a steady-state amplitude of $20mm$. When both forces are acting simultaneously, the steady-state amplitude is $15mm$. What is the phase difference between the two forces?
Traducción
Una fuerza produce una vibración forzada en estado estacionario con una amplitud de $10mm$. Una segunda fuerza de la misma frecuencia de la primera, actúa sobre el mismo sistema y produce una amplitud de $20mm$. Cuando ambas fuerzas actúan de manera simultanea, la amplitud de estado estacionario es de $15mm$. ¿Cuál es la diferencia de fase entre las dos fuerzas?
Solución
La amplitud resultante para la superposición de dos vibraciones forzadas con la misma frecuencia, está dada por la ecuación $(5.25)$ del texto(Main):
donde $A$ es la amplitud resultante, $A_1$ y $A_2$ las amplitudes de las vibraciones que actuan sobre el sistema, $\alpha_1$ es la fase de la primera fuerza y $\alpha_2$ la fase de la segunda fuerza.
Para este problema en específico, sabemos que $A_1 = 10 mm$, $A_2 = 20mm$ y $A = 15mm$, por lo que podemos escribir $A_2 = 2A_1$ y $A = 3/2 A_1$. Entonces, reescribiendo la ecuación para la amplitud resultante, tenemos que:
Y resolviendo para $\alpha_2 - \alpha_1$:
$ \dfrac{9}{4} A_1^2 - A_1^2 - 4A_1^2 = 4A_1^2 \cos(\alpha_2 - \alpha_1) \\ \dfrac{9}{4} A_1^2 - \dfrac{4}{4} A_1^2 - \dfrac{16}{4} A_1^2 = 4A_1^2 \cos(\alpha_2 - \alpha_1) \\ - \dfrac{11}{4} A_1^2 = 4A_1^2 \cos(\alpha_2 - \alpha_1) \\ \left(\dfrac{- \dfrac{11}{4} A_1^2}{4A_1^2}\right) = \cos(\alpha_2 - \alpha_1) \\ \cos(\alpha_2 - \alpha_1) = - \dfrac{11}{16} $
Por lo que:
Por lo tanto, la diferencia de fases entre las dos fuerzas es de $\approx 133.4^o$.
Resultado por usuario: Ivan de Jesús Pompa García (discusión) 17:09 10 mar 2015 (CDT)
Problema 5.18
A simple seismometer consists of a mass hung on a spring attached to a rigid framework, which is fixed to the ground, with critical damping. The vertical displacement of the mass relative to the framework is recorded.
a) Show that the measured amplitude A of the steady-state vibration resulting from a vertical displacement $Hcos(\omega t)$ of the earth´s surface is given by
\begin{equation} \frac{A}{H}=\frac{\omega}{2\omega_{0}}[R_{(\omega)}]^{\frac{1}{2}} \end{equation}
b) Show that, if the frecuencies of the detected disturbances lie in the region of mass controlled motion, the mass remains almost stationary when the ground moves.
Interpretación al español latino
5.18 Un simple sismómetro consiste en una masa colgada en un resorte unido a un marco rígido, que está fijado al suelo, con amortiguamiento crítico. El desplazamiento vertical de la masa en relación con el marco se registra.
a) Demostrar que la amplitud A medida de la vibración de estado estacionario resultante de un desplazamiento vertical $Hcos(\omega t)$ de la superficie de la tierra está dado por
\begin{equation} \frac{A}{H}=\frac{\omega}{2\omega_{0}}[R_{(\omega)}]^{\frac{1}{2}} \end{equation}
b) Demostrar que, si las frecuencias de las alteraciones detectadas se encuentran en la región del movimiento de masas controladas, la masa permanece casi estacionario cuando el suelo se mueve.
Solución
El movimiento del sismómetro puede verse como un oscilador forzado, donde el movimiento terrestre es la fuerza externa oscilante, llamaremos:
\begin{equation} \upsilon_{(t)}=Hcos(\omega t) \end{equation}
Encontramos que el cambio de momento:
\begin{equation}
p=m\dot{\upsilon} \Longrightarrow \frac{\delta p}{\delta t}=m\ddot{\upsilon}
\end{equation}
donde: \begin{equation} \ddot{\upsilon}=-H\omega^{2}cos(\omega t) \end{equation}
Entonces por segunda ley de newton y tomando en cuenta que el movmiento es unidimensional. \begin{equation} F=\frac{\delta p}{\delta t} \Longrightarrow F(t)=-mH\omega^{2}cos(\omega t) \end{equation}
Ahora bien para la descripción del movimiento del sismógrafo, tenemos de la anterior ecuación diferencial.
\begin{equation} m\ddot{h}+2m\beta\dot{h}+m\omega_{0}^{2}h=-mH\omega^{2}cos(\omega t) \end{equation}
La cual para simplificar dividimos entre la masa.
\begin{equation}
\ddot{h}+2\beta\dot{h}+\omega_{0}^{2}h=-H\omega^{2}cos(\omega t)
\end{equation}
Sin embargo la solución homogénea es como lo indica el problema: amortiguamiento critico, por tanto nos quedaremos con una solución de la forma:
\begin{equation} h_{(t)}=Acos(\omega t-\phi) \end{equation}
Evaluando derivadas.
\begin{equation} \dot{h_{(t)}}=-A\omega sen(\omega t-\phi) \end{equation}
\begin{equation} \ddot{h}_{(t)}=-A\omega^{2}cos(\omega t-\phi) \end{equation}
Sustituimos en la ecuación diferencial.
\begin{equation} -A\omega^{2}cos(\omega t-\phi)-2A\beta\omega sen(\omega t-\phi)+A\omega_{0}^{2}cos(\omega t-\phi)=-H\omega^{2}cos(\omega t) \end{equation}
Y reagrupamos términos.
\begin{equation} A(\omega_{0}^{2}-\omega^{2})cos(\omega t-\phi)-2A\beta\omega sen(\omega t-\phi)]=-H\omega^{2}cos(\omega t) \end{equation}
De aquí se procederá, partiendo del producto interno entre dos funciones, se puede demostrar que:
\begin{equation}
\int_{0}^{T}cos(\omega t-\phi)sen(\omega t-\phi)=0
\end{equation}
De esto se puede concluir que ambas funciones son ortogonales, y de allí que forman un triangulo rectángulo donde la magnitud de sus catetos es el coeficiente de cada función. Ahora, la fuerza al no poseer el mismo argumento se dice oblicua a las anteriores, y de allí que su argumento corresponda a la hipotenusa, por lo tanto se puede armar por teorema de pitágoras.
\begin{equation} H^{2}\omega^{4}=A^{2}[(\omega_{0}^{2}-\omega^{2})^{2}+4\beta^{2}\omega^{2}] \end{equation}
Lo cual tras algunas manipulaciones algebraicas.
\begin{equation}
\frac{A^{2}}{H^{2}}=\frac{\omega^{4}}{[(\omega_{0}^{2}-\omega^{2})^{2}+4\beta^{2}\omega^{2}]}
\end{equation}
Por la definición de
\begin{equation} R_{(\omega)}\equiv\frac{4\beta^{2}\omega^{2}}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2}+4\beta^{2}\omega^{2}}} \end{equation}
Multiplicamos la original por el termino del numerador, tomando en cuenta las condiciones de amortiguamiento critico.
\begin{equation} \frac{A^{2}}{H^{2}}=\frac{\omega^{4}}{[(\omega_{0}^{2}-\omega^{2})^{2}+4\beta^{2}\omega^{2}]}\frac{4\omega_{0}^{2}\omega^{2}}{4\omega_{0}^{2}\omega^{2}} \end{equation}
Al simplificar y reducir obtenemos.
\begin{equation} \frac{A}{H}=\frac{\omega}{2\omega_{0}}[R_{(\omega)}]^{\frac{1}{2}} \end{equation}
De aquí que la máxima resonancia es cuando ambas frecuencias angulares son iguales, y entonces la amplitud es igual a un medio de la amplitud con que la tierra oscila.
Aportación por usuarios: Angel Nahir Molina Guadarrama (discusión) 12:35 21 feb 2014 (UTC) ,Andrés Arturo Cerón Téllez (discusión) 21:55 29 jun 2013 (CDT) ,Se agregaron los símbolos para que apareciera una ecuación con el formato adecuado. Andrés Arturo Cerón Téllez (discusión) 22:37 5 jul 2013 (CDT)
Problema 5.19
Una masa de 4 kg alarga 1cm un resorte, la masa se libera desde el reposo inicialmente desde ese punto que esta por arriba de la posición de equilibrio y el movimiento posterior ocurre en un medio que ofrece una fuerza de amortiguamiento igual a un cuarto de la velocidad instantánea; encuentre la ecuación de movimiento si se aplica una una fuerza externa igual a la velocidad instantánea.
Solución
Datos
m= 2 kg
k=2
condiciones iniciales
y
sustituimos términos
la solución a esta ecuación diferencial es
Aportación por usuarios: David Alberto Rojas Solis (discusión) 09:08 6 jul 2013 (CDT) , mfg-wiki (discusión) 12:01 9 may 2013 (CDT)
Problema Extra 3
Una masa que pesa $8lb$ alarga $6in$ un resorte por una masa que pesa $8 lb$. La masa esta sujeta a un mecanismo de amortiguación viscosa que tiene una constante de amortiguamiento de $0.25lb/ft$ y sobre ella actúa una fuerza externa de $4\cos(2t) lb$. Encuentre la posición de la masa en cada instante de tiempo.
Solución
- Hallamos el valor de la constante $k$ y de masa $m$,
- $m=\frac{w}{g}=\frac{8 lb}{32ft/s^{2}}=\frac{1lb⋅s^{2}}{4ft}$
- $k=\frac{w}{l}=\frac{8 lb}{6ft}=16\frac{lb}{ft}$
- Buscamos el modelo estándar de una oscilación forzada,
- $m\frac{d^{2}y}{dx^{2}}+b\frac{dy}{dx}+ky=g(t)$
- Entonces, con $m=\frac{1}{4}, b=0.25, k=16, g(t)=4\cos(2t)$
- $\frac{1}{4}\frac{d^{2}y}{dx^{2}}+\frac{1}{4}\frac{dy}{dx}+16y=4\cos(2t)=\frac{d^{2}y}{dx^{2}}+\frac{dy}{dx}+64y=16\cos(2t)\qquad\qquad (1)$
- El problema estriba en hallar la función $y(t)$ que satisfaga la ecuación $(1)$. La solución general de la ecuación $(1)$ consta de una solución homogénea y una solución particular,
- $y(t)=y_{h}(t)+y_{p}(t)$
- Para hallar la solución de la ecuación diferencial homogénea, buscamos el polinomio característico de la ecuación,
- Tenemos los valores, $a=1, b=1, c=64$
- $r^{2}+r+64=0$
- Con discriminante,
- $D=b^{2}-4ac=(1)-4(1)(64)=-255<0$
- Obtenemos el valor de $r$,
- $r_{1,2}=λ±іμ=-\frac{b}{2a}±і\frac{\sqrt{D}}{2a}=-\frac{1}{2}±і\frac{\sqrt{255}}{2}$
- Por lo tanto, las soluciones de $(1)$ linealmente independientes son,
- $y_{1}(t)=e^{λt}\cos(μt)$
- $y_{1}(t)=e^{-\frac{t}{2}}\cos(\frac{\sqrt{255}}{2}t)$
- $y_{2}(t)=e^{λt}\sin(μt)$
- $y_{2}(t)=e^{-\frac{t}{2}}\sin(\frac{\sqrt{255}}{2}t)$
- Y la solución general homogénea de $(1)$ es,
- $y_{h}(t)=C_{1}y_{1}(t)+C_{2}y_{2}(t)=C_{1}e^{-\frac{t}{2}}\cos(\frac{\sqrt{255}}{2}t)+C_{2}e^{-\frac{t}{2}}\sin(\frac{\sqrt{255}}{2}t)$
- Para encontrar la solución particular de $(1)$ utilizamos el método de los coeficientes indeterminados. Proponemos la solución,
- $y_{p}(t)=A\cos(2t)+B\sin(2t)$
- $y'_{p}(t)=-2A\sin(2t)+2B\cos(2t)$
- $y’’_{p}(t)=-4A\cos(2t)-4B\sin(2t)$
- Igualamos la ecuación $(1)$ con la solución particular propuesta y sus derivadas,
- $\frac{d^{2}y}{dx^{2}}+\frac{dy}{dx}+64y=[-4A\cos(2t)-4B\sin(2t)]+[-2A\sin(2t)+2B\cos(2t)]+64[A\cos(2t)+B\sin(2t)]$
- $=16\cos(2t)$
- Factorizando los senos y cosenos,
- $[-4A+2B+64A]\cos(2t)+[-4B-2A+64B]\sin(2t)=16\cos(2t)$
- Igualamos los términos en grado y coeficiente de ambos miembros de la igualdad, y se resuelve el sistema,
- $60A+2B=16$
- $-2A+60B=0$
- $A=\frac{240}{901}$
- $B=\frac{8}{901}$
- Por lo tanto la solución particular es,
- $y_{p}(t)=A\cos(2t)+B\sin(2t)=\frac{240}{901}\cos(2t)+\frac{8}{901}\sin(2t) \qquad\qquad (3)$
- Entonces, tomando en cuenta las ecuaciones $(2)$ y $(3)$, la solución general de la ecuación diferencial es,
- $y(t)=y_{h}(t)+y_{p}(t)=C_{1}e^{-\frac{t}{2}}\cos(\frac{\sqrt{255}}{2}t)+C_{2}e^{-\frac{t}{2}}\sin(\frac{\sqrt{255}}{2}t)+\frac{240}{901}\cos(2t)+\frac{8}{901}\sin(2t)$
En conclusión, $y(t)$ satisface la ecuación $(1)$ y representa la posición de la masa en cualquier instante de tiempo.
Aportación por usuario: Rodrigo (discusión) 20:10 3 jul 2020 (CDT)
Problemas Adicionales del French
Problema 2, capítulo 4 del French
Considerar el procedimiento de resolver el movimiento de estado estaciona- rio de un oscilador forzado si la fuerza impulsora es de la forma $F=f_{0}\sin(\omega t)$ en lugar de $F=f_{0}cos(\omega t)$
Solución
el sistema se rige por la ecuación
${\ddot{x}+\omega^{2}x=f_{0}\sin(\omega t)}$
donde $f_{0}=\frac{F_{0}}{m}$ proponemos que $x=A\sin(\omega t+\alpha)$
nos da:
$-A\omega^{2}\sin(\omega t+\alpha)+A\omega_{0}^{2}\sin(\omega t+\alpha)=f_{0}\sin(\omega t)$
$A(\omega_{0}^{2}-\omega)A\left[cos(\omega t)\sin\alpha+\sin(\omega t)cos\alpha\right]=f_{0}\sin(\omega t)$
$\sin(\omega t)cos\alpha\left[A(\omega_{0}^{2}-\omega)-f_{0}\right]+cos(\omega t)\sin\alpha A(\omega_{0}^{2}-\omega)=0$
esto seria igual a cero solo cuando ambos coeficientes junto sin($\omega t)$ y cos ($\omega t)$ sean cero por separado. Esto da:
$A=\frac{f_{0}}{\omega_{0}^{2}-\omega}$
para $\alpha=0$ o $\alpha=\pi$
Problema Adicional 2 FRENCH Problema 4-13
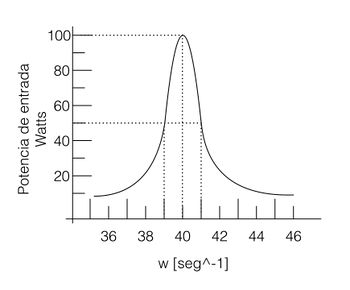
Vibraciones y ondas. A. P. FRENCH pág. 132. Problema 4-13.
El gráfico muestra la curva de resonancia de potencia de un determinado sistema mecánico cuando se ve accionado por una fuerza , en donde es constante y es variable.
a)Hallar los valores numéricos de y Q para este sistema. b)Si suprime la fuerza impulsora.¿Después de cuántos ciclos de oscilación libre ha descendido la energía del sistema a 1/e de su valor inicial?
Solución
Inciso a
a) Observando la gráfica se tiene como punto mas alto a
Para Q, usando
se sabe que es la anchura de la curva a la mitad de la altura máxima.
Sustituyendo en
Inciso b
b) De
sabemos que la energía decae por un factor de 1/e al tiempo
El número de ciclos se obtiene con
Resuelto por: Luis Velázquez (discusión) 21:49 11 mar 2015 (CDT)
Problema Adicional 3 French 4.17
Problema 4.17 , Vibraciones y Ondas, A.P. French, Publicación del MIT
Un objeto de masa de 2 kg cuelga de un muelle de masa despreciable. El muelle se alarga en 2.5 cm cuando se le sujeta dicho objeto. El extremo superior del muelle se hace oscilar hacia arriba y hacia abajo con un movimiento armónico simple de amplitud 1 mm. La Q del sistema es 15.
a) ¿Cuál es para el sistema?
b) ¿Cuál es la amplitud de la oscilación formada para ?
c) ¿Cuál es la potencia media de entrada para mantener la osculación formada a una frecuencia 2% mayor que ?
usando la expresión
Solución:
Consideraciones:
1. Por el enunciado el problema se solucionará tomando la descripción de un movimiento armónico simple, considerando la oscilación forzada, dado que el resorte que es colgado tiene un término de fuerza restitutiva, fuerza amortiguada, una fuerza forzada y a una fuerza externa, por ende la expresión que cumple esta descripción es de la forma:
\[
\ddot{\psi}+\gamma\dot{\psi}+\omega_{0}^{2}\psi=\frac{F_{0}}{m}\cos\omega t\qquad\
\]
2. Una solución es , Donde la amplitud "A", es descrita por en donde se puede demostrar que (Problema 5.5) la amplitud máxima está dada por \[ A_{m}=\frac{F_{0}}{s}\frac{\omega_{0/}\omega}{\left[\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}+\frac{1}{Q^{2}}\right]^{1/2}} \] .
3. Como el resorte está colgado, dejaremos la suma de fuerzas es cero, dado que está en reposo y por Newton tenemos que: Por lo tanto , donde es la constante del resorte y es el desplazamiento con respecto de la vertical en donde el sistema está en reposo.
Inciso a
a) Tomamos a , donde Donde , por obtenemos que
Inciso b
b) Tomando la expresión: En donde Conociendo podemos expresar la ecuación anterior como: Donde para se obtiene que:
resolviendo el problema:
Inciso c
c) Con la expresión, dada en el problema es: Tomando a y y resolviendo el la expresión obtenemos que:
Hecho por: Pablo (discusión) 22:53 14 mar 2015 (CDT) . Correcciones por: Pablo (discusión) 23:00 14 mar 2015 (CDT), Rodrigo (discusión) 10:20 3 jul 2020 (CDT)
Problemas Adicionales
Problema Adicional 1
Cuando un automóvil va por un camino con ondulaciones regulares (como una tabla de lavar), los golpes hacen que las ruedas oscilen sobre los amortiguadores. Encontrar la velocidad del coche a la cual resuena la oscilación, sabiendo que al subir en el auto cuatro personas de 80 kg, este se une dos centímetros, cada eje con sus dos ruedas tiene una masa total de 50kg, y las ondulaciones en el piso están cada 80cm.
Solución:
Se tienen cuatro amortiguadores (resortes de Hooke), en paralelo, los que se comprimen 2cm al colocar
sobre ellos cuatro masas de 80kg. Por la ley de Hooke se tiene:
\[
k_{e}=\frac{F}{4x}=\frac{(4)(80kg)(9.81\frac{m}{s})}{(4)(0.002m)}
\]
\[
k_e \approx 4 \times 10 ^{4} \frac{N}{m}
\]
Cada par de llantas con su eje y amortiguadores constituyen un oscilador armónico descrito por:
\[ m\ddot{x}+2k_e x =0 \] \[ \ddot{x}+\frac{2K_e}{m} x =0 \]
\[ \ddot{x}+\omega_0^2 x =0 \]
con \[\omega_0 ^2 = \frac{2k_e}{m}=\frac{2(4 \times 10^4 \frac{N}{m})}{50 kg}=1600 s^2 \]
Y con una frecuencia natural de oscilación de:
\[\nu =\frac{\omega_0}{2 \pi}\]
\[\nu=6 Hz\]
Al pasar por un tramo de carretera ondulado, cada par de llantas será un oscilador forzado, por lo que ahora su comportamiento queda descrito por:
\[ \ddot{x}+\omega_0 ^2 x = (\frac{f_0}{m})cos(\omega t) \qquad\qquad (2) \]
Para esta ED se propone la solución: \[ x=c_1 cos (\omega t) + c_2 sin(\omega t) \]
con derivadas: \[\dot{x}= -c_1 \omega sin(\omega t) +c_2 \omega cos (\omega t)\]
\[\ddot{x}=-c_1\omega^2 cos(\omega t)-c_2 \omega^2 sen(\omega t)\]
Sustutuyendo en (2) se tiene:
\[-c_1\omega^2 cos(\omega t)-c_2 \omega^2 sen(\omega t)+c_1 \omega_0 ^2 cos (\omega t) + c_2\omega_0 ^2 sin(\omega t)=(\frac{f_0}{m})cos(\omega t) \]
De donde se tiene:
\[c_2 =0\]
\[c_1 (\omega_0 ^2 -\omega ^2)= \frac{f_0}{m}\]
\[c_1 = A =\frac{f_0}{m(\omega_0 ^2 - \omega^2)}\]
De esta ultima expresión, podemos ver que la amplitud sera pequeña cuando $\omega _0^2 -\omega^2$ sea grande pero crece abruptamente cuando $\omega \longrightarrow \omega _0$. El fenómeno de resonancia esta representado por el hecho de que el valor de A, sin tomar en cuenta el signo, resulta infinitamente grande si:
\[\omega = \omega _0 =40 s\]
Siendo \[V=\frac{\lambda}{\omega}= \frac{.08m}{40 s}\]
Por lo que las llantas del auto estarán en resonancia cuando la velocidad sea:
\[V\approx 5 ms^-1\]
Tomado de: Mecánica clásica John R. Taylor ISBN:978-84-291-4312-6 PP.234
Resuelto por Luis Enrique Santos.
Realizado por usuario: Luis Santos (discusión) 22:58 5 mar 2015 (CST)
Ejercicio adicional 2, Oscilaciones Acopladas
se considera una cuerda discreta compuesta por 3 partículas espaciadas regularmente sobre la misma. En el instante t=0, la partícula central sufre un desplazamiento (a) y después se deja libre desde el reposo.
Calcular el movimiento subsiguiente.
en primer lugar las condiciones iniciales son :
q2(0)=a, q1(0)=q3(0)=0 q1(0)=q2(0)=q3(0)=0
como las velocidades iniciales son nulas, las (V) se anularan y las vendran dadas por :
entonces : ,
las cantidades r y j para la partícula 1 son :
r=1, j=
r=2, j = 1
r=3,j=
para la partícula 2 :
r=1,j=1
r=2,j=0
r=3,j=-1
para la partícula 3
r=1,j=
r=2, j= -1
r=3, j= -
y por consiguiente el desplazamiento de las 3 partículas serán:
q1(t) =
q2(t)=
q3(t) =
Realizado por usuario: Luisa Alejandra Vega Sanchez (discusión) 12:13 15 mar 2015 (CDT) usuario : Luisa Alejandra Vega Sanchez
Problema Adicional 3, de vibraciones forzadas
Dos esferas de masa cada una están soldadas a una barra ligera que esta articulada en el punto B. Una segunda barra ligera esta solada a la anterior. Se aplica una perturbación en el punto A igual a $F=F_{0}\sin{\omega}t$. En el otro extremo C, se encuentra un muelle recuperador que cuando AC esta horizontal no presenta deformación. Si la amplitud de rotación estacionaria sistema se mantiene por debajo de 0.0020 ¿Que rango de frecuencias esta permitido?. Utiliza los siguientes datos:
Solución:
Aplicando las ecuaciones de movimiento, se tiene
$\sum M_{B}=I_{B}\alpha$
$F(a\cos{\theta})+Mgl\sin{\theta}-F_{e}a\cos{\theta}=I_{B}\alpha$
Para ángulos pequeños $\cos{\theta}\simeq 1$
$F(a)-F_{e}(a)=I_{B}\alpha$
$aF_{0}\sin{\omega}t=I_{B}\alpha+(kx_{e})a$
$aF_{0}\sin{\omega}t=(Ml^{2}+Ml^{2})\alpha+(kx_{e})a$
$aF_{0}\sin{\omega}t=(2Ml^{2})\ddot{\theta}+(kx_{e})a$ .....$(1)$
Sustituyendo valores en $(1)$ tenemos:
$0.36\ddot{\theta}+70\theta=\sin{\omega}t$
L solución permanente es de la forma
$\theta=\theta_{0}\sin{\omega}t$
y resolviendo para $\omega$ se tiene que
$\omega=\pm7.rad/s$
Aportación por usuario: Héctor Reséndiz (discusión) 21:11 15 mar 2015 (CDT)
Problema adicional 4, interpretación de un problema de valores iniciales
Un peso de 16 libras se une al extremo inferior de un muelle helicoidal suspendido del techo, la constante de resorte del resorte siendo 10 libras / ft. El peso viene a descansar en su posición de equilibrio. Comenzando en t = 0 una fuerza externa dada por F (t) = 5 cos (2t) se aplica al sistema. Determinar el movimiento resultante si la fuerza de amortización en libras es numéricamente igual a 2 (dx / dt), fueron dx / dt es la velocidad instantánea en pies por segundo.
Solución
Tenemos que : $m=\frac{w}{g}=\frac{16}{32}=\frac{1}{6}slug$, $a=2$, $k=10$, $F(t)=5cos(2t)$.
La ecuación que describe el sistema mencionado es
\begin{equation} \frac{1}{2}\frac{dx^{2}}{dt^{2}}+2\frac{dx}{dt}+10x=5cos(2t) \end{equation}
Multiplicando por 2 la ecua ion anterior
\begin{equation} \frac{dx^{2}}{dt^{2}}+4\frac{dx}{dt}+20x=10cos(2t) \end{equation}
La solución general de la ecuación homogénea esta dada por:
\[ x_{h}(t)=exp(-2t)[c_{1}sin(4t)+c_{2}cos(4t)] \]
Por el método de coeficientes indeterminados, la solución particular para ecuación (1) es de la forma
\begin{equation} x{}_{p}=Acos(2t)+Bsin(2t) \end{equation}
Calculando la primera y la segunda derivada de la ecuación (3) y sustituyéndolas
en la ecuación (2) obtenemos el siguiente sistema de ecuaciones.
\[ 16A+8B=10 \]
\[
16B-8A=0
\]
Resolviendo, $A=\frac{1}{2},B=\frac{1}{4}$. Entonces:
\[ x(t)=x_{h}+x_{p}=exp(-2t)[c_{1}sin(4t)+c_{2}cos(4t)]+\frac{1}{2}cos(2t)+\frac{1}{4}sin(2t) \]
Realizado por Rosario Maya (discusión) 22:13 15 mar 2015 (CDT)
Problema Adicional 5 Resonancia
Muestra que el valor máximo de la amplitud es de la forma , en la cual se dice que el sistema está en resonancia.
Solución
Se tiene la ecuación diferencial básica, que es:
$ \ddot{\varPsi}+2\lambda\dot{\varPsi}+\omega^{2}\varPsi=F(t)\qquad\qquad (1) $
donde , y .
Supondremos que es suficientemente pequeño, de modo que el amortiguamiento es menor que el crítico; es decír, .
La solución complementaria de la ecuación (1) es
$ \varPsi_{C}(t)=e^{-\lambda t}\left\{ c_{1}\cos\left(\sqrt{\omega^{2}-\lambda^{2}}t\right)+c_{2}\sin\left(\sqrt{\omega^{2}-\lambda^{2}}t\right)\right\} $
con
Constantes arbitrarios, que dependen de las condiciones iniciales, o equivalentes; entonces
$ \varPsi_{C}(t)=Ae^{-\lambda t}\sin\left(\sqrt{\omega^{2}-\lambda^{2}}t+\phi\right)\qquad\qquad (2) $
donde , , .
Ahora determinaremos una solución particular partiendo de la ecuación (1) utilizando el método de los coeficientes indeterminados
$ \varPsi_{P}(t)=B\cos\left(\alpha t\right)+C\sin\left(\alpha t\right) $
entonces
$ \dot{\varPsi}_{P}(t)=-\alpha B\sin\left(\alpha t\right)+\alpha C\cos\left(\alpha t\right) $
$ \varPsi_{P}(t)=-\alpha^{2}B\cos\left(\alpha t\right)-\alpha^{2}C\sin\left(\alpha t\right). $
Sustituyendo
$ \varPsi_{P}\left(t\right),\dot{\varPsi}_{P}(t),\ddot{\varPsi}_{P}(t) $ en (1) se obtiene
Igualando los coeficientes en la última igualdad, resulta el sistema de ecuaciones
cuya solución es
Consecuentemente
$ \varPsi_{P}(t)=-\frac{2\alpha\lambda F_{0}}{\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}}\cos\left(\alpha t\right)+\frac{\left(\omega^{2}-\lambda^{2}\right)F_{0}}{\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}}\sin\left(\alpha t\right). $
Podemos escribir la solución particular en la forma
$ \varPsi_{P}(t)=\tilde{A}\sin\left(\alpha t+\theta\right), $
donde
es decir,
El ángulo está determinado por las relaciones
Así que
$ \varPsi_{P}(t)=\frac{F_{0}}{\sqrt{\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}}}\sin\left(\alpha t+\theta\right)\qquad\qquad (3) $
Observemos que la solución completa es la suma de dos términos
$ \varPsi(t)=\varPsi_{C}(t)+\varPsi_{P}(t). $
El primero de la ecuación (2) representa la oscilación amortiguada, que sería todo el movimiento del sistema si la fuerza externa “F(t)” no actuara. El segundo término de la ecuación (3), resulta de la presencia de la fuerza externa, representa un movimiento armónico simple de periodo y amplitud
Para fijos, la amplitud es función de . Consideremos la función en el intervalo . Se tiene que
Luego, si y solo si o . Se puede verificar que la amplitud de las oscilaciones alcanza un valor máximo cuando
Por lo que el valor máximo de la amplitud es
Bibliografía:
Birkhoff, G. y Rotta, G,. Ordinary Differencial Equations 3 era edicion, New York 1978
Resuelto por usuario : Ricardo García HernándezRicardo Garcia Hernandez (discusión) 23:58 15 mar 2015 (CDT)
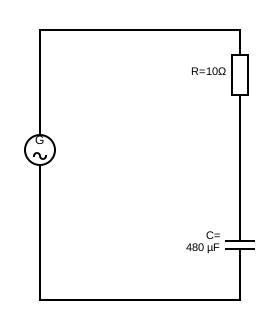
Problema Circuito RC
Un circuito está formado por una resistencia de 10$\Omega$ en serie con un condensador de 480µf. El circuito está alimentado por una tensión de 220V(eficaces) a una frecuencia de 50Hz.
Hallar:
a) Valor de la impedancia del circuito(módulo y argumento).
b) Valor instantáneo y eficaz de la corriente que atraviesa el circuito y su fase respecto de V.
Solución
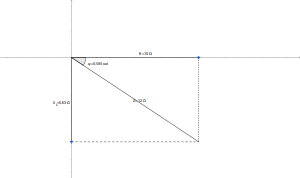
Inciso a
a)Valor de Z.
valor del argumento:
Con estos valores se puede hacer el triangulo de Z:
Inciso b
b)Valor instantáneo de la corriente. Una tensión eficaz de $220V/50Hz$ corresponde con una tensión de:
por tanto:
donde $I_0 = 25.92A$
y el valor eficaz de la corriente está dado por:
Resultado por usuario: Luis Martínez (discusión) 08:31 15 mar 2015 (CDT)--Luis Martínez (discusión) 08:31 15 mar 2015 (CDT)
Problemas Extra
Problema Extra 1
Si un sistema resorte - masa no amortiguado con una masa que pesa $6lb$ y una constante de resorte de $ 1 \frac{lb}{in}$ se pone repentinamente en movimiento en $t=0$ por una fuerza externa de $4\cos(7t) lb$, determine la posición de la masa en cualquier instante de tiempo.
Solución
- Primero calculamos la masa,
- $m=\frac{w}{g}=\frac{6 lb}{32 ft/s^{2}}=\frac{3 lb·s^{2}}{16ft}=\frac{1 lb·s^{2}}{64in}$
- Buscamos el modelo estándar de una oscilación forzada,
- $m\frac{d^{2}y}{dx^{2}}+b\frac{dy}{dx}+ky=g(t)$
- Entonces, con $m=\frac{1}{64}, b=0, k=1, g(t)=4\cos(7t)$
- $\frac{1}{64}\frac{d^{2}y}{dx^{2}}+0\frac{dy}{dx}+y=4\cos(7t) \qquad\qquad (1)$
- El problema estriba en hallar la función $y(t)$ que satisfaga la ecuación $(1)$. La solución general de la ecuación $(1)$ consta de una solución homogénea y una solución particular,
- $y(t)=y_{h}(t)+y_{p}(t)$
- Para hallar la solución de la ecuación diferencial homogénea, buscamos el polinomio característico de la ecuación,
- Tenemos los valores; $a=\frac{1}{64}, b=0, c=1$
- $\frac{1}{64}r^{2}+1=0$
- Con el discriminante,
- $D=b^{2}-4ac=-4(\frac{1}{64})(1)=\frac{-1}{16}<0$
- Obtenemos el valor de $r$,
- $r_{1,2}=λ±іμ=-\frac{b}{2a}±і\frac{\sqrt{D}}{2a}=±і\frac{\sqrt{\frac{1}{16}}}{2\frac{1}{64}}=$ $±8і$
- Por lo tanto, las soluciones de $(1)$ linealmente independientes son,
- $y_{1}(t)=e^{λt}\cos(μt)$
- $y_{1}(t)=\cos(8t)$
- $y_{2}(t)=e^{λt}\sin(μt)$
- $y_{2}(t)=\sin(8t)$
- Y la solución general homogénea de $(1)$ es,
- $y_{h}(t)=C_{1}y_{1}(t)+C_{2}y_{2}(t)=C_{1}\cos(8t)+C_{2}\sin(8t) \qquad\qquad (2)$
- Para encontrar la solución particular de $(1)$ utilizamos el método de los coeficientes indeterminados. Proponemos la solución,
- $y_{p}(t)=A\cos(7t)+B\sin(7t)$
- $y'_{p}(t)=-7A\sin(7t)+7B\cos(7t)$
- $y’’_{p}(t)=-49A\cos(7t)-49B\sin(7t)$
- Igualamos la ecuación $(1)$ con la solución particular propuesta y sus derivadas,
- $\frac{1}{64}\frac{d^{2}y}{dx^{2}}+y=6[-49A\cos(7t)-49B\sin(7t)]+[A\cos(7t)+B\sin(7t)]=4\cos(7t)$
- Factorizando los senos y cosenos,
- $[-\frac{49}{64}A+A]\cos(7t)+[-\frac{49}{64}B+B]\sin(7t)=4\cos(7t)$
- Igualamos los términos en grado y coeficiente de ambos miembros de la igualdad, y se resuelve el sistema,
- $\frac{15}{64}A=4$
- $\frac{15}{64}B=0$
- Entonces,
- $A=\frac{256}{15}$
- $B=0$
- Por lo tanto la solución particular es,
- $y_{p}(t)=A\cos(7t)+B\sin(7t)=\frac{256}{15}\cos(7t) \qquad\qquad (3)$
- Entonces, tomando en cuenta las ecuaciones $(2)$ y $(3)$, la solución general de la ecuación diferencial es,
- $y(t)=y_{h}(t)+y_{p}(t)=C_{1}\cos(8t)+C_{2}\sin(8t)+\frac{256}{15}\cos(7t)$
En conclusión, $y(t)$ satisface la ecuación $(1)$ y representa la posición de la masa en cualquier instante de tiempo.
Realizado por usuario: Rodrigo (discusión) 15:20 3 jul 2020 (CDT) , Rodrigo (discusión) 10:32 3 jul 2020 (CDT)
Problema Extra 2
Una masa que pesa $8 lb$ alarga $6 in$. Sobre el sistema actúa una fuerza externa de $8\sin(8t) lb$. Si se tira hacia abajo de la masa $3 in$ y luego se suelta, determine la posición de la masa en cualquier instante. Determine las primeras cuatro veces en las que la velocidad de la masa es cero.
Solución
- Hallamos el valor de la constante $k$ y de masa $m$,
- $m=\frac{w}{g}=\frac{8 lb}{32ft/s^{2}}=\frac{1lb⋅s^{2}}{4ft}$
- $k=\frac{w}{l}=\frac{8 lb}{0.5ft}=16\frac{lb}{ft}$
- Buscamos el modelo estándar de una oscilación forzada,
- $m\frac{d^{2}y}{dx^{2}}+b\frac{dy}{dx}+ky=g(t)$
- Entonces, con $m=\frac{1}{4}, b=0, k=16, g(t)=8\sin(8t)$
- $\frac{1}{4}\frac{d^{2}y}{dx^{2}}+0\frac{dy}{dx}+16y=8\sin(8t) \qquad\qquad (1)$
- El problema estriba en hallar la función $y(t)$ que satisfaga la ecuación $(1)$. La solución general de la ecuación $(1)$ consta de una solución homogénea y una solución particular,
- $y(t)=y_{h}(t)+y_{p}(t)$
- Para hallar la solución de la ecuación diferencial homogénea, buscamos el polinomio característico de la ecuación,
- Tenemos los valores, $a=\frac{1}{4}, b=0, c=16$
- $\frac{1}{4}r^{2}+16=0$
- Con discriminante,
- $D=b^{2}-4ac=-4(\frac{1}{4})(16)=-16<0$
- Obtenemos el valor de $r$,
- $r_{1,2}=λ±іμ=-\frac{b}{2a}±і\frac{\sqrt{D}}{2a}=±і\frac{\sqrt{16}}{2\frac{1}{4}}=$ $±8і$
- Por lo tanto, las soluciones de $(1)$ linealmente independientes son,
- $y_{1}(t)=e^{λt}\cos(μt)$
- $y_{1}(t)=\cos(8t)$
- $y_{2}(t)=e^{λt}\sin(μt)$
- $y_{2}(t)=\sin(8t)$
- Y la solución general homogénea de $(1)$ es,
- $y_{h}(t)=C_{1}y_{1}(t)+C_{2}y_{2}(t)=C_{1}\cos(8t)+C_{2}\sin(8t) \qquad\qquad (2)$
- Para encontrar la solución particular de $(1)$ utilizamos el método de los coeficientes indeterminados. Proponemos la solución,
- $y_{p}(t)=A\cos(8t)+B\sin(8t)$
- Sin embargo, notamos que existe dependencia lineal entre las soluciones particular y homogénea. Por lo que proponemos una solucion de la forma,
- $y_{p}(t)=At\cos(8t)+Bt\sin(8t)$
- $y'_{p}(t)=A[\cos(8t)-8t\sin(8t)]+B[\sin(8t)+8t\cos(8t)]$
- $y’’_{p}(t)=A[-16\sin(8t)-64t\cos(8t)]+B[16\cos(8t)-64t\sin(8t)]$
- Igualamos la ecuación $(1)$ con la solución particular propuesta y sus derivadas,
- $\frac{1}{4}\frac{d^{2}y}{dx^{2}}+16y=\frac{1}{4}[A[-16\sin(8t)-64t\cos(8t)]+B[16\cos(8t)-64t\sin(8t)]+16[At\cos(8t)+Bt\sin(8t)]=$
- $=8\sin(8t)$
- Factorizando los senos y cosenos,
- $t\cos(8t): -16A+16A=0$
- $t\sin(8t): -16B+16B=0$
- $\cos(8t): -4B$
- $\sin(8t): 4B$
- Igualamos los términos en grado y coeficiente de ambos miembros de la igualdad, y se resuelve el sistema,
- $-4A=4$
- $4B=0$
- Entonces,
- $A=-2$
- $B=0$
- Por lo tanto la solución particular es,
- $y_{p}(t)=At\cos(8t)+Bt\sin(8t)=-2t\cos(8t) \qquad\qquad (3)$
- Entonces, tomando en cuenta las ecuaciones $(2)$ y $(3)$, la solución general de la ecuación diferencial es,
- $y(t)=y_{h}(t)+y_{p}(t)=C_{1}\cos(8t)+C_{2}\sin(8t)-2t\cos(8t)$
En conclusión, $y(t)$ satisface la ecuación $(1)$ y representa la posición de la masa en cualquier instante de tiempo.
- Para hallar la ecuación especifica $y(t)$ debemos prestar atención a las condiciones iniciales que nos dan en el problema. El resorte se estira $3in$, es decir, $\frac{1}{4} ft$ en el tiempo $t=0$. Entonces,
- $y(0)=\frac{1}{4}$
- Ademas, nos piden buscar los valores de $t$, para los cuales la velocidad es cero, por lo que podemos decir que,
- $y'(0)=0$
- Reacomodando estas condiciones,
- $y(0)=C_{1}\cos(8t)+C_{2}\sin(8t)-2t\cos(8t)=C_{1}=\frac{1}{4}$
- $y'(0)=16t\sin(8t)-8C_{1}\sin(8t)+8C_{2}\cos(8t)-2\cos(8t)=8C_{2}-2=0$
- Despejando constantes, tenemos,
- $C_{1}=\frac{1}{4}$
- $C_{2}=\frac{1}{4}$
- Entonces la solución especifica con valores iniciales de $y(t)$ es,
- $y_{e}(t)=\frac{1}{4}\cos(8t)+\frac{1}{4}\sin(8t)-2t\cos(8t) \qquad\qquad 4)$
- Para hallar los valores de $t$ en los que $y'_{e}(t)=0$, separamos $y'_{e}(t)=0$ en dos factores e igualamos a cero.
- $y'_{e}(t)=(16t-2)(\sin(8t))=0$
- Uno de los factores debe de ser cero, para el primer factor tenemos,
- $(16t-2)=0 ⇒ t=\frac{1}{8}$
- Mientras que para $(\sin(8t))$, la función se hará cero en múltiplos de $π$, por lo tanto los primeros múltiplos de $π$ son: $1,2,3$, para que la función seno se haga cero, hacemos las siguientes igualdades en el argumento,
- $8t=π ⇒ t=\frac{π}{8}$
- $8t=2π ⇒ t=\frac{π}{4}$
- $8t=3π ⇒ t=\frac{3π}{8}$
- Los primeros valores de $t$ para los que $y'_{e}(t)=0$ son,
- Valores de t:$⟨ \frac{1}{8}, \frac{π}{8}, \frac{π}{4}, \frac{3π}{8} ⟩$
Realizado por usuario: Rodrigo (discusión) 18:55 3 jul 2020 (CDT)




























































![{\displaystyle \psi =(7.5mm)cos[(6.28s^{-1})t+27^{\circ }]-(2.3mm)sin[(6.20s^{-1})t-121^{\circ }]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/13c0654359615c4c6eabc94072e7a667bdd53dc2)

























+[1.4\cos(1.4t)+6.3\sin(1.4t)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b4de33afd774b8ceac7751361980fcc09ea7d9af)














![A=\frac{F_{0}}{m}\left[\frac{1}{(\omega_{0}^{2}-\omega^{2})^{2}+\gamma^{2}\omega^{2}}\right]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/78182b2da155a200bb6c60bc7f3a79b0547d01aa)









![A_{m}=\frac{F_{0}}{s}\frac{\omega_{0/}\omega}{\left[\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}+\frac{1}{Q^{2}}\right]^{1/2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/69be53b684a6b6077fea675654beb182da6b45cb)

![A_{m}= A_{0} \frac{\omega_{0/}\omega}{\left[\left(\frac{\omega_{0}}{\omega}-\frac{\omega}{\omega_{0}}\right)^{2}+\frac{1}{Q^{2}}\right]^{1/2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/db363d145858f1dce30d5711b88af0cae70150bc)





























![\left(-\alpha^{2}B+2\lambda\alpha C+\omega^{2}B\right)\cos\left(\alpha t\right)+\left[\left(\omega^{2}-\alpha^{2}\right)C-2\alpha\lambda B\right]\sin\left(\alpha t\right)=F_{0}\sin\left(\alpha t\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/117b7687f71cf21b3851ce8d329a5ace60f58363)




![\tilde{A}=\sqrt{\left[\frac{2\alpha\lambda F_{0}}{\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}}\right]^{2}+\left[\frac{\left(\omega^{2}-\lambda^{2}\right)F_{0}}{\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}}\right]^{2}},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8ac6560e0a57dbb23f8bb8f0a1f9924f00ac398e)









![\dot{g}\left(\alpha\right)=\frac{2F_{0}\alpha\left(\omega^{2}-\alpha^{2}-2\lambda^{2}\right)}{\left[\left(\omega^{2}-\lambda^{2}\right)^{2}+4\alpha^{2}\lambda^{2}\right]^{3/2}}.](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2cba5017214735766a37afb93fb49b7c639fc6fa)