aproximación paraxial: soluciones Gaussianas
Ecuación diferencial de onda paraxial
La ecuacion de onda
(1.1)

para una onda monocromática
 deviene en la ecuación de Helmholtz
deviene en la ecuación de Helmholtz
(1.2)

donde  .
Considere que la onda se propaga preferencialmente en la dirección z,
.
Considere que la onda se propaga preferencialmente en la dirección z,
(1.3)

donde  es un campo complejo [1]. El gradiente es entonces
es un campo complejo [1]. El gradiente es entonces
(1.4)
![\nabla\left[\tilde{u}\exp\left(ikz\right)\right]=\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2c3f4b80c06a814c43f8ae340604f3a3ddeacf0c)
y el laplaciano escrito como la divergencia del gradiente es
(1.5)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\right]\exp\left(ikz\right)+\nabla\left[\exp\left(ikz\right)\right]\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31e42a8f437ab9151ad25f46c66eca43088e88c0)
pero
(1.6)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+ik\frac{\partial\tilde{u}}{\partial z}\right]\exp\left(ikz\right)+\left[ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b93d34eaec7b52be0d1b57bdc759ad791089795d)
de manera que
(1.7)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/50fad1b556e75b30fd71652bb6ba6f849e6fcfb7)
La ecuación de Helmhlotz (sin aproximaciones aún) es entonces
(1.8)

La aproximación paraxial requiere que  y
y
(1.9)

El operador nabla se puede expresar en términos de un operador transversal
 mas un operador longitudinal
mas un operador longitudinal  .
En coordenadas cartesianas
.
En coordenadas cartesianas  o en coordenadas cilíndricas
o en coordenadas cilíndricas 
 .
De manera que el laplaciano se puede sustituir por el laplaciano transversal para obtener la ecuación de onda paraxial
.
De manera que el laplaciano se puede sustituir por el laplaciano transversal para obtener la ecuación de onda paraxial
(1.10)

que es una ecuación parabólica.
Solución de onda esférica
Una solución exacta de la ecuación de onda son las ondas esféricas
(2.1)

Demostración: El gradiente de la magnitud radial es  . De manera que
. De manera que
(2.2)

El laplaciano es entonces
(2.3)
![{\displaystyle \nabla ^{2}\psi _{esf}=\nabla \cdot \left[\left(-{\frac {1}{r}}+ik\right){\hat {\mathbf {r} }}\psi _{esf}\right]=\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\nabla \cdot {\hat {\mathbf {r} }}+\nabla \left[\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\right]\cdot {\hat {\mathbf {r} }},}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/adaf8bd94ea63c067299dddd8df7b7051f35384a)
pero  y
y
(2.4)
![\nabla\left[\left(-\frac{1}{r}+ik\right)\psi_{esf}\right]\cdot\hat{\mathbf{r}}=\frac{1}{r^{2}}\psi_{esf}+\left(-\frac{1}{r}+ik\right)^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4f5b3a915bf747ef380ee56aba270007ca02033e)
de manera que el laplaciano deviene
(2.5)
![\nabla^{2}\psi_{esf}=\left[\frac{2}{r}\left(-\frac{1}{r}+ik\right)+\frac{2}{r^{2}}-2\frac{ik}{r}-k^{2}\right]\psi_{esf}=-k^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9b68ef43402ff74fc32333ae259ec3b9f922b725)
y se satisface la ecuación de onda monocromática.
Solución aproximada de ecuación de onda
La expansión de la distancia radial  en ejes cartesianos con una dirección preferencial, digamos z
es
en ejes cartesianos con una dirección preferencial, digamos z
es
(3.1)

La solución aproximada del resultado esférico exacto es entonces
(3.2)

Si se expresa ésta ecuación en términos de la forma preferencial  , se obtiene
, se obtiene
(3.3)

Solución exacta de la ecuación paraxial
Éste resultado es la solución exacta a la ecuación diferencial aproximada.
Demostración: El gradiente transversal es
(3.1.1)
![\nabla_{T}\tilde{u}=\frac{ik}{\left(z-z_{1}\right)}\tilde{u}\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5c244d15af3515d4831330d2b0ef6d3f297794f0)
y el laplaciano transversal
(3.1.2)
![{\displaystyle \nabla _{T}^{2}{\tilde {u}}={\frac {ik}{\left(z-z_{1}\right)}}{\tilde {u}}\nabla _{T}\cdot \left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right]+\left[{\frac {ik}{\left(z-z_{1}\right)}}\nabla _{T}{\tilde {u}}\right].\left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right],}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ae3650ae5c87377568210f5559682b3d0b56ae7e)
que puede escribirse como
(3.1.3)
![\nabla_{T}^{2}\tilde{u}=\frac{2ik}{\left(z-z_{1}\right)}\tilde{u}+\frac{-k^{2}}{\left(z-z_{1}\right)^{2}}\tilde{u}\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a56a95744b3ce95544686bb2fc1301716f515543)
Mientras que la primera derivada longitudinal es
(3.1.4)

de manera que satisface exactamente la ecuación paraxial.
Ondas Gaussianas - solución acotada
Considere la solución para  compleja,
compleja,  .
El término involucrando la dirección de propagación puede escribirse como
.
El término involucrando la dirección de propagación puede escribirse como
(4.1)

El primer término involucra la fase y se describe por el inverso de la función radio de curvatura
(4.2)

El segundo término, puesto que en la fase
está multiplicada por  , es una amplitud decreciente en las direcciones transversales
, es una amplitud decreciente en las direcciones transversales
(4.3)
![\exp\left(-\frac{k}{2}\frac{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}{b\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right]}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c87490eb3f4760b0c241e701795f75f5c33e458)
De manera que corresponde a una Gaussiana en ambos ejes transversales
 que decae a
que decae a  a una distancia
a una distancia
(4.4)
![w^{2}=b\frac{\lambda}{\pi}\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c040188a2a7ae81c2eb9b162b3eb3e5c9fe3a9cb)
donde hemos utilizado la relación  . Para
definir el valor de las constantes a, b en términos de cantidades
con mayor significado físico, considere el plano
. Para
definir el valor de las constantes a, b en términos de cantidades
con mayor significado físico, considere el plano  , entonces
, entonces
(4.5)

donde  es el valor mínimo de la función
es el valor mínimo de la función  y se conoce como la cintura del haz
y se conoce como la cintura del haz
(4.6)

Por otro lado, si se consideran dos planos el primero como  entonces
entonces  y el área el haz es
y el área el haz es  , el segundo plano como
, el segundo plano como  , entonces
, entonces
 , puesto que el área del haz es
, puesto que el área del haz es
 , i.e. la distancia
, i.e. la distancia  es aquella en la cual el área crece el doble de
es aquella en la cual el área crece el doble de  . Ésta distancia
se conoce en física como distancia de Rayleigh.
. Ésta distancia
se conoce en física como distancia de Rayleigh.
(4.7)

En el ámbito fotográfico, es una medida de la profundidad de campo
que estima la nitidez de las imágienes en distintos planos.
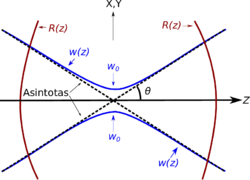
Figura. 4.1 Esquema del comportamiento del diámetro de un haz gaussiano y de los frentes de onda.
El radio del haz (donde decae a  ) es entonces
) es entonces
(4.8)

notar que si  se obtiene que
se obtiene que  la cual es una representación más real de un haz, pues en los experimentos no vemos que el diámetro de un haz se reduzca a un punto en
la cual es una representación más real de un haz, pues en los experimentos no vemos que el diámetro de un haz se reduzca a un punto en  , también en el límite cuando
, también en el límite cuando  obtenemos el caso asintótico (ver Figura. 4.1).
obtenemos el caso asintótico (ver Figura. 4.1).
El radio de curvatura es
(4.9)

para el radio de curvatura también vemos los casos límite, cuando  y cuando
y cuando  el radio de curvatura diverge i.e. tiene comportamiento como onda plana.
el radio de curvatura diverge i.e. tiene comportamiento como onda plana.
La representación polar de  es
es
(4.10)
![\frac{1}{R}+\frac{2i}{kw^{2}}=\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c4a559097b8235dd3110d204c510ac7ffebf6d62)
 puede reescribirse como
puede reescribirse como
(4.11)

y
(4.12)

de manera que
(4.13)
![\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right]=\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d2214d2ba8b8c489df222bbf07c3bb0090827ebb)
mientras que la fase es
(4.14)

La amplitud compleja es entonces
(4.15)
![\tilde{u}=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d6549678113b515ff4af6f9a85ceed8fd67c8af0)
La solución de la ecuación diferencial en la aproximación paraxial es una Gaussiana dada por
(4.16)
![\psi=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right)\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76dd4db3d6a49e2709aecf354596a3ee8f07df08)
Gráficas de esta función se encuentran en la página de Ondas: Gaussianas
- ↑ Siegman A., Lasers, University Science Books, 1986 [cap.16 p. 626]
--LPM 11:30 25 nov 2015 (CDT)
--Mfg 16:57 1 jul 2008 (CDT)
corrección
--CAZ 00:50 9 jul 2008 (CDT)
--Mfg 21:48 6 ago 2008 (CDT)






![\nabla\left[\tilde{u}\exp\left(ikz\right)\right]=\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2c3f4b80c06a814c43f8ae340604f3a3ddeacf0c)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\right]\exp\left(ikz\right)+\nabla\left[\exp\left(ikz\right)\right]\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31e42a8f437ab9151ad25f46c66eca43088e88c0)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+ik\frac{\partial\tilde{u}}{\partial z}\right]\exp\left(ikz\right)+\left[ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b93d34eaec7b52be0d1b57bdc759ad791089795d)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/50fad1b556e75b30fd71652bb6ba6f849e6fcfb7)












![{\displaystyle \nabla ^{2}\psi _{esf}=\nabla \cdot \left[\left(-{\frac {1}{r}}+ik\right){\hat {\mathbf {r} }}\psi _{esf}\right]=\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\nabla \cdot {\hat {\mathbf {r} }}+\nabla \left[\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\right]\cdot {\hat {\mathbf {r} }},}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/adaf8bd94ea63c067299dddd8df7b7051f35384a)

![\nabla\left[\left(-\frac{1}{r}+ik\right)\psi_{esf}\right]\cdot\hat{\mathbf{r}}=\frac{1}{r^{2}}\psi_{esf}+\left(-\frac{1}{r}+ik\right)^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4f5b3a915bf747ef380ee56aba270007ca02033e)
![\nabla^{2}\psi_{esf}=\left[\frac{2}{r}\left(-\frac{1}{r}+ik\right)+\frac{2}{r^{2}}-2\frac{ik}{r}-k^{2}\right]\psi_{esf}=-k^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9b68ef43402ff74fc32333ae259ec3b9f922b725)






![\nabla_{T}\tilde{u}=\frac{ik}{\left(z-z_{1}\right)}\tilde{u}\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5c244d15af3515d4831330d2b0ef6d3f297794f0)
![{\displaystyle \nabla _{T}^{2}{\tilde {u}}={\frac {ik}{\left(z-z_{1}\right)}}{\tilde {u}}\nabla _{T}\cdot \left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right]+\left[{\frac {ik}{\left(z-z_{1}\right)}}\nabla _{T}{\tilde {u}}\right].\left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right],}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ae3650ae5c87377568210f5559682b3d0b56ae7e)
![\nabla_{T}^{2}\tilde{u}=\frac{2ik}{\left(z-z_{1}\right)}\tilde{u}+\frac{-k^{2}}{\left(z-z_{1}\right)^{2}}\tilde{u}\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a56a95744b3ce95544686bb2fc1301716f515543)






![\exp\left(-\frac{k}{2}\frac{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}{b\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right]}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c87490eb3f4760b0c241e701795f75f5c33e458)


![w^{2}=b\frac{\lambda}{\pi}\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c040188a2a7ae81c2eb9b162b3eb3e5c9fe3a9cb)
























![\frac{1}{R}+\frac{2i}{kw^{2}}=\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c4a559097b8235dd3110d204c510ac7ffebf6d62)



![\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right]=\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d2214d2ba8b8c489df222bbf07c3bb0090827ebb)

![\tilde{u}=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d6549678113b515ff4af6f9a85ceed8fd67c8af0)
![\psi=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right)\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76dd4db3d6a49e2709aecf354596a3ee8f07df08)