Una guía de onda es un dispositivo que se usa para transportar energía electromagnética y/o información de un sitio a otro. Generalmente se usa el término línea de transmisión a la guía de ondas usada en el extremo de menor frecuencia del espectro.
Introducción
El nombre de guías de onda se utiliza para designar los tubos de un material conductor de sección rectangular (figura 1), circular o elíptica, en los cuales la dirección de la energía electromagnética debe ser principalmente conducida a lo largo de la guía y limitada en sus fronteras. Las paredes conductoras del tubo confinan la onda al interior por reflexión en la superficie, donde el tubo puede estar vacío o relleno con un dieléctrico. El dieléctrico le da soporte mecánico al tubo (las paredes pueden ser delgadas), pero reduce la velocidad de propagación. Algunos sistemas de comunicaciones utilizan la propagación de ondas en el espacio libre, sin embargo también se puede transmitir información mediante la confinación de las ondas en cables o guías. En altas frecuencias las líneas de transmisión y los cables coaxiales presentan atenuaciones muy elevadas por lo que impiden que la transmisión de la información sea la adecuada, son imprácticos para aplicaciones en alta frecuencia (HF) o de bajo consumo de potencia, especialmente en el caso de señales cuyas longitudes de onda son del orden de centímetros, esto es, microondas.
En las guías los campos eléctrico y magnético están confinados en el espacio que se encuentra en su interior, de este modo no hay pérdidas de potencia por radiación y las pérdidas en el dieléctrico son muy bajas debido a que suele ser aire. Este sistema evita que existan interferencias en el campo por otros objetos, al contrario de lo que ocurría en los sistemas de transmisión abiertos. La guía está diseñada fundamentalmente para operar un solo modo de propagación con el ancho de banda requerido, atenuando los demás modos de orden superior. Esto quiere decir que transmite óptimamente la frecuencia portadora, para la cual se ha seleccionado la guía con su respectivo ancho de banda de transmisión.
Guías de onda
Estamos interesados entonces en la solución de la ecuación homogénea de las ondas en presencia de fronteras conductoras. Es el caso, por ejemplo, de ondas electromagnéticas de longitudes de onda del orden de los centímetros, llamadas microondas, que tienen diversas aplicaciones tecnológicas. Para su propagación, se necesita precisamente disponer de tubos conductores de secciones apropiadas, de dimensiones similares a las longitudes de onda en cuestión. El análisis que sigue lo realizamos en el caso de superficies conductoras perfectas, de conductividad infinita. Las condiciones de contorno nos enseñan que en la región inmediata a la superficie de esos conductores ideales, sólo pueden existir la componente normal del campo eléctrico $\mathbf E_{\bot} = 0$, y la componente tangencial de intensidad magnética  .
.
A fin de analizar las posibles oscilaciones electromagnéticas que pueden propagarse por el interior de la guía de ondas, comenzamos por suponer, que los campos dependen armónicamente del tiempo. Además usamos la notación exponencial compleja, a fin de simplificar el tratamiento. Tomando al eje z como la dirección longitudinal de la guía, suponemos para los campos la forma
\begin{equation}
\mathbf{E}{(\mathbf{r},t) = \mathbf{E_0}({x,y}) }{e}^{i(\mathit{k \cdot z- \omega t})}
\label{1}
\end{equation}
\begin{equation}
\mathbf{B}{(\mathbf{r},t) =\mathbf{B_0}({x,y}) }{e}^{i(\mathit{k \cdot z- \omega t})}
\label{2}
\end{equation}
Utilizando estas definiciones de los campos en las ecuaciones de Maxwell. Los campos eléctrico y magnético deben satisfacer las ecuaciones de Maxwell, en el interior de la guía de onda
\begin{equation}
\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}
\label{3}
\end{equation}
\begin{equation}
\nabla\cdot \mathbf{B}=0
\label{4}
\end{equation}
\begin{equation}
\nabla\times \mathbf{E}=-\frac{\partial\mathbf{B}}{\partial\mathit{t}}
\label{5}
\end{equation}
\begin{equation}
\nabla \times \mathbf{B} = \mu_0 \mathbf{j} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}
\label{6}
\end{equation}
Debemos asumir que esta guía de onda es un conductor perfecto, esto es que tanto el campo eléctrico, como el magnético son nulos dentro del conductor y por lo tanto las condiciones a la frontera en el interior del conductor serán :


Suponiendo un conductor perfecto,  , y por la ley de Faraday, la cual establece que la corriente inducida en un circuito es directamente proporcional a la rapidez con que cambia el flujo magnético que lo atraviesa, implicará que
, y por la ley de Faraday, la cual establece que la corriente inducida en un circuito es directamente proporcional a la rapidez con que cambia el flujo magnético que lo atraviesa, implicará que  .
.
El problema es encontrar las funciones  y
y  que los campos (\ref{1}) y (\ref{2}) obedecen a las ecuaciones diferenciales de Maxwell, sujetas a las condiciones de frontera
que los campos (\ref{1}) y (\ref{2}) obedecen a las ecuaciones diferenciales de Maxwell, sujetas a las condiciones de frontera
\begin{equation}
\mathbf{E_0} = E_x\hat{x} + E_y\hat{y} +E_z\hat{z}
\label{7}
\end{equation}
\begin{equation}
\mathbf{B_0} = B_x\hat{x} + B_y\hat{y} +B_z\hat{z}
\label{8}
\end{equation}
Veamos que (\ref{7}) y (\ref{8}), cumplen con la ecuación de Maxwell
 .
.
Entonces recordemos que  , por lo que hacemos el rotacional para las 3 componentes , es decir ;
, por lo que hacemos el rotacional para las 3 componentes , es decir ;
 ,
,  y
y  .
.
Comencemos entonces con la componente 

de aquí vemos que
 .
.
Ahora lo hacemos para la componente  , y tenemos
, y tenemos

de donde obtenemos:
 .
.
Y por último para la componente en  , tenemos
, tenemos
 .
.
De manera que

Ahora este mismo procedimiento lo aplicamos a :

para el caso cuando la  y
y  , recordemos que estamos analizando para el caso dentro del material.
, recordemos que estamos analizando para el caso dentro del material.
Entonces para cumplir con ecuación de Maxwell necesitamos que :
 .
.
Lo cual se obtiene de manera similar al procedimiento anterior para  , es decir ;
, es decir ;

Continuando con este mismo proceso, llegamos a que las ecuaciones vectoriales resueltas en componentes, que conducen a las relaciones:
i)  , ii)
, ii) 
iii)  , iv)
, iv) 
v)  , vi)
, vi) 
Con este sistema de ecuaciones, resolvemos para encontrar  , en términos de
, en términos de  , untilizando las eciaciones de i-iv, tenemos:
, untilizando las eciaciones de i-iv, tenemos:
i) 
ii) 
iii) 
iv) 
Ahora consideramos la ecuación de la divergencia del campo electrico y que este campo depende armonicamente del tiempo, tomando el eje z como propagación de la onda.

lo cual implica,
\begin{equation}
\left (\frac{\partial\mathit{E_x}}{\partial\mathit{x}}+\frac{\partial\mathit{E_y}}{\partial\mathit{x}} + ik\mathbf{E_z} \right ) = 0
\label{9}
\end{equation}
Utilizando las expresiones i) y ii), sustituyendo en (\ref{9}) obtenemos:

simplificando nos queda,
![\frac{\partial^2\mathbf{E_z}}{\partial\mathit{x}^2}+\frac{\partial^2\mathbf{E_z}}{\partial\mathit{y}^2}+[{\mathrm({\omega/c})^2-k^2}]\mathbf{E_z}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c158dffe96438d7e5dae73c91cb4f955b4f14a5)
y factorizando  , tenemos:
, tenemos:
\begin{equation}
\left [{{\frac{\partial^2}{\partial\mathit{x}^2}}+{\frac{\partial^2}{\partial\mathit{y}^2}}+{\mathrm({\omega/c})^2-k^2}} \right ]\mathbf{E_z}=0
\label{10}
\end{equation}
De igual forma lo hacemos para

obteniendo de manera similar:
\begin{equation}
\left [{{\frac{\partial^2}{\partial\mathit{x}^2}}+{\frac{\partial^2}{\partial\mathit{y}^2}}+{\mathrm({\omega/c})^2-k^2}} \right ]\mathbf{B_z}=0
\label{11}
\end{equation}
Las ondas electromagnéticas viajan a través de las guías por medio de diversas configuraciones a las que llamamos modos de propagación. Un modo es la manera en la que la energía se puede propagar a lo largo de la guía de onda, estos modos deben satisfacer ciertas condiciones de frontera para que se puedan dar. A medida que se va aumentando la frecuencia se irá incrementando el número de modos a partir de cada frecuencia de corte, de cada modo respectivamente. Específicamente una guía soporta tres modos de propagación los cuales son:
1. Modo transversal magnético (TM): también denominado modo  , en el cual las soluciones se derivan a través de la componente del campo eléctrico
, en el cual las soluciones se derivan a través de la componente del campo eléctrico  , con la condición de que
, con la condición de que  , esto es, la componente axial del campo magnético es cero, por lo cual se asegura la transmisión de la potencia en la dirección z que es la que se ha seleccionado como la dirección de propagación de la línea.
, esto es, la componente axial del campo magnético es cero, por lo cual se asegura la transmisión de la potencia en la dirección z que es la que se ha seleccionado como la dirección de propagación de la línea.
2. Modo transversal eléctrico (TE): también denominado modo  , en el cual las soluciones se derivan a través de la componente del campo eléctrico
, en el cual las soluciones se derivan a través de la componente del campo eléctrico  , con la condición de que
, con la condición de que  .
.
3. Modo transversal eléctromagnético (TEM): si eligiésemos simultaneamente  y
y  . Esta última opción es posible en problemas similares; sin embargo, en guías huecas de paredes conductoras no resulta una solución adecuada. Para verlo se puede razonar del siguiente modo: si ambas componentes longitudinales fueran nulas, por las leyes de Gauss y de Faraday, resultaía que el campo eléctrico tendría divergencia y rotacional nulos, es decir, se podría expresar el campo en función de un potencial escalar que cumpliría la ecuación de Laplace. Entonces, ya que
. Esta última opción es posible en problemas similares; sin embargo, en guías huecas de paredes conductoras no resulta una solución adecuada. Para verlo se puede razonar del siguiente modo: si ambas componentes longitudinales fueran nulas, por las leyes de Gauss y de Faraday, resultaía que el campo eléctrico tendría divergencia y rotacional nulos, es decir, se podría expresar el campo en función de un potencial escalar que cumpliría la ecuación de Laplace. Entonces, ya que  , y que las condiciones de contorno del campo sobre la superficie la fuerzan a ser equipotencial, resultando que
, y que las condiciones de contorno del campo sobre la superficie la fuerzan a ser equipotencial, resultando que  en todos los puntos sería una solución posible(y única), y el campo se anularía forzosamente (no habría onda). Sería diferente si en el interior de la guía hubiesse otro conductor, aislado del conductor externo, porque entonces los potenciales en ambos podrían ser distintos, y sí serían posibles soluciones no triviales en ese contexto.
en todos los puntos sería una solución posible(y única), y el campo se anularía forzosamente (no habría onda). Sería diferente si en el interior de la guía hubiesse otro conductor, aislado del conductor externo, porque entonces los potenciales en ambos podrían ser distintos, y sí serían posibles soluciones no triviales en ese contexto.
Los tres modos de propagación son validos para cualquier geometría de guía hueca de paredes conductoras. A continuación tratamos dos ejemplos de guías de onda huecas, la guía rectangular y la guía circular.
Guía de onda rectangular
Si consideramos una guía de dimensiones  , como se muestra en la figura 2:
, como se muestra en la figura 2:
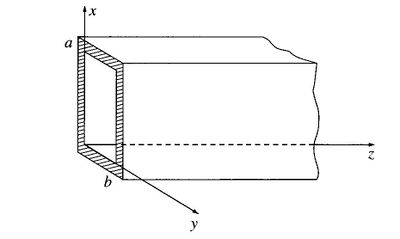
figuira 2. Guía de onda rectangular de dimensión axb y se propaga en el eje z
Modo TE
Supongamos que nuestra onda que incide en la guía es del tipo TE, es decir,  , entonces resolvemos la ecuación (\ref{11})
, entonces resolvemos la ecuación (\ref{11})
![{[{\frac{\partial^2}{\partial\mathit{x}^2}}+{\frac{\partial^2}{\partial\mathit{y}^2}}+{\mathrm({\omega/c})^2-k^2}]}\mathbf{B_z}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33502eadbade3846c151bc27cea5422fb82174f0) .
.
cuya condición de frontera es

Proponemos una solución para (\ref{11})
 .
.
Sustituyendo en (\ref{11}), tenemos que
\begin{equation}
\mathit{Y} \frac {\mathrm d^2X}{\mathrm dx^2} + \mathit{X} \frac {\mathrm d^2Y}{\mathrm dy^2} + [{\mathit({\omega/c})^2-k^2}]\mathit{X}\mathit{Y} = 0
\label{12}
\end{equation}
Esta ecuación se cumple sí y solo sí

y

con
\begin{equation}
{\mathit{-k_x^2}} {\mathit{-k_y^2}}+ [{\mathit({\omega/c})^2-k^2}]\mathit{X}\mathit{Y} = 0
\label{13}
\end{equation}
Entonces la solución para  sera :
sera :

Usando condiciones a la frontera, tenemos que  y
y  ,
,  .
.
Hacemos el mismo procedimiento para  , y vemos que
, y vemos que
 ,
, 
juntando ambas soluciones tenemos la solución general para el modo transversal eléctrico:
\begin{equation}
\mathbf{B_z}= B_0 \cos \left (\frac{\mathit{m}\pi}{a} \right ) \cos \left (\frac{\mathit{n}\pi}{b} \right )
\label{14}
\end{equation}
De esta ecuación notamos los modos normales, a esta solución se lo conoce como modo  , donde al menos un indice debe ser distinto de 0.
, donde al menos un indice debe ser distinto de 0.
Si sustituimos los valores de  y
y  en la ecuación (\ref{13}), obtendremos el numero de onda (k)
en la ecuación (\ref{13}), obtendremos el numero de onda (k)
![\mathit{K} = \sqrt{({\omega/c})^2- \pi^2[({m/a})^2 + ({n/b})^2]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7a7b64c98bee98944257597ddd3b58c10e8708fe)
Notemos que si

el numero de onda (k) es imaginario, y en vez de una onda se tiene campo exponencialmente atenuado. Por esta razón  es llamado frecuencia de corte para el modo TE. La frecuencia de corte mas baja para una guía de onda en dicho modo es
es llamado frecuencia de corte para el modo TE. La frecuencia de corte mas baja para una guía de onda en dicho modo es  . Frecuencias mas bajas que esto no se propagarán en absoluto.
. Frecuencias mas bajas que esto no se propagarán en absoluto.
El numero de onda más simple que podemos encontrar con la frecuencia de corte más baja es
 .
.
Si la velocidad de onda es

con velocidad mayor a c. Sin embargo la energía llevada por la onda viajera es la velocidad de grupo
 .
.
Consideremos que hay reflexión total por la guía de onda de las ondas transmitidas, donde el vector de propagación de las ondas planas, que se puede obtener de la figura 3, es:
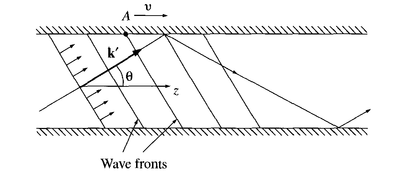
figura 3. Velocidad de grupo se propaga en el eje z
 ,
,
y frecuencia
![\omega=c| k' |=c\sqrt{k^2+\pi^2[(m/a)^2+(n/b)^2]}=\sqrt{(ck)^2+\omega_{mn}^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fb0d5c210ad8ab9ced8533d11cc7e99551537301) .
.
Sólo ciertos ángulos darán lugar a uno de los patrones de ondas permitidos
 .
.
La onda plana viaja a velocidad $c$, pero debido a que se va a un ángulo  con el eje z, esta velocidad neta hacia abajo de la guía de onda es
con el eje z, esta velocidad neta hacia abajo de la guía de onda es
 .
.
La velocidad de la onda, es la velocidad de los frentes de onda hacia abajo de la guía
 .
.
Modo TM
La obtención de los modos TM sigue los mismos pasos que en la sección anterior. Ahora la solución propuesta es

y, sustitullendo en la ecuacion  , llegamos a la solución
, llegamos a la solución
 .
.
Con la condición de frontera

y aplicándolo inmediatamente, puesto que  es una componente del campo eléctrico tangencial a las cuatro paredes de la guía, y debe cancelarse g ¡Junto a todas ellas. Teniendo la expresión final
es una componente del campo eléctrico tangencial a las cuatro paredes de la guía, y debe cancelarse g ¡Junto a todas ellas. Teniendo la expresión final
\begin{equation}
\mathbf{E_z}= E_0 \sin \left (\frac{\mathit{m}\pi}{a} \right ) \sin \left (\frac{\mathit{n}\pi}{b} \right )
\label{15}
\end{equation}
Guía de onda circular
Las leyes que rigen la propagación de las ondas en las guías son independientes da la forma de la sección transversal de la guía y sus dimensiones, debido a esto el concepto de campos eléctricos y magnéticos, así como la frecuencia de corte y en general todos los parámetros presentados en guías de onda rectangulares se cumplen también para guías de onda circulares exceptuando que el problema de los modos de transmisión para guías circulares se presentan en coordenadas cilíndricas.
La guía de onda rectangular se utiliza en distancias cortas y debido a su rigidez no se puede doblar, lográndose que la señal se refleje en otra dirección. La guía circular es un ducto flexible de unos cuantos centímetros de diámetro, el cual puede doblarse sin excesivas reflexiones. Para que la propagación tenga un lugar en la guía de onda circular, la configuración de campo eléctrico y magnético de las ondas deben satisfacer ciertas condiciones. Hay muchas posibles configuraciones, llamadas modos. Los modos se designan según las direcciones que los campos eléctricos y magnéticos de la onda electromagnética asumen respecto de la dirección de propagación.
Modo TM
Consideremos una guía de onda cilíndrica de radio a, formada por un conductor perfecto. Condiciones de frontera

Vamos a considerar una onda monocrómatica, propagándose en la dirección z

donde r y  son las componentes radial y azimutal en coordenadas cilíndricas. Sustituimos en la ecuación de onda para
son las componentes radial y azimutal en coordenadas cilíndricas. Sustituimos en la ecuación de onda para 

Aplicando el operador  en coordenadas cilíndricas:
en coordenadas cilíndricas:

Aplicamos el método de separación de variables con

Fibra Óptica
Consideraremos una fibra óptica que consiste en un núcleo y revestimiento, y que la diferencia entre sus indices de refracción es mínima.
Así el campo óptico está en gran parte confinado al núcleo de la fibra.
La fibra es circular, y tiene un núcleo de radio  con un índice de refracción uniforme
con un índice de refracción uniforme  , lijeramente mayor que el índice de refracción del revestimiento
, lijeramente mayor que el índice de refracción del revestimiento  , asi las permitividades relativas del núcleo y el revestimiento son respectivamente
, asi las permitividades relativas del núcleo y el revestimiento son respectivamente  y
y  .
.
Ecuaciones de Maxwell
Supongamos ahora que existe un campo electromagnético  que oscila a una sola frecuencia
que oscila a una sola frecuencia  , dicho vector se puede escribir.
, dicho vector se puede escribir.
![\mathbf{A}{(\mathbf{r},t) = Re[\mathbf{\bar{A}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23344bb0b313f67af5ce946ff04ab30e5020bf82)
De esta misma manera.
![\mathbf{E}{(\mathbf{r},t) = Re[\mathbf{\bar{E}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d0fafd7a3b6685dcdea6986067bb137ae2e7a25c)
![\mathbf{H}{(\mathbf{r},t) = Re[\mathbf{\bar{H}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58cf5b30507a7aaf291bf38df9254271ba72736d)
![\mathbf{D}{(\mathbf{r},t) = Re[\mathbf{\bar{D}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3bbd0450ad8f1c58e369c923b0a7ccd587225870)
![\mathbf{B}{(\mathbf{r},t) = Re[\mathbf{\bar{B}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/29372078897036e09f31f2ff141f621f0f8bbeff)
En donde los vectores con barra son fasores de los vectores sin barra. es decir que cada vector con barra tiene la información de la propagación (el vector de onda k).
Al aplicar las ecuaciones de Maxwell sin fuentes y con  .
.




recordando que


Sabemos de la fórmula vectorial para dos rotacionales seguidos.

En donde  es el Laplaciano
es el Laplaciano
Al aplicar esta formula a la ecuación 3 y sustituyendo la ecuación 4


Dado que la ecuación 1 está igualada a cero y es una constante se puede escribir de la siguiente forma.
es una constante se puede escribir de la siguiente forma.

y después

Al despejar se obtiene

Al sustituir este resultado en la ecuación 5

Sabemos tambien que  , el níumero de onda en el vacío es:
, el níumero de onda en el vacío es:

y dado que

usando que el número de onda  en un medio se relaciona con número de onda en el vacío.
en un medio se relaciona con número de onda en el vacío.

y tenemos

En el caso que la permeabilidad relativa sea constante eso se reducirá a la ecuación de Helmholtz.

Usando pasos similares llegamos a que

y de igual manera

Pongamos atención ahora en una guia óptica cuya estructura es uniforme en la dirección  .La derivada de un campo electromagnético con respecto la coordenada
.La derivada de un campo electromagnético con respecto la coordenada  es constante asi que:
es constante asi que:

En donde  es la constante de propagación y es la componente en la dirección de
es la constante de propagación y es la componente en la dirección de  de el vector de onda
de el vector de onda  .La razón entre la constante de propagación en un medio
.La razón entre la constante de propagación en un medio  y el número de onda
y el número de onda  se le conoce como el índice de refracción efectiva
se le conoce como el índice de refracción efectiva

y donde  es la longitud de onda en el vacío,
es la longitud de onda en el vacío,

aqui  es la componente de la longitud de onda en la dirección
es la componente de la longitud de onda en la dirección  en el medio. El significado físico de la constante de propagación
en el medio. El significado físico de la constante de propagación  es la fase de rotación por unidad de distancia de propagación. Asi el índice de refracción efectiva
es la fase de rotación por unidad de distancia de propagación. Asi el índice de refracción efectiva  se puede interpretar como la razón entre la longitud de onda en un medio y la longitud de onda en el vacío o como la razón entre la rotación de fase en el medio y la rotación de fase en el vacío.
se puede interpretar como la razón entre la longitud de onda en un medio y la longitud de onda en el vacío o como la razón entre la rotación de fase en el medio y la rotación de fase en el vacío.
Entonces podemos escribir la ecuación de Helmholtz de la siguiente manera.

o de otra manera

y para el campo magnético

tambien

en donde:

Para obtener una solución exacta se debe usar un análisis de modos híbridos, no obstante se puede hacer un análisis más simple si hablamos que la diferencia entre los índices de refracción en el núcleo y el revestimiento es muy pequeña (aprox. 1%), esta solución da lugar a modos linealmente polarizados.(LP Modes)
Simetría Cilíndrica
Podemos escribir al laplaciano en coordenadas cilíndricas como:

Para poder resolver la ecuación de Helmholtz asumiremos que la función de campo eléctrico es el producto de dos funciones así.

Aqui 
Al sustituir en la ecuación 6 se tiene.



y al dividir entre  se obtiene
se obtiene

Y quedamos con la ecuación

Obtenemos entonces las dos ecuaciones diferenciales


que al igualarlas a cero quedan


La solución para la ecuación de  es simple, pues corresponde a la solución del oscilador armónico
es simple, pues corresponde a la solución del oscilador armónico

Ecuación diferencial de Bessel
Definamos

y el cambio de variable

para la primera derivada

asi

y la segunda derivada

entonces

Usando esto la ecuación 10 se puede reescribir de la siguiente manera



Las soluciones de esta ecuación son las funciones Bessel de orden  .
.

y sustituyendo el valor de 


pero como las permitividades relativas son distintas en el núcleo y el revestimiento.


como:

las funciones de Bessel para el revestimiento(  ) resultan tener un argumento imaginario entonces podemos escribir
) resultan tener un argumento imaginario entonces podemos escribir

A estas se les llama funciones Bessel modificadas y se escriben

Definiendo los parámetros


Soluciones de la ecuación diferencial de Bessel
Las funciones de bessel para el núcleo y el revestimiento quedan


Aquí  y
y  son las funciones besel de orden
son las funciones besel de orden  de primer y segundo tipo, y
de primer y segundo tipo, y  y
y  son las funciones Bessel modificadas de orden
son las funciones Bessel modificadas de orden  de primer y segundo tipo.
de primer y segundo tipo.
Podemos obtener una importante relación para los parametros

en donde

es la frecuencia normalizada. Los parametros  y
y  son considerados respectivamente como la constante de propagación lateral normalizada en el núcleo y la constante de decaimiento lateral normalizada en el revestimiento. El índice de refracción effectiva
son considerados respectivamente como la constante de propagación lateral normalizada en el núcleo y la constante de decaimiento lateral normalizada en el revestimiento. El índice de refracción effectiva  debe satisfacer la relación:
debe satisfacer la relación:

Sabemos que las funciones de Bessel de segundo tipo, ,divergen para
,divergen para  y que las funciones de Bessel modificada tambien de segundo tipo,
y que las funciones de Bessel modificada tambien de segundo tipo,  , diverje para
, diverje para  , entonces sus coeficientes B y D deben de ser cero quedandonos solo:
, entonces sus coeficientes B y D deben de ser cero quedandonos solo:


ahora aplicaremos las condiciones de frontera (interfaz dielectrico dielectrico, tambien quiere decir que las ondas en propagación son contínuas y son almenos clase  )
)

y

En esta última condición las primas significan derivadas con respecto de r, siguiendo esto en la solución queda


Para resolver el sistema escribamos la matriz correspondiente.

Para que el sistema tenga soluciones no triviales el determinante de la matriz de coeficietes debe ser cero.

Ecuación característica
Así llegamos a la ecuación característica

El índice  puede ser encontrado al resolver en combinación las ecuaciones (11) y (12), En otras palabras, ya que
puede ser encontrado al resolver en combinación las ecuaciones (11) y (12), En otras palabras, ya que  y
y  son funciones del índice de refracción efectivo
son funciones del índice de refracción efectivo  la ecuación caracretistica (12) es una función de
la ecuación caracretistica (12) es una función de  . Las soluciones de esta ecuación son los llamados modos linealmente polarizados (LP Modes).
. Las soluciones de esta ecuación son los llamados modos linealmente polarizados (LP Modes).
Calculemos ahora las formas explícitas para la ecuación característica, en particular para el modo 


y haciendo uso de la fórmula de recurrencia


lo que lleva a

esto también se puede escribir

haremos el mismo desarrollo pero para el modo 
haciendo uso de las fórmulas


Podemos escribir la ecuación (12) como:

Lo cuál lleva a

Rango de valores de $ u $
La ecuación 13 es de suma importancia pues nos da información de cuando es que existen soluciones para la ecuación diferencial de bessel, en particular podemos usar a  y su relación con
y su relación con  y así determinar el rango de valores de
y así determinar el rango de valores de  (y por tanto de
(y por tanto de  ). El rango de valores se puede encontrar a través de los límites
). El rango de valores se puede encontrar a través de los límites  y
y  .
.
Sabemos de la ecuación (11) que cuando  ,
, 
aplicaremos este límite para:



Sabemos que las funciones Bessel modificadas de primer tipo para valores de z cercanos a 0 son:


al sustituir esto en la parte derecha de la ecuación (14)


asi obtenemos

podemos notar que mientras que la función Bessel de orden cero  la función Bessel de orden 1
la función Bessel de orden 1  , es decir que la solución es
, es decir que la solución es  . Esto implica que el valor de cierre
. Esto implica que el valor de cierre  para la frecuencia normalizada
para la frecuencia normalizada  es cero, en otras palabras el modo
es cero, en otras palabras el modo  no tiene condición de cierre.
no tiene condición de cierre.
No obstante  no es la única solución, muchas otras soluciones son las raíces de la función de Bessel de primer tipo y de orden 1
no es la única solución, muchas otras soluciones son las raíces de la función de Bessel de primer tipo y de orden 1
 en donde
en donde  es la (m-1)ésima raíz de
es la (m-1)ésima raíz de  . Claro esto solo si
. Claro esto solo si  y
y  tiene el mismo signo para
tiene el mismo signo para  , esto significa que el valor de cierre
, esto significa que el valor de cierre  para el modo
para el modo  está dado por:
está dado por:

así, en resumen las condiciones de corte para los modos  :
:


Por otro lado, cuando  , la expansión asintótica de orden
, la expansión asintótica de orden  de la funcion modificada de bessel de primer tipo es
de la funcion modificada de bessel de primer tipo es




entonces

Por otro lado recordemos

entonces

esto implica que los valores de u deben ser las raíces de la función de Bessel de primer tipo y de orden 0

así, en resúmen los valores asintóticos de  para los modos
para los modos  :
:


Ahora repetiremos el proceso para encontrar las condiciones de cierre y la aproximación asintótica para los modos 
La función modificada de Bessel de  ésimo orden para
ésimo orden para  se puede escribir como.
se puede escribir como.

Haciendo uso de esta aproximación

cuando  entonces
entonces

mientras que del otro lado de (13)

Las posibles soluciones de esta ecuación son aquellas en las que los signos de  y
y  sean opuestos y que además
sean opuestos y que además  , esto en las raíces de la función besel de primer tipo y orden
, esto en las raíces de la función besel de primer tipo y orden  , es decir
, es decir  .
.
Entonces la condición de cierre para el modo 
 .
.
Ahora hagamos la expansión asintótica  , es claro que cuando
, es claro que cuando  la ecuación (13) queda:
la ecuación (13) queda:

y entonces los valores asintóticos para  están dados por las raíces de
están dados por las raíces de  , es decir
, es decir

Podemos resumir que el rango de valores posibles para el parametro u es
 .
.
 .
.
 .
.
Soluciones
Los siguientes gráficos se hicieron tomando en cuenta medidas reales para una fibra óptica monomodo:
Núcleo de 9 micrómetros
Revestimiento de 125 micrómetros
Índice de refracción del núcleo 1.48
Índice de refracción del Revestimiento 1.46
Índice de refracción efectiva 1.47
El número de onda en el vacío se calculó con la relación sencilla:

Las imágenes verdes corresponden a un láser de  , las azules a un láser azul de
, las azules a un láser azul de  y las rojas corresponden a un láser rojo de
y las rojas corresponden a un láser rojo de  .
.
Referencias
|
K. Kawano, K. Tsutomu, Introduction to Optical Waveguide Analysis, John Wiley and Sons.
F. Bowman, Introduction to Bessel Functions, Dover Publications, New York.
Z.X Wang, D.R. Guo, Special Functions, World Scientific, London.
|
Aportación por usuarios: Tomás Salinas Sánchez 09:52 23 jul 2012 (UTC), Usuario:Aoi sasori









































![\frac{\partial^2\mathbf{E_z}}{\partial\mathit{x}^2}+\frac{\partial^2\mathbf{E_z}}{\partial\mathit{y}^2}+[{\mathrm({\omega/c})^2-k^2}]\mathbf{E_z}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c158dffe96438d7e5dae73c91cb4f955b4f14a5)











![{[{\frac{\partial^2}{\partial\mathit{x}^2}}+{\frac{\partial^2}{\partial\mathit{y}^2}}+{\mathrm({\omega/c})^2-k^2}]}\mathbf{B_z}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/33502eadbade3846c151bc27cea5422fb82174f0)














![\mathit{K} = \sqrt{({\omega/c})^2- \pi^2[({m/a})^2 + ({n/b})^2]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7a7b64c98bee98944257597ddd3b58c10e8708fe)








![\omega=c| k' |=c\sqrt{k^2+\pi^2[(m/a)^2+(n/b)^2]}=\sqrt{(ck)^2+\omega_{mn}^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fb0d5c210ad8ab9ced8533d11cc7e99551537301)





















![\mathbf{A}{(\mathbf{r},t) = Re[\mathbf{\bar{A}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23344bb0b313f67af5ce946ff04ab30e5020bf82)
![\mathbf{E}{(\mathbf{r},t) = Re[\mathbf{\bar{E}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d0fafd7a3b6685dcdea6986067bb137ae2e7a25c)
![\mathbf{H}{(\mathbf{r},t) = Re[\mathbf{\bar{H}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58cf5b30507a7aaf291bf38df9254271ba72736d)
![\mathbf{D}{(\mathbf{r},t) = Re[\mathbf{\bar{D}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3bbd0450ad8f1c58e369c923b0a7ccd587225870)
![\mathbf{B}{(\mathbf{r},t) = Re[\mathbf{\bar{B}}({\mathbf{r}}) }{e}^{-i\mathit{\omega t}}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/29372078897036e09f31f2ff141f621f0f8bbeff)















































































































































































