Ondas: planas
Introducción
En la historia de la física, un ejemplo claro de los alcances del trabajo conjunto entre la física teórica y experimental es sin duda el desarrollo de la teoría electromagnética, un conglomerado de conocimientos teóricos desarrollados a partir del pensamiento científico de grandes mentalidades de la época y evidencia experimental que respaldaba los avances en esta rama de la física, el electromagnetismo. El primer indicio fue la relación imprevista entre los fenómenos eléctricos y la velocidad de la luz.
Velocidad de la luz
En la naturaleza, las fuerzas eléctricas se originan de dos formas. Primero está la atracción o la repulsión eléctricas entre las cargas eléctricas positivas y negativas. Es posible definir una unidad de carga eléctrica como la carga que repele a otra carga similar a la distancia de, podemos decir, 1 metro con la fuerza de la unidad de fuerza utilizada (las fórmulas usuales lo definen con más precisión).
Pero en segundo lugar están la atracción y la repulsión entre corrientes eléctricas paralelas. Por lo que podremos definir la unidad de corriente como la corriente que circulando por un hilo recto, atrae a una corriente similar que circule por un hilo paralelo separado 1 metro, con la fuerza de la unidad utilizada, en cada metro de la longitud de los hilos.
En los tiempos de Faraday ya se conocía cual era la velocidad de la luz, aunque sin la precisión actual. Fue deducida por vez primera por Ole (Olaus) Røemer, un astrónomo danés que trabajaba en París. Røemer intentaba predecir los eclipses de Ío, la luna de Júpiter y encontró una diferencia entre los tiempos reales y los previstos, que crecían y disminuían de nuevo cuando la Tierra circunvalaba el Sol. Adivinó la razón correctamente: cuando la Tierra se movía en su órbita, su distancia a Júpiter también aumentaba y disminuía, y así la luz necesitaba un tiempo extra para cubrir esa distancia extra.
Faraday y Maxwell
Faraday también mostró que un campo magnético que cambia en el tiempo, como el producido por la corriente alterna (CA), podría conducir corrientes eléctricas, si los hilos de cobre estuvieran colocados de la forma adecuada. Esto era la "inducción magnética", el fenómeno en el que se basan los transformadores eléctricos.
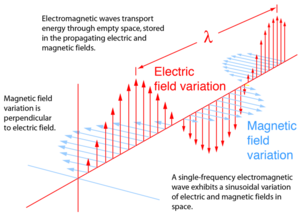
Por lo tanto, los campos magnéticos podían producir corrientes eléctricas y ya sabemos que las corrientes eléctricas producen campos magnéticos. ¿Sería quizá posible que el espacio sustentara un movimiento ondulatorio alternante entre los dos? Del tipo de:
Campo Magnético $\rightarrow $ Corriente Eléctrica $\rightarrow$ Campo Magnético $\rightarrow $ Corriente Eléctrica $\rightarrow $ ...
Esto era un obstáculo. Esta onda no existiría en el espacio vacío, debido a que el espacio vacío no tiene hilos de cobre y no podría conducir la corriente necesaria para completar el ciclo anterior. Un brillante joven escocés, James Clerk Maxwell, solucionó el problema en 1861 proponiendo que las ecuaciones de la electricidad necesitaban un término adicional, que representase a una corriente eléctrica que pudiera viajar a través del espacio vacío, pero solo mediante oscilaciones muy rápidas.
Añadiendo ese término (la "corriente de desplazamiento"), las ecuaciones de la electricidad y del magnetismo permitían que existiese una onda que se propagase a la velocidad de la luz.
Maxwell propuso que eso era luz. Hubo anteriores indicios --como se citó anteriormente, la velocidad de la luz apareció inesperadamente en las ecuaciones de la electricidad y del magnetismo-- y estudios posteriores lo confirmaron.
Después Heinrich Hertz, en Alemania, mostró que una corriente eléctrica saltando adelante y atrás en un hilo (actualmente se le podría llamar "antena") podía ser la fuente de esas ondas. (La corriente, de acuerdo con la ley de Ampere, también produce un campo magnético, pero este campo disminuye rápidamente con la distancia).
Poco a poco se descubrieron otras ondas electromagnéticas. La naturaleza de onda de la luz origina que los diferentes colores se reflejen de forma diferente por una superficie, generando finas rayas paralelas --a esto se debe el que un disco compacto láser (para uso musical o para ordenador) brille en todos los colores del arco iris. Las filas ordenadas de los átomos en un cristal también forman líneas paralelas pero mucho menos espaciadas y resultan tener el mismo efecto sobre los rayos X, mostrando que los rayos X, al igual que la luz, también son ondas electromagnéticas, pero con una longitud de onda mucho más corta. Se encontró posteriormente que los haces de electrones en un campo magnético, dentro de un tubo de vacío, podían hacerse inestables y emitir ondas más largas que la luz: el tubo magnetrón donde ocurría esto fue un dispositivo de radar de alto secreto durante la II Guerra Mundial e hizo posible posteriormente la fabricación del horno microondas.[1]
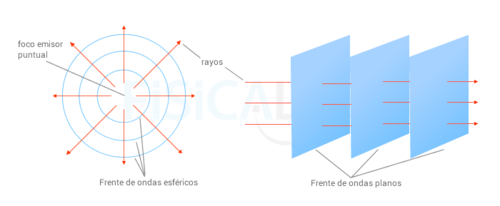
Existen casos donde la ecuación de onda se puede resolver directamente. Por ejemplo en coordenadas cartesianas, cuando no existe variación respecto a $x$ y $y$ la ecuación de onda tiene la solución conocida de ondas planas unidimensionales. Este es el ejemplo más sencillo de onda tridimensional. Existe en un instante dado cuando todas las superficies sobre las cuales una perturbación tiene fase constante, forman un conjunto de planos, cada uno generalmente perpendicular a la dirección de propagación.
Forma Vectorial
Para deducir la expresión matemática de un plano perpendicular a un vector dado k y que pasa a través de algún punto , primero se escribe el vector de posición en coordenadas cartesianas, en términos de los vectores unitarios de la base. [2]
$\textbf{r}=x \hat{\mathbf{e}}_x+y \hat{\mathbf{e}}_y+z \hat{\mathbf{e}}_z$
Comienza en el origen arbitrario $\textbf{0}$ y termina en el punto $(x,y,z)$ que en este caso será cualquier lugar en el espacio.
Sabemos por la ecuación del plano que un vector único paralelo a un plano no basta para definir la dirección del plano, pero un vector perpendicular al plano sí puede definir a este último. Así un plano en el espacio está determinado por un punto en el plano y un vector kque es ortogonal a éste. Dicho vector k se denomina vector normal. Así, sea un punto arbitrario en el plano, y sean y los vectores de posición y . Entonces, el vector esta representado por . El vector normal es ortogonal a cada vector director que define un plano determinado. En particular, es ortogonal a ver (fig 1), por lo que tenemos
$(\textbf{r}-\textbf{r}_{0})=(x-x_{0})\hat{\mathbf{e}}_x+(y-y_{0})\hat{\mathbf{e}}_y+(z-z_{0})\hat{\mathbf{e}}_z$
Estableciendo así:
\begin{equation} (\textbf{r}-\textbf{r}_{0})\cdot\textbf{k}=0, \label{eq1} \end{equation}
Obligando al vector $(\textbf{r}-\textbf{r}_{0})$ a barrer un plano perpendicular a k, al ir adquiriendo su punto extremo $( x ,y, z )$ todos los valores permitidos.
Con
\begin{equation} \textbf{k}=k\hat{\mathbf{e}}_x+k\hat{\mathbf{e}}_y+k\hat{\mathbf{e}}_z \end{equation}
La ecuación (\ref{eq1}) puede expresarse como
\begin{equation} k_{x}(x-x_{0}) + k_{y}(y-y_{0}) + k_{z}(z-z_{0})=0 \end{equation}
O como
\begin{equation} k_{x}x + k_{y}y + k_{z}z =0 \end{equation}
De donde
\begin{equation} a = k_{x}x_{0} + k_{y}y_{0} + k_{z}z_{0}\ =\text{constante} \end{equation}
La forma más concisa de la ecuación de un plano perpendicular a $k$ es entonces
\begin{equation} \textbf{k}\cdot\textbf{r}= \text{constante} = a \end{equation}
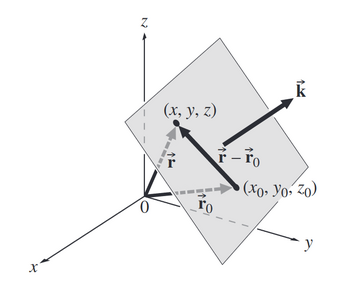
El plano es el lugar de todos los puntos cuyos vectores de posición tienen cada uno la misma proyección en la dirección de $\textbf{k}$
Ahora podemos construir un conjunto de planos sobre los cuales $\psi(\textbf{r})$ varía de manera sinusoidal en el espacio, es decir
\begin{equation}
\psi(\textbf{r})=A \sin (\textbf{k}\cdot\textbf{r})
\end{equation}
\begin{equation} \psi(\textbf{r})=A \cos (\textbf{k}\cdot\textbf{r}) \end{equation}
O bien,
\begin{equation} \psi(\textbf{r})=A e^{i\textbf{k}\cdot\textbf{r}}. \end{equation}
Por todas estas expresiones se mantiene constante sobre cada plano definido por . Como estamos analizando las funciones armónicas, deberían repetirse en el espacio después de un desplazamiento de $\lambda$ en la dirección de k (Fig. 1) . En (Fig. 2) se representa esta clase de expresión. Del infinito número de planos se han dibujado sólo unos pocos, cada uno con una diferente. Los planos deberían también haberse dibujado con una extensión espacial infinita, ya que no se han puesto límites a . La perturbación ocupa claramente todo el espacio.

La naturaleza repetitiva espacial de estas funciones armónicas se puede expresar por:
\begin{equation} \psi(\textbf{r})=\psi(\textbf{r}+\frac{\lambda\textbf{r}}{k}) \label{eq10} \end{equation}
Donde $k$ es la magnitud de $\textbf{k}$ y $\textbf{k}/{k}$ es un vector unitario paralelo a él.
En la forma exponencial, esto equivale a:
\[
A e^{i\vec{k}\cdot \vec{r} }=A e^{i k \cdot (\vec{r} + \lambda \vec{k}/k)}=A e^{i \vec{k} \cdot \vec{r}} e^{i\lambda k}
\]
Para que sea cierto, debemos tener :
\[ e^{i\,\lambda k}=1=e^{2\pi\,i} \]
Por consiguiente, por la igualdad
\[ \lambda k=2\pi, \]
se concluye que
\[ k=\frac{2\pi}{\lambda}. \]
El vector k, cuya magnitud es el número de propagación , se llama vector de onda o de propagación. Ver ondas: vector de onda
En cualquier punto fijo del espacio donde r es constante, la fase es constante y también lo es ; en resumen, los planos están inmóviles. Para hacer que se muevan, debe hacerse variar en el tiempo, algo que puede lograrse introduciendo la dependencia del tiempo en una forma análoga a la de una onda unidimensional.
Aquí entonces
\[ \psi(\boldsymbol{r},t)=Ae^{[i(\boldsymbol{k}\cdot\boldsymbol{r}\pm\omega t)]} \]
Donde son constantes. Mientras que esta perturbación viaja a lo largo de la dirección k, podemos asignarle una fase correspondiente en cada punto en el espacio y en el tiempo. En cualquier instante, las superficies que unen todos los puntos de igual fase se conocen como frentes de onda . Observe que la función de onda tendrá un valor constante sobre el frente de onda solamente si la amplitud A tiene un valor fijo en todos los puntos del frente de onda. Por lo general, A es una función de r y puede que no sea constante en todo el espacio o en todo un frente de onda. En este último caso, la onda se dice in-homogénea.
Velocidad de fase para una onda plana
La velocidad de fase de una onda plana dada por la ecuación (\ref{eq10}) es equivalente a la velocidad de propagación del frente de onda. En la (Fig. 2) la componente escalar de r en la dirección de k es . La perturbación en un frente de onda es constante, de manera que al cabo de un tiempo dt, si el frente recorre una distancia a lo largo de k, debemos tener
\begin{equation} \psi(\textbf{r},t)=\psi(r_{k}+d_{rk},t+dt)=\psi(r_{k},t) \end{equation}
En forma exponencial, sería
\[ Ae^{[i(\boldsymbol{k}\cdot\boldsymbol{r}\pm\omega t)]}=Ae^{[i(\boldsymbol{kr_{k}}+\boldsymbol{k\,dr_{k}}\pm\omega t\pm\omega\,dt)]}=Ae^{[i(\boldsymbol{kr_{k}}\pm\omega t)]} \]
Por consiguiente
.
La magnitud de la velocidad de la onda, es
\begin{equation} \frac{dr_{k}}{dt}=\pm\frac{\omega}{k}=\pm{v} \end{equation}
Podríamos haber anticipado este resultado girando el sistema coordenado de la figura 4 de tal forma que k fuera paralelo al eje x. Para esa orientación
\[ \psi(\boldsymbol{r},t)=Ae^{[i(\boldsymbol{k}x\pm\omega t)]}, \]
Ya que . La onda ha sido reducida efectivamente de esa manera a la perturbación unidimensional de la que ya se habló.
Ahora, considérense dos ondas de la (Fig. 3) ; ambas tienen la misma longitud de onda de tal manera que . La onda 1 que se propaga a lo largo del eje z puede escribirse
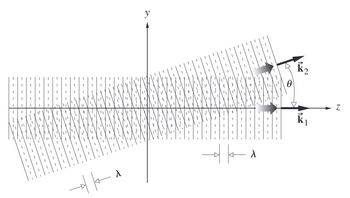
Donde, puesto que y son paralelos
.
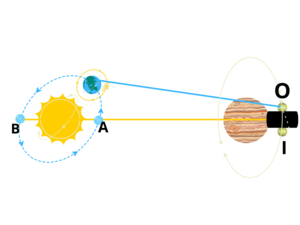
De forma análoga, para la onda 2:
Además de,
.
La onda armónica plana a menudo se escribe en coordenadas cartesianas como
\[ \psi(x,y,z,t)=Ae^{[i(\boldsymbol{k_{x}}x+\boldsymbol{k_{y}}y+\boldsymbol{k_{z}}y\pm\omega t)]} \]
o bien se tiene,
\[ \psi(x,y,z,t)=Ae^{[ik(\alpha x+\beta y+\gamma y\pm\omega t)]}; \]
Donde $\alpha$, $\beta$ y $\gamma$ son los cosenos directores de $k$. En términos de sus componentes, la magnitud del vector de propagación esta dado por
\begin{equation} \textbf{k}=k=(k_{x}^{2}+k_{y}^{2}+k_{z}^{2})^{1/2} \end{equation}
y por supuesto,
\begin{equation} \alpha^{2}+ \beta ^{2}+ \gamma^{2}=1. \end{equation}
Hemos examinado ondas planas poniendo de relieve particularmente las funciones armónicas. La ondas sinusoidales pueden generarse de manera relativamente simple, usando alguna forma de oscilador armónico. Cualquier onda tridimensional puede expresarse como una combinación de ondas planas, cada una con amplitud y dirección de propagación distintas.
Tipos de ondas planas
Onda plana viajera
Comúnmente el término de "onda plana" hace referencia de manera específica a una onda plana que se traslada a través del espacio, cuya evolución a través del tiempo puede ser descrita simplemente como una traslación del campo de la misma a una velocidad igual a la de la luz de manera perpendicular a los frentes de onda. Tal campo puede ser descrito como:
\[ F(\boldsymbol{x},t)=G(\boldsymbol{x}\cdot\boldsymbol{n}-ct) \]
donde $G(u)$ es ahora una función o un solo parámetro real $u=d-ct$, que describe el 'perfil' de la onda, por nombrarlo el valor del campo en el tiempo $t=0$, para cada desplazamiento $d=\boldsymbol{x}\cdot\boldsymbol{n}$. En este caso, $\boldsymbol{n}$ es llamado el ``vector de dirección de propagación. Para cada desplazamiento $d$, el plano en movimiento perpendicular a $\boldsymbol{n}$ a una distancia $d+ct$ desde el origen es llamado un ``frente de onda. Este plano viaja a través de la dirección de propagación de $\boldsymbol{n}$ con velocidad $c$; y el valor de este campo es entonces el mismo, y constante en el tiempo, en cada uno de estos puntos (en el plano o frente de onda).
Onda plana sinusoidal
El término es también usado, aún más específicamente, para referirse a una onda ``monocromática o una onda plana sinusoidal como aque onda viajera cuyo perfil $G(u)$ es una función sinusoidal. Esto es,
\[ F(\boldsymbol{x},t)=A\text{sin}(2\pi f(\boldsymbol{x}\cdot\boldsymbol{n}-ct)+\varphi). \]
El parámetro $A$, el cual puede ser un escalar o un vector, es llamado la 'amplitud' de la onda; el coeficiente escalar $f$ es la 'frecuencia espacial' y el escalar $\varphi$ es la fase.
Propiedades
Una onda plana puede ser estudiada aún ignorando las direcciones perpendiculares al vector director $\boldsymbol{n}$, esto es, al considerar la función $G(z,t)=F(z\boldsymbol{n},t)$ como una onda un medio uni-dimensional.
Cualquier operador matemático local, lineal o no, aplicado a una onda plana resulta en otra onda plana. Cualquier combinación lineal de ondas planas con el mismo vector normal $\boldsymbol{n}$, es también una onda plana.
Además, para una onda escalar plana en dos o tres dimensiones, el gradiente del campo es siempre colineal con la dirección $\boldsymbol{n}$.
Ondas electromagnéticas
Desde el punto de vista clásico la radiación electromagnética son las ondas electromagnéticas generadas por las fuentes del campo electromagnético y que se propagan a la velocidad de la luz. La generación y la propagación de estas ondas son compatibles con el modelo de ecuaciones matemáticas definido en las ecuaciones de Maxwell.
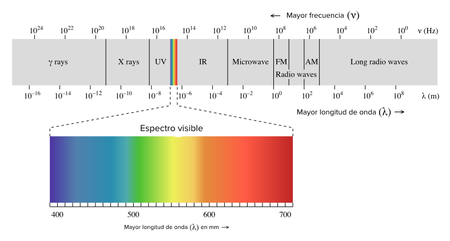
Es importante tener en cuenta el espectro electromagnético, ya que nos da una idea general sobre las características de las ondas electromagnéticas; como se muestra en la siguiente figura, las ondas electromagnéticas abarcan una amplia gama de tipos de radiación, con los cuales estamos en contacto de manera cotidiana.
Ecuaciones de Maxwell
La radiación electromagnética está formada por la emisión de un tipo de partícula responsable de transmitir una de las cuatro fuerzas fundamentales de la naturaleza llamada precisamente interacción electromagnética, es decir, la emisión de fotones.[4]
Se sabe que un campo electromagnético se propaga en el vacío con una velocidad igual a la de la luz en el vacío, es decir a una velocidad
\[ c=\frac{1}{\sqrt{\epsilon_{0}\mu_{0}}}\approx3*10^{8}\text{ms}^{-1}. \]
La existencia de dichas ondas había sido predicha por James Clerk Maxwell y confirmada por Heinrich Hertz. El trabajo de Maxwell lo llevó a sintetizar en 4 ecuaciones los fenómenos electromagnéticos clásicos; dichas ecuaciones, conocidas comúnmente con el nombre de 'Ecuaciones de Maxwell', son las siguientes, donde $E$ es el campo eléctrico y $B$ es el campo de inducción magnética (campo magnético variable en el tiempo)[5]:
- I) Relación de Gauss para campo eléctrico.
Forma integral:
\[ \oint_{s}\boldsymbol{\boldsymbol{E}}\cdot\boldsymbol{u_{n}}\,dS=\frac{q}{\epsilon_{0}}. \]
Forma diferencial:
\[ \nabla\cdot\boldsymbol{E}=\frac{\rho}{\epsilon_{0}}. \]
Donde
$\rho:=$densidad de carga eléctrica,
$\epsilon_{0}:=$permitividad eléctrica del vacío.
- II) Relación de Gauss para campo magnético.
Forma integral:
\[ \oint_{s}\boldsymbol{B}\cdot\boldsymbol{u_{n}}\,dS=0. \]
Forma diferencial:
\[ \nabla\cdot\boldsymbol{\boldsymbol{B}}=0. \]
- III) Relación de Faraday-Henry.
Forma integral:
\[ \oint_{L}\boldsymbol{\boldsymbol{E}}\cdot d\boldsymbol{l}=-\frac{d}{dt}\oint_{s}\boldsymbol{B}\cdot\boldsymbol{u_{n}}\,dS. \]
Forma diferencial:
\[ \nabla\times\boldsymbol{\boldsymbol{E}}=-\frac{\partial\boldsymbol{B}}{\partial t}. \]
- IV) Relación de Ampere-Maxwell.
Forma integral:
\[ \oint_{L}\boldsymbol{B}\cdot d\boldsymbol{l}=\mu_{0}\boldsymbol{I}+\epsilon_{0}\mu_{0}\frac{d}{dt}\oint_{s}\boldsymbol{\boldsymbol{E}}\cdot\boldsymbol{u_{n}}\,dS. \]
Forma diferencial:
\[ \nabla\times\boldsymbol{B}=\mu_{0}\boldsymbol{j}+\epsilon_{0}\mu_{0}\frac{\partial\boldsymbol{\boldsymbol{E}}}{\partial t}. \]
Donde
$I:=$ corriente eléctrica,
$j:=$ densidad de corriente eléctrica,
$\epsilon_{0}:=$ permitividad eléctrica del vacío,
$\rho:=$ densidad de carga eléctrica,
$\mu_{0}:=$ permitividad magnética del vacío.
Para todas las expresiones anteriores, $\boldsymbol{u_{n}}$ simboliza un vector unitario normal a las superficies en cuestión. [6]
Así, se abordará el cuestionamiento sobre si las ecuaciones de Maxwell para el campo electromagnético admiten como solución particular, un campo eléctrico $E$ y un campo magnético variable en el tiempo $B$ perpendiculares entre sí.
Ejemplos comunes de ondas electromagnéticas son las ondas de radio, las señales de televisión, los haces de radar y los rayos luminosos. Para más información véase Radiacion:_antenas
Ondas electromagnéticas planas
Se aborda una situación particular en la que la dirección del campo eléctrico $E$ y la dirección de $B$ son siempre perpendiculares entre sí, abordando de esta manera el concepto de ondas electromagnéticas planas. Tomaremos el eje Y paralelo al campo $E$ y eje Z paralelo al campo $B$. En este caso particular:
\[ E_{x}=0,\:\,\,\,E_{y}=E,\,\,\,\,E_{z}=0, \]
y
\[ B_{x}=0,\:\,\,\,B_{y}=0,\,\,\,\,B_{z}=B. \]
Supondremos también que el campo se encuentra en el vacío, es decir, que no hay cargas libre ni corrientes; esto implica que $\rho=0$ y $\boldsymbol{j}=0$, densidad de carga y densidad de corriente respectivamente. En estas condiciones, las ecuaciones de Maxwell se expresan como:
(a) Relación de Gauss para campo eléctrico,
\[ \frac{\partial\boldsymbol{E}}{\partial y}=0; \]
(b) Relación de Gauss para campo magnético.
\[ \frac{\partial\boldsymbol{B}}{\partial z}=0; \]
(c) Relación de Faraday-Henry,
\[ \frac{\partial\boldsymbol{B}}{\partial z}=0, \]
\begin{equation} \frac{\partial\boldsymbol{E}}{\partial x}=-\frac{\partial\boldsymbol{B}}{\partial t}; \label{eq15} \end{equation}
(d) Relación de Ampere-Maxwell,
\[ \frac{\partial\boldsymbol{B}}{\partial z}=0, \]
\begin{equation} -\frac{\partial\boldsymbol{B}}{\partial x}=\epsilon_{0}\mu_{0}\frac{\partial\boldsymbol{E}}{\partial t}. \label{eq16} \end{equation}
Las ecuaciones anteriores indican que ni $E$ ni $B$ dependen de Y o de Z. En consecuencia ambos cambios dependen sólo de X y de t, y en cada instante cada uno de ellos tiene el mismo valor sobre cualquier plano perpendicular al eje X. Por lo tanto nos quedan las ecuaciones distintas de cero para determinar las dependencias de los campos descritos con las variables X y t, posición y tiempo, respectivamente. Derivando la ecuación (\ref{eq15}) con respecto a x, obtenemos:
\[ \frac{\partial^{2}E}{\partial x^{2}}=-\frac{\partial^{2}B}{\partial x\partial t}. \]
Análogamente, derivando la ecuación (\ref{eq16}) con respecto a t, resulta
\[ -\frac{\partial^{2}B}{\partial x\partial t}=\epsilon_{0}\mu_{0}\frac{\partial{}^{2}E}{\partial t^{2}}. \]
Combinando estos dos resultados se tiene
\[ \frac{\partial^{2}E}{\partial t^{2}}=\frac{1}{\epsilon_{0}\mu_{0}}\frac{\partial^{2}E}{\partial x^{2}}. \]
Inmediatamente se identifica la forma de una ecuación de onda
\[ \frac{\partial^{2}\psi}{\partial t^{2}}=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial x^{2}}=\frac{1}{c^{2}}\frac{\partial^{2}\psi}{\partial x^{2}}. \]
en donde el campo eléctrico se propaga en la dirección del eje X con velocidad
\[ c=\frac{1}{\sqrt{\epsilon_{0}\mu_{0}}}, \]
por tanto se puede expresar de la forma
\[ E(x,t)=E_{0}(x-ct). \]
De manera análoga se tiene
\[ \frac{\partial^{2}B}{\partial t^{2}}=\frac{1}{\epsilon_{0}\mu_{0}}\frac{\partial^{2}B}{\partial x^{2}}, \]
de donde
\[ B(x,t)=B(x-ct). \]
Consideremos en particular el caso de las ondas armónicas de frecuencia $\nu=\frac{\omega}{2\pi}$ y longitud de onda $\lambda=\frac{2\pi}{k}$. En tal caso
\[ E=E_{0}\text{sin}k(x-ct)=E_{0}\text{sin}(kx-\omega t) \]
y
\[ B=B_{0}\text{sin}k(x-ct)=B_{0}\text{sin}(kx-\omega t). \]
De donde observamos que
\[ k=\omega\sqrt{\mu_{0}\epsilon_{0}}=\frac{\omega}{c}, \]
podemos además definir una contante llamada 'impedancia intrínseca del vacío' dada por:
\[ \eta_{0}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}=120\pi\simeq377\,\Omega; \]
por lo tanto podemos reescribir las ecuaciones de onda para campo eléctrico y de inducción magnética de manera vectorial como:
\[ \boldsymbol{\boldsymbol{E}}=E_{0}\text{sin}(kx-\omega t)\,\hat{\boldsymbol{e_{E}}}=E_{0}\text{sin}(kx-\omega t)\,\boldsymbol{\widehat{j}}, \]
y, en el caso de $B$,
\[ \boldsymbol{B}=B_{0}\text{sin}(kx-\omega t)\,\boldsymbol{\widehat{e}_{B}}=B_{0}\text{sin}(kx-\omega t)\,\boldsymbol{\widehat{k}}=\frac{\E_{0}}{\eta_{0}}\text{sin}(kx-\omega t)\boldsymbol{\widehat{k}}. \]
Al usar la notación de vectores canónicos unitarios, se puede observar claramente que ambos campos son siempre normales entre sí, tal que
\[ \boldsymbol{\widehat{e}_{E}}\times\boldsymbol{\widehat{e}_{B}}=\boldsymbol{\widehat{k}}. \]
Esto significa que se sitúan en un plano transversal u ortogonal a esa dirección. Así, forma una onda electromagnética sin componentes de campo eléctrico y magnético a lo largo de la dirección de propagación, llamada 'onda electromagnética transversal (ET)'. $E$ y $B$ son a su vez, y por separado, una 'onda plana uniforme', puesto que $E$ (o $B$) mantiene igual magnitud a todo lo largo de un plano transversal, definido por x constante. La dirección en la que apunta el campo eléctrico es la polarización de una onda ET.[7] Para entender mejor el efecto descrito a través de ondas polarizadas véase Ondas:_Polarizacion
Derivando cada ecuación hallada respecto del tiempo, en el caso de la inducción magnética, y respecto a la posición, en el caso del campo eléctrico se tienen:
\[ \frac{dE}{dx}=kE_{0}\text{cos}(k(x-ct)), \]
y
\[ \frac{dB}{dt}=-kcE_{0}\text{cos}(k(x-ct)); \]
sustituyendo en la ecuación (\ref{eq15}) se tiene:
\[ \frac{\partial E}{\partial x}=-\frac{\partial B}{\partial t}\Rightarrow kE_{0}\text{cos}(k(x-ct))=kcE_{0}\text{cos}(k(x-ct)), \]
por lo tanto
\[ E_{0}=cB_{0}\leftrightarrow B_{0}=\frac{1}{c}E_{0}. \]
Por otra parte, la existencia física de una onda plana uniforme es imposible, ya que se extendería al infinito y representaría una energía infinita. Pese a su simplicidad, no carece de importancia pues sirve como aproximación de ondas prácticas -las procedentes de una antena de radio, por ejemplo- alejadas de fuentes de radiación.
Referencias
|
Aportación de: Mautona97 (discusión) 03:38 14 jul 2020 (CDT)



























![{\displaystyle \psi _{2}=A_{2}\cos[{\frac {2\pi }{\lambda }}(z\cos \theta +y{\text{sen}}\theta )-\omega {t}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a4ec42cc4676b82769e937a932e8945fe3c4c65c)