Ondas: Polarizacion
Introducción
El estudio acerca del comportamiento y la naturaleza de la luz incluye nombres de grandes maestros a través de la historia, además de ser un tema bastante amplio.
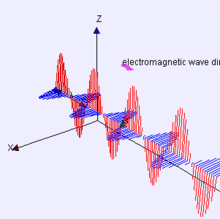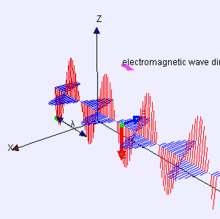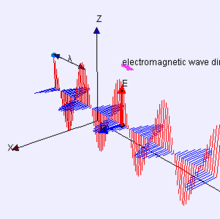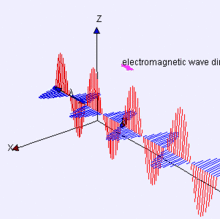
Una de las propiedades físicas de la luz es que puede ser polarizada. Siendo la luz un tipo de radiación electromagnética, posee tanto campo eléctrico como campo magnético; es precisamente su campo eléctrico el que produce el fenómeno de la polarización.
Se sabe que los campos eléctrico y magnético guardan una cierta relación entre sí, por lo que una vez conocido el campo eléctrico, entonces se puede determinar el campo magnético (transversal al campo eléctrico):
El campo eléctrico de la luz puede ser descrito mediante un vector, el cuál se encuentra en un plano perpendicular a la dirección de propagación de la misma, oscilando a medida que la luz avanza en el medio o en el vacío. Es debido a esto que a la luz se le considera una onda electromagnética transversal (conviene recordar que una onda transversal es aquella donde la perturbación o vibración ocurre en los planos perpendiculares a la dirección del movimiento).
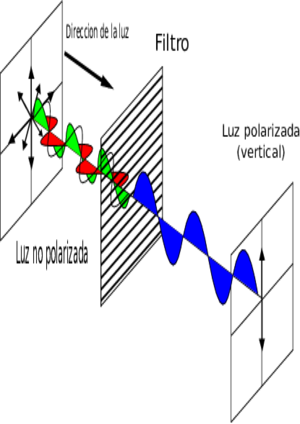
La orientación de las oscilaciones del campo eléctrico de la luz en el plano (si se considera al eje como el eje de la dirección de propagación) son las que generan el efecto de polarización. Para que la luz sea polarizada, el campo eléctrico debe vibrar principalmente en una dirección.
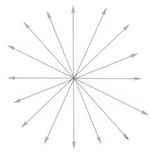
La mayoría de las fuentes de luz no se encuentran polarizadas. Se puede hablar de luz no polarizada cuando ésta no es estrictamente monocromática y no es posible determinar si está polarizada o no [2]. Es en el caso de la luz no polarizada donde no todos los átomos emiten luz en el mismo estado de polarización, por lo que el vector campo eléctrico vibra en todas las direcciones (Fig.2) de forma aleatoria, cancelando el efecto de polarización.
Animación
https://emanim.szialab.org/index.html
Polarización Lineal

En general, la magnitud y dirección del vector campo eléctrico en cualquier punto a lo largo de la trayectoria de la onda es una función del tiempo y del espacio.
Se dice que la luz es linealmente polarizada (o polarizada plana) cuando la componente-x y la componente-y del vector del campo eléctrico se encuentran en fase, conservando constante su dirección y cambiando únicamente (de forma senoidal con el tiempo y el espacio) su magnitud y sentido.
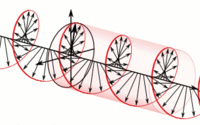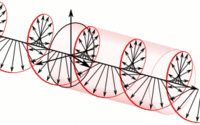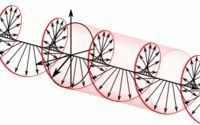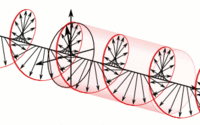
Imaginemos dos ondas de luz linealmente polarizadas de la misma frecuencia, moviéndose a través de la misma región del espacio, en la misma dirección, siendo sus vectores campo eléctrico colineales. Las perturbaciones superpuestas se combinarán simplemente para formar una onda resultante linealmente polarizada. Si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería lineal, o una recta.
Tomando el plano como referencia, podemos considerar a las vibraciones del campo eléctrico () en ese plano como una onda armónica simple, la cuál se propaga a lo largo del eje-. Así, por considerarse a la luz una onda electromagnética, el campo eléctrico oscila en el eje- perpendicularmente a , a determinada frecuencia.
Análogamente, tomando el plano como referencia, se consideran de igual forma las vibraciones del campo eléctrico en ese plano como una onda armónica simple, que también se propaga a lo largo de , y cuyas oscilaciones se dan en el eje- perpendicularmente a .
La onda en y la onda en pueden se descritas, matemáticamente, por las siguientes ecuaciones: [4]
\begin{equation}
\vec{\mathbf{E}}_x(z,t)=\mathbf{\hat e_x} E_{0x}\cos(kz - \omega t) \qquad
\label{1a}
\end{equation}
\begin{equation} \vec{\mathbf{E}}_y(z,t)=\mathbf{\hat e_y} E_{0y}\cos(kz - \omega t + \varepsilon) \qquad \label{2a} \end{equation}
En estas expresiones, es la diferencia de fase entre las ondas, las cuáles viajan en dirección de . La amplitud de estas ondas puede ser diferente, y esta diferencia únicamente determina la dirección de la línea recta (o qué tanto se inclina en el plano ) que traza el vector del campo eléctrico mientras se propaga.
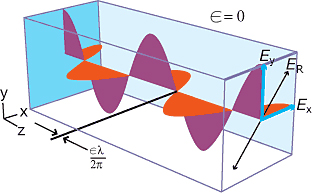
Hablando del campo eléctrico como una perturbación óptica, la suma vectorial de sus componentes produce un resultante:
\begin{equation}
\vec{\mathbf{E}}(z,t) = \vec E_x(z,t)+\vec E_y(z,t) \qquad
\label{3a}
\end{equation}
Si es cero, o un múltiplo entero de , ambas componentes se dicen que se encuentran en fase. En ese caso, la suma vectorial de ambas sería:
\begin{equation}
\vec{\mathbf{E}} = (\mathbf{\hat e_x} \vec E_{0x}+\mathbf{\hat e_y} \vec E_{0x})\cos(kz-\omega t) \qquad
\label{4a}
\end{equation}
Es la superposición de las ondas y (en fase) que resulta en la ecuación (\ref{4a}), con una amplitud fija igual a , lo cuál significa que la suma de ambas genera otra onda que también es linealmente polarizada.
Las magnitudes relativas de las componentes determinarán la orientación de la polarización, es decir:
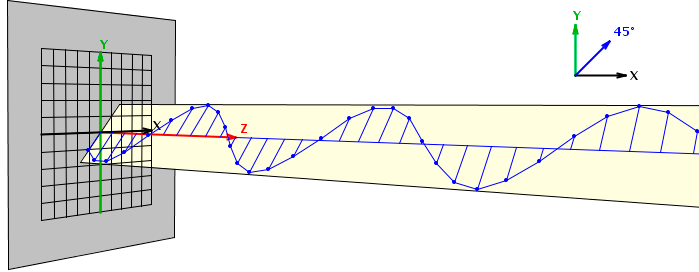
Aportación de: Roberto Martínez Sosa 07:27 5 abr 2012 (UTC)
Polarización Circular

Cuando la luz es linealmente polarizada, las ondas en el eje-x y el eje-y del campo eléctrico deben estar en fase (es decir, ). Es cuando se encuentran desfasadas por 90°, y cuando la amplitud de ambas es exactamente la misma, que hablamos de polarización circular. En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz linealmente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería circular.
Bajo esta definición, las ondas en el eje-x y el eje-y que describen a este tipo de polarización pueden representarse, matemáticamente, por las siguientes ecuaciones: [7]
\begin{equation} \vec{\mathbf{E}}_x(z,t)=\mathbf{\hat e_x} E_{0}\cos(kz - \omega t) \qquad \label{1b} \end{equation}
\begin{equation} \vec{\mathbf{E}}_y(z,t)=\mathbf{\hat e_y} E_{0}\sin(kz - \omega t) \qquad \label{2b} \end{equation}
Donde la amplitud de y es la misma (). Por el desfase de 90°, la componente del campo eléctrico en el eje-y cambia de a , por lo que la fase debe ser equivalente a (con ,...).
Luego, la suma vectorial de las componentes en el eje-x () y el eje-y () es:
\begin{equation} \vec{\mathbf{E}}=E_{0}[\mathbf{\hat e_x} \cos(kz - \omega t) + \mathbf{\hat e_y} \sin(kz - \omega t)] \qquad \label{3b} \end{equation}
La polarización circular puede presentarse como polarización circular derecha y polarización circular izquierda. Los nombres sólo hacen referencia a la dirección en la que el campo eléctrico rota mientras la onda se propaga (hacia la derecha es en sentido de las manecillas del reloj y hacia la izquierda en sentido opuesto a las manecillas del reloj).
Una forma de representar la polarización circular derecha es haciendo , a un valor arbitrario . En este caso, el vector del campo eléctrico quedaría en un eje de referencia situado en el primer cuadrante del plano , por lo que las componentes en el eje-x y en el eje-y quedarían así:
\begin{equation} \vec{\mathbf{E}}_x=\mathbf{\hat e_x} E_{0}\cos(kz_0) \qquad \label{4b} \end{equation}
\begin{equation} \vec{\mathbf{E}}_y=\mathbf{\hat e_y} E_{0}\sin(kz_0) \qquad \label{5b} \end{equation}
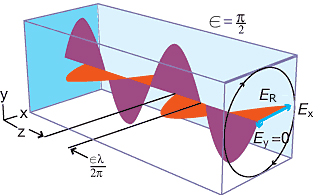
Si avanzamos en el tiempo de tal forma que ahora , obtenemos que y . Con esto podemos deducir que del eje de referencia, el campo eléctrico rotó de tal forma que ahora se encuentra sobre el eje-x, por lo que su dirección de rotación fue en sentido de las manecillas del reloj.
Para representar su caso opuesto (polarización circular izquierda), basta con tener una onda cuya ecuación corresponda a:
\begin{equation} \vec{\mathbf{E}}=E_{0}[\mathbf{\hat e_x} \cos(kz - \omega t) - \mathbf{\hat e_y} \sin(kz - \omega t)] \qquad \label{6b} \end{equation}
Donde el signo negativo en el eje-y, a una fase de (con ,...), genera una rotación en sentido contrario a las manecillas del reloj.
Si sumamos las ecuaciones de polarización circular izquierda (\ref{6b}) y polarización circular derecha (\ref{3b}), podemos obtener una ecuación que representaría una onda linealmente polarizada:
\begin{equation} \vec{\mathbf{E}}=2E_{0}\mathbf{\hat e_x} \cos(kz - \omega t) \qquad \label{7b} \end{equation}
Aportación de: Roberto Martínez Sosa 07:22 5 abr 2012 (UTC)
Polarización Elíptica.

La polarización elíptica se presenta cuando las componentes y se encuentran desfasadas un valor arbitrario, y a su vez presentan una amplitud arbitraria.
Si podemos considerar "arbitrario" como cualquier valor, entonces se pueden presentar los casos donde , (o múltiplos enteros de éste), así como cuando la amplitud de las componentes sea la misma, que es cuando se manifiesta la polarización lineal y polarización circular. Es por esto que a la polarización lineal y polarización circular se les considera casos especiales de polarización elíptica, a pesar de que éstos no manifiesten estrictamente un movimiento elíptico.
En este caso, si pudiéramos observar las oscilaciones del campo eléctrico en un haz de luz elípticamente polarizada, viniendo de frente (saliendo de la pantalla), entonces el movimiento descrito sería, en la mayoría de los casos, elíptico.
Para tener una mejor idea de cómo se describe el movimiento elíptico en este tipo de polarización, recordemos que, matemáticamente, los componentes del vector en el eje-x y el eje-y se ven así:
\begin{equation} E_x =E_{0x} \cos(kz-\omega t) \label{1c} \end{equation}
\begin{equation}
E_y =E_{0y} \cos(kz-\omega t+\varepsilon)
\label{2c}
\end{equation}
Al tomar haciendo uso de las siguientes relaciones:
Despejando y sustituyéndola adecuadamente, podemos llegar a la siguiente relación:
\begin{equation}
E_{y}=E_{0y}\frac{E_{x}}{E_{0x}}E_{x}\cos\varepsilon-E_{0y}\left[1-\left(\frac{E_{x}}{E_{0x}^{2}}\right)^{2}\right]\sin\varepsilon
\label{3c}
\end{equation}
Ordenando términos y tomando así la expresión:
\begin{equation} \left(\frac{E_{y}}{E_{0y}}-\frac{E_{x}}{E_{0x}}\cos\varepsilon\right)^{2}=\left[1-\left(\frac{E_{x}}{E_{0x}^{2}}\right)^{2}\right]\sin^{2}\varepsilon \label{4c} \end{equation}
Podemos transformarla de la siguiente manera:
\begin{equation}
\frac{E_{x}^{2}}{E_{0x}^{2}}+\frac{E_{y}^{2}}{E_{0y}^{2}}-\frac{2E_{x}E_{y}}{E_{0x}E_{0y}}\cos\varepsilon=\sin^{2}\varepsilon
\label{5c}
\end{equation}
Es posible mostrar que esta es la ecuación de una elipse, para ello rotamos esta ecuación a un nuevo sistema de coordenadas (η,ξ) giradas un ángulo Ψ con respecto al sistema de coordenadas (x,y) como se muestra en la Figura 9:
Si para la ecuación (\ref{5c}) ó ...., podemos obtener la ecuación ya conocida:
\begin{equation} \frac{E_{x}^{2}}{E_{0x}^{2}}+\frac{E_{y}^{2}}{E_{0y}^{2}}=1 \label{6c} \end{equation}
Además si sabemos que:
\begin{equation}
E_{x}^{2}+E_{y}^{2}=E_{0}^{2}
\label{7c}
\end{equation}
Lo cual es un círculo. Si es un múltiplo par de encontramos en la ecuación (\ref{5c}) que:
\begin{equation} E_{y}=\frac{E_{0y}}{E_{0x}}E_{x} \label{8c} \end{equation}
De manera similar si es un múltiplo impar de :
Ambas son líneas rectas con pendiente:
Podemos llevar a cabo la rotación a un nuevo sistema de coordenadas por medio de las siguientes ecuaciones de transformación:
\begin{equation} E_{x}=E_{\eta}\cos\psi-E_{\xi}\sin\psi \label{9c} \end{equation}
\begin{equation} E_{y}=E_{\eta}\sin\psi+E_{\xi}\cos\psi \label{10c} \end{equation}
Que al ser empleadas para transformar (\ref{5c}) nos dan:
\begin{equation} \left[E_{0y}^{2}\cos^{2}\psi+E_{0x}^{2}\sin^{2}\psi-2E_{0x}E_{0y}\sin\psi \cos\psi \cos\varepsilon\right]E_{\eta}^{2}+\left[E_{0y}^{2}\sin\psi+E_{0x}^{2}\cos^{2}\psi+2E_{0x}E_{0y}\sin\psi \cos\psi \cos\varepsilon\right]E_{\xi}^{2} -2\left[\left(E_{0y}^{2}-E_{0x}^{2}\right)\sin\psi \cos\psi+E_{0x}E_{0y}(\cos^{2}\psi-\sin^{2}\psi)\cos\varepsilon\right]E_{\eta}E_{\xi}=E_{0y}^{2}E_{0x}^{2}\sin^{2}\varepsilon \label{11c} \end{equation}
El ángulo Ψ se escoge de tal manera que los semiejes de la elipse coincidan con los ejes η,ξ. Esto se logra haciendo que el coeficiente de de la ecuación (\ref{11c}) sea igual a cero, por tanto:
Que al utilizar las identidades:
Podemos obtener una orientación de la elipse dada por:
Al escribir la ecuación (\ref{5c}) sin el término del coeficiente que igualamos con cero anteriormente, tendríamos una ecuación la cual puede ser reescrita, para finalmente obtener la forma general siguiente:
\begin{equation} \frac{E_{\eta}^{2}}{a^{2}}+\frac{E_{\xi}^{2}}{b^{2}}=1 \end{equation}
En donde las constantes a y b son los semiejes mayor y menor, respectivamente.
Es posible demostrar que:
\begin{equation} a^{2}b^{2}=E_{0x}E_{0y}\sin^{2}\zeta \label{12c} \end{equation}
\begin{equation} a^{2}+b^{2}=E_{0x}^{2}+E_{0y}^{2} \label{13c} \end{equation}
Aportación de: Roberto Martínez Sosa 07:42 5 abr 2012 (UTC)
Polarizadores dicroicos.
El artefacto que divide la luz no polarizada en dos componentes y descarta una, se llama polarizador. Si el proceso para separar es imperfecto, de modo que una fracción de la componente que no se desea, no se descarta, el polarizador se llama parcial. Existen muchos tipos de polarizadores que se pueden usar en muchos procesos de óptica: absorción, reflexión, refracción, o dispersión cualquiera de estos puede usarse para resolver un haz en componentes polarizadas. La clave para el proceso de polarización es la asimetría ( por ejemplo la asimetría estructural interna del polarizador, la asimetría, oblicuidad, de la armadura del polarizador o la asimetría de la dirección de visión relativa a la dirección de incidencia del haz, asimetría de en la absorción o dricroísmo.
El Polarizador de rejilla de alambre
Este aparato consta de un conjunto de finos alambres colocados paralelamente, siendo los alambres metálicos de gran conductividad para los campos eléctricos paralelos a ellos. Tales campos producen corrientes eléctricas en los alambres de forma que su energía se invierte en calor, debido a la pequeña pero significativa, resistencia eléctrica de los alambres. Sin embargo, debido a que en los espacios entre los alambres no hay conducción, no hay flujo de corriente perpendicular a ellos. Así, pues, los campos eléctricos perpendiculares a los alambres no producen corrientes ni pierden energía. Entonces, el colocar la rejilla de alambre frente a un haz no polarizado se disipa la energía de una de las componentes y permite la otra pasar casi sin disminución.
La Lámina H
Son largas y delgadas cadenas de Yodo, absorben las vibraciones eléctricas paralelas a su eje de alineación y transmiten libremente las vibraciones perpendiculares. Así el eje de transmisión es perpendicular a la dirección del estiramiento.En condiciones ideales se transmite el cincuenta por ciento de la potencia de un haz incidente. La componente de en una onda incidente, que es paralela a las moléculas, impulsa a los electrones, hace trabajo sobre ellos, y es fuertemente absorbida La hoja H es un polarizador muy efectivo sobre todo en el espectro visible pero es algo menos en el extremo azul. Cuando se observa una luz blanca brillante a través de un par de hojas H polaroides cruzadas, el color de extinción será un color azul profundo como resultado de esta fuga.
Polarizadores en un reloj(Animación)
https://www.vascak.cz/data/android/physicsatschool/templateimg.php?s=opt_polarizacefiltr&l=es
Figura activa con dos polarizadores
http://micro.magnet.fsu.edu/primer/java/polarizedlight/filters/index.html
Vídeo de polarización
https://www.youtube.com/watch?v=82Cux9Q9afk
Polarizadores de reflexión:
Casi cualquier objeto pulido, no metálico tiende a polarizar a luz que choca oblicuamente. Uno de los polarizadores de reflexión más sencillos es una placa de vidrio montada oblicuamente en el haz de luz dado. Cuando se monta la placa perpendicular al haz no hay polarización; todas las componentes de la luz se transmiten ( cerca del 92% por lo general) y el haz transmitido esta no polarizado. Cerca del 8 % se refleja y también es no polarizada.
Pero cuando la placa está inclinada, de modo que la asimetría del proceso de reflexión queda destruida, suceden cosas interesantes . El haz transmitido se halla parcialmente polarizado y el haz reflejado aún más.Las formas de polarización de los dos haces son ortogonales
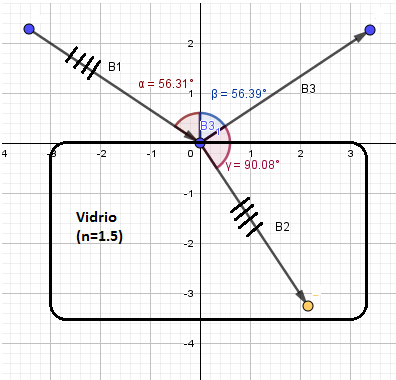
Como se ve en la figura, para un caso particular, el caso en el que haz B1 incide a 56.3° de la normal en una placa de vidrio cuyo índice de reflexión es 1.5 .
se supondrá en primer lugar que el haz está 100 % polarizado linealmente y que la dirección de vibración eléctrica es paralela al plano del papel. Considérese enseguida al haz refractado B2 que penetra al vidrio y el B3 que está reflejado de la superficie superior.
El haz refractado tiene una dirección más inclinada que B1, como lo describe la ley de Snell, y las vibraciones en el haz refractado , B2, son paralelas exactamente a la dirección del haz reflejado, B3.
Y esto a su vez , significa que el haz reflejado, B3 no puede existir. No hay tal haz y ninguna energía puede fluir en esa dirección.
¿Por qué? porque , de acuerdo con la teoría electromagnética, la luz necesita una vibración transversal; sin embargo, en el punto en el que empieza la luz entrar al vidrio las vibraciones son exactamente paralelas a la dirección B3 y por tanto, no tiene componente que sea transversal a B3.
Finalmente suponga que el haz incidente B1 no esta polarizado. El haz reflejado consta, por tanto, de una segunda componente y tiene una polarización de 100 %. El transmitido también se polariza; por en un grado mucho menor y , por supuesto predomina la dirección de vibración ortogonal. El único ángulo en el que el haz reflejado queda completamente polarizado es el que se conoce como de Brewster o ángulo de polarización. Esto es lo único que se necesita para producir un haz completamente polarizado, Conociendo el índice de refracción, n, de una placa de vidrio, plástico o algún material semejante, y conociendo la ley de Snell se puede calcular el ángulo de polarización; este resulta ser el ángulo cuya tangente es precisamente n, Así, pues, una placa de cloruro de plata n=2, tiene un ángulo de polarización de arco tan 2, o aproximadamente de 63°.
El agua tiene un índice de 1.33; por tanto la luz natural que se refleja a un arco tan 1.33, o aproximadamente a 53°, de la superficie de un estanque está completamente polarizada.
El vector de Stokes
El vector de Stokes
El vector de Stokes es un conjunto de números, se aplica igualmente a luz polarizada, a luz parcialmente polarizada y a la luz no polarizada. Inventado en 1852 por el físico británico G.G Stokes, proporciona el método más sencillo para predecir el resultado de superponer dos haces incoherentes.
Más importante aún es el hecho de que el vector de Stokes de un método numérico simple para predecir cómo se afecta un haz por efecto de un polarizador o un retardador. La especificación del haz emergente se determina multiplicando el vector de Stokes que representa el haz incidente por una matriz que representa al polarizador o retardador.
- La intensidad total de la luz (polarizada + no polarizada)
- La intensidad de la polarización lineal horizontal o vertical
- La intensidad de la polarización lineal + 45 ° o -45 °
- La intensidad de polarización circular derecha o izquierda
La intensidad de la parte polarizada de la onda de luz viene dada por:
La intensidad total es:
Así:
(Luz completamente polarizada)
(Luz parcialmente polarizado y no polarizado)
Para representar (14) en términos de los observables del campo óptico, debemos tomar un promedio durante el tiempo de observación.
Dado que la vibración es tan rápida, el tiempo de observación puede verse como infinito. Pero, dado que y son periódicos, en realidad podemos promediar (\ref{5c}) solo en un solo período de oscilación.
El tiempo promedio está representado por los corchetes angulares <...>, por lo que (\ref{5c}) puede escribirse como:
\begin{equation}
\frac { \left< { E }_{ x }^{ 2 }(t) \right> }{ { E }_{ 0x }^{ 2 } } +\frac { \left< { E }_{ y }^{ 2 }(t) \right> }{ { E }_{ 0y }^{ 2 } } -2\frac { \left< { E }_{ y }(t){ E }_{ x }(t) \right> }{ { E }_{ 0y }(t){ E }_{ 0x }(t) } \cos\varepsilon ={ \sin }^{ 2 }\varepsilon
\label{14}
\end{equation}
Dónde
\begin{equation} \left< { E }_{ y }(t){ E }_{ x }(t) \right> ={ Lim }_{ T\longrightarrow \infty }\frac { 1 }{ T } \int _{ 0 }^{ T }{ { E }_{ y }(t){ E }_{ x }(t)dt } \label{15} \end{equation}
Luego multiplicamos (\ref{14}) por , y luego obtenemos:
\begin{equation} { { 4E }_{ 0y } }^{ 2 }\left< { E }_{ x }^{ 2 }(t) \right> +{ { 4E }_{ 0x } }^{ 2 }\left< { E }_{ y }^{ 2 }(t) \right> -8{ E }_{ 0y }(t){ E }_{ 0x }(t)\left< { E }_{ y }(t){ E }_{ x }(t) \right> \cos\varepsilon ={ (2{ E }_{ 0y }(t){ E }_{ 0x }(t){ \sin }\varepsilon ) }^{ 2 } \label{16} \end{equation}
Podemos encontrar los valores promedio de la ecuación (\ref{16}) usando la ecuación (\ref{15}):
\begin{equation} \left< { E }_{ x }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }^{ 2 } \label{17} \end{equation}
\begin{equation}
\left< { E }_{ y }^{ 2 }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0y } }^{ 2 }
\label{18}
\end{equation}
\begin{equation} \left< { E }_{ y }(t){ E }_{ x }(t) \right> =\frac { 1 }{ 2 } { { E }_{ 0x } }{ { E }_{ 0y } }\cos\varepsilon \label{19} \end{equation}
Sustituyendo (\ref{17}), (\ref{18}),(\ref{19})en (\ref{16}) y obtenemos:
\begin{equation} { { 2E }_{ 0x } }^{ 2 }{ { E }_{ 0y } }^{ 2 }+{ { 2E }_{ 0x } }^{ 2 }{ { E }_{ 0y } }^{ 2 }-{ ({ { 2E }_{ 0x } }{ { E }_{ 0y } }\cos\varepsilon ) }^{ 2 }={ (2{ E }_{ 0y }{ E }_{ 0x }{ \sin }\varepsilon ) }^{ 2 } \label{20} \end{equation}
Como queremos expresar el resultado final en términos de intensidad, podemos sumar y restar la cantidad al lado izquierdo de (\ref{20}); Haciendo esto se obtienen cuadrados perfectos.
Entonces podemos obtener:
\begin{equation}
{ { ({ E }_{ ox }^{ 2 } }{ +{ { E }_{ oy }^{ 2 } } }) }^{ 2 }-{ { { ({ E }_{ ox }^{ 2 } } }{ -{ { E }_{ oy }^{ 2 } } }) }^{ 2 }-{ ({ { 2E }_{ 0x } }{ { E }_{ 0y } }cos\varepsilon ) }^{ 2 }={ (2{ E }_{ 0y }{ E }_{ 0x }{ \sin }\varepsilon ) }^{ 2 }
\label{21}
\end{equation}
Escribimos las cantidades dentro de los paréntesis como:
\begin{equation}
{ S }_{ 0 }={ { E }_{ ox }^{ 2 } }{ +{ { E }_{ oy }^{ 2 } } }
\label{22}
\end{equation}
\begin{equation}
{ S }_{ 1 }={ { E }_{ ox }^{ 2 } }{ -{ { E }_{ oy }^{ 2 } } }
\label{23}
\end{equation}
\begin{equation}
{ S }_{ 2 }={ { { 2E }_{ 0x } }{ { E }_{ 0y } }\cos\varepsilon }
\label{24}
\end{equation}
\begin{equation}
{ S }_{ 3 }={ { { 2E }_{ 0x } }{ { E }_{ 0y } }\sin\varepsilon }
\label{25}
\end{equation}
Tenga en cuenta que $S_0$ , $S_1$ , $S_2$ , $S_3$ son cantidades promediadas en el tiempo realizadas en un intervalo de tiempo $T_D$ que es la constante de tiempo característica del proceso de detección.
Luego reescribimos (\ref{21}) como:
\begin{equation}
{ S }_{ 0 }^{ 2 }={ S }_{ 1 }^{ 2 }+{ S }_{ 2 }^{ 2 }+{ S }_{ 3 }^{ 2 }
\label{26}
\end{equation}
Las cuatro ecuaciones (\ref{22}), (\ref{23}),(\ref{24})y(\ref{25}) son los parámetros de polarización de Stokes para una onda plana .
Nota:
Los parámetros de Stokes se expresan en términos de intensidades (que podemos medir) Los parámetros de Stokes son cantidades reales (en lugar de números complejos como en las matrices de Jones)
Basándonos en la desigualdad de Schwartz, podemos decir que para cualquier estado de luz polarizada:
En (\ref{17}), la igualdad es verdadera para la luz completamente polarizada, y la desigualdad es verdadera para la luz parcialmente polarizada o no polarizada.
Grado de polarización (DOP) en términos de parámetros de Stokes.
Podemos usar los parámetros de Stokes para describir el grado de polarización para cualquier estado de polarización (completamente polarizado, parcialmente polarizado y no polarizado).
El grado de polarización P se define como (basado en la intensidad de la luz):
Entonces el significado de P es:
- Si $P = 1$ La luz es completamente polarizada
- Si $P = 0$ La luz no es polarizada
- $0 < P <1$ La luz parcialmente polarizada
Ejemplos de parametros de Stokes para luz completamente polarizada.
Ahora discutimos los parámetros de Stokes para algunos casos especiales.
Luz Linealmente Polarizada Horizontalmente (LHP)
Para este caso, no hay componente de campo vertical, por lo que . De (\ref{22}), (\ref{23}), (\ref{24}) y (\ref{25}) obtenemos:
Luz Linealmente Polarizada Verticalmente (LVP)
Para este caso, no hay componente de campo horizontal, por lo que . De(\ref{22}) a (\ref{25})obtenemos:
Lineal $+45°$ Luz Polarizada $(L + 45)$
Las condiciones para obtener luz polarizada lineal de $(+ 45)$ son:
y
Esto significa que esta polarización es una superposición de campos horizontales y verticales en fase, de igual amplitud. Con (\ref{22}) a (\ref{25}), obtenemos:
Lineal $-45°$ Luz Polarizada $(L - 45)$
Las condiciones para obtener luz polarizada lineal de -45 ° son:
y $\varepsilon =180°$
Entonces obtenemos:
Luz Circularmente Polarizada Derecha (RCP)
Las condiciones para obtener una luz polarizada circularmente correcta son:
y $\varepsilon =90°$
Entonces obtenemos:
Luz Circularmente Polarizada Izquierda (LCP)
Las condiciones para obtener luz polarizada circularmente a la izquierda son:
y $\varepsilon =-90°$
Entonces obtenemos:
Luz polarizada elípticamente.
Los parámetros de Stokes para luz polarizada elípticamente en general son como la definición:
Aplicaciones: El resultado de combinar dos haces incoherentes se halla sumando los dos vectores de Stokes adecuados. Considérese, por ejemplo,la suma de un haz polarizado horizontalmente de intensidad uno y un haz polarizado circularmente en sentido derecho de intensidad tres. Los vectores correspondientes son ( 1,1,0,0) y (3,0,0,3),hay que notar los vectores los pusimos horizontal solo para ahorrar espacio.
La suma obtenida añadiendo los números situados en lugares correspondientes es (4,1,0,3). Este vector resultante significa que la intensidad del haz resultante es 4, ya que el primer número es 4.
El modelo seccional elíptico tiene gran parecido con un círculo, ya que la magnitud del último número es grande y el sentido circular de la elipse es hacia la derecha, pues el último número es positivo. La elipse es más horizontal que vertical, ya que el segundo número es positivo. El grado de polarización es
o sea 79 por ciento.
Otro ejemplo es la combinación de dos haces polarizados horizontal y verticalmente que son incoherentes y de intensidad unidad. sus vectores son (1,1,0,0) y (1,-1,,0,0), en tanto que la suma es (2,0,0,0). Este representa un haz no polarizado, pues los últimos tres números son cero.
Para determinar la forma completa del estado de polarización de un haz de luz (bien sea natural o parcialmente polarizado) son necesarios tres parámetros independientes, como por ejemplo los semiejes a y b, y la orientación Ψ de la elipse.
Los parámetros: y , que determinan por completo la elipse de polarización.
Estos parámetros estan definidos en términos de , Ψ y son:
Donde representa la irradiancia del haz. Solamente tres de estos parámetros son independientes, ya que ellos se relacionan entre sí por:
Si definimos ahora una cantidad χ mediante :
Entonces:
pero usando 4 y 5 se pueden escribir como:
y substituyendo aquí los valores de tenemos:
por otro lado podemos ver que:
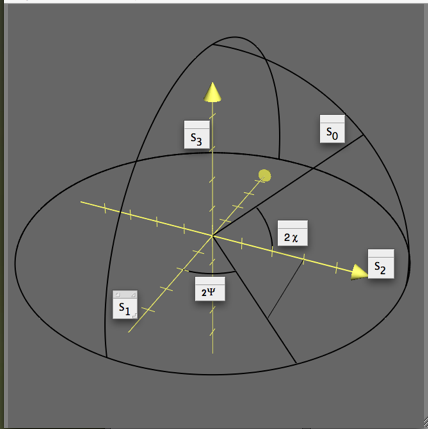
La relación dada por la ecuación (1c) sugiere que se pueden representar los parámetros por puntos en una esfera con radio .
Los parámetros de Stokes se pueden representar con base a la esfera de Poincaré de la manera siguiente:
Hemos visto en general que un haz completamente polarizado tiene en general polarización elíptica, la cual puede tomar las formas particulares circular o lineal.
La luz esta completamente polarizada sólo si las componentes son coherentes entre sí, es decir, si tienen una diferencia de fase $\varepsilon$ constante.
Podemos pensar en una onda no polarizada como una en la cual el estado de polarización cambia al azar en forma sumamente rápida. Una onda tal tiene la característica de que su irradiancia es la misma en cualquier plano de polarización que se mida.
Para representar en forma completa el estado de polarización, incluyendo los de luz parcialmente polarizada, es necesario especificar cuatro parámetros independientes. Dichos parámetros son los siguientes:
Estos parámetros (que están definidos como los promedios temporales de los parámetros de Stokes para luz completamente polarizada) representan físicamente lo siguiente:
I representa la irradiancia total del haz.
M indica el predominio de la componente horizontal o vertical, segun sea positivo o negativo.
C representa la tendencia del angulo χ para la orientación de la elipse, hacia -45º o +45º según sea positivo o negativo.
S indica si la polarización es derecha o izquierda, según sea positivo o negativo. Este parámetro es cero si la polarización es lineal.
El vector de Jones
El vector de de Jones, inventado en 1941 por un físico americano de 25 años, R.Clark Jones, es superior al vector de Stokes en algunos sentidos, pero inferior a otros. Es superior en el sentido de que es aplicable a la adición de haces coherentes. Es inferior en el sentido de que no puede aplicarse a la luz no polarizada o parcialmente polarizada y en que, además, utiliza números complejos.
Dado que la luz se compone de campos eléctricos y magnéticos oscilantes, Jones razonó que la forma más natural de representar la luz es en términos del vector de campo eléctrico.
Cuando se escribe como un vector de columna, este vector se conoce como un vector de Jones y tiene la forma:
Donde y son los componentes escalares instantáneos del campo eléctrico. Nota que estos valores pueden ser números complejos, por lo que la información de amplitud y fase es presente. A menudo, sin embargo, no es necesario conocer las amplitudes y fases exactas de los componentes del vector. Por lo tanto los vectores de Jones pueden ser normalizados y en fase común, los factores pueden ser descuidados. Esto resulta en una pérdida de información, pero puede simplificar enormemente expresiones. Por ejemplo, los siguientes vectores contienen diversos grados de información, pero son todas las representaciones vectoriales de Jones para el mismo estado de polarización:
Tenga en cuenta que se dice que un vector complejo se normaliza cuando el producto punto del vector con su conjugado complejo produce un valor de unidad. En la mayoría de los casos, se elige la base para el vector de Jones como los estados de polarización lineal horizontal y vertical. En este caso las representaciones de estos dos estados son:
y
o, en forma normalizada,
y
Donde y representan la luz polarizada horizontal y verticalmente, respectivamente. La suma de dos haces de luz coherentes viene dada por la suma de sus componentes correspondientes del vector de Jones, por lo que la suma de y cuando viene dada por :
Donde la flecha indica normalización. Tenga en cuenta que esta es la representación de la polarización. Estado en el que el campo eléctrico está orientado en un ángulo de 45 grados con respecto a la estados base. Otros dos estados de polarización comunes son circular derecho y circular izquierdo. En ambos casos los dos componentes tienen la misma amplitud,pero tienen una diferencia de fase de 90°. Así, la representación vectorial de Jones para la derecha-circular es
Normalizando esta expresión y factorizando un factor de fase constante :
Del mismo modo, la representación normalizada para la luz circular izquierda es:
La intensidad del haz es proporcional a la suma de los cuadrados de las magnitudes de los elementos. Si cada elemento del vector se multiplica por 4,la intensidad aumenta por un factor de 16. Aplicaciones: Una aplicación sencilla del vector de Jones es la predicción del resultado de componer dos haces coherentes. Considérese un haz polarizado horizontalmente de intensidad 1 y otro verticalmente polarizado de intensidad de 16 veces mayor. Los haces se suponen coherentes y de la misma fase.
Los vectores correspondientes son y El resultado de componer los dos haces se encuentra sumando los vectores. La suma es
Este corresponde a un haz linealmente polarizado a un angulo dado por ; esto es ,76°. La intensidad esta dada por osea 17.
A continuación, consideremos un haz de luz representado por el vector de Jones
incidente en un dispositivo óptico. La luz interactuará con el dispositivo, y el nuevo estado de polarización de la luz al salir del dispositivo será:
El acoplamiento entre estos dos vectores se puede describir completamente mediante un conjunto de cuatro coeficientes de acuerdo con el siguiente par de ecuaciones lineales:
Estas dos ecuaciones pueden reescribirse usando la notación matricial como
dónde
Es la matriz de Jones del dispositivo óptico. Una lista de matrices de Jones para algunos dispositivos ópticos comunes aparece en la Tabla 1. Es posible representar el paso de un haz de luz a través de múltiples dispositivos como la multiplicación de matrices de Jones. Tenga en cuenta que las matrices no conmutan, como se ilustra en el siguiente ejemplo. Supongamos una señal de entrada polarizada horizontalmente, y veamos su propagación a través de dos dispositivos, un polarizador lineal orientado a y una placa de cuarto de onda con su eje vertical rápido. Si la luz pasa a través del polarizador primero, seguido por la placa de onda, tenemos:
donde hemos descuidado los factores de amplitud y fase comunes por simplicidad. La salida es polarizado circularmente a la derecha.
Si bien la multiplicación de matrices no es conmutativa, es asociativa, por lo que una cadena de múltiples matrices de Jones que representan varios dispositivos se puede multiplicar para obtener una sola matriz de Jones que describe el sistema óptico en su conjunto. Por lo tanto, es posible condensar las propiedades de N dispositivos ópticos que actúan en serie hasta una sola matriz simplemente multiplicando las matrices de Jones de los dispositivos:
Cómo funcionan las gafas 3-D
Visualización en 3-D
En una sala de cine, la razón por la que usas gafas 3-D es para introducir diferentes imágenes en tus ojos como lo hace un View-Master. En realidad, la pantalla muestra dos imágenes y las gafas hacen que una de las imágenes entre en un ojo y la otra en el otro. Hay dos sistemas comunes para hacer esto:
Rojo / Verde o Rojo / Azul
Aunque el sistema rojo / verde o rojo / azul ahora se usa principalmente para efectos de televisión en 3D, y se usó en muchas películas antiguas en 3D. En este sistema, se muestran dos imágenes en la pantalla, una en rojo y la otra en azul (o verde). Los filtros en las gafas permiten que solo una imagen entre en cada ojo, y su cerebro hace el resto. Realmente no puede tener una película en color cuando está usando el color para proporcionar la separación, por lo que la calidad de la imagen no es tan buena como con el sistema polarizado.
Polarización
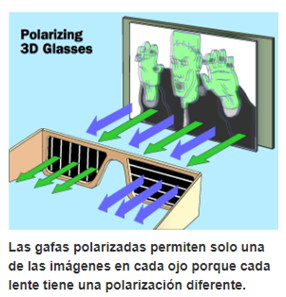
En Disney World , Universal Studios y otros lugares tridimensionales, el método preferido utiliza lentes polarizados porque permiten la visualización del color. Dos proyectores sincronizados proyectan dos vistas respectivas en la pantalla, cada una con una polarización diferente. Las gafas permiten solo una de las imágenes en cada ojo porque contienen lentes con polarización diferente.
Como se había dicho anteriormente un filtro polarizador tiene pequeñas líneas paralelas grabadas en él, un poco como las lamas de un conjunto de persianas venecianas. Esto significa que solo permitirá que la luz vibre en un plano particular a través.
Al igual que en el antiguo estilo 3D, la película se graba utilizando dos lentes de cámara, sentados uno al lado del otro. Pero en el cine, los dos carretes de película se proyectan a través de diferentes filtros polarizados. Así que las imágenes destinadas a los ojos izquierdos de los espectadores están polarizadas en un plano horizontal, mientras que las imágenes destinadas a sus ojos derechos están polarizadas en un plano vertical. Las gafas de los espectadores de cine usan los mismos filtros polarizadores para separar las dos imágenes nuevamente, dando a cada ojo una perspectiva ligeramente diferente y engañando al cerebro para que "vea" el planeta Pandora de Avatar.
En un par de gafas digitales 3D, cada lente está polarizada de manera diferente. En algunas gafas, hay una diferencia de 90 grados en la polarización. Otros utilizan diferentes alineaciones de polarización circular. La pantalla está especialmente diseñada para mantener la polarización correcta cuando la luz de los proyectores rebota en ella. En lugar de verse como una malla de rojo y verde, las películas que usan esta tecnología parecen normales, pero borrosas, cuando se ven sin gafas.
Aportación de: Luis Manuel Chávez Antonio
Actividad Óptica
Un rayo de luz no polarizado puede ser polarizado linealmente haciéndolo pasar por una hoja de polarización. En un polarizador existe una cierta dirección, indicada por líneas paralelas (eje óptico), que transmite sólo los componentes de la luz cuyos vectores de campo eléctrico vibran paralelamente a esa dirección, y absorben aquellas que lo hacen de forma perpendicular. La luz proveniente del polarizador sale linealmente polarizada.
Si colocamos una segunda hoja de polarización (llamada analizador cuando se usa en esta forma), entonces la cantidad de luz transmitida dependerá de la orientación del eje de la segunda hoja en relación a la primera; si los ejes son paralelos el rayo de luz podrá pasar, en el mejor de los casos, sin pérdida de intensidad. Si los ejes son perpendiculares, entonces no habrá paso de luz a través de él.
Existen materiales que presentan actividad óptica, es decir, aquellas sustancias que son capaces de hacer girar el plano de vibración de la luz polarizada cuando dicha luz la atraviesa. Los cristales de cuarzo y las soluciones en azúcar son ejemplos de materiales ópticamente activos. El polarizador y el analizador pueden alinearse cuidadosamente cuando no hay un material ópticamente activo entre ellos; cuando lo hay, el ángulo en que el analizador debe girar para lograr la transmisión máxima o mínima indica la rotación del plano de polarización al cruzar el material.
La actividad óptica es un tipo de birrefringencia, es decir, de doble refracción. Cualquier luz polarizada linealmente puede ser escrita como una combinación de polarización circular derecha o izquierda, RHC y LHC respectivamente (por sus siglas en inglés)
Donde es el campo eléctrico de la luz. La fase relativa entre las dos polarizaciones circulares () da la polarización lineal a . En un material ópticamente activo, las dos polarizaciones circulares experimentan diferentes índices de refracción. La diferencia entre estos índices cuantifica la fuerza de la actividad óptica.
Esta diferencia es una característica del material (para sustancias en solución, esta dado como la rotación específica). Después de viajar a través de la distancia del material, las dos polarizaciones toman una fase relativa de
Donde es la longitud de onda de la luz. Como una consecuencia de esto, la polarización final es rotada a un ángulo:
>> Rotación específica.
La rotación específica () es la cantidad que indica el grado de actividad óptica de ciertas sustancias en una solución. Su magnitud y signo depende de la estructura de la molécula y generalmente varía con la longitud de onda de la luz utilizada para la medición, así como la concentración de la sustancia.
donde (grados) es el ángulo medido de rotación (observado por el analizador de polarización) por una solución con concentación (g/cm^3) y longitud L (cm). La rotación específica, (grados/(g/cm^2)), es la propiedad de una sustancia en particular, a determinada longitud de onda (la utilizada para su medición).
--Roberto Martínez Sosa 07:26 5 abr 2012 (UTC)
Fuentes y Referencias
"Optica Básica", Daniel Malacara, Fondo de la cultura económica 1989.
"Polarized Light In Optics And Spectroscopy", David S. Kliger, James W. Lewis y Cora E. Randall, Academic Press,Inc. 1990 .
"Ondas (Berkeley Physics Course - Volumen 3)", Frank S.Crawford, Jr., Edit Reverté 1994.
"Optics", Eugene Hecht, 4ta edición, Addison Wesley 2002.
"The Feynman Lectures of Physics: Volume 1", Richard Feynman, Robert Leighton, y Matthew Sands.
"Óptica.". E. Hecht, A. Zajac. Ed. Addison Wesley, 2000
"Luz Polarizada". WILLIAM A. SHURCLIFF. Ed.Reverté Mexicana, 1968
"Polarized Light:Production and Use". W.A. SHURCLIFF, Harvard University Press,1962.
E. Collett, Field Guide to Polarization, SPIE Press, Bellingham, WA (2005).
|
--Roberto Martínez Sosa 07:41 5 abr 2012 (UTC)



![\vec B(z,t)=\mathbf{\hat{e}_{z}}\times[E^{+}(z,t)-E^{-}(z,t))]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5caf0f830f395da1c9ee5a62d3677e8900d78601)





































![\sin(\omega t-kz)=\left[1-cos^{2}(kz-\omega t)\right]^{\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f0995e75214cc574c46e6aaee126b026992fbc25)