Introducción
En esencia, una antena es un sistema conductor metálico capaz de radiar y recibir ondas electromagnéticas, y una guía de onda es un tubo metálico conductor por medio del cual se propaga energía electromagnética de alta frecuencia, por lo general entre una antena y un transmisor, un receptor, o ambos.
Electromagnetismo en las antenas
El comportamiento de las ondas electromagnéticas y de cómo se desplazan en el medio queda expresado analíticamente por medio de las ecuaciones de Maxwell[1], que se transcriben a continuación:




Para nuestro caso, las ondas electromagnéticas se propagan en el espacio libre y se tiene  y la ecuación (1) se reduce a:
y la ecuación (1) se reduce a:

Por lo tanto, la ecuación (4) se cumple si el campo magnético se expresa como el rotacional de un potencial, al cual se le asigna el nombre de potencial vectorial  .
.
Como la divergencia de un rotacional es cero, se puede establecer entonces:

donde  es la permeabilidad magnética.
es la permeabilidad magnética.
De la misma manera, se establece una relación entre el campo eléctrico y el potencial escalar  . En este caso se tiene sustituyendo la ecuación (5) en la ecuación (2),
. En este caso se tiene sustituyendo la ecuación (5) en la ecuación (2),

Factorizando los rotacionales:

Esta ecuación indica que el campo  es conservativo, ya que su rotacional es cero, y en este caso se puede expresar como menos el gradiente de un potencial escalar
es conservativo, ya que su rotacional es cero, y en este caso se puede expresar como menos el gradiente de un potencial escalar  , donde el signo menos indica que la fuerza decrece con la distancia.
, donde el signo menos indica que la fuerza decrece con la distancia.
Tenemos entonces:

O sea,

El campo eléctrico se expresa a través de un potencial vectorial  y otro escalar
y otro escalar  .
.
Campos y radiación de una fuente oscilante localizada
Si consideramos que los potenciales, los campos y la radiación debidos a un sistema de cargas y corrientes varían sinusoidalmente con el tiempo

La solución para el potencial vectorial es:

La integral puede ponerse en forma más familiar si se integra por partes:

Recordemos que: 
Pero  .
.
Por lo tanto  .
.
En consecuencia 
Usando el Teorema de la divergencia [ecuación (f)] el primer términos nos queda  , y como
, y como  esta dentro del volumen V, es cero en la superficie.
esta dentro del volumen V, es cero en la superficie.
Por lo tanto  o, combinando esto con las componentes de
o, combinando esto con las componentes de  y
y  ,
, 
Entonces la ec (10) nos queda:

Para encontrar la ecuación de continuidad, tomamos

Ahora, haciendo uso de la divergencia en esta última ecuación, tenemos

Pero 
Entonces nos queda

O sea:
 , pero de la ecuación (8) obtenemos
, pero de la ecuación (8) obtenemos

Sustituyendo este resultado en la ecuación (10), nos queda:

Así que el vector potencial se puede escribir como:

en donde  es el momento dipolar eléctrico.
es el momento dipolar eléctrico.
Dipolo
Un dipolo corto es un dipolo que esta formado por dos conductores de longitud total  muy pequeña comparada a la longitud de onda
muy pequeña comparada a la longitud de onda  . Los dos conductores están alimentados en el centro del dipolo. Esta vez se toma como hipótesis que la corriente es máxima en el centro del dipolo (en donde está alimentada) y que decae linealmente hacia cero a las extremidades del dipolo.
. Los dos conductores están alimentados en el centro del dipolo. Esta vez se toma como hipótesis que la corriente es máxima en el centro del dipolo (en donde está alimentada) y que decae linealmente hacia cero a las extremidades del dipolo.
Hay que notar que la corriente circula en la misma dirección en los dos brazos del dipolo: hacia la derecha en los dos o hacia la izquierda en los dos.
El dipolo corto se diferencia del de Hertz por la distribución no uniforme de la corriente a lo largo de su longitud. No obstante, la teoría del dipolo de Hertz permite descubrir las propiedades del dipolo simétrico.
En particular, en el dipolo simétrico varía la distancia entre las secciones simétricas del conductor y sus parámetros lineales a medida que nos vamos alejando de las terminales del generador.
Dipolo infinitesimal
Un cable lineal infinitesimal  se sitúa simétricamente en el origen del sistema de coordenadas y se orienta a lo largo del eje
se sitúa simétricamente en el origen del sistema de coordenadas y se orienta a lo largo del eje  . El cable, además de ser muy pequeño
. El cable, además de ser muy pequeño  , es muy delgado. La corriente se asume como constante y esta dada por
, es muy delgado. La corriente se asume como constante y esta dada por

donde 
Distribución de corriente en una antena
El movimiento de las cargas crea una corriente de onda que viaja, con magnitud  , a lo largo de cada uno de los cables. Cuando la corriente llega el final de cada uno de los cables, experimenta una reflexión (de igual magnitud).
, a lo largo de cada uno de los cables. Cuando la corriente llega el final de cada uno de los cables, experimenta una reflexión (de igual magnitud).
Si el diámetro de cada cable es muy pequeño, el patrón de onda estacionaria de la corriente a lo largo de los brazos del dipolo es sinusoidal con un valor nulo al final. La corriente de un dipolo es muy pequeña
y puede ser aproximada por una distribución triangular desde  donde
donde  es muy pequeño. Esto se puede ver en la Figura 2.
es muy pequeño. Esto se puede ver en la Figura 2.
Dipolo corto
El arreglo geométrico más conveniente para el análisis de un dipolo es generalmente hacerlo simétricamente sobre el origen con su longitud dirigida a lo largo del eje  , tal como se muestra en la Figura (2). Esto no es necesario, pero por lo general es la forma más simple. Por lo tanto la distribución de corriente esta dada por
, tal como se muestra en la Figura (2). Esto no es necesario, pero por lo general es la forma más simple. Por lo tanto la distribución de corriente esta dada por

donde  es constante
es constante
La primera derivada del momento dipolar de un sistema de cargas 
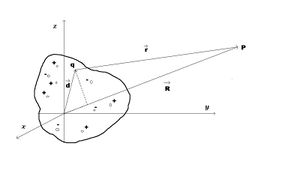
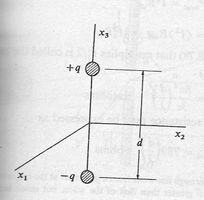
Sistema de cargas 

Haciendo ahora los vectores  fijos y haciendo cambiar las cargas
fijos y haciendo cambiar las cargas  con respecto al tiempo. Un ejemplo sencillo de esta situación se muestra en la fig (2) donde podemos considerar la variación temporal de las cargas como equivalentes al flujo de corrientes entre
con respecto al tiempo. Un ejemplo sencillo de esta situación se muestra en la fig (2) donde podemos considerar la variación temporal de las cargas como equivalentes al flujo de corrientes entre  y
y  . Así,
. Así,

Según la ecuación de continuidad (11), la densidad lineal de carga  es constante a lo largo de cada brazo de la antena, y tiene el valor:
es constante a lo largo de cada brazo de la antena, y tiene el valor:

el signo superior corresponde a los valores positivos de  y el inferior a los negativos. El momento dipolar es paralelo al eje
y el inferior a los negativos. El momento dipolar es paralelo al eje  y tiene el valor:
y tiene el valor:

La distribución angular de potencia radiada es

mientras que la potencia radiada total es

Vemos que para una corriente de excitación, la potencia radiada aumenta con el cuadrado de la frecuencia.
Antenas Lineales
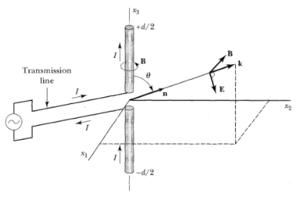
Para comenzar este tema primeramente describiremos una antena compuesta de 2 delgados alambres. Ambos de longitud d/2, los cuales tienen una ligera separación entre ellos. En dicha separación se aplicara una señal forzada. Para este caso despreciaremos la radiación producida por la señal.
En este caso supondremos que la corriente es senoidal y que dicha corriente es cero en los extremos exteriores de la antena. Es decir:
![\vec{J}(\vec{r}',t_{r})dv'=I(x_{3}^{'},t_{r})d\vec{x}_{3}^{'}=\hat{e}_{3}I_{0}e^{-i\omega t_{r}}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]dx_{3}^{'} (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e7cc7d36eb1714be38e1ec2428a9b3328628cfdd)
y la señal de entrada sería:

La ecuación (1) es un resultado aproximado de la ecuación Pocklington.
Tomaremos en cuenta unicamente la radiación de campo lejano, es decir, de los campos retardados sólo tomaremos aquellos términos que van como 1/R. Por ello, tomando en cuenta esto, la expresión del campo magnético se reduce a:
![\vec{B}_{rad}=\int_{v}\frac{[\partial\vec{J}/\partial t]\times\hat{n}}{c^{2}R}dv' (3)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8956640d04d1bd11ac689f007b9a69539d6245c3)
Ahora de la ecuación (1) podemos ver que ![I(x_{3}^{'},t_{r})=I_{0}e^{-i\omega t_{r}}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a12e4c3971104e99c541cb2eeb9a159ab284e2a4) y tambien podemos ver que
y tambien podemos ver que ![[\partial\vec{J}/\partial t]dv'=[\partial I(x_{3}^{'},t_{r})/\partial t]d\vec{x}_{3}^{'}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d441da2707ccd0a77e0d69f0d0ac884379f677dd)
![=\hat{e}_{3}[\partial I(x_{3}^{'},t_{r})/\partial t]dx_{3}^{'}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1f3f24e80306f50914aaebcf94229e6a7afbe20f) . Por tanto con base en ello tenemos que:
. Por tanto con base en ello tenemos que:
![\vec{B}_{rad}=\hat{e}_{3}\times\hat{n}\int\frac{[\partial I(x_{3}^{'},t_{r})/\partial t]}{c^{2}R}dx_{3}^{'} (4)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fae86f330be79e4a3d1a4c2a80cddc3b786929d9)

Ahora como la distancia de observación es muy grande comparada con el tamaño de la antena, R que se define como  , se reduce a $r$, por tanto la fórmula (5) se reduce a:
, se reduce a $r$, por tanto la fórmula (5) se reduce a:

Es importante mencionar que dos limites que usaremos (de los cuales el paraxial ya usamos) son:

Llamamos limite paraxial a r  d, debido a lo siguiente.
El término aproximación paraxial es utilizado en óptica cuando los rayos de luz que inciden en un objeto, forman ángulos pequeños con el eje principal. En otras palabras el tamaño del objeto es despreciable en comparación con su distancia al sistema óptico. Es por ello, que en este caso llamamos a
r
d, debido a lo siguiente.
El término aproximación paraxial es utilizado en óptica cuando los rayos de luz que inciden en un objeto, forman ángulos pequeños con el eje principal. En otras palabras el tamaño del objeto es despreciable en comparación con su distancia al sistema óptico. Es por ello, que en este caso llamamos a
r  d, limite paraxial. Porque si se hacemos una analogía, en este caso el objeto sería la antena y la posición del sistema óptico sería el punto de observación r. Por esta razón r
d, limite paraxial. Porque si se hacemos una analogía, en este caso el objeto sería la antena y la posición del sistema óptico sería el punto de observación r. Por esta razón r  d, es llamado limite paraxial.
Siguiendo con el tema, debido a que el campo magnético y eléctrico son ortogonales, podemos encontrar el campo eléctrico, con la siguiente expresión:
d, es llamado limite paraxial.
Siguiendo con el tema, debido a que el campo magnético y eléctrico son ortogonales, podemos encontrar el campo eléctrico, con la siguiente expresión:


Pero en realidad para los cálculos que prosiguen sólo requerimos la magnitud del vector  , (es importante mencionar que la magnitud de
, (es importante mencionar que la magnitud de  y
y  son iguales debido a que estamos trabajando en unidades gaussianas), con base en los mencionado y sabiendo que el vector de Poynting es:
son iguales debido a que estamos trabajando en unidades gaussianas), con base en los mencionado y sabiendo que el vector de Poynting es:

podemos reescribir la expresión de la siguiente manera:

Con base en esto vemos que nuestro verdadero objetivo es resolver la integral (6). A pesar, de que, para obtener la ecuación (6) tuvimos que despreciar  , no podemos hacer lo mismo, cuando sustituyamos la expresión del tiempo retardado, debemos hacer una aproximación mediante una expansión binomial. Esto se debe a que sólo de esta manera observaremos con detalle la fase de oscilación de la antena. Para ello sustituiremos
, no podemos hacer lo mismo, cuando sustituyamos la expresión del tiempo retardado, debemos hacer una aproximación mediante una expansión binomial. Esto se debe a que sólo de esta manera observaremos con detalle la fase de oscilación de la antena. Para ello sustituiremos  en la integral (6) y usaremos que
en la integral (6) y usaremos que  y que
y que  .
.
Ahora debido a que  es radial el producto
es radial el producto  , no es igual debido a que el ángulo entre
, no es igual debido a que el ángulo entre  y
y  no es 90°. Por tanto de acuerdo a la definición de producto cruz,
no es 90°. Por tanto de acuerdo a la definición de producto cruz,  .
.
De acuerdo a lo que hemos mencionado, la ecuación (6) se reduce a:


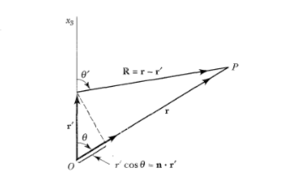
Ahora de acuerdo a la figura de la derecha tenemos que, 
Ahora realizando la expansión binomial de,  tenemos:
tenemos:
![|\vec{r}-\vec{r}'|=r[1-\frac{\hat{n}\cdot\vec{r}'}{r}+\frac{r'^{2}}{2r^{2}}-\frac{1}{8}\left(\frac{2\hat{n}\cdot\vec{r}'}{r}\right)^{2}+...]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/36c65224932c21146ffbe54c1c3fae97321ac178)
![\Rightarrow|\vec{r}-\vec{r}'|=r[1-\frac{r'}{r}Cos(\theta)+\frac{r'^{2}}{2r^{2}}Sen^{2}(\theta)+...] (12)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e702a07c9bf0cd6070c7e597025ebc89e11e07f6)
Ahora , para despreciar los términos de orden cuadrático requerimos que, cuando los sustituyamos en la ecuación (11), estos sean muy pequeños comparados con 2 . Es decir que
. Es decir que  . Debido al tipo de antena que estamos tratando, el valor más grande de
. Debido al tipo de antena que estamos tratando, el valor más grande de  . Por tanto, para despreciar los términos de orden cuadrático se debe cumplir:
. Por tanto, para despreciar los términos de orden cuadrático se debe cumplir:




Esta aproximación, junto con las dos de la ecuación (7), se pueden escribir en una sola expresión, de la siguiente manera:

Vemos que usando el limite de Fraunhofer, podemos reescribir  como
como  . Lo que nos permite reescribir la ecuación (11) de la siguiente manera:
. Lo que nos permite reescribir la ecuación (11) de la siguiente manera:

pero de la ecuación (1) sabemos que ![I(x_{3}^{'})=I_{0}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cb8b9eb357c69c833eccb7ea846c7195b031fcf3) , por tanto:
, por tanto:
![B_{\phi}=-I_{0}\frac{i\omega}{c^{2}r}Sen(\theta)e^{i(kr-\omega t)}\int_{-d/2}^{d/2}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]e^{ikx_{3}^{'}Cos(\theta)}dx_{3}^{'} (15)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce26b0dc09718cee40c52239e6d510d721a3baca)
Resolviendo la ecuación (15) obtenemos:

Ahora sabemos que:



Por tanto:

Donde la ecuación (18) es el promedio en el tiempo de la potencia radiada por unidad de ángulo-sólido, emitido por la antena.
Podemos ver que la distribución angular de la potencia radiada depende en gran medida del valor kd/2. Situaciones de gran interes, son aquellas, en las que la relación entre la longitud de la antena y la longitud de onda de la señal aplicada, forma una relación sencilla. Por ejemplo digamos que d es un multiplo de  /2 (donde
/2 (donde  es la longitud de onda de la señal que se está aplicando a la antena, para que está emita), entonces tendremos:
es la longitud de onda de la señal que se está aplicando a la antena, para que está emita), entonces tendremos:

Por tanto:

Las corrientes de distribución para m=1,2,3,4, son mostradas a continuación:
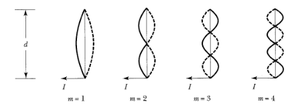
Corrientes de distribucion con la señal conectada en el centro
La curvas sólidas corresponden a la primera mitad del ciclo de las oscilaciones y las punteadas a la otra mitad. Claro esta que valores positivos y negativos en la corriente, representan cambios en la dirección de la corriente que fluye a tráves de la antena.
Las distribuciones angulares para m=1 y m=2, se muestran a continuación:


El promedio sobre el tiempo de la potencia total radiada está dada por la siguiente expresión:

![=\frac{I_{0}^{2}}{c}\int_{0}^{\pi}\frac{\left[Cos\left(\frac{m\pi}{2}Cos(\theta)\right)-Cos\left(\frac{m\pi}{2}\right)\right]^{2}}{Sen(\theta)}d\theta (23)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/558ecf2cf06cc00ea3459b227585d6d28c37402c)
Dicha integral se puede evaluar numéricamente. Para el caso de la antena de media onda,m=1, tenemos:

Pero sabemos que  , lo que implica que:
, lo que implica que:

El equivante de dicha expresión (ecuación (25)) en unidades del SI es:
 ohms
ohms
donde  ohms es la impedancia del vacío en el sistema internacional. En este caso (así como cuando m sea par), el punto de alimentación que está en el centro de la antena coincide con el antinodo de la corriente y debido a esto
ohms es la impedancia del vacío en el sistema internacional. En este caso (así como cuando m sea par), el punto de alimentación que está en el centro de la antena coincide con el antinodo de la corriente y debido a esto  será la resistencia de la señal forzada; y se encontrará en el punto de alimentación. Para otros casos (m impar), dicha resistencia está en términos de
será la resistencia de la señal forzada; y se encontrará en el punto de alimentación. Para otros casos (m impar), dicha resistencia está en términos de  :
:

![=\frac{2}{cSen^{2}\left(\frac{m\pi}{2}\right)}\int_{0}^{\pi}\frac{\left[Cos\left(\frac{m\pi}{2}Cos(\theta)\right)-Cos\left(\frac{m\pi}{2}\right)\right]^{2}}{Sen(\theta)}d\theta (26)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cf76a52f67cabbd8f3fb97d2583ae75b31ce3475)
Podemos ver, de la ecuación (26), que dicha expresión diverge cuando m es par, que es cuando, la onda, tiene su nodo, en el centro de la antena. Podemos reducir la resistencia de entrada a un valor más practico si aumentamos la distancia entre los alambres. Similarmente, podemos variar dicha resistencia variando la posición en la que se conecte la señal sobre la antena.
De la ultima figura, podemos ver que la antena de onda total (m=2), es equivalente a 2 antenas de media onda. Es por ello que la antena de media onda es la unidad básica para la construcción de muchos sistemas de antenas. Tomando en cuenta esto colocando dichas antenas en los lugares adecuados, con las fases de corriente adecuadas, podemos construir un amplia gama de patrones de radiación.
Ahora, a continuación veremos las distribución de las corrientes, pero con la señal colocada al final de la antena:
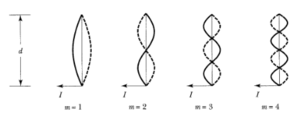
Corrientes de distribucion con la señal conectada en un extremo
Podemos ver que para el caso de m impar, la situación es la misma, que teníamos cuando la señal estaba conectada en el centro de la antena. Pero para el resto de los casos una de las mitades va en dirección opuesta, como se puede observar.
Para el caso de m impar tenemos que la ecuación (18) se simplifica a:

Y para el caso par:

A continuación se muestran los patrones de radiación que se forman, de acuerdo a en que parte conectemos la señal que alimenta a la antena:
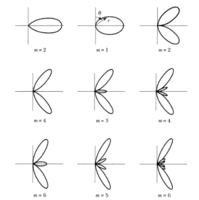
Patrones de radiación con la señal conectada en diferentes partes
De la imagen de arriba, la columna izquierda corresponde a aquellas antenas con la señal colocada en el centro, la de la derecha corresponde a la situación en que la señal se coloco al final de la antena y la de enmedio corresponde a aquella antena que se le conectaron dos señales, una en el centro y otra en su extremo.
De la imágen de arriba podemos ver que conforme la antena aumenta de tamaño, la emisión de esta tiende a acercarse a la dirección de la antena.
Por último queda agregar que suponer que la corriente es senoseidal es algo muy idealista. Esto debido a que la distribución de la corriente se ve afectada por la resistencia del alambre del que esta hecho la antena. Además de que hay que tomar en cuenta que la presencia de la tierra así como otras estructuras conductoras modifican el patrón de radiación producido por la antena. Además veamos que la suposición de trabajar con un valor específico de m implica que la antena opere a una frecuencia particular y sabemos que en la realidad las antenas tienen que trabajar eficientemente en una rango amplio de frecuencias.
--Daniel Quiroga González 18:48 23 jul 2012 (UTC)
Directividad de la Antena y Área Efectiva
Hemos visto que las antenas no emiten de manera uniforme. De hecho, es imposible topologicamente que una antena emita ondas transversales de manera uniforme. Por lo general los ingenieros que diseñan estos aparatos buscan que la antena, emite la mayor parte de su radiación en una determinada dirección. En el caso de que la antena sea un receptor esperamos que dicha antena sea más sensible en una determinada dirección.
La directividad o ganancia la definiremos como el cociente del valor máximo de la potencia radiada por unidad de ángulo sólido entre el promedio de la potencia radiada por unidad de ángulo-sólido.

Es decir, la directividad mide cuánta radiación es emitidad en una determinada dirección, respecto a la que es emitida en esa misma dirección por una antena isotrópica que trabaja a la misma potencia que la real (es importante saber que una antena isotrópica es una idealización). De las ecuaciones (21) y (23) es fácil ver que la direcitividad de una antena de media onda es 1.64. Sin embargo en la vida real se requieren directividades mucho más grandes que 1. Para alcanzar directividades de dicha magnitud se usan antenas que están hechas a base de una gran número de pequeñas antenas (es decir, antenas de media onda), para que de esta manera la antena tenga una longitud mucho mayor a la longitud de onda, que se está propagando en el espacio.
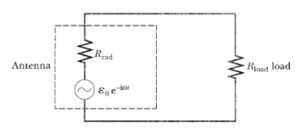
Para introducir el concepto de área efectiva trataremos la antena como un receptor. Una antena que funciona como receptor, primero que nada capta una onda electromagnética. Esto provoca que se induzca una corriente en la antena, dicha corriente es depurada en un filtro electrónico (conocida como “antenna's load”), esto con el propósito de quedarnos únicamente con la señal deseada. Es decir en otras palabras, una antena receptora es un circuito, que produce una fuerza electromotriz (debido a la onda electromǵnetica incidente), de magnitud  , con una determinada resistencia interna
, con una determinada resistencia interna  , cuyo valor dependerá del material de la antena. A continuación se muestra el circuito de una antena receptora.
, cuyo valor dependerá del material de la antena. A continuación se muestra el circuito de una antena receptora.
Debido a que queremos que la máxima potencia llegue al filtro electrónico, la resistencia de dicho filtro debe ser igual a la resistencia interna de la antena. Por ello dicha potencia se expresaría de la siguiente manera:

Definiendo A como el área efectiva, y sabiendo que en dicha área se concentra la potencia máxima que recibirá la antena. Podemos concluir que:

Ahora, la dependencia de la fuerza electromotriz, con la amplitud del campo eléctrico para un dipolo hertziano (usaremos dicha expresión para obtener la relación entre el área efectiva y la directividad) es:

Donde l es la longitud del dipolo. Ahora el vector de Poynting de una onda electromagnética aproximándose se expresa de la siguiente forma:

Ahora usando, las ecuaciones (30) y (33), tenemos:

Y sabiendo que  , la ecuación (34), se reduce a la siguiente expresión:
, la ecuación (34), se reduce a la siguiente expresión:

Podemos de este caso particular, obtener una expresión más general. Para ello hay que saber que  donde
donde  es el área efectiva de una antena isotrópica. De acuerdo a esto, debido a que la directividad o ganancia de un dipolo hertziano es
es el área efectiva de una antena isotrópica. De acuerdo a esto, debido a que la directividad o ganancia de un dipolo hertziano es  , tendremos:
, tendremos:


Ahora con base en la ecuación (37) y reciente definición de G que se hizo, obtenemos la siguiente expresión, que es válida para cualquier antena:

Con esta fórmula terminamos, el texto, pues la intención era dar una definición de la directividad y del área efectiva. Hay que recordar que en este texto hubo varias aproximaciones, además de que no detallamos aquellas partes que tenían que ver con la electrónica. Por ello es de esperarse que algunas de estas propiedades no se cumplan al pie de la letra en todos los tipos de antenas.
--Daniel Quiroga González 18:48 23 jul 2012 (UTC)
Apéndice
Operadores Diferenciales Vectoriales




Teoremas de integrales
Integral por partes

Teorema de la divergencia (Teorema de Gauss)

Teorema de Stokes

Demostración detallada para el vector potencial

Ahora, sacando factor común  de la raíz
de la raíz
![\frac{1}{\mathbf{|r-r'|}}=\left(r^{2}\right)^{-\frac{1}{2}}\left(1-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)^{-\frac{1}{2}}=\frac{1}{r}\left[1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)\right]^{-\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e13452e06304a7cf4ca32dfa465a2b6766bf072a)
Hasta aquí no hay aproximación alguna. Observamos que en el último factor tenemos 1 más algo mucho más pequeño que la unidad (pues  ). La fórmula general del binomio de Newton nos dice que si
). La fórmula general del binomio de Newton nos dice que si 

Aplicando esto al resultado anterior
![\frac{1}{\mathbf{|r-r'|}}=\frac{1}{r}\left[1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)\right]^{-\frac{1}{2}}=\frac{1}{r}\left[1-\frac{1}{2}\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)+\mathcal{O}\left(\delta^{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a790093f5b3df8ac6848508f6d58f8bdfa4b5ed5)
pero de hecho, el segundo de los dos sumandos del paréntesis también es de orden  , por lo que podemos despreciarlo y reducir el desarrollo a
, por lo que podemos despreciarlo y reducir el desarrollo a
![\frac{1}{\mathbf{|r-r'|}}=\frac{1}{r}\left[1+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\mathcal{O}\left(\delta^{2}\right)\right]=\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{3}}+...](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/167ac9b46b89fd7dac79f20047379e752d165d0d)
El segundo paso es sustituir esto en la expresión del potencial vector. Nos queda

La primera de estas dos integrales es el desplazamiento neto al recorrer una curva cerrada, por lo que se anula idénticamente,

Véase también
Referencias
Classical Electromagnetic Radiation, Jerry B. Marion, Second Edition, pp.245-252
Electrodinámica Clasica, J. D. Jackson, Segunda Edición, pp. 398-410
Radiación, propagación y antenas, María José Salmerón, Ed. Trillas, pp. 15-17
Anthenna Theory, Balanis C.,pp. 11-14, 100-112































































![\vec{J}(\vec{r}',t_{r})dv'=I(x_{3}^{'},t_{r})d\vec{x}_{3}^{'}=\hat{e}_{3}I_{0}e^{-i\omega t_{r}}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]dx_{3}^{'} (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e7cc7d36eb1714be38e1ec2428a9b3328628cfdd)

![\vec{B}_{rad}=\int_{v}\frac{[\partial\vec{J}/\partial t]\times\hat{n}}{c^{2}R}dv' (3)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8956640d04d1bd11ac689f007b9a69539d6245c3)
![I(x_{3}^{'},t_{r})=I_{0}e^{-i\omega t_{r}}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a12e4c3971104e99c541cb2eeb9a159ab284e2a4)
![[\partial\vec{J}/\partial t]dv'=[\partial I(x_{3}^{'},t_{r})/\partial t]d\vec{x}_{3}^{'}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d441da2707ccd0a77e0d69f0d0ac884379f677dd)
![=\hat{e}_{3}[\partial I(x_{3}^{'},t_{r})/\partial t]dx_{3}^{'}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1f3f24e80306f50914aaebcf94229e6a7afbe20f)
![\vec{B}_{rad}=\hat{e}_{3}\times\hat{n}\int\frac{[\partial I(x_{3}^{'},t_{r})/\partial t]}{c^{2}R}dx_{3}^{'} (4)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fae86f330be79e4a3d1a4c2a80cddc3b786929d9)























![|\vec{r}-\vec{r}'|=r[1-\frac{\hat{n}\cdot\vec{r}'}{r}+\frac{r'^{2}}{2r^{2}}-\frac{1}{8}\left(\frac{2\hat{n}\cdot\vec{r}'}{r}\right)^{2}+...]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/36c65224932c21146ffbe54c1c3fae97321ac178)
![\Rightarrow|\vec{r}-\vec{r}'|=r[1-\frac{r'}{r}Cos(\theta)+\frac{r'^{2}}{2r^{2}}Sen^{2}(\theta)+...] (12)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e702a07c9bf0cd6070c7e597025ebc89e11e07f6)










![I(x_{3}^{'})=I_{0}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cb8b9eb357c69c833eccb7ea846c7195b031fcf3)
![B_{\phi}=-I_{0}\frac{i\omega}{c^{2}r}Sen(\theta)e^{i(kr-\omega t)}\int_{-d/2}^{d/2}Sen[k(\frac{d}{2}-|x_{3}^{'}|)]e^{ikx_{3}^{'}Cos(\theta)}dx_{3}^{'} (15)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ce26b0dc09718cee40c52239e6d510d721a3baca)











![=\frac{I_{0}^{2}}{c}\int_{0}^{\pi}\frac{\left[Cos\left(\frac{m\pi}{2}Cos(\theta)\right)-Cos\left(\frac{m\pi}{2}\right)\right]^{2}}{Sen(\theta)}d\theta (23)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/558ecf2cf06cc00ea3459b227585d6d28c37402c)








![=\frac{2}{cSen^{2}\left(\frac{m\pi}{2}\right)}\int_{0}^{\pi}\frac{\left[Cos\left(\frac{m\pi}{2}Cos(\theta)\right)-Cos\left(\frac{m\pi}{2}\right)\right]^{2}}{Sen(\theta)}d\theta (26)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cf76a52f67cabbd8f3fb97d2583ae75b31ce3475)




























![\frac{1}{\mathbf{|r-r'|}}=\left(r^{2}\right)^{-\frac{1}{2}}\left(1-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)^{-\frac{1}{2}}=\frac{1}{r}\left[1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)\right]^{-\frac{1}{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e13452e06304a7cf4ca32dfa465a2b6766bf072a)



![\frac{1}{\mathbf{|r-r'|}}=\frac{1}{r}\left[1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)\right]^{-\frac{1}{2}}=\frac{1}{r}\left[1-\frac{1}{2}\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\frac{r'^{2}}{r^{2}}\right)+\mathcal{O}\left(\delta^{2}\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a790093f5b3df8ac6848508f6d58f8bdfa4b5ed5)

![\frac{1}{\mathbf{|r-r'|}}=\frac{1}{r}\left[1+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{2}}+\mathcal{O}\left(\delta^{2}\right)\right]=\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^{3}}+...](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/167ac9b46b89fd7dac79f20047379e752d165d0d)

