|
|
| (No se muestran 287 ediciones intermedias de 7 usuarios) |
| Línea 1: |
Línea 1: |
| Building
| | == Difracción de apertura Círculo-Cuadrado. == |
|
| |
|
| | La ecuación <ref> Manuel Fernandez Guasti,''Analytic geometry of some rectilinear figures'',INT.J.MATH.EDUC.SCI.TECHNOL., 1992, VOL.23,No.6</ref> |
|
| |
|
| == 1. Apertura rectangular. == | | <center> |
| | <math>x^{2}+y^{2}-\frac{s^{2}}{a^{2}}x^{2}y^{2}=a^{2}\qquad \qquad\qquad\qquad\qquad (1) |
| | </math></center> |
|
| |
|
| | * Representa un círculo en el plano <math>xy</math> de radio <math>a</math> si <math>s=0</math> |
|
| |
|
| * Según el principio de Huygens-Fresnel(Cada punto en una
| | <center> |
| fuente de ondas sirve como frente de trenes de onda esféricas
| | <math>x^{2}+y^{2}=a^{2}\qquad \qquad\qquad\qquad\qquad |
| secundarias),
| | </math></center> |
| * un área diferencial <math>dS</math> dentro de la abertura se
| |
| visualiza como si estuviera cubierta con fuentes secundarias
| |
| coherentes
| |
| * Si <math>varepsilon _{A} </math>es la intensidad de la fuente
| |
| por unidad de área, suponiendo que es constante en toda la abertura
| |
| * La perturbación óptica en P debida a <math> dS</math>
| |
|
| |
|
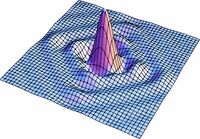
| | * Representa un cuadrado de lado <math>2a</math> si <math>s=1</math> [[Imagen:circcuadlisto.jpg |right|thumb|400x400px|Figura1. Solución para el cuadrado con las restricciones mencionadas]] |
|
| |
|
| <math> | | <center> |
| dE=\frac{\varepsilon _{A}}{r}e^{\imath(\omega t-kr)}dS
| | <math>(1-\frac{x^{2}}{a^{2}})^{1/2}(1-\frac{y^{2}}{a^{2}})^{1/2}=0</math> |
| </math>
| | </center> |
| La distancia de <math>dS</math> a <math>P</math>es
| | |
| <math>
| | Debido a que las variables están restringidas a valores mas pequeños o iguales a <math>a</math> tenemos |
| r^{2}=x^{2}+(Y-y)^{2}+(Z-z)^{2}
| |
| </math> | |
|
| |
|
| | <center> |
| | <math>a^{2}\geq x^{2},y^{2}</math> |
| | </center> |
|
| |
|
| -Como la condición de Fraunhofer se satisface para $r$ muy grande
| | Por lo tanto obtenemos la Fig6. |
| y si abertura es muy pequeña remplazamos <math>r</math> por <math>R</math> y hacemos una aproximación para la fase
| |
| <math>
| |
| R=[X^{2}+Y^{2}+Z^{2}]^{\frac{1}{2}}
| |
| </math>
| |
|
| |
|
| entonces
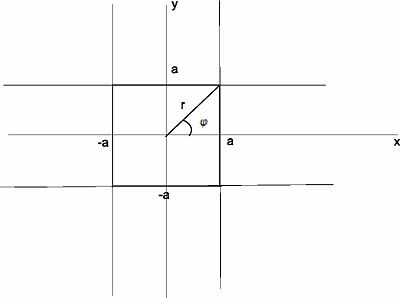
| | La ecuación (1) representa una figura intermedia con esquinas redondeadas que escribiéndola en coordenadas polares <math>(r,\varphi)</math> |
|
| |
|
| <math> | | <center> |
| r=R[1+\frac{(y^{2}+z^{2})}{R^{2}}-\frac{2(Yy+Zz)^{2}}{R^{2}}]^{\frac{1}{2}}\
| | <math>[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0 |
| </math> | | </math> |
| | </center> |
|
| |
|
| -Para el campo lejano <math>R</math> es muy grande comparado con las dimensiones de la apertura
| | Encontramos que tiene solución |
|
| |
|
| <math> | | <center> |
| R=\frac{(y^{2}+z^{2})}{R^{2}}\simeq 0
| | <math>r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2} |
| </math> | | </math></center> |
|
| |
|
| Por lo tanto
| | Puede demostrarse que el signo negativo en la expresión implica una y solo una posible solución que cumple la condición <math>r^{2}\leq 2a^{2}</math> |
| <math> | |
| r=R[1-\frac{2(Yy+Zz)^{2}}{R^{2}}]^{\frac{1}{2}} | |
| </math> | |
|
| |
|
| -Y con una expansión binomial obtenemos.
| | La transformada de Fourier para una apertura arbitraria es como dijimos antes |
|
| |
|
| <math> | | <center> |
| r=R[1-\frac{(Yy+Zz)^{2}}{R^{2}}]
| | <math>E(k_{q},K_{\phi})=\int_{0}^{\infty}\rho \int_{0}^{2\pi}\mathcal{A}(\rho,\varphi)e^{\imath (kq\rho/R) \cos(\varphi-\phi)}\rho d\rho d\varphi</math> |
| </math> | | </center> |
|
| |
|
| Por lo tanto la perturbación total que llega a <math>P</math> es
| | La función de apertura para este caso particular es |
|
| |
|
| <math> | | <center> |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}\int_{Abertura}\int e^{\imath k (Yy+Zz)/R} dS | | <math>\mathcal{A}(\rho,\varphi)=\{ ^{1\quad para \quad \rho < r(a,\varphi)}_{0 \quad para\quad \rho >r(a,\varphi)} |
| </math> | | </math></center> |
|
| |
|
| | Si reescribimos esta función como el producto de una parte radial y una angular entonces |
|
| |
|
| -Consideramos ahora la figura siguiente
| | <math>r(a,\varphi)=aM_{s}(\varphi)</math> |
|
| |
|
| Podemos escribir la ecuación (1) como
| | con |
|
| |
|
| <math> | | <center> |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}\int_{-b/2}^{b/2}e^{\imath k Yy/R}dy \int_{-a/2}^{a/2}e^{\imath k Zz/R} dz
| | <math>M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2} |
| </math> | | </math></center> |
|
| |
|
| Si definimos <math>\beta=\frac{kby}{2R}</math>,<math>\alpha=\frac {kaz}{2R}</math> obtenemos
| | Esta función tiene fronteras entre |
|
| |
|
| <math> | | <math> \quad 1\leq M_{s}(\varphi)\leq \sqrt 2 </math> |
| \int_{-b/2}^{b/2}e^{\imath k Yy/R}dy=\frac{R}{\imath kY}(e^{\imath kYb/2R}-e^{-\imath kYb/2R})=\frac{2R}{kY}\sin (\frac{bkY}{2R})=b\frac{\sin( \beta)}{\beta} | |
| </math> | |
|
| |
|
| <math> | | Y puede verse que en el limite cuando <math>s\longrightarrow 0, \qquad M_{s}(\varphi)\longrightarrow 1</math> |
| \int_{-a/2}^{a/2}e^{\imath k Zz/R}dz=\frac{R}{\imath kZ}(e^{\imath kZa/2R}-e^{-\imath kZa/2R})=\frac{2R}{kY}\sin (\frac{akZ}{2R})= a\frac{\sin\alpha}{\alpha} | |
| </math> | |
|
| |
|
| Por lo tanto
| | Si reescribimos la variable radial |
| <math>
| |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}A(\frac{\sin \beta}{\beta})(\frac{\sin\alpha}{\alpha})
| |
| </math>
| |
|
| |
|
| -Como <math>I=<(Re)\tilde{E}>_{T}</math>
| | <center> <math>\rho = \rho \prime M_{s}(\varphi)\quad |
| | d\rho =d\rho \prime M_{s}(\varphi) |
| | </math></center> |
|
| |
|
| <math> | | Entonces la ecuación de la función de apertura puede ser escrita independiente del ángulo <math>\varphi</math> |
| I(Y,Z)=I(0)(\frac{\sin \beta}{\beta})(\frac{\sin\alpha}{\alpha})
| |
| </math> | |
|
| |
|
| -Donde <math>I(0)</math> es la Irradiancia en <math>P_{0}</math>
| | <center> |
| | <math>U(\rho\prime)=\{ ^{1\quad para \quad \rho\prime < a}_{0 \quad para\quad \rho\prime >a} |
| | </math></center> |
|
| |
|
| | Tal que |
|
| |
|
| En valores de Y,Z tales que <math>\alpha, \beta</math> sean cero <math>I(Y,Z)</math> adquiere la forma de la difracción de una rendija
| | <center> |
| | <math>\mathcal{A}(a,\varphi)=\mathcal{A}(\rho\prime,\varphi)=U(\rho\prime)U(\phi)=U(\rho\prime)</math> <math>\varphi</math> |
| | </center> |
|
| |
|
| == 2. Apertura circular. ==
| | Entonces la transformada de Fourier de un circulo-cuadrado es<ref> M. Fernandez Guasti y M. de la Cruz Heredia,''Difracction pattern of a circle/square aperture'', JOURNAL OF MODERN OPTICS, 1993, VOL.40,No.6</ref> |
|
| |
|
| | <center> |
| | <math>E(k_{q},K_{\phi})=\int_{0}^{\infty}\rho \prime U(\rho\prime)\int_{0}^{2\pi}M_{s}^{2}(\varphi) |
| | e^{\imath (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}d\rho\prime d\varphi |
| | </math>\</center> |
|
| |
|
| Las aberturas circulares son muy importantes para el estudio de la instrumentación óptica.
| | == Círculo == |
| Partimos de
| |
| <math>
| |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}\int_{Abertura}\int e^{\imath k (Yy+Zz)/R} dS (1)
| |
| </math>
| |
|
| |
|
| En coordenadas esféricas
| | Si ponemos <math>s=0</math> entonces <math>M_{s}(\varphi)=1</math> y obtenemos |
| <math> | |
| z=\rho \cos \varphi, Z=q\cos \phi
| |
| </math> | |
|
| |
|
| <math> | | <math>\begin{alignat}{4} |
| y=\rho \sin \varphi, Y=q\sin \phi
| | E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi) |
| </math>
| | e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \\ |
|
| |
|
| Entonces
| | &=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\\ |
|
| |
|
| <math>
| | &=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\\ |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}\int_{\rho=0}^{a}\int _{\varphi=0}^{2\pi}e^{(\imath k \rho q/R)\cos (\varphi-\phi)}\rho d\rho d\varphi
| |
| </math>
| |
|
| |
|
| -Por la simetría axial la solución es independiente de <math>\phi</math>
| | &=&(R/kqa)J_{1}(kqa/R)\\ |
| <math>
| | \end{alignat} |
| \int _{\varphi=0}^{2\pi}e^{(\imath k \rho q/R)\cos (\varphi)} d\varphi
| |
| </math> | | </math> |
|
| |
|
| Es una función única que no puede reducirse
| | Y recobramos el resultado ya presentado |
|
| |
|
| -La cantidad
| | == Cuadrado == |
| | |
| <math>
| |
| J_{0}(u)=\frac{1}{2\pi}\int _{0}^{2\pi}e^{\imath u\cos v} dv
| |
| </math>
| |
|
| |
|
| Es la función de Bessel de primera especie y orden cero
| | Obtenemos un cuadrado para <math>s=1</math> |
|
| |
|
| | Por consideraciones de simetría y tomando la parte real de la transformada de Fourier para el circulo-cuadrado obtenemos |
|
| |
|
| En general
| | <math>E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi) |
| <math> | | \cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi |
| J_{m}(u)=\frac{\imath ^{-m}}{2\pi }\int _{0}^{2\pi}e^{\imath( mv+u\cos v)} dv
| |
| </math> | | </math> |
| Representa la función de Bessel de orden m
| |
|
| |
|
| Si <math>u=\frac {k\rho q}{R}</math>
| | Tomando en cuenta que la función angular del cuadrado es |
|
| |
|
| | | <math>M_{s=1}(\varphi)=\{^{\frac{1}{|\cos \varphi|} \quad para \quad -\pi/4 \quad a\quad (\pi/4)+n\pi} |
| Podemos escribir
| | _{\frac{1}{|\sin \varphi|}\quad para \quad \pi/4 \quad a\quad (3\pi/4)+n\pi} |
| | |
| <math> | |
| \tilde{E}=\frac{\varepsilon _{A} e^{\imath(\omega t-kR)}}{R}\int_{0}^{a}J_{0}(\frac{k\rho q}{R})\rho d\rho
| |
| </math> | | </math> |
|
| |
|
| -Otra propiedad de la funciones de Bessel es la relación de recurrencia
| | Tenemos entonces que |
|
| |
|
| <math> | | <math>E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4} |
| \frac{d}{du}[u^{m}J_{m}(u)]=u^{m}J_{m-1}(u) | | \frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime + \int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4} |
| | \frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sin^{2}\varphi} d\varphi d\rho\prime |
| </math> | | </math> |
|
| |
|
| Con <math>m=1</math>
| | Nombramos la primera de la ecuación <math>G_{1}</math>,y la segunda parte <math>G_{2}</math> quedando |
|
| |
|
| <math> | | <math>E(k_{q},K_{\phi})=G_{1}+G_{2} |
| \int_{0}^{u}u\prime J_{0}(u\prime)du\prime =uJ_{1}(u)
| |
| </math>}
| |
| | |
| Entonces si nombramos
| |
| | |
| <math> w=\frac{k\rho q}{R}</math> , <math>dw=\frac{kq}{R}d\rho</math>, <math>d\rho=\frac{R}{kq}dw</math>, y <math>\rho =\frac{wR}{kq}</math>
| |
| | |
| Mediante la regla de recurrencia tenemos
| |
| | |
| <math>
| |
| \tilde{E}=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R} 2\pi a^{2}(\frac{R}{kaq})J_{1}(\frac{k a q}{R})
| |
| </math> | | </math> |
|
| |
|
| Y la irradiancia en P es <math>\frac{1}{2}\tilde{E}\tilde{E}^{*}</math>
| | Haciendo las integrales angulares |
|
| |
|
| <math> | | <math>G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi] |
| I=2(\frac{\varepsilon _{A}}{R}A)^{2}[\frac{J_{1}(\frac{k a q}{R})}{\frac{k a q}{R}}]^{2}
| |
| </math> | | </math> |
| | | <math>G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi] |
| Para calcular la irradiancia en el centro ponemos <math>q=0</math>
| |
| Y usando la ley de recurrencia.
| |
| | |
| Verificamos que
| |
| <math>
| |
| \lim_{u\rightarrow 0}\frac{J_{1}(u)}{u}=\frac{1}{2}
| |
| </math> | | </math> |
|
| |
|
| La irradiancia en <math>P_{0}</math> es
| | Integrando nuevamente |
| | |
| <math>I(0)=\frac{\varepsilon _{A}^{2}}{2R^{2}}A^{2}</math>
| |
| | |
| Que es el mismo resultado que la apertura rectangular
| |
| Como <math>\sin \theta =q/r</math>, la irradiancia se puede escribir como función de <math>\theta </math>
| |
|
| |
|
| | | <math>G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi}) |
| <math>I=I(0)[\frac{2J_{1}(ka\sin \theta)}{k a\sin \theta }]^{2} | |
| </math> | | </math> |
| | | <math>+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})] |
| }
| |
| | |
| -El máximo central corresponde e llamado disco de Airy
| |
| | |
| | |
| si hacemos
| |
| | |
| <math>\frac{dI}{dq}=-2I(0)u/q[\frac{J_{1}(u)}{u}][\frac{J_{2}(u)}{u}]=0 | |
| | |
| </math> | | </math> |
|
| |
|
| -El primer mínimo corresponde al primer cero de la función <math>J_{1}(0)</math>, con <math>u=3.83</math>
| | <math>G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi}) |
| | |
| <math>kaq/R=3.83\
| |
| q_{1}=1.22 R\lambda/D</math>
| |
| | |
| | |
| -Los máximos secundarios ocurren para <math>J_{2}=0</math>
| |
| | |
| == 3. Métodos de Fourier. ==
| |
| | |
| | |
| -La transformada de Fourier aporta una percepción de diferente del mecanismo de difracción de Fraunhofer
| |
| Partimos de la ecuación
| |
| | |
| <math>\tilde{E}(Y,Z)=\frac{\varepsilon _{A}e^{\imath(\omega t-kR)}}{R}\int_{Abertura}\int e^{\imath k (Yy+Zz)/R} dS
| |
| </math> | | </math> |
| | | <math>+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})] |
| | |
| * La cantidad R es la distancia del centro de la apertura
| |
| * si nos limitamos a una pequeña región <math>R</math> puede conciderarse constante
| |
| <math>\varepsilon_{A} </math> no es necesariamente invariante | |
| * Las variaciones en <math>\varepsilon_{A}</math> y la constante multlipicativa pueden combinarse en una sola cantidad compleja
| |
| | |
| | |
| | |
| <math>\mathscr{A}(y,z)=\mathscr{A}_{0}(y,z)e^{\imath \phi (y,z)}</math>
| |
| | |
| Denominada función de abertura
| |
| | |
| -Con esto podemos reformular la ecuación anterior
| |
| | |
| <math>\tilde{E}(Y,Z)=\int\int_{-\infty}^{\infty}\mathscr{A}(y,z) e^{\imath k (Yy+Zz)/R} dydz
| |
| </math> | | </math> |
|
| |
|
| Donde los limites de la integral pueden extenderse hasta <math>\pm \infty</math> por que la función de la abertura
| | Sumando <math>G_{1}+G_{2}</math> tenemos |
| es no nula únicamente en la region de la abertura
| |
| -Definimos la frecuencias espaciales
| |
|
| |
|
| <math> | | <math> |
| K_{y}=kY/R=k\sin \phi =k\cos \beta \quad
| | \begin{array}{lcl} |
| K_{z}=kZ/R=k\sin \theta =k\cos \gamma</math>
| | E(k_{q},K_{\phi})&=&G_{1}+G_{2}\\ |
| | | &=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\\ |
| El campo difractado puede ahora escribirse como
| | &=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\\ |
| | | \end{array} |
| | |
| <math>\tilde{E}(K_{y},K_{z})=\int\int_{-\infty}^{\infty}\mathscr{A}(y,z) e^{\imath k (K_{y}y+K_{z}z)/R} dydz
| |
| </math>
| |
| | |
| Ahora tenemos que "la distribución del campo en la figura de difracción de Fraunhofer es la transformada de Fourier de la distribución
| |
| del campo sobre la abertura"
| |
| -Simbolicamente
| |
| | |
| | |
| <math>E(K_{y},K_{z})=\mathscr{F}{\mathscr{A}(y,z)}
| |
| </math> | | </math> |
|
| |
|
|
| |
| La distribucion del campo en el plano imagen es el espectro de frecuencia espacial de la función de la abertura.
| |
| Entonces
| |
|
| |
| <math>\mathscr{A}(y,z)=\frac{1}{(2\pi)^{2}}\int\int_{-\infty}^{\infty}E(K_{y},K_{z}) e^{\imath k (K_{y}y+K_{z}z)/R} dydz
| |
| </math>
| |
|
| |
| o
| |
|
| |
|
| |
| <math>\mathscr{A}(y,z)=\mathscr{F}^{-1}E(K_{y},K_{z})
| |
| </math>
| |
|
| |
| == 4. Difracción de apertura circulo-cuadrado. ==
| |
|
| |
|
| |
| La ecuación
| |
|
| |
|
| |
| <math>x^{2}+y^{2}-\frac{s^{2}}{a^{2}}x^{2}y{2}=a^{2}
| |
| </math>
| |
|
| |
|
| |
| * Representa un circulo en el plano <math>xy</math> de radio <math>a</math> si <math>s=0</math>
| |
| * Representa un cuadrado de lado <math>2a</math> si <math>s=1</math>
| |
|
| |
| Debido a que las variables estan restringidas a valores mas pequeños o iguales a <math>a</math>
| |
|
| |
| <math>a^{2}\geq x^{2},y^{2}</math>
| |
|
| |
| La ecuación (3) representa una figura intermedia con esquinas redondeadas
| |
|
| |
| Escribimos en coordenadas Polares <math>(r,\varphi)</math>
| |
|
| |
| <math>[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0
| |
| </math>
| |
|
| |
|
| |
| Con solución
| |
|
| |
| <math>r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2}
| |
| </math>
| |
|
| |
| -Puede demostrarse que el signo negativo en la expresión implica una y solo una posible solución que cumple la condición <math>r^{2}\leq 2a^{2}</math>
| |
|
| |
| La transformada de Fourier para una apertura es
| |
|
| |
|
| |
| <math>E(k_{q},K_{\phi})=\int_{0}^{\infty}\rho \int_{0}^{2\pi}\mathscr{A}(\rho,\varphi)e^{\imath (kq\rho/R) \cos(\varphi-\phi)}\rho d\rho d\varphi</math>
| |
|
| |
|
| |
| La función de apertura es.
| |
|
| |
|
| |
| <math>\mathscr{A}(\rho,\varphi)=\{ ^{1\quad para \quad \rho < r(a,\varphi)}_{0 \quad para\quad \rho >r(a,\varphi)}
| |
| </math>
| |
|
| |
| Reescribimos esta función como el producto de una parte radial y una angular entonces
| |
| <math>r(a,\varphi)=aM_{s}(\varphi)</math>
| |
|
| |
|
| |
| <math>M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2}
| |
| </math>
| |
|
| |
| Esta función tiene fronteras entre <math>1\leq M_{s}(\varphi)\leq \sqrt 2 </math>
| |
|
| |
| Y puede verse que en el limite cuando <math>s\longrightarrow 0</math> <math>M_{s}(\varphi)\longrightarrow 1</math>
| |
|
| |
| Si reescribimos la variable radial a
| |
|
| |
| \textcolor[rgb]{0.00,0.59,0.00}{\begin{displaymath}
| |
| \rho = \rho \prime M_{s}(\varphi)\quad
| |
| d\rho =d\rho \prime M_{s}(\varphi)
| |
| \end{displaymath}}
| |
|
| |
| Entonces la ecuación de la función de apertura puede ser escrita independiente del angulo $\varphi$
| |
|
| |
| \textcolor[rgb]{1.00,0.50,0.00}{\begin{displaymath}
| |
| U(\rho\prime)=\{ ^{1\quad para \quad \rho\prime < a}_{0 \quad para\quad \rho\prime >a}
| |
| \end{displaymath}}
| |
| \end{frame}
| |
|
| |
| \begin{frame}
| |
|
| |
| Tal que \textcolor[rgb]{0.00,0.53,0.68}{$\mathscr{A}(a,\varphi)=\mathscr{A}(\rho\prime,\varphi)=U(\rho\prime)U(phi)=U(\rho\prime)$} para todo $\varphi$
| |
|
| |
| Entonces la transformada de Fourier de un circulo-cuadrado es
| |
|
| |
| \textcolor[rgb]{1.00,0.00,0.00}{\begin{displaymath}
| |
| E(k_{q},K_{\phi})=\int_{0}^{\infty}\rho \prime U(\rho\prime)\int_{0}^{2\pi}M_{s}^{2}(\varphi)
| |
| e^{\imath (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}d\rho\prime d\varphi
| |
| \end{displaymath}}
| |
| \end{frame}
| |
|
| |
|
| |
| \subsection{circulo}
| |
|
| |
| \begin{frame}
| |
|
| |
| \textcolor[rgb]{0.00,0.00,1.00}{Circulo}
| |
|
| |
| Si ponemos $s=0$ entonces $M_{s}(\varphi)=1$ y obtenemos
| |
|
| |
| \textcolor[rgb]{0.00,0.59,0.00}{\begin{eqnarray}
| |
| E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi)
| |
| e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \nonumber\\
| |
| &=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\nonumber\\
| |
| &=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\nonumber\\
| |
| &=&(R/kqa)J_{1}(kqa/R)\nonumber\
| |
| \end{eqnarray}}
| |
|
| |
| Y recobramos el resultado ya presentado
| |
| \end{frame}
| |
|
| |
|
| |
|
| |
| \subsection{cuadrado}
| |
|
| |
| \begin{frame}
| |
|
| |
| \textcolor[rgb]{0.00,0.00,1.00}{Cuadrado}
| |
|
| |
| Obtenemos un cuadro para $s=1$
| |
|
| |
| Por consideraciones de simetria y tomando la parte real de la transformada de Fourier para el circulo-cuadrado obtenemos
| |
|
| |
| \textcolor[rgb]{0.00,0.50,0.00}{\begin{displaymath}
| |
| E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi)
| |
| \cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi
| |
| \end{displaymath}}
| |
|
| |
| Tomando en cuenta que la función angular del cuadrado es
| |
| \textcolor[rgb]{1.00,0.00,0.00}{\begin{displaymath}
| |
| M_{s=1}(\varphi)=\{^{\frac{1}{|\cos \varphi|} \quad para \quad -\pi/4 \quad a\quad (\pi/4)+n\pi}
| |
| _{\frac{1}{|\sin \varphi|}\quad para \quad \pi/4 \quad a\quad (3\pi/4)+n\pi}
| |
| \end{displaymath}}
| |
| \end{frame}
| |
|
| |
| \begin{frame}
| |
|
| |
| Tenemos entonces que
| |
|
| |
| \textcolor[rgb]{0.00,0.50,1.00}{\begin{displaymath}
| |
| E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4}
| |
| \frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime
| |
| \end{displaymath}}
| |
| \textcolor[rgb]{0.00,0.50,1.00}{\begin{displaymath}
| |
| +\int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4}
| |
| \frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sen^{2}\varphi} d\varphi d\rho\prime=G_{1}+G_{2}
| |
| \end{displaymath}}
| |
|
| |
| Haciendo las integrales angulares
| |
|
| |
| \textcolor[rgb]{0.50,0.00,1.00}{\begin{displaymath}
| |
| G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi]
| |
| \end{displaymath}}
| |
| \textcolor[rgb]{1.00,0.00,0.50}{\begin{displaymath}
| |
| G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi]
| |
| \end{displaymath}}
| |
| \end{frame}
| |
|
| |
| \begin{frame}
| |
|
| |
| Integrando nuevamente\\
| |
|
| |
| \textcolor[rgb]{0.00,0.59,0.00}{\begin{displaymath}
| |
| G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi})
| |
| \end{displaymath}}
| |
| \textcolor[rgb]{0.00,0.59,0.00}{\begin{displaymath}
| |
| +(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]
| |
| \end{displaymath}}
| |
|
| |
| \textcolor[rgb]{0.00,0.00,1.00}{\begin{displaymath}
| |
| G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi})
| |
| \end{displaymath}}
| |
| \textcolor[rgb]{0.00,0.00,1.00}{\begin{displaymath}
| |
| +(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]
| |
| \end{displaymath}}
| |
|
| |
| Sumando $G_{1}+G_{2}$ tenemos
| |
| \end{frame}
| |
|
| |
| \begin{frame}
| |
|
| |
| \textcolor[rgb]{0.50,0.50,0.00}{\begin{eqnarray}
| |
| E(k_{q},K_{\phi})&=&G_{1}+G_{2}\nonumber\\
| |
| &=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\nonumber\\
| |
| &=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\nonumber\
| |
| \end{eqnarray}}
| |
| como | | como |
| \\
| |
| \textcolor[rgb]{0.50,0.25,0.00}{\begin{displaymath}
| |
| z=\rho \cos \varphi, Z=q\cos \phi
| |
| \end{displaymath}}
| |
|
| |
| \textcolor[rgb]{0.00,0.87,0.00}{\textcolor[rgb]{0.50,0.00,0.50}{\begin{displaymath}
| |
| y=\rho \sin \varphi, Y=q\sin \phi
| |
| \end{displaymath}}}
| |
|
| |
| \textcolor[rgb]{0.98,0.00,0.00}{\begin{displaymath}
| |
| E(k_{q},K_{\phi})=4a^{2} \mathrm{sinc}(ka/R Y)\mathrm{sinc}(ka/R Z)
| |
| \end{displaymath}}
| |
|
| |
| \end{frame}
| |
| \begin{frame}
| |
|
| |
| \includegraphics[height=.9\textheight]{cc1.pdf}
| |
| \end{frame}
| |
| \begin{frame}
| |
|
| |
| \includegraphics[height=.9\textheight]{cc2.pdf}
| |
| \end{frame}
| |
| \begin{frame}
| |
|
| |
| \includegraphics[height=.9\textheight]{cc3.pdf}
| |
| \includegraphics[height=.9\textheight]{cc4.pdf}
| |
| \includegraphics[height=.9\textheight]{cc5.pdf}
| |
| \includegraphics[height=.9\textheight]{cc6.pdf}
| |
| \end{frame}
| |
|
| |
|
| |
| \end{document}
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| | <math>z=\rho \cos \varphi, Z=q\cos \phi</math> |
|
| |
|
| | <math>y=\rho \sin \varphi, Y=q\sin \phi</math> |
|
| |
|
| | Obtenemos finalmente |
|
| |
|
| | <center> <math>E(k_{q},k_{\phi})=4a^{2}\mathrm{sinc}[(ka/R)\quad Y]\mathrm{sinc}[(ka/R)\quad Z]</math></center> |
|
| |
|
| | Que es la ecuación para el campo de un cuadrado. |
|
| |
|
| | == Valores Intermedios de $\mathit{S}$ == |
|
| |
|
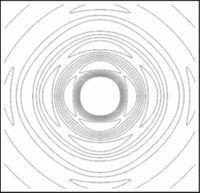
| | [[Imagen:anipic.gif|right|thumb|300x300px|Figura2. Variación de s para la ecuación del círculo-cuadrado]] |
|
| |
|
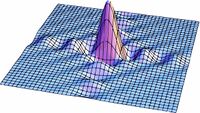
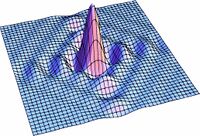
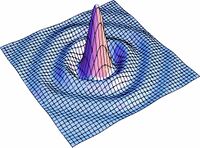
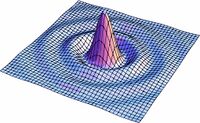
| | Las soluciones para los valores intermedios de la ecuación (1) pueden observarse en la Fig7. en donde se realizo una simulación para valores de <math>s</math> entre <math>0</math> y <math>1</math>. Podemos ver como poco a poco pasamos de un círculo a un cuadrado. |
|
| |
|
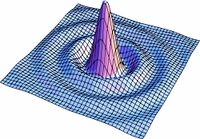
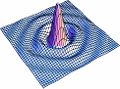
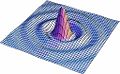
| | La distribución para la amplitud del campo se realizo calculando primeramente la integral angular para la transformada de Fourier y se hizo una animación variando el parametro <math>S</math> como se presenta en la Fig8. |
|
| |
|
| | [[Imagen:irrapic1.gif|left|thumb|360px292px|Figura9. Variación de s para la distribucion de l campo]] |
|
| |
|
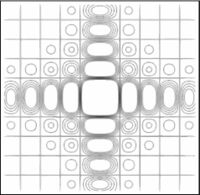
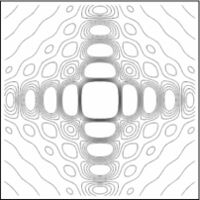
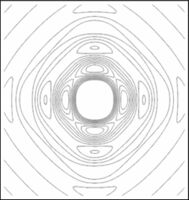
| | En las figuras subsecuentes se muestra la distribución del campo para varios valores de <math>S</math> asi como la curva de nivel del campo. |
| | <br><br><br><br><br><br><br><br><br><br><br><br><br><br> |
|
| |
|
| | <center> |
| | <gallery caption="parámetro de cuadradez" widths="200px" heights="200px" perrow="2"> |
| | c-c-1.jpg|left|thumb|400x400px|<math>s=1</math> |
| | cnivel1.jpg|right|thumb|300x300px|<math>s=1</math> |
| | c-c-999.jpg|left|thumb|400x400px|<math>s=0.99</math> |
| | cnivel99.jpg|right|thumb|300x300px|<math>s=.99</math> |
| | c-c-95.jpg|left|thumb|400x400px|<math>s=0.95</math> |
| | c-c-95.jpg|left|thumb|400x400px|<math>s=0.95</math> |
| | c-c-8.jpg|left|thumb|400x400px|<math>s=0.8</math> |
| | cnivel8.jpg|right|thumb|300x300px|<math>s=.8</math> |
| | c-c-6.jpg|left|thumb|400x400px|<math>s=0.6</math> |
| | cnivel6.jpg|right|thumb|300x300px|<math>s=.6</math> |
| | c-c-cero.jpg|left|thumb|400x400px|<math>s=0</math> |
| | cnivel0.jpg|right|thumb|300x300px|<math>s=0</math> |
| | </gallery> |
| | </center> |
| | <!-- |
| | [[Imagen:c-c-1.jpg|left|thumb|400x400px|<math>s=1</math>]] |
| | [[Imagen:cnivel1.jpg|right|thumb|300x300px|<math>s=1</math>]] |
| | [[Imagen:c-c-999.jpg|left|thumb|400x400px|<math>s=0.99</math>]] |
| | [[Imagen:cnivel99.jpg|right|thumb|300x300px|<math>s=1</math>]] |
| | [[Imagen:c-c-95.jpg|left|thumb|400x400px|<math>s=0.95</math>]] |
| | [[Imagen:c-c-8.jpg|left|thumb|400x400px|<math>s=0.8</math>]] |
| | [[Imagen:cnivel8.jpg|right|thumb|300x300px|<math>s=1</math>]] |
| | [[Imagen:c-c-6.jpg|left|thumb|400x400px|<math>s=0.6</math>]] |
| | [[Imagen:cnivel6.jpg|right|thumb|300x300px|<math>s=1</math>]] |
| | [[Imagen:c-c-cero.jpg|left|thumb|400x400px|<math>s=0</math>]] |
| | [[Imagen:cnivel0.jpg|right|thumb|300x300px|<math>s=1</math>]] |
| | --> |
|
| |
|
| | == Variación con el parámetro de cuadradez $\mathit{S}$ == |
| | Aqui se muestra una serie de imágenes con distintos párametros de cuadradez. El eje vertical representa intensidad, mientras que los otros dos ejes ortogonales representan posición bidimensional. |
| | <!-- comentario --> |
| | <gallery caption="galería" mode="slideshow" heights="300px" > |
| | c-c-1.jpg|<math>s=1</math> |
| | c-c-999.jpg|<math>s=0.99</math> |
| | c-c-95.jpg|<math>s=0.95</math> |
| | c-c-8.jpg|<math>s=0.8</math> |
| | c-c-6.jpg|<math>s=0.6</math> |
| | c-c-cero.jpg|<math>s=0.0</math> |
| | </gallery> |
|
| |
|
| | <references/> |
|
| |
|
| | [[Usuario:Mfgwi|Mfgwi]] ([[Usuario discusión:Mfgwi|discusión]]) 13:43 6 dic 2019 (CST) |
|
| |
|
| Building
| | [[Usuario:Carlos A.Z.|CAZ]] 16:32 29 ago 2008 (CDT) |
|
| |
|
| --[[Usuario:Carlos A.Z.|CAZ]] 00:20 19 ago 2008 (CDT)
| | [[Category:optica]] |
Difracción de apertura Círculo-Cuadrado.
La ecuación [1]

- Representa un círculo en el plano
 de radio
de radio  si
si 


Debido a que las variables están restringidas a valores mas pequeños o iguales a  tenemos
tenemos

Por lo tanto obtenemos la Fig6.
La ecuación (1) representa una figura intermedia con esquinas redondeadas que escribiéndola en coordenadas polares 
![[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/28fdf9357f272ebe100580e205a6f59045f3d1e8)
Encontramos que tiene solución
![r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7dc197672aa7b8984ba2d1a8e68e9cbf2dd05271)
Puede demostrarse que el signo negativo en la expresión implica una y solo una posible solución que cumple la condición 
La transformada de Fourier para una apertura arbitraria es como dijimos antes

La función de apertura para este caso particular es

Si reescribimos esta función como el producto de una parte radial y una angular entonces

con
![M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/756bff1a4b259e4ae8cc4762fd3068900d091650)
Esta función tiene fronteras entre

Y puede verse que en el limite cuando 
Si reescribimos la variable radial

Entonces la ecuación de la función de apertura puede ser escrita independiente del ángulo 

Tal que


Entonces la transformada de Fourier de un circulo-cuadrado es[2]
 \
\
Círculo
Si ponemos  entonces
entonces  y obtenemos
y obtenemos
![\begin{alignat}{4}
E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi)
e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \\
&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&(R/kqa)J_{1}(kqa/R)\\
\end{alignat}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7d265afe2e186cb351fa9cd21c5a40ada90a8d8a)
Y recobramos el resultado ya presentado
Cuadrado
Obtenemos un cuadrado para 
Por consideraciones de simetría y tomando la parte real de la transformada de Fourier para el circulo-cuadrado obtenemos
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi)
\cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f20eed37013feefc1440acb5066f0eb2d75833c)
Tomando en cuenta que la función angular del cuadrado es

Tenemos entonces que
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4}
\frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime + \int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4}
\frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sin^{2}\varphi} d\varphi d\rho\prime](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f20de9f724dac8cc05b453eeb9558a8b9f011289)
Nombramos la primera de la ecuación  ,y la segunda parte
,y la segunda parte  quedando
quedando

Haciendo las integrales angulares
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a142e178cf2ed7d23e8516977966a62c418e2b76)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4e1208e1f67c0e4d0b0fe0e91f6d3cce42174442)
Integrando nuevamente
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/14d033b7db039943ca71cbb186d8b54070776fd0)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85d58ac0ac8a2c831617c33881263a5ffc63ea70)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
Sumando  tenemos
tenemos
![\begin{array}{lcl}
E(k_{q},K_{\phi})&=&G_{1}+G_{2}\\
&=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\\
&=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\\
\end{array}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/665c1266ada0e9c88606f0148ad22e0b8af7d892)
como


Obtenemos finalmente
![{\displaystyle E(k_{q},k_{\phi })=4a^{2}\mathrm {sinc} [(ka/R)\quad Y]\mathrm {sinc} [(ka/R)\quad Z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9b38c945d3dad1ac561bfbcc51cca0480aa3fef)
Que es la ecuación para el campo de un cuadrado.
Valores Intermedios de $\mathit{S}$
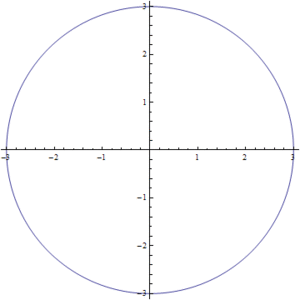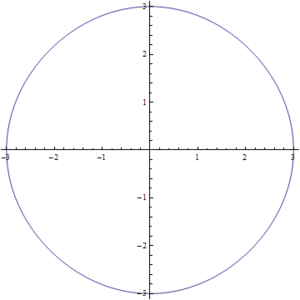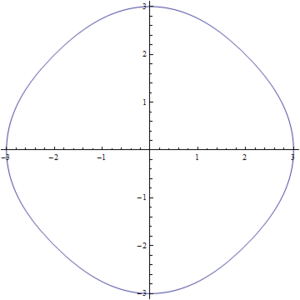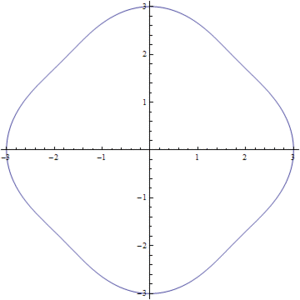
Figura2. Variación de s para la ecuación del círculo-cuadrado
Las soluciones para los valores intermedios de la ecuación (1) pueden observarse en la Fig7. en donde se realizo una simulación para valores de  entre
entre  y
y  . Podemos ver como poco a poco pasamos de un círculo a un cuadrado.
. Podemos ver como poco a poco pasamos de un círculo a un cuadrado.
La distribución para la amplitud del campo se realizo calculando primeramente la integral angular para la transformada de Fourier y se hizo una animación variando el parametro  como se presenta en la Fig8.
como se presenta en la Fig8.
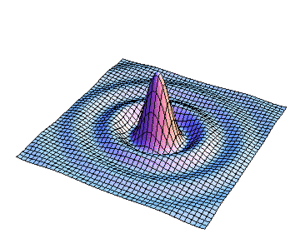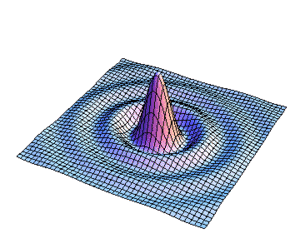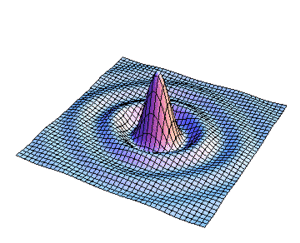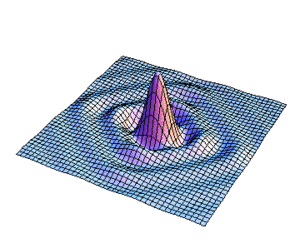
Figura9. Variación de s para la distribucion de l campo
En las figuras subsecuentes se muestra la distribución del campo para varios valores de  asi como la curva de nivel del campo.
asi como la curva de nivel del campo.
- parámetro de cuadradez












Variación con el parámetro de cuadradez $\mathit{S}$
Aqui se muestra una serie de imágenes con distintos párametros de cuadradez. El eje vertical representa intensidad, mientras que los otros dos ejes ortogonales representan posición bidimensional.
- galería






- ↑ Manuel Fernandez Guasti,Analytic geometry of some rectilinear figures,INT.J.MATH.EDUC.SCI.TECHNOL., 1992, VOL.23,No.6
- ↑ M. Fernandez Guasti y M. de la Cruz Heredia,Difracction pattern of a circle/square aperture, JOURNAL OF MODERN OPTICS, 1993, VOL.40,No.6
Mfgwi (discusión) 13:43 6 dic 2019 (CST)
CAZ 16:32 29 ago 2008 (CDT)










![[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/28fdf9357f272ebe100580e205a6f59045f3d1e8)
![r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7dc197672aa7b8984ba2d1a8e68e9cbf2dd05271)




![M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/756bff1a4b259e4ae8cc4762fd3068900d091650)








![\begin{alignat}{4}
E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi)
e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \\
&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&(R/kqa)J_{1}(kqa/R)\\
\end{alignat}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7d265afe2e186cb351fa9cd21c5a40ada90a8d8a)
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi)
\cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f20eed37013feefc1440acb5066f0eb2d75833c)

![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4}
\frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime + \int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4}
\frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sin^{2}\varphi} d\varphi d\rho\prime](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f20de9f724dac8cc05b453eeb9558a8b9f011289)



![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a142e178cf2ed7d23e8516977966a62c418e2b76)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4e1208e1f67c0e4d0b0fe0e91f6d3cce42174442)
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/14d033b7db039943ca71cbb186d8b54070776fd0)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85d58ac0ac8a2c831617c33881263a5ffc63ea70)

![\begin{array}{lcl}
E(k_{q},K_{\phi})&=&G_{1}+G_{2}\\
&=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\\
&=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\\
\end{array}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/665c1266ada0e9c88606f0148ad22e0b8af7d892)


![{\displaystyle E(k_{q},k_{\phi })=4a^{2}\mathrm {sinc} [(ka/R)\quad Y]\mathrm {sinc} [(ka/R)\quad Z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9b38c945d3dad1ac561bfbcc51cca0480aa3fef)