Difracción de apertura Círculo-Cuadrado.
La ecuación [1]

- Representa un círculo en el plano
 de radio
de radio  si
si 


Debido a que las variables están restringidas a valores mas pequeños o iguales a  tenemos
tenemos

Por lo tanto obtenemos la Fig6.
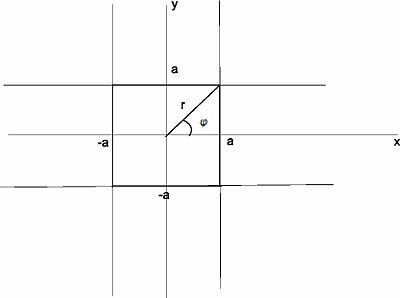
La ecuación (1) representa una figura intermedia con esquinas redondeadas que escribiéndola en coordenadas polares 
![[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/28fdf9357f272ebe100580e205a6f59045f3d1e8)
Encontramos que tiene solución
![r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7dc197672aa7b8984ba2d1a8e68e9cbf2dd05271)
Puede demostrarse que el signo negativo en la expresión implica una y solo una posible solución que cumple la condición 
La transformada de Fourier para una apertura arbitraria es como dijimos antes

La función de apertura para este caso particular es

Si reescribimos esta función como el producto de una parte radial y una angular entonces

con
![M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/756bff1a4b259e4ae8cc4762fd3068900d091650)
Esta función tiene fronteras entre

Y puede verse que en el limite cuando 
Si reescribimos la variable radial

Entonces la ecuación de la función de apertura puede ser escrita independiente del ángulo 

Tal que


Entonces la transformada de Fourier de un circulo-cuadrado es[2]
 \
\
Círculo
Si ponemos  entonces
entonces  y obtenemos
y obtenemos
![\begin{alignat}{4}
E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi)
e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \\
&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&(R/kqa)J_{1}(kqa/R)\\
\end{alignat}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7d265afe2e186cb351fa9cd21c5a40ada90a8d8a)
Y recobramos el resultado ya presentado
Cuadrado
Obtenemos un cuadrado para 
Por consideraciones de simetría y tomando la parte real de la transformada de Fourier para el circulo-cuadrado obtenemos
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi)
\cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f20eed37013feefc1440acb5066f0eb2d75833c)
Tomando en cuenta que la función angular del cuadrado es

Tenemos entonces que
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4}
\frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime + \int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4}
\frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sin^{2}\varphi} d\varphi d\rho\prime](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f20de9f724dac8cc05b453eeb9558a8b9f011289)
Nombramos la primera de la ecuación  ,y la segunda parte
,y la segunda parte  quedando
quedando

Haciendo las integrales angulares
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a142e178cf2ed7d23e8516977966a62c418e2b76)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4e1208e1f67c0e4d0b0fe0e91f6d3cce42174442)
Integrando nuevamente
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/14d033b7db039943ca71cbb186d8b54070776fd0)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85d58ac0ac8a2c831617c33881263a5ffc63ea70)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
Sumando  tenemos
tenemos
![\begin{array}{lcl}
E(k_{q},K_{\phi})&=&G_{1}+G_{2}\\
&=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\\
&=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\\
\end{array}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/665c1266ada0e9c88606f0148ad22e0b8af7d892)
como


Obtenemos finalmente
![{\displaystyle E(k_{q},k_{\phi })=4a^{2}\mathrm {sinc} [(ka/R)\quad Y]\mathrm {sinc} [(ka/R)\quad Z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9b38c945d3dad1ac561bfbcc51cca0480aa3fef)
Que es la ecuación para el campo de un cuadrado.
Valores Intermedios de $\mathit{S}$
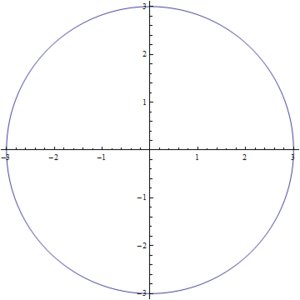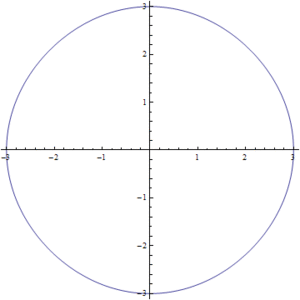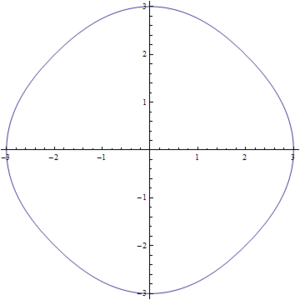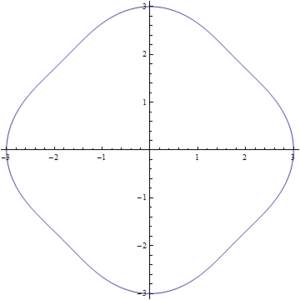
Figura2. Variación de s para la ecuación del círculo-cuadrado
Las soluciones para los valores intermedios de la ecuación (1) pueden observarse en la Fig7. en donde se realizo una simulación para valores de  entre
entre  y
y  . Podemos ver como poco a poco pasamos de un círculo a un cuadrado.
. Podemos ver como poco a poco pasamos de un círculo a un cuadrado.
La distribución para la amplitud del campo se realizo calculando primeramente la integral angular para la transformada de Fourier y se hizo una animación variando el parametro  como se presenta en la Fig8.
como se presenta en la Fig8.
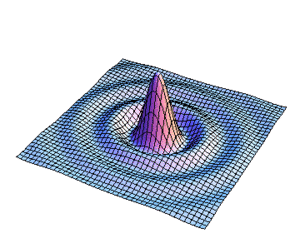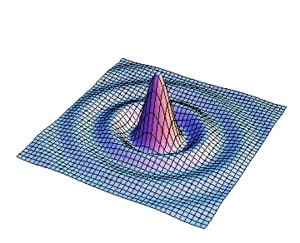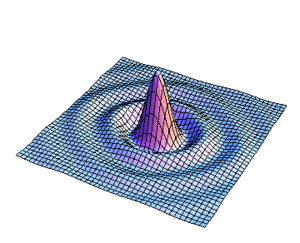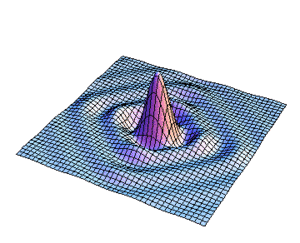
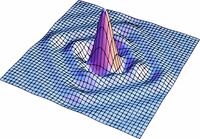
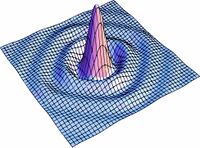
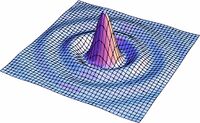
Figura9. Variación de s para la distribucion de l campo
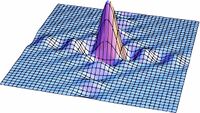
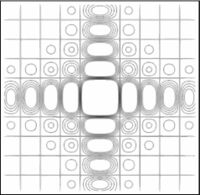
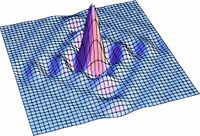
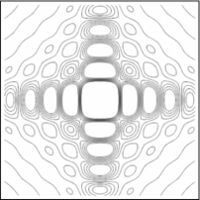
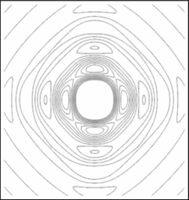
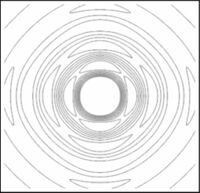
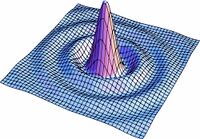
En las figuras subsecuentes se muestra la distribución del campo para varios valores de  asi como la curva de nivel del campo.
asi como la curva de nivel del campo.
- parámetro de cuadradez












Variación con el parámetro de cuadradez $\mathit{S}$
Aqui se muestra una serie de imágenes con distintos párametros de cuadradez. El eje vertical representa intensidad, mientras que los otros dos ejes ortogonales representan posición bidimensional.
- galería






- ↑ Manuel Fernandez Guasti,Analytic geometry of some rectilinear figures,INT.J.MATH.EDUC.SCI.TECHNOL., 1992, VOL.23,No.6
- ↑ M. Fernandez Guasti y M. de la Cruz Heredia,Difracction pattern of a circle/square aperture, JOURNAL OF MODERN OPTICS, 1993, VOL.40,No.6
Mfgwi (discusión) 13:43 6 dic 2019 (CST)
CAZ 16:32 29 ago 2008 (CDT)










![[\frac{s^{2}}{4}\sin ^{2}2\varphi]r^{4}-a^{2}r^{2}+a^{2}=0](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/28fdf9357f272ebe100580e205a6f59045f3d1e8)
![r(a,\varphi)=\{[2a^{2}\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}\}^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7dc197672aa7b8984ba2d1a8e68e9cbf2dd05271)




![M_{s}(\varphi)=[2\frac{1-[1-s^{2}\sin ^{2}(2\varphi)]^{1/2}}{s^{2}\sin ^{2}(2\varphi)}]^{1/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/756bff1a4b259e4ae8cc4762fd3068900d091650)








![\begin{alignat}{4}
E(k_{q},K_{\phi})&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[\int_{0}^{2\pi}(\varphi)
e^{\imath (kq\rho \prime /R) \cos(\varphi-\phi)} d\varphi]d\rho\prime \\
&=&\int_{0}^{\infty}\rho \prime U(\rho\prime)[J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&\int_{0}^{a}\rho \prime [J_{0}(k q \rho\prime/R)]d\rho\prime\\
&=&(R/kqa)J_{1}(kqa/R)\\
\end{alignat}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7d265afe2e186cb351fa9cd21c5a40ada90a8d8a)
![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{3\pi /4}M_{s}^{2}(\varphi)
\cos[ { (kq\rho \prime M_{s}(\varphi)/R) \cos(\varphi-\phi)}]d\rho\prime d\varphi](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6f20eed37013feefc1440acb5066f0eb2d75833c)

![E(k_{q},K_{\phi})=\int_{0}^{a}\rho \prime \int_{-\pi/4}^{\pi /4}
\frac{\cos [(kq\rho\prime/R) (\cos\phi+\sin\phi\tan\varphi]}{\cos^{2}\varphi} d\varphi d\rho\prime + \int_{0}^{a}\rho \prime \int_{\pi/4}^{3\pi /4}
\frac{\cos [(kq\rho\prime/R) (\sin\phi+\cos\phi\cot\varphi)]}{\sin^{2}\varphi} d\varphi d\rho\prime](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f20de9f724dac8cc05b453eeb9558a8b9f011289)



![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi} \int_{0}^{a}\sin[(kq\rho\prime/R)\sin\phi]\cos[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a142e178cf2ed7d23e8516977966a62c418e2b76)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi} \int_{0}^{a}\cos[(kq\rho\prime/R)\sin\phi]\sin[(kq\rho\prime/R)\cos\phi]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4e1208e1f67c0e4d0b0fe0e91f6d3cce42174442)
![G_{1}=\frac{4}{(kq/R)^{2}\sin\phi}[(\frac{1-\cos[kqa/R(\sin\phi-cos\phi)]}{\sin\phi-\cos\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/14d033b7db039943ca71cbb186d8b54070776fd0)
![+(\frac{1-\cos[kqa/R(\sin\phi+\cos\phi)]}{\sin\phi+\cos\phi})]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cefdd8809aedcb8405bda5aba7e6b55ed217eea1)
![G_{2}=\frac{4}{(kq/R)^{2}\cos\phi}[(\frac{1-\cos[kqa/R(\cos\phi-\sin\phi)]}{\cos\phi-\sin\phi})](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/85d58ac0ac8a2c831617c33881263a5ffc63ea70)

![\begin{array}{lcl}
E(k_{q},K_{\phi})&=&G_{1}+G_{2}\\
&=&\frac{4}{(kq/R)^{2}\cos\phi\sin\phi}[\sin(kqa/R\sin\phi)\sin(kqa/R\cos\phi)]\\
&=&4a^{2}\mathrm{sinc}(kqa/R \sin\phi)\mathrm{sinc} (kqa/R\cos\phi)\\
\end{array}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/665c1266ada0e9c88606f0148ad22e0b8af7d892)


![{\displaystyle E(k_{q},k_{\phi })=4a^{2}\mathrm {sinc} [(ka/R)\quad Y]\mathrm {sinc} [(ka/R)\quad Z]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d9b38c945d3dad1ac561bfbcc51cca0480aa3fef)