Diferencia entre revisiones de «Ondas: probs c2 mov osc»
Sin resumen de edición |
|||
| (No se muestran 89 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
Problemas capítulo 2 Óptica | Problemas capítulo 2 Óptica <big>'''Hecht'''</big>, '''Movimiento Ondulatorio''' | ||
Ejercicios resueltos acerca del movimiento ondulatorio. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema. | |||
Algunas ediciones del Hetch, tienen distintas numeraciones para problemas idénticos. | |||
= Primeras Ediciones (1°,2°,3°) en Ingles.= | |||
==Problema 2.9(Hecht 1ra edición) == | |||
'''Considere una onda luminosa teniendo una velocidad de fase de $3\times10^{8}\frac{m}{s}$ y una frecuencia de $6\times10^{14}Hz.$ Encontrar: la frecuencia angular, el valor del número de propagación $k$, la longitud de onda y comprobar que esta onda se encuentre dentro del espectro de luz visible. ¿Qué desplazamiento de fase ocurre en un punto dado a $10^{-6}s$, y cuántas ondas han pasado hasta ese momento? | |||
SOLUCIÓN: | |||
Consideramos la ecuación de la propagación de onda: | |||
\[ | |||
\psi(x,t)=Asen(kx-\omega t+\varepsilon) | |||
\] | |||
donde \varepsilon=0 dado que consideraremos que la fase inicial | |||
$\varepsilon$ es nula. Por lo que: | |||
= | \[ | ||
\psi(x,t)=Asen(kx-\omega t)......(1) | |||
\] | |||
Para obtener el valor del número de propagación consideramos que la | |||
velocidad de fase $V_{\phi}=\frac{\omega}{k}\Longrightarrow k=\frac{\omega}{V_{\phi}}$ | |||
y sabemos que $\omega=2\pi\upsilon$ donde $\upsilon$ es la conocida | |||
frecuencia por lo que substituyendo tendremos: | |||
\[\ | \[ | ||
\omega=2\pi(6\times10^{14})=12\times10^{14}\pi\frac{rad}{seg} | |||
\] | |||
Y por lo tanto: | |||
\[ | |||
k=\frac{\omega}{V_{\phi}}=\frac{12\times10^{14}\pi}{3\times10^{8}}=4\times10^{6}\pi | |||
\] | |||
\ | De aquí sabremos que la longitud de onda $\lambda$ dada por \lambda=\frac{2\pi}{k} | ||
será: | |||
\[ | |||
\lambda=\frac{2\pi}{4\times10^{6}\pi}=500\times10^{-9}=500nm | |||
\] | |||
y como en el espectro monocromático la luz visible va desde los 400nm | |||
hasta los 700nm, aproximadamente, se comprueba entonces que esta onda | |||
está dentro el rango del espectro visible de la luz. | |||
Para calcular el desplazamiento de fase recurrimos la ec.(1) donde | |||
el tiempo es dado y donde ya conocemos la frecuencia: | |||
\[ | |||
\psi(x,t)=Asen(kx-\omega t) | |||
\] | |||
Y el desplazamiento de fase es $x=(V_{\phi})(t)=(3\times10^{8})(10^{-6})=3\times10^{2}$ | |||
Para calcular el número de ondas que han pasado en ese tiempo, simplemente | |||
calculamos para $\omega$; si sabemos cuanto pasa en un segundo sólo | |||
multiplicamos $\omega$ por $10^{-6}seg$, así: | |||
\[ | |||
(12\times10^{14}\pi)(10^{-6})=12\times10^{8} | |||
\] | |||
que es el número de ondas que han pasado en ese intervalo de tiempo. | |||
---- | |||
Realizado por: [[Usuario:A. Martín R. Rabelo|A. Martín R. Rabelo]] ([[Usuario discusión:A. Martín R. Rabelo|discusión]]) 01:34 30 mar 2015 (CDT) | |||
---- | |||
== Problema 2.18 2da Edición == | |||
Dada la ecuación de onda <math>\psi\left(x,t\right)=5.0\exp\left(-ax^{2}-bt^{2}-2\sqrt{ab}xt\right)</math>, determina la dirección de propagación. | |||
\ | |||
'''Procedimiento''' | |||
Calcule algunos valores de <math>\psi</math> y haz un bosquejo de la onda en t=0 dado <math>a=25m^{-2}</math> y <math>b=9.0s^{-2}</math>. ¿Cual es la velocidad de la onda? | |||
[[Imagen:graficaa1.jpg|200px|thumb|right|Grafica para t=0]] | |||
[[Imagen:graficaa2.jpg|200px|thumb|right|Grafica para t=1]] | |||
De las gráficas de la derecha y no siendo una onda ondas armónicos en forma de coseno o seno, se ve que el la onda se va desplazando hacia la izquierda cuando en este caso t va desde t=0s hasta t =1s | |||
Para la velocidad de onda se hace uso de la misma ecuación diferencial de onda y se despeja de esta misma ecuación la velocidad. Así tenemos: | |||
<math>\frac{\partial^{2}\psi}{\partial x^{2}}=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial t^{2}}</math>: | |||
<math>v^{2}=\frac{\frac{\partial^{2}\psi}{\partial t^{2}}}{\frac{\partial^{2}\psi}{\partial x^{2}}}</math>: | |||
<math>v=\sqrt{\frac{\frac{\partial^{2}\psi}{\partial t^{2}}}{\frac{\partial^{2}\psi}{\partial x^{2}}}}</math>: | |||
<math>\frac{\partial^{2}\psi}{\partial t^{2}}=5\left(-18\exp\left(-9t^{2}-30tx-25x^{2}\right)+\exp\left(-9t^{2}-30tx-25x^{2}\right)\left(-18t-30x\right)^{2}\right)</math>: | |||
<math>\frac{\partial^{2}\psi}{\partial x^{2}}=5\left(-50\exp\left(-9t^{2}-30tx-25x^{2}\right)+\exp\left(-9t^{2}-30tx-25x^{2}\right)\left(-30t-50x\right)^{2}\right)</math> | |||
Factorizando el exponenciales las dos segundas derivadas se tiene: | |||
<math>\frac{\partial^{2}\psi}{\partial t^{2}}=5\exp\left(-9t^{2}-30tx-25x^{2}\right)\left(-18+\left(-18t-30x\right)^{2}\right)</math>; | |||
\ | <math>\frac{\partial^{2}\psi}{\partial x^{2}}=5\exp\left(-9t^{2}-30tx-25x^{2}\right)\left(-50+\left(-30t-50x\right)^{2}\right)</math> | ||
2=\ | |||
\ | |||
Que al hacer la división se elimina y ahora ademas factorizando del termino restante <math>3t+5x^{2}</math>: | |||
<math>\frac{\frac{\partial^{2}\psi}{\partial t^{2}}}{\frac{\partial^{2}\psi}{\partial x^{2}}}</math>: | |||
'''Conclusión''' | |||
<math>=\frac{-18(1-2\left(3t+5x\right)^{2})}{-10(5+\left(3t+5x\right)^{2})}</math> | |||
Que finalmente resulta en que v=0.6 rad/s | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Uziel Sanchez Gutierrez|Uziel Sanchez Gutierrez]] ([[Usuario discusión:Uziel Sanchez Gutierrez|discusión]]) 17:38 30 mar 2015 (CDT) Hecho por Uziel Sanchez Gutierrez | ||
---- | ---- | ||
= | = 4ta Edición en Ingles.= | ||
==Problema 2.1 4ta Edición.== | |||
'''2.1¿Cuantas ondas de luz amarillas (<math>\lambda=580nm</math>) caben en una distancia en el espacio igual a un trozo de papel de (0.003 pulgadas)? ¿Hasta donde se extenderá el mismo número de microondas <math>\displaystyle{(\nu=10^{10}Hhz}</math>, es decir, <math>\displaystyle{10GHz}</math> y <math>\displaystyle{v=3x10^8\frac{m}{s}})</math>?''' | |||
Para responder a la primera pregunta, basta con dividir el espesor del papel con el de la longitud de onda dada, es decir: | |||
<center><math>ondas=\displaystyle{\frac{0.003 in}{580 mm}=\frac{0.003 in}{580 nm}\frac{25.4mm}{1 in}=\frac{0.0762 mm}{580 nm}=131 ondas}</math></center> | |||
Una microonda con frecuencia de <math>\displaystyle{10 GHz}</math> tiene una longitud de onda de | |||
$ | $\displaystyle{\lambda=\frac{c}{\nu}=\frac{3x10⁸}{10 GHz}=0.03m}$ | ||
Por lo tanto 131 ondas con dicha longitud se extenderán | |||
$\displaystyle{extensión=(131)(0.03m)=3.93 m}$ | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 20:28 17 mar 2014 (UTC) | ||
---- | ---- | ||
== Problema 2. | ==Problema 2.1 Solución Secundaria == | ||
'''¿Cuántas ondas de luz <<amarillas>> $(\lambda=580nm)$ caben en una distancia en el espacio igual al espesor de un trozo de papel $(0.003 pulgadas)$? ¿Hasta dónde se extenderá el mismo número de microondas $(\nu=10^{10}Hz$, es decir, $10GHz$ y $v=3x10^8m/s)$?''' | |||
''' | '''Solución''' | ||
La longitud de onda es la relación entre la velocidad de la onda y su frecuencia, que está dada por; | |||
:<math>\lambda=\frac{v}{\nu}</math> | |||
Donde $v$ es la velocidad de la onda y $\nu$ es la frecuencia de la onda. | |||
La distancia $d$ recorrida por la onda es: | |||
<math>d=k*\lambda</math> | |||
Donde $k$ es el número de ondas propagadas, y $\lambda$ es la longitud de onda. | |||
ahora para saber cuántas ondas caben en el espesor del trozo de papel, convierto la longitud de onda de la luz amarilla a metros: | |||
<math>\lambda_{amarillo} = (580nm) * \left(\frac{10^{-9}m}{1nm}\right)=580*10^{-9}m</math> | |||
después convierto el espesor del papel en metros: | |||
\ | <math>0.003in=(0.003in)* \left(\frac{2.54*10^{-2}m}{1in}\right)=7.62*10^{-5}m</math> | ||
calculamos el numero de ondas en la distancia en el espacio del espesor del papel, utilizamos lo que ya sabemos: | |||
:<math>d=k*\lambda_{amarillo}</math> | |||
despejando y sustituyendo tenemos: | |||
:<math>k=\frac{d_{papel}}{\lambda_{amarillo}}=\frac{7.62*10^{-5}m}{580*10^{-9}m}=131ondas</math> | |||
<math>\therefore</math> $131$ $ondas$ de luz amarilla caben en una distancia de $0.003$ $pulgadas$ | |||
para la segunda pregunta calculamos la longitud de onda con los datos que nos dan: | |||
:<math>\lambda=\frac{v}{\nu}=\frac{3*10^8m/s}{10^{10}Hz}=0.03m</math> | |||
'''Conclusión''' | |||
Ahora calculamos cuanta distancia se extenderá el mismo número de ondas con ésta longitud de onda: | |||
:<math>\therefore d=k*\lambda=(131)(0.03m)= 3.9m</math> | |||
---- | |||
Realizado por: [[Usuario:Luis Martínez|Luis Martínez]] ([[Usuario discusión:Luis Martínez|discusión]]) 08:09 27 mar 2015 (CDT) | |||
---- | |||
==Problema 2.2 4ta Edición.== | |||
2.2''' La velocidad de la luz en el vació es aproximadamente de''' $3x10^{8}\frac{m}{s}$.'''Calcule la longitud de onda de la luz roja con una frecuencia de''' $5x10^{14}Hz$.'''Compárela con la longitud de onda de una onda electromagnética de'''$60Hz.$ | |||
'''Procedimiento''' | |||
= | Utilizamos la ecuación $\lambda=\frac{c}{\nu}$,donde $c$ es la velocidad de la luz y $\nu$ la frecuencia de la onda. Tendremos entonces: | ||
\[\lambda=\frac{c}{\nu}=\frac{3x10^{8}\frac{m}{s}}{5x10^{14}Hz}=6x10^{-7}m\] | |||
o la ecuación: | |||
\[\lambda=600nm\] | |||
Que es la longitud de onda de la luz roja a la frecuencia solicitada en el problema. Ahora calculamos la longitud de onda de la onda electromagnética: | |||
\[\lambda_{1}=\frac{c}{\nu}=\frac{3x10^{8}\frac{m}{s}}{60Hz}=5x10^{6}m\]. | |||
'''Conclusión''' | |||
'''Conclusión''' | |||
Al comparar $\lambda$ con $\lambda_{1}$ notamos que la longitud de onda ${\lambda}_{1}$correspondiente a la onda electromagnética es mucho mayor que la de la luz roja. | |||
---- | ---- | ||
Realizado por: [[Usuario:Pedro Pablo Ramírez Martínez|Pedro Pablo Ramírez Martínez]] ([[Usuario discusión:Pedro Pablo Ramírez Martínez|discusión]]) 02:15 17 mar 2014 (UTC) | |||
---- | ---- | ||
==Problema 2. | ==Problema 2.3 4ta Edición.== | ||
''' | |||
''' | '''Es posible generar ondas ultrasónicas en cristales con longitudes de onda similares a la luz $(5\times10^{-5}cm)$ | ||
'''pero con frecuencias mas bajas''' $(6\times10^{8}Hz)$. '''Calcule la velocidad correspondiente de dicha onda.''' | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Pues bien teniendo los datos: $\lambda=5\times10^{-7}m$ y $f=6\times10^{8}Hz$ | |||
y | |||
De la ecuación $v=f\cdot\lambda$ | |||
$v=f\cdot\lambda$ | |||
$v=(5\times10^{-7}m)(6\times10^{8}Hz)$ | |||
'''Solución''' | |||
$v=300\frac{m}{s}$ | |||
---- | |||
Realizado por: [[Usuario:Mario Moranchel|Mario Moranchel]] ([[Usuario discusión:Mario Moranchel|discusión]]) 06:29 18 mar 2014 (UTC) | |||
---- | |||
==Ejercicio 2.3 Solución Alternativa == | |||
Es posible generar ondas ultrasonicas en cristales con longitudes de onda similares a la luz $5x10^-5$ pero con frecuencias mas bajas $6x10^8 HZ$. | |||
Calcular la velocidad correspondiente de dicha onda. | |||
'''Procedimiento''' | |||
Teniendo : <math>\lambda=5x10^-7 m </math> | |||
<math>F= 6x10^8 HZ </math> | |||
'''Conclusión''' | '''Conclusión''' | ||
Donde de la ecuación :<math> V = F\lambda </math> | |||
<math> V=(5X10^-7)(6X10^8HZ) = 300\frac{m}{s}</math> | |||
\ | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 17:03 30 mar 2015 (CDT)luisa alejandra vega sanchez | ||
---- | ---- | ||
== | ==Ejercicio 2.3 Solución Alterna == | ||
Es posible generar ondas ultrasonicas en cristales con longitudes de onda similares a la luz $5x10^-5$ pero con frecuencias mas bajas $6x10^8 HZ$. | |||
Calcular la velocidad correspondiente de dicha onda. | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Teniendo : <math>\lambda=5x10^-7 m </math> | |||
<math>F= 6x10^8 HZ </math> | |||
'''Conclusión''' | |||
Donde de la ecuación :<math> V = F\lambda </math> | |||
<math> V=(5X10^-7)(6X10^8HZ) = 300\frac{m}{s}</math> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 17:03 30 mar 2015 (CDT)luisa alejandra vega sanchez | ||
---- | ---- | ||
==Problema 2. | == Problema 2.4 4ta Edición.== | ||
'''Un joven en un barco sobre un lago está mirando las ondas que parecen''' | |||
de | '''una sucesión infinita de crestas idénticas, produciéndose con''' | ||
'''un intervalo de medio segundo cada una. Si cada perturbación tarda''' | |||
'''1.5s en cubrir la extensión del barco de 4.5 ¿cuál es la frecuencia,''' | |||
'''el periodo y la longitud de onda de las olas?''' | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Los datos dados en el problema, son los siguientes: | |||
t = 1.5s, l = 4.5m, | |||
\ | Del enunciado, se deduce que el periodo, es el siguiente: $\tau=$0.5s. | ||
De donde se calcula la frecuencia utilizando la definición de frecuencia: | |||
\ | \[ | ||
\ | \nu=\frac{1}{\tau} | ||
\ | \] | ||
Al sustituir, en la ecuación, se obtiene el siguiente resultado: | |||
\[ | |||
\nu=\frac{1}{0.5s}=2Hz | |||
\] | |||
Para obtener la longitud de onda, se utiliza la siguiente relación: | |||
== | \[ | ||
\tau=\frac{\lambda}{v}\rightarrow\lambda=v\tau | |||
\] | |||
De donde la velocidad se obtiene a partir de la siguiente definición: | |||
$v=\frac{l}{t}=\frac{4.5m}{1.5s}=3m/s$ | |||
Entonces $\lambda=(3m/s)(0.5s)=1.5m$. | |||
'''Conclusión''' | |||
Frecuencia | |||
\ | \[ | ||
\nu=\frac{ | \nu=\frac{1}{0.5s}=2Hz | ||
\] | |||
Periodo | |||
$\tau=$0.5s | |||
Longitud de onda | |||
$\lambda=1.5m$. | |||
---- | |||
Realizado por: [[Usuario:Ana Alarid|Ana Alarid]] ([[Usuario discusión:Ana Alarid|discusión]]) 01:46 12 mar 2014 (UTC) | |||
---- | |||
==Problema 2.5 4ta Edición== | |||
\ | '''Con un martillo vibrante se golpea el extremo de una barra de metal larga de manera que una onda de compresión periódica con una longitud de onda de 4.3m recorra todo lo largo de la barra con una velocidad de $v=3.5\frac{km}{s}$''' | ||
\ | |||
'''¿Cual sera la frecuencia de la vibración?''' | |||
'''Procedimiento''' | |||
Teniendo los datos: $\lambda=4.3m$ y $v=3500\frac{m}{s}$ | |||
De la ecuación $v=f\cdot\lambda$ obtendremos la frecuencia. | |||
\ | |||
$v=f\cdot\lambda$ | |||
$f=\frac{v}{\lambda}$ | |||
$f=\frac{3500 \frac{m}{s}} {4.3m}$ | |||
'''Conclusión''' | '''Conclusión''' | ||
$f=813.95 Hz$ | |||
---- | ---- | ||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | ---- | ||
==Problema 2. | ==Problema 2.6 4ta Edición== | ||
'''Durante la boda de dos buceadores, se sumerge un violín en la''' | |||
'''piscina. Dado que la velocidad de las ondas de compresión en agua''' | |||
'''pura es de 1498 m/s. ¿Cual es la longitud de una nota la, de 440''' | |||
, en | '''Hz que se toca en dicho instrumento?''' | ||
de | |||
'''Procedimiento''' | |||
Conocemos la velocidad de la onda en el agua que es $\upsilon=1498\frac{m}{s}$ | |||
y conocemos también la frecuencia de la nota que es $\upsilon=440Hz=440\frac{ciclos}{s}$ | |||
Ahora bien si queremos encontrar la longitud de la onda, recurrimos | |||
a la ecuación | |||
\[ | |||
\upsilon=\nu\lambda | |||
\] | |||
De donde conocemos todo excepto la longitud de onda, solo requiere | |||
de un sencillo despeje para encontrar $\lambda$ | |||
Haciendo el despeje la ecuación queda: | |||
\[ | |||
\lambda=\frac{\upsilon}{\nu} | |||
\] | |||
Sustituimos nuestros datos | |||
\[ | |||
\lambda=\frac{1498\frac{m}{s}}{440\frac{ciclos}{s}} | |||
\] | |||
'''Conclusión''' | |||
Y obtendremos que: | |||
\[ | |||
\lambda=3.40m | |||
\] | |||
---- | |||
Realizado por: [[Usuario:Daniel Olvera Moreno]] ) 05:29 21 mar 2014 (UTC) | |||
---- | |||
==Problema 2.7 4ta Edición == | |||
'''Un pulso de onda tarda $2.0 s$ en recorrer $10 m$ a lo largo de una cuerda, se genera una perturbación armónica con una longitud de onda de $0.5 m$ en la cuerda. ¿Cuál es su frecuencia?''' | |||
'''Procedimiento''' | |||
De los datos proporcionados sabemos que si la perturbación armónica tiene una longitud de onda de $\lambda=0.5 m$ de manera que el pulso completa 20 "ciclos" en los $10 m$ recorridos. | |||
De esta forma el periodo de la perturbación es: | |||
<math> \tau= \frac{2 s}{20}= 0.1 s</math> | |||
'''Solución''' | |||
Entonces la frecuencia es: | |||
<math> f= \frac{1}{\tau}=\frac{1}{0.1 s}=10 Hz </math> | |||
---- | |||
Realizado por: [[Usuario:Brenda Pérez Vidal|Brenda Pérez Vidal]] ([[Usuario discusión:Brenda Pérez Vidal|discusión]]) 18:16 27 mar 2014 (UTC) | |||
---- | |||
==Problema 2.8 5ta Edición== | |||
Calcule la longitud de onda de las ondas de ultrasonido con una frecuencia | |||
de 500 MHz en el aire. La velocidad del sonido en el aire es de 343 m/s | |||
'''Procedimiento''' | |||
Para este caso, la resolución del problema es fácil ya que solo aplicamos la Ecuación \ref{eq:last} y solamente aplicamos sustitución de datos. | |||
\begin{equation}\label{eq:last} | |||
v=f * \lambda | |||
\end{equation} | |||
Por lo tanto, despejando la $\lambda$ llegamos a la Ecuación \ref{eq:last1}. | |||
\begin{equation}\label{eq:last1} | |||
\lambda= \frac{v}{f} | |||
\end{equation} | |||
Sustituyendo los datos. | |||
\begin{equation} | |||
\lambda= \frac{343}{500000000} | |||
\end{equation} | |||
'''Conclusión''' | '''Conclusión''' | ||
Por lo tanto llegamos a la solución de que la longitud de onda del ultrasonido es de: 0.000000686 m. | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Misa cabca|Misa cabca]] ([[Usuario discusión:Misa cabca|discusión]]) 20:31 16 nov 2020 (CST) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.8 4ta Edición== | ||
'''2.8 Demuestre que para una onda periódica $\omega=(\frac{2\pi}{\lambda})v$ | |||
''' | '''Procedimiento''' | ||
La mayoría de las ondas son el resultado de muchas perturbaciones sucesivas del medio. Cuando dichas perturbaciones se producen a intervalos regulares y todas son de la misma forma, estamos frente a una onda periódica. | |||
Una onda periódica posee periodo (número de unidades de tiempo por onda) y frecuencia (número de ondas por unidad de tiempo), establecidas por: | |||
\ | $Periodo$ | ||
\ | \begin{equation} | ||
\ | \tau=\frac{\lambda}{v}.... (i) | ||
\end{equation} | |||
donde $\tau$ es el periodo de onda, $\lambda$ es la longitud de onda y $v$ se refiere a la velocidad con la que viaja la onda. | |||
$Frecuencia$ | |||
\begin{equation} | |||
\nu=\frac{\omega}{2\pi}....(ii) | |||
\end{equation} | |||
donde $\nu$ es la frecuencia de la onda, $\omega$ es la frecuencia angular de la onda. | |||
De $(ii)$ despejamos $\omega$ | |||
$\ | |||
\ | \begin{equation} | ||
\ | \omega=\nu 2\pi ....(iii) | ||
\ | \end{equation} | ||
También sabemos que el inverso del periodo es la frecuencia $(\nu=\frac{1}{\tau})$ | |||
Utilizando la expresión $(iv)$ y sustituyendola en $(iii)$ | |||
y | |||
\ | \begin{equation} | ||
\ | \nu=\frac{1}{\tau} ....(iv) | ||
\end{equation} | |||
\begin{equation} | |||
\omega= \frac{2\pi}{\tau} | |||
\end{equation} | |||
Sustituyendo $(i)$ en $\tau$ | |||
\ | \begin{equation} | ||
\omega= \frac{2\pi}{\frac{\lambda}{v}} | |||
\end{equation} | |||
'''Conclusión''' | |||
Por lo tanto: | |||
\ | \begin{equation} | ||
\ | \omega= (\frac{2\pi}{\lambda})(v) | ||
\end{equation} | |||
---- | |||
Realizado por: [[Usuario:Angel Nahir Molina Guadarrama|Angel Nahir Molina Guadarrama]] ([[Usuario discusión:Angel Nahir Molina Guadarrama|discusión]]) 11:13 23 mar 2014 (UTC) | |||
---- | |||
==Problema 2.9 4ta Edición== | |||
\ | Hacer una tabla con las columnas encabezadas por los valores de $\theta$ | ||
\ | corriendo de $-\frac{\pi}{2}$ a $2\pi$ en intervalos de $\frac{\pi}{4}$ | ||
\ | , en cada fila el valor correspondiente de $\sin\theta$ , debajo | ||
de esos valores los de $\cos\theta$ , por debajo de los valores de | |||
$\sin\left(\theta-\frac{\pi}{4}\right)$ , y similarmente con las | |||
funciones $\sin\left(\theta-\frac{\pi}{2}\right)$ , $\sin\left(\theta-\frac{3\pi}{4}\right)$ | |||
, y $\sin\left(\theta+\frac{\pi}{2}\right)$) . Trazar cada una de | |||
estas funciones, sin los efectos del desplazamiento de fase. La funcion | |||
$\sin\theta$ se atrasa o se adelantade la funcion $\sin\left(\theta-\frac{\pi}{2}\right)$ | |||
. en otras palabras, Una de las funciones alcanza una magnitud particular, | |||
en un valor menor de $\theta$ que la otra y , por tanto, una conduce | |||
a la otra ( como $\cos\theta$ conduce $\sin\theta$ ) ? | |||
'''Tabla''' | |||
[[Archivo:Grafica2.9.png|700px|thumb|left|Las funciones $\sin\left(\theta+\frac{\pi}{2}\right)$ y $\cos\theta$ son iguales y las otras funciones se desplazan a la izquierda de la función $\sin\theta$ cada $\frac{\pi}{4}$ a excepción de la función $\sin\left(\theta+\frac{\pi}{2}\right)$ que de desplaza a la derecha ]] | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
! $ \theta $ | |||
! $-\frac{\pi}{4}$ | |||
\ | ! $-\frac{\pi}{4}$ | ||
! $ 0 $ | |||
! $ \frac{\pi}{4}$ | |||
! $ \frac{\pi}{2}$ | |||
! $ \frac{3\pi}{4}$ | |||
! $ \pi $ | |||
! $ \frac{5\pi}{4}$ | |||
! $ \frac{3\pi}{2}$ | |||
! $ \frac{7\pi}{4}$ | |||
! $ 2\pi$ | |||
|- | |- | ||
| $ \sin(\theta) $ | |||
| $ -1 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 1 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ -1 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
|- | |- | ||
| $ | | $ \cos(\theta) $ | ||
| $ | | $ 0 $ | ||
| $ | | $ \frac{\sqrt{2}}{2} $ | ||
| $ 1 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | | $ 0 $ | ||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ -1 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 1 $ | |||
| $ -\frac{\sqrt{2}}{2}$ | |||
| $ - | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $ | |||
| $ | |||
| $ | |||
|- | |- | ||
| $\ | | $ \sin(\theta-\frac{\pi}{4}) $ | ||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ -1 $ | |||
| $ -\frac{\sqrt{2}}{2}$ | | $ -\frac{\sqrt{2}}{2} $ | ||
| $ - | | $ 0 $ | ||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 1 $ | |||
| $-\frac{\sqrt{2}}{2}$ | | $ \frac{\sqrt{2}}{2} $ | ||
| $ 0 $ | |||
| $ | | $ -\frac{\sqrt{2}}{2} $ | ||
| $ | | $ -1 $ | ||
| $ | | $ -\frac{\sqrt{2}}{2} $ | ||
| $ | |||
| $ | |||
| $ | |||
| $ | |||
| $ | |||
|- | |- | ||
| $ | | $ \sin(\theta-\frac{\pi}{2}) $ | ||
| $ | | $ 0 $ | ||
| $ | | $ -\frac{\sqrt{2}}{2} $ | ||
| $ | | $ -1 $ | ||
| $ | | $ -\frac{\sqrt{2}}{2} $ | ||
| $ | | $ 0 $ | ||
| $ | | $ \frac{\sqrt{2}}{2} $ | ||
| $ | | $ 1 $ | ||
| | | $ \frac{\sqrt{2}}{2} $ | ||
| $ 0 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ -1 $ | |||
|- | |- | ||
| $ \sin(\theta-\frac{3 \pi}{4}) $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ -1 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 1 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ -\frac{\sqrt{2}}{2} $ | |||
|- | |- | ||
| $ \sin(\theta+\frac{\pi}{2}) $ | |||
| $ 0 $ | |||
| | | $ \frac{\sqrt{2}}{2} $ | ||
| $ 1 $ | |||
| $ | | $ \frac{\sqrt{2}}{2} $ | ||
| | | $ 0 $ | ||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $-\frac | | $ -1 $ | ||
| $ -\frac{\sqrt{2}}{2} $ | |||
| $ 0 $ | |||
| $ \frac{\sqrt{2}}{2} $ | |||
| $ 1 $ | |||
|} | |} | ||
| Línea 716: | Línea 670: | ||
'''Conclusión''' | |||
Respuesta: $\sin\left(\theta+\frac{\pi}{2}\right)$ que es igual al $\cos(\theta)$ se desplaza a la izquierda del $\sin\theta$ | |||
---- | |||
Realizado por: [[Usuario:Rosario Maya|Rosario Maya]] ([[Usuario discusión:Rosario Maya|discusión]]) 20:37 29 mar 2015 (CDT) | |||
---- | |||
==Problema 2.10 (4ta Edición)== | |||
Hacer una tabla con columnas encabezadas por los valores de $kx$ | |||
correr desde $x=-\frac{\lambda}{2}$ a $x=+\lambda$ en intervalos | |||
de $x$ de $\frac{\lambda}{4}$ , por supuesto, $k=\frac{2\pi}{\lambda}$ | |||
. En cada columna colocar los correspondientes valores de $\cos\left(kx+\frac{3\pi}{4}\right)$ | |||
y para las funciones $15\cos\left(kx-\frac{\pi}{4}\right)$ y $25\cos\left(kx+\frac{3\pi}{4}\right)$. | |||
'''Tabla''' | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
! $ x $ | |||
! $-\frac{\lambda}{2}$ | |||
! $-\frac{\lambda}{4}$ | |||
! $ 0 $ | |||
! $\frac{\lambda}{4}$ | |||
! $\frac{\lambda}{2}$ | |||
! $\frac{3\lambda}{2} $ | |||
! $ \lambda $ | |||
|- | |||
| $ kx=2\pi\frac{\lambda}{2} $ | |||
| $ -\pi $ | |||
| $ -\frac{\pi}{2}$ | |||
| $ 0 $ | |||
| $ \frac{\pi}{2}$ | |||
| $ \pi $ | |||
| $ \frac{3\pi}{2}$ | |||
| $ 2\pi$ | |||
|- | |||
| $\cos\left(kx-\frac{\pi}{2}\right)$ | |||
| $ -\frac{\sqrt{2}}{2}$ | |||
| $ -\frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $-\frac{\sqrt{2}}{2}$ | |||
| $-\frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
|- | |||
| $\cos\left(kx+\frac{3\pi}{4}\right)$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $ -\frac{\sqrt{2}}{2}$ | |||
| $ -\frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $ \frac{\sqrt{2}}{2}$ | |||
| $-\frac{\sqrt{2}}{2}$ | |||
|- | |||
| $15\cos\left(kx-\frac{\pi}{4}\right)$ | |||
| $ 15-\frac{\sqrt{2}}{2}$ | |||
| $ 15-\frac{\sqrt{2}}{2}$ | |||
| $ 15\frac{\sqrt{2}}{2}$ | |||
| $ 15\frac{\sqrt{2}}{2}$ | |||
| $ 15-\frac{\sqrt{2}}{2}$ | |||
| $ 15-\frac{\sqrt{2}}{2}$ | |||
| $ 15\frac{\sqrt{2}}{2}$ | |||
|- | |||
| $25\cos\left(kx+\frac{3\pi}{4}\right)$ | |||
| $ 25\frac{\sqrt{2}}{2}$ | |||
| $ 25\frac{\sqrt{2}}{2}$ | |||
| $ 25-\frac{\sqrt{2}}{2}$ | |||
| $ 25-\frac{\sqrt{2}}{2}$ | |||
| $ 25\frac{\sqrt{2}}{2}$ | |||
| $ 25\frac{\sqrt{2}}{2}$ | |||
| $ 25-\frac{\sqrt{2}}{2}$ | |||
|} | |||
---- | ---- | ||
Ejercicio Resuelto por :[[Usuario:Rosario Maya|Rosario Maya]] ([[Usuario discusión:Rosario Maya|discusión]]) 00:05 30 mar 2015 (CDT) | |||
---- | ---- | ||
== Problema 2. | ==Problema 2.11 4ta Edición== | ||
'''Haga una tabla con columnas encabezadas por valores de $\omega \, t$ que van desde a $t=-\tau /2$ to $t=+\tau$ en intervalos de $t$ of $\tau/4$; por supuesto $\omega=2\,\pi/\tau$. En cada columna coloque los valores correspondientes de$\sin(\omega\,t+\pi/4)$ y $\sin(\pi/4-\omega\,t)$ y trace estas dos funciones. ''' | |||
$ | Se realiza la tabla usando $\omega=2\,\pi/\tau$ en el argumento de cada función. | ||
{| class="wikitable" style="width:60%; height:200px" align="center" border="2" cellpadding="2" | |||
|- | |||
!width="75"|$t$ !!width="25"| $-\frac{\tau}{2}$ !!width="25"| $-\frac{\tau}{4}$ !!width="25"| $0$ !!width="25"| $\frac{\tau}{4}$ !!width="25"| $\frac{\tau}{2}$ !!width="25"| $\frac{3\tau}{4}$ !!width="25"| $\tau$ | |||
|- | |||
! $\omega \, t$ | |||
| $-\pi$ || $-\frac{\pi}{2}$ || $0$ || $\frac{\pi}{4}$ || $\frac{\pi}{2}$ || $\frac{3\pi}{2}$ || $2\pi$ | |||
|- | |||
! $\sin(\omega\,t+\frac{\pi}{4})$ | |||
| $-\frac{1}{\sqrt{2}}$ || $-\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ || $-\frac{1}{\sqrt{2}}$ || $-\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ | |||
|- | |||
! $\sin(\frac{\pi}{4}-\omega\,t)$ | |||
| $-\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ || $-\frac{1}{\sqrt{2}}$ || $-\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ || $\frac{1}{\sqrt{2}}$ | |||
|} | |||
La gráfica se realizó en ''Mathematica 10.0''. El comando utilizado fue: | |||
Plot[ | |||
{Sin[wt + Pi/4], Sin[Pi/4 - wt]}, {wt, -Pi, 2 Pi}, | |||
PlotStyle -> Thickness[.01], PlotLegends -> "Expressions", | |||
AxesStyle -> {Directive[Black, 12, Thick], Directive[Black, 12, Thick]}, | |||
Ticks -> {Table[-Pi + n Pi/2, {n, 0, 6}], {-1, -(Sqrt[2]/2), 0, Sqrt[2]/2, 1}}, | |||
TicksStyle -> Directive["Label", 18, Black, Thick], | |||
GridLines -> {Table[-Pi + n Pi/4, {n, 0, 12}], {-1, -(Sqrt[2]/2), 0, Sqrt[2]/2, 1}}, | |||
GridLinesStyle -> Directive[Dashed, GrayLevel[.76], Thickness[.0025]], | |||
ImageSize -> Large | |||
] | |||
[[Image:Problema 2.11 Hecht wikiluz.png|thumb|Gráfica acorde a los datos de la tabla mostrada arriba.|left|800px]] | |||
----- | |||
Problema hecho por: [[Usuario:Adolfo Calderón Alcaraz|Adolfo Calderón Alcaraz]] ([[Usuario discusión:Adolfo Calderón Alcaraz|discusión]]) 01:58 30 mar 2015 (CDT) | |||
----- | |||
''' | ==Problema 2.12 4ta Edición== | ||
'''2.12 El perfil de una onda armónica, que viaja con velocidad de 1.2 m/s en una cuerda,esta dado por''' | |||
<center><math>\displaystyle{y=\left(0.02m\right)\sin\left(157m^{-1}\right)x}</math></center> | |||
''' | '''Calcule su amplitud, su longitud de onda, su frecuencia y su periodo''' | ||
''' | ''' Procedimiento ''' | ||
Se observa que la ecuación no muestra dependencia del tiempo, por lo obedece a la ecuación (2.12) del libro | |||
<center><math>\displaystyle{\psi(x)=A\sin(kx)}</math></center> | |||
de donde es inmediatos su amplitud '''A=0.02m''' y número de onda '''<math>k=157m^{-1}</math>''', por lo que su longuitud de onda esta dada por: | |||
<center><math>\displaystyle{\lambda=\frac{2\pi}{k}=\frac{2\pi}{157m^{-1}}=0.04m}</math></center> | |||
su frecuencia esta dada ṕor la ecuación (2.19), entonces: | |||
<center><math>\displaystyle{\nu=\frac{v}{\lambda}=\frac{1.2\frac{m}{s}}{0.04m}=30Hhz}</math></center> | |||
Finalmente, su periodo esta dado por: | |||
'''Conclusión''' | |||
<center><math>\displaystyle{\tau=\frac{1}{\nu}=\frac{1}{30}s}</math></center> | |||
---- | |||
Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 17:56 26 mar 2014 (UTC) | |||
---- | |||
== Problema 2.12 2do método == | |||
El perfil de velocidad de una onda armónica, que viaja a una velocidad de $1.2 m/s$ en una cuerda, esta dado por: | |||
$ y=\left(0.02\right)\sin\left(157/m\right)x $ | |||
\ | |||
\ | |||
Calcule su amplitud, su longitud de onda, su frecuencia y su periodo. | |||
. | |||
Solución | |||
Se tiene la ecuación de onda (2.13) que es: | |||
\ | $\varPsi\left(x,t\right)=a\sin\kappa\left(x-vt\right)$ | ||
\ | |||
Donde $A$ | |||
es la amplitud , y $\kappa$ | |||
el numero de onda (constante). | |||
Tomando en cuenta que el tiempo es independiente de la función de onda, y con t=0; se tiene: | |||
: $\varPsi(x,0)=A\sin\left[x-v(0)\right]=A\sin\kappa x$ | |||
'''Inciso a''' | |||
a) Comparando la ecuación del ejercicio, con la parte teórica, se sabe por inspección que la amplitud $ A=0.02m$ | |||
y $\kappa=157m^{-1}$. | |||
'''Inciso b''' | |||
b) Se tiene la relación $\kappa=\frac{2\pi}{\lambda}$ | |||
; despejando la longitud de onda $"\lambda"$ se tiene: | |||
$\lambda$ | |||
$= \frac{2\pi}{\kappa}$ | |||
$= \frac{2\pi}{157m^{-1}}$ | |||
$= 0.0400 m $ | |||
'''Inciso c''' | |||
c) Para la frecuencia se tiene la relación $v=\nu\lambda$ | |||
Despejando la frecuencia $"\nu"$ se tiene: | |||
$\frac{ | $\nu$ | ||
=$\frac{v}{\lambda}$ | |||
= $\frac{1.2m/s}{0.0400m}$ | |||
=$ 30 Hz $ | |||
'''Inciso d''' | |||
d) Para el período se tiene el recíproco de la frecuencia: | |||
$\frac{1}{\nu}=0. | $\tau$ | ||
= $\frac{1}{\nu}$ | |||
= $\frac{1}{30Hz}$ | |||
= $0.033 s$ | |||
---- | |||
Elaborado por Ricardo García Hernández.[[Usuario:Ricardo Garcia Hernandez|Ricardo Garcia Hernandez]] ([[Usuario discusión:Ricardo Garcia Hernandez|discusión]]) 00:25 30 mar 2015 (CDT) | |||
---- | |||
==Problema 2.16 4ta Edición== | |||
'''2.13 Usando las funciones de onda''' | |||
$\ | $\psi_{1}=4\sin2\pi\left(0.2x-3t\right)$ | ||
$\psi_{2}=\frac{\sin\left(7x+3.5t\right)}{2.5}$ | |||
Determine en cada caso los valores de | |||
'''a)Frecuencia.''' | |||
'''b)Longitud de onda.''' | |||
'''c)Periodo.''' | |||
'''d)Amplitud.''' | |||
'''e)Velocidad de fase.''' | |||
'''f)Dirección del movimiento.''' | |||
'''El tiempo se expresa en segundos y x en metros.''' | |||
= | Partimos de la ecuación de onda: | ||
\[ | |||
\psi=Asin(kx \pm \omega t)...(1) | |||
\] | |||
En donde podemos factorizar $2 \pi$ del argumento y escribir: | |||
\[ | |||
\psi=Asin2 \pi (\frac{k}{2 \pi} x \pm \frac{\omega}{2\pi}t) | |||
...(2)\] | |||
Definimos a: | |||
\[ | |||
\frac{k}{2\pi}=\chi | |||
\] | |||
\[ | |||
\frac{\omega}{2\pi}=\nu | |||
\] | |||
\[ | |||
\psi=Asin 2\pi(\chi x \pm \nu t)...(3) | |||
\] | |||
De esta ecuación podemos identificar la: | |||
Amplitud: $A$ | |||
Frecuencia: $\nu$ | |||
Número de onda: $\chi$ | |||
También sabemos que: | |||
Velocidad de fase: $V= \pm \frac{\omega}{k}$ | |||
Longitud de onda: $\frac{V}{\nu}$ | |||
'''Primera función de onda.''' | |||
- | Con lo anterior, dada $ \psi_1 = 4 sin2\pi (0.2 x - 3t)$ | ||
'''a) Frecuencia''' | |||
$\nu=3 Hz$ | |||
'''b) Longitud de Onda''' | |||
$\lambda=\frac{V}{\nu}= \frac{15}{3}=5 m$ | |||
'''c) Periodo''' | |||
$\tau=\frac{1}{\nu}=0.333... s$ | |||
'''d) Amplitud''' | |||
$A= 4 m$ | |||
'''e) Velocidad de fase''' | |||
$v=\frac{\omega}{k}=\frac{\nu}{\chi}=\frac{3 Hz}{0.2 m^{-1}}=15 m/s$ | |||
'''f) Dirección de movimiento''' | |||
Hacia la derecha. | |||
'''Segunda Función de onda''' | |||
\ | Para la función $ \psi_2 \frac{1}{2.5} sin(7x + 3.5t) $ | ||
\frac{ | |||
'''a) Frecuencia.''' | |||
$\nu=\frac{\omega}{2\pi}=\frac{3.5}{2\pi}=0.55 Hz$ | |||
'''b) Longitud de onda.''' | |||
$\lambda=\frac{2\pi}{k}= \frac{2/pi}{7}=0.897 m$ | |||
'''c) Periodo.''' | |||
$\tau=\frac{2\pi}{\omega}=1.795 s$ | |||
'''d) Amplitud.''' | |||
$A=\frac{1}{2.5}=0.4 m$ | |||
'''e) Velocidad de fase.''' | |||
$v=\frac{\omega}{k}=-\frac{3.5}{7}=-0.5 m/s$ | |||
'''f) Dirección de movimiento.''' | |||
Dado el signo negativo, de la velocidad de fase, el movimiento es Hacia la izquierda. | |||
---- | ---- | ||
Resuelto por:[[Usuario:Luis Santos|Luis Santos]] ([[Usuario discusión:Luis Santos|discusión]]) 13:13 28 mar 2015 (CDT) | |||
---- | ---- | ||
==Problema 2. | ==Problema 2.18 4ta Edición== | ||
Demuestre que, <math>\psi(x,t)=A\sin\left [k(x-vt) \right ]</math> es una solución de la ecuación diferencial de onda. | |||
''' | '''Demostración''' | ||
De la solución propuesta se observa que se trata de la ecuación de diferencial de onda en una dimensión, luego, para ser solución debe satisfacer la ecuación. | |||
$\frac{\partial^2 \psi }{\partial x^2}=\frac{1}{v^{2}}\frac{\partial^{2} \psi}{\partial t^{2}}$ | |||
La segunda derivada parcial respecto de x esta dada por: | |||
$\frac{\partial^2 \psi}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial \psi}{\partial x}=\frac{\partial}{\partial x}(kA\cos(kx-kvt))=-k^2 A \sin(kx-kvt)$ | |||
La segunda derivada parcial respecto de t esta dada por: | |||
$\frac{\partial^2 \psi }{\partial t^2}=\frac{\partial}{\partial t}\frac{\partial \psi}{\partial t}=\frac{\partial}{\partial t}(-kvA\cos(kx-kvt))=-k^2v^2A\sin(kx-kvt)$ | |||
Al sustituirlas en la ecuación diferencial de onda se tiene: | |||
<math>\ | <center><math>\displaystyle{-k^{2}A\sin(kx-kvt)=-\frac{1}{v^{2}}kv^{2}A\sin(kx-kvt)}</math></center> | ||
Como la última igualdad es cierta, entonces es solución de la ecuación diferencial de onda en una dimensión. | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 21:17 17 mar 2014 (UTC) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.18 4ta Edición== | ||
Demuestre que, <math>\psi(x,t)=A\sin\left [k(x-vt) \right ]</math> es una solución de la ecuación diferencial de onda. | |||
''' | '''Demostración''' | ||
De la solución propuesta se observa que se trata de la ecuación de diferencial de onda en una dimensión, luego, para ser solución debe satisfacer la ecuación. | |||
$\frac{\partial^2 \psi }{\partial x^2}=\frac{1}{v^{2}}\frac{\partial^{2} \psi}{\partial t^{2}}$ | |||
La segunda derivada parcial respecto de x esta dada por: | |||
$\frac{\partial^2 \psi}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial \psi}{\partial x}=\frac{\partial}{\partial x}(kA\cos(kx-kvt))=-k^2 A \sin(kx-kvt)$ | |||
La segunda derivada parcial respecto de t esta dada por: | |||
$\frac{\partial^2 \psi }{\partial t^2}=\frac{\partial}{\partial t}\frac{\partial \psi}{\partial t}=\frac{\partial}{\partial t}(-kvA\cos(kx-kvt))=-k^2v^2A\sin(kx-kvt)$ | |||
Al sustituirlas en la ecuación diferencial de onda se tiene: | |||
<center><math>\displaystyle{-k^{2}A\sin(kx-kvt)=-\frac{1}{v^{2}}kv^{2}A\sin(kx-kvt)}</math></center> | |||
Como la última igualdad es cierta, entonces es solución de la ecuación diferencial de onda en una dimensión. | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 21:17 17 mar 2014 (UTC) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.22 4ta Edición== | ||
Escriba la expresión para la onda armónica de amplitud <math>10^{3}V/m</math> , periodo <math>2.2\times 10^{-15}s</math> ,y velocidad <math>3\times 10^{8}m/s</math> .La onda se propaga en la dirección negativa de X y tiene un valor de <math>10^{3} V/m</math> en t=0 y x=0 | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Sabemos que una función de onda, puede escribirse como: | |||
\ | $\Psi(x,t)=A \sin\left [ kx \pm \omega t \right ]$ | ||
\ | $\Psi(x,t)=A \cos\left [ kx \pm \omega t \right ]$ | ||
Dado que en $x=0$ y $t=0$ tiene un valor de $10^{3}V/m$, usamos la función coseno (Dado que la función Seno nos daría un valor de 0 en esos valores). ademas sabemos que se propaga en dirección negativa de X usamos el signo positivo. | |||
\ | $\Psi(x,t)=A \cos\left [ kx + \omega t \right ]$ | ||
Para encontrar los valores, tenemos que encontrar el valor de $\omega$ | |||
\ | $\omega=\frac{2\pi}{T}=\frac{2\pi}{2.2 \times 10^{-15}s}=2.856 \times 10^{15} s^{-1}$ | ||
El valor de $k$ se puede encontrar usando: | |||
$k=\frac{\omega}{\nu}=\frac{2.856 \times10^{15} \frac{rad}{s}}{3 \times 10^8 \frac{m}{s}}=9.52 \times 10^{6} m^{-1}$ | |||
'''Conclusión''' | |||
Sustituyendo estos valores, se tiene la siguiente función de onda: | |||
$\Psi(x,t)=\left (10^{3} \frac{V}{m} \right ) \cos\left [ \left (9.52 \times 10^{6} m^{-1} \right ) x + \left (2.856 \times 10^{15} s^{-1} \right ) t \right ]$ | |||
que cumple con: | |||
$\Psi(0,0)=\left (10^{3} \frac{V}{m} \right )$ | |||
---- | ---- | ||
Re elaborado por [[Usuario: Manuel Rodríguez |Manuel Rodríguez]] | |||
---- | ---- | ||
== Problema 2. | |||
==Problema 2.36 4ta Edición == | |||
''' Escribe una expresión para la onda mostrada en la figura P.2.36. Encuentra la velocidad de onda, velocidad, frecuencia y periodo.''' | |||
[[Archivo:Figure P.2.36.png|350px]] | |||
'''Inciso a''' | |||
a) La forma matemática de la descripción de una función de onda es: | |||
<math>\psi(z,t)=Asen(kz \mp \omega t \pm \epsilon)</math> | |||
Dado lo anterior podemos encontrar el número de onda K y la frecuencia <math>\omega</math>, donde <math>\epsilon</math> a un tiempo cero, es igual a cero por lo tanto <math>\epsilon =0 </math>. | |||
<math> | De las expresiones para el numero de onda <math>K = \frac{2 \pi}{ \lambda}</math> y <math>\omega= \frac{2 \pi}{\tau}</math>, en donde <math>\tau</math> y <math>\lambda</math> son la frecuencia y la longitud de onda respectivamente, podremos reescribir la expresión para la onda como: | ||
<math> | |||
<math> | <math>\psi(z,t)=A sen 2 \pi (\frac{z}{\lambda}-\frac{t}{\tau})</math> | ||
<math> | |||
<math> | El signo menos es por el desplazamiento de la función de onda a la derecha. | ||
Por el gráfico se observa que la longitud de onda es de cuatrocientos nanómetros, la amplitud es de 60 nanómetros y el periodo es de | |||
<math>1.33x10^{-15}s</math>, dado que da un ciclo en ese tiempo. Por ende la expresión buscada es: | |||
<math>\psi(z,t)=A sen 2 \pi (\frac{z}{400x10^{-9} m}-\frac{t}{1.33X10^{-15}s})</math> | |||
'''Inciso b''' | |||
b)Calculando la velocidad de onda: | |||
<math>\frac{\ | <math>v= \frac{\lambda}{\tau}=\frac{400x10^{-9}m}{1.33x10^{-15} s}=3x10^{8} \frac{m}{s}</math> | ||
'''Inciso c''' | |||
c) Calculando la frecuencia y el periodo: | |||
<math>\ | <math>\nu = \frac{1}{\tau}= \frac{1}{1.33} x10^{15} Hz</math> | ||
<math>\tau= 1.33x 10^{-15} s</math> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Pablo|Pablo]] ([[Usuario discusión:Pablo|discusión]]) 22:23 21 mar 2015 (CDT) | ||
---- | ---- | ||
= | = 5ta Edición en Ingles.= | ||
==Problema 2.2 5ta Edición== | |||
'''Mostrar que la función''' | |||
\begin{equation}\label{eq:1} | |||
\psi (y,t)=(y-4t)^{2} | |||
\end{equation} | |||
'''Es una succiona de la ecuación de onda diferencial. ¿En que dirección viaja?''' | |||
'''Procedimiento''' | |||
Para resolver este problema, debemos tener presente que le Ecuación de Onda es de la forma | |||
\begin{equation}\label{eq:2} | |||
\frac{\partial^{2}{\psi}}{\partial{y}^{2}}=\frac{1}{v^{2}} \frac{\partial^{2}{\psi}}{\partial{t}^{2}} | |||
\end{equation} | |||
Para comprobar, comenzamos realizando la primer derivada de la función (Ecuación \ref{eq:1}) respecto a $y$ | |||
\begin{equation} | |||
\frac{\partial{\psi}}{\partial{y}}=\frac{\partial}{\partial{y}}((y-4t)^{2})=2(y-4t)=2y-8t | |||
\end{equation} | |||
Ahora derivamos el resultado anterior para así obtener la segunda derivada respeto a la variable $y$ | |||
\begin{equation} | |||
\frac{\partial^{2}{\psi}}{\partial{y}^{2}}=\frac{\partial}{\partial{y}}(\frac{\partial{\psi}}{\partial{y}})=\frac{\partial}{\partial{y}}(2y-8t)=2 | |||
\end{equation} | |||
Realizamos el mismo procedimiento para llegar a la segunda derivada de la Ecuación \ref{eq:1} pero ahora respecto a la variable $t$ | |||
\ | |||
pero | |||
\begin{equation} | |||
\ | \frac{\partial{\psi}}{\partial{t}}=\frac{\partial}{\partial{t}}((y-4t)^{2})=2(y-4t)(-4)=-8(y-4t)=32t-8y | ||
\end{equation} | |||
\begin{equation} | |||
\frac{\partial^{2}{\psi}}{\partial{t}^{2}}=\frac{\partial}{\partial{t}}(\frac{\partial{\psi}}{\partial{t}})=\frac{\partial}{\partial{t}}(32t-8y)=32 | |||
\end{equation} | |||
Como se observa en la Ecuación \ref{eq:2} solo nos hace falta obtener la variable $v$, pero como vemos, esta se obtiene despejandola para finalmente llegar a la siguiente expresión | |||
\ | |||
$ | |||
\begin{equation} | |||
v^{2}=\frac{\frac{\partial^{2}{\psi}}{\partial{t}^{2}}}{\frac{\partial^{2}{\psi}}{\partial{y}^{2}}} | |||
\end{equation} | |||
$ | Sustituimos los datos de las segundas derivadas que habíamos encontrado y vemos que la $v^{2}=16$. | ||
= | |||
$ | |||
'''Conclusión''' | |||
Realizando la sustitución de los datos, encontramos | |||
\begin{equation} | |||
2=\frac{1}{16}(32)=2 | |||
\end{equation} | |||
que la función es solución de la ecuación de onda. | |||
La onda viaja de izquierda a derecha ya que la función (Ec.\ref{eq:1}) tiene un signo menos. | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Misa cabca|Misa cabca]] ([[Usuario discusión:Misa cabca|discusión]]) 10:24 27 oct 2020 (CDT) | ||
---- | ---- | ||
==Problema 2.27 5ta Edición== | |||
Demuestre que si el desplazamiento de la cuerda de la figura 2.7 está dado por <math>y(x,t)=A \sin[kx - \omega t + \varepsilon]</math> entonces la mano que genera la onda se debe mover verticalmente con movimiento armónico simple. | |||
Vemos que el movimiento de la cuerda en la figura $2.7$ corresponde al de una onda armónica que se desplaza a lo largo del eje $x$ durante un tiempo de un período, en este caso cualquier punto de la cuerda se desplaza sólo verticalmente, entonces podemos derivar la ecuación de movimiento como sigue: | |||
[[Archivo:Hetch 2da edicion problema (2.15).png|miniaturadeimagen|derecha|Figura 2.7]] | |||
'''Procedimiento''' | |||
\[ | |||
\frac{\partial}{\partial x} y(x,t)=k A \cos[kx - \omega t + \varepsilon] | |||
\] | |||
\[ | |||
\frac{\partial^2}{\partial x^2} y(x,t) = k^2 A \sin[kx - \omega t + \varepsilon] | |||
\] | |||
Vemos que en la segunda derivada aparece la primer derivada, al sustituirla se llega a la siguiente expresión: | |||
''' | '''Conclusión''' | ||
\[ | \[ | ||
\ | \ddot{y}=-k^2 y(x,t) \rightarrow \ddot{y}+k^2y=0 | ||
\] | \] | ||
Se observa que corresponde a la ecuación de un movimiento armónico simple realizado verticalmente. | |||
---- | |||
Realizado por: [[Usuario:Brenda Pérez Vidal|Brenda Pérez Vidal]] ([[Usuario discusión:Brenda Pérez Vidal|discusión]]) 16:49 27 mar 2014 (UTC) | |||
---- | |||
==Problema 2.28 5ta Edición== | |||
Escriba la expresión para la onda armónica de amplitud <math>10^{3}V/m</math> , periodo <math>2.2x10^{-15}s</math> ,y velocidad <math>3x10^{8}m/s</math> .La onda se propaga en la dirección negativa de X y tiene un valor de <math>10^{3}V/m</math> en t=0 y x=0.''' | |||
'''Procedimiento''' | |||
<math>\tau=2.2x10^{-15}s</math> | |||
\ | sabiendo que <math>\nu=\frac{1}{\tau}</math> | ||
<math>\nu=\frac{1}{2.2x10^{-15}s}=4.5x10^{14}Hz</math> | |||
obtenemos la longitud de onda con <math>v=\nu\lambda</math> | |||
es decir <math>\lambda=\frac{v}{\nu}=\frac{3.8x10^{8}m/s}{4.5x10^{14}Hz}</math> | |||
<math>\lambda=6.6x10^{-7}m</math> | |||
obtenemos K de la formula <math>k=\frac{2\pi}{\lambda}=9.5x10^{6}m^{-1}</math> | |||
\frac{\ | |||
Sabiendo que la expresión de la ecuación de onda es | |||
<math>\psi(x,t)=A\cos\left[kx+\omega t\right]</math> | |||
'''Conclusión''' | '''Conclusión''' | ||
sustituimos los datos antes encontrados para hallar la expresión que nos piden. | |||
<math>\psi(x,t)=\left(10^{3}\right)\cos\left[9.5x10^{6}\left(x+3x10^{8}t\right)\right]</math> | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Leticia González Zamora|Leticia González Zamora]] ([[Usuario discusión:Leticia González Zamora|discusión]]) 15:27 20 jun 2013 (CDT) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.29 5ta Edición== | ||
Considere el pulso descrito en términos de sus desplazamientos en $t=0$ por $y(x,t)|_{t=0}=\frac{C}{2+x^{2}}$ donde $C$ es una constante. Dibuje el perfil de onda. Escriba una expresión para la onda que tiene una velocidad $v$ en la dirección negativa de $x$, como función del tiempo $t$. Si $v=1\frac{m}{s}$, dibuje el perfil en $t=2s$. | |||
''' | '''Procedimiento''' | ||
De la expresión $y(x,t)|_{t=0}=\frac{C}{2+x^{2}}$ notamos que el | |||
máximo de la función se encuentra cuando $x=0$ y por tanto el máximo | |||
siempre estará en $y_{max}=\frac{C}{2}$. | |||
[[Archivo:Perfil11.png]] | |||
De la expresión anterior debido a que esta al tiempo $t=0$ la velocidad | |||
de la onda no contribuía, ahora bien la expresión para una onda con | |||
cierta velocidad para ester perfil esta dada por | |||
\[ | |||
y(x,t)=\frac{C}{2+(x+vt)^{2}} | |||
\] | |||
el sigo se debe a que queremos ver la onda desplazada a la izquierda | |||
o dirección negativa del $eje\; x$. | |||
La gráfica al tiempo $t=2s$ con una velocidad $v=1\frac{m}{s}$ se | |||
muestra a continuación. | |||
[[Archivo:Perfil123.png]] | |||
Nuevamente se toman 3 valores distintos para $C$. | |||
---- | |||
Realizado por: [[Usuario:Luis Miguel Sánchez Mtz.|Luis Miguel Sánchez Mtz.]] ([[Usuario discusión:Luis Miguel Sánchez Mtz.|discusión]]) 05:46 26 mar 2014 (UTC) | |||
---- | |||
==Problema 2.60 5ta Edición== | |||
Haga una tabla con columnas encabezadas por valores de $kx$ que va de $x=\frac{\lambda}{2}$ a $x=\lambda$ en intervalos de x de $\frac{\lambda}{4}$ en cada columna coloque los valores correspondientes de $\cos(kx)$ y debajo de eso los valores de cos(kx+ p). Luego grafique las tres funciones $\cos(kx)$, $\cos (kx + p)$. | |||
'''Tablas''' | |||
[[Archivo:tabla30.jpg|500px|thumb|center|]] | |||
[[Archivo:Graf30.jpg|400px|thumb|center|]] | |||
---- | |||
Problema resuelto por: [[Usuario:Luis Velázquez|Luis Velázquez]] ([[Usuario discusión:Luis Velázquez|discusión]]) 20:08 27 mar 2015 (CDT) | |||
---- | |||
= 3ra Edición en Español.= | |||
==Problema 2. | ==Problema 2.18 3ra Edición en español== | ||
Determine la magnitud de la función de onda''' $\psi(z,t)=Acos[k(z+vt)+\pi]$ '''en el punto''' $z=0$, '''cuanto''' $t=\frac{\tau}{2}$ '''y cuando '''$t=\frac{3\tau}{4}$. | |||
el | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Partimos de la ecuación de la onda | |||
\[ | |||
\ | \[\psi(z,t)=Acos[k(z+vt)+\pi]\] | ||
\] | |||
Evaluamos en $z=0$ y nos queda | |||
\[\psi(0,t)=Acos[kvt+\pi]\] | |||
Sustituimos $kv=\omega$ y entonces tenemos | |||
\[ | \[\psi(z,t)=Acos[\omega t+\pi]\] | ||
\ | |||
\] | |||
Pero como $-Acos[\omega t]=Acos[\omega t+\pi]$ tenemos que | |||
\[ | \[\psi(z,t)=-Acos[\omega t]\] | ||
\ | |||
\] | |||
'''Conclusión''' | '''Conclusión''' | ||
Finalmente sustituimos para $t=\frac{\tau}{2}$ y luego para $t=\frac{3\tau}{4}$ y obtenemos los resultados siguientes para cada caso. | |||
\ | $\psi(0,\frac{\tau}{2})=-Acos[\omega\frac{\tau}{2}]=-Acos(\pi)^{-1}=A$ | ||
y para $\psi(0,\frac{3\tau}{4})=-Acos[\omega\frac{3\tau}{4}]=-Acos(\frac{3}{4}\pi)=0$ | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Pedro Pablo Ramírez Martínez|Pedro Pablo Ramírez Martínez]] ([[Usuario discusión:Pedro Pablo Ramírez Martínez|discusión]]) 01:48 28 mar 2014 (UTC) | ||
---- | ---- | ||
==Problema 2.19 3ra Edición en español== | |||
¿La siguiente función en la que''' $A$ '''es una constante,''' $\psi(y,t)=(y-vt)A$ | |||
'''representa una onda? Explique su razonamiento.''' | |||
'''Procedimiento''' | '''Procedimiento''' | ||
$\;$ | |||
Como $\psi(y,t)=(y-vt)A$ es solo función de $(y-vt)$ cumple las | |||
\psi( | condiciones de una ecuación de onda, donde | ||
\ | \[ | ||
\frac{\partial^{2}\psi}{\partial y^{2}}=\frac{\partial^{2}\psi}{\partial t^{2}}=0 | |||
\] | |||
y así esta función es una solución a la ecuación de onda. Sin embargo, | |||
\[ | |||
\psi(y,0)=Ay, | |||
\] | |||
por lo que no puede representar un perfil de onda. | |||
---- | |||
Realizado por: [[Usuario:Luis Miguel Sánchez Mtz.|Luis Miguel Sánchez Mtz.]] ([[Usuario discusión:Luis Miguel Sánchez Mtz.|discusión]]) 06:50 22 mar 2014 (UTC) | |||
---- | |||
==Problema 2.20 3ra Edición en español== | |||
''' Utilice la ecuación (2.33) para calcular la velocidad de la onda cuya representación en unidades SI es $\psi(y,t) = A \cos\left[\pi\left(3x10^6 y + 9x10^{14} t\right)\right]$ ''' | |||
\psi( | |||
\ | |||
'''Procedimiento''' | |||
La ecuación (2.33) nos dice que: | |||
$ | |||
\left(\dfrac{\partial x}{\partial t}\right)_\varphi = \pm \dfrac{\omega}{k} = \pm v \hspace{20pt} \cdots \hspace{20pt} (2.33) | |||
$ | |||
pero nuestra representación está dada en términos de $\psi(y,t)$, por lo que podemos reescribir la ecuación como: | |||
\ | $ | ||
\left(\dfrac{\partial y}{\partial t}\right)_\psi = \pm \dfrac{\omega}{k} = \pm v | |||
\ | $ | ||
y también sabemos que la ecuación está dada en términos del siguiente cociente(ecuación 2.32 del texto con las variables adecuadas): | |||
$ | |||
\left(\dfrac{\partial y}{\partial t}\right)_\psi = \dfrac{-\left(\dfrac{\partial \psi}{\partial t}\right)_y}{\left(\dfrac{\partial \psi}{\partial y}\right)_t} \hspace{20pt} \cdots \hspace{20pt} (2.32) | |||
$ | |||
Calculando ahora las derivadas: | |||
$ | |||
\ | -\left(\dfrac{\partial \psi}{\partial t}\right)_y = - \left\{ - 9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] \right\} | ||
A(\ | = 9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] \\ | ||
\ | \left(\dfrac{\partial \psi}{\partial y}\right)_t = - 3x10^{6} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] | ||
$ | |||
Por lo que, sustituyendo en la ecuación (2.32): | |||
$ | |||
\left(\dfrac{\partial y}{\partial t}\right)_\psi = \dfrac{-\left(\dfrac{\partial \psi}{\partial t}\right)_y}{\left(\dfrac{\partial \psi}{\partial y}\right)_t} | |||
= \dfrac{9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right]}{- 3x10^{6} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right]} | |||
= - \dfrac{9x10^{14}}{3x10^{6}} | |||
$ | |||
Y realizando la operación obtenemos la velocidad deseada(en unidades SI como lo indica el enunciado): | |||
'''Conclusión''' | |||
$ | |||
v = \left(\dfrac{\partial y}{\partial t}\right)_\psi = -3x10^8 m/s = -c | |||
$ | |||
Donde el signo negativo($-$) indica que la dirección de propagación es hacia la izquierda. | |||
---- | |||
Realizado por: [[Usuario:Ivan de Jesús Pompa García|Ivan de Jesús Pompa García]] ([[Usuario discusión:Ivan de Jesús Pompa García|discusión]]) 00:50 27 mar 2015 (CDT) | |||
---- | |||
==Problema 2.21 3ra Edición en Español== | |||
( | Comenzando por el siguiente teorema: sí <math>Z=f_{(x,y)}</math>,<math>x=g_{(t)}</math> y <math>y=h_{(t)}</math> | ||
'''Procedimiento''' | |||
<math>\frac{\delta Z}{\delta t}=\frac{\partial Z}{\partial x}\frac{\delta x}{\delta t}+\frac{\partial Z}{\partial y}\frac{\delta y}{\delta t}</math> | |||
Derivar la ecuación: (2.34)''' | |||
<math>\left.v=-\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial y}}\right\} 2.35</math> | |||
En general tenemos que una función de onda cualquiera posee la forma. | |||
<math>\Psi_{(\bar{r},t)}=\psi</math> | |||
Sin perdida de generalidad consideramos el movimiento sobre un eje de propagación “y” | |||
<math>\Psi_{(y,t)}=\psi</math> | |||
Entonces por regla de la cadena (el teorema propuesto.) | |||
<math>\frac{\delta\psi}{\delta t}=\frac{\partial\psi}{\partial y}\frac{\delta y}{\delta t}+\frac{\partial\psi}{\partial t}\frac{\delta t}{\delta t}</math> | |||
De aquí sabemos que para una perturbación que no cambia con el tiempo: | |||
= | <math>\frac{\delta\psi}{\delta t}=0</math> | ||
Asimismo la diferencial del tiempo respecto al tiempo es uno, entonces, tras estas simplificaciones obtenemos. | |||
''' | <math>0=\frac{\partial\psi}{\partial y}\frac{\delta y}{\delta t}+\frac{\partial\psi}{\partial t}</math> | ||
'''Conclusión''' | |||
Despejando: <math>\frac{\delta y}{\delta t}=v</math> | |||
<math>v=-\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial y}}</math> | |||
La cual es la ecuación 2.34. | |||
---- | |||
Realizado por: [[Usuario:Andrés Arturo Cerón Téllez|Andrés Arturo Cerón Téllez]] ([[Usuario discusión:Andrés Arturo Cerón Téllez|discusión]]) 23:48 5 jul 2013 (CDT) | |||
---- | |||
'''Forma alternativa''' | |||
El problema yo lo realice de la siguiente manera: | |||
'''2.21. Empezando por el siguiente teorema: Si $z=f(x,y)$ y $x=g(t)$,''' | |||
'''$y=h(t)$, entonces:''' | |||
\[ | |||
\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} | |||
\] | |||
'''Derive la ecuación (2.34)''' | |||
Sabemos que la ecuación (2.34) es: | |||
\[ | |||
\pm v=-\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{t}} | |||
\] | |||
Ya que sabemos que | |||
\[ | |||
\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} | |||
\] | |||
Luego: | |||
\[ | |||
\left(\frac{d\psi}{d\varphi}\right)_{\varphi}=\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi}+\frac{\partial\psi}{\partial y}\frac{dy}{d\varphi} | |||
\] | |||
Y ya que en nuestro caso $\left(\frac{d\psi}{d\varphi}\right)$ es | |||
constante en $\varphi$, entonces la ecuación se vuelve | |||
\[ | |||
\text{-}\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}=\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi} | |||
\] | |||
\[ | |||
\frac{dx}{d\varphi}=-\frac{\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}} | |||
\] | |||
Pero ádemas, es posible reescribir a $\frac{dx}{d\varphi}=\frac{\partial x}{\partial t}\frac{dt}{d\varphi}$, | |||
asi: | |||
\[ | |||
\frac{\partial x}{\partial t}=-\frac{\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}} | |||
\] | |||
'''Conclusión''' | |||
Así finalmente, la ecuación se puede reescribir como: | |||
\[ | |||
\pm v=\left(\frac{\partial x}{\partial t}\right)_{\varphi}=-\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{t}} | |||
\] | |||
---- | |||
Realizado por: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21:29 (CDT) | |||
---- | |||
==Problema 2.22 3ra Edición en Español== | |||
Utilizando los resultados del problema anterior, demuestre que''' | |||
'''para una onda armónica con una fase $\varphi(x,t)=k(x-vt)$ podemos''' | |||
'''calcular la velocidad estableciendo $\frac{d\varphi}{dt}=0$.''' | |||
'''Aplique la técnica al problema 2.20 a fin de calcular la velocidad''' | |||
'''de dicha onda.''' | |||
'''Procedimiento''' | |||
Veamos primero que dicha fase cumple con la definición, entonces tenemos | |||
lo siguiente: | |||
\[ | |||
\psi(x,t)=Asen(k(x-vt)) | |||
\] | |||
[ | \[ | ||
\frac{\partial\psi}{\partial x}=kAsen(k(x-vt)) | |||
\] | |||
-- | \[ | ||
\frac{\partial\psi}{\partial t}=-kvAsen(k(x-vt)) | |||
\] | |||
Luego: | |||
\[ | |||
-\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial x}}=-\frac{(-kv)Asen(k(x-vt))}{kAsen(k(x-vt))}=v | |||
\] | |||
$ | Por lo cuál, la función cumple con la definición. Ahora veamos que | ||
si $\frac{d\varphi}{dt}=0$ entonces la función sigue cumpliendo. | |||
Del problema (2.21) tenemos que por definición: | |||
\[ | |||
\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}=\frac{d\psi}{d\varphi}-\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi} | |||
\] | |||
\[ | |||
\frac{\partial x}{\partial t}=\frac{\frac{d\psi}{d\varphi}-\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}} | |||
\] | |||
'''Conclusión''' | |||
\[ | |||
\frac{\partial x}{\partial t}=\frac{\frac{d\psi}{d\varphi}\frac{d\varphi}{dt}\frac{dt}{d\varphi}-\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}}=-\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial t}} | |||
\] | |||
---- | |||
Aportación de: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21:36 (CDT) | |||
---- | |||
==Problema 2.23 3ra Edición en Español== | |||
$ | Una onda gaussiana, tiene la forma $\psi(x,t)=A^{-a(bx+ct)^{2}}$. Utilice | ||
el que $\psi(x,t)=f(x\pm vt)$''' '''para calcular su velocidad, comprobando | |||
luego su respuesta con la ecuación (2.3).''' | |||
'''Procedimiento''' | |||
Se utiliza la siguiente definición de velocidad: | |||
\[ | |||
\pm v=-\left(\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{y}}\right) | |||
\] | |||
Se resuelven ambas partes de la ecuación por separado: | |||
= | \[ | ||
\psi_{x}=(-2a)A(b)e^{-(abx+ct)^{2}} | |||
\] | |||
\[ | |||
\psi_{y}=-(2a)Ace^{-(bx+ct)^{2}} | |||
\] | |||
'''Conclusión''' | |||
Al sustituir los resultados obtenidos en la definición de velocidad: | |||
\[ | |||
v=\frac{(-2a)Ace^{-(abx+ct)^{2}}}{(-2a)Abe^{-(abx+ct)^{2}}}=\frac{c}{b} | |||
\] | |||
Se obtiene el resultado de la ecuación 2.3: $v=\frac{c}{b}$ | |||
---- | |||
Realizado por: [[Usuario:Ana Alarid|Ana Alarid]] ([[Usuario discusión:Ana Alarid|discusión]]) 18:43 27 mar 2014 (UTC) | |||
---- | |||
==Problema 2.24 3ra Edición en Español== | |||
Encuentre una expresión para el perfil de una onda armónica que viaja en la dirección de $z$ cuya magnitud en $z=-\frac{\lambda}{12}$ es 0.866, en $z=+\frac{\lambda}{6}$ es $\frac{1}{2}$ y en $z=\frac{\lambda}{4}$ es 0. | |||
'''Procedimiento''' | |||
$ | Utilizamos la función de onda armónica en el que $t=0$ puesto que $\varepsilon$ es una contribución constante a la fase y además es independiente del recorrido de la onda en términos de espacio y de tiempo: | ||
\begin{equation} | |||
\psi(z,0)=Asen(kz+\varepsilon); | |||
\end{equation} | |||
Donde $\psi$ es la propagación de la onda, $A$ es la amplitud, $k$ es el número de onda que está dada por $k=\frac{2\pi}{\lambda}$, $z$ corresponde a la dirección de propagación y $\varepsilon$ es la fase inicial. | |||
A continuación escribimos las condiciones iniciales: | |||
\begin{equation} | |||
\psi(-\frac{\lambda}{12},0)=Asen(-\pi/6 + \varepsilon)=0.866 ....(I) | |||
\end{equation} | |||
\begin{equation} | |||
\psi(\frac{\lambda}{6},0)=Asen(-\pi/3 + \varepsilon)=\frac{1}{2} ....(II) | |||
\end{equation} | |||
\begin{equation} | |||
\psi(\frac{\lambda}{4},0)=Asen(-\pi/2 + \varepsilon)=0 ....(III) | |||
\end{equation} | |||
Para obtener el valor numérico de $\psi$ es necesario encontrar los valores para $\varepsilon$ y por consiguiente la amplitud $A$ y en conclusión obtener el perfil que se nos pide. | |||
Para ello utilizamos la expresión $(III)$ puesto que es más sencilla de manipular y está igualada a 0. Utilizamos la identidad trigonométrica de suma de dos ángulos que involucra a senos y cosenos. | |||
\begin{equation} | |||
A=sen(\pi/2+\varepsilon)=A[sen(\pi/2)cos(\varepsilon)+cos(\pi/2)sen(\varepsilon)] | |||
\end{equation} | |||
Simplificamos | |||
\begin{equation} | |||
=Acos(\varepsilon)=0 | |||
\end{equation} | |||
Despejamos $\varepsilon$ y obtenemos su valor | |||
\begin{equation} | |||
\varepsilon=\frac{\pi}{2} | |||
\end{equation} | |||
Ahora bien para encontrar $A$ podemos utilizar la expresión $(I)$ o $(II)$. Utilizando la expresión $(II)$ y sustituyendo el valor encontrado para $\varepsilon$: | |||
== | \begin{equation} | ||
Asen(\pi/3 + \pi/2)=Asen(5\pi/6)=\frac{1}{2} | |||
\end{equation} | |||
Así | |||
\begin{equation} | |||
A(\frac{1}{2})=\frac{1}{2}; A=1 | |||
\end{equation} | |||
''' | '''Conclusión''' | ||
Por lo tanto, la expresión para el perfil de una onda armónica que viaja en la dirección de $z$ es: | |||
es | |||
\begin{equation} | |||
\psi(z,0)=sen(kz+\pi/2) | |||
\end{equation} | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Angel Nahir Molina Guadarrama|Angel Nahir Molina Guadarrama]] ([[Usuario discusión:Angel Nahir Molina Guadarrama|discusión]]) 01:37 23 mar 2014 (UTC) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.26 3ra Edición en Español== | ||
Establezca cuáles de las expresiones siguientes describen ondas '''viajeras:''' | |||
(a) $\psi(y,t)=\exp-(a^{2}y^{2}+b^{2}t^{2}-2aybt)$ | |||
(b) $\psi(z,t)=Asen(az^{2}-bt^{2})$ | |||
(c) $\psi(x,t)=Asen2\pi\left(\frac{x}{a}+\frac{t}{b}\right)^{2}$ | |||
(d) $\psi(x,t)=Acos^{2}2\pi(t-x)$ | |||
'''Procedimiento''' | '''Procedimiento''' | ||
Para la onda (a), si la reescribimos como sigue: | |||
$\psi(y,t)=\exp-(a^{2}y^{2}+b^{2}t^{2}-2aybt)\Rightarrow\exp-a^{2}(y-\frac{b}{a}t)^{2}$ | |||
'''Es evidente que se trata de una onda viajera, ya que cumple con las | |||
características de una.''' | |||
Para la onda (b), es claro que no se comporta como una onda viajera, | |||
ya que la función no es lineal, una característica de las ondas viajeras. | |||
Para la | '''Para la onda (c), es viajera, por que el término dentro del argumento | ||
es lineal, y nos dice que la onda se desplaza en una dirección diferente, | |||
hacia la izquierda.''' | |||
Para la onda (d), no es viajera, por que la función $cos^{2}(x)$ | |||
no cumple con la definición de onda viajera. | |||
---- | ---- | ||
Realizado por: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21: | Realizado por: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21:37 (CDT) | ||
---- | ---- | ||
==Problema 2. | ==Problema 2.31 3ra Edición en Español== | ||
Trabajando directamente con exponenciales, demuestre que la magnitud de $\psi=A\exp iwt$ es A. A continuación, vuelva a calcular el mismo resultado utilizando la fórmula de Euler, demuestre que $e^{i\left ( \alpha \right )}e^{i\left ( \beta \right )}=e^{i\left ( \alpha + \beta \right )}$ | |||
'''Usando exponenciales''' | |||
Sabemos que la magnitud de $\psi$ sera igual a su modulo, es decir: | |||
$|\psi|=\left (\psi\psi* \right )^{\frac{1}{2}}$ y que $\psi*=A\exp-iwt$ por | |||
definición. | |||
Luego: | |||
$|\psi|=\left[\left(A\exp iwt\right)\left(A\exp-iwt\right)\right]^{\frac{1}{2}}=\left[A^{2}\exp iwt-iwt\right]^{\frac{1}{2}}=\left(A^{2}\exp0\right)^{\frac{1}{2}}=A$ | |||
Ahora, usando la fórmula de Euler, tenemos que: | |||
$|\psi|=\left[\left(A\exp iwt\right)\left(A\exp-iwt\right)\right]^{\frac{1}{2}}$ | |||
$|\psi|=\left[A(coswt+isenwt)A(coswt-isenwt)\right]^{\frac{1}{2}}$ | |||
$|\psi|=\left[A^{2}\left(cos^{2}wt-isen(wt)cos(wt)+isen(wt)cos(wt)+sen^{2}wt\right)\right]^{\frac{1}{2}}$ | |||
$|\psi|=\left[A^{2}(cos^{2}wt+sen^{2}wt)\right]^{\frac{1}{2}}=(A^{2})^{\frac{1}{2}}=A$ | |||
'''Usando la formula de Euler''' | |||
Demostremos ahora que $e^{i\left ( \alpha \right )}e^{i\left ( \beta \right )}=e^{i\left ( \alpha + \beta \right )}$ | |||
$e ^{i\alpha} e ^{i\beta} = \left(cos\alpha+isen\alpha\right)\left(cos\beta+isen\beta\right)$ | |||
$e^{i\alpha}e^{i\beta}=cos\alpha cos\beta+icos\alpha sen\beta-icos\beta sen\alpha+i^{2}sen\beta sen\alpha$ | |||
$e ^{i\alpha} e^{ i\beta}=\cos\alpha cos\beta+icos\alpha sen\beta-icos\beta sen\alpha-sen\beta sen\alpha=(cos\alpha cos\beta-sen\alpha sen\beta)+i(cos\alpha sen\beta+sen\alpha cos\beta)$ | |||
$e^{i\alpha} e^{i\beta} =cos(\alpha+\beta)+isen(\alpha+\beta)=e^{i(\alpha+\beta)}$ | |||
---- | ---- | ||
Realizado por: [[Usuario: | Realizado por: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21:38 (CDT) | ||
---- | ---- | ||
==Problema | ==Problema 2.32 3ra Edición en Español== | ||
Demuestre que la parte imaginaria de un número complejo z esta dada por $\left(z-z^{\star}\right)/2i$.''' | |||
'''Solución''' | |||
Sea z perteneciente a los complejos | |||
$z=a+ib$ | |||
y su conjugado | |||
$z^{\star}=a-ib$ | |||
entonces: | |||
$z-z^{\star}=a+ib-(a-ib)$ | |||
$z-z^{\star}=2ib$ | |||
Dividimos entre $2i$ | |||
$z-z^{\star}/2i=2ib/2i$ | |||
'''Conclusión''' | |||
$\left(z-z^{\star}\right)/2i=b$ | |||
que es la parte imaginaria del número complejo $z=a+ib$. | |||
---- | |||
Realizado por: [[Usuario:Edgar Ortega Roano|Edgar Ortega Roano]] ([[Usuario discusión:Edgar Ortega Roano|discusión]]) 17:43 18 mar 2014 (CDT) y [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] ([[Usuario discusión:Cesar Ivan Avila Vasquez|discusión]]) 21:53 26 Marzo 2014 (UTC) | |||
---- | |||
==Problema 2.34 3ra Edición en Español== | |||
'''Demuestre que las ecuaciones $\psi(x,y,z,t)=f(\alpha x+\beta y+\gamma z-vt)$ y $\psi(x,y,z,t)=f(\alpha x+\beta y+\gamma z+vt)$ que son ondas planas de forma arbitraria, cumplen con la ecuación diferencial de onda tridimensional.''' | |||
'''Solución:''' | |||
De la ecuación de onda tridimensional ,$\nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial t^{2}}$, obtenemos el Laplaciano para nuestras ecuaciones, así $\nabla^{2}\psi=\alpha^{2}f^{´´}+\beta^{2}f^{´´}+\gamma^{2}f^{´´}$ | |||
es el Laplaciano para ambas ecuaciones. | |||
Ahora al calcular $\frac{\partial^{2}\psi}{\partial t^{2}}$ obtenemos que $\frac{\partial^{2}\psi}{\partial t^{2}}=v^{2}f^{´´}$ para ambas ecuaciones. | |||
Por lo que al sustituir en la ecuación de onda tridimensional obtenemos. | |||
$f^{´´}(\alpha^{2}+\beta^{2}+\gamma^{2})=f^{´´}$ | |||
Por lo que para cualquier onda tridimensional se debe cumplir que $\alpha^{2}+\beta^{2}+\gamma^{2}=1$. | |||
---- | |||
Realizado por: [[Usuario:Edgar Ortega Roano|Edgar Ortega Roano]] ([[Usuario discusión:Edgar Ortega Roano|discusión]]) 17:52 18 mar 2014 (CDT) | |||
---- | |||
==Problema 2.35 3ra Edición en Español== | |||
La hipótesis de De Broglie afirma que cada partícula tiene asociada''' | |||
'''a ella una longitud de onda dada por la constante de Planck ($h=6.6x10^{-34}Js$),''' | |||
'''dividida por el momento de la partícula.''' | |||
'''Compare la longitud de onda de una piedra de 6.0 kg moviéndose a una''' | |||
'''velocidad de 1 m/s con la de la luz.''' | |||
''' | '''Procedimiento''' | ||
Tenemos que: | |||
\[ | |||
\lambda=\frac{h}{p} | |||
\] | |||
Para la piedra tenemos entonces que: | |||
\[ | |||
\lambda=\frac{6.6x10^{-34}Js}{(6kg)(1m/s)}=1.1x10^{-34}m | |||
\] | |||
Y sabemos ademas que la longitud de onda de la luz se encuentra en | |||
un intervalo de $\lambda=\left[3.8,7.5\right]x10^{-7}m$, entonces, | |||
comparando ambas longitudes de onda notamos que la asociada a la piedra | |||
es mucho más pequeña que la de la luz, si la longitud de onda de la | |||
luz fuera más pequeña que la de la piedra, la luz atravesaría la piedra. | |||
---- | |||
Realizado por: [[Usuario:Cesar Ivan Avila Vasquez|Cesar Ivan Avila Vasquez]] 23 Marzo 2014 21:40 (CDT) | |||
---- | |||
==Problema 2.37 3ra Edición en Español== | |||
<math>\ | Escriba una expresión en coordenadas cartesianas para una onda plana armónica de amplitud <math>A</math> y frecuencia <math>\omega</math> que se propaga en dirección positiva de <math>x</math>. | ||
'''Procedimiento''' | |||
<math>\ | Primero se escribe un vector de posición <math>\textbf{r}=x \hat{\mathbf{e}}_x+y \hat{\mathbf{e}}_y+z \hat{\mathbf{e}}_z</math> que comienza en el origen y termina en cualquier otro punto <math>(x,y,x)</math>. | ||
De esta forma, lo podemos escribir como | |||
<math>(\textbf{r}-\textbf{r}_{0})=(x-x_{0})\hat{\mathbf{e}}_x+(y-y_{0})\hat{\mathbf{e}}_y+(z-z_{0})\hat{\mathbf{e}}_z</math> y | |||
-- | <math>(\textbf{r}-\textbf{r}_{0})\cdot\textbf{k}=0</math> donde obligamos al vector <math>(\textbf{r}-\textbf{r}_{0})</math> a barrer un plano perpendicalar a <math>\hat{\mathbf{e}}_x</math> | ||
al ir adquiriendo su punto exremo <math>(x,y,z)</math> com <math>i=i_{x}\hat{\mathbf{e}}_x+i_{y}\hat{\mathbf{e}}_y+i_{z}\hat{\mathbf{e}}_z</math> que se puede escribir también como | |||
<math>i_{x}(x-x_{0})+i_{y}(y-y_{0})+i_{z}(z-z_{0})=0</math> | |||
o también | |||
<math>i_{x}x+i_{y}y+i_{z}z=a</math> donde <math>a=cte</math> | |||
Asi un plano perpendicular a <math>i</math> es <math> </math> <math>\textbf{i}\cdot\textbf{r}=a</math> | |||
Tomemos la funcion <math>\psi{(r)}=A\sin{(\textbf{i}\cdot\textbf{r})}</math> | |||
<math>\psi{(r)}=Acos{(\textbf{i}\cdot\textbf{r})}</math> | |||
o <math>\psi{(r)}=Ae^{i\hat{\imath}\cdot\textbf{r}}</math> | |||
y la función armónica se puede escribir como | |||
<math>\psi{(r)}=\psi{(r+\frac{\lambda \hat{\imath}}{k})}</math> | |||
Para que esta función sea cierta se debe tener que | |||
<math>e^{i\lambda \hat{\imath}}=e^{i2\pi}</math> | |||
Por consiguiente <math>\lambda i = 2\pi</math> | |||
despejando <math>i</math> se tiene <math>i= \frac{2\pi}{\lambda}</math> | |||
Se tiene entonces que | |||
<math>\psi{(r,t)}=Ae^{i(\hat{\imath}\cdot\textbf{r}\pm\omega t)}</math> | |||
Para que esta función este orientada sobre el eje <math>x</math> solo se toma la coordenada <math>x</math> del vector <math>\vec{r}</math> | |||
'''Conclusión''' | |||
<math> | <math>\psi{(r,t)}=Ae^{i(ix\pm\omega t)}</math> asi que | ||
<math> | <math>\psi{(x)}=Ae^{i(ix\pm\omega t)}</math> | ||
Por tanto esta es la onda armónica en coordenadas cartesianas que se propaga en el eje <math>x</math>. | |||
---- | |||
Realizado por: Hector resendiz [[Usuario:Héctor Reséndiz|Héctor Reséndiz]] ([[Usuario discusión:Héctor Reséndiz|discusión]]) 19:23 29 mar 2015 (CDT) Libro hecht | |||
---- | |||
== Problema 2.42 3ra Edición en Español == | |||
'''Escriba una expresión en coordenadas cartesianas para una onda plana armónica de amplitud $A$ y frecuencia $w$, que se propaga en la dirección del verctor $\overrightarrow{k}$, que a su vez, se encuentra en una línea que va desde el origen hasta el punto $(4,2,1)$. Hint: primero calcule $\overrightarrow{k}$ y luego haga el producto escalar con $\overrightarrow{r}=x\hat{i} + y\hat{j} + z\hat{k}$. ''' | |||
'''Procedimiento''' | |||
para obtener el vector $\overrightarrow{k}$ necesitamos encontrar un vector unitario en la dirección que nos piden y multiplicándolo por $k$. el vector unitario es: | |||
<math> | <math>\hat{a}= \frac{\left[(4-0)\hat{i} + (2-0)\hat{j} + (1-0)\hat{k} \right]}{\sqrt{4^2 + 2^2 + 1^2}}= \frac{4\hat{i} + 2\hat{j} + 1\hat{k}}{\sqrt{21}} </math> | ||
ahora el vector $\overrightarrow{k}$ está dado por: | |||
<math>\overrightarrow{k}= k*\hat{a}=\frac{k*(4\hat{i} + 2\hat{j} + 1\hat{k})}{\sqrt{21}}</math> | |||
la expresión en coordenadas cartesianas de una onda plana armónica viene dada por: | |||
<math>\psi (x,y,z,t)=A*sen(\overrightarrow{k}\cdot \overrightarrow{r} - wt)</math>: | |||
'''Conclusión''' | |||
<math>\psi | <math>\therefore \psi (x,y,z,t)=A*sen \left[\frac{4k}{\sqrt{21}}x + \frac{2k}{\sqrt{21}}y + \frac{k}{\sqrt{21}}z - wt\right]</math> | ||
---- | |||
Realizado por: [[Usuario:Luis Martínez|Luis Martínez]] ([[Usuario discusión:Luis Martínez|discusión]]) 17:05 27 mar 2015 (CDT) | |||
---- | |||
=Problemas Adicionales= | |||
== Problema Adicional 1 == | |||
'''La ecuación de onda transversal que se mueve a lo largo de una cuerda está dada por:''' | |||
<math>\Psi(z,t)=0.3\sin\pi\left(0.5z-50t\right) | |||
</math> | |||
'''Hallar la amplitud, la longitud de onda, el número de ondas, la frecuencia, el período y la velocidad de onda. ''' | |||
'''Solución''' | |||
Usando la ecuación | |||
\[ | |||
\psi=A\sin2\pi\left(kz\pm\nu t\right) | |||
\] | |||
\[ | |||
\psi=A\sin\pi\left(2kz\ - 2\nu t\right) | |||
\] | |||
La amplitud: | |||
<math>A=0.3m</math> | |||
Longitud de onda | |||
<math>0.5=\frac{2}{\lambda}</math> | |||
<math>\lambda=4m</math> | |||
Número de onda | |||
<math> | <math>2k=0.5</math> | ||
entonces | |||
<math>\ | <math>k=\frac{0.5}{2}</math> | ||
<math>k=0.25m^-1</math> | |||
La velocidad de onda | |||
<math>v=(2) (50)</math> | |||
<math>v=100 m/s</math> | |||
Tomado de : Vibraciones y ondas. A. P. FRENCH pág. 277. Problema 7-2. | |||
---- | |||
Resuelto por: [[Usuario:Luis Velázquez|Luis Velázquez]] ([[Usuario discusión:Luis Velázquez|discusión]]) 10:56 26 mar 2015 (CDT) | |||
---- | |||
== Problema adicional 2== | |||
Física General 10° Edición, Frederick J. Bueche. Eugene Hetch. | |||
= | '''Una onda se propaga por una cuerda según la ecuación $ y = 0.2\sin(6\pi t + \pi x + \dfrac{\pi}{4})$. Calcular:''' | ||
''' | '''a) La frecuencia, el periodo, la longitud de onda y la velocidad de propagación.''' | ||
'''b) El estado de vibración, la velocidad y aceleración de una partícula situada en x = 0.2 m en 0.3 s ''' | |||
'''c) La diferencia de fase entre dos puntos separados 0.3 m''' | |||
'''Inciso a''' | |||
$y | a) La forma general de la ecuación de onda $y(x, t)= A \sin(\omega t + Kx +\delta)$ | ||
$ | Partiremos de la frecuencia angular $\omega = 2 \pi ; f = 6\pi rad/s ; f= 3 Hz $ | ||
El periodo $ T = \dfrac{1}{f}= 0.333s$ | |||
$ | Para la velocidad usamos $c= \dfrac{\omega}{k} = \dfrac{6\pi}{\pi} = 6 m/s $ | ||
'''Inciso b''' | |||
b) Para x = 0.2 m, t= 0.3s. | |||
$y= 0.2\sin(6\pi*0.3 + \pi*0.2 + \dfrac{\pi}{4})= 0.2 \sin(7.069) = 0.1414 m $ | |||
$ | Velocidad $\dfrac{dy}{dx} = 0.2 *6 \pi \cos (6 \pi t + \pi x \dfrac{\pi}{4})= 0.2*6 \pi \cos (7.069)= 2.66 m/s$ | ||
Aceleración $\dfrac{d^{2}y}{dt^{2}}= -0.2(36\pi^{2})\sin(6\pi t + \pi x + \dfrac{\pi}{4} = 0,2(36\pi^{2}cos (7.069)= -50.25 m/s^{2}$ | |||
'''Inciso c''' | |||
c) $\vartriangle x= 0.3 m$ | |||
. | |||
$\delta_{1} = 6 \pi t + \pi x + \dfrac{\pi}{4}$ | |||
$\vartriangle \delta = \delta_{2} - \delta_{1}= 0.3\pi rad $ | |||
$\delta_{2} = 6 \pi t + \pi (x + 0.3) + \dfrac{\pi}{4}$ | |||
---- | |||
Realizado por: [[Usuario:Esther Sarai|Esther Sarai]] ([[Usuario discusión:Esther Sarai|discusión]]) 18:25 28 mar 2015 (CDT)Esther Sari García González | |||
---- | |||
3 | ==Problemas adicional 3== | ||
Un foco genera ondas de 2 mm de amplitud con una frecuencia de 250 Hz, que se propagan por un medio con una velocidad de 250 m/s. Determina el periodo y la longitud de onda de la perturbacion. Si en el instante inicial la elongacion de un punto situado a 3 m del foco es $y = -2 mm$, determina la elongacion de un punto situado a 2,75 m del foco en el mismo instante. | |||
Un foco | |||
Periodo: $T=\frac{1}{f}=\frac{1}{250}=4\times 10^{-3}$s | |||
Frecuencia angular: $w=2\pi f= 500\pi$ $rad/s$ | |||
Longitud de onda: $\lambda=\frac{v}{f}=\frac{250}{250}=1m$ | |||
numero de onda: $k=\frac{2\pi}{\lambda}=2\pi$ $m^{-1}$ | |||
En este caso y como los datos de vibracion no son los del foco, debe introducirse una fase inicial $\phi_0$ que se determina con las condiciones de vibracion del punto x = 3 m. | |||
$y = A Cos(wt-kx+ \phi_0 ) =2 \times 10^{-3} | |||
Cos(500\pi t-2 \pi x+\phi_0)$ | |||
Operando: | |||
$y=2\times 10^{-3}Cos[2\pi(250t-x) + \phi_0]$ | |||
Sustituyendo los datos de vibracion del punto considerado, resulta que: | |||
$y(x=3, t=0)=y=2\times 10^{-3}Cos[2π(250(0)-3) + ϕ0]=2\times 10^{-3}m \rightarrow Cos(-6\pi +\phi_0)=-1$ | |||
Por lo que la fase inicial es: $\phi_0= \pi$ rad | |||
La ecuacion general de la onda es: | |||
$y=2\times 10^{-3}Cos[2\pi(250t-x)+\pi]$ | |||
La elongacion del punto x = 2,75 m en el instante pedido es: | |||
$y(x=2.75, t=0)=y=2\times 10^{-3}Cos[2π(250(0)-2.75)+\pi]=Cos(6.5\pi)=0m$ | |||
---- | |||
--[[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez | [[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez | ||
[[Usuario:Estefaniantin|Estefaniantin]] | [[Usuario:Estefaniantin|Estefaniantin]] | ||
---- | |||
== Problema Adicional 4 == | |||
Un oscilador vibra con una frecuencia de 500 Hz y genera ondas que | |||
se propagan con una velocidad de 350 m/s. | |||
1. La separacion de dos puntos consecutivos que vibren con una diferencia | |||
de fase de 60 | |||
2. El intervalo de tiempo que transcurre entre dos estados de vibracion | |||
consecutivos de un punto con una diferencia de fase de 180 | |||
. | |||
3. Diferencia de fase en un instante cualquiera entre dos puntos separados | |||
por una distancia de 3,15 m. | |||
1.-Para hallar la separacion de los funtos con un $\phi$=60 lo cual | |||
es equivalente a $\frac{\pi}{3}$ rad | |||
sabiendo que $\lambda=\frac{\upsilon}{v}$=$\frac{500Hz}{350m/s}$=.7m | |||
Por una regla de proporcionalidad a 2$\pi$le corresponden $\lambda=.7m,$por | |||
lo que la separacion de los puntos $\triangle x=\frac{\pi}{3}$$\lambda$$\frac{1}{2\pi}$=.117m | |||
2.-Del mismo modo por una regla de proporcionalidad como T=$\frac{1}{\nu}$=$\frac{1}{500Hz}$=2$^{-3}$s | |||
$\triangle t=$$\frac{\pi T}{2\pi}$=$\frac{2(10^{-3})\pi s}{2\pi}$=10$^{-3}s$ | |||
3.- Se busca un $\triangle\varphi\triangle\varphi=T\frac{\triangle x}{\lambda}$y | |||
usando los valores del punto 1 se obtiene que $\triangle\varphi$=2$\pi\frac{.117m}{.7m}$=2.1 | |||
---- | |||
[[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez | |||
[[Usuario:Estefaniantin|Estefaniantin]] | |||
---- | |||
== Problema adicional 5 == | |||
Un foco F1 situado en el punto de coordenadas (0,0) entre ondas armónicas transversales de frecuencia 500Hz y amplitud 0.3m. Las ondas se propagan en el sentido positivo del eje x con una velocidad de 250 m/s. | |||
donde de la | ¿Cual es la longitud de onda y el periodo de las ondas emitidas?. Escribir la función de onda | ||
V= 500 Hz , A= 0.3 m, v= 250m/s , donde | |||
<math>\lambda=\frac{v}{V}= \frac{250}{500}= 0.5 m </math> es la longitud de onda | |||
<math>T=\frac{1}{V}=\frac{1}{500}= 2x10^{-3}s</math> es el periodo | |||
La expresión general para la función de onda es | |||
<math>y(x,t)=Asen(kx-\omega (t))</math> | |||
<math>\frac{2\pi}{(\lambda)}=4\pi rad m^-1</math> | |||
<math>\omega=2\pi V= 2\pi 500 = 1000 \pi rad s^-1</math> | |||
<math> y1(x,t)= 0.3 sen ( 4\pi - 1000\pi) m</math> | |||
--[[Usuario: | ---- | ||
[[Usuario:Luisa Alejandra Vega Sanchez|Luisa Alejandra Vega Sanchez]] ([[Usuario discusión:Luisa Alejandra Vega Sanchez|discusión]]) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez | |||
[[Usuario:Estefaniantin|Estefaniantin]] | |||
---- | |||
[[categoría:ondas]] | |||
Revisión actual - 05:20 5 oct 2023
Problemas capítulo 2 Óptica Hecht, Movimiento Ondulatorio
Ejercicios resueltos acerca del movimiento ondulatorio. Incluye problemas de libro de Óptica de Eugene HECHT, de sus diversas ediciones tanto en inglés como en español, así como problemas adicionales acerca de este tema.
Algunas ediciones del Hetch, tienen distintas numeraciones para problemas idénticos.
Primeras Ediciones (1°,2°,3°) en Ingles.
Problema 2.9(Hecht 1ra edición)
Considere una onda luminosa teniendo una velocidad de fase de $3\times10^{8}\frac{m}{s}$ y una frecuencia de $6\times10^{14}Hz.$ Encontrar: la frecuencia angular, el valor del número de propagación $k$, la longitud de onda y comprobar que esta onda se encuentre dentro del espectro de luz visible. ¿Qué desplazamiento de fase ocurre en un punto dado a $10^{-6}s$, y cuántas ondas han pasado hasta ese momento?
SOLUCIÓN:
Consideramos la ecuación de la propagación de onda:
\[ \psi(x,t)=Asen(kx-\omega t+\varepsilon) \]
donde \varepsilon=0 dado que consideraremos que la fase inicial
$\varepsilon$ es nula. Por lo que:
\[ \psi(x,t)=Asen(kx-\omega t)......(1) \]
Para obtener el valor del número de propagación consideramos que la
velocidad de fase $V_{\phi}=\frac{\omega}{k}\Longrightarrow k=\frac{\omega}{V_{\phi}}$
y sabemos que $\omega=2\pi\upsilon$ donde $\upsilon$ es la conocida
frecuencia por lo que substituyendo tendremos:
\[ \omega=2\pi(6\times10^{14})=12\times10^{14}\pi\frac{rad}{seg} \]
Y por lo tanto:
\[ k=\frac{\omega}{V_{\phi}}=\frac{12\times10^{14}\pi}{3\times10^{8}}=4\times10^{6}\pi \]
De aquí sabremos que la longitud de onda $\lambda$ dada por \lambda=\frac{2\pi}{k}
será:
\[ \lambda=\frac{2\pi}{4\times10^{6}\pi}=500\times10^{-9}=500nm \]
y como en el espectro monocromático la luz visible va desde los 400nm
hasta los 700nm, aproximadamente, se comprueba entonces que esta onda
está dentro el rango del espectro visible de la luz.
Para calcular el desplazamiento de fase recurrimos la ec.(1) donde el tiempo es dado y donde ya conocemos la frecuencia:
\[ \psi(x,t)=Asen(kx-\omega t) \]
Y el desplazamiento de fase es $x=(V_{\phi})(t)=(3\times10^{8})(10^{-6})=3\times10^{2}$
Para calcular el número de ondas que han pasado en ese tiempo, simplemente calculamos para $\omega$; si sabemos cuanto pasa en un segundo sólo multiplicamos $\omega$ por $10^{-6}seg$, así:
\[ (12\times10^{14}\pi)(10^{-6})=12\times10^{8} \] que es el número de ondas que han pasado en ese intervalo de tiempo.
Realizado por: A. Martín R. Rabelo (discusión) 01:34 30 mar 2015 (CDT)
Problema 2.18 2da Edición
Dada la ecuación de onda , determina la dirección de propagación.
Procedimiento
Calcule algunos valores de y haz un bosquejo de la onda en t=0 dado y . ¿Cual es la velocidad de la onda?
De las gráficas de la derecha y no siendo una onda ondas armónicos en forma de coseno o seno, se ve que el la onda se va desplazando hacia la izquierda cuando en este caso t va desde t=0s hasta t =1s
Para la velocidad de onda se hace uso de la misma ecuación diferencial de onda y se despeja de esta misma ecuación la velocidad. Así tenemos:
: : : :
Factorizando el exponenciales las dos segundas derivadas se tiene:
;
Que al hacer la división se elimina y ahora ademas factorizando del termino restante :
:
Conclusión
Que finalmente resulta en que v=0.6 rad/s
Realizado por: Uziel Sanchez Gutierrez (discusión) 17:38 30 mar 2015 (CDT) Hecho por Uziel Sanchez Gutierrez
4ta Edición en Ingles.
Problema 2.1 4ta Edición.
2.1¿Cuantas ondas de luz amarillas () caben en una distancia en el espacio igual a un trozo de papel de (0.003 pulgadas)? ¿Hasta donde se extenderá el mismo número de microondas , es decir, y ?
Para responder a la primera pregunta, basta con dividir el espesor del papel con el de la longitud de onda dada, es decir:
Una microonda con frecuencia de tiene una longitud de onda de
$\displaystyle{\lambda=\frac{c}{\nu}=\frac{3x10⁸}{10 GHz}=0.03m}$
Por lo tanto 131 ondas con dicha longitud se extenderán
$\displaystyle{extensión=(131)(0.03m)=3.93 m}$
Realizado por: Pérez Córdoba Sabino (discusión) 20:28 17 mar 2014 (UTC)
Problema 2.1 Solución Secundaria
¿Cuántas ondas de luz <<amarillas>> $(\lambda=580nm)$ caben en una distancia en el espacio igual al espesor de un trozo de papel $(0.003 pulgadas)$? ¿Hasta dónde se extenderá el mismo número de microondas $(\nu=10^{10}Hz$, es decir, $10GHz$ y $v=3x10^8m/s)$?
Solución
La longitud de onda es la relación entre la velocidad de la onda y su frecuencia, que está dada por;
Donde $v$ es la velocidad de la onda y $\nu$ es la frecuencia de la onda. La distancia $d$ recorrida por la onda es:
Donde $k$ es el número de ondas propagadas, y $\lambda$ es la longitud de onda.
ahora para saber cuántas ondas caben en el espesor del trozo de papel, convierto la longitud de onda de la luz amarilla a metros:
después convierto el espesor del papel en metros:
calculamos el numero de ondas en la distancia en el espacio del espesor del papel, utilizamos lo que ya sabemos:
despejando y sustituyendo tenemos:
$131$ $ondas$ de luz amarilla caben en una distancia de $0.003$ $pulgadas$
para la segunda pregunta calculamos la longitud de onda con los datos que nos dan:
Conclusión
Ahora calculamos cuanta distancia se extenderá el mismo número de ondas con ésta longitud de onda:
Realizado por: Luis Martínez (discusión) 08:09 27 mar 2015 (CDT)
Problema 2.2 4ta Edición.
2.2 La velocidad de la luz en el vació es aproximadamente de $3x10^{8}\frac{m}{s}$.Calcule la longitud de onda de la luz roja con una frecuencia de $5x10^{14}Hz$.Compárela con la longitud de onda de una onda electromagnética de$60Hz.$
Procedimiento
Utilizamos la ecuación $\lambda=\frac{c}{\nu}$,donde $c$ es la velocidad de la luz y $\nu$ la frecuencia de la onda. Tendremos entonces:
\[\lambda=\frac{c}{\nu}=\frac{3x10^{8}\frac{m}{s}}{5x10^{14}Hz}=6x10^{-7}m\]
o la ecuación:
\[\lambda=600nm\]
Que es la longitud de onda de la luz roja a la frecuencia solicitada en el problema. Ahora calculamos la longitud de onda de la onda electromagnética:
\[\lambda_{1}=\frac{c}{\nu}=\frac{3x10^{8}\frac{m}{s}}{60Hz}=5x10^{6}m\].
Conclusión
Al comparar $\lambda$ con $\lambda_{1}$ notamos que la longitud de onda ${\lambda}_{1}$correspondiente a la onda electromagnética es mucho mayor que la de la luz roja.
Realizado por: Pedro Pablo Ramírez Martínez (discusión) 02:15 17 mar 2014 (UTC)
Problema 2.3 4ta Edición.
Es posible generar ondas ultrasónicas en cristales con longitudes de onda similares a la luz $(5\times10^{-5}cm)$ pero con frecuencias mas bajas $(6\times10^{8}Hz)$. Calcule la velocidad correspondiente de dicha onda.
Procedimiento
Pues bien teniendo los datos: $\lambda=5\times10^{-7}m$ y $f=6\times10^{8}Hz$
De la ecuación $v=f\cdot\lambda$
$v=f\cdot\lambda$
$v=(5\times10^{-7}m)(6\times10^{8}Hz)$
Solución
$v=300\frac{m}{s}$
Realizado por: Mario Moranchel (discusión) 06:29 18 mar 2014 (UTC)
Ejercicio 2.3 Solución Alternativa
Es posible generar ondas ultrasonicas en cristales con longitudes de onda similares a la luz $5x10^-5$ pero con frecuencias mas bajas $6x10^8 HZ$.
Calcular la velocidad correspondiente de dicha onda.
Procedimiento
Teniendo :
Conclusión
Donde de la ecuación :
Realizado por: Luisa Alejandra Vega Sanchez (discusión) 17:03 30 mar 2015 (CDT)luisa alejandra vega sanchez
Ejercicio 2.3 Solución Alterna
Es posible generar ondas ultrasonicas en cristales con longitudes de onda similares a la luz $5x10^-5$ pero con frecuencias mas bajas $6x10^8 HZ$.
Calcular la velocidad correspondiente de dicha onda.
Procedimiento
Teniendo :
Conclusión
Donde de la ecuación :
Realizado por: Luisa Alejandra Vega Sanchez (discusión) 17:03 30 mar 2015 (CDT)luisa alejandra vega sanchez
Problema 2.4 4ta Edición.
Un joven en un barco sobre un lago está mirando las ondas que parecen una sucesión infinita de crestas idénticas, produciéndose con un intervalo de medio segundo cada una. Si cada perturbación tarda 1.5s en cubrir la extensión del barco de 4.5 ¿cuál es la frecuencia, el periodo y la longitud de onda de las olas?
Procedimiento
Los datos dados en el problema, son los siguientes:
t = 1.5s, l = 4.5m,
Del enunciado, se deduce que el periodo, es el siguiente: $\tau=$0.5s.
De donde se calcula la frecuencia utilizando la definición de frecuencia:
\[ \nu=\frac{1}{\tau} \]
Al sustituir, en la ecuación, se obtiene el siguiente resultado:
\[ \nu=\frac{1}{0.5s}=2Hz \]
Para obtener la longitud de onda, se utiliza la siguiente relación:
\[ \tau=\frac{\lambda}{v}\rightarrow\lambda=v\tau \]
De donde la velocidad se obtiene a partir de la siguiente definición: $v=\frac{l}{t}=\frac{4.5m}{1.5s}=3m/s$
Entonces $\lambda=(3m/s)(0.5s)=1.5m$.
Conclusión
Frecuencia \[ \nu=\frac{1}{0.5s}=2Hz \]
Periodo $\tau=$0.5s
Longitud de onda
$\lambda=1.5m$.
Realizado por: Ana Alarid (discusión) 01:46 12 mar 2014 (UTC)
Problema 2.5 4ta Edición
Con un martillo vibrante se golpea el extremo de una barra de metal larga de manera que una onda de compresión periódica con una longitud de onda de 4.3m recorra todo lo largo de la barra con una velocidad de $v=3.5\frac{km}{s}$
¿Cual sera la frecuencia de la vibración?
Procedimiento
Teniendo los datos: $\lambda=4.3m$ y $v=3500\frac{m}{s}$
De la ecuación $v=f\cdot\lambda$ obtendremos la frecuencia.
$v=f\cdot\lambda$
$f=\frac{v}{\lambda}$
$f=\frac{3500 \frac{m}{s}} {4.3m}$
Conclusión
$f=813.95 Hz$
Re elaborado por Manuel Rodríguez
Problema 2.6 4ta Edición
Durante la boda de dos buceadores, se sumerge un violín en la piscina. Dado que la velocidad de las ondas de compresión en agua pura es de 1498 m/s. ¿Cual es la longitud de una nota la, de 440 Hz que se toca en dicho instrumento?
Procedimiento
Conocemos la velocidad de la onda en el agua que es $\upsilon=1498\frac{m}{s}$ y conocemos también la frecuencia de la nota que es $\upsilon=440Hz=440\frac{ciclos}{s}$
Ahora bien si queremos encontrar la longitud de la onda, recurrimos a la ecuación
\[ \upsilon=\nu\lambda \]
De donde conocemos todo excepto la longitud de onda, solo requiere
de un sencillo despeje para encontrar $\lambda$
Haciendo el despeje la ecuación queda:
\[ \lambda=\frac{\upsilon}{\nu} \]
Sustituimos nuestros datos
\[ \lambda=\frac{1498\frac{m}{s}}{440\frac{ciclos}{s}} \]
Conclusión
Y obtendremos que:
\[ \lambda=3.40m \]
Realizado por: Usuario:Daniel Olvera Moreno ) 05:29 21 mar 2014 (UTC)
Problema 2.7 4ta Edición
Un pulso de onda tarda $2.0 s$ en recorrer $10 m$ a lo largo de una cuerda, se genera una perturbación armónica con una longitud de onda de $0.5 m$ en la cuerda. ¿Cuál es su frecuencia?
Procedimiento
De los datos proporcionados sabemos que si la perturbación armónica tiene una longitud de onda de $\lambda=0.5 m$ de manera que el pulso completa 20 "ciclos" en los $10 m$ recorridos.
De esta forma el periodo de la perturbación es:
Solución
Entonces la frecuencia es:
Realizado por: Brenda Pérez Vidal (discusión) 18:16 27 mar 2014 (UTC)
Problema 2.8 5ta Edición
Calcule la longitud de onda de las ondas de ultrasonido con una frecuencia de 500 MHz en el aire. La velocidad del sonido en el aire es de 343 m/s
Procedimiento
Para este caso, la resolución del problema es fácil ya que solo aplicamos la Ecuación \ref{eq:last} y solamente aplicamos sustitución de datos.
\begin{equation}\label{eq:last} v=f * \lambda \end{equation}
Por lo tanto, despejando la $\lambda$ llegamos a la Ecuación \ref{eq:last1}.
\begin{equation}\label{eq:last1} \lambda= \frac{v}{f} \end{equation}
Sustituyendo los datos.
\begin{equation} \lambda= \frac{343}{500000000} \end{equation}
Conclusión
Por lo tanto llegamos a la solución de que la longitud de onda del ultrasonido es de: 0.000000686 m.
Realizado por: Misa cabca (discusión) 20:31 16 nov 2020 (CST)
Problema 2.8 4ta Edición
2.8 Demuestre que para una onda periódica $\omega=(\frac{2\pi}{\lambda})v$
Procedimiento
La mayoría de las ondas son el resultado de muchas perturbaciones sucesivas del medio. Cuando dichas perturbaciones se producen a intervalos regulares y todas son de la misma forma, estamos frente a una onda periódica.
Una onda periódica posee periodo (número de unidades de tiempo por onda) y frecuencia (número de ondas por unidad de tiempo), establecidas por:
$Periodo$ \begin{equation} \tau=\frac{\lambda}{v}.... (i) \end{equation} donde $\tau$ es el periodo de onda, $\lambda$ es la longitud de onda y $v$ se refiere a la velocidad con la que viaja la onda.
$Frecuencia$ \begin{equation} \nu=\frac{\omega}{2\pi}....(ii) \end{equation} donde $\nu$ es la frecuencia de la onda, $\omega$ es la frecuencia angular de la onda.
De $(ii)$ despejamos $\omega$
\begin{equation} \omega=\nu 2\pi ....(iii) \end{equation}
También sabemos que el inverso del periodo es la frecuencia $(\nu=\frac{1}{\tau})$
Utilizando la expresión $(iv)$ y sustituyendola en $(iii)$
\begin{equation} \nu=\frac{1}{\tau} ....(iv) \end{equation}
\begin{equation} \omega= \frac{2\pi}{\tau} \end{equation}
Sustituyendo $(i)$ en $\tau$
\begin{equation} \omega= \frac{2\pi}{\frac{\lambda}{v}} \end{equation}
Conclusión
Por lo tanto:
\begin{equation} \omega= (\frac{2\pi}{\lambda})(v) \end{equation}
Realizado por: Angel Nahir Molina Guadarrama (discusión) 11:13 23 mar 2014 (UTC)
Problema 2.9 4ta Edición
Hacer una tabla con las columnas encabezadas por los valores de $\theta$ corriendo de $-\frac{\pi}{2}$ a $2\pi$ en intervalos de $\frac{\pi}{4}$ , en cada fila el valor correspondiente de $\sin\theta$ , debajo de esos valores los de $\cos\theta$ , por debajo de los valores de $\sin\left(\theta-\frac{\pi}{4}\right)$ , y similarmente con las funciones $\sin\left(\theta-\frac{\pi}{2}\right)$ , $\sin\left(\theta-\frac{3\pi}{4}\right)$ , y $\sin\left(\theta+\frac{\pi}{2}\right)$) . Trazar cada una de estas funciones, sin los efectos del desplazamiento de fase. La funcion $\sin\theta$ se atrasa o se adelantade la funcion $\sin\left(\theta-\frac{\pi}{2}\right)$ . en otras palabras, Una de las funciones alcanza una magnitud particular, en un valor menor de $\theta$ que la otra y , por tanto, una conduce a la otra ( como $\cos\theta$ conduce $\sin\theta$ ) ?
Tabla
| $ \theta $ | $-\frac{\pi}{4}$ | $-\frac{\pi}{4}$ | $ 0 $ | $ \frac{\pi}{4}$ | $ \frac{\pi}{2}$ | $ \frac{3\pi}{4}$ | $ \pi $ | $ \frac{5\pi}{4}$ | $ \frac{3\pi}{2}$ | $ \frac{7\pi}{4}$ | $ 2\pi$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $ \sin(\theta) $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ |
| $ \cos(\theta) $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ |
| $ \sin(\theta-\frac{\pi}{4}) $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ |
| $ \sin(\theta-\frac{\pi}{2}) $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ |
| $ \sin(\theta-\frac{3 \pi}{4}) $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ |
| $ \sin(\theta+\frac{\pi}{2}) $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ | $ \frac{\sqrt{2}}{2} $ | $ 0 $ | $ -\frac{\sqrt{2}}{2} $ | $ -1 $ | $ -\frac{\sqrt{2}}{2} $ | $ 0 $ | $ \frac{\sqrt{2}}{2} $ | $ 1 $ |
Conclusión
Respuesta: $\sin\left(\theta+\frac{\pi}{2}\right)$ que es igual al $\cos(\theta)$ se desplaza a la izquierda del $\sin\theta$
Realizado por: Rosario Maya (discusión) 20:37 29 mar 2015 (CDT)
Problema 2.10 (4ta Edición)
Hacer una tabla con columnas encabezadas por los valores de $kx$ correr desde $x=-\frac{\lambda}{2}$ a $x=+\lambda$ en intervalos de $x$ de $\frac{\lambda}{4}$ , por supuesto, $k=\frac{2\pi}{\lambda}$ . En cada columna colocar los correspondientes valores de $\cos\left(kx+\frac{3\pi}{4}\right)$ y para las funciones $15\cos\left(kx-\frac{\pi}{4}\right)$ y $25\cos\left(kx+\frac{3\pi}{4}\right)$.
Tabla
| $ x $ | $-\frac{\lambda}{2}$ | $-\frac{\lambda}{4}$ | $ 0 $ | $\frac{\lambda}{4}$ | $\frac{\lambda}{2}$ | $\frac{3\lambda}{2} $ | $ \lambda $ |
|---|---|---|---|---|---|---|---|
| $ kx=2\pi\frac{\lambda}{2} $ | $ -\pi $ | $ -\frac{\pi}{2}$ | $ 0 $ | $ \frac{\pi}{2}$ | $ \pi $ | $ \frac{3\pi}{2}$ | $ 2\pi$ |
| $\cos\left(kx-\frac{\pi}{2}\right)$ | $ -\frac{\sqrt{2}}{2}$ | $ -\frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ |
| $\cos\left(kx+\frac{3\pi}{4}\right)$ | $ \frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ | $ -\frac{\sqrt{2}}{2}$ | $ -\frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ | $ \frac{\sqrt{2}}{2}$ | $-\frac{\sqrt{2}}{2}$ |
| $15\cos\left(kx-\frac{\pi}{4}\right)$ | $ 15-\frac{\sqrt{2}}{2}$ | $ 15-\frac{\sqrt{2}}{2}$ | $ 15\frac{\sqrt{2}}{2}$ | $ 15\frac{\sqrt{2}}{2}$ | $ 15-\frac{\sqrt{2}}{2}$ | $ 15-\frac{\sqrt{2}}{2}$ | $ 15\frac{\sqrt{2}}{2}$ |
| $25\cos\left(kx+\frac{3\pi}{4}\right)$ | $ 25\frac{\sqrt{2}}{2}$ | $ 25\frac{\sqrt{2}}{2}$ | $ 25-\frac{\sqrt{2}}{2}$ | $ 25-\frac{\sqrt{2}}{2}$ | $ 25\frac{\sqrt{2}}{2}$ | $ 25\frac{\sqrt{2}}{2}$ | $ 25-\frac{\sqrt{2}}{2}$ |
Ejercicio Resuelto por :Rosario Maya (discusión) 00:05 30 mar 2015 (CDT)
Problema 2.11 4ta Edición
Haga una tabla con columnas encabezadas por valores de $\omega \, t$ que van desde a $t=-\tau /2$ to $t=+\tau$ en intervalos de $t$ of $\tau/4$; por supuesto $\omega=2\,\pi/\tau$. En cada columna coloque los valores correspondientes de$\sin(\omega\,t+\pi/4)$ y $\sin(\pi/4-\omega\,t)$ y trace estas dos funciones.
Se realiza la tabla usando $\omega=2\,\pi/\tau$ en el argumento de cada función.
| $t$ | $-\frac{\tau}{2}$ | $-\frac{\tau}{4}$ | $0$ | $\frac{\tau}{4}$ | $\frac{\tau}{2}$ | $\frac{3\tau}{4}$ | $\tau$ |
|---|---|---|---|---|---|---|---|
| $\omega \, t$ | $-\pi$ | $-\frac{\pi}{2}$ | $0$ | $\frac{\pi}{4}$ | $\frac{\pi}{2}$ | $\frac{3\pi}{2}$ | $2\pi$ |
| $\sin(\omega\,t+\frac{\pi}{4})$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ |
| $\sin(\frac{\pi}{4}-\omega\,t)$ | $-\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{\sqrt{2}}$ |
La gráfica se realizó en Mathematica 10.0. El comando utilizado fue:
Plot[
{Sin[wt + Pi/4], Sin[Pi/4 - wt]}, {wt, -Pi, 2 Pi},
PlotStyle -> Thickness[.01], PlotLegends -> "Expressions",
AxesStyle -> {Directive[Black, 12, Thick], Directive[Black, 12, Thick]},
Ticks -> {Table[-Pi + n Pi/2, {n, 0, 6}], {-1, -(Sqrt[2]/2), 0, Sqrt[2]/2, 1}},
TicksStyle -> Directive["Label", 18, Black, Thick],
GridLines -> {Table[-Pi + n Pi/4, {n, 0, 12}], {-1, -(Sqrt[2]/2), 0, Sqrt[2]/2, 1}},
GridLinesStyle -> Directive[Dashed, GrayLevel[.76], Thickness[.0025]],
ImageSize -> Large
]
Problema hecho por: Adolfo Calderón Alcaraz (discusión) 01:58 30 mar 2015 (CDT)
Problema 2.12 4ta Edición
2.12 El perfil de una onda armónica, que viaja con velocidad de 1.2 m/s en una cuerda,esta dado por
Calcule su amplitud, su longitud de onda, su frecuencia y su periodo
Procedimiento
Se observa que la ecuación no muestra dependencia del tiempo, por lo obedece a la ecuación (2.12) del libro
de donde es inmediatos su amplitud A=0.02m y número de onda , por lo que su longuitud de onda esta dada por:
su frecuencia esta dada ṕor la ecuación (2.19), entonces:
Finalmente, su periodo esta dado por:
Conclusión
Realizado por: Pérez Córdoba Sabino (discusión) 17:56 26 mar 2014 (UTC)
Problema 2.12 2do método
El perfil de velocidad de una onda armónica, que viaja a una velocidad de $1.2 m/s$ en una cuerda, esta dado por:
$ y=\left(0.02\right)\sin\left(157/m\right)x $
Calcule su amplitud, su longitud de onda, su frecuencia y su periodo.
Solución
Se tiene la ecuación de onda (2.13) que es:
$\varPsi\left(x,t\right)=a\sin\kappa\left(x-vt\right)$
Donde $A$
es la amplitud , y $\kappa$ el numero de onda (constante).
Tomando en cuenta que el tiempo es independiente de la función de onda, y con t=0; se tiene:
- $\varPsi(x,0)=A\sin\left[x-v(0)\right]=A\sin\kappa x$
Inciso a
a) Comparando la ecuación del ejercicio, con la parte teórica, se sabe por inspección que la amplitud $ A=0.02m$ y $\kappa=157m^{-1}$.
Inciso b
b) Se tiene la relación $\kappa=\frac{2\pi}{\lambda}$
- despejando la longitud de onda $"\lambda"$ se tiene
$\lambda$
$= \frac{2\pi}{\kappa}$ $= \frac{2\pi}{157m^{-1}}$ $= 0.0400 m $
Inciso c
c) Para la frecuencia se tiene la relación $v=\nu\lambda$
Despejando la frecuencia $"\nu"$ se tiene:
$\nu$ =$\frac{v}{\lambda}$ = $\frac{1.2m/s}{0.0400m}$ =$ 30 Hz $
Inciso d
d) Para el período se tiene el recíproco de la frecuencia:
$\tau$ = $\frac{1}{\nu}$ = $\frac{1}{30Hz}$ = $0.033 s$
Elaborado por Ricardo García Hernández.Ricardo Garcia Hernandez (discusión) 00:25 30 mar 2015 (CDT)
Problema 2.16 4ta Edición
2.13 Usando las funciones de onda
$\psi_{1}=4\sin2\pi\left(0.2x-3t\right)$
$\psi_{2}=\frac{\sin\left(7x+3.5t\right)}{2.5}$
Determine en cada caso los valores de
a)Frecuencia.
b)Longitud de onda.
c)Periodo.
d)Amplitud.
e)Velocidad de fase.
f)Dirección del movimiento.
El tiempo se expresa en segundos y x en metros.
Partimos de la ecuación de onda:
\[
\psi=Asin(kx \pm \omega t)...(1)
\]
En donde podemos factorizar $2 \pi$ del argumento y escribir:
\[ \psi=Asin2 \pi (\frac{k}{2 \pi} x \pm \frac{\omega}{2\pi}t) ...(2)\]
Definimos a:
\[ \frac{k}{2\pi}=\chi \] \[ \frac{\omega}{2\pi}=\nu \]
\[ \psi=Asin 2\pi(\chi x \pm \nu t)...(3) \] De esta ecuación podemos identificar la:
Amplitud: $A$
Frecuencia: $\nu$
Número de onda: $\chi$
También sabemos que:
Velocidad de fase: $V= \pm \frac{\omega}{k}$
Longitud de onda: $\frac{V}{\nu}$
Primera función de onda.
Con lo anterior, dada $ \psi_1 = 4 sin2\pi (0.2 x - 3t)$
a) Frecuencia
$\nu=3 Hz$
b) Longitud de Onda
$\lambda=\frac{V}{\nu}= \frac{15}{3}=5 m$
c) Periodo
$\tau=\frac{1}{\nu}=0.333... s$
d) Amplitud
$A= 4 m$
e) Velocidad de fase
$v=\frac{\omega}{k}=\frac{\nu}{\chi}=\frac{3 Hz}{0.2 m^{-1}}=15 m/s$
f) Dirección de movimiento
Hacia la derecha.
Segunda Función de onda
Para la función $ \psi_2 \frac{1}{2.5} sin(7x + 3.5t) $
a) Frecuencia.
$\nu=\frac{\omega}{2\pi}=\frac{3.5}{2\pi}=0.55 Hz$
b) Longitud de onda.
$\lambda=\frac{2\pi}{k}= \frac{2/pi}{7}=0.897 m$
c) Periodo.
$\tau=\frac{2\pi}{\omega}=1.795 s$
d) Amplitud.
$A=\frac{1}{2.5}=0.4 m$
e) Velocidad de fase.
$v=\frac{\omega}{k}=-\frac{3.5}{7}=-0.5 m/s$
f) Dirección de movimiento.
Dado el signo negativo, de la velocidad de fase, el movimiento es Hacia la izquierda.
Resuelto por:Luis Santos (discusión) 13:13 28 mar 2015 (CDT)
Problema 2.18 4ta Edición
Demuestre que, es una solución de la ecuación diferencial de onda.
Demostración
De la solución propuesta se observa que se trata de la ecuación de diferencial de onda en una dimensión, luego, para ser solución debe satisfacer la ecuación.
$\frac{\partial^2 \psi }{\partial x^2}=\frac{1}{v^{2}}\frac{\partial^{2} \psi}{\partial t^{2}}$
La segunda derivada parcial respecto de x esta dada por:
$\frac{\partial^2 \psi}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial \psi}{\partial x}=\frac{\partial}{\partial x}(kA\cos(kx-kvt))=-k^2 A \sin(kx-kvt)$
La segunda derivada parcial respecto de t esta dada por:
$\frac{\partial^2 \psi }{\partial t^2}=\frac{\partial}{\partial t}\frac{\partial \psi}{\partial t}=\frac{\partial}{\partial t}(-kvA\cos(kx-kvt))=-k^2v^2A\sin(kx-kvt)$
Al sustituirlas en la ecuación diferencial de onda se tiene:
Como la última igualdad es cierta, entonces es solución de la ecuación diferencial de onda en una dimensión.
Realizado por: Pérez Córdoba Sabino (discusión) 21:17 17 mar 2014 (UTC)
Problema 2.18 4ta Edición
Demuestre que, es una solución de la ecuación diferencial de onda.
Demostración
De la solución propuesta se observa que se trata de la ecuación de diferencial de onda en una dimensión, luego, para ser solución debe satisfacer la ecuación.
$\frac{\partial^2 \psi }{\partial x^2}=\frac{1}{v^{2}}\frac{\partial^{2} \psi}{\partial t^{2}}$
La segunda derivada parcial respecto de x esta dada por:
$\frac{\partial^2 \psi}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial \psi}{\partial x}=\frac{\partial}{\partial x}(kA\cos(kx-kvt))=-k^2 A \sin(kx-kvt)$
La segunda derivada parcial respecto de t esta dada por:
$\frac{\partial^2 \psi }{\partial t^2}=\frac{\partial}{\partial t}\frac{\partial \psi}{\partial t}=\frac{\partial}{\partial t}(-kvA\cos(kx-kvt))=-k^2v^2A\sin(kx-kvt)$
Al sustituirlas en la ecuación diferencial de onda se tiene:
Como la última igualdad es cierta, entonces es solución de la ecuación diferencial de onda en una dimensión.
Realizado por: Pérez Córdoba Sabino (discusión) 21:17 17 mar 2014 (UTC)
Problema 2.22 4ta Edición
Escriba la expresión para la onda armónica de amplitud , periodo ,y velocidad .La onda se propaga en la dirección negativa de X y tiene un valor de en t=0 y x=0
Procedimiento
Sabemos que una función de onda, puede escribirse como:
$\Psi(x,t)=A \sin\left [ kx \pm \omega t \right ]$
$\Psi(x,t)=A \cos\left [ kx \pm \omega t \right ]$
Dado que en $x=0$ y $t=0$ tiene un valor de $10^{3}V/m$, usamos la función coseno (Dado que la función Seno nos daría un valor de 0 en esos valores). ademas sabemos que se propaga en dirección negativa de X usamos el signo positivo.
$\Psi(x,t)=A \cos\left [ kx + \omega t \right ]$
Para encontrar los valores, tenemos que encontrar el valor de $\omega$
$\omega=\frac{2\pi}{T}=\frac{2\pi}{2.2 \times 10^{-15}s}=2.856 \times 10^{15} s^{-1}$
El valor de $k$ se puede encontrar usando:
$k=\frac{\omega}{\nu}=\frac{2.856 \times10^{15} \frac{rad}{s}}{3 \times 10^8 \frac{m}{s}}=9.52 \times 10^{6} m^{-1}$
Conclusión
Sustituyendo estos valores, se tiene la siguiente función de onda:
$\Psi(x,t)=\left (10^{3} \frac{V}{m} \right ) \cos\left [ \left (9.52 \times 10^{6} m^{-1} \right ) x + \left (2.856 \times 10^{15} s^{-1} \right ) t \right ]$
que cumple con:
$\Psi(0,0)=\left (10^{3} \frac{V}{m} \right )$
Re elaborado por Manuel Rodríguez
Problema 2.36 4ta Edición
Escribe una expresión para la onda mostrada en la figura P.2.36. Encuentra la velocidad de onda, velocidad, frecuencia y periodo.
Inciso a
a) La forma matemática de la descripción de una función de onda es:
Dado lo anterior podemos encontrar el número de onda K y la frecuencia , donde a un tiempo cero, es igual a cero por lo tanto .
De las expresiones para el numero de onda y , en donde y son la frecuencia y la longitud de onda respectivamente, podremos reescribir la expresión para la onda como:
El signo menos es por el desplazamiento de la función de onda a la derecha. Por el gráfico se observa que la longitud de onda es de cuatrocientos nanómetros, la amplitud es de 60 nanómetros y el periodo es de
, dado que da un ciclo en ese tiempo. Por ende la expresión buscada es:
Inciso b
b)Calculando la velocidad de onda:
Inciso c
c) Calculando la frecuencia y el periodo:
Realizado por: Pablo (discusión) 22:23 21 mar 2015 (CDT)
5ta Edición en Ingles.
Problema 2.2 5ta Edición
Mostrar que la función
\begin{equation}\label{eq:1} \psi (y,t)=(y-4t)^{2} \end{equation}
Es una succiona de la ecuación de onda diferencial. ¿En que dirección viaja?
Procedimiento
Para resolver este problema, debemos tener presente que le Ecuación de Onda es de la forma
\begin{equation}\label{eq:2} \frac{\partial^{2}{\psi}}{\partial{y}^{2}}=\frac{1}{v^{2}} \frac{\partial^{2}{\psi}}{\partial{t}^{2}} \end{equation}
Para comprobar, comenzamos realizando la primer derivada de la función (Ecuación \ref{eq:1}) respecto a $y$
\begin{equation} \frac{\partial{\psi}}{\partial{y}}=\frac{\partial}{\partial{y}}((y-4t)^{2})=2(y-4t)=2y-8t \end{equation}
Ahora derivamos el resultado anterior para así obtener la segunda derivada respeto a la variable $y$
\begin{equation} \frac{\partial^{2}{\psi}}{\partial{y}^{2}}=\frac{\partial}{\partial{y}}(\frac{\partial{\psi}}{\partial{y}})=\frac{\partial}{\partial{y}}(2y-8t)=2 \end{equation}
Realizamos el mismo procedimiento para llegar a la segunda derivada de la Ecuación \ref{eq:1} pero ahora respecto a la variable $t$
\begin{equation} \frac{\partial{\psi}}{\partial{t}}=\frac{\partial}{\partial{t}}((y-4t)^{2})=2(y-4t)(-4)=-8(y-4t)=32t-8y \end{equation}
\begin{equation} \frac{\partial^{2}{\psi}}{\partial{t}^{2}}=\frac{\partial}{\partial{t}}(\frac{\partial{\psi}}{\partial{t}})=\frac{\partial}{\partial{t}}(32t-8y)=32 \end{equation}
Como se observa en la Ecuación \ref{eq:2} solo nos hace falta obtener la variable $v$, pero como vemos, esta se obtiene despejandola para finalmente llegar a la siguiente expresión
\begin{equation} v^{2}=\frac{\frac{\partial^{2}{\psi}}{\partial{t}^{2}}}{\frac{\partial^{2}{\psi}}{\partial{y}^{2}}} \end{equation}
Sustituimos los datos de las segundas derivadas que habíamos encontrado y vemos que la $v^{2}=16$.
Conclusión
Realizando la sustitución de los datos, encontramos
\begin{equation} 2=\frac{1}{16}(32)=2 \end{equation}
que la función es solución de la ecuación de onda.
La onda viaja de izquierda a derecha ya que la función (Ec.\ref{eq:1}) tiene un signo menos.
Realizado por: Misa cabca (discusión) 10:24 27 oct 2020 (CDT)
Problema 2.27 5ta Edición
Demuestre que si el desplazamiento de la cuerda de la figura 2.7 está dado por entonces la mano que genera la onda se debe mover verticalmente con movimiento armónico simple.
Vemos que el movimiento de la cuerda en la figura $2.7$ corresponde al de una onda armónica que se desplaza a lo largo del eje $x$ durante un tiempo de un período, en este caso cualquier punto de la cuerda se desplaza sólo verticalmente, entonces podemos derivar la ecuación de movimiento como sigue:
Procedimiento
\[
\frac{\partial}{\partial x} y(x,t)=k A \cos[kx - \omega t + \varepsilon]
\]
\[ \frac{\partial^2}{\partial x^2} y(x,t) = k^2 A \sin[kx - \omega t + \varepsilon] \]
Vemos que en la segunda derivada aparece la primer derivada, al sustituirla se llega a la siguiente expresión:
Conclusión
\[ \ddot{y}=-k^2 y(x,t) \rightarrow \ddot{y}+k^2y=0 \]
Se observa que corresponde a la ecuación de un movimiento armónico simple realizado verticalmente.
Realizado por: Brenda Pérez Vidal (discusión) 16:49 27 mar 2014 (UTC)
Problema 2.28 5ta Edición
Escriba la expresión para la onda armónica de amplitud , periodo ,y velocidad .La onda se propaga en la dirección negativa de X y tiene un valor de en t=0 y x=0.
Procedimiento
sabiendo que
obtenemos la longitud de onda con
es decir
obtenemos K de la formula
Sabiendo que la expresión de la ecuación de onda es
Conclusión
sustituimos los datos antes encontrados para hallar la expresión que nos piden.
Realizado por: Leticia González Zamora (discusión) 15:27 20 jun 2013 (CDT)
Problema 2.29 5ta Edición
Considere el pulso descrito en términos de sus desplazamientos en $t=0$ por $y(x,t)|_{t=0}=\frac{C}{2+x^{2}}$ donde $C$ es una constante. Dibuje el perfil de onda. Escriba una expresión para la onda que tiene una velocidad $v$ en la dirección negativa de $x$, como función del tiempo $t$. Si $v=1\frac{m}{s}$, dibuje el perfil en $t=2s$.
Procedimiento
De la expresión $y(x,t)|_{t=0}=\frac{C}{2+x^{2}}$ notamos que el máximo de la función se encuentra cuando $x=0$ y por tanto el máximo siempre estará en $y_{max}=\frac{C}{2}$.
De la expresión anterior debido a que esta al tiempo $t=0$ la velocidad de la onda no contribuía, ahora bien la expresión para una onda con cierta velocidad para ester perfil esta dada por \[ y(x,t)=\frac{C}{2+(x+vt)^{2}} \] el sigo se debe a que queremos ver la onda desplazada a la izquierda o dirección negativa del $eje\; x$.
La gráfica al tiempo $t=2s$ con una velocidad $v=1\frac{m}{s}$ se muestra a continuación.
Nuevamente se toman 3 valores distintos para $C$.
Realizado por: Luis Miguel Sánchez Mtz. (discusión) 05:46 26 mar 2014 (UTC)
Problema 2.60 5ta Edición
Haga una tabla con columnas encabezadas por valores de $kx$ que va de $x=\frac{\lambda}{2}$ a $x=\lambda$ en intervalos de x de $\frac{\lambda}{4}$ en cada columna coloque los valores correspondientes de $\cos(kx)$ y debajo de eso los valores de cos(kx+ p). Luego grafique las tres funciones $\cos(kx)$, $\cos (kx + p)$.
Tablas
Problema resuelto por: Luis Velázquez (discusión) 20:08 27 mar 2015 (CDT)
3ra Edición en Español.
Problema 2.18 3ra Edición en español
Determine la magnitud de la función de onda $\psi(z,t)=Acos[k(z+vt)+\pi]$ en el punto $z=0$, cuanto $t=\frac{\tau}{2}$ y cuando $t=\frac{3\tau}{4}$.
Procedimiento
Partimos de la ecuación de la onda
\[\psi(z,t)=Acos[k(z+vt)+\pi]\]
Evaluamos en $z=0$ y nos queda
\[\psi(0,t)=Acos[kvt+\pi]\]
Sustituimos $kv=\omega$ y entonces tenemos
\[\psi(z,t)=Acos[\omega t+\pi]\]
Pero como $-Acos[\omega t]=Acos[\omega t+\pi]$ tenemos que
\[\psi(z,t)=-Acos[\omega t]\]
Conclusión
Finalmente sustituimos para $t=\frac{\tau}{2}$ y luego para $t=\frac{3\tau}{4}$ y obtenemos los resultados siguientes para cada caso.
$\psi(0,\frac{\tau}{2})=-Acos[\omega\frac{\tau}{2}]=-Acos(\pi)^{-1}=A$
y para $\psi(0,\frac{3\tau}{4})=-Acos[\omega\frac{3\tau}{4}]=-Acos(\frac{3}{4}\pi)=0$
Realizado por: Pedro Pablo Ramírez Martínez (discusión) 01:48 28 mar 2014 (UTC)
Problema 2.19 3ra Edición en español
¿La siguiente función en la que $A$ es una constante, $\psi(y,t)=(y-vt)A$ representa una onda? Explique su razonamiento.
Procedimiento
$\;$
Como $\psi(y,t)=(y-vt)A$ es solo función de $(y-vt)$ cumple las condiciones de una ecuación de onda, donde \[ \frac{\partial^{2}\psi}{\partial y^{2}}=\frac{\partial^{2}\psi}{\partial t^{2}}=0 \]
y así esta función es una solución a la ecuación de onda. Sin embargo,
\[
\psi(y,0)=Ay,
\]
por lo que no puede representar un perfil de onda.
Realizado por: Luis Miguel Sánchez Mtz. (discusión) 06:50 22 mar 2014 (UTC)
Problema 2.20 3ra Edición en español
Utilice la ecuación (2.33) para calcular la velocidad de la onda cuya representación en unidades SI es $\psi(y,t) = A \cos\left[\pi\left(3x10^6 y + 9x10^{14} t\right)\right]$
Procedimiento
La ecuación (2.33) nos dice que:
$ \left(\dfrac{\partial x}{\partial t}\right)_\varphi = \pm \dfrac{\omega}{k} = \pm v \hspace{20pt} \cdots \hspace{20pt} (2.33) $ pero nuestra representación está dada en términos de $\psi(y,t)$, por lo que podemos reescribir la ecuación como:
$ \left(\dfrac{\partial y}{\partial t}\right)_\psi = \pm \dfrac{\omega}{k} = \pm v $
y también sabemos que la ecuación está dada en términos del siguiente cociente(ecuación 2.32 del texto con las variables adecuadas):
$ \left(\dfrac{\partial y}{\partial t}\right)_\psi = \dfrac{-\left(\dfrac{\partial \psi}{\partial t}\right)_y}{\left(\dfrac{\partial \psi}{\partial y}\right)_t} \hspace{20pt} \cdots \hspace{20pt} (2.32) $
Calculando ahora las derivadas:
$ -\left(\dfrac{\partial \psi}{\partial t}\right)_y = - \left\{ - 9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] \right\} = 9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] \\ \left(\dfrac{\partial \psi}{\partial y}\right)_t = - 3x10^{6} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right] $
Por lo que, sustituyendo en la ecuación (2.32):
$ \left(\dfrac{\partial y}{\partial t}\right)_\psi = \dfrac{-\left(\dfrac{\partial \psi}{\partial t}\right)_y}{\left(\dfrac{\partial \psi}{\partial y}\right)_t} = \dfrac{9x10^{14} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right]}{- 3x10^{6} A \pi \sin \left[ \pi \left(3x10^6 y + 9x10^{14} t\right) \right]} = - \dfrac{9x10^{14}}{3x10^{6}} $
Y realizando la operación obtenemos la velocidad deseada(en unidades SI como lo indica el enunciado):
Conclusión
$ v = \left(\dfrac{\partial y}{\partial t}\right)_\psi = -3x10^8 m/s = -c $
Donde el signo negativo($-$) indica que la dirección de propagación es hacia la izquierda.
Realizado por: Ivan de Jesús Pompa García (discusión) 00:50 27 mar 2015 (CDT)
Problema 2.21 3ra Edición en Español
Comenzando por el siguiente teorema: sí , y
Procedimiento
Derivar la ecuación: (2.34)
En general tenemos que una función de onda cualquiera posee la forma.
Sin perdida de generalidad consideramos el movimiento sobre un eje de propagación “y”
Entonces por regla de la cadena (el teorema propuesto.)
De aquí sabemos que para una perturbación que no cambia con el tiempo:
Asimismo la diferencial del tiempo respecto al tiempo es uno, entonces, tras estas simplificaciones obtenemos.
Conclusión
Despejando:
La cual es la ecuación 2.34.
Realizado por: Andrés Arturo Cerón Téllez (discusión) 23:48 5 jul 2013 (CDT)
Forma alternativa
El problema yo lo realice de la siguiente manera:
2.21. Empezando por el siguiente teorema: Si $z=f(x,y)$ y $x=g(t)$, $y=h(t)$, entonces:
\[ \frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} \]
Derive la ecuación (2.34)
Sabemos que la ecuación (2.34) es:
\[ \pm v=-\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{t}} \]
Ya que sabemos que
\[ \frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt} \]
Luego:
\[ \left(\frac{d\psi}{d\varphi}\right)_{\varphi}=\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi}+\frac{\partial\psi}{\partial y}\frac{dy}{d\varphi} \]
Y ya que en nuestro caso $\left(\frac{d\psi}{d\varphi}\right)$ es
constante en $\varphi$, entonces la ecuación se vuelve
\[ \text{-}\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}=\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi} \]
\[
\frac{dx}{d\varphi}=-\frac{\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}}
\]
Pero ádemas, es posible reescribir a $\frac{dx}{d\varphi}=\frac{\partial x}{\partial t}\frac{dt}{d\varphi}$,
asi:
\[ \frac{\partial x}{\partial t}=-\frac{\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}} \]
Conclusión
Así finalmente, la ecuación se puede reescribir como:
\[ \pm v=\left(\frac{\partial x}{\partial t}\right)_{\varphi}=-\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{t}} \]
Realizado por: Cesar Ivan Avila Vasquez 23 Marzo 2014 21:29 (CDT)
Problema 2.22 3ra Edición en Español
Utilizando los resultados del problema anterior, demuestre que
para una onda armónica con una fase $\varphi(x,t)=k(x-vt)$ podemos
calcular la velocidad estableciendo $\frac{d\varphi}{dt}=0$.
Aplique la técnica al problema 2.20 a fin de calcular la velocidad
de dicha onda.
Procedimiento
Veamos primero que dicha fase cumple con la definición, entonces tenemos lo siguiente:
\[ \psi(x,t)=Asen(k(x-vt)) \]
\[
\frac{\partial\psi}{\partial x}=kAsen(k(x-vt))
\]
\[
\frac{\partial\psi}{\partial t}=-kvAsen(k(x-vt))
\]
Luego:
\[ -\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial x}}=-\frac{(-kv)Asen(k(x-vt))}{kAsen(k(x-vt))}=v \]
Por lo cuál, la función cumple con la definición. Ahora veamos que
si $\frac{d\varphi}{dt}=0$ entonces la función sigue cumpliendo.
Del problema (2.21) tenemos que por definición:
\[
\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}=\frac{d\psi}{d\varphi}-\frac{\partial\psi}{\partial x}\frac{dx}{d\varphi}
\]
\[
\frac{\partial x}{\partial t}=\frac{\frac{d\psi}{d\varphi}-\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}}
\]
Conclusión
\[ \frac{\partial x}{\partial t}=\frac{\frac{d\psi}{d\varphi}\frac{d\varphi}{dt}\frac{dt}{d\varphi}-\frac{\partial\psi}{\partial t}\frac{dt}{d\varphi}}{\frac{\partial\psi}{\partial x}\frac{dt}{d\varphi}}=-\frac{\frac{\partial\psi}{\partial t}}{\frac{\partial\psi}{\partial t}} \]
Aportación de: Cesar Ivan Avila Vasquez 23 Marzo 2014 21:36 (CDT)
Problema 2.23 3ra Edición en Español
Una onda gaussiana, tiene la forma $\psi(x,t)=A^{-a(bx+ct)^{2}}$. Utilice el que $\psi(x,t)=f(x\pm vt)$ para calcular su velocidad, comprobando luego su respuesta con la ecuación (2.3).
Procedimiento
Se utiliza la siguiente definición de velocidad: \[ \pm v=-\left(\frac{\left(\frac{\partial\psi}{\partial t}\right)_{x}}{\left(\frac{\partial\psi}{\partial x}\right)_{y}}\right) \]
Se resuelven ambas partes de la ecuación por separado:
\[ \psi_{x}=(-2a)A(b)e^{-(abx+ct)^{2}} \]
\[
\psi_{y}=-(2a)Ace^{-(bx+ct)^{2}}
\]
Conclusión
Al sustituir los resultados obtenidos en la definición de velocidad:
\[ v=\frac{(-2a)Ace^{-(abx+ct)^{2}}}{(-2a)Abe^{-(abx+ct)^{2}}}=\frac{c}{b} \]
Se obtiene el resultado de la ecuación 2.3: $v=\frac{c}{b}$
Realizado por: Ana Alarid (discusión) 18:43 27 mar 2014 (UTC)
Problema 2.24 3ra Edición en Español
Encuentre una expresión para el perfil de una onda armónica que viaja en la dirección de $z$ cuya magnitud en $z=-\frac{\lambda}{12}$ es 0.866, en $z=+\frac{\lambda}{6}$ es $\frac{1}{2}$ y en $z=\frac{\lambda}{4}$ es 0.
Procedimiento
Utilizamos la función de onda armónica en el que $t=0$ puesto que $\varepsilon$ es una contribución constante a la fase y además es independiente del recorrido de la onda en términos de espacio y de tiempo:
\begin{equation} \psi(z,0)=Asen(kz+\varepsilon); \end{equation}
Donde $\psi$ es la propagación de la onda, $A$ es la amplitud, $k$ es el número de onda que está dada por $k=\frac{2\pi}{\lambda}$, $z$ corresponde a la dirección de propagación y $\varepsilon$ es la fase inicial.
A continuación escribimos las condiciones iniciales:
\begin{equation} \psi(-\frac{\lambda}{12},0)=Asen(-\pi/6 + \varepsilon)=0.866 ....(I) \end{equation}
\begin{equation} \psi(\frac{\lambda}{6},0)=Asen(-\pi/3 + \varepsilon)=\frac{1}{2} ....(II) \end{equation}
\begin{equation} \psi(\frac{\lambda}{4},0)=Asen(-\pi/2 + \varepsilon)=0 ....(III) \end{equation}
Para obtener el valor numérico de $\psi$ es necesario encontrar los valores para $\varepsilon$ y por consiguiente la amplitud $A$ y en conclusión obtener el perfil que se nos pide.
Para ello utilizamos la expresión $(III)$ puesto que es más sencilla de manipular y está igualada a 0. Utilizamos la identidad trigonométrica de suma de dos ángulos que involucra a senos y cosenos.
\begin{equation} A=sen(\pi/2+\varepsilon)=A[sen(\pi/2)cos(\varepsilon)+cos(\pi/2)sen(\varepsilon)] \end{equation}
Simplificamos
\begin{equation} =Acos(\varepsilon)=0 \end{equation}
Despejamos $\varepsilon$ y obtenemos su valor \begin{equation} \varepsilon=\frac{\pi}{2} \end{equation}
Ahora bien para encontrar $A$ podemos utilizar la expresión $(I)$ o $(II)$. Utilizando la expresión $(II)$ y sustituyendo el valor encontrado para $\varepsilon$:
\begin{equation} Asen(\pi/3 + \pi/2)=Asen(5\pi/6)=\frac{1}{2} \end{equation}
Así \begin{equation} A(\frac{1}{2})=\frac{1}{2}; A=1 \end{equation}
Conclusión
Por lo tanto, la expresión para el perfil de una onda armónica que viaja en la dirección de $z$ es:
\begin{equation} \psi(z,0)=sen(kz+\pi/2) \end{equation}
Realizado por: Angel Nahir Molina Guadarrama (discusión) 01:37 23 mar 2014 (UTC)
Problema 2.26 3ra Edición en Español
Establezca cuáles de las expresiones siguientes describen ondas viajeras:
(a) $\psi(y,t)=\exp-(a^{2}y^{2}+b^{2}t^{2}-2aybt)$
(b) $\psi(z,t)=Asen(az^{2}-bt^{2})$
(c) $\psi(x,t)=Asen2\pi\left(\frac{x}{a}+\frac{t}{b}\right)^{2}$
(d) $\psi(x,t)=Acos^{2}2\pi(t-x)$
Procedimiento
Para la onda (a), si la reescribimos como sigue:
$\psi(y,t)=\exp-(a^{2}y^{2}+b^{2}t^{2}-2aybt)\Rightarrow\exp-a^{2}(y-\frac{b}{a}t)^{2}$
Es evidente que se trata de una onda viajera, ya que cumple con las características de una.
Para la onda (b), es claro que no se comporta como una onda viajera, ya que la función no es lineal, una característica de las ondas viajeras.
Para la onda (c), es viajera, por que el término dentro del argumento es lineal, y nos dice que la onda se desplaza en una dirección diferente, hacia la izquierda.
Para la onda (d), no es viajera, por que la función $cos^{2}(x)$ no cumple con la definición de onda viajera.
Realizado por: Cesar Ivan Avila Vasquez 23 Marzo 2014 21:37 (CDT)
Problema 2.31 3ra Edición en Español
Trabajando directamente con exponenciales, demuestre que la magnitud de $\psi=A\exp iwt$ es A. A continuación, vuelva a calcular el mismo resultado utilizando la fórmula de Euler, demuestre que $e^{i\left ( \alpha \right )}e^{i\left ( \beta \right )}=e^{i\left ( \alpha + \beta \right )}$
Usando exponenciales
Sabemos que la magnitud de $\psi$ sera igual a su modulo, es decir:
$|\psi|=\left (\psi\psi* \right )^{\frac{1}{2}}$ y que $\psi*=A\exp-iwt$ por definición.
Luego:
$|\psi|=\left[\left(A\exp iwt\right)\left(A\exp-iwt\right)\right]^{\frac{1}{2}}=\left[A^{2}\exp iwt-iwt\right]^{\frac{1}{2}}=\left(A^{2}\exp0\right)^{\frac{1}{2}}=A$
Ahora, usando la fórmula de Euler, tenemos que:
$|\psi|=\left[\left(A\exp iwt\right)\left(A\exp-iwt\right)\right]^{\frac{1}{2}}$
$|\psi|=\left[A(coswt+isenwt)A(coswt-isenwt)\right]^{\frac{1}{2}}$
$|\psi|=\left[A^{2}\left(cos^{2}wt-isen(wt)cos(wt)+isen(wt)cos(wt)+sen^{2}wt\right)\right]^{\frac{1}{2}}$
$|\psi|=\left[A^{2}(cos^{2}wt+sen^{2}wt)\right]^{\frac{1}{2}}=(A^{2})^{\frac{1}{2}}=A$
Usando la formula de Euler
Demostremos ahora que $e^{i\left ( \alpha \right )}e^{i\left ( \beta \right )}=e^{i\left ( \alpha + \beta \right )}$
$e ^{i\alpha} e ^{i\beta} = \left(cos\alpha+isen\alpha\right)\left(cos\beta+isen\beta\right)$
$e^{i\alpha}e^{i\beta}=cos\alpha cos\beta+icos\alpha sen\beta-icos\beta sen\alpha+i^{2}sen\beta sen\alpha$
$e ^{i\alpha} e^{ i\beta}=\cos\alpha cos\beta+icos\alpha sen\beta-icos\beta sen\alpha-sen\beta sen\alpha=(cos\alpha cos\beta-sen\alpha sen\beta)+i(cos\alpha sen\beta+sen\alpha cos\beta)$
$e^{i\alpha} e^{i\beta} =cos(\alpha+\beta)+isen(\alpha+\beta)=e^{i(\alpha+\beta)}$
Realizado por: Cesar Ivan Avila Vasquez 23 Marzo 2014 21:38 (CDT)
Problema 2.32 3ra Edición en Español
Demuestre que la parte imaginaria de un número complejo z esta dada por $\left(z-z^{\star}\right)/2i$.
Solución
Sea z perteneciente a los complejos
$z=a+ib$
y su conjugado
$z^{\star}=a-ib$
entonces:
$z-z^{\star}=a+ib-(a-ib)$
$z-z^{\star}=2ib$
Dividimos entre $2i$
$z-z^{\star}/2i=2ib/2i$
Conclusión
$\left(z-z^{\star}\right)/2i=b$
que es la parte imaginaria del número complejo $z=a+ib$.
Realizado por: Edgar Ortega Roano (discusión) 17:43 18 mar 2014 (CDT) y Cesar Ivan Avila Vasquez (discusión) 21:53 26 Marzo 2014 (UTC)
Problema 2.34 3ra Edición en Español
Demuestre que las ecuaciones $\psi(x,y,z,t)=f(\alpha x+\beta y+\gamma z-vt)$ y $\psi(x,y,z,t)=f(\alpha x+\beta y+\gamma z+vt)$ que son ondas planas de forma arbitraria, cumplen con la ecuación diferencial de onda tridimensional.
Solución:
De la ecuación de onda tridimensional ,$\nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial t^{2}}$, obtenemos el Laplaciano para nuestras ecuaciones, así $\nabla^{2}\psi=\alpha^{2}f^{´´}+\beta^{2}f^{´´}+\gamma^{2}f^{´´}$ es el Laplaciano para ambas ecuaciones.
Ahora al calcular $\frac{\partial^{2}\psi}{\partial t^{2}}$ obtenemos que $\frac{\partial^{2}\psi}{\partial t^{2}}=v^{2}f^{´´}$ para ambas ecuaciones.
Por lo que al sustituir en la ecuación de onda tridimensional obtenemos.
$f^{´´}(\alpha^{2}+\beta^{2}+\gamma^{2})=f^{´´}$
Por lo que para cualquier onda tridimensional se debe cumplir que $\alpha^{2}+\beta^{2}+\gamma^{2}=1$.
Realizado por: Edgar Ortega Roano (discusión) 17:52 18 mar 2014 (CDT)
Problema 2.35 3ra Edición en Español
La hipótesis de De Broglie afirma que cada partícula tiene asociada a ella una longitud de onda dada por la constante de Planck ($h=6.6x10^{-34}Js$), dividida por el momento de la partícula.
Compare la longitud de onda de una piedra de 6.0 kg moviéndose a una velocidad de 1 m/s con la de la luz.
Procedimiento
Tenemos que:
\[ \lambda=\frac{h}{p} \]
Para la piedra tenemos entonces que:
\[ \lambda=\frac{6.6x10^{-34}Js}{(6kg)(1m/s)}=1.1x10^{-34}m \]
Y sabemos ademas que la longitud de onda de la luz se encuentra en
un intervalo de $\lambda=\left[3.8,7.5\right]x10^{-7}m$, entonces,
comparando ambas longitudes de onda notamos que la asociada a la piedra
es mucho más pequeña que la de la luz, si la longitud de onda de la
luz fuera más pequeña que la de la piedra, la luz atravesaría la piedra.
Realizado por: Cesar Ivan Avila Vasquez 23 Marzo 2014 21:40 (CDT)
Problema 2.37 3ra Edición en Español
Escriba una expresión en coordenadas cartesianas para una onda plana armónica de amplitud y frecuencia que se propaga en dirección positiva de .
Procedimiento
Primero se escribe un vector de posición que comienza en el origen y termina en cualquier otro punto .
De esta forma, lo podemos escribir como
y
donde obligamos al vector a barrer un plano perpendicalar a
al ir adquiriendo su punto exremo com que se puede escribir también como
o también
donde
Asi un plano perpendicular a es
Tomemos la funcion
o
y la función armónica se puede escribir como
Para que esta función sea cierta se debe tener que
Por consiguiente
despejando se tiene
Se tiene entonces que
Para que esta función este orientada sobre el eje solo se toma la coordenada del vector
Conclusión
asi que
Por tanto esta es la onda armónica en coordenadas cartesianas que se propaga en el eje .
Realizado por: Hector resendiz Héctor Reséndiz (discusión) 19:23 29 mar 2015 (CDT) Libro hecht
Problema 2.42 3ra Edición en Español
Escriba una expresión en coordenadas cartesianas para una onda plana armónica de amplitud $A$ y frecuencia $w$, que se propaga en la dirección del verctor $\overrightarrow{k}$, que a su vez, se encuentra en una línea que va desde el origen hasta el punto $(4,2,1)$. Hint: primero calcule $\overrightarrow{k}$ y luego haga el producto escalar con $\overrightarrow{r}=x\hat{i} + y\hat{j} + z\hat{k}$.
Procedimiento
para obtener el vector $\overrightarrow{k}$ necesitamos encontrar un vector unitario en la dirección que nos piden y multiplicándolo por $k$. el vector unitario es:
ahora el vector $\overrightarrow{k}$ está dado por:
la expresión en coordenadas cartesianas de una onda plana armónica viene dada por:
:
Conclusión
Realizado por: Luis Martínez (discusión) 17:05 27 mar 2015 (CDT)
Problemas Adicionales
Problema Adicional 1
La ecuación de onda transversal que se mueve a lo largo de una cuerda está dada por:
Hallar la amplitud, la longitud de onda, el número de ondas, la frecuencia, el período y la velocidad de onda.
Solución
Usando la ecuación
\[
\psi=A\sin2\pi\left(kz\pm\nu t\right)
\]
\[ \psi=A\sin\pi\left(2kz\ - 2\nu t\right) \]
La amplitud:
Longitud de onda
Número de onda
entonces
La velocidad de onda
Tomado de : Vibraciones y ondas. A. P. FRENCH pág. 277. Problema 7-2.
Resuelto por: Luis Velázquez (discusión) 10:56 26 mar 2015 (CDT)
Problema adicional 2
Física General 10° Edición, Frederick J. Bueche. Eugene Hetch.
Una onda se propaga por una cuerda según la ecuación $ y = 0.2\sin(6\pi t + \pi x + \dfrac{\pi}{4})$. Calcular:
a) La frecuencia, el periodo, la longitud de onda y la velocidad de propagación.
b) El estado de vibración, la velocidad y aceleración de una partícula situada en x = 0.2 m en 0.3 s
c) La diferencia de fase entre dos puntos separados 0.3 m
Inciso a
a) La forma general de la ecuación de onda $y(x, t)= A \sin(\omega t + Kx +\delta)$
Partiremos de la frecuencia angular $\omega = 2 \pi ; f = 6\pi rad/s ; f= 3 Hz $
El periodo $ T = \dfrac{1}{f}= 0.333s$
Para la velocidad usamos $c= \dfrac{\omega}{k} = \dfrac{6\pi}{\pi} = 6 m/s $
Inciso b
b) Para x = 0.2 m, t= 0.3s.
$y= 0.2\sin(6\pi*0.3 + \pi*0.2 + \dfrac{\pi}{4})= 0.2 \sin(7.069) = 0.1414 m $
Velocidad $\dfrac{dy}{dx} = 0.2 *6 \pi \cos (6 \pi t + \pi x \dfrac{\pi}{4})= 0.2*6 \pi \cos (7.069)= 2.66 m/s$
Aceleración $\dfrac{d^{2}y}{dt^{2}}= -0.2(36\pi^{2})\sin(6\pi t + \pi x + \dfrac{\pi}{4} = 0,2(36\pi^{2}cos (7.069)= -50.25 m/s^{2}$
Inciso c
c) $\vartriangle x= 0.3 m$
$\delta_{1} = 6 \pi t + \pi x + \dfrac{\pi}{4}$
$\vartriangle \delta = \delta_{2} - \delta_{1}= 0.3\pi rad $
$\delta_{2} = 6 \pi t + \pi (x + 0.3) + \dfrac{\pi}{4}$
Realizado por: Esther Sarai (discusión) 18:25 28 mar 2015 (CDT)Esther Sari García González
Problemas adicional 3
Un foco genera ondas de 2 mm de amplitud con una frecuencia de 250 Hz, que se propagan por un medio con una velocidad de 250 m/s. Determina el periodo y la longitud de onda de la perturbacion. Si en el instante inicial la elongacion de un punto situado a 3 m del foco es $y = -2 mm$, determina la elongacion de un punto situado a 2,75 m del foco en el mismo instante.
Periodo: $T=\frac{1}{f}=\frac{1}{250}=4\times 10^{-3}$s
Frecuencia angular: $w=2\pi f= 500\pi$ $rad/s$
Longitud de onda: $\lambda=\frac{v}{f}=\frac{250}{250}=1m$
numero de onda: $k=\frac{2\pi}{\lambda}=2\pi$ $m^{-1}$
En este caso y como los datos de vibracion no son los del foco, debe introducirse una fase inicial $\phi_0$ que se determina con las condiciones de vibracion del punto x = 3 m.
$y = A Cos(wt-kx+ \phi_0 ) =2 \times 10^{-3} Cos(500\pi t-2 \pi x+\phi_0)$
Operando:
$y=2\times 10^{-3}Cos[2\pi(250t-x) + \phi_0]$
Sustituyendo los datos de vibracion del punto considerado, resulta que:
$y(x=3, t=0)=y=2\times 10^{-3}Cos[2π(250(0)-3) + ϕ0]=2\times 10^{-3}m \rightarrow Cos(-6\pi +\phi_0)=-1$
Por lo que la fase inicial es: $\phi_0= \pi$ rad
La ecuacion general de la onda es:
$y=2\times 10^{-3}Cos[2\pi(250t-x)+\pi]$
La elongacion del punto x = 2,75 m en el instante pedido es:
$y(x=2.75, t=0)=y=2\times 10^{-3}Cos[2π(250(0)-2.75)+\pi]=Cos(6.5\pi)=0m$
Luisa Alejandra Vega Sanchez (discusión) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez Estefaniantin
Problema Adicional 4
Un oscilador vibra con una frecuencia de 500 Hz y genera ondas que se propagan con una velocidad de 350 m/s.
1. La separacion de dos puntos consecutivos que vibren con una diferencia de fase de 60
2. El intervalo de tiempo que transcurre entre dos estados de vibracion consecutivos de un punto con una diferencia de fase de 180 .
3. Diferencia de fase en un instante cualquiera entre dos puntos separados por una distancia de 3,15 m.
1.-Para hallar la separacion de los funtos con un $\phi$=60 lo cual es equivalente a $\frac{\pi}{3}$ rad
sabiendo que $\lambda=\frac{\upsilon}{v}$=$\frac{500Hz}{350m/s}$=.7m
Por una regla de proporcionalidad a 2$\pi$le corresponden $\lambda=.7m,$por lo que la separacion de los puntos $\triangle x=\frac{\pi}{3}$$\lambda$$\frac{1}{2\pi}$=.117m
2.-Del mismo modo por una regla de proporcionalidad como T=$\frac{1}{\nu}$=$\frac{1}{500Hz}$=2$^{-3}$s
$\triangle t=$$\frac{\pi T}{2\pi}$=$\frac{2(10^{-3})\pi s}{2\pi}$=10$^{-3}s$
3.- Se busca un $\triangle\varphi\triangle\varphi=T\frac{\triangle x}{\lambda}$y usando los valores del punto 1 se obtiene que $\triangle\varphi$=2$\pi\frac{.117m}{.7m}$=2.1
Luisa Alejandra Vega Sanchez (discusión) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez Estefaniantin
Problema adicional 5
Un foco F1 situado en el punto de coordenadas (0,0) entre ondas armónicas transversales de frecuencia 500Hz y amplitud 0.3m. Las ondas se propagan en el sentido positivo del eje x con una velocidad de 250 m/s.
¿Cual es la longitud de onda y el periodo de las ondas emitidas?. Escribir la función de onda
V= 500 Hz , A= 0.3 m, v= 250m/s , donde
es la longitud de onda
es el periodo
La expresión general para la función de onda es
Luisa Alejandra Vega Sanchez (discusión) 23:58 29 mar 2015 (CDT)luisa alejandra vega sanchez Estefaniantin





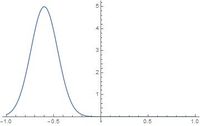






























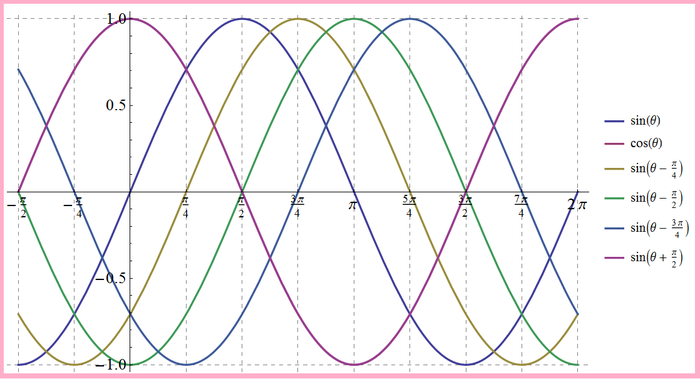
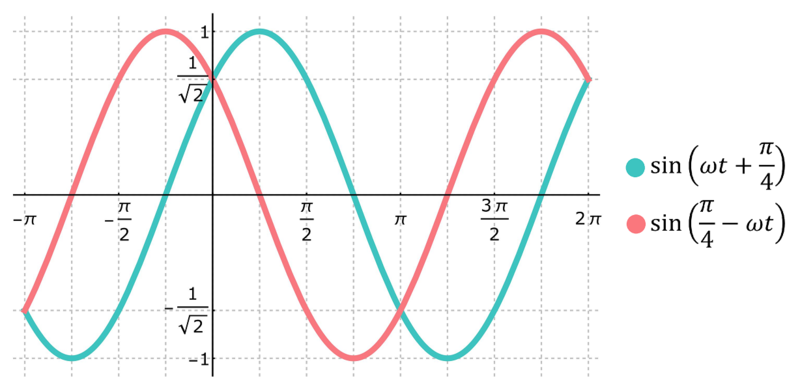






![{\displaystyle \psi (x,t)=A\sin \left[k(x-vt)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e7e8129bb1c29a4a49eb9f8473a3f1d48c5b940c)




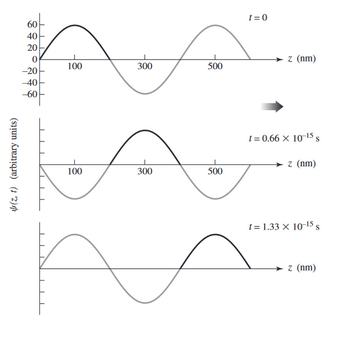














![y(x,t)=A \sin[kx - \omega t + \varepsilon]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6ab4756ac9b801f6d5122c5711658e05619492e1)
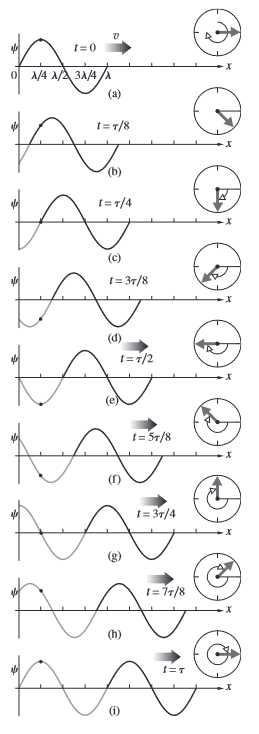









![\psi(x,t)=A\cos\left[kx+\omega t\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/aa9b642964809e58c3a51ef3bfa3d41e9dd78c70)
![\psi(x,t)=\left(10^{3}\right)\cos\left[9.5x10^{6}\left(x+3x10^{8}t\right)\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f668662e1658dca652c6a70cb807cae9392d2b50)

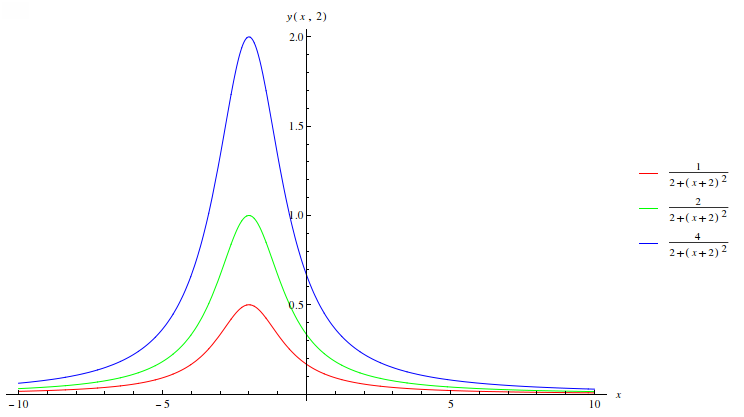
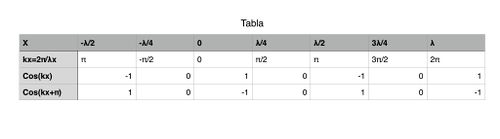
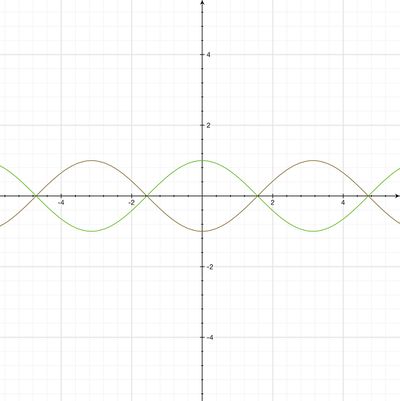







































![\hat{a}= \frac{\left[(4-0)\hat{i} + (2-0)\hat{j} + (1-0)\hat{k} \right]}{\sqrt{4^2 + 2^2 + 1^2}}= \frac{4\hat{i} + 2\hat{j} + 1\hat{k}}{\sqrt{21}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fd74bfa18e7e2e1d721103c96cb905dca67da159)


![\therefore \psi (x,y,z,t)=A*sen \left[\frac{4k}{\sqrt{21}}x + \frac{2k}{\sqrt{21}}y + \frac{k}{\sqrt{21}}z - wt\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8227864efdfc87cfa34e7d948ad0e260efd0e7a3)














