1. Demuestre que el producto de números complejos cumple con la ley asociativa
Sean  con
con 
Por demostrar 
 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
Por otra parte
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)
Entonces se cumple  .
.
--Gabita 22:15 28 sep 2009 (UTC)
1.1.2
1. Demuestre que 
Sean 


![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)
Por otra parte

--Gabita 22:15 28 sep 2009 (UTC)
2. Exprese  de la forma
de la forma 
Por las propiedades  ,
, 

Simplificando, se obtiene:

Resolviendo la división de números complejos, de la forma:
 :
:

= .
.
--Josua Da Vinci 23:00 28 sep 2009 (UTC)
3. Demuestre que  es raiz de un polinomio real si y solo si
es raiz de un polinomio real si y solo si  lo es.
lo es.
Sea  solucion de un polinomio real,
solucion de un polinomio real,
entonces 
como  , por lo tanto
, por lo tanto  tambien es solucion.
tambien es solucion.
--Luis Nava 06:35 30 sep 2009 (UTC)
5. Sean  tales que cumplen
tales que cumplen  , demuestre que estos tres puntos determinan un triángulo equilátero.
, demuestre que estos tres puntos determinan un triángulo equilátero.
Tenemos que

y, por lo tanto,

De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

De (2) y (3) tenemos que:

Por triángulos semejantes, se tiene que el ángulo  es igual al ángulo
es igual al ángulo  y éste a su vez al ángulo
y éste a su vez al ángulo  , es decir,
, es decir,

Y la ecuación (5) es precisamente la condición para que el triángulo ABC de la Figura 1 sea equilátero.
--Belen 02:48 29 sep 2009 (UTC)
6. Sea  , pruebe que
, pruebe que

Puesto que el número complejo z puede escribirse como

![{\begin{align}\left|{z}\right| & = \sqrt{[Re(z)]^2+[Im(z)]^2} \end{align}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6ce755bb71159f65f036bfd5f2fe0558120200fe)
Se deduce que


Como el cuadrado de un número real no puede ser negativo
![{{[\left|{Re(z)}\right|-\left|{Im(z)}\right|]^2}{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/978669b16b44e568056d312dc705389713ab77d3)
Entonces
![{[Re(z)]^2+[Im(z)]^2-2\left|{Re(z)}\right|\left|{Im(z)}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7b0f476c3d8973b1600fca31412b10b1ac7f73a)
O sea
![{{[Re(z)]^2+[Im(z)]^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fed125498b2c36e65792cd5398d4f6b6a81a0ed7)
O de otra manera

Sumando  , a ambos lados se tiene
, a ambos lados se tiene

Como

Entonces

De donde
![{{2\left|{z}\right|^2}{\ge }[\left|{Re(z)}\right|+\left|{Im(z)}\right|]^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/25881ff9f07d97b28f96aa6f6619afa320e7571b)
Sacando raíces cuadradas positivas

Por lo tanto

--Ralf Gutierrez 19:18 29 sep 2009 (UTC)
6-bis. Sea  , pruebe que
, pruebe que

Tenemos que  , entonces de la teoria sabemos que
, entonces de la teoria sabemos que
![{\begin{align}\left|{z}\right| & = \sqrt{[x]^2+[y]^2} \end{align}}\qquad (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cc1a4b669a6ef738a4c62479047618f1e43188f8)


Tambien es inmediato que para z  ,
,  , y que el cuadrado de cualquier numero real es siempre positivo, entonces de esto se tiene que
, y que el cuadrado de cualquier numero real es siempre positivo, entonces de esto se tiene que
![{{[\left|{x}\right|-\left|{y}\right|]^2}{\ge}0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8fa44a4b80670114ab92e33372745f673d1898a)
Desarrollando el binomio se tiene que
![{[x]^2+[y]^2-2\left|{x}\right|\left|{y}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/713aec1fca2fe1b369986232bd50201f383ae306)
![{{[x]^2+[y]^2}{\ge }2\left|{x}\right|\left|{y}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c9e0cd7ac7b4884edd34e46175066247da7544c)
Y por la identidad (1) esto se puede escribir como

Ahora sumando en ambos lados  obtenemos lo siguiente
obtenemos lo siguiente

Pero ademas como  , lo sustituimos en el resultado anterior
, lo sustituimos en el resultado anterior

Es facil ver que
![{{[\left|{x}\right|+\left|{y}\right|]^2}={[x]^2+[y]^2+2\left|{x}\right|\left|{y}\right|}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a6f07c61fcbfff5a8e8ba6b651f1ffea8ea29339)
Utilizando este resultado se deduce que
![{{2\left|{z}\right|^2}{\ge }{[\left|{x}\right|+\left|{y}\right|]^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f96dc4fb554170cf471278862b51cbb43ca3cbe4)
Y tomando las raices positivas llegamos al siguiente resultado

Que es lo que se queria mostrar.
--Oscar Adrian 03:56 1 oct 2009 (UTC)
REVISADO'7. Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.
Archivo:Dibujobueno.jpg
Sacamos las normas de los números complejos
|z|= |w|=
|w|=
Por algebra de vectores

Donde |h| es la resultante de |z|+|w|
 +
+ 
De la misma forma el dibujo nos indica q trasladamos la magnitudes de los vectores
|w| y |z| y por tanto también tendremos |z|+|w| =|h|
Entonces si |z|+|w| = |h|
Aplicando el teorema de pitagoras q nos dice
d = cateto
f = cateto

entonces tenemos que


Aplicamos pitagoras

Por tanto
 se cumple la suma de los cuadrados de los lados es igual a la suma de los cuadrados de la diagonal.
se cumple la suma de los cuadrados de los lados es igual a la suma de los cuadrados de la diagonal.
--Karla 22:47 4 oct 2009 (UTC)Sanchez
1.1.3
'REVISADO'1. Calcule las raìces cuadradas de  y de
y de  .
.
Aplicando la formula para calcular raices cuadradas de numeros complejos.
 si
si 
Por lo tanto las raices de  , son:
, son:



y para  , son:
, son:



--Josua Da Vinci 23:44 30 sep 2009 (UTC)
2.- Calcule las raices sextas de -64 y las raices cubicas de 8i
Tenemos que  definicion en forma polar
definicion en forma polar

r=64
n=6 porque nos piden las raíces sextas
Entonces el argumento 
Si 
Entonces utilizando la definición de Moivre para obtener las raíces

Ahora tenemos
 y g= raíz enesima
y g= raíz enesima  = = 2
= = 2
y  los
los  es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de
es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de  entonces sacando las raíces
entonces sacando las raíces
 k=0
k=0
 k=1
k=1
 k=2
k=2
 k=3
k=3
 k=4
k=4
 k=5
k=5
Las soluciones son
r1= 2 
r2= 2 
r3= 2 
r4= 2 
r5= 2 
r6= 2 
Graficando en coordenadas polares nos queda:
Archivo:POLIGONO2.jpg
Haciendo algo similar para el 8i Tenemos

Archivo:DEMO3.jpg
el argumento 
r= 8
n=3 porque nos pinden las raíces cubicas
 y g= raíz enesima
y g= raíz enesima  = = 2
= = 2

 k=0
k=0
 k=1
k=1
 k=2
k=2
r1= 2 
r2= 2 
r3= 2 
Graficando en coordenadas polares tenemos

--Karla 21:35 4 oct 2009 (UTC)Sanchez
2.- Calcule las raices sextas de -64 y las raices cubicas de 8i
Sea 
Por la formula de De Moivre
 para k = 0,1,2,3,4,5
para k = 0,1,2,3,4,5
Evaluando k se obtiene
con k = 0

con k = 1

con k = 2

con k = 3

con k = 4

con k = 5

..............
Sea 
 para k = 0,1,2
para k = 0,1,2
Evaluando a k se obtiene
con k = 0

con k = 1

con k = 2

--Luis Nava 21:07 3 oct 2009 (UTC)
3. Demuestre que  donde z es una raíz n-ésima de la unidad,
donde z es una raíz n-ésima de la unidad,

Sea 
Ahora multiplicamos ambos lados por Z

Restando la segunda ecuación de la primera

Tenemos que

De donde

Como z es una raíz enesima de la unidad



Entonces

y

porque

Por lo tanto

--Ralf Gutierrez 22:00 2 oct 2009 (UTC)
4. Demuestre que:

Sugerencia: Factoriza la expresión  usando las raices n-ésimas de la unidad, posteriormente evalue en
usando las raices n-ésimas de la unidad, posteriormente evalue en  .
.
Solución:
Las raices de  son
son

entonces podemos escribir

dividiendo ambos lados por  y haciendo
y haciendo  :
:

de aqui hallamos que

tomando el conjugado complejo de ambos lados de (1)

Multiplicando la ecuación (1) por la (2) y aplicando que

tenemos

puesto que

la ecuación anterior se transforma en

despejando y sacando la raíz en ambos lados de la expresión:

lo que queda demostrada la igualdad.
--Wendy 23:10 4 oct 2009 (UTC)
5. Demuestre que
 ,
,
donde  no es un multiplo par de
no es un multiplo par de  .
.
Esta identidad se le atribuye a Lagrange.
Sugerencia: calcular la parte real de
 , donde
, donde  .
.
Solucion.
Sea
 si multiplicamos por
si multiplicamos por  a
a  se tiene que
se tiene que
 ahora restemos estas dos ultimas expresiones
ahora restemos estas dos ultimas expresiones
 de lo que se obtiene que
de lo que se obtiene que

Si en esta última expresion utilizamos  entonces
entonces

toma la siguiente forma

que es equivalente a esta

Tomando el lado derecho de esta ultima expresión y llevar a cabo el producto con su conjugado , es decir:

Se obtiene del numerador lo siguiente

si tomamos solo la parte real se tiene que




por otra parte para el denominador se tiene:



al tomar la parte real de
 ,
,
sustituir lo encontrado para el numerador (parte real) y el denominador , y utilizar la siguiente
identidad

tenemos lo siguiente:

Lo cual es casi a lo que se queria llegar.
--Dali 00:01 5 oct 2009 (UTC)
1.1.4
1. Demuestre que:

Se conoce como igualdad de Lagrange
Solución.
Esta demostración se hará por inducción, es decir, empezaremos suponiendo que el elemento  se encuentra en el conjunto, pues entonces el resultado implica que el elemento
se encuentra en el conjunto, pues entonces el resultado implica que el elemento  esta en el conjunto.
esta en el conjunto.
Sea 
Supongamos que  esta en
esta en  , es decir,
, es decir,

Tenemos que:




Pero veamos la forma que toman las siguientes expresiones al expandir la suma,


Al comparar las expresiones  con
con  se observa que:
se observa que:

Entonces si ahora utilizamos las expresiones  ,
,  e
e  podemos re-escribir
podemos re-escribir  de la manera siguiente:
de la manera siguiente:


![\begin{align}
\aleph=\left|\sum_{k=1}^{n}Z_{k}W_{k}\right|^2 - \overline{Z}_{n}\overline{W}_{n} \sum_{k=1}^n Z_{k}W_{k}-Z_{n}W_{n} \sum_{l=1}^n \overline{Z}_{k}\overline{W}_{k}+ \left|Z_{n}W_{n}\right|^2 - \left[\sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{j}W_{n}- \sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{n}W_{j}- \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j}\overline{Z}_{j}W_{n} + \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j} \overline{Z}_{n}W_{j}\right] + \left|W_{n}\right|^2 \sum_{k=1}^{n-1} \left|Z_{k}\right|^2 + \left|Z_{n}\right|^2 \sum_{l=1}^{n-1} \left|W_{l} \right|^2 + \left|Z_{n}\right|^2 \left|W_{n}\right|^2
\qquad (xi)\\
\end{align}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58db6fac073a7e82f0f422967dcbfe5cdc665a23)





por lo tanto si 




 .
.
--Dali 03:31 14 oct 2009 (UTC)
2.- Sean  numeros complejos, ¿Bajo que condiciones se tiene que
numeros complejos, ¿Bajo que condiciones se tiene que  ?
?
Si  , entonces
, entonces

por otro lado

y por lo tanto

--Luis Nava 02:52 5 oct 2009 (UTC)
2.- Sean  numeros complejos, ¿Bajo que condiciones se tiene que
numeros complejos, ¿Bajo que condiciones se tiene que  ?
?
Tomando como punto de partida la demostracion de la desigualdad del triangulo. Podemos generalizar por medio de la inducción matemática a sumas de cualquier número finito de términos.
 .
.
Es claro ver que cuando n = 2 se cumple la desigualdad del triangulo.

Ahora suponiendo que (1) es válida cuando n=m, debe ser tambien para n=m+1, y aplicando la desigualdad del triangulo:


En donde los primeros m terminos los redefiniremos como Z y el termino m+1 como Z
y el termino m+1 como Z . Entonces lo anterior queda como:
. Entonces lo anterior queda como:

Ahora escribiendolo como igualdad


Esta desigualdad solo se cumple como igualdad cuando los numeros son colineales y tienen la misma direccion, esto tambien puede ser en los real (Re) o el imaginario (Im).
Esto es muy claro ver cuando n=2, en una grafica.
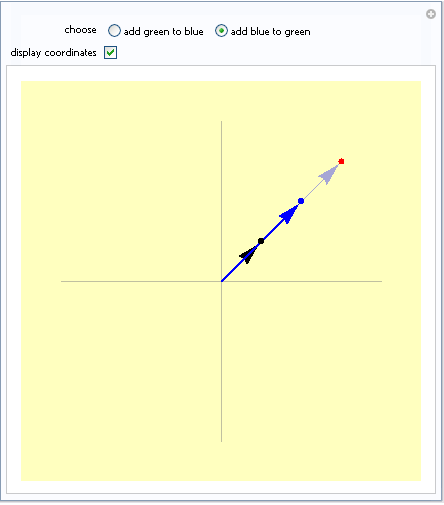
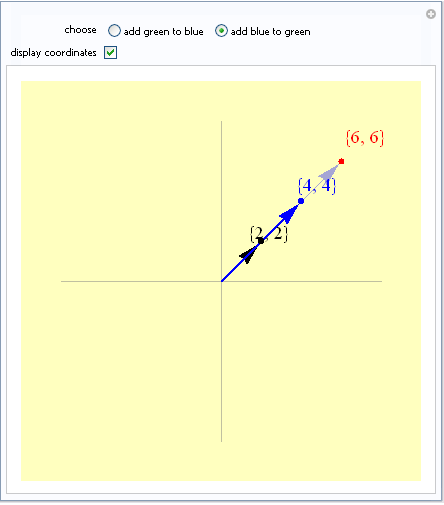
Aquí les dejo el enlace de la pagina donde consulte el código para generar las graficas para los que les interese.
Demostracion grafica
--Oscar Adrian 03:41 16 oct 2009 (UTC)
--Oscar Adrian 03:07 6 oct 2009 (UTC)
3. Encuentre el ínfimo de  en la región
en la región  , y describa en qué puntos se alcanza.
, y describa en qué puntos se alcanza.
Con una variante de la desigualdad del triángulo, tenemos que

Por tanto,

Entonces, el ínfimo de la expresión es 7.
Por otro lado, tenemos que, si 

Si tomamos la cota inferior,  , la expresión anterior es entonces:
, la expresión anterior es entonces:

Ya que la función coseno tiene su mínimo en el valor -1, tomemos una  tal que
tal que  . Para este caso, tenemos dos valores:
. Para este caso, tenemos dos valores:  y
y  ,
,
de tal forma que, con estos valores,

Con la fórmula de De Moivre, tenemos que el ínfimo de la expresión dada toma ese valor en  y
y  tales que
tales que

y

Pero, además, por le geometría de los números complejos, tenemos otros dos valores  y
y  tales que
tales que

y

Por tanto, las expresiones (2), (3), (4) y (5) nos proporcionan los valores en que el ínfimo es tomado, a saber,  y
y  .
.
--Belen 04:08 12 oct 2009 (UTC)
Compleja:ej-cap1.2



 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)




![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)


























![{\begin{align}\left|{z}\right| & = \sqrt{[Re(z)]^2+[Im(z)]^2} \end{align}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6ce755bb71159f65f036bfd5f2fe0558120200fe)


![{{[\left|{Re(z)}\right|-\left|{Im(z)}\right|]^2}{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/978669b16b44e568056d312dc705389713ab77d3)
![{[Re(z)]^2+[Im(z)]^2-2\left|{Re(z)}\right|\left|{Im(z)}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d7b0f476c3d8973b1600fca31412b10b1ac7f73a)
![{{[Re(z)]^2+[Im(z)]^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/fed125498b2c36e65792cd5398d4f6b6a81a0ed7)





![{{2\left|{z}\right|^2}{\ge }[\left|{Re(z)}\right|+\left|{Im(z)}\right|]^2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/25881ff9f07d97b28f96aa6f6619afa320e7571b)


![{\begin{align}\left|{z}\right| & = \sqrt{[x]^2+[y]^2} \end{align}}\qquad (1)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/cc1a4b669a6ef738a4c62479047618f1e43188f8)




![{{[\left|{x}\right|-\left|{y}\right|]^2}{\ge}0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d8fa44a4b80670114ab92e33372745f673d1898a)
![{[x]^2+[y]^2-2\left|{x}\right|\left|{y}\right|{\ge }0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/713aec1fca2fe1b369986232bd50201f383ae306)
![{{[x]^2+[y]^2}{\ge }2\left|{x}\right|\left|{y}\right|}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4c9e0cd7ac7b4884edd34e46175066247da7544c)




![{{[\left|{x}\right|+\left|{y}\right|]^2}={[x]^2+[y]^2+2\left|{x}\right|\left|{y}\right|}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a6f07c61fcbfff5a8e8ba6b651f1ffea8ea29339)
![{{2\left|{z}\right|^2}{\ge }{[\left|{x}\right|+\left|{y}\right|]^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f96dc4fb554170cf471278862b51cbb43ca3cbe4)







































































































































![\begin{align}
\aleph=\left|\sum_{k=1}^{n}Z_{k}W_{k}\right|^2 - \overline{Z}_{n}\overline{W}_{n} \sum_{k=1}^n Z_{k}W_{k}-Z_{n}W_{n} \sum_{l=1}^n \overline{Z}_{k}\overline{W}_{k}+ \left|Z_{n}W_{n}\right|^2 - \left[\sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{j}W_{n}- \sum_{j=1}^{n-1} Z_{j}\overline{W}_{n}\overline{Z}_{n}W_{j}- \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j}\overline{Z}_{j}W_{n} + \sum_{j=1}^{n-1} Z_{n}\overline{W}_{j} \overline{Z}_{n}W_{j}\right] + \left|W_{n}\right|^2 \sum_{k=1}^{n-1} \left|Z_{k}\right|^2 + \left|Z_{n}\right|^2 \sum_{l=1}^{n-1} \left|W_{l} \right|^2 + \left|Z_{n}\right|^2 \left|W_{n}\right|^2
\qquad (xi)\\
\end{align}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58db6fac073a7e82f0f422967dcbfe5cdc665a23)















































