Diferencia entre revisiones de «Compleja:ej-cap1.1»

Revisión del 22:28 6 dic 2009

1. Demuestre que el producto de números complejos cumple con la ley asociativa

Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = a + i b, \quad w = c + i d, \quad s = e + i f \, \quad con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \quad a,b,c,d,e,f \in \mbox{R}

Por demostrar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (zw)s = z(ws)\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (zw)s = [(a + i b)(c + i d)](e + i f) = [(ac - bd) + i (bc + ad)](e + i f)\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,

Por otra parte

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,

Entonces se cumple Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (zw)s = z(ws)\, .

--Gabita 22:15 28 sep 2009 (UTC)

SECCION 1.1.2

1. Demuestre que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left|\frac{z}{w}\right| = \frac{\left|z\right|}{\left|w\right|}

Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = a + i b \quad y \quad w = c + i d\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left|\frac{z}{w}\right|= \left|\frac{a + i b }{c + i d}\right|= \left|\frac{(a + i b)(c - i d)}{(c + i d)(c - i d)}\right|

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\left|\frac{(ac + bd) + i (bc - ad)}{c^2 + d^2}\right|= \sqrt{\bigg ( \frac{ac + bd}{c^2 + d^2}\bigg )^2 + \bigg (\frac{bc - ad}{c^2 + d^2}\bigg )^2} = \frac{1}{c^2 + d^2}\sqrt{ (ac + bd)^2 + (bc - ad)^2 }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2 } = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] } = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}

Por otra parte

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\left|z\right|}{\left|w\right|} = \frac{\left|a + i b\right|}{\left|c + i d\right|} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}} = \left|\frac{z}{w}\right|

--Gabita 22:15 28 sep 2009 (UTC)

2. Exprese Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\left(\frac{\left(2+3i\right)^2}{4+i}\right)} de la forma Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x+iy

Por las propiedades Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\left ( \frac{z}{w} \right )}=\frac\bar{z}\bar{w} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{zw}=\bar{z}\bar{w}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\overline{\left ({2+3i}\right)^2}}{\overline{\left({4+i}\right)}}=\frac{\overline{\left ({2+3i}\right)}\overline{\left ({2+3i}\right)}}{\overline{\left({4+i}\right)}}=\frac{\left(2-3i\right)\left(2-3i\right)}{\left(4-i\right)}

Simplificando, se obtiene:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{4-6i-6i-9}{4-i}=\frac{-5-12i}{4-i}

Resolviendo la división de números complejos, de la forma:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{z}{w}=\frac{z\bar{w}}{w\bar{w}}=\frac{z\bar{w}}{\left|w\right|^2} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\left(-5-12i\right)\left(4+i\right)}{\left(4-i\right)\left(4+i\right)}=\frac{-20-5i-48i+12}{17}=\frac{-8-53i}{17}

=Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): -\frac{8}{17}-\frac{53}{17}i .

--Josua Da Vinci 23:00 28 sep 2009 (UTC)

3. Demuestre que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha es raiz de un polinomio real si y solo si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\alpha} lo es.

Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\alpha} solucion de un polinomio real,

entonces Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\alpha} \in \mathbb{R}

como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline{\alpha} = \alpha , por lo tanto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha tambien es solucion.

--Luis Nava 06:35 30 sep 2009 (UTC)

5. Sean Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z_1 , z_2 , z_3 \in \mathbb{C} tales que cumplen Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{z_2 - z_1}{z_3 - z_1} = \frac{z_1 - z_3}{z_2 - z_3} , demuestre que estos tres puntos determinan un triángulo equilátero.

Archivo:Comp triang eq2.jpg

Figura 1

Tenemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left | \frac{z_2 - z_1}{z_3 - z_1} \right | = \left | \frac{z_1 - z_3}{z_2 - z_3} \right |,\qquad (1)

y, por lo tanto,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{|z_2 - z_1|}{|z_3 - z_1|} = \frac{|z_1 - z_3|}{|z_2 - z_3|}.\qquad (2)

De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left . \begin{matrix}|z_2 - z_1| = A\\ |z_3 - z_1| = B = |z_1 - z_3|\\ |z_2 - z_3| = C\\ \end{matrix} \right \} \qquad (3)

De (2) y (3) tenemos que:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{A}{B} = \frac{B}{C}. \qquad (4)

Por triángulos semejantes, se tiene que el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \beta es igual al ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \gamma y éste a su vez al ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha , es decir,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha = \beta = \gamma. \qquad (5)

Y la ecuación (5) es precisamente la condición para que el triángulo ABC de la Figura 1 sea equilátero.

--Belen 02:48 29 sep 2009 (UTC)

6. Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}z & = x+iy \end{align}} , pruebe que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{x}\right|+\left|{y}\right|}{\le}{\sqrt{2} \ \left|{z}\right|}

Puesto que el número complejo z puede escribirse como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}z & = Re(z)+iIm(z) \end{align}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}\left|{z}\right| & = \sqrt{[Re(z)]^2+[Im(z)]^2} \end{align}}

Se deduce que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{z}\right|}{\ge }{\left|{Re(z)}\right|}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{z}\right|}{\ge }{\left|{Im(z)}\right|}

Como el cuadrado de un número real no puede ser negativo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{[\left|{Re(z)}\right|-\left|{Im(z)}\right|]^2}{\ge }0}

Entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {[Re(z)]^2+[Im(z)]^2-2\left|{Re(z)}\right|\left|{Im(z)}\right|{\ge }0}

O sea

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{[Re(z)]^2+[Im(z)]^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}

O de otra manera

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\left|{z}\right|^2}{\ge }2\left|{Re(z)}\right|\left|{Im(z)}\right|}

Sumando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{z}\right|^2} , a ambos lados se tiene

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{2\left|{z}\right|^2}{\ge }\left|{z}\right|^2+2\left|{Re(z)}\right|\left|{Im(z)}\right|}

Como

${\begin{aligned}\left|{z}\right|^{2}&=\left|{Re(z)}\right|^{2}+\left|{Im(z)}\right|^{2}\end{aligned}}$

Entonces

${{2\left|{z}\right|^{2}}{\geq }\left|{Re(z)}\right|^{2}+\left|{Im(z)}\right|^{2}+2\left|{Re(z)}\right|\left|{Im(z)}\right|}$

De donde

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{2\left|{z}\right|^2}{\ge }[\left|{Re(z)}\right|+\left|{Im(z)}\right|]^2}

Sacando raíces cuadradas positivas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\sqrt{2} \ \left|{z}\right|}{\ge} \left|{Re(z)}\right|+\left|{Im(z)}\right|}

Por lo tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\sqrt{2} \ \left|{z}\right|}{\ge}{\left|{x}\right|+\left|{y}\right|}}

--Ralf Gutierrez 19:18 29 sep 2009 (UTC)

6-bis. Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}z & = x+iy \end{align}} , pruebe que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{x}\right|+\left|{y}\right|}{\le}{\sqrt{2} \ \left|{z}\right|}

Tenemos que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}z & = x+iy \end{align}} , entonces de la teoria sabemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\begin{align}\left|{z}\right| & = \sqrt{[x]^2+[y]^2} \end{align}}\qquad (1)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{x}\right|=\left|{Re(z)}\right|}{\le}{ \left|{z}\right|}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\left|{y}\right|=\left|{Im(z)}\right|}{\le}{ \left|{z}\right|}

Tambien es inmediato que para z Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \in \mathbb{R} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \overline z = z , y que el cuadrado de cualquier numero real es siempre positivo, entonces de esto se tiene que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{[\left|{x}\right|-\left|{y}\right|]^2}{\ge}0}

Desarrollando el binomio se tiene que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {[x]^2+[y]^2-2\left|{x}\right|\left|{y}\right|{\ge }0}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{[x]^2+[y]^2}{\ge }2\left|{x}\right|\left|{y}\right|}

Y por la identidad (1) esto se puede escribir como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\left|{z}\right|^2}{\ge }2\left|{x}\right|\left|{y}\right|}

Ahora sumando en ambos lados Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\left|{z}\right|^2}} obtenemos lo siguiente

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{2\left|{z}\right|^2}{\ge }\left|{z}\right|^2+2\left|{x}\right|\left|{y}\right|}

Pero ademas como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{\left|{z}\right|^2}={\left|{x}\right|^2}+{\left|{y}\right|^2}} , lo sustituimos en el resultado anterior

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{2\left|{z}\right|^2}{\ge }\left|{x}\right|^2}+{\left|{y}\right|^2+2\left|{x}\right|\left|{y}\right|}

Es facil ver que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{[\left|{x}\right|+\left|{y}\right|]^2}={[x]^2+[y]^2+2\left|{x}\right|\left|{y}\right|}}

Utilizando este resultado se deduce que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {{2\left|{z}\right|^2}{\ge }{[\left|{x}\right|+\left|{y}\right|]^2}}

Y tomando las raices positivas llegamos al siguiente resultado

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\sqrt{2}\left|{z}\right|}{\ge }{\left|{x}\right|+\left|{y}\right|}

Que es lo que se queria mostrar.

--Oscar Adrian 03:56 1 oct 2009 (UTC)

REVISADO

7. Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.

Archivo:Dibujobueno.jpg

Sacamos las normas de los números complejos

|z|=Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{(a)^2+(b)^2} |w|=Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{(c)^2+(d)^2}

Por algebra de vectores

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): |z|+|w|=|h|

Donde |h| es la resultante de |z|+|w|

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{(a)^2+(b)^2} + Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{(c)^2+(d)^2}=|h|

De la misma forma el dibujo nos indica q trasladamos la magnitudes de los vectores

|w| y |z| y por tanto también tendremos |z|+|w| =|h|

Entonces si |z|+|w| = |h|

Aplicando el teorema de pitagoras q nos dice

d = cateto

f = cateto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^2=d^2+f^2

entonces tenemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (a)^2+(b)^2=|z|^2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (c)^2+(d)^2=|w|^2

Aplicamos pitagoras

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (c)^2+(d)^2+(a)^2+(b)^2=(c)^2+(d)^2+(a)^2+(b)^2

Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): |z|^2 +|w|^2 = |h|^2 se cumple la suma de los cuadrados de los lados es igual a la suma de los cuadrados de la diagonal.

--Karla 22:47 4 oct 2009 (UTC)Sanchez

SECCION 1.1.3

1. Calcule las raìces cuadradas de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 3+4i y de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+2i .

Aplicando la formula para calcular raices cuadradas de numeros complejos.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \pm\left(\sqrt{\frac{a+\sqrt{a^2+b^2}}{2}} + i\sqrt{\frac{-a+\sqrt{a^2+b^2}}{2}}\right) si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \quad b>0

Por lo tanto las raices de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 3+4i , son:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(\sqrt{\frac{3+\sqrt{25}}{2}} + i\sqrt{\frac{-3+\sqrt{25}}{2}}\right)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(\sqrt{\frac{8}{2}} + i\sqrt{1}\right)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(2+i\right)

y para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+2i , son:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(\sqrt{\frac{1+\sqrt{5}}{2}} + i\sqrt{\frac{-1+\sqrt{5}}{2}}\right)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(\sqrt{1.61} + i\sqrt{0.61}\right)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): =\pm\left(1.27 + i 0.78\right).

--Josua Da Vinci 23:44 30 sep 2009 (UTC)

REVISADO

2.- Calcule las raices sextas de -64 y las raices cubicas de 8i

Tenemos que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): cos\boldsymbol{\theta}+i sen\boldsymbol{\theta}= -64 definicion en forma polar

r=64

n=6 porque nos piden las raíces sextas

Entonces el argumento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi

Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): x+iy=re^{i\boldsymbol{\theta}}

Entonces utilizando la definición de Moivre para obtener las raíces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (g e^{i\boldsymbol{\phi}n})= r e^{i\boldsymbol{\theta}}

Ahora tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): g^n=r y g= raíz enesima Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{64} = = 2

y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\phi}n=\boldsymbol{\theta}+2k\pi los Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2\pi es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2\pi entonces sacando las raíces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/6 k=0

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi / 6 + 2\pi / 6 = 3\pi / 6 k=1

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/6+2(2)\pi/6= 5\pi/6 k=2

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/6+(3)2\pi/6= 7\pi/6 k=3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/6+2(4)\pi/6= 9\pi/6 k=4

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/6+2(5)\pi/6= 11\pi/6 k=5

Las soluciones son

r1= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( \pi/6)}

r2= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 3\pi/6)}

r3= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 5\pi/6)}

r4= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 7\pi/6)}

r5= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 9\pi/6)}

r6= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 11\pi/6)}

Graficando en coordenadas polares nos queda:

Archivo:POLIGONO2.jpg

Haciendo algo similar para el 8i Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): cos\boldsymbol{\theta}+i sen\boldsymbol{\theta}= 8i

Archivo:DEMO3.jpg

el argumento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\theta}=\pi/2

r= 8

n=3 porque nos pinden las raíces cubicas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): g^n=r y g= raíz enesima Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \sqrt{8} = = 2

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\phi}n = \boldsymbol{\theta}+2k\pi

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\phi} = \boldsymbol{\theta}+2k\pi =\pi/6 k=0

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\phi}=\pi/6+2\pi/3= 5\pi/6 k=1

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \boldsymbol{\phi}==\pi/6+2(2)\pi/3= 9\pi/6 k=2

r1= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( \pi/6)}

r2= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 5\pi/6)}

r3= 2 Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): e^{i( 9\pi/6)}

Graficando en coordenadas polares tenemos

--Karla 21:35 4 oct 2009 (UTC)Sanchez

2.- Calcule las raices sextas de -64 y las raices cubicas de 8i

Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = -64 = 64(cos\pi + isen\pi)\,

Por la formula de De Moivre

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z^{1/6} = 64^{1/6}(cos\pi + sen\pi)^{1/6} = 2 (cos(\frac{\pi+2k\pi}{6}) + isen(\frac{\pi+2k\pi}{6})) para k = 0,1,2,3,4,5

Evaluando k se obtiene

con k = 0

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{0} = 2(cos(\frac{\pi}{6}) + isen(\frac{\pi}{6})) = \sqrt{3} + i

con k = 1

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{1} = 2(cos(\frac{\pi+2\pi}{6}) + isen(\frac{\pi+2\pi}{6})) = 2(cos(\frac{\pi}{2}) + isen(\frac{\pi}{2})) = 2i

con k = 2

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{2} = 2(cos(\frac{\pi+4\pi}{6}) + isen(\frac{\pi+4\pi}{6})) = 2(cos(\frac{5\pi}{6}) + isen(\frac{5\pi}{6})) = -\sqrt{3} + i

con k = 3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{3} = 2(cos(\frac{\pi+6\pi}{6}) + isen(\frac{\pi+6\pi}{6})) = 2(cos(\frac{7\pi}{6}) + isen(\frac{7\pi}{6})) = -\sqrt{3} - i

con k = 4

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{4} = 2(cos(\frac{\pi+8\pi}{6}) + isen(\frac{\pi+8\pi}{6})) = 2(cos(\frac{3\pi}{2}) + isen(\frac{3\pi}{2})) = -2i

con k = 5

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{5} = 2(cos(\frac{\pi+10\pi}{6}) + isen(\frac{\pi+10\pi}{6})) = 2(cos(\frac{11\pi}{6}) + isen(\frac{11\pi}{6})) = \sqrt{3} - i

..............

Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z = 8i = 8(cos(\frac{\pi}{2}) + sen(\frac{\pi}{2})\,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z^{1/3} = 8^{1/3}(cos(\frac{\pi}{2}) + isen(\frac{\pi}{2}))^{1/3} = 2(cos(\frac{\frac{\pi}{2}+2k\pi}{3}) + isen(\frac{\frac{\pi}{2}+2k\pi}{3})) para k = 0,1,2

Evaluando a k se obtiene

con k = 0

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{0} = 2(cos(\frac{\pi}{6}) + isen(\frac{\pi}{6}) = \sqrt{3} + i

con k = 1

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{1} = 2(cos(\frac{\frac{\pi}{2}+2\pi}{3}) + isen(\frac{\frac{\pi}{2}+2\pi}{3})) = 2(cos(\frac{5\pi}{6}) + isen(\frac{5\pi}{6}) = -\sqrt{3} + i

con k = 2

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): w_{2} = 2(cos(\frac{\frac{\pi}{2}+4\pi}{3}) + isen(\frac{\frac{\pi}{2}+4\pi}{3})) = 2(cos(\frac{3\pi}{2}) + isen(\frac{3\pi}{2})) = -2i

--Luis Nava 21:07 3 oct 2009 (UTC)

3. Demuestre que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ 1+Z+Z^2+...+Z^{n-1}=0 donde z es una raíz n-ésima de la unidad, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z\neq 1

Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ S=1+Z+Z^2+...+Z^{n-1}

Ahora multiplicamos ambos lados por Z

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ ZS=Z+Z^2+Z^3+...+Z^{n-1}+Z^n

Restando la segunda ecuación de la primera

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {(s=1+z+z^2+...+z^{n-1})-(zs=z+^2+z^3+...+z^{n-1}+z^n)}

Tenemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {s-zs=1-z^n}

entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {s(1-z)=1-z^n}

De donde

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): s=\frac{1-z^n}{1-z}

Como z es una raíz enesima de la unidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 0=\frac{1-z^n}{1-z}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {1-z^n=0}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {z^n=1}

Entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \ {z^n=1}

y

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {1-z}\ne{0}

porque

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {z}\ne{1}

Por lo tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {s=0}

--Ralf Gutierrez 22:00 2 oct 2009 (UTC)

4. Demuestre que:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{n}{2^{n-1}}=\prod_{k=1}^{n-1}\sin\frac{\pi}{k}

Sugerencia: Factoriza la expresión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+z+z^2+\cdots+z^n usando las raices n-ésimas de la unidad, posteriormente evalue en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z=1 .

Solución:

Las raices de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z^m=1 son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z=1,e^{\frac{2\pi i}{m}},e^{\frac{4\pi i}{m}},\dots,e^{\frac{(2m-1)\pi i}{m}}

entonces podemos escribir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z^{m-1}=(z-e^{\frac{2\pi i}{m}})(z-e^{\frac{4\pi i}{m}})\cdots(z-e^{\frac{(2m-1)\pi i}{m}})

dividiendo ambos lados por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z-1 y haciendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z=1 :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{z^{m-1}}{z-1}=1+z+z^2+\cdots+z^{m-1}

de aqui hallamos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): m=(1-e^{\frac{2\pi i}{m}})(1-e^{\frac{4\pi i}{m}})\cdots(1-e^{\frac{(2m-1)\pi i}{m}})\qquad (1)

tomando el conjugado complejo de ambos lados de (1)

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): m=(1-e^{\frac{-2\pi i}{m}})(1-e^{\frac{-4\pi i}{m}})\cdots(1-e^{\frac{-(2m-1)\pi i}{m}})\qquad (2)

Multiplicando la ecuación (1) por la (2) y aplicando que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-(1-e^{\frac{2k\pi i}{m}})(1-e^{\frac{2k\pi i}{m}})= 2 - 2\cos\frac{2k\pi}{m}

tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): m^2=2^{m-1}(1-\cos\frac{2\pi}{m})(1-\cos\frac{4\pi}{m})\cdots(1-\cos\frac{2(m-1)\pi}{m})

puesto que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-\cos\frac{2k\pi}{m}=2\sin^2\frac{k\pi}{m}

la ecuación anterior se transforma en

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): m^2=2^{2m-2}(\sin^2\frac{\pi}{m})(\sin^2\frac{2\pi}{m})\cdots(\sin^2\frac{(m-1)\pi}{m})

despejando y sacando la raíz en ambos lados de la expresión:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{m}{2^{m-1}}=(\sin\frac{\pi}{m})(\sin\frac{2\pi}{m})\cdots(\sin\frac{(m-1)\pi}{m})

lo que queda demostrada la igualdad. --Wendy 23:10 4 oct 2009 (UTC)

5. Demuestre que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+cos\phi+cos2\phi+...............+cos n\phi=\frac{1}{2}+\frac{sen\left(n\phi+\frac{\phi}{2}\right)}{2sen\left(\frac{\phi}{2}\right)} ,

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \phi no es un multiplo par de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \pi .

Esta identidad se le atribuye a Lagrange.

Sugerencia: calcular la parte real de

$1+z+z^{2}+..........+z^{n}$ , donde $z=cos\phi +isen\phi$ .

Solucion.

Sea

$S=1+z+z^{2}+.......+z^{n}$ si multiplicamos por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): S se tiene que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): zS=z+z^{2}+z^{3}+......+z^{n}+z^{n+1} ahora restemos estas dos ultimas expresiones

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left(S-zS\right)=\left(1-z\right)S=1-z^{n+1} de lo que se obtiene que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): S=\frac{1-z^{n+1}}{1-z}

Si en esta última expresion utilizamos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): z=cos\phi+isen\phi entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): S=\frac{1-z^{n+1}}{1-z}

toma la siguiente forma

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+\left(cos\phi+isen\phi\right)+\left(cos\phi+isen\phi\right)^{2}+........+\left(cos\phi+isen\phi\right)^{n}=\frac{1-\left(cos\phi+isen\phi\right)^{n+1}}{1-\left(cos\phi+isen\phi\right)}

que es equivalente a esta

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+\left(cos\phi+isen\phi\right)+\left(cos2\phi+isen2\phi\right)+........+\left(cosn\phi+isen\left(n\phi\right)\right)=\frac{1-\left(cos\left(n+1\right)\phi+isen\left(n+1\right)\phi\right)}{1-\left(cos\phi+isen\phi\right)}

Tomando el lado derecho de esta ultima expresión y llevar a cabo el producto con su conjugado , es decir:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left(\frac{1-cos\left(n\phi+\phi\right)-isen\left(n\phi+\phi\right)}{1-cos\phi-isen\phi}\right)\star\left(\frac{1-cos\phi+isen\phi}{1-cos\phi+isen\phi}\right)

Se obtiene del numerador lo siguiente

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-cos\phi+isen\phi-cosn\left(n\phi+\phi\right)+cos\phi cos\left(n\phi+\phi\right)-isen\phi cos\left(n\phi+\phi\right)-isen\left(n\phi+\phi\right)+icos\phi sen\left(n\phi+\phi\right)+sen\phi sen\left(n\phi+\phi\right)

si tomamos solo la parte real se tiene que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-cos\phi-cos\left(n\phi+\phi\right)+cos\phi cos\left(n\phi+\phi\right)+sen\phi sen\left(n\phi+\phi\right)=

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-cos\phi+cos\left(n\phi-\phi\right)-cos\left(n\phi+\phi\right) Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): = Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-cos\phi+2sen\phi sen\phi

por otra parte para el denominador se tiene:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \left(1-cos\phi\right)^{2}+sen^{2}\phi=

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1-2cos\phi+sen^{2}\phi+cos^{2}\phi= Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2\left(1-cos\phi\right)

al tomar la parte real de

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+\left(cos\phi+isen\phi\right)+\left(cos2\phi+isen2\phi\right)+........+\left(cosn\phi+isenn\phi\right)=\frac{1-\left(cos\left(n+1\right)\phi+isen\left(n+1\right)\phi\right)}{1-\left(cos\phi+isen\phi\right)} ,

sustituir lo encontrado para el numerador (parte real) y el denominador , y utilizar la siguiente identidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): sen\left(\frac{\phi}{2}\right)=\sqrt{\frac{1-cos\phi}{2}}

tenemos lo siguiente:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 1+cos\phi+cos2\phi+...............+cosn\phi=\frac{2sen\left(\frac{\phi}{2}\right)+sen\phi sen\left(n\phi\right)}{2\left(2sen\left(\frac{\phi}{2}\right)\right)}=\frac{1}{2}+\frac{sen\phi sen\left(n\phi\right)}{2sen\left(\frac{\phi}{2}\right)}

Lo cual es casi a lo que se queria llegar.

--Dali 00:01 5 oct 2009 (UTC)

1.1.4

1. Demuestre que:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \begin{align}\left | \textstyle \sum_{k=1}^n Z_{k}W_{k} \right | ^2 = \left (\sum_{k=1}^n \left| Z_{k} \right|^2 \right) \left(\sum_{k=1}^n \left| W_{k} \right|^2 \right) -\sum_{1<j<k\leq n} \left|Z_{j}\overline{W}_{k}-Z_{k}\overline{W}_{j}\right|^2. \qquad (I)\\ \end{align}

Se conoce como igualdad de Lagrange

Solución.

Esta demostración se hará por inducción, es decir, empezaremos suponiendo que el elemento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): n-1 se encuentra en el conjunto, pues entonces el resultado implica que el elemento $n$ esta en el conjunto.

Sea $\eth =\left\{\omega \in \mathbb {N\,} tal\,que\left(I\right)\,se\,cumpla\right\}$

Supongamos que $n-1$ esta en $\eth$ , es decir,

{\begin{aligned}\left|\textstyle \sum _{k=1}^{n-1}Z_{k}W_{k}\right|=\left(\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}\right)\left(\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}\right)-\sum _{1<j<k<n-1}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}\qquad (i)\\\end{aligned}}

Tenemos que:

{\begin{aligned}\aleph =\left(\sum _{k=1}^{n}\left|Z_{k}\right|^{2}\right)\left(\sum _{l=1}^{n}\left|W_{l}\right|^{2}\right)-\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}\qquad (ii)\\\end{aligned}}

{\begin{aligned}\aleph =\left(\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\right)\left(\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|W_{n}\right|^{2}\right)-\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}\qquad (iii)\\\end{aligned}}

{\begin{aligned}\aleph =\left(\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}\right)\left(\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}\right)+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}-\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}\qquad (iv)\\\end{aligned}}

{\begin{aligned}\aleph =\left(\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}\right)\left(\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}\right)-\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (v)\\\end{aligned}}

Pero veamos la forma que toman las siguientes expresiones al expandir la suma,

{\begin{aligned}\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}=\left|Z_{1}{\overline {W}}_{2}-Z_{2}{\overline {W}}_{1}\right|^{2}+\left|Z_{1}{\overline {W}}_{3}-Z_{3}{\overline {W}}_{1}\right|^{2}+..............+\left|Z_{1}{\overline {W}}_{n}-Z_{1}{\overline {W}}_{n}\right|^{2}+...........+\left|Z_{2}{\overline {W}}_{3}-Z_{3}{\overline {W}}_{2}\right|^{2}+...........+\left|Z_{2}{\overline {W}}_{n}-Z_{n}{\overline {W}}_{2}\right|^{2}+..........+\left|Z_{n-1}{\overline {W}}_{n}-Z_{n}{\overline {W}}_{n-1}\right|^{2}\qquad (vi)\\\end{aligned}}

{\begin{aligned}\sum _{1<j<k\leq n-1}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}=\left|Z_{1}{\overline {W}}_{2}-Z_{2}{\overline {W}}_{1}\right|^{2}+\left|Z_{1}{\overline {W}}_{3}-Z_{3}{\overline {W}}_{1}\right|^{2}+..........+\left|Z_{1}{\overline {W}}_{n-1}-Z_{n-1}{\overline {W}}_{1}\right|^{2}+..........+\left|Z_{2}{\overline {W}}_{3}-Z_{3}{\overline {W}}_{2}\right|^{2}+...........+\left|Z_{2}{\overline {W}}_{n-1}-Z_{n-1}{\overline {W}}_{2}\right|^{2}+...........+\left|Z_{n-2}{\overline {W}}_{n-1}-Z_{n-1}{\overline {W}}_{n-2}\right|^{2}\qquad (vii)\\\end{aligned}}

Al comparar las expresiones $vi$ con $vii$ se observa que:

{\begin{aligned}\sum _{1<j<k\leq n}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}=\sum _{1<j<k\leq n-1}\left|Z_{j}{\overline {W}}_{k}-Z_{k}{\overline {W}}_{j}\right|^{2}+\sum _{j=1}^{n-1}\left|Z_{j}{\overline {W}}_{n}-Z_{n}{\overline {W}}_{j}\right|^{2}\qquad (viii)\\\end{aligned}}

Entonces si ahora utilizamos las expresiones $viii$ , $I$ e $i$ podemos re-escribir $\aleph$ de la manera siguiente:

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n-1}Z_{k}W_{k}\right|^{2}-\sum _{j=1}^{n-1}\left|Z_{j}{\overline {W}}_{n}-Z_{n}{\overline {W}}_{j}\right|^{2}+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (ix)\\\end{aligned}}

{\begin{aligned}\aleph =\left(\sum _{k=1}^{n}Z_{k}W_{k}-Z_{n}W_{n}\right)\left(\sum _{l=1}^{n}{\overline {Z}}_{k}{\overline {W}}_{k}-{\overline {Z}}_{n}{\overline {W}}_{n}\right)-\sum _{j=1}^{n-1}\left(Z_{j}{\overline {W}}_{n}-Z_{n}{\overline {W}}_{j}\right)\left({\overline {Z}}_{j}W_{n}-{\overline {Z}}_{n}W_{j}\right)+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (x)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}-{\overline {Z}}_{n}{\overline {W}}_{n}\sum _{k=1}^{n}Z_{k}W_{k}-Z_{n}W_{n}\sum _{l=1}^{n}{\overline {Z}}_{k}{\overline {W}}_{k}+\left|Z_{n}W_{n}\right|^{2}-\left[\sum _{j=1}^{n-1}Z_{j}{\overline {W}}_{n}{\overline {Z}}_{j}W_{n}-\sum _{j=1}^{n-1}Z_{j}{\overline {W}}_{n}{\overline {Z}}_{n}W_{j}-\sum _{j=1}^{n-1}Z_{n}{\overline {W}}_{j}{\overline {Z}}_{j}W_{n}+\sum _{j=1}^{n-1}Z_{n}{\overline {W}}_{j}{\overline {Z}}_{n}W_{j}\right]+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (xi)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}-{\overline {Z}}_{n}{\overline {W}}_{n}\sum _{k=1}^{n}Z_{k}W_{k}-Z_{n}W_{n}\sum _{k=1}^{n}{\overline {Z}}_{k}{\overline {W}}_{k}+\left|Z_{n}W_{n}\right|^{2}-W_{n}{\overline {W}}_{n}\sum _{j=1}^{n-1}Z_{j}{\overline {Z}}_{j}+{\overline {W}}_{n}{\overline {Z}}_{n}\sum _{j=1}^{n-1}Z_{j}W_{j}+W_{n}Z_{n}\sum _{j=1}^{n-1}{\overline {W}}_{j}{\overline {Z}}_{j}-Z_{n}{\overline {Z}}_{n}\sum _{j=1}^{n-1}W_{j}{\overline {W}}_{j}+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (xii)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}-{\overline {Z}}_{n}{\overline {W}}_{n}\sum _{k=1}^{n}Z_{k}W_{k}-Z_{n}W_{n}\sum _{k=1}^{n}{\overline {Z}}_{k}{\overline {W}}_{k}+\left|Z_{n}W_{n}\right|^{2}-\left|W_{n}\right|^{2}\sum _{j=1}^{n-1}\left|Z_{j}\right|^{2}+{\overline {W}}_{n}{\overline {Z}}_{n}\sum _{j=1}^{n-1}Z_{j}W_{j}+W_{n}Z_{n}\sum _{j=1}^{n-1}{\overline {W}}_{j}{\overline {Z}}_{j}-\left|Z_{n}\right|^{2}\sum _{j=1}^{n-1}\left|W_{j}\right|^{2}+\left|W_{n}\right|^{2}\sum _{k=1}^{n-1}\left|Z_{k}\right|^{2}+\left|Z_{n}\right|^{2}\sum _{l=1}^{n-1}\left|W_{l}\right|^{2}+\left|Z_{n}\right|^{2}\left|W_{n}\right|^{2}\qquad (xiii)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}-{\overline {Z}}_{n}{\overline {W}}_{n}\sum _{k=1}^{n}Z_{k}W_{k}-Z_{n}W_{n}\sum _{k=1}^{n}{\overline {Z}}_{k}{\overline {W}}_{k}+\left|Z_{n}W_{n}\right|^{2}+{\overline {W}}_{n}{\overline {Z}}_{n}\sum _{j=1}^{n-1}Z_{j}W_{j}+W_{n}Z_{n}\sum _{j=1}^{n-1}{\overline {W}}_{j}{\overline {Z}}_{j}+\left|Z_{n}W_{n}\right|^{2}\qquad (xiv)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}-{\overline {Z}}_{n}{\overline {W}}_{n}Z_{n}W_{n}-Z_{n}W_{n}{\overline {Z}}_{n}{\overline {W}}_{n}+\left|Z_{n}W_{n}\right|^{2}+\left|Z_{n}W_{n}\right|^{2}\qquad (xv)\\\end{aligned}}

{\begin{aligned}\aleph =\left|\sum _{k=1}^{n}Z_{k}W_{k}\right|^{2}\qquad (xvi)\\\end{aligned}}

por lo tanto si $n-1$ $\in$ $\eth$ $\Longrightarrow$ $n\in$ $\eth$ .

--Dali 03:31 14 oct 2009 (UTC)

2.- Sean $z_{1},z_{2},...,z_{n}\,$ numeros complejos, ¿Bajo que condiciones se tiene que $|z_{1}+z_{2}+...+z_{n}|=|z_{1}|+|z_{2}|+...+|z_{n}|\,$ ?

Si $z_{1}=z_{2}=...=z_{n}\,$ , entonces

$|z_{1}|+|z_{2}|+...+|z_{n}|=n|z_{1}|\,$

por otro lado

$|z_{1}+z_{2}+...+z_{n}|=|nz_{1}|=n|z_{1}|\,$

y por lo tanto

$|z_{1}|+|z_{2}|+...+|z_{n}|=|z_{1}+z_{2}+...+z_{n}|\,$

--Luis Nava 02:52 5 oct 2009 (UTC)

2.- Sean $z_{1},z_{2},...,z_{n}\,$ numeros complejos, ¿Bajo que condiciones se tiene que $|z_{1}+z_{2}+...+z_{n}|=|z_{1}|+|z_{2}|+...+|z_{n}|\,$ ?

Tomando como punto de partida la demostracion de la desigualdad del triangulo. Podemos generalizar por medio de la inducción matemática a sumas de cualquier número finito de términos.

$\left|z_{1}+z_{2}+...+z_{n}\right|\leq \left|z_{1}\right|+\left|z_{2}\right|+...+\left|z_{n}\right|,(n=1,2,3,...)\qquad (1)$ .

Es claro ver que cuando n = 2 se cumple la desigualdad del triangulo.

$\left|z_{1}+z_{2}\right|\leq \left|z_{1}\right|+\left|z_{2}\right|$

Ahora suponiendo que (1) es válida cuando n=m, debe ser tambien para n=m+1, y aplicando la desigualdad del triangulo:

$\left|\left(z_{1}+z_{2}+...+z_{m}\right)+z_{m+1}\right|\leq \left|z_{1}+z_{2}+...+z_{m}\right|+\left|z_{m+1}\right|$

$\left|(z_{1}+z_{2}+...+z_{m})+z_{m+1}\right|\leq (\left|z_{1}\right|+\left|z_{2}\right|+...+\left|z_{m}\right|)+\left|z_{m+1}\right|$

En donde los primeros m terminos los redefiniremos como Z $_{I},$ y el termino m+1 como Z $_{II},$ . Entonces lo anterior queda como:

$\left|Z_{I}+Z_{II}\right|\leq \left|Z_{I}\right|+\left|Z_{II}\right|$

Ahora escribiendolo como igualdad

$\left|Z_{I}+Z_{II}\right|=\left|Z_{I}\right|+\left|Z_{II}\right|\equiv \left|z_{1}+z_{2}+...+z_{m}+z_{m+1}\right|=\left|z_{1}\right|+\left|z_{2}\right|+...+\left|z_{m}\right|+\left|z_{m+1}\right|$

$\left|z_{1}+z_{2}+...+z_{m}+z_{m+1}\right|=\left|z_{1}\right|+\left|z_{2}\right|+...+\left|z_{m}\right|+\left|z_{m+1}\right|\equiv \left|z_{1}+z_{2}+...+z_{n}\right|=\left|z_{1}\right|+\left|z_{2}\right|+...+\left|z_{n}\right|$

Esta desigualdad solo se cumple como igualdad cuando los numeros son colineales y tienen la misma direccion, esto tambien puede ser en los real (Re) o el imaginario (Im).

Esto es muy claro ver cuando n=2, en una grafica.

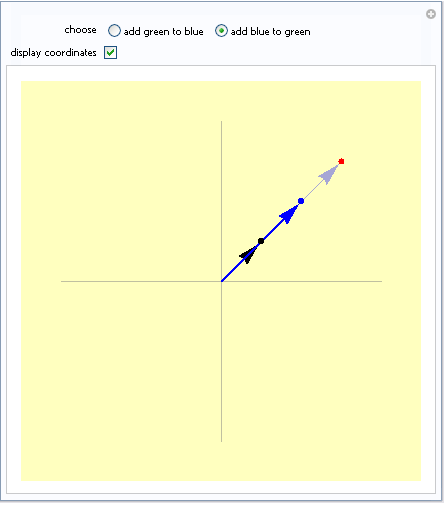
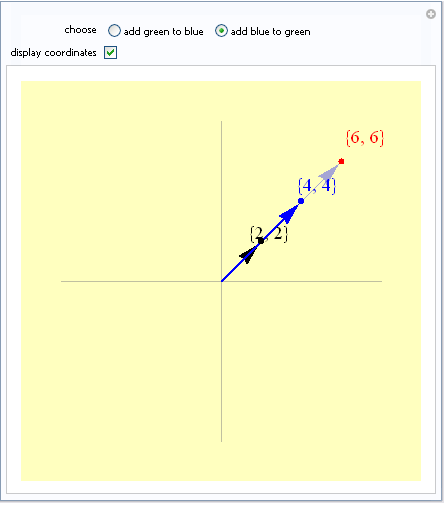
Aquí les dejo el enlace de la pagina donde consulte el código para generar las graficas para los que les interese. Demostracion grafica

--Oscar Adrian 03:41 16 oct 2009 (UTC) --Oscar Adrian 03:07 6 oct 2009 (UTC)

3. Encuentre el ínfimo de $\left|z^{3}+2i\right|$ en la región $\left\{z\mid |z|\geq 2\right\}$ , y describa en qué puntos se alcanza.

Con una variante de la desigualdad del triángulo, tenemos que

\left|z^{3}+i\right|\geq \left||z|^{3}-1\right|\geq 8-1.

Por tanto,

7\leq \left|z^{3}+i\right|.\qquad (1)

Entonces, el ínfimo de la expresión es 7.

Por otro lado, tenemos que, si $z=r\left(cos\theta +1\sin \theta \right)$

{\begin{aligned}\left|z^{3}+i\right|^{2}&=\left|r^{3}\left(\cos 3\theta +i\sin 3\theta \right)+1\right|^{2}\\&=\left|r^{3}\cos 3\theta +1+ir^{3}\sin 3\theta \right|^{2}\\&=r^{6}+2r^{3}\cos 3\theta +1.\\\end{aligned}}

Si tomamos la cota inferior, $\left|z\right|=2$ , la expresión anterior es entonces:

{\begin{aligned}\left|z^{3}+i\right|^{2}&=r^{6}+2r^{3}\cos 3\theta +1\\&=65+2r^{3}\cos 3\theta .\\\end{aligned}}

Ya que la función coseno tiene su mínimo en el valor -1, tomemos una $\theta$ tal que $\cos 3\theta {=}-1$ . Para este caso, tenemos dos valores: $\theta _{1}{=}{\frac {\pi }{3}}$ y $\theta _{2}{=}\pi$ ,

de tal forma que, con estos valores,

\left|z^{3}+i\right|^{2}=65-16=49.

Con la fórmula de De Moivre, tenemos que el ínfimo de la expresión dada toma ese valor en $z_{1}$ y $z_{2}$ tales que

{\begin{aligned}z_{1}&=2\left(\cos \theta _{1}+i\sin \theta _{1}\right)\\&=2\left(\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}\right)\\&=2\left({\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)\\z_{1}&=1+i{\sqrt {3}},\qquad (2)\\\end{aligned}}

y

{\begin{aligned}z_{2}&=2\left(\cos \theta _{2}+i\sin \theta _{2}\right)\\&=2\left(\cos \pi +i\sin \pi \right)\\z_{2}&=-2.\qquad (3)\\\end{aligned}}

Pero, además, por le geometría de los números complejos, tenemos otros dos valores $z_{3}$ y $z_{4}$ tales que

{\begin{aligned}z_{3}&=2\left(\cos \theta _{1}+\pi +i\sin \theta _{1}+\pi \right)\\&=2\left(\cos {\frac {4\pi }{3}}+i\sin {\frac {4\pi }{3}}\right)\\&=2\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)\\&=-1-i{\sqrt {3}}\\z_{3}&=-z_{1},\qquad (4)\\\end{aligned}}

y

{\begin{aligned}z_{4}&=2\left(\cos \theta _{2}+\pi +i\sin \theta _{2}+\pi \right)\\&=2\left(\cos 2\pi +i\sin 2\pi \right)\\&=2\\z_{4}&=-z_{2}.\qquad (5)\\\end{aligned}}

Por tanto, las expresiones (2), (3), (4) y (5) nos proporcionan los valores en que el ínfimo es tomado, a saber, $\pm (1+i{\sqrt {3}})$ y $\pm 2$ .

--Belen 04:08 12 oct 2009 (UTC)

Compleja:ej-cap1.2

Compleja:ej-cap1.3

Compleja:ej-cap1.4

@@ Línea 328: / Línea 328: @@
 --[[Usuario:Karla|Karla]] 22:47 4 oct 2009 (UTC)Sanchez
-== 1.1.3 ==
+== '''SECCION 1.1.3''' ==
 '''1. Calcule las raìces cuadradas de <math>3+4i</math> y de <math>1+2i</math>.'''
@@ Línea 788: / Línea 788: @@
 --[[Usuario:Dali|Dali]] 00:01 5 oct 2009 (UTC)
 == 1.1.4 ==

Anónimo

Buscar

Diferencia entre revisiones de «Compleja:ej-cap1.1»

Espacios de nombres

Más

Acciones de página

Revisión del 22:28 6 dic 2009

SECCION 1.1.2

SECCION 1.1.3

1.1.4

Navegación

Navegación

Herramientas wiki

Herramientas wiki

Anónimo

Buscar

Diferencia entre revisiones de «Compleja:ej-cap1.1»

Revisión del 22:28 6 dic 2009

SECCION 1.1.2

SECCION 1.1.3

1.1.4

Navegación

Herramientas wiki

Herramientas de página

Categorías