Ondas contrapropagantes en musica: cuerdas de guitarra
¿Qué son las ondas contrapropagantes?
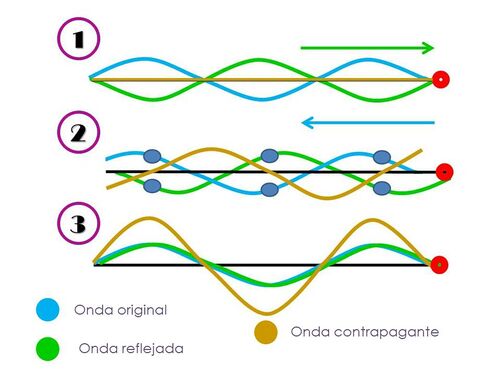
En instrumentos de cuerda, como las guitarras, las ondas sonoras en el aire son creadas por la resonancia transversal de ondas contrapropagantes en las cuerdas, es por esto que nos interesa conocer qué son este tipo de ondas y cómo se forman. Al tocar la guitarra, producimos perturbaciones en sus cuerdas con nuestros dedos, estas perturbaciones viajan a lo largo de la cuerda hasta llegar a un nodo, el cual provoca que la onda se refleje sobre su eje de propagación y viaje en dirección opuesta. La superposición de estas ondas, la onda original con la reflejada, es a lo que llamamos onda contrapropagante. El siguiente esquema refleja distintos momentos para comprender la formación de la onda contrapropagante
- En $1$ cuando la onda reflejada es inversa a la original, se anulan entre sí y no hay perturbación.
- En $2$ a medida que avanzan las ondas van formando la onda contrapropagante, siendo los nodos puntos fijos en la cuerda donde siempre se anulará el movimiento de la cuerda. Los puntos azules en el esquema, muestran distancias iguales en cada onda al eje de propagación, para comprender cómo es que se anula el movimiento en los nodos.
- En $3$ vemos la amplitud máxima de la onda contrapropagante, que es el doble de la amplitud de la onda original, ya que en ese momento, ambas ondas coinciden. [1]
Usualmente se le llama ondas "estacionarias" a este tipo de ondas, ya que la onda resultante no se propaga en alguna dirección como lo hacen las ondas que la forman. No obstante, el usar ese término para ondas que se propagan en direcciones opuestas puede ser engañoso, ya que las ondas nunca están "fijas" no son estacionarias. Los nombres como introducción del tema pueden causar malas interpretaciones. Si las ondas contrapropagantes tienen mismas amplitudes el flujo neto es cero, sin embargo con seguridad, sabemos que existe un flujo producido por cada una de las ondas. Una analogía muy distinta pero ilustrativa, son las autopistas en la ciudad, donde dos escenarios diferentes tienen flujo total cero: i) Cuando hay mucho tráfico (embotellamiento), tanto que ningún vehículo puede moverse, en esta situación el flujo neto es cero. En contraste, ii) Un flujo constante y rápido de coches en ambos sentidos, donde otra vez el flujo total es cero. Las ondas contrapropagantes se parecen más a la segunda situación ii) donde difícilmente podemos hablar de algo "estacionario". Algunas veces se ha mencionado que este nombre se debe a los nodos, que se encuentran espacialmente fijos pero, estos son los únicos dos puntos estacionarios en un intervalo $2\pi$ mientras que el resto de puntos continúa moviéndose de arriba a abajo.[2]
Ecuación de onda contrapropagante
La ecuación diferencial de movimiento de la cuerda es \begin{equation} \frac{\partial^2\psi}{\partial x^2}= \frac{\mu}{T} \frac{\partial^2\psi}{\partial t^2}\label{eq:movdif} \end{equation} Donde $T$ es la tensión en la cuerda y $\mu=m/L$ es la densidad lineal de la cuerda.[3]
El desplazamiento de la onda inicial $\Psi_1$ es la solución de la EDO (\ref{eq:movdif}) \begin{equation} \ \Psi_1= \Psi_0 \mathrm{sen} (kx+\omega t)\label{eq:onda inicial} \end{equation} Ya que la onda reflejada $\Psi_2$ va en dirección opuesta y tiene la misma amplitud $\Psi_0$ podemos escribir \[ \ \Psi_2= \Psi_0\mathrm{sen}(kx-\omega t) \]
La onda contrapropagante $\Psi$ al ser la superposición de estas ondas es entonces $\Psi_1+\Psi_2$ \[ \ \Psi=\Psi_1+\Psi_2=\Psi_0\mathrm{sen}(kx-\omega t) + \Psi_0\mathrm{sen}(kx+\omega t) \] Simplificando esta ecuación \begin{equation} \ \Psi= \Psi_0 [\mathrm{sen}(kx-\omega t)+\mathrm{sen}(kx+\omega t)]\label{eq:ondacontrap} \end{equation} Utilizando la propiedad \[ \ \mathrm{sen}(kx-\omega t)+\mathrm{sen}(kx+\omega t)=2\mathrm{cos}(\omega t)\mathrm{sen}(kx) \] Sustituyendo esta propiedad en (\ref{eq:ondacontrap}) obtenemos la ecuación de onda contrapropagante \begin{equation} \ \Psi= 2\Psi_0 \mathrm{cos}(\omega t)\mathrm{sen}(kx)\label{eq:ondacontraprop} \end{equation}
Por otro lado, podemos encontrar una relación entre la velocidad del sonido en la cuerda $v_s$ y la tensión $T$ de la cuerda, para ello conviene expresar algunas relaciones de onda como[4]
- Número de onda: $k=\frac{2\pi}{\lambda}$
- Frecuencia angular: $\omega=2\pi\nu$
- Velocidad de propagación, velocidad del sonido en la cuerda: $v_s=\nu\lambda$
Así podemos expresar a $\omega$ como $\omega=\frac{2\pi v_s}{\lambda}$
Sustituyendo estos valores para $k$ y $\omega~$ en la ecuación de onda (\ref{eq:onda inicial}) \begin{equation} \ \Psi_1= \Psi_0 \mathrm{sen} (\frac{2\pi}{\lambda}x+\frac{2\pi v_s}{\lambda} t)\label{eq:onda inicial'} \end{equation} Factorizando $\frac{2\pi}{\lambda}$ \begin{equation} \ \Psi_1= \Psi_0 \mathrm{sen} \frac{2\pi}{\lambda}(x+v_s t)\label{eq:onda2} \end{equation} Posteriormente, al seguir la ecuación (\ref{eq:movdif}), debemos obtener las segundas derivadas parciales de $\psi$ de (\ref{eq:onda2}), primeramente respecto del tiempo \[ \frac{\partial^2\psi}{\partial t^2}=\frac{-4\pi^2}{\lambda^2}\psi_0 v_s^2 \mathrm{sen}\frac{2\pi}{\lambda}(x+v_s t) \] Y posteriormente, respecto de la posición en $x$ \[ \frac{\partial^2\psi}{\partial x^2}=\frac{-4\pi^2}{\lambda^2}\psi_0 \mathrm{sen}\frac{2\pi}{\lambda}(x+v_s t) \] Sustituyendo estos resultados en (\ref{eq:movdif}) \[ \frac{-4\pi^2}{\lambda^2}\psi_0 \mathrm{sen}\frac{2\pi}{\lambda}(x+v_s t)=\frac{\mu}{T}\frac{-4\pi^2}{\lambda^2}\psi_0 v_s^2 \mathrm{sen}\frac{2\pi}{\lambda}(x+v_s t) \] Así, al simplificar esta expresión podemos llegar a que \begin{equation} \ 1=\frac{\mu}{T}v_s^2\label{eq:velocidadcuadrada} \end{equation} Y finalmente \begin{equation} \ v_s=\sqrt\frac{T}{\mu}\label{eq:velso1} \end{equation}
Modos de vibración
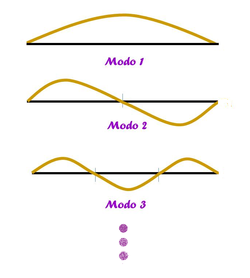
La cuerda de una guitarra, a diferencia de la masa en un resorte, puede oscilar en muchas frecuencias o patrones de onda conocidos como modos de vibración (Figura 1). Cada modo de vibración tiene propiedades de "onda" (tales como longitud de onda, frecuencia, étc.).
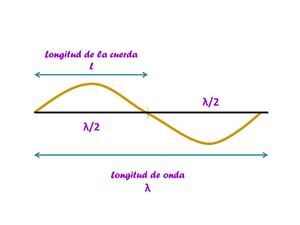
En las cuerdas de una guitarra hablamos de patrones de onda (por su forma sinusoidal) ya que si analizamos su movimiento no es una onda completa; una onda parte del reposo, crece hasta su cresta, vuelve a la posición de equilibrio, decrece hasta un valle y vuelve a su posición de equilibrio en un ciclo completo; mientras que en una cuerda, la oscilación en la frecuencia fundamental, sólo se produce la mitad de una onda en toda la longitud de la cuerda. Por lo que la longitud de onda $\lambda$ es dos veces la longitud de la cuerda $L$.
A la frecuencia fundamental le llamamos primer modo de vibración, es el modo con la longitud de onda más larga y la frecuencia más baja, también es el modo que produce un sonido más fuerte. La frecuencia depende de la velocidad del sonido en la cuerda.
Si suponemos que esta velocidad es $V_{s}=107 \frac{m}{s}$, la longitud de la cuerda es $L=65 cm$ y dado que $\lambda=2L=1.3m$ entonces
\begin{equation} \ \nu=\nu_{1}=\frac{V_{s}}{\lambda}=\frac{107}{1.3}=82.3 Hz\label{eq:frecuencia1} \end{equation}
Esta es la frecuencia fundamental de la cuerda más baja, correspondiente a la nota Mi.
Ya que la longitud de onda es dos veces la longitud de la cuerda podemos expresar en forma general la ecuación (\ref{eq:frecuencia1}) como
\begin{equation} \ \nu=\nu_{1}=\frac{V_{s}}{2L}\label{eq:frecuencia1'} \end{equation}
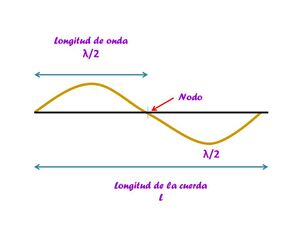
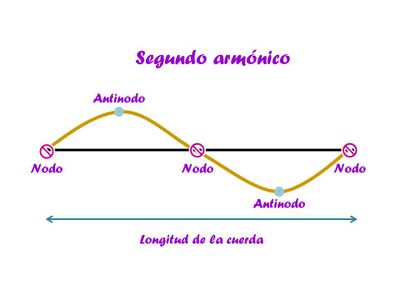
El segundo modo de vibración comprende de un nodo más, que se encuentra a distancias iguales de la cuerda. Para los fines de esta sección, supongamos que podemos ver a este nodo como un punto donde se parte a la cuerda en dos secciones iguales, podemos ver cada parte como dos cuerdas con longitudes de onda $\frac{\lambda}{2}$
Entonces, para este caso, podemos notar que la longitud de onda de la cuerda es igual a la longitud de la cuerda, ya que tenemos dos medios de $\lambda$ en toda la cuerda.
Así la frecuencia para el segundo modo de vibración es
\begin{equation}
\ \nu_{2}= 2\frac{V_{s}}{2L}= \frac{V_{s}}{L}=\frac{107}{0.65}=165 Hz\label{eq:frecuencia2}
\end{equation}
Para el 3er modo de vibración se añade otro nodo, cada nodo está igualmente espaciado a lo largo de la de la cuerda, por lo que podemos ver que para este modo de vibración tenemos $ 3\frac{\lambda}{2}$ en toda la longitud de la cuerda
La frecuencia del tercer modo es \begin{equation} \ \nu_{3}= 3\frac{V_{s}}{2L}= 3\frac{107}{130}=247 Hz\label{eq:frecuencia3} \end{equation}
En este punto, es claro que no existe un límite para los posibles modos de vibración en los que puede oscilar la cuerda de una guitarra, creando cada uno de ellos los diferentes armónicos de un tono. El primer modo de vibración corresponde al primer armónico o tono fundamental, el segundo modo crea el segundo armónico y así sucesivamente. Cada frecuencia armónica es un múltiplo entero de la frecuencia fundamental.
Armónicos
Se le llama armónicos a dos o más componentes de un tono si sus frecuencias son múltiplos enteros pequeños de una misma frecuencia fundamental. Por ejemplo, las ecuaciones (\ref{eq:frecuencia2}) y (\ref{eq:frecuencia3}) muestran frecuencias que son múltiplos enteros de la frecuencia fundamental que arroja la ecuación (\ref{eq:frecuencia1}) para la cuerda más baja de una guitarra. El primer modo corresponde al primer armónico o armónico fundamental, el segundo modo es el segundo armónico y así sucesivamente. Como vimos en la sección anterior los nodos hacen distintos a un modo de otro o, en otras palabras a un armónico de otro, sin embargo, no los hemos definido como tal. Los nodos son puntos donde la cuerda no se mueve, puntos de no desplazamiento, donde no importa cuanto esperemos no veremos a la cuerda oscilar. El primer armónico tiene dos nodos, los cuales son los extremos de la guitarra, su puente y las clavijas que sujetan a las cuerdas.
Entre cada dos nodos existe un antinodo, si en los nodos la amplitud de la onda es mínima (no hay amplitud realmente), en los antinodos la amplitud es máxima, ambos son puntos donde la velocidad de la cuerda es cero.
En la siguiente tabla podemos visualizar la relación que hay según el número de armónico n, con las ondas en una cuerda de guitarra, cuántos nodos y antinodos hay, la longitud de onda y sus frecuencias utilizando la información para $v{_s}$ y $L$ de la sección anterior. [5] Donde se utilizó esta expresión para calcular la longitud de onda \begin{equation} \ \lambda=\frac{2L}{n}\label{eq:lambda1} \end{equation}
| Armónico
n |
Ondas en la cuerda | #
De nodos |
#
De antinodos |
Longitud de onda
(cm) |
Frecuencia
(Hz) |
|---|---|---|---|---|---|
| $1$ | $\frac{1}{2}$ | $2$ | $1$ | $2L=130$ | $82.3$ |
| $2$ | $1$ | $3$ | $2$ | $L=65$ | $165$ |
| $3$ | $\frac{3}{2}$ | $4$ | $3$ | $\frac{2}{3}L=43.3$ | $247$ |
| $4$ | $2$ | $5$ | $4$ | $\frac{1}{2}L=32.5$ | $329$ |
| $5$ | $\frac{5}{2}$ | $6$ | $5$ | $\frac{2}{5}L=26$ | $416$ |
Ya hemos mencionado que las frecuencias de los armónicos son siempre múltiplos enteros de la frecuencia fundamental, este hecho hace que se puedan crear tonos consistentes con los componentes de vibración que son armónicos, estos componentes son ondas sinusoidales llamadas "partes" ya que un tono completo se compone de varias de estas. Cada componente sinusoidal es "parte" de una onda completa, las partes de un tono creado por una cuerda estirada son armónicas debido a esta relación entre las frecuencias de las partes, hecho que se enfatiza con la expresión \begin{equation} \ \nu_{n}= n\nu_{1}\label{eq:frecuenciaarm} \end{equation}
La cual determina la frecuencia de cualquier armónico o modo de vibración.
La ecuación del guitarrista
Para tocar melódica y armoniosamente un guitarrista debe tocar notas con una correcta frecuencia fundamental. Como hemos visto, la frecuencia fundamental de una nota o tono está relacionada con la velocidad del sonido en la cuerda y a su vez, la velocidad del sonido depende de la tensión en la cuerda $T$ y su densidad de masa lineal $ \mu$ de acuerdo con la expresión (\ref{eq:velso1}), la cual conviene reescribir \[ \ v_{s}=\sqrt\frac{T}{\mu}\ \]
Al sustiuir $v_{s}$ dada por (\ref{eq:velso1}) en la ecuación (\ref{eq:frecuencia1'}) obtenemos la ecuación del guitarrista para la frecuencia fundamental de un tono \begin{equation} \ \nu_{1}=\frac{1}{2L}\sqrt\frac{T}{\mu}\label{eq:guitar'splayer} \end{equation}
Esta expresión muestra que la creación de un tono depende de las propiedades de la cuerda: Tensión $T$, Longitud $L$ y densidad lineal $\mu$.
Cabe mencionar que la expresión (\ref{eq:guitar'splayer}) es sólo la idealización de la realidad. Ya que considera que la tensión es la única fuerza que actúa sobre la cuerda, lo cual es falso. Analicemos un poco lo que pasa: Cuando tocamos la guitarra nuestros dedos hacen que la cuerda oscile, la fuerza restauradora es la que hace que la cuerda busque su posición de equilibrio, esta fuerza, en mayor medida, está compuesta por la tensión pero también contribuye la rigidez de la cuerda. Para comprender qué es la rigidez, imaginemos que le quitamos una cuerda a la guitarra, por tanto ya no hay tensión, si intentamos doblar por completo la cuerda encontraremos que existe cierta resistencia, esa resistencia es la rigidez. Para hablar de cuerdas reales necesitamos incluir la rigidez en nuestro razonamiento. [6]
Series de Fourier para la forma inicial de una cuerda y armónicos para ondas contrapropagantes [7]
Cuando tocamos la nota Mi, esta no sólo consiste en la frecuencia fundamental dada en (\ref{eq:frecuencia1}), también se conforma de otros armónicos más altos que se pueden obtener de la expresión (\ref{eq:frecuenciaarm}). El conjunto de estas cantidades relativas define un tono musical, aún con esto el tono que produzca la guitarra depende también de la forma en la que toque las notas el guitarrista.
Para determinar las amplitudes de los armónicos (fundamentales o más altos) para las cuerdas de una guitarra, es usualmente utilizado un análisis de Fourier de la forma de onda. Cuando se toca una nota en una guitarra en diferentes puntos sobre la cuerda podemos notar que los timbres entre ellas son notablemente diferentes. Las amplitudes correspondientes a los armónicos dependen de en qué punto de la cuerda estos se toquen. Las amplitudes iniciales esperadas para los armónicos cuando tocamos una cuerda de una forma particular pueden ser calculadas como coeficientes de Fourier de una serie infinita de armónicos representando la forma inicial de la cuerda de una guitarra.
La forma inicial de la cuerda no es exactamente triangular debido a la rigidez de la cuerda, sin embargo, este hecho también será despreciable para este análisis.
Para una cuerda sujeta en sus extremos $x=0$ y $x=L$, podemos escribir la ecuación (\ref{eq:movdif}) sustituyendo $\frac{\mu}{T}$ por $\frac{1}{v_s^2}$ al despejar $\frac{1}{v_s}$ de la ecuación (\ref{eq:velocidadcuadrada}) \begin{equation} \frac{\partial^2\psi}{\partial x^2}= \frac{1}{v_s} \frac{\partial^2\psi}{\partial t^2}\label{eq:dif2} \end{equation}
Donde $v_s$ está dada por la expresión (\ref{eq:velso1}) Para el caso en el que se toque la cuerda en cierta posición en $t=0$, las condiciones iniciales pueden ser descritas como $\psi(x,0)=\psi(x)$, donde $\psi(x)$ es la forma inicial de la cuerda y $\frac{\partial \psi}{\partial t}_{t=0}=0$ para cualquier x. Podemos escribir una solución para la ecuación (\ref{eq:dif2}) dadas estas condiciones iniciales, de la ecuación para las ondas contrapropagantes mostrada en (\ref{eq:ondacontraprop}) considerando los n armónicos \begin{equation} \ \psi(x,t)= \sum_{n=1}^{∞} \psi_n \mathrm{sen}(\frac{n\pi x}{L})\mathrm{cos}(\frac{n\pi v_s t}{L})\label{eq:fourier} \end{equation}
- Donde $\psi_n$ es la amplitud correspondiente al n-ésimo armónico.
- Podemos obtener $\nu_n=\frac{nv_s}{2L}$, al substituir (\ref{eq:frecuencia1'}) en (\ref{eq:frecuenciaarm}) por lo que en (\ref{eq:fourier}) hemos sustituido a $\omega=2\pi\nu_n$, por $\omega=\frac{n\pi v_s }{L}$
- Análogamente para $k=\frac{2\pi}{\lambda}$, se sustituyó $\lambda$ de la expresión (\ref{eq:lambda1}) para poder sustituir $k=\frac{n\pi}{L}$ en (\ref{eq:fourier}).
Podemos definir \[ \ y_n=\psi_n \mathrm{sen}(\frac{n\pi x}{L}) \] Así la ecuación (\ref{eq:fourier}) se expresa como \begin{equation} \ \psi(x,t)= \sum_{n=1}^{∞} y_n \mathrm{cos}(\frac{n\pi v_s t}{L}) \end{equation} Las frecuencias de los armónicos se pueden variar al cambiar la tensión en la cuerda (por ejemplo al afinar la guitarra) o cambiando la longitud $L$ de la sección vibrante de la cuerda (como cuando se coloca un capo).
Es fácil ver que para cada armónico, el desplazamiento $y_n(x,t)=0$ en $x=0$, $x=L$, $x=\frac{L}{n}$. Como coeficiente de Fourier $\psi_n$ que representan las amplitudes de los armónicos puede ser calculado de la forma inicial de la cuerda en $\psi_0(x,0)=f(x)$ siguiendo esta expresión [8] \begin{equation} \ \psi_n= \frac{2}{L}\int_{0}^{L}f(x) \mathrm{sen}(\frac{n\pi x}{L})dx\label{eq:armamp} \end{equation} Para una cuerda de largo $L$ que se toca en la posición $x_1$ (distancia desde el extremo final de la cuerda) a una distancia $A$ (Figura 5), podemos escribir $f(x)$ como
\begin{equation} \ f(x)=\frac{A}{x_1}x\label{eq:xl1} \end{equation} Para $0\leq x \leq x_1$
y \begin{equation} \ f(x)=\frac{A}{L-x_1}(L-x)\label{eq:xl2} \end{equation} Para $x_1\leq x \leq L$
Por lo tanto al sustituir (\ref{eq:xl1}) y(\ref{eq:xl2}) en (\ref{eq:armamp}) las amplitudes de los componentes de Fourier (armónicos) en la forma inicial de la guitarra se pueden calcular como \[ \ \psi_n= \frac{2A}{Lx_1}\int_{0}^{x_1} x \mathrm{sen}(\frac{n\pi x}{L})dx + \frac{2A}{L(L-x_1)}\int_{x_1}^{L} (L-x) \mathrm{sen}(\frac{n\pi x}{L})dx \] y finalmente al resolver la integral \[ \ \psi_n= \frac{2A \mathrm{sen}(\frac{n\pi x_1}{L})}{\frac{x_1}{L}(1-\frac{x_1}{L})\pi^2n^2} \] Obteniendo así la magnitud o amplitud del n-ésimo armónico de la forma inicial de la cuerda de guitarra.
Referencias
|