Ondas periodicas: armonicas y anarmonicas

Introducción

Onda periódica se denomina al conjunto de pulsos que son emitidos a intervalos iguales de tiempo. Es decir en cada período se provoca una perturbación idéntica a la anterior.

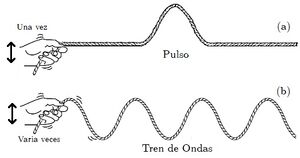
Una imagen ilustrativa:

Que nos muestra un (a) Pulso, que es una perturbación aislada, no periódica, que tiene lugar en un movimiento ondulatorio de algún tipo. Y un (b) Tren de Ondas: Un Tren de Ondas es una colección de pulsos. Si el movimiento es periódico, entonces se originará un tren de ondas periódico (donde cada partícula de la cuerda tendrá un movimiento periódico). El caso especial más sencillo de una onda periódica es una onda armónica, donde cada partícula experimenta un movimiento armónico simple.

Ondas periódicas armónicas

Cuando la fuente que produce la perturbación describe un movimiento armónico simple la onda generada se denomina onda armónica.

Supongamos una cuerda infinita en la que se fuerza a uno de sus extremos a realizar un movimiento armónico simple de amplitud $A$ y de frecuencia $f$ o $ν$. Su desplazamiento vertical (y) será:

$y(x,t)=A\cdot \cos(2\pi \nu t)=A\cdot \cos(\omega t)$

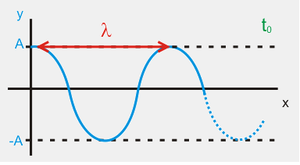
Cada uno de los pulsos de onda generados se propaga por la cuerda de forma continua produciendo una onda armónica de la misma amplitud y de la misma frecuencia. En un instante de tiempo determinado $t_0$ la cuerda tendría esta forma:

La distancia entre dos puntos consecutivos con el mismo desplazamiento vertical se denomina longitud de onda $\lambda$ y en el S.I. se mide en metros. Se define también otra variable relacionada llamada número de ondas $k$:

$k={\frac {2\pi }{\lambda }}$

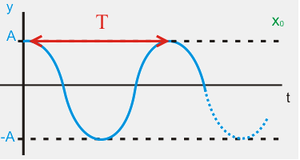
Representando el desplazamiento vertical en función del tiempo para un punto de coordenada fija $x_0$:

El tiempo que tarda un punto en describir una oscilación completa es el periodo (T) cuyas unidades en el S. I. son los segundos. La inversa del periodo es la frecuencia (f o ν) que representa el número de oscilaciones por segundo y se mide en Hertz.

La velocidad de fase se calcula entonces como el cociente entre la longitud de onda y el periodo:

$v={\frac {\lambda }{T}}=\lambda \nu$

La función de onda que describe el desplazamiento vertical y para un punto de coordenada x en función del tiempo se expresa:

$y(x,t)=A \cos \left [\frac{2\pi\nu}{v}(x-vt)\right ]$

O de otra forma más sencilla:

$y(x,t)=A\cos(kx-\omega t)$

La función tiene las siguientes características:

La función seno es periódica (periódicamente, al aumentar t, varía entre +1 y -1) : se repite cuando el argumento se incrementa en $2\pi$.

La función describe la posición respecto al punto de equilibrio de un punto del medio, situado a una distancia "x"del origen, por el que se propaga una perturbación que le comunica un Movimiento Vibratorio Armónico Simple.

A es la amplitud o separación máxima respecto al punto de equilibrio.

La frecuencia angular es $\omega=k v$

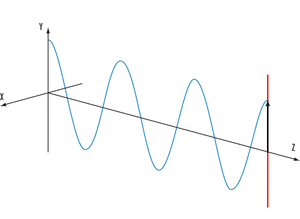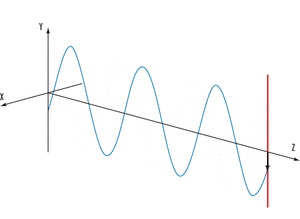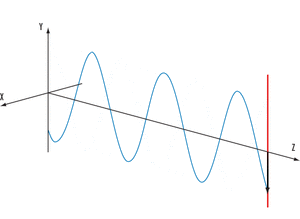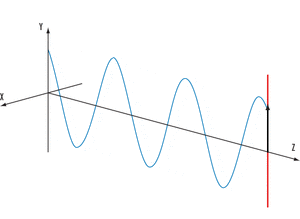
Ejemplo de onda periódica armónica

Ondas periódicas anarmónicas

Las ondas anarmónicas son todas aquellas cuyos perfiles no son curvas armónicas (senos o cosenos), sin importar si permanecen constantes o no al transcurrir el tiempo.

Figura 1. Perfiles de ondas anarmónicas

La figura 2 sugiere que al emplear varias funciones periódicas sinusoidales cuyas amplitudes, longitudes de onda y fases relativas hayan sido juiciosamente seleccionadas, sería posible sintetizar algunos perfiles de onda muy interesantes. Una técnica matemática excepcionalmente bella que lleva precisamente a eso fue diseñada por el físico francés Jean Baptiste Joseph, Barón de Fourier.

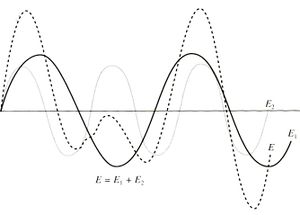
Figura 2. Superposición de dos ondas armónicas de diferente frecuencia.

Ya se ha afirmado, sin pruebas, que cualquier onda real en el espacio puede construirse a partir de ondas armónicas seleccionadas apropiadamente que tengan las frecuencias espaciales, amplitudes y fases relativas correctas. La técnica que logra esta hazaña se llama análisis de Fourier, y es una de las metodologías más importantes en toda la física teórica. Debido a que el método analítico habitual es matemáticamente un poco oscuro, comenzamos con un enfoque gráfico más intuitivo que hará evidente lo que realmente hace la matemática formal. Los métodos desarrollados se aplican por igual a los eventos espaciales (es decir, los que existen en muchas ubicaciones en el espacio al mismo tiempo, como las ondas en una cuerda) y a los eventos temporales (es decir, los que existen en una ubicación en el espacio en muchos momentos en el tiempo.

Teoría de Fourier

J. B. J. Fourier (1768–1830), matemático aplicado y egiptólogo, fue uno de los grandes científicos franceses que trabajaban en la época de Napoleón. Hoy en día, es mejor recordado por el método de la serie de Fourier, que inventó para la representación de cualquier función periódica como una suma de armónicos sinusoidales discretos de su frecuencia fundamental. Por extrapolación, su nombre también se asocia a transformadas de Fourier o integrales de Fourier, que permiten que casi cualquier función se represente en términos de una integral de funciones sinusoidales en un rango continuo de frecuencias. Los métodos de Fourier tienen aplicaciones en casi todos los campos de la ciencia y la ingeniería. Dado que la óptica se ocupa de los fenómenos de onda, el uso de las series de Fourier y las transformaciones para analizarlos ha sido particularmente fructífero.

El teorema de Fourier demuestra que una función anarmónica cualquiera se puede definir mediante una suma términos de funciones armónicas. Para ello en la función original del perfil de la onda, expresamos a $f(x)$ como una suma de términos armónicos de la siguiente forma:

$f(x)={\frac {A_{0}}{2}}+\sum _{m=1}^{\infty }\left[A_{m}\cos(mkx)+B_{m}\mathrm {sen} (mkx)\right]$

Esta serie puede tener varias simplificaciones.

$a)$ Si la función es par $( f(-x) = f(x) )$, o sea es simétrica alrededor de x=0 la serie tendrá solamente términos coseno.

$b)$ Si la función es impar $( f(-x) = -f(x) )$, o sea es antisimétrica alrededor de x=0 la serie tendrá solamente términos seno.

$c)$ En general, con el cálculo de 3 a 5 términos (los coeficientes $A_m$ ó $B_m$), es suficiente

Serie de Fourier

La forma de una onda en el espacio (es decir, su perfil), o una señal en el tiempo, a menudo se conoce como una forma de onda. Se muestra cómo varias formas de onda armónicas de la misma frecuencia se suman para producir una forma de onda armónica resultante de la misma frecuencia. Esa observación puede generalizarse: independientemente de sus amplitudes y fases relativas, la superposición de cualquier número de formas de onda armónicas de la misma frecuencia da como resultado una forma de onda armónica de esa misma frecuencia. Por el contrario, al agregar formas de onda de diferentes frecuencias, como en la Fig. 3, se obtiene un compuesto que es anarmónico (es decir, no sinusoidal).

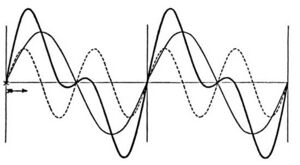
Figura 3. La superposición de dos ondas armónicas de diferente frecuencia. La onda resultante es periódica pero anarmónica.

La Figura 3 comienza a sugerir que, al utilizar varias funciones sinusoidales seleccionadas con criterio, sería posible sintetizar algunos perfiles de onda interesantes. Las longitudes de onda de los sinusoides en esa ilustración, $\lambda _{1}$ y $\lambda _{2}$, son diferentes, y después de un ciclo están fuera de fase. Pero después de $N _{1}$ ciclos de uno y $N_{2}$ ciclos del otro (donde $N _{1}$ y $N _{2}$ son números enteros), de manera que $\lambda _{1}N_{1}=\lambda _{2}N_{2}$ , volverán a estar en fase y la resultante se repetirá una y otra vez; La función sintetizada es periódica con un periodo espacial $\lambda $.

Cuando se agregan varias formas de onda armónicas sin mucha preocupación por la longitud de onda, la periodicidad de la resultante puede requerir muchos ciclos de sus componentes antes de que se establezca. Por el contrario, comenzando con la forma de onda más larga, de longitud de onda $\lambda $, y agregándole formas de onda con longitud de onda de $ \frac{\lambda }{2}$, $\frac{\lambda }{3}$ , $ \frac{\lambda }{2}$, etc., produce una resultante que también tiene una longitud de onda o un período espacial de $\lambda $ . Esto se debe a que todas las formas de onda más cortas que contribuyen se ajustan exactamente un número entero de veces en la longitud de onda $\lambda $. fundamental.

Supongamos que queremos sintetizar alguna forma de onda periódica $f(x)$ , del periodo espacial $\lambda$ , usando contribuciones armónicas. La discusión anterior sugiere que haríamos bien en comenzar con una sinusoide o cosinusoide que también tenga una longitud de onda de $\lambda$ y agregarle términos armónicos cuyos argumentos contengan fracciones de números enteros de $\lambda$.

La Serie de Fourier establece que cualquier función periódica $f(x)$ se puede expresar como la suma de una serie de funciones sinusoidales que tienen longitudes de onda que son fracciones integrales de la longitud de onda $\lambda$ de $f(x)$. Para completar esta afirmación, el cero se cuenta como un número entero, dando un término inicial constante a la serie:

$f(x)={\frac {1}{2}}C_{0}+C_{1}\cos \left({\frac {2\pi x}{\lambda }}+\alpha _{1}\right)+C_{2}\cos \left({\frac {2\pi x}{\frac {\lambda }{2}}}+\alpha _{2}\right)+\cdot \cdot \cdot +C_{m}\cos \left({\frac {2\pi x}{\frac {\lambda }{n}}}+\alpha _{m}\right)+\cdot \cdot \cdot$ (1)

Donde $f(x)$ es la onda viajera $f(x-vt)$

$f(x)={\frac {1}{2}}C_{0}+C_{1}\cos \left(kx+\alpha _{1}\right)+C_{2}\cos \left(2kx+\alpha _{2}\right)+\cdot \cdot \cdot +C_{m}\cos \left(mkx+\alpha _{m}\right)$

$f(x)={\frac {1}{2}}C_{0}+\sum _{m=1}^{\infty }C_{m}\cos \left(mk_{0}x+\alpha _{m}\right)$

Donde $k_{0}={\frac {2\pi }{\lambda }}$ es la frecuencia espacial fundamental. Las ns se denominan órdenes de los términos, que son armónicos. El siguiente argumento demuestra el teorema como razonable. Si cortamos la serie después del primer término, la elección de $C_{0}$ permite que la ecuación se cumpla en un número discreto de puntos, al menos dos por longitud de onda. Si agregamos un segundo término, la cantidad de puntos de acuerdo aumentará; a medida que continuamos agregando términos, se puede hacer que el número de intersecciones entre la función sintética y el original aumente sin límite.

Esto no prueba que las funciones deben ser idénticas cuando el número de términos se vuelve infinito; hay ejemplos que no convergen a la función requerida, pero las regiones de error deben volverse muy pequeñas. Este razonamiento, por supuesto, se aplicaría a funciones básicas distintas de las ondas sinusoidales. Sin embargo, la curva sinusoidal, que es la solución de todas las ecuaciones de onda, es de particular importancia en la física y, por lo tanto, le da al teorema de Fourier su significado fundamental.

Cada término de la serie tiene dos coeficientes de Fourier, una amplitud $C_{m}$ y un ángulo de fase $(\alpha _{m})$. La última cantidad proporciona el grado de libertad necesario para los desplazamientos relativos de los términos de la serie a lo largo del eje x. La determinación de estas cantidades para cada término de la serie se llama análisis de Fourier. Otra forma de expresar los coeficientes de Fourier es escribir como una suma de términos de seno y coseno.

$f(x)={\frac {A_{0}}{2}}+\sum _{m=1}^{\infty }\left[A_{m}\cos(mkx)+B_{m}\mathrm {sen} (mkx)\right]$.....(2)

$C_{m}cos\left(mkx+\alpha _{m}\right)=A_{m}\cos(mkx)+B_{m}\mathrm {sen} (mkx)$

dónde: $A_{m}=C_{m}\cos(\alpha _{m}),B_{m}=-C_{m}\mathrm {sen} (\alpha _{m})$

Coeficientes de Fourier

El proceso que permite establecer los coeficientes $A_{0},A_{m}$ y $B_{m}$ para una función (ecuacion 2) especifica $f(x)$ recibe el nombre de Analisis de Fourier . Ahora deduciremos un conjunto de ecuaciones para estos coeficientes que podrán utilizarse de qui en adelante.

A fin de definir $A_{0}$,$A_{m}$ y $B_{m}$ usaremos la ortogonalidad de las funciones sinusoidales, es decir, el hecho de que

$\int \limits _{0}^{\lambda }\mathrm {sen} (mkx)\cos(nkx)dx=0\qquad i)$

$\int \limits _{0}^{\lambda }\cos(mkx)\cos(nkx)dx={\frac {\lambda }{2}}\delta _{mn}\qquad ii)$

$\int \limits _{0}^{\lambda }\mathrm {sen} (mkx)\mathrm {sen} (nkx)dx={\frac {\lambda }{2}}\delta _{mn}\qquad iii)$

$\int \limits _{0}^{\lambda }\mathrm {sen} (mkx)dx=\int \limits _{0}^{\lambda }\cos(mkx)dx=0\qquad iv)$

Donde $m$ y $n$ son números enteros positivos diferentes de cero y $\delta _{mn}$, denominada delta de Kronecker, es una expresión abreviada igual a cero cuando $m\neq n$ e igual a $1$ cuando $m=n$.

Para encontrar el coeficiente $A_{0}$ partimos de la ecuacion (2)

$f(x)={\frac {{A}_{0}}{2}}+\sum _{m=1}^{\infty }{\left\{{A}_{m}\cos \left(mkx\right)+{B}_{m}\mathrm {sen} \left(mkx\right)\right\}}$

Integramos la ecuación con los limites $0$ a $\lambda $

$\int_{0}^{\lambda }f(x)dx=\int_{0}^{\lambda }\frac{A_{0}}{2}dx+\int_{0}^{\lambda }\sum_{m=1}^{\infty }\left [ A_{m}\cos(mkx)+B_{m}\mathrm{sen}(mkx) \right ]dx$

$\int_{0}^{\lambda }f(x)dx=\frac{A_{0}}{2}\int_{0}^{\lambda }dx+\sum_{m=1}^{\infty }A_{m}\int_{0}^{\lambda } \cos(mkx)dx+\sum_{m=1}^{\infty }B_{m}\int_{0}^{\lambda }\mathrm{sen}(mkx) dx$

Pero usando la la relación $iv)$$\qquad \int \limits _{0}^{\lambda }\mathrm {sen} (mkx)dx=\int \limits _{0}^{\lambda }\cos(mkx)dx=0$

$\int _{0}^{\lambda }f(x)dx={\frac {A_{0}}{2}}\int _{0}^{\lambda }dx$

$\int _{0}^{\lambda }f(x)dx=\left[{\frac {A_{0}}{2}}x\right]_{0}^{\lambda }$

$\int _{0}^{\lambda }f(x)dx={\frac {A_{0}}{2}}\left(\lambda \right)$

$\therefore A_{0}={\frac {2}{\lambda }}\int _{0}^{\lambda }f(x)dx$ .....(3)

Para encontrar el coeficiente $A_{m}$ multiplicamos toda la ecuación (2) por $cos(nkx)$ e integramos la ecuación con los limites $0$ hasta $\lambda$

$f(x)\cos(nkx)={\frac {A_{0}}{2}}\cos(nkx)+\sum _{m=1}^{\infty }A_{m}\cos(mkx)\cos(nkx)+\sum _{m=1}^{\infty }B_{m}\mathrm {sen} (mkx)\cos(nkx)$

$\int _{0}^{\lambda }f(x)\cos(nkx)dx={\frac {A_{0}}{2}}\int _{0}^{\lambda }\cos(nkx)dx+\sum _{m=1}^{\infty }A_{m}\int _{0}^{\lambda }\cos(mkx)\cos(nkx)dx+\sum _{m=1}^{\infty }B_{m}\int _{0}^{\lambda }\mathrm {sen} (mkx)\cos(nkx)dx$

Por la relación $i)$ $\qquad \int \limits _{0}^{\lambda }\mathrm {sen} (mkx)\cos(nkx)dx=0$

Por la relación $ii)$ $\qquad \int \limits _{0}^{\lambda }\cos(mkx)\cos(nkx)dx={\frac {\lambda }{2}}\delta _{mn}$

$\int _{0}^{\lambda }f(x)\cos(nkx)dx=\sum _{m=1}^{\infty }A_{m}\int _{0}^{\lambda }\cos(mkx)\cos(nkx)dx$

con: $m=n$

$\int _{0}^{\lambda }f(x)\cos(nkx)dx=A_{m}\int _{0}^{\lambda }\cos(mkx)\cos(nkx)dx$

$\int _{0}^{\lambda }f(x)\cos(nkx)dx=A_{m}{\frac {\lambda }{2}}\delta _{mn}$

$\int _{0}^{\lambda }f(x)\cos(nkx)dx=A_{m}{\frac {\lambda }{2}}$

$\therefore A_{m}={\frac {2}{\lambda }}\int _{0}^{\lambda }f(x)\cos(mkx)dx$.....(4)

Para encontrar el coeficiente $B_{m}$ multiplicamos toda la ecuación (2) por $\mathrm{sen}(nkx)$ e integramos la ecuación con los limites $0$ hasta $\lambda$

$f(x)\mathrm {sen} (nkx)={\frac {A_{0}}{2}}\mathrm {sen} (nkx)+\sum _{m=1}^{\infty }A_{m}\cos(mkx)\mathrm {sen} (nkx)+\sum _{m=1}^{\infty }B_{m}\mathrm {sen} (mkx)\mathrm {sen} (nkx)$

$\int _{0}^{\lambda }f(x)\mathrm {sen} (nkx)dx={\frac {A_{0}}{2}}\int _{0}^{\lambda }\mathrm {sen} (nkx)dx+\sum _{m=1}^{\infty }A_{m}\int _{0}^{\lambda }\cos(mkx)\mathrm {sen} (nkx)dx+\sum _{m=1}^{\infty }B_{m}\int _{0}^{\lambda }\mathrm {sen} (mkx)\mathrm {sen} (nkx)dx$

Por la relación $i)$ $\qquad \int \limits _{0}^{\lambda }\mathrm {sen} (mkx)\cos(nkx)dx=0$

Por la relación $iii)$ $\qquad \int \limits _{0}^{\lambda }\mathrm {sen} (mkx)\mathrm {sen} (nkx)dx={\frac {\lambda }{2}}\delta _{mn}$

$\int _{0}^{\lambda }f(x)\mathrm {sen} (nkx)dx=\sum _{m=1}^{\infty }B_{m}\int _{0}^{\lambda }\mathrm {sen} (mkx)\mathrm {sen} (nkx)dx$

con $m=n$

$\int _{0}^{\lambda }f(x)\mathrm {sen} (nkx)dx=B_{m}\int _{0}^{\lambda }\mathrm {sen} (mkx)\mathrm {sen} (nkx)dx$

$\int _{0}^{\lambda }f(x)\mathrm {sen} (nkx)dx=B_{m}{\frac {\lambda }{2}}\delta _{mn}$

$\int _{0}^{\lambda }f(x)\mathrm {sen} (nkx)dx=B_{m}{\frac {\lambda }{2}}$

$\therefore B_{m}={\frac {2}{\lambda }}\int _{0}^{\lambda }f(x)\mathrm {sen} (mkx)dx$

En resumen, entonces una función periódica $f(x)$ puede representarse como serie de Fourier

$f(x)={\frac {{A}_{0}}{2}}+\sum _{m=1}^{\infty }{\left\{{A}_{m}\cos \left(mkx\right)+{B}_{m}\mathrm {sen} \left(mkx\right)\right\}}$

Donde conociendo $f(x)$, los coeficientes se calculan usando $(3),(4)$ y $(5)$.

Existen determinadas condiciones de simetría que vale la pena considerar porque proporcionan algunos atajos a los cálculos. Así, si una función $f(x)$ es par, es decir, si $f(-x)=f(x)$ o, de manera equivalente, si la misma es simétrica alrededor de $x=0$, su serie de Fourier contendrá solamente términos coseno ($B_{m}=0$ para todo $m$) los cuales son, de por sí, funciones pares. De la misma forma, las funciones impares que son antisimétricas alrededor de $x=0$, es decir, $f(-x)=-f(x)$ tendrá desarrollos en serie que contiene sólo funciones seno ($A_{m}=0$ para cualquier valor de $m$). En cualquiera de los dos casos, no es preciso calcular ambas series. Esto resulta ser particularmente útil cuando la posición del origen $(x=0)$ es arbitraria pudiendo escogerse para simplificar las cosas todo lo posible. No obstante cabe recordar que muchas funciones comunes no son ni pares ni impares (por ejemplo, $e^{x}$)

Serie de Fourier: Ejemplo 1

Desarrolle $f(x)=1$ cuando $0<x<{\frac {\lambda }{2}}$ , $-1$ cuando ${\frac {\lambda }{2}}<x<\lambda$

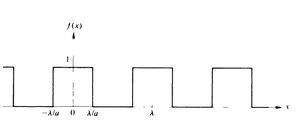
Figura 4.Perfil de una onda cuadrada periodica

Para poner un ejemplo, calculamos la serie de Fourier que corresponde a una onda cuadrada. Seleccionamos la posición de origen como se muestra en la figura 4:

Partimos de nuestra función:

$f(x)={\frac {A_{0}}{2}}+\sum _{m=1}^{\infty }\left[A_{m}\cos(mkx)+B_{m}\mathrm {sen} (mkx)\right]$

Calculamos el coeficiente $A_{0}$ usando la ecuación (3):

$A_{0}={\frac {2}{\lambda }}\int _{0}^{\lambda }f(x)dx$

$A_{0}={\frac {2}{\lambda }}\left[\int _{0}^{\frac {\lambda }{2}}dx-\int _{\frac {\lambda }{2}}^{\lambda }dx\right]$

$A_{0}={\frac {2}{\lambda }}\left[\left[x\right]_{0}^{\frac {\lambda }{2}}+\left[-x\right]_{\frac {\lambda }{2}}^{\lambda }\right]$

$A_{0}={\frac {2}{\lambda }}\left[{\frac {\lambda }{2}}+\left[-\lambda +{\frac {\lambda }{2}}\right]\right]$

$A_{0}={\frac {2}{\lambda }}\left[{\frac {\lambda }{2}}+\left[-{\frac {\lambda }{2}}\right]\right]$

$A_{0}={\frac {2}{\lambda }}\left[{\frac {\lambda }{2}}-{\frac {\lambda }{2}}\right]$

$A_{0}={\frac {2}{\lambda }}(0)$

$\therefore A_{0}=0$

Ahora calculamos el coeficiente $A_{m}$ usando la ecuación (4):

$A_{m}={\frac {2}{\lambda }}\left[\int _{0}^{\frac {\lambda }{2}}\cos(mkx)dx-\int _{\frac {\lambda }{2}}^{\lambda }\cos(mkx)dx\right]$

$A_{m}={\frac {2}{\lambda }}\left[{\frac {1}{mk}}\left[\mathrm {sen} (mkx)\right]_{0}^{\frac {\lambda }{2}}-{\frac {1}{mk}}\left[\mathrm {sen} (mkx)\right]_{\frac {\lambda }{2}}^{\lambda }\right]$

$A_{m}={\frac {2}{\lambda }}\left[{\frac {1}{mk}}\left[\mathrm {sen} \left({\frac {mk\lambda }{2}}\right)\right]-{\frac {1}{mk}}\left[\mathrm {sen} (mk\lambda )-\mathrm {sen} \left({\frac {mk\lambda }{2}}\right)\right]\right]$

$A_{m}={\frac {2}{\lambda }}\left[-{\frac {1}{mk}}\left[\mathrm {sen} (mk\lambda )\right]\right]$

Pero $k={\frac {2\pi }{\lambda }}$

$A_{m}={\frac {2}{\lambda }}\left[-{\frac {\lambda }{2\pi m}}\left[\mathrm {sen} (2\pi m)\right]\right]$

$A_{m}={\frac {1}{\pi m}}\left[-\mathrm {sen} (2\pi m)\right]$

El termino $\left[-\mathrm {sen} (2\pi m)\right]$ es igual a cero ya que cualquier múltiplo de m dará cero

$\therefore A_{m}=0$

Ahora calculamos el coeficiente $B_{m}$ usando la ecuación (5):

$B_{m}={\frac {2}{\lambda }}\left[\int _{0}^{\frac {\lambda }{2}}\mathrm {sen} (mkx)dx-\int _{\frac {\lambda }{2}}^{\lambda }\mathrm {sen} (mkx)dx\right]$

$B_{m}={\frac {2}{\lambda }}\left[{\frac {1}{mk}}\left[-\cos(mkx)\right]_{0}^{\frac {\lambda }{2}}+{\frac {1}{mk}}\left[\cos(mkx)\right]_{\frac {\lambda }{2}}^{\lambda }\right]$

$B_{m}={\frac {2}{\lambda }}\left[{\frac {1}{mk}}\left[-\cos \left({\frac {mk\lambda }{2}}\right)+cos(0)\right]+{\frac {1}{mk}}\left[\cos(mk\lambda )-\cos \left({\frac {mk\lambda }{2}}\right)\right]\right]$

$B_{m}={\frac {2}{\lambda }}\left[{\frac {1}{mk}}\left[-\cos \left({\frac {mk\lambda }{2}}\right)+1+\cos(mk\lambda )-\cos \left({\frac {mk\lambda }{2}}\right)\right]\right]$

Pero $k={\frac {2\pi }{\lambda }}$

$B_{m}={\frac {2}{\lambda }}\left[{\frac {\lambda }{2\pi m}}\left[-\cos(\pi m)+1+\cos(2\pi m)-\cos(\pi m)\right]\right]$

$B_{m}={\frac {1}{\pi m}}\left[-2\cos(\pi m)+2\right]$

$\therefore B_{m}={\frac {2}{\pi m}}\left[1-\cos(\pi m)\right]$

Sustituyendo en nuestra función (ecuación (2)), la respuesta queda de la siguiente manera:

$\therefore f(x)={\frac {2}{\pi }}\sum _{m=1}^{\infty }{\frac {1-\cos(\pi m)}{m}}\mathrm {sen} (mx)$

Figura 5. Representación gráfica de unas sumas parciales de la serie a medida que el número de términos aumenta.

Serie de Fourier: Ejemplo 2

Desarrolle $f(x)=x$ , en $-2<x<2$

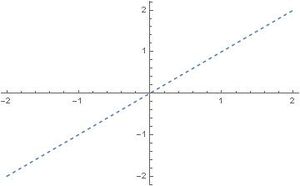
Figura 6. Perfil de una función impar

La inspección de la Figura (6) muestra que la función dada es impar en el intervalo $(-2,2)$ por lo que desarrollamos $f$ en una serie de senos.

Tenemos la función:

$f(x)={\frac {A_{0}}{2}}+\sum _{m=1}^{\infty }\left[A_{m}\cos(mkx)+B_{m}\mathrm {sen} (mkx)\right]$

Como ya mencionamos, la función es impar por lo que los coeficientes son:

$A_{0}=0$

$A_{m}=0$

Resolvemos:

$B_{m}={\frac {2}{\lambda }}\int _{0}^{\lambda }f(x)\mathrm {sen} (mkx)dx$

donde $\lambda =2$

$B_{m}=\int _{-2}^{0}x\mathrm {sen} (mkx)dx+\int _{0}^{2}x\mathrm {sen} (mkx)dx$

$B_{m}=-{\frac {1}{mk}}\left[x\cos(mkx)\right]_{-2}^{0}+{\frac {1}{m^{2}k^{2}}}\left[\mathrm {sen} (mkx)\right]_{-2}^{0}-{\frac {1}{mk}}\left[x\cos(mkx)\right]_{0}^{2}+{\frac {1}{m^{2}k^{2}}}\left[\mathrm {sen} (mkx)\right]_{0}^{2}$

$B_{m}=-{\frac {1}{mk}}\left[2\cos(2mk)\right]+{\frac {1}{m^{2}k^{2}}}\left[\mathrm {sen} (2mk)\right]-{\frac {1}{mk}}\left[2\cos(2mk)\right]+{\frac {1}{m^{2}k^{2}}}\left[\mathrm {sen} (2mk)\right]$

Pero : $k={\frac {2\pi }{\lambda }}={\frac {2\pi }{2}}=\pi$

$B_{m}=-{\frac {1}{m\pi }}\left[2\cos(2\pi m)\right]+{\frac {1}{m^{2}\pi ^{2}}}\left[\mathrm {sen} (2\pi m)\right]-{\frac {1}{m\pi }}\left[2\cos(2\pi m)\right]+{\frac {1}{m^{2}\pi ^{2}}}\left[\mathrm {sen} (2\pi m)\right]$

Vemos que $\mathrm {sen} (2\pi m)=0$ ya que cualquier múltiplo de $m$ que le demos nos dará $0$

$B_{m}=-{\frac {1}{m\pi }}\left[2\cos(2\pi m)\right]-{\frac {1}{m\pi }}\left[2\cos(2\pi m)\right]$

$B_{m}=-{\frac {4}{m\pi }}\left[\cos(2\pi m)\right]$

$B_{m}=-{\frac {4}{m\pi }}\left[(-1)^{n}\right]$

$\therefore B_{m}={\frac {4}{m\pi }}\left[(-1)^{n+1}\right]$

Sustituyendo en nuestra función (ecuación (2)), la respuesta queda de la siguiente manera:

$\therefore f(x)={\frac {4}{\pi }}\sum _{m=1}^{\infty }{\frac {(-1)^{n+1}}{m\pi }}\mathrm {sen} \left({\frac {m\pi x}{2}}\right)$

De ahora en adelante podemos visualizar este tipo de perturbación como superposición consecutivas armónicas de diferentes frecuencias cuyo comportamiento individual puede estudiarse separadamente. Por lo tanto, podemos escribir

$f(x\pm vt)={\frac {A_{0}}{2}}+\sum _{m=1}^{\infty }A_{m}\cos mk(x\pm vt)+\sum _{m=1}^{\infty }B_{m}\mathrm {sen} mk(x\pm vt)\qquad (6)$

para cualquiera de tales ondas periódicas anarmónicas.

Referencias

"Óptica.". E. Hecht, A. Zajac. Ed. Addison Wesley, 2000

"Optical physics" 4th Edition / S. G. Lipson, H. Lipson and D. S. Tannhauser.

"Fundamentals of Optics." F.A. Jenkins, H.E. White. Ed. McGraw-Hill, 1981.

---

Aportación de: Nayomi (discusión) 21:35 13 jul 2020 (CDT) Nayomi Russell