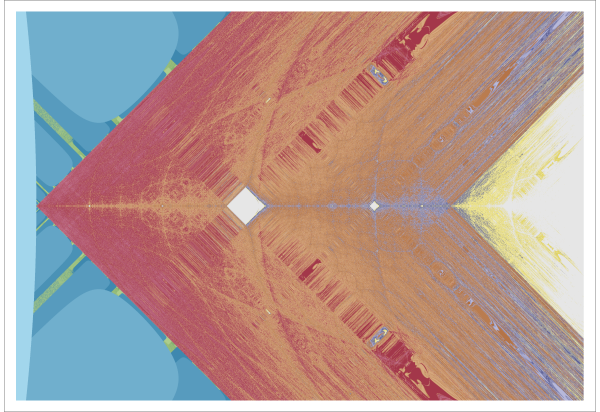
In the parameter space , both imaginary and real, the initial point is always in the origin. The first iteration corresponds to the point that is being evaluated (see quadratic mapping).
In the images below, the complete bound real scator set under the quadratic iteration in 1+2 dimensions is depicted, it's labeled as $c2i0 \mathbb{E}_{+}^{1+2}$.
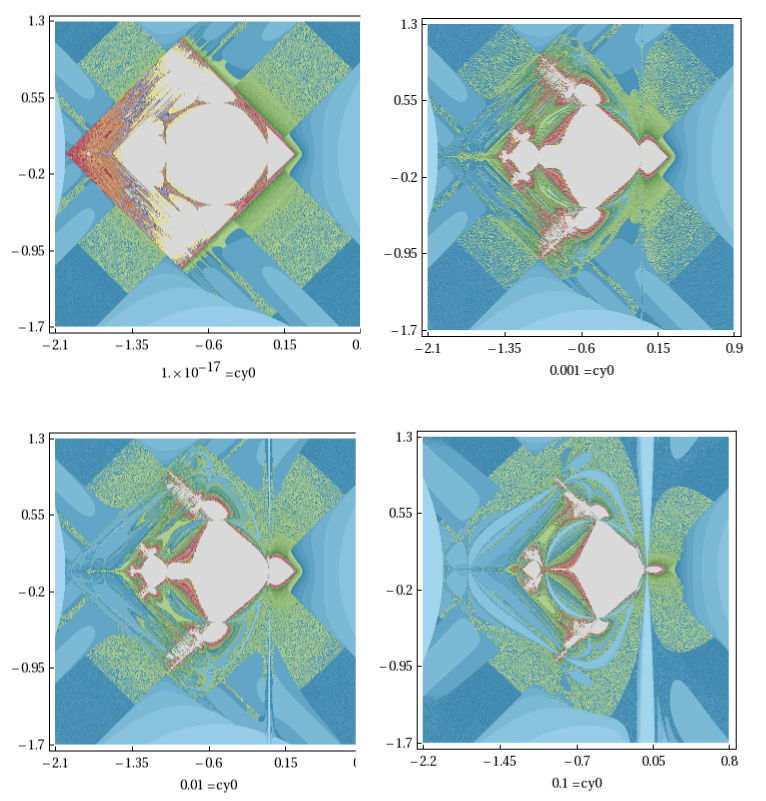
The rendering was performed with the fantastic programme Mandelbulber v.2.07 modified accordingly to cope with scator algebra. The file modifications are described in the following link: hun: parameter programme .
In this case, the images are obtained by means of planes s, x, along "y" axis. In the previous image conforming it moves along the "y" hyper-axis, you can observe different behavior.