Here we describe an experiment where the position and momentum of photons in two closely separated modes were, for the first time, simultaneously measured in the same space-time region.
Many articles have been written regarding the intrinsic uncertainty between conjugate variables in quantum mechanics ... However, very few of them involve experiments. Most realizations with light evaluate uncertainty from a diffraction setup. However, as has been pointed out, the position uncertainty is measured in one place (the diffracting aperture) while the momentum is evaluated from the diffraction pattern (at the observation screen). Thus, it is not, stricktly speaking, a simultaneous measurement.
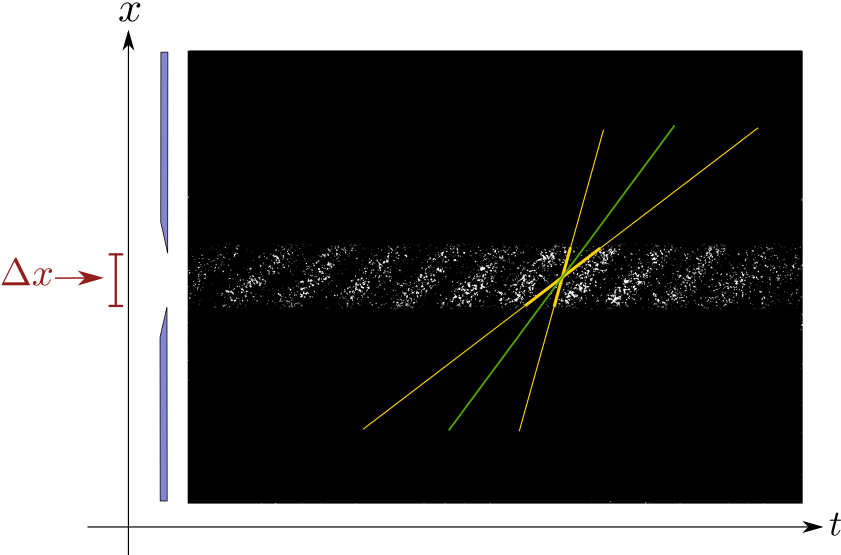
The position uncertainty $\Delta x$ depends on the entrance pupil aperture. The momentum is given by the slope of the fringes in a space versus time interferogram. The momenumt uncertainty $\Delta p$, is proportional to the difference between the maximum and minimum slopes (shown in yellow in the figures). In this experiment, the limitation of the simultaneous measurement of the photon's position and momentum is directly visualized. In the external link https://dx.doi.org/10.2139/ssrn.4105108 the experiment is reported in detail.
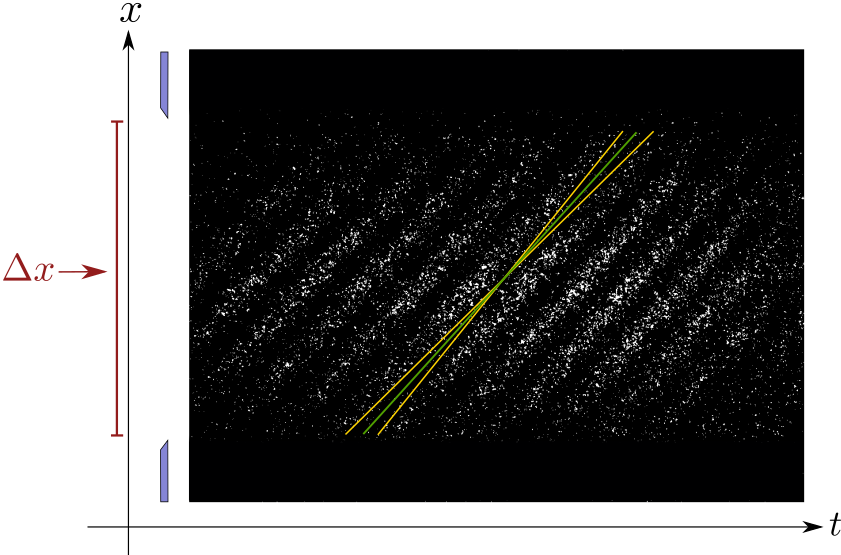
When the entrance aperture is fully opened, the position uncertainty $\Delta x$ is large. The momentum uncertainty $\Delta p$ is quite narrow, as can be seen from the first figure. The average slope (in green) and the maximum and minimum slopes (in yellow), differ very little from each other.
If the entrance aperture is reduces, the position uncertainty $\Delta x$ is reduced. However, the slope uncertainty $\Delta p$ increases considerably, as can be seen from the second figure.
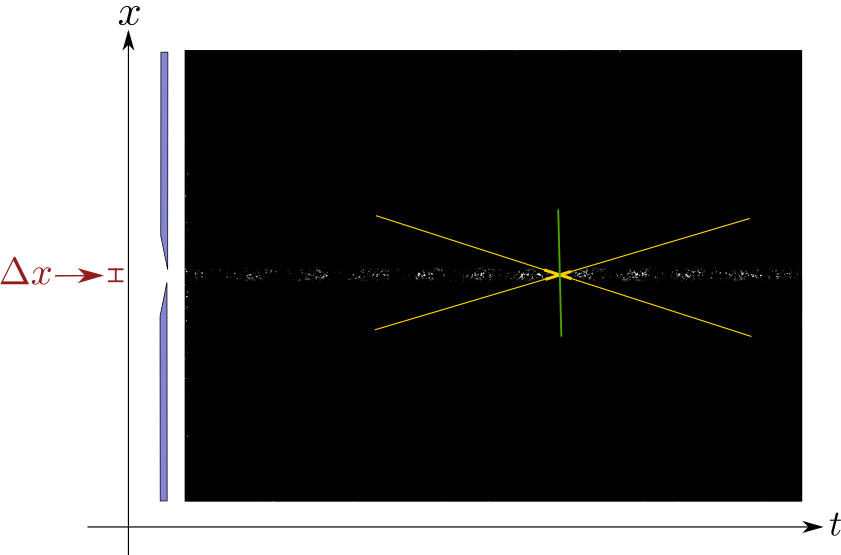
If the entrance aperture is still further reduced to minimum, while letting some light to be detected, the position uncertainty $\Delta x$ is very small. However, the slope (in green) is almost a guess, for the inclination of the fringes is not discernible. Thus, the slope uncertainty becomes huge, and thus the momentum uncertainty $\Delta p$ is very large.
Notice that the position instrumental resolution is of the size of a white dot, that is, much smaller than the position quantum uncertainty $\Delta x$. The slope instrumental resolution is actually smaller than the slopes difference (in green) in the first figure. Therefore, the simultaneous measurement of position and momentum in the quantum limit does not depend on the instrument resolution. Even if the instrument can resolve much smaller distances or momenta, as in this case, it is not possible to achieve a simultaneous measurement with better resolution than that established by Heisenberg's inequality $$\Delta x \; \Delta p \geq\frac{\hbar}{2}.$$

