Mucha tinta ha corrido respecto a la incertidumbre intrínseca entre variables conjugadas en mecánica cuántica ...
Aquí se describe un experimento donde se midió la posición y momentum de fotones que se encuentran en dos modos muy cercanos. La incertidumbre en la posición $\Delta x$ depende de la apertura de entrada del sistema. El momento está dado por la pendiente de las franjas en el interferograma de espacio contra tiempo. La incertidumbre en el momento $\Delta p$, es proporcional a la diferencia entre las pendientes máxima y mínima (mostradas en amarillo en las figuras). En el experimento se visualiza la limitación que existe al realizar una medición simultánea de posición y momentum de los fotones. En el vínculo externo https://dx.doi.org/10.2139/ssrn.4105108 se describe el experimento.
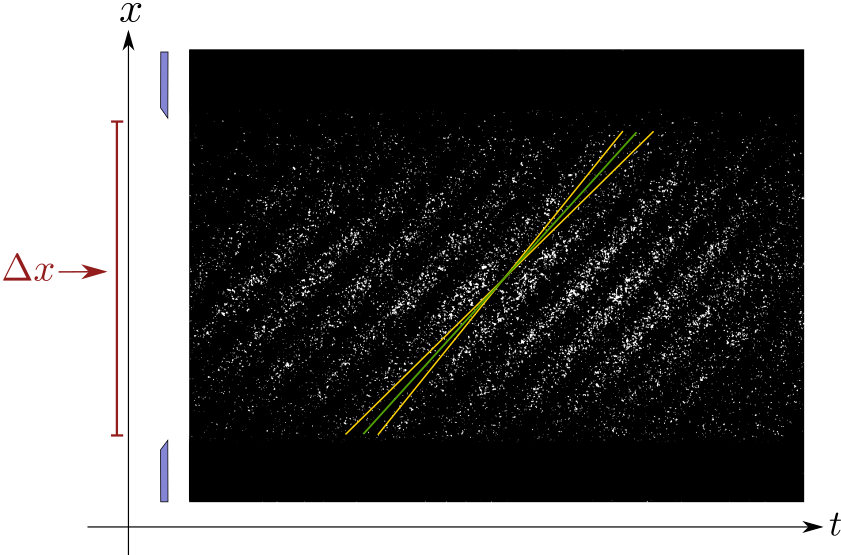
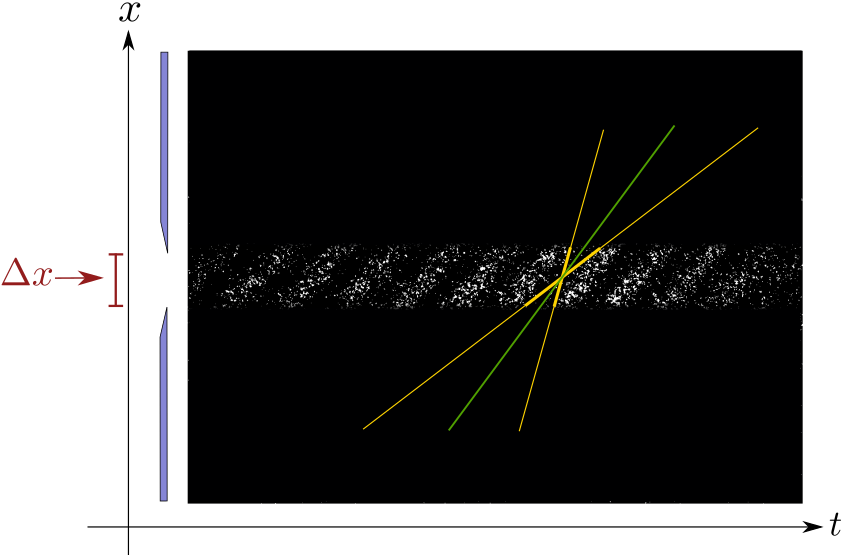
Cuando la apertura de entrada es máxima, la incertidumbre en la posición $\Delta x$ es grande. La incertidumbre en en el momento $\Delta p$ es bastante reducido, pues como se ve de la primera figura, la pendiente promedio (en verde) y las pendientes máxima y mínima (en amarillo) difieren poco.
Si se reduce la apertura de entrada, la incertidumbre en la posición $\Delta x$ es menor. Sin embargo, la incertidumbre en la pendiente $\Delta p$ aumenta considerablemente.
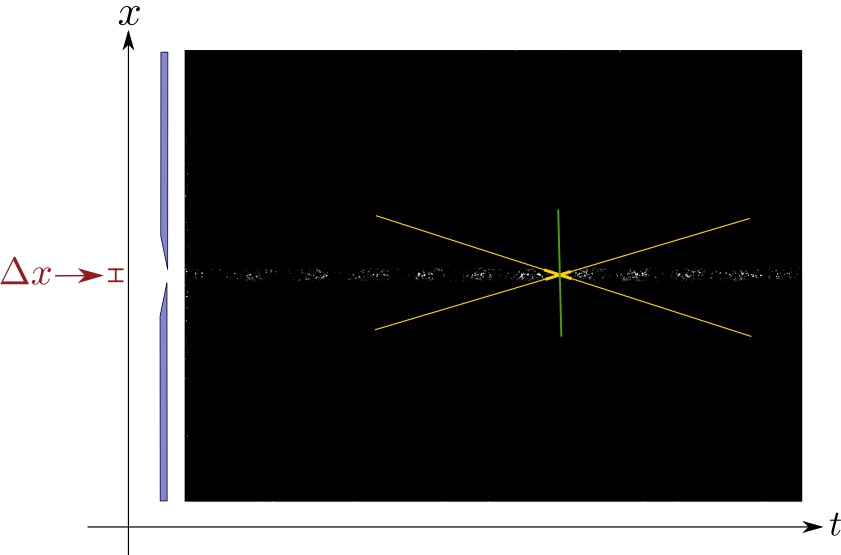
Si la apertura de entrada se reduce al mínimo, de manera que la incertidumbre en la posición $\Delta x$ sea mínima, la pendiente (en verde) es casi una adivinanza, pues no es posible visualizar la inclinación de las franjas. Entonces, la incertidumbre en la pendiente es enorme, y por lo tanto la incertidumbre en el momentum $\Delta p$ es muy grande.
Reflexionemos que la incertidumbre instrumental en la posición es del tamaño de una de las motas blancas, es decir, mucho menor que la incertidumbre cuántica $\Delta x$. La incertidumbre instrumental en la pendiente, es menor aún que la diferencia de pendientes en la primera figura. Esto ilustra que el problema de la medición simultánea de la posición y momentum en el límite cuántico no depende de la resolución de los instrumentos, pues aunque estos tengan una mejor resolución, como en este caso, no es posible lograr una medición simultánea más allá del límite que establece la desigualdad de Heisenberg $$\Delta x \; \Delta p \geq\frac{\hbar}{2}.$$

