Diferencia entre revisiones de «Vibra: probs c8»
| Línea 5: | Línea 5: | ||
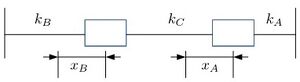
Dos osciladores armónicos A y B, de masa m y constantes $k_{A}$ y $k_{B}$ respectivamente, se acoplan juntos mediante un muelle de constante $k_{C}$. Hallar las frecuencias normales $ \omega_{1}$ y $ \omega_{2}$ y describir los modos normales de oscilación si $k_{C}^2 = k_{A} k_{B}$. | Dos osciladores armónicos A y B, de masa m y constantes $k_{A}$ y $k_{B}$ respectivamente, se acoplan juntos mediante un muelle de constante $k_{C}$. Hallar las frecuencias normales $ \omega_{1}$ y $ \omega_{2}$ y describir los modos normales de oscilación si $k_{C}^2 = k_{A} k_{B}$. | ||
[[Archivo:Diagrama01.jpg|miniaturadeimagen|Diagrama de masas unidas a los muelles.]] | [[Archivo:Diagrama01.jpg|miniaturadeimagen|Diagrama de masas unidas a los muelles.]] | ||
Teniendo a consideración la $2^a$ ley de Newton, las ecuaciones de movimiento pueden ser descritas de la sig. manera. | Teniendo a consideración la $2^a$ ley de Newton, las ecuaciones de movimiento pueden ser descritas de la sig. manera. | ||
| Línea 14: | Línea 13: | ||
\[ | \[ | ||
m\ddot{x_B} = -k_B x_B - k_C (x_B - x_A) | m\ddot{x_B} = -k_B x_B - k_C (x_B - x_A) | ||
\] | |||
Ahora dividimos todo entre la masa "m", distribuimos los términos de la multiplicación y pasamos todo del lado izquierdo quedando todo igualado a 0. | |||
\begin{equation} | |||
\ddot{x_A} + \frac{k_A + k_C}{m}x_A -\frac{k_C}{m}x_B = 0 | |||
\end{equation} | |||
\begin{equation} | |||
\ddot{x_B} + \frac{k_B + k_C}{m}x_B -\frac{k_C}{m}x_A = 0 | |||
\end{equation} | |||
Ahora usando la forma $x_A = Ae^{i \omega t}$ y $x_B = Be^{i \omega t}$. Y sustituyéndolo en (1) y (2), tenemos: | |||
\[ | |||
[- \omega^2 + \frac{k_A +k_C}{m}]A - \frac{k_C}{m}B = 0 | |||
\] | |||
\[ | |||
- \frac{k_C}{m}A + [- \omega^2 + \frac{k_B +k_C}{m}]B = 0 | |||
\] | |||
Una vez teniendo esto, puedo ver que tengo un sistema de ecuaciones, por lo tanto al reescribirlo en forma matricial queda: | |||
\[ | |||
\begin{bmatrix} | |||
- \omega^2 + \frac{k_A +k_C}{m} & - \frac{k_C}{m} \\ | |||
- \omega^2 + \frac{k_B +k_C}{m}& - \frac{k_C}{m} | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
A \\ | |||
B | |||
\end{bmatrix} =0 | |||
\] | |||
Este sistema no tendrá una solución trivial por lo tanto su determinante es cero. Al evaluar el determinante tenemos: | |||
\[ | |||
(- \omega^2 + \frac{k_A +k_C}{m})(- \omega^2 + \frac{k_B +k_C}{m}) -\frac{k_C^2}{m^2} = 0 | |||
\] | |||
\[ | |||
\omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m}- \frac{k_C^2}{m^2}+ \frac{1}{m^2}(k_A + k_C)(k_B + k_C) | |||
\] | |||
\[ | |||
\omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m} + \frac{k_A k_B + k_A k_C + k_B k_C}{m^2} = 0 | |||
\] | |||
Resolviendo esta ecuación cuadrática para $ \omega^2 $ | |||
\[ | |||
\omega_{1,2}^{2} = \frac{1}{2}[\frac{k_A+2k_C+k_B}{m} \pm \sqrt{(\frac{k_A+2k_C+k_B}{m})^2 - \frac{4}{m^2}(k_A k_B + k_A k_C + k_B k_C)}] | |||
\] | |||
\[ | |||
= \frac{1}{m}[\frac{k_A+k_B}{2}+ k_C \pm \sqrt{\frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C)}] | |||
\] | |||
Ahora para la expresión dentro de la raíz es: | |||
\[ | |||
I = \frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C) | |||
\] | |||
\[ | |||
= \frac{1}{4}(k_A^2 +k_B^2 + 2k_C^2 + 2k_A k_B + 4k_A k_C + 4k_Bk_C) - (k_A k_B + k_A k_C + k_B k_C) | |||
\] | |||
\[ | |||
= \frac{1}{4}(k_A^2 + k_B^2 -2k_A k_B) + k_C^2 = (\frac{k_A - k_B}{2})^2 + k_C^2 | |||
\] | |||
Así por lo tanto: | |||
\[ | |||
{\Large \fbox{$ \omega_{1,2}^{2} = \frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_C^2}]$}} | |||
\] | |||
Ahora para el caso de $ k_C^2 = k_A k_B $ tenemos: | |||
\[ | |||
\omega_{1,2}^{2} = \frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_A k_B}] | |||
\] | |||
\[ | |||
= \frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A + k_B}{2})^2}] | |||
\] | |||
\[ | |||
= \frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \frac{1}{2}(k_A + k_B)] | |||
\] | |||
Por lo tanto $ \omega_1$ y $ \omega_2$ en el caso de suma y resta $ \pm$ respectivamente, tenemos: | |||
\[ | |||
{\Large \fbox{$ \omega_1 = \sqrt{\frac{k_A + k_B + k_C}{m}}$}} | |||
\] | |||
\[ | |||
{\Large \fbox{$ \omega_2 = \sqrt{\frac{k_C}{m}}$}} | |||
\] | \] | ||
Revisión del 11:11 10 nov 2020
Mfgwi (discusión) 09:17 10 nov 2020 (CST)
Problema 5-4. Capítulo 5. French
Dos osciladores armónicos A y B, de masa m y constantes $k_{A}$ y $k_{B}$ respectivamente, se acoplan juntos mediante un muelle de constante $k_{C}$. Hallar las frecuencias normales $ \omega_{1}$ y $ \omega_{2}$ y describir los modos normales de oscilación si $k_{C}^2 = k_{A} k_{B}$.
Teniendo a consideración la $2^a$ ley de Newton, las ecuaciones de movimiento pueden ser descritas de la sig. manera.
\[ m\ddot{x_A} = -k_A x_A - k_C (x_A - x_B) \]
\[ m\ddot{x_B} = -k_B x_B - k_C (x_B - x_A) \] Ahora dividimos todo entre la masa "m", distribuimos los términos de la multiplicación y pasamos todo del lado izquierdo quedando todo igualado a 0.
\begin{equation} \ddot{x_A} + \frac{k_A + k_C}{m}x_A -\frac{k_C}{m}x_B = 0 \end{equation} \begin{equation} \ddot{x_B} + \frac{k_B + k_C}{m}x_B -\frac{k_C}{m}x_A = 0 \end{equation}
Ahora usando la forma $x_A = Ae^{i \omega t}$ y $x_B = Be^{i \omega t}$. Y sustituyéndolo en (1) y (2), tenemos:
\[ [- \omega^2 + \frac{k_A +k_C}{m}]A - \frac{k_C}{m}B = 0 \] \[ - \frac{k_C}{m}A + [- \omega^2 + \frac{k_B +k_C}{m}]B = 0 \]
Una vez teniendo esto, puedo ver que tengo un sistema de ecuaciones, por lo tanto al reescribirlo en forma matricial queda:
\[ \begin{bmatrix} - \omega^2 + \frac{k_A +k_C}{m} & - \frac{k_C}{m} \\ - \omega^2 + \frac{k_B +k_C}{m}& - \frac{k_C}{m} \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} =0 \]
Este sistema no tendrá una solución trivial por lo tanto su determinante es cero. Al evaluar el determinante tenemos: \[ (- \omega^2 + \frac{k_A +k_C}{m})(- \omega^2 + \frac{k_B +k_C}{m}) -\frac{k_C^2}{m^2} = 0 \] \[ \omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m}- \frac{k_C^2}{m^2}+ \frac{1}{m^2}(k_A + k_C)(k_B + k_C) \] \[ \omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m} + \frac{k_A k_B + k_A k_C + k_B k_C}{m^2} = 0 \]
Resolviendo esta ecuación cuadrática para $ \omega^2 $
\[ \omega_{1,2}^{2} = \frac{1}{2}[\frac{k_A+2k_C+k_B}{m} \pm \sqrt{(\frac{k_A+2k_C+k_B}{m})^2 - \frac{4}{m^2}(k_A k_B + k_A k_C + k_B k_C)}] \] \[ = \frac{1}{m}[\frac{k_A+k_B}{2}+ k_C \pm \sqrt{\frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C)}] \]
Ahora para la expresión dentro de la raíz es:
\[ I = \frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C) \] \[ = \frac{1}{4}(k_A^2 +k_B^2 + 2k_C^2 + 2k_A k_B + 4k_A k_C + 4k_Bk_C) - (k_A k_B + k_A k_C + k_B k_C) \] \[ = \frac{1}{4}(k_A^2 + k_B^2 -2k_A k_B) + k_C^2 = (\frac{k_A - k_B}{2})^2 + k_C^2 \]
Así por lo tanto:
\[ {\Large \fbox{$ \omega_{1,2}^{2} = \frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_C^2}]$}} \]
Ahora para el caso de $ k_C^2 = k_A k_B $ tenemos:
\[
\omega_{1,2}^{2} = \frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_A k_B}]
\]
\[
= \frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A + k_B}{2})^2}]
\]
\[
= \frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \frac{1}{2}(k_A + k_B)]
\]
Por lo tanto $ \omega_1$ y $ \omega_2$ en el caso de suma y resta $ \pm$ respectivamente, tenemos:
\[ {\Large \fbox{$ \omega_1 = \sqrt{\frac{k_A + k_B + k_C}{m}}$}} \] \[ {\Large \fbox{$ \omega_2 = \sqrt{\frac{k_C}{m}}$}} \]