Vibra: probs c8

Mfgwi (discusión) 09:17 10 nov 2020 (CST)

Problema 5-4. Capítulo 5. French

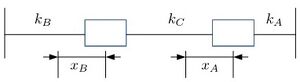
Dos osciladores armónicos . A y B, de masa m y constantes $k_{A}$ y $k_{B}$ respectivamente, se acoplan juntos mediante un muelle de constante $k_{C}$. Hallar las frecuencias normales $ \omega_{1}$ y $ \omega_{2}$ y describir los modos normales de oscilación si $k_{C}^2 = k_{A} k_{B}$.

Diagrama de masas unidas a los muelles.

Teniendo a consideración la $2^a$ ley de Newton, las ecuaciones de movimiento pueden ser descritas de la sig. manera.

\[ m\ddot{x_A} = -k_A x_A - k_C (x_A - x_B). \]

\[ m\ddot{x_B} = -k_B x_B - k_C (x_B - x_A). \] Ahora dividimos todo entre la masa "m", distribuimos los términos de la multiplicación y pasamos todo del lado izquierdo quedando todo igualado a 0.

\begin{equation} \ddot{x_A} + \frac{k_A + k_C}{m}x_A -\frac{k_C}{m}x_B = 0. \end{equation} \begin{equation} \ddot{x_B} + \frac{k_B + k_C}{m}x_B -\frac{k_C}{m}x_A = 0. \end{equation}

Ahora usando la forma $x_A = Ae^{i \omega t}$ y $x_B = Be^{i \omega t}$. Y sustituyéndolo en (1) y (2), tenemos:

\[ [- \omega^2 + \frac{k_A +k_C}{m}]A - \frac{k_C}{m}B = 0. \] \[ - \frac{k_C}{m}A + [- \omega^2 + \frac{k_B +k_C}{m}]B = 0. \]

Una vez teniendo esto, puedo ver que tengo un sistema de ecuaciones, por lo tanto al reescribirlo en forma matricial queda:

\[ \begin{bmatrix} - \omega^2 + \frac{k_A +k_C}{m} & - \frac{k_C}{m} \\ - \omega^2 + \frac{k_B +k_C}{m}& - \frac{k_C}{m} \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} =0 \]

Este sistema no tendrá una solución trivial por lo tanto su determinante es cero. Al evaluar el determinante tenemos: \[ (- \omega^2 + \frac{k_A +k_C}{m})(- \omega^2 + \frac{k_B +k_C}{m}) -\frac{k_C^2}{m^2} = 0, \] Resolviendo la multiplicación de polinomios \[ \omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m}- \frac{k_C^2}{m^2}+ \frac{1}{m^2}(k_A + k_C)(k_B + k_C), \] Por lo tanto \[ \omega^4 - \omega^2 \frac{k_A+2k_C+k_B}{m} + \frac{k_A k_B + k_A k_C + k_B k_C}{m^2} = 0. \]

Resolviendo esta ecuación cuadrática para $ \omega^2 $

\[ \omega_{1,2}^{2} = \frac{1}{2}[\frac{k_A+2k_C+k_B}{m} \pm \sqrt{(\frac{k_A+2k_C+k_B}{m})^2 - \frac{4}{m^2}(k_A k_B + k_A k_C + k_B k_C)}], \] \[ = \frac{1}{m}[\frac{k_A+k_B}{2}+ k_C \pm \sqrt{\frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C)}]. \]

Ahora para la expresión dentro de la raíz es:

\[ I = \frac{1}{4}(k_A +2k_C + k_B)^2 - (k_A k_B + k_A k_C + k_B k_C), \] Desarrollando el polinomio y simplificando \[ = \frac{1}{4}(k_A^2 +k_B^2 + 2k_C^2 + 2k_A k_B + 4k_A k_C + 4k_Bk_C) - (k_A k_B + k_A k_C + k_B k_C), \] \[ = \frac{1}{4}(k_A^2 + k_B^2 -2k_A k_B) + k_C^2 = (\frac{k_A - k_B}{2})^2 + k_C^2. \]

Así por lo tanto:

\[ {\Large \fbox{$ \omega_{1,2}^{2} = \frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_C^2}].$}} \]

Ahora para el caso de $ k_{C}^{2} = k_A k_B $ tenemos

\[ \omega_{1,2}^{2} =\frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A - k_B}{2})^2 + k_A k_B}] \] \[ =\frac{1}{m}[\frac{k_A + k_B}{2} + \sqrt{k_A k_B} \pm \sqrt{(\frac{k_A + k_B}{2})^2}] \] \[ =\frac{1}{m}[\frac{k_A + k_B}{2} + k_C \pm \frac{1}{2}(k_A + k_B)] \]

Por lo tanto $ \omega_1$ y $ \omega_2$ en el caso de suma y resta $ \pm$ respectivamente, tenemos:

\[ {\Large \fbox{$ \omega_1 = \sqrt{\frac{k_A + k_B + k_C}{m}}.$}} \] \[ {\Large \fbox{$ \omega_2 = \sqrt{\frac{k_C}{m}}.$}} \] Fernando M (discusión) 10:44 10 nov 2020 (CST)