Radiacion: Guias de onda

Guías de onda

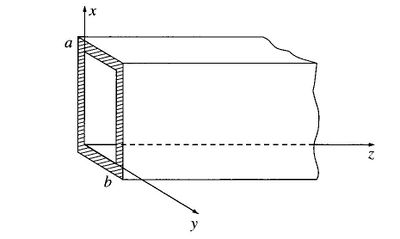
Consideremos ondas electromagnéticas confinadas en el interior de un tubo hueco, o una guia de onda. (véase fig. 4.2)

Debemos asumir que esta guía de onda es un conductor perfecto, esto es que tanto el campo eléctrico, como el magnético son nulos dentro del conductor.

$\mathbf {E} =0$ y $\mathbf {B} =0$ y por lo tanto las condiciones a la frontera en el interior del conductor serán :

$\mathbf {E} _{paralelo}=0\quad \quad \quad (i)$

$\mathbf {B} _{perpendicular}=0\quad \quad \quad (ii)$

Las condiciones (i) y (ii) , se deben a que , suponiendo un conductor perfecto, es decir, $\mathbf {E} =0$ y por lo tanto por ley de Faraday [1] , la cual establece que la corriente inducida en un circuito es directamente proporcional a la rapidez con que cambia el flujo magnético que lo atraviesa, en este caso al ser $\mathbf {E} =0$ , implicará que ${\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}=0$ .

Ahora , por otra parte las cargas y corrientes inducidas en la superficie , deben ser de tal forma para que se les puedan aplicar estas condiciones de frontera.

Entonces estamos interesados en buscar Ondas planas monocromáticas que se propaguen por la guía , por lo que $\mathbf {E}$ y $\mathbf {B}$ , se escriben de la siguiente manera:

$\mathbf {E} {(\mathbf {r} ,t)=\mathbf {E_{0}} ({x,y})}{e}^{i({\mathit {k\cdot z-\omega t}})}\quad \quad \quad (1)$

$\mathbf {B} {(\mathbf {r} ,t)=\mathbf {B_{0}} ({x,y})}{e}^{i({\mathit {k\cdot z-\omega t}})}\quad \quad \quad (2)$

donde consideramos $\mathbf {k} \in \ Re$ , pues es lo que necesitamos.

Tanto el campo eléctrico $\mathbf {E}$ , como el campo magnético $\mathbf {B}$ , deben por supuesto satisfacer las ecuaciones de Maxwell [2] , que se escriben a continuación:

$\nabla \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}\quad \quad \quad (3)$

$\nabla \cdot \mathbf {B} =0\quad \quad \quad (4)$

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}\quad \quad \quad (5)$

$\nabla \times \mathbf {B} =\mu _{0}\mathbf {j} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\quad \quad \quad (6)$

Objetivo

El objetivo es entonces encontrar funciones $\mathbf {E_{0}} ({x,y})$ y $\mathbf {B_{0}} ({x,y})$ tales que satisfagan las ecuaciones de Maxwell (3-6) , sujetas a las condiciones de fronteras (i) y (ii). Como se verá mas adelante , las ondas confinadas en general no son siempre transversales , por lo que con la finalidad de satisfacer las condiciones de frontera , incluimos la componente longitudinal. $E_{z}(\mathbf {x,y} )$ y $B_{z}(\mathbf {x,y} )$ .

Por lo que escribimos $\mathbf {E_{0}} ({x,y})$ y $\mathbf {B_{0}} ({x,y})$ de la siguiente manera:

$\mathbf {E_{0}} =E_{x}(\mathbf {x,y} ){\hat {x}}+E_{y}(\mathbf {x,y} ){\hat {y}}+E_{z}(\mathbf {x,y} ){\hat {z}}\quad \quad \quad (7)$

$\mathbf {B_{0}} =B_{x}(\mathbf {x,y} ){\hat {x}}+B_{y}(\mathbf {x,y} ){\hat {y}}+B_{z}(\mathbf {x,y} ){\hat {z}}\quad \quad \quad (8)$

Verificando ecuación de Maxwell

Veamos que (7) y (8), cumplen con la ecuación de Maxwell $\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}$ .

Entonces recordemos que $\mathbf {E} =({\mathit {E_{x}}}{\hat {x}}+{\mathit {E_{y}}}{\hat {y}}+{\mathit {E_{z}}}{\hat {z}})\ {e}^{i({\mathit {k\cdot z-\omega t}})}$ , por lo que hacemos el rotacional para las 3 componentes , es decir ;

$(\nabla \times \mathbf {E} )_{\hat {x}}$ , $(\nabla \times \mathbf {E} )_{\hat {y}}$ y $(\nabla \times \mathbf {E} )_{\hat {z}}$.

Comencemos entonces con la componente ${\hat {x}}$

$(\nabla \times \mathbf {E} )_{\hat {x}}=({\frac {\partial {\mathit {E_{z}}}}{\partial {\mathit {y}}}}-{\frac {\partial {\mathit {E_{y}}}}{\partial {\mathit {z}}}}){\hat {x}}=({\frac {\partial {\mathit {E_{0}z}}}{\partial {\mathit {y}}}}-ik{\mathit {E_{0}y}}){\mathit {e}}^{i({\mathit {k\cdot z-\omega t}})}$

de aqui vemos que

$({\frac {\partial {\mathit {E_{z}}}}{\partial {\mathit {y}}}}-ik{\mathit {E_{y}}})=i\omega {\mathit {B_{x}}}$

.

Ahora lo hacemos para la componente ${\hat {y}}$ , y tenemos

$(\nabla \times \mathbf {E} )_{\hat {y}}=({\frac {\partial {\mathit {E_{x}}}}{\partial {\mathit {z}}}}-{\frac {\partial {\mathit {E_{z}}}}{\partial {\mathit {x}}}}){\hat {y}}=(ik{\mathit {E_{0}x}}-{\frac {\partial {\mathit {E_{0}z}}}{\partial {\mathit {x}}}}){\mathit {e}}^{i({\mathit {k\cdot z-\omega t}})}$

de donde obtenemos:

$(ik{\mathit {E_{x}}}-{\frac {\partial {\mathit {E_{z}}}}{\partial {\mathit {x}}}})=i\omega {\mathit {B_{y}}}$

.

Y por último para la componente en ${\hat {z}}$, tenemos

$({\frac {\partial {\mathit {E_{y}}}}{\partial {\mathit {x}}}}-{\frac {\partial {\mathit {E_{x}}}}{\partial {\mathit {y}}}})=i\omega {\mathit {B_{z}}}$

.

De manera que

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}=i\omega \mathbf {B_{0}} {\mathit {e}}^{i({\mathit {k\cdot z-\omega t}})}$

Ahora este mismo procedimiento lo aplicamos a :

$\nabla \times \mathbf {B} =\mu _{0}\mathbf {j} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial {\mathit {t}}}}$ para el caso cuando la $\mathbf {j} =0$ , recordemos que estamos analizando para el caso dentro del material.

Entonces para cumplir con ecuación de Maxwell necesitamos que :

$({\frac {\partial {\mathit {B_{z}}}}{\partial {\mathit {y}}}}-ik{\mathit {B_{y}}})=-i\omega \mu _{0}\epsilon _{0}{\mathit {E_{x}}}$

.

Lo cual se obtiene de manera similar al procedimiento anterior para $\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}$ , es decir ;

$(\nabla \times \mathbf {B} ){\hat {x}}=({\frac {\partial {\mathit {B_{z}}}}{\partial {\mathit {y}}}}-{\frac {\partial {\mathit {B_{y}}}}{\partial {\mathit {z}}}}){\hat {x}}=({\frac {\partial {\mathit {B_{0}z}}}{\partial {\mathit {y}}}}-ik{\mathit {B_{0}y}}){\mathit {e}}^{i({\mathit {k\cdot z-\omega t}})}$

Continuando con este mismo proceso , llegamos a la siguiente tabla :

Soluciones de $\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial {\mathit {t}}}}$	Soluciones de $\nabla \times \mathbf {B} =\mu _{0}\mathbf {j} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial {\mathit {t}}}}$
1 ${\partial _{x}{\mathit {E_{y}}}}-{\partial _{y}{\mathit {E_{x}}}}=i\omega {\mathit {B_{z}}}$	1´ ${\partial _{x}{\mathit {B_{y}}}}-{\partial _{y}{\mathit {B_{x}}}}=-i\omega \mu _{0}\epsilon _{0}{\mathit {E_{z}}}$
2 ${\partial _{y}{\mathit {E_{z}}}}-ik{\mathit {E_{y}}}=i\omega {\mathit {B_{x}}}$	2´ ${\partial _{y}{\mathit {B_{z}}}}-ik{\mathit {B_{y}}}=-i\omega \mu _{0}\epsilon _{0}{\mathit {E_{x}}}$
3 $ik{\mathit {E_{x}}}-{\partial _{x}{\mathit {E_{z}}}}=i\omega {\mathit {B_{y}}}$	3´ $ik{\mathit {B_{x}}}-{\partial _{x}{\mathit {B_{z}}}}=-i\omega \mu _{0}\epsilon _{0}{\mathit {E_{y}}}$

Ya con estas ecuaciones, queremos encontrar $\mathbf {E_{x}} ,\mathbf {E_{y}} ,\mathbf {B_{x}} ,\mathbf {B_{y}}$, en términos de $\mathbf {E_{z}} ,\mathbf {B_{z}}$.

Entonces resolviendo el conjunto de ecuaciones de la tabla . tenemos:

$\mathbf {E_{x}} ={\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{x}\mathbf {E_{z}} }+w{\partial _{y}\mathbf {B_{z}} })$

$\mathbf {E_{y}} ={\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{y}\mathbf {E_{z}} }-w{\partial _{x}\mathbf {B_{z}} })$

$\mathbf {B_{x}} ={\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{x}\mathbf {B_{z}} }-\omega {\mathrm {\mu _{0}\epsilon _{0}} ^{2}}{\partial _{y}\mathbf {E_{z}} })$

$\mathbf {B_{y}} ={\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{y}\mathbf {B_{z}} }+\omega {\mathrm {\mu _{0}\epsilon _{0}} ^{2}}{\partial _{x}\mathbf {E_{z}} })$

.

Ahora considerando

$\nabla \cdot \mathbf {E} ={\partial _{x}\mathbf {E_{x}} }+{\partial _{y}\mathbf {E_{y}} }+{\partial _{z}\mathbf {E_{z}} }=({\partial _{x}\mathbf {E_{x}} }+{\partial _{y}\mathbf {E_{y}} }+ik\mathbf {E_{0}z} )\mathbf {e} ^{i({\mathit {k\cdot z-\omega t}})}=0$

lo cual implica,

$({\partial _{x}\mathbf {E_{x}} }+{\partial _{y}\mathbf {E_{y}} }+ik\mathbf {E_{0}z} )=0\quad \quad \quad (9)$

Y utilizando las expresiones para $\mathbf {E_{x}} ,\mathbf {E_{y}}$ , podemos sustituir en $(9)$ obteniendo:

${\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{x}^{2}\mathbf {E_{z}} }+w{\partial _{x}^{2}y\mathbf {B_{z}} })+{\frac {i}{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}}(k{\partial _{y}^{2}\mathbf {E_{z}} }-w{\partial _{x}^{2}y\mathbf {B_{z}} }+ik\mathbf {E_{z}} )=0$

o bien ,

${\partial _{y}^{2}\mathbf {E_{z}} }+{\partial _{x}^{2}\mathbf {E_{z}} }+[{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]\mathbf {E_{z}} =0$

que factorizando , tenemos  ;

${[{\partial _{y}^{2}}+{\partial _{x}^{2}}+{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]}\mathbf {E_{z}} =0\quad \quad \quad (10)$

.

y ahora al hacerlo para

$\nabla \cdot \mathbf {B} =0$ , obtenemos algo similar:

${[{\partial _{x}^{2}}+{\partial _{y}^{2}}+{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]}\mathbf {B_{z}} =0\quad \quad \quad (11)$

.

De (10) y (11) , podemos decir lo siguiente:

Si $\mathbf {E_{z}} =0$ , llamamos TE (onda transversal eléctrica)

Si $\mathbf {B_{z}} =0$ , llamamos TM (onda transversal magnética)

Si $\mathbf {E_{z}} =\mathbf {B_{z}} =0$ , llamamos TEM (onda transversal electromagnética) , sin embargo se puede ver que el tipo de onda TEM , no puede existir en una guía de onda.

Archivo:TEM.gif

Durante la propagación de la onda, el campo electrico (rayas rojas) oscila en un eje perpendicular a la dirección de propagación. El campo magnético (rayas azules) también oscila pero en dirección perpendicular al campo eléctrico.

Ejemplo clásico

Guía de onda rectangular

Tenemos una guía de dimensiones $a\times \ b$

Supongamos que nuestra onda que incide en la guía es del tipo TE, es decir, $\mathbf {E_{z}} =0$ , entonces resolvemos la ecuación (11)

${[{\partial _{x}^{2}}+{\partial _{y}^{2}}+{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]}\mathbf {B_{z}} =0$

.

cuya condicion de frontera es

$\mathbf {E_{paralelo}} =0\quad \quad \quad (i)$

Ahora proponemos una solución para (11)

$\mathbf {B_{z}} (x,y)=X(x)Y(y)$

.

Sustituyendo en (11), tenemos que

$\mathrm {Y} {dx^{2}\mathrm {X} }+\mathrm {X} {dy^{2}\mathrm {Y} }+[{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]\mathrm {X} \mathrm {Y} =0\quad \quad (12)$

Esta ecuación se cumple sí y solo sí

${\frac {1}{X}}{dx^{2}\mathrm {X} }={\mathrm {-k_{x}^{2}} }$

y

${\frac {1}{Y}}{dy^{2}\mathrm {Y} }={\mathrm {-k_{y}^{2}} }$

con

${\mathrm {-k_{x}^{2}} }{\mathrm {-k_{y}^{2}} }+[{\mathrm {(} {\omega \mu _{0}\epsilon _{0}})^{2}-k^{2}}]\mathrm {X} \mathrm {Y} =0\quad \quad \quad (13)$

entonces la solucion para $\mathbf {X}$ sera :

${\mathbf {X(x)} }=A\sin(k_{x}\mathrm {x} )+B\cos(k_{x}\mathrm {x} )$

usando condiciones a la frontera , tenemos que ${\mathrm {A} }=0$ y ${\mathrm {k_{x}} }={\frac {\mathrm {n} \pi }{a}}$ , $\forall (n)\in \mathbb {N}$

Hacemos el mismo procedimiento para $\mathbf {Y}$

y vemos que

${\mathrm {k_{y}} }={\frac {\mathrm {n} \pi }{b}}$ $\forall (n)\in \mathbb {N}$

por lo tanto juntando ambas soluciones , llego a ;

$\mathbf {B_{z}} =B_{0}\cos({\frac {\mathrm {m} \pi }{a}})x\cos({\frac {\mathrm {n} \pi }{b}})x$

.

De esta ecuacuación notamos los modos normales [3], a esta solución se lo conoce como modo $\ TE_{mn}$, donde al menos un indice debe ser distinto de 0.

Ahora de $(13)$ , se tiene que

$\mathrm {K} ={\sqrt {({\omega }{\mu _{0}\epsilon _{0}})^{2}-\pi ^{2}[({\frac {m}{a}})^{2}+({\frac {n}{b}})^{2}]}}$

Notemos que si

$\omega <\pi /\mathrm {\mu _{0}\epsilon _{0}} {\sqrt {({\frac {m}{a}})^{2}+({\frac {n}{b}})^{2}}}\equiv {\mathit {\omega _{mn}}}$

implica que

$\mathrm {K} \in \mathbb {C}$ , lo cual nos indica una Onda atenuada , este tema no se verá a fondo solo se menciona el comportamiento de una onda atenuada.

Entonces si escribimos a $\mathrm {K}$ de la siguiente manera

$\mathrm {K} =\mathrm {K_{1}} +i\mathrm {K_{2}}$

tendremos que ;

$\mathbf {e} ^{i(kx-\omega t)}=\mathbf {e} ^{i(\mathrm {K_{1}} +i\mathrm {K_{2}} -i\omega t)}$ $=\mathbf {e} ^{i(\mathrm {K_{1}z} -\omega t)}\mathbf {e} ^{\mathrm {-K_{z}} }$

Archivo:Atenuada.jpg

A ${\mathit {\omega _{mn}}}$ , se le define como frecuencia de corte para el modo ${\mathit {mn}}$ , la frecuencia de corte mas baja es para el modo ${\mathit {TE_{10}}}$ . ${\mathit {\omega _{mn}}}=({\frac {\pi \mathrm {\mu _{0}\epsilon _{0}} }{a}})$ , a frecuencias mas bajas que esta , no hay propagación.