Optica: Difraccion de Fraunhofer circulo-cuadrado

Building

1. Apertura Rectangular.

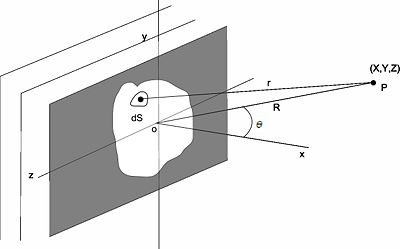
Consideramos la configuración de la Fig.1 en tres dimenciones la cual puede verse de una forma mas simple si rotamos los ejes y solo vemos el perfil del eje $y$ como en Fig.2, en donde tenemos una onda plana monocromática que se propaga en el eje $x$ e incide en una pantalla que contiene una

Fig.1

Fig.2

abertura de forma arbitraria .Deseamos calcular la distribución de la densidad de flujo correspondiente al campo lejano en un punto P distante arbitrario. De acuerdo con el principio de Huygens-Fresnel un area diferencial $dS$ de la apertura puede visualizarse como cubierta de fuentes puntuales secundarias coherentes. Tomando que $dS$ es mas pequeña que $\lambda$ tal que todas las contribuciones en el punto P permanecen en fase interfiriendo constructivamente.

• Si $\varepsilon _{A}$ es la intensidad de la fuente

por unidad de área, suponiendo que es constante en toda la abertura

• La perturbación óptica en P debida a $dS$ es

$dE={\frac {\varepsilon _{A}}{r}}e^{\imath (\omega t-kr)}dS$

La distancia de $dS$ a $P$ es

$r=[X^{2}+(Y-y)^{2}+(Z-z)^{2}]^{\frac {1}{2}}$

Donde tomamos en cuenta la Fig.1 y posteriormente una figura similar para el perfil del eje z.

Como la condición de Fraunhofer se satisface para $r$ muy grande, ademas si la abertura es muy pequeña remplazamos $r$ por $R$ y hacemos una aproximación para la fase

$R=[X^{2}+Y^{2}+Z^{2}]^{\frac {1}{2}}$

entonces

$r=R[1+{\frac {(y^{2}+z^{2})}{R^{2}}}-{\frac {2(Yy+Zz)^{2}}{R^{2}}}]^{\frac {1}{2}}$

Para el campo lejano $R$ es muy grande comparado con las dimensiones

 de la apertura y el termino $R={\frac {(y^{2}+z^{2})}{R^{2}}}\simeq 0$

Por lo cual

$r=R[1-{\frac {2(Yy+Zz)^{2}}{R^{2}}}]^{\frac {1}{2}}$

Y mediane una expansión binomial obtenemos.

$r=R[1-{\frac {(Yy+Zz)^{2}}{R^{2}}}]$

Por lo tanto la perturbación total que llega a $P$ es

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{Abertura}\int e^{\imath k(Yy+Zz)/R}dS$

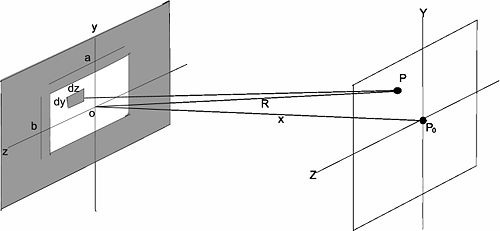
Consideramos ahora la configuración de la fig.3 con lo cual la ecuación para el campo se puede escribir como

Fig.3

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{-b/2}^{b/2}e^{\imath kYy/R}dy\int _{-a/2}^{a/2}e^{\imath kZz/R}dz$

Si definimos $\beta ={\frac {kby}{2R}},\qquad \alpha ={\frac {kaz}{2R}}$ obtenemos

$\int _{-b/2}^{b/2}e^{\imath kYy/R}dy={\frac {R}{\imath kY}}(e^{\imath kYb/2R}-e^{-\imath kYb/2R})={\frac {2R}{kY}}\sin({\frac {bkY}{2R}})=b{\frac {\sin(\beta )}{\beta }}$

$\int _{-a/2}^{a/2}e^{\imath kZz/R}dz={\frac {R}{\imath kZ}}(e^{\imath kZa/2R}-e^{-\imath kZa/2R})={\frac {2R}{kY}}\sin({\frac {akZ}{2R}})=a{\frac {\sin \alpha }{\alpha }}$

Por lo tanto

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}A({\frac {\sin \beta }{\beta }})({\frac {\sin \alpha }{\alpha }})$

Como $I=<(Re){\tilde {E}}>_{T}$

$I(Y,Z)=I(0)({\frac {\sin \beta }{\beta }})({\frac {\sin \alpha }{\alpha }})$

Donde $I(0)$ es la Irradiancia en $P_{0}$

En valores de Y,Z tales que $\alpha ,\beta$ sean cero $I(Y,Z)$ adquiere la forma de la difracción de una rendija

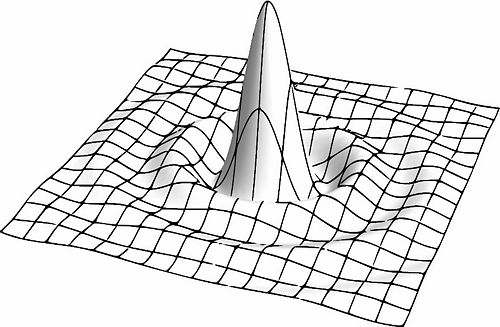
Distribución de campo lejano de una apertura cuadrada

La misma distribución a color

Distribución de la irradiancia para una apertura cuadrada

2. Apertura Circular.

Fig.4

• Ahora consideramos nuevamente la Fig.4 solo que en esta ocacion la apertura es circular.
• Las aberturas circulares son muy importantes para el estudio de la instrumentación óptica.
• Retomando nuevamente la expresión de la perturbación óptica en P para la abertura arbitraria en el caso del campo lejano

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{Abertura}\int e^{\imath k(Yy+Zz)/R}dS(1)$

La simetría del problema sugiere el uso de coordenadas esféricas tanto en el plano de la apertura como en el plano de observación

$z=\rho \cos \varphi ,Z=q\cos \phi$ $y=\rho \sin \varphi ,Y=q\sin \phi$

Entonces sustitullendo en la expresión de la rendija arbitraria

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{\rho =0}^{a}\int _{\varphi =0}^{2\pi }e^{(\imath k\rho q/R)\cos(\varphi -\phi )}\rho d\rho d\varphi$

Por la simetría axial la solución es independiente de $\phi$

$\int _{\varphi =0}^{2\pi }e^{(\imath k\rho q/R)\cos(\varphi )}d\varphi$

Esta ultima ecuación es una función única que no puede reducirse otra forma más corriente, como funciones hiperbólicas exponenciales o trigonometricas

La cantidad

$J_{0}(u)={\frac {1}{2\pi }}\int _{0}^{2\pi }e^{\imath u\cos v}dv$

Se denomina función de Bessel de primera especie y orden cero

En general

$J_{m}(u)={\frac {\imath ^{-m}}{2\pi }}\int _{0}^{2\pi }e^{\imath (mv+u\cos v)}dv$

Representa la función de Bessel de orden m

Si

$u={\frac {k\rho q}{R}}$

Podemos escribir

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{0}^{a}J_{0}({\frac {k\rho q}{R}})\rho d\rho$

Otra propiedad de la funciones de Bessel es la relación de recurrencia

${\frac {d}{du}}[u^{m}J_{m}(u)]=u^{m}J_{m-1}(u)$

Con $m=1$

$\int _{0}^{u}u\prime J_{0}(u\prime )du\prime =uJ_{1}(u)$

Entonces si nombramos a $w$ como $w={\frac {k\rho q}{R}}\quad$

obtenemos

$\qquad dw={\frac {kq}{R}}d\rho ,\qquad d\rho ={\frac {R}{kq}}dw\qquad \rho ={\frac {wR}{kq}}$

Mediante la regla de recurrencia tenemos

${\tilde {E}}={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}2\pi a^{2}({\frac {R}{kaq}})J_{1}({\frac {kaq}{R}})$

Y la irradiancia en P es ${\frac {1}{2}}{\tilde {E}}{\tilde {E}}^{*}$

$I=2({\frac {\varepsilon _{A}}{R}}A)^{2}[{\frac {J_{1}({\frac {kaq}{R}})}{\frac {kaq}{R}}}]^{2}$

Para calcular la irradiancia en el centro ponemos $q=0$ Y usando la ley de recurrencia.

Verificamos que

$\lim _{u\rightarrow 0}{\frac {J_{1}(u)}{u}}={\frac {1}{2}}$

La irradiancia en $P_{0}$ es

$I(0)={\frac {\varepsilon _{A}^{2}}{2R^{2}}}A^{2}$

Que es el mismo resultado que la apertura rectangular

Fig5. Disco de Airy

Como $\sin \theta =q/r$, la irradiancia se puede escribir como función de $\theta$

$I=I(0)[{\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}]^{2}$

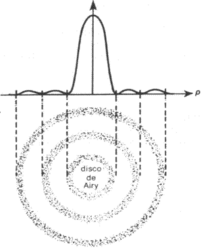
El máximo central corresponde al llamado disco de Airy (Fig5.)

si derivamos respecto a la distancia q obtenemos la condición para los minimos y maximos

${\frac {dI}{dq}}=-2I(0)u/q[{\frac {J_{1}(u)}{u}}][{\frac {J_{2}(u)}{u}}]=0$

El primer mínimo corresponde al primer cero de la función $J_{1}(0)$, con $u=3.83$

Podemos calcular la distancia del centro de la distribucion a los maximos y minimos.

${\frac {kaq}{R}}=3.83$,$q_{1}={\frac {1.22R\lambda }{D}}$

Los máximos secundarios ocurren para $J_{2}=0$

Distribución de campo lejano de una apertura cuadrada

Distribución para difracción de rayos X

Distribución de la irradiancia para una apertura circular

3. Métodos de Fourier.

-La transformada de Fourier aporta una percepción de diferente del mecanismo de difracción de Fraunhofer Partimos de la ecuación

${\tilde {E}}(Y,Z)={\frac {\varepsilon _{A}e^{\imath (\omega t-kR)}}{R}}\int _{Abertura}\int e^{\imath k(Yy+Zz)/R}dS$

• La cantidad R es la distancia del centro de la apertura
• si nos limitamos a una pequeña región $R$ puede conciderarse constante

$\varepsilon _{A}$ no es necesariamente invariante

• Las variaciones en $\varepsilon _{A}$ y la constante multlipicativa pueden combinarse en una sola cantidad compleja

${\mathcal {A}}(y,z)={\mathcal {A}}_{0}(y,z)e^{\imath \phi (y,z)}$

Denominada función de abertura

-Con esto podemos reformular la ecuación anterior

${\tilde {E}}(Y,Z)=\int \int _{-\infty }^{\infty }{\mathcal {A}}(y,z)e^{\imath k(Yy+Zz)/R}dydz$

Donde los limites de la integral pueden extenderse hasta $\pm \infty$ por que la función de la abertura es no nula únicamente en la region de la abertura -Definimos la frecuencias espaciales

$K_{y}=kY/R=k\sin \phi =k\cos \beta \quad K_{z}=kZ/R=k\sin \theta =k\cos \gamma$

El campo difractado puede ahora escribirse como

${\tilde {E}}(K_{y},K_{z})=\int \int _{-\infty }^{\infty }{\mathcal {A}}(y,z)e^{\imath k(K_{y}y+K_{z}z)/R}dydz$

Ahora tenemos que "la distribución del campo en la figura de difracción de Fraunhofer es la transformada de Fourier de la distribución del campo sobre la abertura" -Simbolicamente

$E(K_{y},K_{z})={\mathcal {F}}{{\mathcal {A}}(y,z)}$

La distribucion del campo en el plano imagen es el espectro de frecuencia espacial de la función de la abertura. Entonces

${\mathcal {A}}(y,z)={\frac {1}{(2\pi )^{2}}}\int \int _{-\infty }^{\infty }E(K_{y},K_{z})e^{\imath k(K_{y}y+K_{z}z)/R}dydz$

o

${\mathcal {A}}(y,z)={\mathcal {F}}^{-1}E(K_{y},K_{z})$

4. Difracción de apertura circulo-cuadrado.

La ecuación

$x^{2}+y^{2}-{\frac {s^{2}}{a^{2}}}x^{2}y{2}=a^{2}$

• Representa un circulo en el plano $xy$ de radio $a$ si $s=0$
• Representa un cuadrado de lado $2a$ si $s=1$

Debido a que las variables estan restringidas a valores mas pequeños o iguales a $a$

$a^{2}\geq x^{2},y^{2}$

La ecuación (3) representa una figura intermedia con esquinas redondeadas

Escribimos en coordenadas Polares $(r,\varphi )$

$[{\frac {s^{2}}{4}}\sin ^{2}2\varphi ]r^{4}-a^{2}r^{2}+a^{2}=0$

Con solución

$r(a,\varphi )=\{[2a^{2}{\frac {1-[1-s^{2}\sin ^{2}(2\varphi )]^{1/2}}{s^{2}\sin ^{2}(2\varphi )}}\}^{1/2}$

-Puede demostrarse que el signo negativo en la expresión implica una y solo una posible solución que cumple la condición $r^{2}\leq 2a^{2}$

La transformada de Fourier para una apertura es

$E(k_{q},K_{\phi })=\int _{0}^{\infty }\rho \int _{0}^{2\pi }{\mathcal {A}}(\rho ,\varphi )e^{\imath (kq\rho /R)\cos(\varphi -\phi )}\rho d\rho d\varphi$

La función de apertura es.

${\mathcal {A}}(\rho ,\varphi )=\{_{0\quad para\quad \rho >r(a,\varphi )}^{1\quad para\quad \rho <r(a,\varphi )}$

Reescribimos esta función como el producto de una parte radial y una angular entonces $r(a,\varphi )=aM_{s}(\varphi )$

$M_{s}(\varphi )=[2{\frac {1-[1-s^{2}\sin ^{2}(2\varphi )]^{1/2}}{s^{2}\sin ^{2}(2\varphi )}}]^{1/2}$

Esta función tiene fronteras entre $1\leq M_{s}(\varphi )\leq {\sqrt {2}}$

Y puede verse que en el limite cuando $s\longrightarrow 0$ $M_{s}(\varphi )\longrightarrow 1$

Si reescribimos la variable radial a

$\rho =\rho \prime M_{s}(\varphi )\quad d\rho =d\rho \prime M_{s}(\varphi )$

Entonces la ecuación de la función de apertura puede ser escrita independiente del angulo $\varphi$

$U(\rho \prime )=\{_{0\quad para\quad \rho \prime >a}^{1\quad para\quad \rho \prime <a}$

Tal que

${\mathcal {A}}(a,\varphi )={\mathcal {A}}(\rho \prime ,\varphi )=U(\rho \prime )U(phi)=U(\rho \prime )\$$ $\varphi$

Entonces la transformada de Fourier de un circulo-cuadrado es

$E(k_{q},K_{\phi })=\int _{0}^{\infty }\rho \prime U(\rho \prime )\int _{0}^{2\pi }M_{s}^{2}(\varphi )e^{\imath (kq\rho \prime M_{s}(\varphi )/R)\cos(\varphi -\phi )}d\rho \prime d\varphi$\

5. circulo.

Si ponemos $s=0$ entonces $M_{s}(\varphi )=1$ y obtenemos

${\begin{alignedat}{4}E(k_{q},K_{\phi })&=&\int _{0}^{\infty }\rho \prime U(\rho \prime )[\int _{0}^{2\pi }(\varphi )e^{\imath (kq\rho \prime /R)\cos(\varphi -\phi )}d\varphi ]d\rho \prime \\&=&\int _{0}^{\infty }\rho \prime U(\rho \prime )[J_{0}(kq\rho \prime /R)]d\rho \prime \\&=&\int _{0}^{a}\rho \prime [J_{0}(kq\rho \prime /R)]d\rho \prime \\&=&(R/kqa)J_{1}(kqa/R)\\\end{alignedat}}$

Y recobramos el resultado ya presentado

5. cuadrado.

Obtenemos un cuadro para $s=1$

Por consideraciones de simetria y tomando la parte real de la transformada de Fourier para el circulo-cuadrado obtenemos

$E(k_{q},K_{\phi })=\int _{0}^{a}\rho \prime \int _{-\pi /4}^{3\pi /4}M_{s}^{2}(\varphi )\cos[{(kq\rho \prime M_{s}(\varphi )/R)\cos(\varphi -\phi )}]d\rho \prime d\varphi$

Tomando en cuenta que la función angular del cuadrado es

$M_{s=1}(\varphi )=\{_{{\frac {1}{|\sin \varphi |}}\quad para\quad \pi /4\quad a\quad (3\pi /4)+n\pi }^{{\frac {1}{|\cos \varphi |}}\quad para\quad -\pi /4\quad a\quad (\pi /4)+n\pi }$

Tenemos entonces que

$E(k_{q},K_{\phi })=\int _{0}^{a}\rho \prime \int _{-\pi /4}^{\pi /4}{\frac {\cos[(kq\rho \prime /R)(\cos \phi +\sin \phi \tan \varphi ]}{\cos ^{2}\varphi }}d\varphi d\rho \prime +\int _{0}^{a}\rho \prime \int _{\pi /4}^{3\pi /4}{\frac {\cos[(kq\rho \prime /R)(\sin \phi +\cos \phi \cot \varphi )]}{\sin ^{2}\varphi }}d\varphi d\rho \prime$

Nombramos la primera de la ecuación $G_{1}$,y la segunda parte $G_{2}$ quedando

$E(k_{q},K_{\phi })=G_{1}+G_{2}$

Haciendo las integrales angulares

$G_{1}={\frac {4}{(kq/R)^{2}\sin \phi }}\int _{0}^{a}\sin[(kq\rho \prime /R)\sin \phi ]\cos[(kq\rho \prime /R)\cos \phi ]$ $G_{2}={\frac {4}{(kq/R)^{2}\cos \phi }}\int _{0}^{a}\cos[(kq\rho \prime /R)\sin \phi ]\sin[(kq\rho \prime /R)\cos \phi ]$

Integrando nuevamente

$G_{1}={\frac {4}{(kq/R)^{2}\sin \phi }}[({\frac {1-\cos[kqa/R(\sin \phi -cos\phi )]}{\sin \phi -\cos \phi }})$ $+({\frac {1-\cos[kqa/R(\sin \phi +\cos \phi )]}{\sin \phi +\cos \phi }})]$

$G_{2}={\frac {4}{(kq/R)^{2}\cos \phi }}[({\frac {1-\cos[kqa/R(\cos \phi -\sin \phi )]}{\cos \phi -\sin \phi }})$ $+({\frac {1-\cos[kqa/R(\sin \phi +\cos \phi )]}{\sin \phi +\cos \phi }})]$

Sumando $G_{1}+G_{2}$ tenemos

${\begin{array}{lcl}E(k_{q},K_{\phi })&=&G_{1}+G_{2}\\&=&{\frac {4}{(kq/R)^{2}\cos \phi \sin \phi }}[\sin(kqa/R\sin \phi )\sin(kqa/R\cos \phi )]\\&=&4a^{2}\mathrm {sinc} (kqa/R\sin \phi )\mathrm {sinc} (kqa/R\cos \phi )\\\end{array}}$

como

$z=\rho \cos \varphi ,Z=q\cos \phi$

$y=\rho \sin \varphi ,Y=q\sin \phi$

$E(k_{q},K_{\phi })=4a^{2}\mathrm {sinc} (ka/RY)\mathrm {sinc} (ka/RZ)$

Building

--CAZ 00:20 19 ago 2008 (CDT) --CAZ 16:28 19 ago 2008 (CDT)