Optica: Capitulo7-problemas

Bienvenidos. En esta página pueden dejar las soluciones a sus problemas del Hecht- Capítulo 7

---

Ejercicio 7.35

Tome la función $f\left(\theta \right)=\theta ^{2}$ en el intervalo $0<\theta <2\pi$ & que sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2\pi periódica. Muestre que su expansión en serie de Fourier es:

$f\left(\theta \right)={\frac {4\pi ^{2}}{3}}+\sum _{m=1}^{\infty }\left({\frac {4\cos(m\theta )}{m^{2}}}-{\frac {4\pi \sin(m\theta )}{m}}\right)$

Solución

Teorema(serie de Fourier trigonométrica). Sea f una función definida en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): -l < x < l , si:

$a_{0}={\frac {1}{2l}}\int _{-l}^{l}f(x)dx$

$b_{n}={\frac {1}{l}}\int _{-l}^{l}f(x)\cos({\frac {n\pi x}{l}})dx,n=1,2,3...$

$a_{n}={\frac {1}{l}}\int _{-l}^{l}f(x)\sin({\frac {n\pi x}{l}})dx,n=1,2,3...$

Entonces la serie

$a_{0}+\sum _{n=1}^{\infty }\left(b_{n}\cos({\frac {n\pi x}{l}})+a_{n}\sin({\frac {n\pi x}{l}})\right)$

converge a f(x).

Sin embargo, tomaremos un corolario del teorema anterior (caso $l=\pi$), para ello basta aplicar una traslación $T:\Re \rightarrow \Re$ dada por:

$T(\theta ):=\left({\frac {2x-2\pi }{2\pi }}\right)\pi$......(1)

Así, tomamos a la función Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): g(x) : = f(\theta =x-\pi) =(x-\pi )^{2} en el intervalo $-\pi <x<\pi$.

Observe que $g(x+2\pi )=\left((x+2\pi )-\pi \right)^{2}=(x+\pi )^{2}:=(\theta +2\pi )^{2}=f(\theta +2\pi ){\stackrel {\mathrm {hip} }{=}}f(\theta ):=g(x)$, bajo (1), pues T es una biyección. Esto indica que la periodicidad se sigue conservando aún al aplicar T.

Entonces, sea que $g(x)$ y, por tanto, $f(\theta )$, admite una expansión en serie de Fourier, tenemos que:

$a_{0}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }g(x)dx={\frac {1}{2\pi }}\int _{-\pi }^{\pi }{\frac {1}{3}}\left({\dfrac {d}{dx}}(x-\pi )^{3}\right)dx={\frac {4}{3}}\pi ^{2}$

Diego de la Cruz López

---

---

Ejercicio 7.7

Utilizando las ecuaciones 7.9, 7.10 y 7.11 muestre que la resultante de las dos ondas

$E_{1}=E_{01}sen\left[\omega t-k(x+\Delta x)\right]$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E_2 = E_{01} sen\left[\omega t - k x\right]

es

Error al representar (error de sintaxis): E = 2 E_{01} cos\left(\dfrac{k \Delta x}{2}\right) sen\left[\omega t - k\left(x+\dfrac{\Delta x}{2}\right)\right]

Solución:

De las ondas 1 y 2 tenemos que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \alpha_1 = - k(x+\Delta x) y $\alpha _{2}=-kx$. La ecuación 7.9 es

Error al representar (error de sintaxis): E_0^2 = E_{01}^2 + E_{02}^2 + 2 E_{01} E_{02} cos(\alpha_2 - \alpha_1)

y nos da la amplitud de la onda resultante, calculando para nuestro caso tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E_0^2 = E_{01}^2 + E_{01}^2 + 2 E_{01}^2 cos\left[-kx+k(x+\Delta x)\right] = 2 E_{01}^2 + 2E_{01}^2 cos(k \Delta x) = 2E_{01}^2 \left[1+cos(k\Delta x)\right] = 4 E_{01}^2 cos^2 \left(\dfrac{k \Delta x}{2}\right)

donde se ha utilizado la identidad trigonométrica

$cos^{2}\left({\dfrac {x}{2}}\right)={\dfrac {1+cosx}{2}}$

Ahora para calcular la fase de la onda resultante utilizamos la ecuación 7.10 que es

$tan\alpha ={\dfrac {E_{01}sen\alpha _{1}+E_{02}sen\alpha _{2}}{E_{01}cos\alpha _{1}+E_{02}cos\alpha _{2}}}$

y en nuestro caso

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): tan \alpha = \dfrac{E_{01} sen[-k(x+\Delta x)] + E_{01} sen(-kx)}{E_{01} cos[-k(x+\Delta x)] + E_{01} cos(-kx)} = \dfrac{sen[-k(x+\Delta x)] + sen(-kx)}{cos[-k(x+\Delta x)] + cos(-kx)}

y definiendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \eta \equiv -k(x+\Delta x) y $\theta \equiv -kx$ tenemos

$tan\alpha ={\dfrac {sen\eta +sen\theta }{cos\eta +cos\theta }}=tan\left({\dfrac {\eta +\theta }{2}}\right)$

donde la igualdad final se cumple gracias a una identidad trigonométrica, por lo que la fase de la onda resultante será

$\alpha ={\dfrac {\eta +\theta }{2}}=-k\left[x+{\dfrac {\Delta x}{2}}\right]$

Y la relación 7.11 es

$E=E_{0}sen(\omega t+\alpha )$

por lo que nuestra onda resultante queda como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E = 4 E_{01}^2 cos^2 \left(\dfrac{k \Delta x}{2}\right) sen \left[\omega t -k \left(x + \dfrac{\Delta x}{2}\right) \right]

Ivan de Jesús Pompa García (discusión) 21:00 5 nov 2018 (CST)

---

Ejercicio 7.8

Sume directamente las dos ondas del problema 7.7 para encontrar la misma solución.

Primero, renombremos los argumentos de la siguiente forma:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): a=wt-kx y $b=k\Delta x$.

Entonces las expreciones de los campos serán de la forma

$E_{1}=E_{0}sen(a-b)$ $E_{2}=E_{0}sen(a)$

Por tanto, al tener la suma de los campos.

$E_{t}=E_{1}+E_{2}=E_{0}sen(a-b)+E_{0}sen(a)=E_{0}[sen(a-b)+sen(a)]$

Asi que sólo los debemos enfocar en la suma trigonométrica. Entonces:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): sen(a-b)+sen(a)=[sen(a)cos(b)-sen(b)cos(a)+sen(a)

Factorizando $sen(a)$:

$sen(a)[cos(b)+1]-sen(b)cos(a)$

Recordando dos identidades trigonométricas importantes que son:

$cos^{2}(b)=1/2[1+cos(b)]$ → $cos(b)+1=2cos^{2}(b)$ y $sen(b)=2sen(b/2)cos(b/2)$.

Entonces:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): sen(a)[cos(b)+1]-sen(b)cos(a)=sen(a)[2cos^2(b/2)]-[2sen(b/2)cos(b/2)]cos(a)

Ahora factorizando $2cos(b/2)$ llegamos a:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): 2cos(b/2){sen(a)cos(b/2)-cos(a)sen(b/2)}=2cos(b/2)[sen(a-b/2)]

Por lo tanto:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): E_t=E_02cos(b/2)[sen(a-b/2)]

Finalmente, regresando a las variables originales.

$E_{t}=E_{0}2cos(k\Delta x/2)[sen(wt-kx-k\Delta x/2)]=E_{0}2cos(k\Delta x)/2)[sen(wt-k[x+\Delta x/2)])]$.

--Fernando Valencia Hernández

---

Ejercicio 7.29

---

La velocidad de propagación de una onda de superficie en un líquido de profundidad mucho mayor que $\lambda$ viene dada por:

$v={\sqrt {{\frac {g\lambda }{2\pi }}+{\frac {2\pi \Upsilon }{\rho \lambda }}}}$

donde g = aceleración de la gravedad, $\lambda$ = longitud de onda, $\rho$ = densidad, $\Upsilon$ = tensión superficial. Calcule la velocidad de grupo de un pulso en el límite de longitud de onda larga (se denominan ondas de gravedad).

Solución:

Para longitudes de onda grandes, notemos que el segundo término de la suma dentro de la raíz es despreciable :

${\frac {2\pi \Upsilon }{\rho \lambda }}$

Entonces la velocidad de propagación de una onda de superficie se convierte en:

$v={\sqrt {\frac {g\lambda }{2\pi }}}$ ........(1)

EL número de onda esta dada,por:

$k={\frac {2\pi }{\lambda }}$ ................(2)

Sustituyendo la ecuación (2) en (1), la velocidad de propagación:

$v={\sqrt {\frac {g}{k}}}$.................(3)

De la relación entre la velocidad de grupo y velocidad de propagación es:

${v}_{g}=v+k{\frac {dv}{dk}}$.............(4)

Donde ${v}_{g}$, es la velocidad de grupo.

De la ecuación (3):

${\frac {dv}{dk}}={\frac {d}{dk}}\left({\sqrt {\frac {g}{k}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}{\frac {d}{dk}}\left({k}^{-{\frac {1}{2}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}\left(-{\frac {1}{2}}\right)\left({k}^{-{\frac {3}{2}}}\right)$

${\frac {dv}{dk}}={\sqrt {g}}\left(-{\frac {1}{2}}\right){\frac {1}{k{\sqrt {k}}}}$

${\frac {dv}{dk}}=\left(-{\frac {1}{2k}}\right){\sqrt {\frac {g}{k}}}$

Sustituyendo (3) en la última expresión:

${\frac {dv}{dk}}=\left(-{\frac {v}{2k}}\right)$..........(5)

Sustituyendo (5) en (4):

${v}_{g}=v+k\left({\frac {-v}{2k}}\right)$

Reduciendo, tenemos que la velocidad de grupo es:

${v}_{g}=v-{\frac {v}{2}}$

${v}_{g}={\frac {v}{2}}$

--Luis Manuel Chávez Antonio

---

Ejercicio 7.30

---

Demuestre que la velocidad de grupo puede escribirse como:

$v_{g}=v-\lambda {\frac {dv}{d\lambda }}$

Solución:

La expresión de la velocidad de grupo se puede escribir como:

$v_{g}=v+{\frac {kdv}{dk}}$

Donde:

$v_{g}$ es la velocidad de grupo

$v$ es la velocidad de fase

$k$ es el numero de onda

La expresión de numero de onda se puede escribir como:

$k={\frac {2\pi }{\lambda }}$

Donde $\lambda$ es la longitud de onda

La expresion de velocidad de grupo se puede escribir como:

$v_{g}=v+k{\frac {dv}{dk}}$

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left({\frac {d\lambda }{dk}}\right)$

La expresión del numero de onda se diferencia con respecto a la longitud de onda como:

$k={\frac {2\pi }{\lambda }}$

${\frac {dk}{d\lambda }}=-2\pi \left({\frac {1}{\lambda ^{2}}}\right)$

${\frac {d\lambda }{dk}}=-{\frac {\lambda ^{2}}{2\pi }}$

Sustituimos ${\frac {d\lambda }{dk}}$ en la expresión anterior.

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left({\frac {d\lambda }{dk}}\right)$

$v_{g}=v+k\left({\frac {dv}{d\lambda }}\right)\left(-{\frac {\lambda ^{2}}{2\pi }}\right)$

$v_{g}=v-{\frac {\lambda ^{2}k}{2\pi }}\left({\frac {dv}{d\lambda }}\right)$

Sustituimos ${\frac {2\pi }{\lambda }}$ por $k$ en la expresión anterior:

$v_{g}=v-{\frac {\lambda ^{2}}{2\pi }}\left({\frac {2\pi }{\lambda }}\right)\left({\frac {dv}{d\lambda }}\right)$

$v_{g}=v-\lambda \left({\frac {dv}{d\lambda }}\right)$

Por lo tanto $v_{g}=v-\lambda \left({\frac {dv}{d\lambda }}\right)$

--Enrique Ortiz Martinez

---

Ejercicio 7.36

---

Demuestre que la velocidad de grupo puede escribirse como:

${\upsilon }_{g}={\frac {c}{n}}+{\frac {\lambda c}{{n}^{2}}}{\frac {dn}{d\lambda }}$

Solución:

La velocidad de grupo esta dada por:

${v}_{g}=v+{\frac {kdv}{dk}}$.......(1)

y sabemos que por regla de la cadena podemos escribir:

${\frac {dv}{dk}}={\frac {dv}{dn}}{\frac {dn}{dk}}$.......(2)

sabemos que la velocidad de la luz en un medio de refracción n es :

$v={\frac {c}{n}}$ donde c= velocidad de la luz en el vacio

derivando con respecto a n tenemos:

${\frac {dv}{dn}}={\frac {-c}{{n}^{2}}}$

sustituyendo este valor en la ecuación (2) obtenemos:

${\frac {dv}{dk}}={\frac {-c}{{n}^{2}}}{\frac {dn}{dk}}$....(3)

y utilizando regla de la cadena tenemos :

${\frac {dn}{dk}}={\frac {d\lambda }{dk}}{\frac {dn}{d\lambda }}$....(4)

sabemos que la constante de propagacion esta dada por:

$k={\frac {2\pi }{\lambda }}$

${\frac {dk}{d\lambda }}={\frac {d}{d\lambda }}\left({\frac {2\pi }{\lambda }}\right)$

${\frac {dk}{d\lambda }}=-{\frac {2\pi }{{\lambda }^{2}}}$

${\frac {d\lambda }{dk}}=-{\frac {{\lambda }^{2}}{2\pi }}$

sustituyendo este valor en la ecuación (4) obtenemos que :

${\frac {dn}{dk}}=-{\frac {{\lambda }^{2}}{2\pi }}{\frac {dn}{d\lambda }}$....(5)

sustituyendo la ecuación (5) en la ecuación (3) obtenemos:

${\frac {dv}{dk}}={\frac {-c}{{n}^{2}}}\left({\frac {{-\lambda }^{2}}{2\pi }}\right){\frac {dn}{d\lambda }}$

${\frac {dv}{dk}}=\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

sustituyendo este valor en la ecuacion (1) obtenemos:

${v}_{g}=v+k\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

donde sabemos que $v={\frac {c}{n}}$, $k={\frac {2\pi }{\lambda }}$

sustituyendo en lo anterior tenemos:

${v}_{g}={\frac {c}{n}}+{\frac {2\pi }{\lambda }}\left({\frac {{c\lambda }^{2}}{2\pi {n}^{2}}}\right){\frac {dn}{d\lambda }}$

${v}_{g}={\frac {c}{n}}+\left({\frac {\lambda c}{{n}^{2}}}\right){\frac {dn}{d\lambda }}$

Como podemos el problema queda demostrado

--Ruben Espinosa Guzman

---

Ejercicio 7.38

---

Para una onda que se propaga en una estructura periódica para la cual $\omega (k)=2{\omega }_{0}\sin {\left({kl}/{2}\right)}$, determine las velocidades de fase y de grupo. Escriba el primer termino como una función seno.

Solución:

Para una onda periódica $\omega (k)=2{\omega }_{0}\sin {\left({kl}/{2}\right)}$ ...$(1)$

Esa es la frecuencia angular de la onda, es una función de constante de propagación.

Sabemos que la velocidad de fase es $v={\frac {\omega }{k}}$

$v={\frac {2{\omega }_{0}\sin {\left({kl}/{2}\right)}}{k}}$

Y la velocidad de grupo ${v}_{g}={\frac {d\omega }{dk}}$

${v}_{g}={\frac {d}{dk}}\left(2{\omega }_{0}\sin {\left({kl}/{2}\right)}\right)$

${v}_{g}=2{\omega }_{0}\left[\cos {\left({kl}/{2}\right)}\left({\frac {l}{2}}\right)\right]$

${v}_{g}={\omega }_{0}l\left[\cos {\left({kl}/{2}\right)}\right]$

Recordando lo siguiente: $\sin {\left({\frac {\pi }{2}}+\theta \right)}=\cos {\left(\theta \right)}$

$\therefore {v}_{g}={\omega }_{0}l\sin {\left[{\frac {\pi }{2}}+\left({\frac {kl}{2}}\right)\right]}$

--Luis Gutiérrez Melgarejo

---

Ejercicio 7.39

---

Un gas o plasma ionizado es un medio dispersivo para las ondas EM. Dado que la ecuación de dispersión es:

${\omega }^{2}={\omega }_{p}^{2}+{c}^{2}{k}^{2}$

donde ${\omega }_{p}^{2}$ es la constante de plasma frecuencial. Determinar expresiones tanto para la fase como para el grupo de velocidades y demostrar que: ${v{v}_{g}}={c}^{2}$.

solución:

sabemos que k= constante de propagacion, ademas la velocidad de fase se expresa como: $v={\frac {\omega }{k}}$

entonces ${\frac {\sqrt {{\omega }_{p}^{2}+{c}^{2}{k}^{2}}}{k}}$

= ${\sqrt {\frac {{\omega }_{p}^{2}+{c}^{2}{k}^{2}}{{k}^{2}}}}$

= ${\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}$ ...(1)

la velocidad de grupo viene dada por: ${v}_{g}={\frac {d\omega }{dk}}$ ...(2)

tenemos: ${\omega }^{2}={\omega }_{p}^{2}+{c}^{2}{k}^{2}$

derivando obtenemos: $2\omega {\frac {d\omega }{dk}}{=c}^{2}2k$

= ${\frac {d\omega }{dk}}={\frac {{c}^{2}k}{\omega }}$ sea ${\omega }_{p}$ una constante

de la ecuacion (2): ${v}_{g}={\frac {{c}^{2}k}{\omega }}$

y ya que $v={\frac {\omega }{k}}$ entonces: ${v}_{g}={\frac {{c}^{2}}{v}}$

sustituyendo ecuacion (1) en lo anterior: ${v}_{g}={\frac {{c}^{2}}{\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}}$ ...(3)

ahora multiplicando (1) y (3)

${v\bullet v}_{g}={\frac {{c}^{2}}{\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}}\bullet {\sqrt {{\frac {{\omega }_{p}^{2}}{{k}^{2}}}+{c}^{2}}}$

${v{v}_{g}}={c}^{2}$.

por tanto queda probado.

--Salvador Morales Carranza

---

---

Ejercicio 7.41

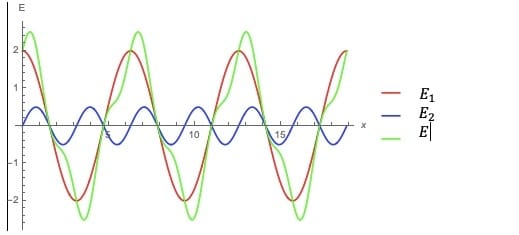
Determine analíticamente la resultante cuando las dos funciones $E_1=2E_0 \cos (\omega t)$ y $E_2=\frac{1}{2}E_0 \sin (2\omega t) $ se superponen. Dibuje $E_1$ , $E_2$ y $E=E_1+E_2$ ¿La resultante es periódica? Si lo es ¿Cuál es su periodo en términos de $\omega$?

Solución:

Realizamos la suma de las dos funciones :

$E=E_1+E_2=2E_0 \cos (\omega t)+\frac{1}{2}E_0 \sin (2\omega t)$

Se hace uso de la identidad trigonométrica : $\sin(2 \theta)=2 \sin \theta \cos \theta $

$E= 2 E_0 \cos ( \omega t ) + \frac{1}{2} E_0 2 \cos (\omega t) \sin (\omega t) $

$E=E_0 \sin \omega t \cos \omega t +2 E_0 \cos \omega t$

$E=E_0 \cos \omega t (1+ \sin (\omega t))$

Se dice que una función f es periódica con período P mayor que cero si cumple que:

$f(t+P)=f(t)$

Así que sustituimos $t$ por ($t+P$) en $E$

$E_0 \cos \omega (t+P) (1+ \sin (\omega (t+P)))$

Usamos la identidad trigonométrica de del coseno de una suma : $\cos (a+b)= \cos a \cos b- \sin a \sin b$

$E_0 \cos (\omega t) \cos (\omega P) - \sin (\omega t) \sin (\omega P)$

Ejercicio 7.27

Usar la relación ${ \frac {1}{v_g}} = { \frac {dk}{dv}}$, probando que:

${ \frac {1}{v_g}} = { \frac {1}{v}}$ - ${ \frac {\upsilon}{v^2}} * { \frac {dv}{d\upsilon}}$

Dado que ${ \frac {1}{v_g}} = { \frac {dk}{dv}}$....(1)

K denota el número de onda  : K = ${ \frac {1}{\lambda}}$

ya que ${\upsilon}=v{\lambda}$

${\lambda}$=${ \frac {\upsilon}{v}}$

${ \frac {1}{\lambda}}$=${ \frac {v}{\upsilon}}$

así que K=${ \frac {v}{\upsilon}}$

así de la ecua 1 se obtiene:

${ \frac {1}{v_g}}= { \frac {d}{dv} { \frac {v}{\upsilon}}}$

Por diferenciación parcial respecto a las ${\upsilon}$ que obtenemos 

${ \frac {1}{v_g}}={ \frac {1}{v}}{ \frac {d\upsilon}{dv}}+v{ \frac {d}{dv}}{ \frac {1}{v}}$

${ \frac {1}{v_g}}={ \frac {1}{v}}+v{ \frac {-1}{v^2}}{ \frac {d\upsilon}{dv}}$

${ \frac {1}{v_g}}={ \frac {1}{v}}-{ \frac {\upsilon}{v^2}}{ \frac {dv}{d\upsilon}}$

por lo que queda probado.

Usuario:Luisa Alejandra Vega Sanchez

Ejercicio 7.30*

Usando la ecuación de dispersión: $n^{2}(\omega)= 1 + \frac{N{q_e}^2}{\varepsilon_{0}m_e}\sum_{j}[\frac{f_Plantilla:J}{{\omega_{0j}}^2 - \omega^{2}}]$------(1)

Mostrar que la velocidad de grupo esta dada por: $v_{g}= \frac{c}{1 + Nq_{e}/2\varepsilon_{0}m_{e}\omega^{2}}$------(2)

para ondas electromagnéticas de frecuencias altas (e.g., rayos X). Mantener en cuenta que como las $f_{j}$ son factores de peso, entonces $\sum_{j}f_{j}=1$.

---

Solución----

Tomando en cuenta el hecho de que se trata de ondas electromagnéticas de alta frecuencia, entonces $\omega>>\omega_{0j}$ y de la ecuación (1) podemos despreciar el término $\omega_{0j}$, por lo que (1) queda como sigue: $n^2(w)\thickapprox 1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}\sum_{j}f_{j}$

Pero $\sum_{j}f_{j}=1$ entonces la última ecuación queda como:

$n^2(w)\thickapprox 1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}$------(3)

Entonces,

$n(w)=(1 - \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2})^{1/2}$------(4)

Usando la expansión binomial,

$(1-x)^{1/2}= 1 - 1/2x - 1/8x^{2} - ...$

Con $x= \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}\omega^2}$ y despreciando términos mayores e iguales que $\omega^{4}$, obtenemos que n($\omega$) es aproximadamente:

$n(\omega)=1 - \frac{N{q_{e}}^2}{2\varepsilon_{0}m_{e}\omega^2}$------(5)

Utilizando la relación:

$v_{g}= c/n_{g}$------(6)

Con $v_{g}$ la velocidad de grupo y $n_{g}$ el índice de grupo de refracción definido como:

$n_{g}= n(\nu) + \nu\frac{dn(\nu)}{d\nu}$

siendo $\nu$ la frecuencia de la onda, sin embargo a $n_{g}$ la escribiremos en terminos de $\omega$:

$\omega= 2\pi\nu ; \longrightarrow \frac{dn}{d\nu}= \frac{dn}{\omega}\frac{d\omega}{d\nu}, \therefore n_{g}(\omega)= n(\omega) + \omega\frac{dn}{\omega}$

$n_{g}(\omega)= n(\omega) + \omega\frac{dn}{d\omega}$------(7)

y,

$\frac{dn(\omega)}{d\omega}= \frac{N{q_{e}}^2}{\varepsilon_{0}m_{e}{\omega}^{3}}$

Sustituyendo todo en (6) llegamos a que la velocidad de grupo $v_{g}$ es:

$v_{g}= \frac{c}{1 + Nq_{e}/2\varepsilon_{0}m_{e}\omega^{2}}$

como se pedía en el problema.

• Es el ejercicio 7.30 del capitulo 7, en el libro de Eugene Hecht edición 4.